Abstract
The step-flow and spiral growth of a multicomponent crystal are considered from vapors, taking into account the different possible Schwoebel barriers for each component within the Burton-Cabrera-Frank model. Analytic expressions for the final growth rates of such a multicomponent crystal are determined while considering the kinetic properties of all the individual components and growth conditions. Possible instabilities inherent in the presence of several components are studied, and a stability criterion for the multicomponent case is proposed. It is shown that, in certain cases, nucleation of nanoislands of pure components behind the moving steps can initiate, significantly distorting the growth process. The criterion for the occurrence of such an unstable regime is found.
1. Introduction
In contemporary technological landscapes, the pivotal role of crystals and thin films is undeniable, with their influence extending across microelectronics, optics, and various technological domains. One of the primary challenges in the development of industrial technologies for synthesizing crystals with desired crystalline quality, doping levels, and other properties is the diversity of growth mechanisms that occur during crystal growth. These mechanisms can significantly impact the growth process, crystal properties, and morphology. As a result, gaining a comprehensive understanding of all the mechanisms and kinetics involved in crystal growth, along with their theoretical elucidation, becomes imperative when introducing new materials into the industry. This need has driven significant developments in the theoretical background since the classic work of Burton, Cabrera, and Frank (BCF) [1]. Their groundbreaking paper bridged the gap between experimental results and the theoretical understanding of atomic-scale processes and surface kinetics, focusing on an industrially important crystal growth regime: step-flow and spiral growth. Numerous surface phenomena have been described both analytically and numerically. These include various types of instabilities, such as step-bunching [2] and step-meandering [3,4], instabilities resulting from electromigration [5,6], the impact of step-step interactions [7], effects of stress [8,9], impurities [10,11], vacancies [12,13], and void formation, as well as the effects of diffusion anisotropy [14] and different terrace types [15]. Many other aspects and effects have also been summarized in various reviews and books [16,17,18,19,20,21]. Different mechanisms of atom incorporation have been thoroughly analyzed [22]. It is important to note that this discussion does not cover other crystal growth modes, such as nucleation or dendritic growth, which have been detailed elsewhere [23,24].
It is worth noting that most of the analytical results obtained thus far are related to single-component crystals, often employing a simple model of a cubic Kossel crystal introduced by Kossel [25] and Stranski in the 1920s. While this model provides a good qualitative and quantitative understanding of surface processes and crystal growth, it often falls short when describing the growth of multicomponent crystals due to its failure to account for kinetic properties like diffusion coefficients and surface lifetimes of each component. Over the past few decades, there has been a strong trend toward the use of increasingly complex crystals composed of multiple components, offering superior characteristics compared to their single-component counterparts. Examples range from two-component wide bandgap semiconductors like GaN [26], SiC [27], and AlN [28], which have begun to replace Si in power and HF devices [29], to metal-organic frameworks (MOFs) [30] used for efficient gas storage, capture [31], and catalysis. Complex crystals have also been developed for solar-blind optical devices [32], perovskites for solar cells [33], cocrystals [34], and many other applications.
To accurately describe the growth of these multicomponent crystals, an extension of existing theoretical models is necessary. These extended models should be capable of properly accounting for the unique properties of each component, their fluxes, and other multicomponent-related characteristics. Furthermore, the presence of multiple components may introduce new types of surface instabilities [35].
Some theoretical approaches and effects have been redeveloped for multicomponent crystal growth [36,37,38,39]. In [40], the classical Burton-Cabrera-Frank theory was extended to the case of multicomponent crystals growing via chemical reactions. In [41], researchers studied the effect of advacancies present on the surface on multicomponent crystal growth. The effect of fast atomic steps on the growth surface was explored in [42], revealing the importance of considering this aspect, as different components exhibit varying surface mobility. As a result, some components incorporate into the steps through convective mechanisms, while others do so diffusively. Under certain conditions, as demonstrated in [35], a ‘dew’ of pure components can fall onto the terraces during the multicomponent crystal growth process, significantly distorting the growth. However, this regime can still be utilized for various bottom-up approaches to nanostructure formation.
One of the crucial properties of crystals is the Schwoebel barrier [43,44], which is associated with a reduced probability of an atom hopping from the upper terrace to the lower one (See Figure 1). In certain cases, it leads to the emergence of various surface instabilities, such as step-meandering [45] and alterations in the crystal surface morphology. This phenomenon has been extensively studied for single-component crystals both theoretically [46,47], experimentally [48,49], and numerically [50,51]. However, there remain numerous unanswered questions about how it manifests itself in a multicomponent system, where each type of atom may have its own Schwoebel barrier.
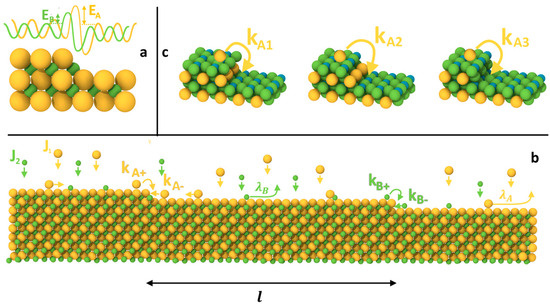
Figure 1.
Schematic representation of the process under consideration: (a,b) Step-flow growth of a two-component crystal AB with different Schwoebel barriers EAs, EBs, and probabilities of integrating components into a step from the upper and lower terraces, and the kinetic processes on the surface. (c) Illustration of the dependence of the Schwoebel barrier for each component on the degree of filling of the crystalline cell, exemplified by a 3-component crystal ABC, with the structure of lead titanate (PbTiO3).
This paper is part of a series of papers dedicated to various theoretical aspects of crystal and pore growth in multicomponent systems [35,38,40,41,42,52,53,54]. Its primary objective is to analyze the growth of a multicomponent crystal within the framework of the classical Burton-Cabrera-Frank model while considering different Schwoebel barriers for the components. We aim to derive analytical expressions for crystal growth under these conditions and to investigate potential instabilities resulting from the presence of these barriers. We also note that the BCF theory, originally proposed for crystal growth from a pure vapor phase, has inspired several important subsequent theories for growth from solutions or diluted vapors of various complexities. These include the theories developed by Chernov, Gilmer-Ghez-Cabrera, and Van Der Eerden [55,56,57]. Unlike the original BCF theory, these theories account for diffusional fluxes not only on the surface but also in the bulk volume of the solution. However, due to their complexity, the impact of the Schwoebel barrier within these multicomponent models will be addressed in separate papers.
2. Formulation of the Problem
In this study, we investigate the growth of a multicomponent non-Kossel crystal via the classical Burton-Cabrera-Frank (BCF) mechanism from its vapor phase. Our problem closely resembles the one explored in [40]. We examine the evolution of an infinite vicinal crystal surface characterized by terraces and equidistant steps separated by the distance . Each step is sufficiently covered with kinks to be treated as a continuous sink for adatoms. Within the framework of the BCF model for a multicomponent system [40], we assume that a constant partial pressure of each component is maintained above the surface. This ensures a uniform flux of atoms for each component onto the surface across the entire area. After deposition, all the components (or building units in the case of MOFs) diffuse along the terrace toward the steps. They may then either evaporate back into the gas phase or incorporate into the kinks on the steps through the following reaction:
Here represents the i-th component in the vapor phase, is its stoichiometric coefficient, and is the solid multicomponent crystal. N denotes the number of components. The schematic illustration of the process is presented in Figure 1. In contrast to [40], we take into account the asymmetry of adatom incorporation into the kinks on steps from the lower and upper terraces. This asymmetry varies for different components due to non-identical Schwoebel barriers. It is important to note that in each incorporation event, the exact value of the Schwoebel barrier for each component may differ depending on the local configuration of the kink and the degree of filling of the multi-component crystalline cell with atoms of other types. However, since the growth process involves many incorporation events, we use averaged “efficient” values, denoted as , for the Schwoebel barriers of the i-th component. These values determine the distribution function of adatoms of the i-th type over the terrace. Another assumption of the model is that equilibrium surface concentrations of different components are sufficiently small, and their surface diffusion, deposition, and evaporation are not interdependent. Therefore, in this model, chemical interactions only occur at kinks according to reaction (1), as atoms incorporate into the kink one after another in stoichiometric ratios.
The primary objective is to derive analytical expressions that describe the rate of step advancement on a crystal surface, taking into account all these phenomena. Subsequently, we will analyze additional effects and instabilities that may arise due to the presence of multiple components.
3. Results and Discussion
3.1. Adatom Distribution on the Surface
To determine the distribution function of adatoms for each component on the surface, their fluxes into the steps, and ultimately, the rate of step advancement over the terrace, we need to formulate the following system of equations:
Here and represent the surface diffusion coefficient, adatom surface concentration, lifetime before evaporation, and flux from the gas phase toward the surface of the i-th component, respectively. According to the principle of detailed balance , where and are the current and equilibrium pressures of the corresponding component, and is the equilibrium surface concentration.
Since we treat the steps as impermeable to adatoms [58], we can apply the following boundary conditions right at the steps for each adatom distribution function :
where and represent the coefficients of incorporation of atoms into the step from the upper and lower terraces, respectively. Following the notation of Pimpinelli et al. [46], we can rewrite the system of equations using the function . In this case, the equation for each component will transform into:
Here represents the diffusion length of the adatom of the i-th component, calculated as . Additionaly, is defined as , representing the concentration of adatoms on the flat surface far away from the steps. These definitions slightly modify the boundary conditions (3) at the steps, which limit the terrace from both sides.
The solution of the system yields expressions for the adatom concentrations of all components, (see Appendix A). Figure 2 illustrates the distribution of adatoms over the surface, normalized by the equilibrium concentration at different ratios of system parameters for qualitative insight.
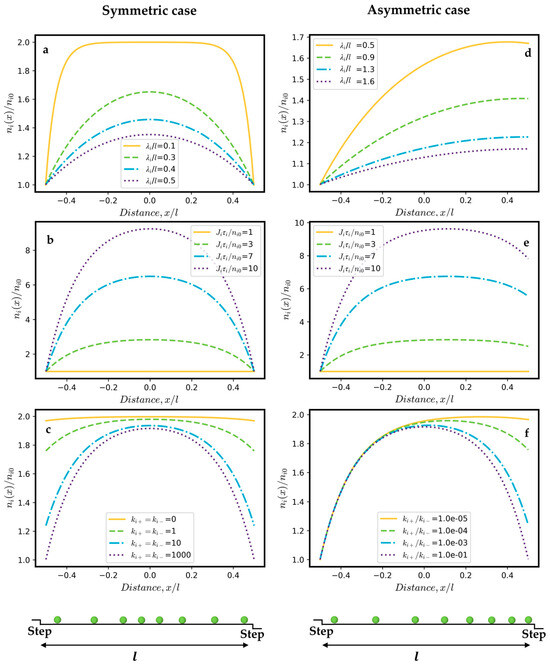
Figure 2.
The dependence of the i-th component’s adatom distribution function , normalized by the equilibrium concentration , on the coordinate at various ratios of system parameters providing qualitative insight. (a–c)—symmetric case ( (a–f)—asymmetric case (; (a,d) varying ; (b,e)—varying ; (c)—varying and ; (f) varying / ratio. The graphs are generated using the following base values: , , , , . The varied parameters that vary are displayed on the respective graphs.
3.2. Rate of Advancement of a Group of Equidistant Steps and Crystal Growth Rate
The net flux of the i-th component toward the step is the sum of the fluxes from the upper and lower terraces:
In Equation (6) we introduce the characteristic lengths and . However, it is important to consider that the fluxes of the components are interconnected by the stoichiometric ratio, as per reaction (1), . To account for this, we can utilize a chain of transformations, as used in [40] (see Appendix A), which provides us with the expression for net “flux” of crystalline cells into the step. With this information, we can immediately determine the rate of advancement of the group of equidistant steps () [40]:
Here, we introduce as the generalized diffusion coefficient, which accounts for the asymmetry of incorporation and the kinetic properties of all components, including Schwoebel barriers, diffusion coefficients, and lengths. represents the generalized supersaturation. These values are defined as:
Additionally, represents the area occupied by a single crystalline cell within the step.
Now, knowing the rate of advancement of a group of equidistant steps in such a system, we can easily calculate the spiral growth rate, as follows [40]:
Here Ω represents the volume of the crystalline cell, and the interstep distance is , with being the critical radius of 2D multicomponent nuclei on the surface [59] (. The parameter represents the surface energy of the multicomponent crystal. It is important to note that the coefficient also depends on the interstep distance, resulting in a rather complex dependence of the growth rate R (Equation (9)) on supersaturation. However, it can be explicitly calculated by knowing the system parameters and supersaturation.
3.3. Instability Analysis
3.3.1. Step System Instability
It is well known that in a single-component system, the Schwoebel barrier may cause surface instabilities during crystal growth. In a multi-component system, however, the tendency for unstable growth caused by the Schwoebel barrier of one component might be suppressed by the inversed Schwoebel barrier of another component. This, in turn, prevents step-meandering but may lead to step-bunching instability. In this section, we analyze the range of growth conditions in which such multicomponent system growth remains stable, and the distances between the steps remain consistent during the growth. The evaluation will follow the approach by Pimpinelli et al. [46] and Bales and Zangwill [3]. For a linear analysis of stability, let us consider a system of equidistant steps and introduce a small periodic fluctuation into each of them according to the equation (see Figure 3):
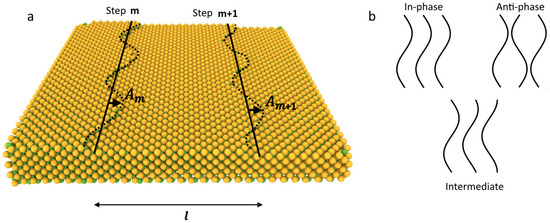
Figure 3.
A schematic representation of the sinusoidal fluctuation in the step system with an amplitude that depends on the step sequential number (a); illustration of different types of perturbations with and without phase shift (b).
Here, represents the ordinal number of a step, is the complex amplitude of fluctuation of m-th step, q is the spatial wave number and is the rate of growth or decay of this fluctuation. Note that CC indicates the complex conjugated value. Such a fluctuation will perturb the equilibrium concentration near the step due to the Gibbs-Thomson effect and the local curvature of the step. Accounting for the boundary condition (5) modified by the local curvature, the distribution of adatoms of the i-th component over the surface near m-th step in this case will be described by a complex expression [46]:
where , and coefficients , are listed in Appendix A.
Using the known distribution functions , we can calculate the fluxes of each component toward the step [40]. Then, we can apply a chain of transformations from the previous section to account for the stoichiometric nature of the fluxes. After performing the necessary mathematical calculations and introducing averaged coefficients for simplicity (See Appendix A and [46]), we will arrive at an equation that relates to the system parameters:
here represents the altered version of the averaged diffusion coefficient for the perturbed system of steps, and is the averaged constant describing the force striving to restore the straightness of the step due to surface tension. The values of and are provided in Appendix A due to their complexity. As one can see, they depend on the amplitude of step fluctuations . Equation (12) allows us to calculate the exact criterion for stable growth in a multi-component case, taking into account the properties of individual components (diffusion lengths, Schwoebel and inverse Schwoebel barriers, etc.). We note that criterion (12) is written in a general form. To apply it, one should substitute the values of and from Appendix A. This substitution directly relates the individual properties of the components, the rate of growth of fluctuation ω, and its complex amplitude . Here, φ represents the phase shift between the fluctuations in two subsequent steps [46], and C is a real constant. The fluctuations can be in-phase (φ = 0), anti-phase (φ = π), or in any intermediate state (see Figure 3b). After making this substitution, it becomes clear that if , then the perturbation grows over time, indicating that the surface is unstable against perturbations with wavenumber q. Conversely, if 0, any perturbation will decay with time, and the surface is stable. It is worth noting that in the limit of a single component, Equation (12) transforms into the corresponding equation from the classical paper by Pimpinelli [46]. Furthermore, in the case of in-phase advancement of the steps (, it resembles the single-component results of Bales and Zangwill [3]. Additionally, it is important to mention that, according to its definitions, the maximal value of the effective diffusion coefficient , which determines the rate of growth of perturbation, is limited by the component (if it exists) for which the product of concentration and diffusion coefficient is the lowest. The impact of each component on the stabilizing factor is also inversely proportional to its equilibrium concentration.
3.3.2. Nucleation of Pure Components behind the Moving Step
In some multicomponent epitaxial processes, another kind of instability has been observed experimentally, which can significantly distort both the growth process and the quality of the film grown. This instability involves the nucleation of liquid nanoislands or droplets of pure components on the terraces between the steps under certain growth conditions. Such instability, for instance, appears in the growth of gallium nitride thin films via molecular-beam epitaxy [60] and even in more complex growth processes involving chemical reactions [61]. In [35], the authors identified a criterion for the appearance of these islands and analyzed their interaction with the steps on the surface. The thermodynamic reason underpinning this unstable regime, which allows for the nucleation of pure islands, is that the rate of reaction (1), as well as multicomponent supersaturation, depends on the product of the concentrations of different components. Therefore, as shown in [35,40], there are various possible combinations of fluxes (, , …, ) at which the surface is near equilibrium in a multicomponent sense, allowing the crystal to grow in a low-supersaturation mode following a step-flow or spiral mechanism. In this scenario, there is no nucleation of multicomponent islands on the terraces. However, single-component supersaturation, which determines the nucleation of pure components, depends linearly on the flux of that specific component. Consequently, at certain combinations of fluxes (, , …, ), there might be an excess of one component, leading to its nucleation. This process is described in detail in [35]. The criterion in [35] relates the maximal concentration of adatoms of the i-th component on the terrace between the steps to its equilibrium single-component concentration in terms of single-component nucleation. It is important to note that in [35], the authors did not take into account the Schwoebel barrier of the components and its asymmetry. Therefore, the maximal concentration was right at the center of the terrace. In some cases, when the diffusion length of adatoms of a particular component is comparable to the distance between steps, and the coefficient of incorporation of this component from the upper terrace is small (i.e., the Schwoebel barrier is large), the distribution of adatoms takes on the shape shown in Figure 3. In this case, immediately behind the moving step, there is a region of increased concentration of this component. If the growth conditions are such that the concentration of this component in this region exceeds the critical value , then the nucleation of nanoislands may also begin.
Note that to determine the criterion for the appearance of islands behind a moving step, one can employ the approach proposed in [35]. Let us compare the nucleation time of islands, denoted as , in the region where an increased concentration is observed, with the time, , required for the subsequent step to advance by a distance equal to the length of this region, denoted as (See Figure 4). This advancement reduces the concentration of adatoms of the i-th component in that region and essentially “restarts” the processes of island nucleation. If the following criterion is met for at least one of the components:
then the islands will have sufficient time to nucleate, and step-flow growth will no longer be described by Equations (7) and (9). It will transition to a different regime, as described in [35]. The key difference from the problem addressed in [35] is that the size of the region with increased supersaturation is now determined not only by the diffusion lengths of the components , as in systems without ta Schwoebel barrier, but is expressed by the formula , where is the solution to the transcendental equation:
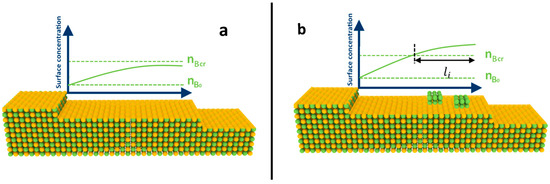
Figure 4.
Illustration for the mechanism of nanoisland formation of pure components behind the moving steps: (a) concentration of i-th component on the terrace is lower than critical, no islands are formed; (b) concentration exceeds critical value right behind the moving step, and nucleation may begin.
If there are two solutions (such a situation is possible, as can be seen from Figure 2d–f), then .
To determine the nucleation time, we can use the expression from [35]:
Here, as in [23,35], is the nucleation rate per unit area. represents the perimeter of the spherical island of the i-th component with the contact angle , is the critical radius of the island, a is the lattice parameter, is the characteristic frequency of atomic vibrations, and is the surface energy of the i-th component. represents the Zeldovich factor, is the activation energy of desorption, is the activation energy of diffusion. is the work of formation of the island of critical radius. is the difference in the chemical potentials of the adatom incorporated into the island, and one adsorbed on the surface between the terraces. As in [35] we assume that the critical radius of the forming island is much smaller than , otherwise the nucleation would also be impossible.
The time required for the multicomponent step to overcome the distance and essentially “restart” the nucleation process is approximately:
Combining Equations (13), (15) and (16) yields the criterion for the manifestation of such an instability:
In contrast to [35], this criterion now takes into account the presence of the Schwobel barrier. There, if condition (16) is satisfied for at least one of the components, nucleation of nanoislands directly behind the step becomes possible, resulting in a significant change in the crystal growth regime. It is important to note that, similar to [35], the criterion is extremely nonlinear in terms of supersaturation and distance between the steps. It should be noted that the nucleation rate itself, and consequently criterion (17), are specifically derived for the case of nucleating hemispherical liquid droplets of the pure component (‘dew’), as observed in the aforementioned experiments. However, this model does not account for the potential mechanical stresses that arise during the nucleation of solid islands. These stresses, caused by differences in lattice parameters between the pure component and the multicomponent surface, typically have a significant impact on the work of nuclei formation. Therefore, to accurately represent scenarios of solid-on-solid nucleation for the pure components which are solid at the growth temperature, further modification of the model is necessary. This modification should also incorporate considerations of the shape of a solid island and the anisotropy of surface energy.
We note that Equations (8), (12) and (17) enable both the determination of the dependence of the growth rate on the growth conditions and the identification of the range of growth conditions in which the surface is stable against the instabilities under consideration. These equations involve numerous system parameters, which are challenging to obtain or measure, especially in the case of multicomponent systems. However, theoretical understanding and knowledge of these dependencies provides us with new practical tools for determining the necessary properties through experiments. As was stated above, a multicomponent system can be in equilibrium at different sets of fluxes (, , …, ). Therefore, one can select a set in which only one specific k-th single component limits the growth process, while the others are in excess and thus do not affect the growth. In this case, the generalized coefficient , according to its definition, becomes dependent only on the properties of that particular k-th component. By measuring the dependence of the step-flow growth rate of a misoriented crystal surface on supersaturation (via increasing the flux of that k-th component), one can obtain information on its kinetic properties. Repeating such an experiment on a series of differently miscut vicinal surfaces with known interstep distances () allows for the determination of all the necessary kinetic coefficients of this component. Subsequently, one may perform the same experiment with other components to obtain these coefficients for each component, which can then be used to describe the growth and stability at any intermediate case with Equations (7), (12), and (17). Another option is to obtain the necessary coefficients from modeling, for example, through quantum chemical calculations [62], which can now describe complex multicomponent systems, given the rapidly growing computing capabilities.
However, it should also be kept in mind that other phenomena on the surface may cause other types of instabilities [18]. Further research is needed to determine the conditions for the most stable growth. This research may involve studying various aspects, such as different mass transport mechanisms, particularly when a carrier gas or solute is present, resulting in non-homogeneous flux towards the surface; exact incorporation mechanisms with the Schwoebel barrier, dependent on the local kink configuration; the impact of surface reconstruction on the diffusion of species; the influence of impurities in a multicomponent case and their combinations. Exploring these factors will contribute to a more comprehensive understanding of stable crystal growth.
4. Conclusions
The growth of a multicomponent crystal is analyzed, taking into account the individual Schwoebel barriers of each component within the framework of the BCF model. Analytical expressions for the step-flow and spiral growth regimes are derived. It is demonstrated that in the multicomponent case, the presence of the Schwoebel barrier, as in the single-component case, may lead to the manifestation of growth instabilities. However, in some cases, when different components demonstrate different ratios of direct and inverse Schwoebel barriers, instability does not arise. A new type of barrier-caused instability is discussed, which leads to the nucleation of liquid nanoislands of pure components on the terrace directly after the step. A kinetic criterion for stable growth is derived, connecting the properties of individual components and growth conditions.
Funding
This research was funded as a part of a state assignement of Institute for Problems in Mechanical Engineering RAS.
Data Availability Statement
Data is contained within the article.
Acknowledgments
The author is grateful to S.A. Kukushkin and V. Tonchev for fruitful discussions.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A
1. The solution of Equation (4) with boundary conditions (5) that is the expression for the concentration of adatoms of the i-th component over the terrace:
Once is determined, one can, on may calculate as described in the main text. Then, it is essential to consider the stoichiometric condition, which states that the fluxes of each component toward the step are proportional to the corresponding stoichiometric coefficient of the component, i.e., . To achieve this, the following chain of transformations [40] can be employed. First, let us express the supersaturation for each component through the flux:
Then, multiply each side by the stoichiometric coefficient and sum over all the components:
Taking out the implied constant value for each component [40] from under the summation operation, and substituting
yields the final expression for the overall flux of crystalline cells toward the steps, which is used for the calculation of the step velocity (as given in Equation (5)):
2. The coefficients for the distribution function of adatoms of i-th component near m-th step are the following:
where values , , and are introduced
3. The expressions for the averaged coefficients (q) and (q) (from Equation (9)) can be obtained using the same approach as in the previous section and in reference [46]. Firstly, one calculates the fluxes of the i-th component toward the perturbed step m, and then applies the stoichiometric rule. After a thorough mathematical analysis, the following results are obtained:
Here coefficient denotes the following expression:
This result in the limit of a single-component crystal coincides with the findings of Pimpinelli et al. [46].
References
- Burton, W.K.; Cabrera, N.; Frank, F.C. The growth of crystals and the equilibrium structure of their surfaces. Philos. Trans. R. Soc. A 1951, 243, 299–358. [Google Scholar]
- Murata, K.I.; Sato, M.; Uwaha, M.; Saito, F.; Nagashima, K.; Sazaki, G. Step-bunching instability of growing interfaces between ice and supercooled water. Proc. Natl. Acad. Sci. USA 2022, 119, e2115955119. [Google Scholar] [CrossRef] [PubMed]
- Bales, G.S.; Zangwill, A. Morphological instability of a terrace edge during step-flow growth. Phys. Rev. B 1990, 41, 5500. [Google Scholar] [CrossRef] [PubMed]
- Kallunki, J.; Krug, J.; Kotrla, M. Competing mechanisms for step meandering in unstable growth. Phys. Rev. B 2002, 65, 205411. [Google Scholar] [CrossRef]
- Toktarbaiuly, O.; Usov, V.; Coileáin, C.Ó.; Siewierska, K.; Krasnikov, S.; Norton, E.; Bozhko, S.I.; Semenov, V.N.; Chaika, A.N.; Murphy, B.E.; et al. Step bunching with both directions of the current: Vicinal W (110) surfaces versus atomistic-scale model. Phys. Rev. B 2018, 97, 035436. [Google Scholar] [CrossRef]
- Latyshev, A.V.; Litvin, L.V.; Aseev, A.L. Peculiarities of step bunching on Si (001) surface induced by DC heating. Appl. Surf. Sci. 1998, 130, 139–145. [Google Scholar] [CrossRef]
- Guin, L.; Jabbour, M.E.; Triantafyllidis, N. Revisiting step instabilities on crystal surfaces. Part I: The quasistatic approximation. J. Mech. Phys. Solids 2021, 156, 104574. [Google Scholar] [CrossRef]
- Hong, W.; Suo, Z.; Zhang, Z. Dynamics of terraces on a silicon surface due to the combined action of strain and electric current. J. Mech. Phys. Solids 2008, 56, 267–278. [Google Scholar] [CrossRef]
- Van der Hoek, B.; Van Der Eerden, J.P.; Bennema, P.; Sunagawa, I. The influence of stress on spiral growth. J. Cryst. Growth 1982, 58, 365–380. [Google Scholar] [CrossRef]
- Cabrera, N.; Levine, M.M. On the dislocation theory of evaporation of crystals. Philos. Mag. 1956, 1, 450–458. [Google Scholar] [CrossRef]
- Sato, M. Effect of the Surface Diffusion and Evaporation of Impurities on Step Bunching Induced by Impurities. J. Phys. Soc. Jpn. 2019, 88, 114801. [Google Scholar] [CrossRef]
- Kosolobov, S. Subsurface diffusion in crystals and effect of surface permeability on the atomic step motion. Sci. Rep. 2019, 9, 13428. [Google Scholar] [CrossRef] [PubMed]
- Sitnikov, S.V.; Latyshev, A.V.; Kosolobov, S.S. Advacancy-mediated atomic steps kinetics and two-dimensional negative island nucleation on ultra-flat Si (111) surface. J. Cryst. Growth 2017, 457, 196–201. [Google Scholar] [CrossRef]
- Meca, E.; Lowengrub, J.; Kim, H.; Mattevi, C.; Shenoy, V.B. Epitaxial graphene growth and shape dynamics on copper: Phase-field modeling and experiments. Nano Lett. 2013, 13, 5692–5697. [Google Scholar] [CrossRef] [PubMed]
- Ju, G.; Xu, D.; Thompson, C.; Highland, M.J.; Eastman, J.A.; Walkosz, W.; Zapol, P.; Stephenson, G.B. Burton-Cabrera-Frank theory for surfaces with alternating step types. Phys. Rev. B 2022, 105, 054312. [Google Scholar] [CrossRef]
- Makoveeva, E.V.; Koroznikova, I.E.; Glebova, A.E.; Alexandrov, D.V. Morphological/dynamic instability of directional crystallization in a finite domain with intense convection. Crystals 2023, 13, 1276. [Google Scholar] [CrossRef]
- Guin, L.; Jabbour, M.E.; Shaabani-Ardali, L.; Triantafyllidis, N. Revisiting step instabilities on crystal surfaces. Part II: General theory. J. Mech. Phys. Solids 2021, 156, 104582. [Google Scholar] [CrossRef]
- Politi, P.; Grenet, G.; Marty, A.; Ponchet, A.; Villain, J. Instabilities in crystal growth by atomic or molecular beams. Phys. Rep. 2000, 324, 271–404. [Google Scholar] [CrossRef]
- Uwaha, M. Introduction to the BCF theory. Prog. Cryst. Growth Charact. Mater. 2016, 62, 58–68. [Google Scholar] [CrossRef]
- Markov, I.V. Crystal Growth for Beginners: Fundamentals of Nucleation, Crystal Growth and Epitaxy; World Scientific: Singapore, 2016; 564p. [Google Scholar]
- Sangwal, K. Effects of impurities on crystal growth processes. Prog. Cryst. Growth Charact. Mater. 1996, 32, 3–43. [Google Scholar] [CrossRef]
- Vekilov, P.G. What Determines the Rate of Growth of Crystals from Solution? Cryst. Growth Des. 2007, 7, 2796–2810. [Google Scholar] [CrossRef]
- Dubrovskii, V.G. Nucleation Theory and Growth of Nanostructures; Springer: Berlin, Germany, 2014; 601p. [Google Scholar]
- Libbrecht, K.G. The physics of snow crystals. Rep. Prog. Phys. 2005, 68, 855. [Google Scholar] [CrossRef]
- Kossel, W. Zur Theorie des Kristallwachstums. Nachrichten Ges. Wiss. Göttingen Math. Phys. Kl. 1927, 1927, 135–143. [Google Scholar]
- Kour, R.; Arya, S.; Verma, S.; Singh, A.; Mahajan, P.; Khosla, A. Recent advances and challenges in indium gallium nitride (InxGa1-xN) materials for solid state lighting. ECS J. Solid State Sci. Technol. 2019, 9, 015011. [Google Scholar] [CrossRef]
- Langpoklakpam, C.; Liu, A.-C.; Chu, K.-H.; Hsu, L.-H.; Lee, W.-C.; Chen, S.-C.; Sun, C.-W.; Shih, M.-H.; Lee, K.-Y.; Kuo, H.-C. Review of Silicon Carbide Processing for Power MOSFET. Crystals 2022, 12, 245. [Google Scholar] [CrossRef]
- Wu, P.; Funato, M.; Kawakami, Y. Environmentally friendly method to grow wide-bandgap semiconductor aluminum nitride crystals: Elementary source vapor phase epitaxy. Sci. Rep. 2015, 5, 17405. [Google Scholar] [CrossRef]
- Kim, M.; Seo, J.H.; Singisetti, U.; Ma, Z. Recent advances in free-standing single crystalline wide band-gap semiconductors and their applications: GaN, SiC, ZnO, β-Ga2O3, and diamond. J. Mater. Chem. C 2017, 5, 8338–8354. [Google Scholar] [CrossRef]
- Wang, Q.; Astruc, D. State of the art and prospects in metal-organic framework (MOF)-based and MOF-derived nanocatalysis. Chem. Rev. 2019, 120, 1438–1511. [Google Scholar] [CrossRef]
- Emam, H.E.; Abdelhameed, R.M.; Ahmed, H.B. Adsorptive performance of MOFs and MOF containing composites for clean energy and safe environment. J. Environ. Chem. Eng. 2020, 8, 104386. [Google Scholar] [CrossRef]
- Voloshin, A.; Rudneva, E.; Manomenova, V.; Vasilyeva, N.; Kovalev, S.; Emelchenko, G.; Masalov, V.; Zhokhov, A. The problem of formation of mixed crystals and high-efficiency K2 (co, ni)(SO4)2• 6H2O optical filters. Crystals 2019, 9, 390. [Google Scholar] [CrossRef]
- Ansari, M.I.H.; Qurashi, A.; Nazeeruddin, M.K. Frontiers, opportunities, and challenges in perovskite solar cells: A critical review. J. Photochem. Photobiol. C Photochem. Rev. 2018, 35, 1–24. [Google Scholar] [CrossRef]
- Karimi-Jafari, M.; Padrela, L.; Walker, G.M.; Croker, D.M. Creating cocrystals: A review of pharmaceutical cocrystal preparation routes and applications. Cryst. Growth Des. 2018, 18, 6370–6387. [Google Scholar] [CrossRef]
- Redkov, A.V.; Kukushkin, S.A. Dynamic interaction of steps and nanoislands during growth of a multicomponent crystal. Cryst. Growth Des. 2021, 21, 4914–4926. [Google Scholar] [CrossRef]
- Tilbury, C.J.; Joswiak, M.N.; Peters, B.; Doherty, M.F. Modeling Step Velocities and Edge Surface Structures during Growth of Non-Centrosymmetric Crystals. Cryst. Growth Des. 2017, 17, 2066–2080. [Google Scholar] [CrossRef]
- Cermelli, P.; Jabbour, M. Multispecies epitaxial growth on vicinal surfaces with chemical reactions and diffusion. Proc. R. Soc. A 2005, 461, 3483–3504. [Google Scholar] [CrossRef]
- Redkov, A. Spiral growth of multicomponent crystals: Theoretical aspects. Front. Chem. 2023, 11, 1189729. [Google Scholar] [CrossRef] [PubMed]
- Cermelli, P.; Jabbour, M.E. Step bunching during the epitaxial growth of a generic binary-compound thin film. J. Mech. Phys. Solids 2010, 58, 810–827. [Google Scholar] [CrossRef]
- Redkov, A.V.; Kukushkin, S.A. Development of Burton–Cabrera–Frank theory for the growth of a non-Kossel crystal via chemical reaction. Cryst. Growth Des. 2020, 20, 2590–2601. [Google Scholar] [CrossRef]
- Redkov, A.; Kukushkin, S. Theoretical aspects of the growth of a non-Kossel crystal from vapours: The role of advacancies. Faraday Discuss. 2022, 235, 362–382. [Google Scholar] [CrossRef]
- Redkov, A.; Kukushkin, S. Influence of the kinetics of atomic steps on the growth of multicomponent crystals under conditions of increased supersaturation. Tech. Phys. Lett. 2023, 13, 35. (In Russian) [Google Scholar] [CrossRef]
- Schwoebel, R.L.; Shipsey, E.J. Step motion on crystal surfaces. J. Appl. Phys. 1966, 37, 3682–3686. [Google Scholar] [CrossRef]
- Schwoebel, R.L. Step Motion on Crystal Surfaces. II. J. Appl. Phys. 1969, 40, 614–618. [Google Scholar] [CrossRef]
- Paulin, S.; Gillet, F.; Pierre-Louis, O.; Misbah, C. Unstable step meandering with elastic interactions. Phys. Rev. Lett. 2001, 86, 5538. [Google Scholar] [CrossRef] [PubMed]
- Pimpinelli, A.; Elkinani, I.; Karma, A.; Misbah, C.; Villain, J. Step motions on high-temperature vicinal surfaces. J. Phys. Condens. Matter 1994, 6, 2661. [Google Scholar] [CrossRef]
- Tonchev, V.; Ranguelov, B.; Omi, H.; Pimpinelli, A. Scaling and universality in models of step bunching: The “C+–C−” model. Eur. Phys. J. B 2010, 73, 539–546. [Google Scholar] [CrossRef]
- Saúl, A.; Métois, J.J.; Ranguis, A. Experimental evidence for an Ehrlich-Schwoebel effect on Si (111). Phys. Rev. B 2002, 65, 075409. [Google Scholar] [CrossRef]
- Rabbering, F.; Wormeester, H.; Everts, F.; Poelsema, B. Quantitative understanding of the growth of Cu/Cu (001) including the determination of the Ehrlich-Schwoebel barrier at straight steps and kinks. Phys. Rev. B 2009, 79, 075402. [Google Scholar] [CrossRef]
- ZaŁuska–Kotur, M.A.; Krzyżewski, F.; Krukowski, S. Emergence of regular meandered step structure in simulated growth of GaN (0001) surface. J. Cryst. Growth 2012, 343, 138–144. [Google Scholar] [CrossRef]
- Bellmann, K.; Pohl, U.W.; Kuhn, C.; Wernicke, T.; Kneissl, M. Controlling the morphology transition between step-flow growth and step-bunching growth. J. Cryst. Growth 2017, 478, 187–192. [Google Scholar] [CrossRef]
- Redkov, A.V.; Kukushkin, S.A.; Osipov, A.V. Growth of faceted pores in a multi-component crystal by applying mechanical stress. CrystEngComm 2020, 22, 5280–5288. [Google Scholar] [CrossRef]
- Redkov, A.V.; Kukushkin, S.A.; Osipov, A.V. Spiral growth of a multicomponent crystal from vapor of its components. J. Cryst. Growth 2020, 548, 125845. [Google Scholar] [CrossRef]
- Kukushkin, S.A.; Osipov, A.V.; Redkov, A.V. Morphological stability criterion for a spherical crystallization front in a multicomponent system with chemical reactions. Phys. Solid State 2014, 56, 2530–2536. [Google Scholar] [CrossRef]
- Chernov, A.A. The spiral growth of crystals. Sov. Phys. Uspekhi 1961, 4, 116. [Google Scholar] [CrossRef]
- Gilmer, G.H.; Ghez, R.; Cabrera, N. An analysis of combined surface and volume diffusion processes in crystal growth. J. Cryst. Growth 1971, 15, 123–128. [Google Scholar] [CrossRef]
- Van Der Eerden, J.P. The advance velocity of steps under the influence of volume and surface diffusion, by direct and indirect incorporation of growth units. J. Cryst. Growth 1982, 56, 174–188. [Google Scholar] [CrossRef]
- Sato, M.; Uwaha, M.; Saito, Y. Instabilities of steps induced by the drift of adatoms and effect of the step permeability. Phys. Rev. B 2000, 62, 8452. [Google Scholar] [CrossRef]
- Kukushkin, S.A. Evolution processes in multicomponent and multiphase films. Thin Solid Film. 1992, 207, 302–312. [Google Scholar] [CrossRef]
- Heying, B.; Smorchkova, I.; Poblenz, C.; Elsass, C.; Fini, P.; Den Baars, S.; Mishra, U.; Speck, J.S. Optimization of the surface morphologies and electron mobilities in GaN grown by plasma-assisted molecular beam epitaxy. Appl. Phys. Lett. 2000, 77, 2885–2887. [Google Scholar] [CrossRef]
- Chen, Y.S.; Liao, C.H.; Kuo, C.T.; Tsiang, R.C.C.; Wang, H.C. Indium droplet formation in InGaN thin films with single and double heterojunctions prepared by MOCVD. Nanoscale Res. Lett. 2014, 9, 334. [Google Scholar] [CrossRef]
- Chugh, M.; Ranganathan, M. Adsorbate interactions on the GaN (0001) surface and their effect on diffusion barriers and growth morphology. Phys. Chem. Chem. Phys. 2017, 19, 2111–2123. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).