Abstract
The fracture of viscoplastic materials is a complex process due to its time-dependent and plastic responses. Numerical simulation for fractures plays a significant role in crack prediction and failure analysis. In recent years, the phase field model has become a competitive approach to predict crack growth and has been extended to inelastic materials, such as elasto-plastic, viscoelastic and viscoplastic materials, etc. However, the contribution of inelastic energy to crack growth is seldom studied. For this reason, we implement the fracture phase field model coupled with a viscoplastic constitutive in a finite element framework, in which the elastic energy and inelastic energy are used as crack driving forces. The implicit algorithm for a viscoplastic constitutive is presented; this procedure is suitable for other viscoplastic constitutive relations. The strain rate effect, creep effect, stress relaxation effect and cyclic loading responses are tested using a single-element model with different inelastic energy contributions. A titanium alloy plate specimen and a stainless-steel plate specimen under tension are studied and compared with the experimental observations in the existing literature. The results show that the above typical damage phenomenon and fracture process can be well reproduced. The inelastic energy significantly accelerates the evolution of the phase field of viscoplastic materials. For cyclic loadings, the acceleration effect for low frequency is more significant than for high frequency. The influence of the weight factor of inelastic energy on the force-displacement curve mainly occurs after reaching the maximum force point. With the increase of , the force drops faster in the force-displacement curve. The inelastic energy has a slight effect on the crack growth paths.
1. Introduction
Numerical simulation methods for fracture failure can be generally classified into two categories: discrete and continuum approaches [1] depending on how to describe the interfacial discontinuity. The former includes the cohesive element [2], the node splitting [3], the hybrid discrete finite element method [4], etc. These methods require additional crack initiation and growth criteria. In the finite element framework, the displacement is discontinuous at the cracking locations; thus, the crack will propagate along or between elements, which leads to a mesh-dependent crack path [5]. To overcome this problem, XFEM [6,7] and some re-meshing strategies [8,9] were developed; however, tracking complicated fracture surfaces is still a difficult task in numerical computations [10]. The continuum approaches, such as the GTN model [11], the Lemaitre damage model [12] and the gradient damage model [13], are widely used for simulating ductile fracture. While the continuum methods cannot describe the crack propagation phase after damage localization, the crack propagation phase is still dealt with using discrete methods, for instance, re-meshing or embedding techniques [14]; meanwhile, the continuum approaches usually need to calibrate many model parameters [15].
As a competitive method to simulate cracking processes, the phase field model has attracted widespread attention for nearly two decades. This diffuse crack model has advantages in predicting complex topologies, including crack branching, coalescence or 3D crack paths. The phase field model origins from Griffith’s [16] energy theory of fracture. However, Griffith’s theory was unable to predict crack initiation, path jumping or branching. Francfort and Marigo [17] proposed a variational approach to overcome this problem, and then Bourdin [18] regularized this approach. Moreover, the extension to fracture simulations in inelastic materials, such as elasto-plastic materials [1,5,10,14,19] viscoelastic materials [20,21,22,23,24] and viscoplastic materials [23,25,26,27] has been studied. Dammaß et al. [25] proposed a unified fracture phase field model for viscoelastic materials via two-way coupling between phase field and relaxation mechanisms. Valverde-González et al. [26] developed a fracture phase field model for visco-hyperelastic materials applied to pre-stressed cylindrical structures. Wang et al. [27] studied the time-dependent deformation and cracking of rocks using a viscous phase field method coupled with a viscoplastic constitutive. Hai et al. [28] proposed a rate-dependent phase field model to characterize the dynamic failure of concrete-like quasi-brittle materials. Xie et al. [29] developed a new phase field model for creep cracks in elasto-plastic materials by introducing a degradation function of creep strain acting on fracture toughness. Arash et al. [30,31] studied the fracture behavior of nanocomposites using the thermos-viscoelastic and nonlinear viscoelastic models. Ullah et al. [32] and ZeiEldin et al. [33] analyzed the Casson hybrid nanofluid by using a Cattaneo–Christov double-diffusion model. Borden et al. [34] first introduced two weight parameters to control the contribution of elastic energy and plastic energy to crack growth in a rate-independent phase field model. Hojjat et al. [23] presented a rate-dependent ductile phase field model incorporating these two weight parameters. However, they did not discuss the influence of the weight parameters on fracture behavior, and the calibration of two weight parameters is more complex. Shen et al. [20] modified the phase field model for the fracture of viscoelastic solid, in which only one weight parameter was used to quantify the viscos crack driving energy. The weight parameter is considered to reflect the influence of temperature, humidity and aging on material damage implicitly. In addition, the influence of the weight parameter on viscoelastic fracture response was studied. Nevertheless, the value of the weight parameter has not been calibrated against relevant experiments.
Therefore, based on existing research, we implemented the phase field model incorporating viscoplastic constitutive, in which one weight parameter is used to control the inelastic energy that contributes to crack growth. The structure of this paper is as follows: Section 2 presents the viscoplastic phase field model and numerical algorithm. Section 3 provides some numerical examples of a few typical viscos tests and two metal plate specimens to discuss the effect of inelastic energy contributions on the fracture response of viscoplastic solid. Section 4 gives some conclusions.
2. Viscoplastic Phase Field Model
2.1. Viscoplastic Constitutive
To simplify the illustration, the uniaxial tensile state is taken as an example. The uniaxial stress considering viscoplasticity is defined as [35]:
where is the yield stress, is the hardening stress, and the effective plastic strain rate . and are material constants related to the viscous behavior.
By rearranging Equation (1), the expression of can be given:
In viscoplasticity, Equation (2) is used to replace the consistency condition in time-independent plasticity. For a von-Mises material, the normality hypothesis is written as:
Here, is the inelastic strain (including plastic strain and viscos strain) rate tensor, the yield function is:
where is the von-Mises stress.
Substituting Equation (4) into Equation (3) gives:
in which is the deviatoric stress tensor.
Hooke’s law in terms of the elastic strain rate tensor is written as:
in which G is the shear modulus, the Lame constant. In viscoplasticity, the strain decomposition still holds:
Here, is the total strain rate tensor, is the elastic strain rate tensor.
2.2. Viscoplastic Phase Field Model
Figure 1 shows an arbitrary domain with external boundary .
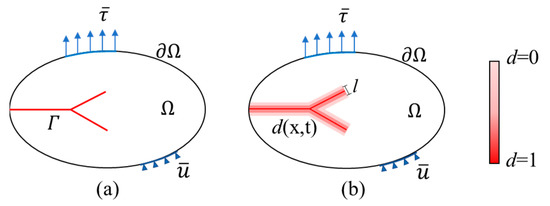
Figure 1.
Crack representation of phase field model: (a) sharp crack model and (b) diffuse crack model.
Here, is the surface traction, applied on the Neumann boundary and is the displacement constraint, applied on the Dirichlet boundary. in Figure 1a represents a set of discrete cracks. The diffuse approximation of the crack through a phase field d is depicted in Figure 1b, where the value d = 0 indicates intact material and d = 1 represents broken material. is the length scale parameter. The total energy functional for viscoplastic materials can be written as:
where the second integral of the right side is the approximation of fracture energy. is elastic strain energy density, is the inelastic strain energy density and is the elastic strain tensor. is the critical energy release rate. is the stiffness degradation function. A common form is , in which k is a tiny value to keep a residual stiffness in fully broken conditions.
According to the minimizing of the total energy functional Equation (8):
The stress equilibrium equation and the phase field governing equation are given:
In order to control the stress state at which the inelastic energy starts to drive the crack growth, the energy density threshold is introduced. is a factor to weight the contribution of inelastic energy to fracture. The Macaulay bracket operators are defined as:
To prevent the crack healing due to the release of elastic energy, the elastic history field is introduced by Miehe et al. [36]:
Substituting Equation (13) into Equation (10), the phase field governing equation turns into:
2.3. Implicit Integration for Viscoplasticity
Here we implement the implicit integration for linear isotropic hardening viscoplasticity with the radial return implicit backward Euler integration method. Regardless of the temperature effect, the sinh-type viscoplastic constitutive equation can be written as [35]:
and are material constants. In order to implement the viscoplastic constitutive in incremental form using Newton’s iterative solution method, Equation (15) is taken to be a function of hardening stress and equivalent inelastic strain increment , which is given by:
All quantities are given at the end of each time increment, that is at time . The procedure for updating stresses and strains of viscoplasticity is as follows:
(I). Calculate the elastic trial stress:
(II). Check for viscoplastic flow:
(III). Solve the effective inelastic strain increment using the Newton–Raphson iterative method:
If the yielding is not active, .
(IV). Update inelastic strain, elastic strain and undegraded stress increment tensors:
(V). Update undegraded stress tensors and effective inelastic strain and degraded stress tensors:
(VI). Exit.
2.4. Numerical Implementation
Algorithmically, solving phase field problems can be classified into monolithic and staggered methods [37]. The monolithic method is more efficient, while the staggered method has proved to be more robust [38]. At each fictitious time step, the equilibrium equation and the phase field evolution equation are solved separately. The displacement field is solved for the fixed phase field at the last loading increment. Meanwhile, the phase field is solved for the fixed displacement field. Bourdin [39] and Burke et al. [40,41] have given the convergence proof of the staggered method. This method needs a small load increment to get a more accurate result. In order to get a better convergence for viscoplastic fracture problem, we adopted the staggered method to solve the phase field problem. The finite element spatial discretization is given below:
where and are the shape functions associated with node i, and are the corresponding values at node i. is the number of nodes of the element. Taking derivatives of and :
where and are the gradient operators of the shape functions. The test functions and corresponding derivatives are given by:
According to the previous definitions, the residual vectors of the equilibrium equation and phase field evolution equation are expressed as:
The Newton iteration equations are written as:
where:
Since the tangential stiffness only affect the convergence rate [34] but does not affect the solution accuracy, and generally, the explicit expression of Jacobian is hard to obtain for viscoplastic constitutive. Hence, the elastic stiffness is used for simplicity. The above equations are implemented in Abaqus subroutines UEL and UMAT using the Fortran language. Some implementation details can be found in [10,37,42,43].
3. Numerical Examples
3.1. One-Dimensional Viscoplastic Test
In this section, a single element is modeled to study the effect of β on crack-driving energy and phase field evolution. The model is a 1 mm × 1 mm × 1 mm element as shown in Figure 2. The axial displacement load and constraint are applied on the bottom and top surfaces, respectively. Table 1 shows the material and phase field parameters.
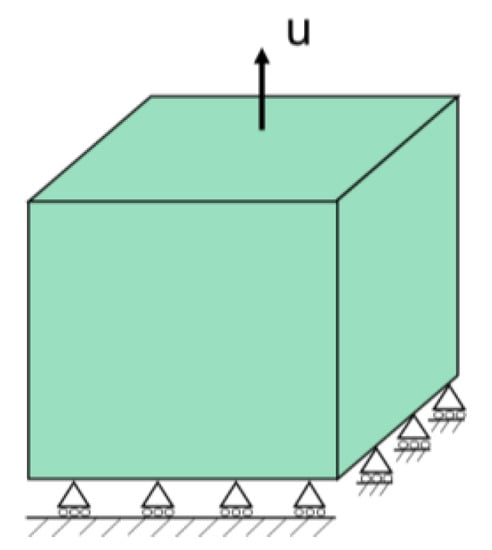
Figure 2.
Single element model and boundary condition, u is axial displacement load.

Table 1.
Material parameters for a single element [44].
In order to verify the correctness of code writing for viscoplastic constitutive, we first simulate three stress–strain curves under strain rates 0.002%/s, 0.02%/s and 0.2%/s. The comparison of experimental data [44] and simulation is plotted in Figure 3. A typical strain rate-dependent effect is observed; the yield stress increases with a higher strain rate. From the perspective of dislocation theory, with the increasing strain rate, overcoming the material resistance of dislocation will take less time, which leads to dislocation density increase and further leads to high strength. The results show that this model can well describe the rate-dependent properties. However, compared with a high-strain rate, the predicted results are slightly worse at a very low-strain rate.
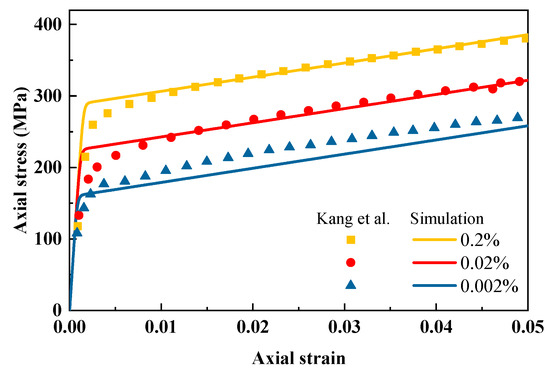
Figure 3.
Comparison of experimental data [44] and simulation for uniaxial tension of different strain rates.
3.1.1. Strain Rate Test
Viscoplasticity describes the rate-dependent behavior of materials; the strain rate affects the mechanical response of viscoplastic solids. Thus, in this subsection, four strain rate loads are selected to illustrate the rate-dependent behavior with the presented phase field model. The stress–strain and phase field-strain relations under different strain rate loads for β = 0.1 and β = 0.3 are shown in Figure 4 and Figure 5. Comparing Figure 4a with Figure 5a, the stress–strain curve becomes greater with increasing strain rate, which exhibits obvious viscoplastic characteristics. A larger value of β may cause greater damage to the stress, resulting from a larger inelastic energy contribution. In Figure 4b with Figure 5b, the phase field curve increases with the increasing strain rate. That is because higher stress may cause more driving energy to be produced under the same strain condition, resulting in greater damage.
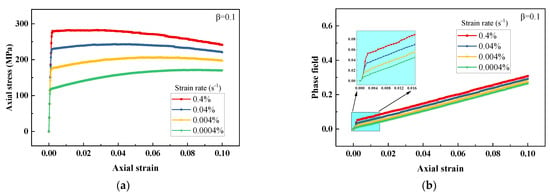
Figure 4.
Response of viscoplastic material under various strain rate loads for β = 0.1: (a) stress–strain relation and (b) phase field-strain relation.
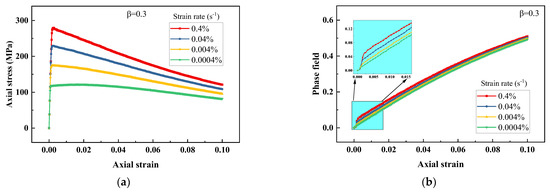
Figure 5.
Response of viscoplastic material under various strain rate loads for β = 0.3: (a) stress–strain relation and (b) phase field-strain relation.
3.1.2. Creep Test
In the creep test, a force load is applied to the top of the model from zero to a fixed value within the first 100 s and then the force load keeps constant. Figure 6a,b show the curves of axial strain and phase field versus time for different values of β. The strain increases gradually under a constant force load, which is usually called the creep phenomenon. The axial strain and phase field increase with the increase of . The model tends to be fully broken when .
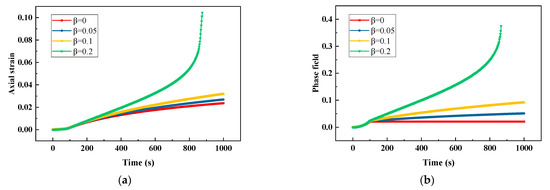
Figure 6.
Response of viscoplastic material under creep load for different values of : (a) strain-time relation and (b) phase field-time relation.
In this creep process, the force does work on the model continually, resulting in continuous phase field evolution. In order to show the evolution of driving energies, we plotted the elastic driving energy , inelastic driving energy and total driving energy . Here, we do not consider the energy density threshold; thus, the crack driving energies are defined below:
The evolution curves of driving energies of Equation (33) for and are plotted in Figure 7a,b. There is little difference between the elastic driving energies. Whereas the inelastic driving energy for is significantly larger than that for . For , the inelastic energy surpasses the elastic energy in a relatively long time (about 250 s); however, for , the inelastic energy surpasses the elastic energy in a relatively short time (about 180 s). This means that a larger value of can accelerate the phase field evolution. Whether or , once the inelastic energy begins to accumulate, it grows significantly faster than elastic energy. It indicates that the inelastic energy is dominant in driving phase field evolution.
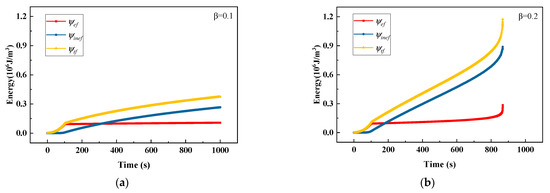
Figure 7.
Crack driving energies of viscoplastic material under creep load: (a) β = 0.1 and (b) β = 0.2.
3.1.3. Stress Relaxation Test
The response of stress relaxation is tested in this subsection. The displacement load increases from zero to a fixed value within the first 100 s and then stays constant. Figure 8a,b show the curves of axial stress and phase field evolution with time for different values of . Figure 9a,b show the corresponding crack driving energies evolution curves. In Figure 8a, within the first 100 s, the axial stresses increase rapidly in the elastic stage and then yield with the increase of displacement. In the stage where the displacement remains constant, the stress decreases gradually to a finite value, this phenomenon is called stress relaxation. In this process, part of the elastic strain converts to inelastic strain, the elastic energy decreases and the inelastic energy increases, which can be observed in Figure 9a,b. The history field will increase as the inelastic energy increases; correspondingly, the phase field also increases after 100 s, which can be seen in Figure 8b. Additionally, a large value of causes greater damage. This is because more inelastic energy contributes to the phase field evolution.
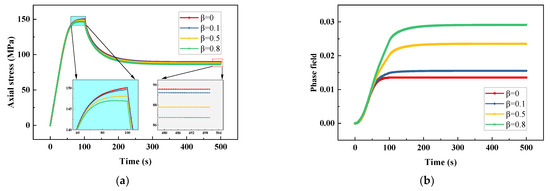
Figure 8.
Response of viscoplastic material under relaxation load for different values of : (a) stress–time relation and (b) phase field-time relation.
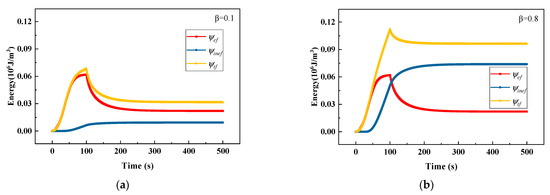
Figure 9.
Crack driving energies of viscoplastic solid subject to relaxation load: (a) β = 0.1 and (b) β = 0.8.
3.1.4. Cyclic Load Test
Sinusoidal displacement loads of low and high frequency are applied to the single-element model. and are selected and the simulation durations are 1000 s and 1 s; the load curves are shown in Figure 10. The axial strains and phase field evolution with time subjected to low- and high-frequency cyclic loads for different values of are plotted in Figure 11 and Figure 12. For this single-element model subjected to displacement-controlled load, the axial strain is not affected by ; therefore, the elastic and inelastic strains only for are plotted as a representative in Figure 11a and Figure 12a. When loading, the crack driving energy increases to exceed the previous history field and the phase field will increase continually, whereas the phase field remains unchanged when unloading, which is controlled by the irreversibility. This phenomenon is consistent with the fact that the crack does not propagate during unloading and compression leads to crack closure in reality. By comparing Figure 11a with Figure 12a, the inelastic strain of the model under low-frequency cyclic load is larger than that under high-frequency cyclic load. This is because the viscoplastic response has more time to develop for low frequency. By comparing Figure 11b with Figure 12b, a larger value of can produce more inelastic crack-driving energy, which then leads to greater damage. The effect of on phase field evolution is more significant for the low-frequency cyclic load.
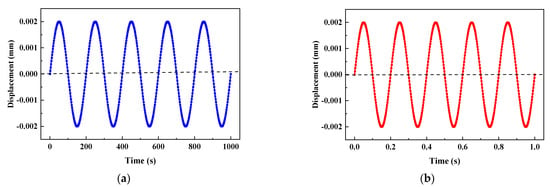
Figure 10.
Sinusoidal displacement loads: (a) low frequency and (b) high frequency.
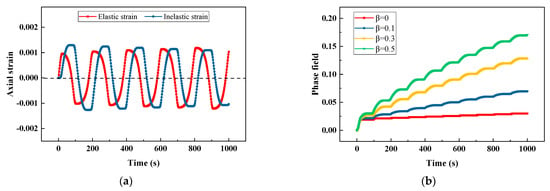
Figure 11.
Response of viscoplastic material under low-frequency cyclic load: (a) strain-time relation for and (b) phase field-time relation for different values of .
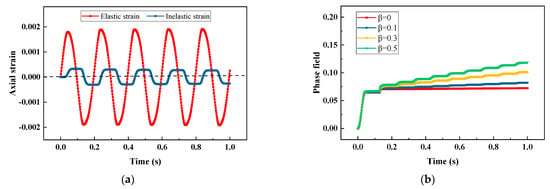
Figure 12.
Response of viscoplastic material under high-frequency cyclic load: (a) strain-time relation for and (b) phase field-time relation for different values of β.
The elastic, inelastic and total crack driving energies are plotted for low-frequency and high-frequency cyclic loads in Figure 13a,b. Under a low-frequency cyclic load, the inelastic energy is larger than elastic energy and the inelastic energy plays a dominant role in driving phase field evolution, whereas under a high-frequency cyclic load, the inelastic energy is smaller than elastic energy; the elastic energy plays a dominant role in driving phase field evolution. This is similar to the creep damage that occurs when materials are loaded for a long duration.
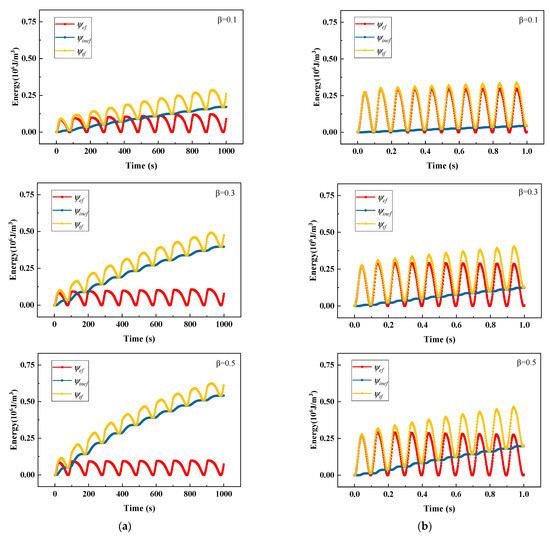
Figure 13.
Crack driving energies of viscoplastic material under (a) low-frequency and (b) high-frequency cyclic load for different values of β.
3.2. Stainless-Steel Plate Tensile Test
In this section, the fracture of a stainless-steel plate specimen with a thickness of 1.5 mm is studied using the presented phase field model. The tensile experiment used for comparison is taken from the literature [45]. The specimen was produced using an additive manufacturing method using the austenitic stainless-steel 316 L powder. The material and phase field parameters of the specimen are given in Table 2. The geometry and finite element discretization are illustrated in Figure 14. The effective element size in the area of crack growth is 0.1 mm. The geometry is meshed using 24,452 hexahedral reduced integration elements eight nodes. The displacement loading rate is 2 × 10−3 mm/s. The reaction force curves for different values of are plotted in Figure 15, in which the curve for agrees well with the experimental result, and a large value of can accelerate the fracture process. Figure 16 shows the final crack paths of the specimen for different values of . Red and blue colors indicate crack and unbroken materials. It is observed that the crack paths for different values of are similar; has no influence on the crack path for this stainless-steel plate specimen.

Table 2.
Material parameters of 316 L [45].
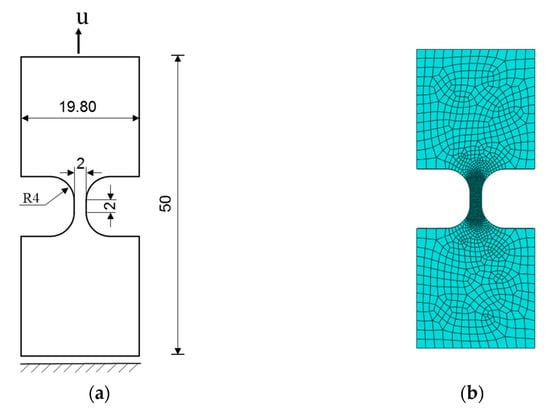
Figure 14.
Stainless-steel plate specimen: (a) geometry and (b) finite element discretization.
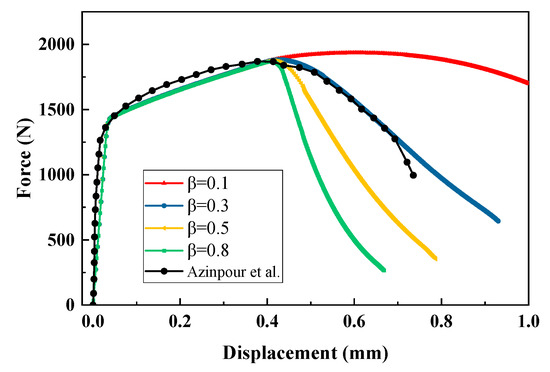
Figure 15.
Force-displacement curves of stainless-steel plate specimen for different values of β [45].
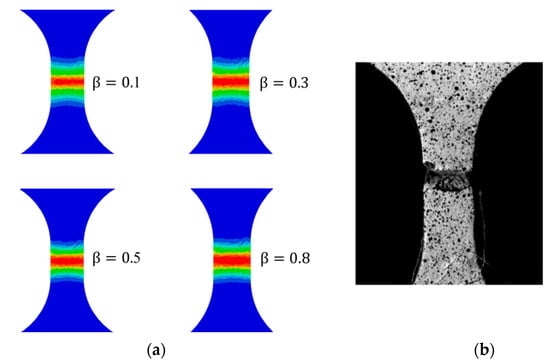
Figure 16.
Fracture of stainless-steel plate specimen: (a) simulation results and (b) experimental observation in literature [45].
3.3. Titanium Alloy Plate Tensile Test
In order to illustrate the influence of β in the present phase field model on crack growth, the fracture behavior of a thin titanium alloy plate under tension load is studied in this subsection. The experiment of this specimen was presented by Verleysen et al. [46]. The material and phase field parameters of titanium alloy Ti6Al4V are shown in Table 3. The geometry and mesh of the specimen are depicted in Figure 17, in which the left end is fixed and the displacement load is imposed on the right end. The thickness of the specimen is 0.6 mm. The geometry is meshed using 12,280 hexahedral reduced integration elements with eight nodes. The effective size of the elements in the refined region is 0.06 mm. The average strain rate of loading is 360/s.

Table 3.
Material parameters of Ti6Al4V [46].
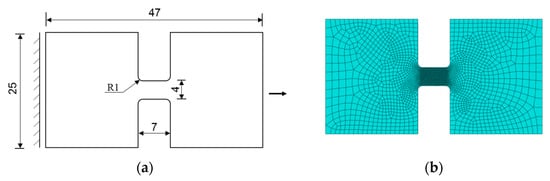
Figure 17.
Titanium alloy plate specimen: (a) geometry and boundary condition and (b) finite element mesh.
The force-displacement curves of the titanium alloy plate specimen for different values of are shown in Figure 18. With the increase of parameter , the force drops faster after reaching the maximum force. For , the force-displacement curve matches the experiment result. Figure 19a shows the crack paths of the titanium alloy plate specimen for different values of , in which the red color indicates crack. The cracks start from the middle of the specimen and then propagate perpendicular to the loading direction (this section of the crack is named the straight crack) and finally develop diagonally to rupture (this section of the crack is named the inclined crack). The length of the straight crack increases with the increasing . The angle between the inclined crack and the loading direction is 55.2° and it is very close to the angle 54.7° of the inclined crack obtained in the experimental observation. Furthermore, the distribution of degraded von-Mises stress of is shown in Figure 20. The stress concentration occurs at the edges of the parallel segment due to discontinuous geometry. Then, the stress of the parallel segment increases almost uniformly as the displacement load increases. When the crack initiates and propagates, the stress at the crack path decreases due to the degradation function.
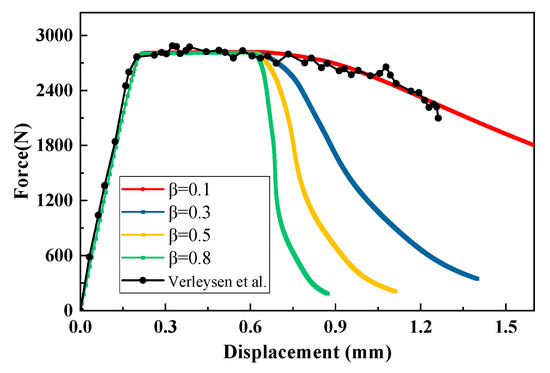
Figure 18.
Force-displacement curves of titanium alloy plate specimen for different values of β [46].
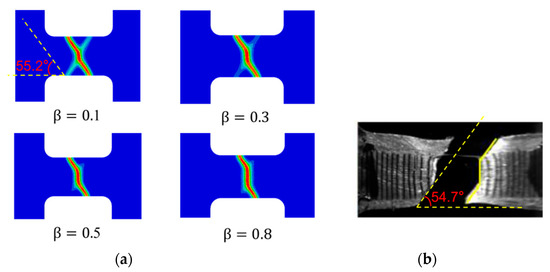
Figure 19.
Crack paths of titanium alloy plate specimen: (a) results of simulation and (b) experimental observation in literature [46].
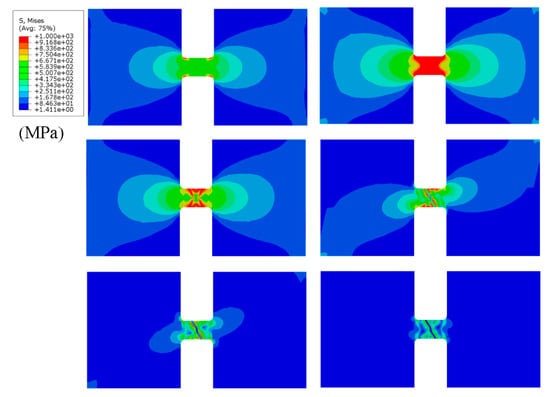
Figure 20.
Degraded von-Mises stress evolution of titanium alloy plate specimen.
4. Conclusions
The phase field model with viscoplastic constitutive was implemented using Abaqus subroutines. The strain rate, creep, stress relaxation and cyclic loading test are studied using a single-element model. The results show that significantly accelerates the evolution of the phase field of viscoplastic materials. For cyclic loadings, the acceleration effect for low frequency is more significant than for high frequency. The fracture response of a stainless-steel plate and a titanium alloy plate subjected to tension load are studied. The influence of on the force-displacement curve mainly occurs after reaching the maximum force point. With the increase of parameter , the force drops faster in the force-displacement curve. for the titanium alloy plate and for the stainless-steel plate are calibrated through the comparison of force-displacement curves. For the mode Ⅰ fracture of stainless-steel plate specimen, has no influence on the crack path. For the mixed fracture of the titanium alloy plate specimen, the angle of the inclined crack path agrees well with the observation in the experiment; however, a higher value of results in a longer straight crack. Based on the specimens tested in this paper, the inelastic energy has a significant effect on post-critical behavior, but has a slight effect on the crack path. In future work, more complex fracture processes need to be tested to study the influence of inelastic energy on the fracture response of viscoplastic material.
Author Contributions
Writing—original draft, software, methodology, investigation, Q.S.; writing—review & editing, supervision, conceptualization, H.Y.; writing—review & editing, investigation, X.W.; writing—review & editing, K.H.; writing—review, funding acquisition, J.H. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by the National Key R&D Program of China (Grant No. 2020YFA0714402), the Natural Science Foundation of China (NSFC) (Grant Nos. 12172103, and 12020101001) and the Natural Science Foundation of Heilongjiang Province of China (Grant No. JJ2023TD0005).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare that they have no known competing financial interest or personal relationships that could have influenced the work reported in this paper.
Nomenclature
| A, B | model parameters of sinh-type viscoplastic constitutive |
| gradient operators of the shape functions | |
| displacement field | |
| degraded stress tensors | |
| undegraded stress tensors | |
| von-Mises stress | |
| uniaxial stress considering viscoplasticity | |
| initial yield stress | |
| trial stress | |
| trial stress tensor | |
| deviatoric stress tensor | |
| effective inelastic strain rate | |
| equivalent inelastic strain increment | |
| total strain increment tensor | |
| elastic strain increment tensor | |
| inelastic strain increment tensor | |
| hardening stress | |
| d | phase field |
| elastic stiffness matrix | |
| yield function | |
| G | shear modulus |
| critical energy release rate | |
| K, m | viscous material constants |
| length scale | |
| stiffness degradation function | |
| shape functions associated with node i | |
| tangent stiffness matrix | |
| identity tensor | |
| residual forms of the nodal displacement and phase field variables | |
| energy density threshold | |
| total strain rate tensor | |
| elastic strain rate tensor | |
| inelastic strain tensors | |
| weight factor of inelastic energy | |
| Lame constant | |
| gradient operator | |
| elastic strain energy density | |
| inelastic strain energy density | |
| elastic crack driving energy | |
| inelastic crack driving energy | |
| total crack driving energy | |
| an arbitrary domain | |
| external boundary | |
| discrete crack set | |
| total energy history field | |
| elastic energy history field | |
| functional form of equivalent inelastic strain rate | |
References
- Ambati, M.; Gerasimov, T.; De Lorenzis, L. Phase-field modeling of ductile fracture. Comput. Mech. 2015, 55, 1017–1040. [Google Scholar] [CrossRef]
- Zhou, F.; Molinari, J.F. Dynamic crack propagation with cohesive elements: A methodology to address mesh dependency. Int. J. Numer. Methods Eng. 2004, 59, 1–24. [Google Scholar] [CrossRef]
- Peng, G.L.; Wang, Y.H. A Node Split Method for Crack Growth Problem. In Applied Mechanics and Materials; Trans. Tech. Publications Ltd.: Stafa-Zurich, Switzerland, 2012; Volume 182–183, pp. 1524–1528. [Google Scholar] [CrossRef]
- Azevedo, N.M.; Lemos, J. Hybrid discrete element/finite element method for fracture analysis. Comput. Methods Appl. Mech. Eng. 2006, 195, 4579–4593. [Google Scholar] [CrossRef]
- Fang, J.; Wu, C.; Li, J.; Liu, Q.; Wu, C.; Sun, G. Phase field fracture in elasto-plastic solids: Variational formulation for multi-surface plasticity and effects of plastic yield surfaces and hardening. Int. J. Mech. Sci. 2019, 156, 382–396. [Google Scholar] [CrossRef]
- Moës, N.; Dolbow, J.; Belytschko, T. A finite element method for crack growth without remeshing. Int. J. Numer. Meth. Eng. 1999, 46, 131–150. [Google Scholar] [CrossRef]
- Moës, N.; Gravouil, A.; Belytschko, T. Non-planar 3D crack growth by the extended finite element and level sets-Part I: Mechanical model. Int. J. Numer. Methods Eng. 2002, 53, 2549–2568. [Google Scholar] [CrossRef]
- Mueller, R.; Maugin, G.A. On material forces and finite element discretizations. Comput. Mech. 2002, 29, 52–60. [Google Scholar] [CrossRef]
- Miehe, C.; Gürses, E.; Birkle, M. A computational framework of configurational-force-driven brittle fracture based on incremental energy minimization. Int. J. Fract. 2007, 145, 245–259. [Google Scholar] [CrossRef]
- Fang, J.; Wu, C.; Rabczuk, T.; Wu, C.; Ma, C.; Sun, G.; Li, Q. Phase field fracture in elasto-plastic solids: Abaqus implementation and case studies. Theor. Appl. Fract. Mech. 2019, 103, 102252. [Google Scholar] [CrossRef]
- Tvergaard, V.; Needleman, A. Analysis of the cup-cone fracture in a round tensile bar. Acta Met. 1984, 32, 157–169. [Google Scholar] [CrossRef]
- Lemaitre, J. A Continuous damage mechanics model for ductile fracture. ASME J. Eng. Mater. Technol. 1985, 107, 83–89. [Google Scholar] [CrossRef]
- Peerlings, R.; Borst, R.; Brekelmans, W.; Vree, J.; Spee, I. Some observations on localisation in non-local and gradient damage models. Eur. J. Mech. A Solids 1996, 15, 937–953. [Google Scholar]
- Ambati, M.; Kruse, R.; De Lorenzis, L. A phase-field model for ductile fracture at finite strains and its experimental verification. Comput. Mech. 2016, 57, 149–167. [Google Scholar] [CrossRef]
- Oh, Y.-R.; Nam, H.-S.; Kim, Y.-J.; Miura, N. Application of the GTN model to ductile crack growth simulation in through-wall cracked pipes. Int. J. Press. Vessel. Pip. 2018, 159, 35–44. [Google Scholar] [CrossRef]
- Griffith, A.A. The phenomena of rupture and flow in solids. Philos. Trans. R. Soc. Lond. Ser. A 1921, 221, 163–198. [Google Scholar]
- Francfort, G.A.; Marigo, J.-J. Revisiting brittle fracture as an energy minimization problem. J. Mech. Phys. Solids 1998, 46, 1319–1342. [Google Scholar] [CrossRef]
- Bourdin, B.; Francfort, G.A.; Marigo, J.-J. Numerical experiments in revisited brittle fracture. J. Mech. Phys. Solids 2000, 48, 797–826. [Google Scholar] [CrossRef]
- Shi, Q.; Yu, H.; Guo, L.; Hao, L.; Huang, K. A phase field model with plastic history field for fracture of elasto-plastic materials. Eng. Fract. Mech. 2022, 268, 108447. [Google Scholar] [CrossRef]
- Shen, R.; Waisman, H.; Guo, L. Fracture of viscoelastic solids modeled with a modified phase field method. Comput. Methods Appl. Mech. Eng. 2019, 346, 862–890. [Google Scholar] [CrossRef]
- Yin, B.; Kaliske, M. Fracture simulation of viscoelastic polymers by the phase-field method. Comput. Mech. 2020, 65, 293–309. [Google Scholar] [CrossRef]
- Huang, K.; Yan, J.; Shen, R.; Wan, Y.; Li, Y.; Ge, H.; Yu, H.; Guo, L. Investigation on fracture behavior of polymer-bonded explosives under compression using a viscoelastic phase-field fracture method. Eng. Fract. Mech. 2022, 266, 108411. [Google Scholar] [CrossRef]
- Dammaß, F.; Ambati, M.; Kästner, M. A unified phase-field model of fracture in viscoelastic materials. Contin. Mech. Thermodyn. 2021, 33, 1907–1929. [Google Scholar] [CrossRef]
- Valverde-González, A.; Reinoso, J.; Jha, N.K.; Merodio, J.; Paggi, M. A phase field approach to fracture for hyperelastic and visco-hyperelastic materials applied to pre-stressed cylindrical structures. Mech. Adv. Mater. Struct. 2022, 29, 1–20. [Google Scholar] [CrossRef]
- Hojjat, B.; Elahe, E.; Mohammed, M. A phase field model for rate-dependent ductile fracture. Metals 2017, 7, 180. [Google Scholar]
- Gmati, H. Phase Field Modelling of Fracture of Elastic and Elasto-Viscoplastic Solid Materials. Ph.D. Thesis, HESAM Université, Paris, France, 2020. [Google Scholar]
- Wang, M.; Yu, Z.; Shen, W.; Shao, J. Numerical study of time-dependent deformation and cracking in brittle rocks with phase-field method and application to slope instability analysis. Int. J. Rock Mech. Min. Sci. 2022, 155, 105144. [Google Scholar] [CrossRef]
- Hai, L.; Li, J. A rate-dependent phase-field framework for the dynamic failure of quasi-brittle materials. Eng. Fract. Mech. 2021, 252, 107847. [Google Scholar] [CrossRef]
- Xie, Q.; Qi, H.; Li, S.; Yang, X.; Shi, D.; Li, F. Phase-field fracture modeling for creep crack. Theor. Appl. Fract. Mech. 2023, 124, 103798. [Google Scholar] [CrossRef]
- Arash, B.; Exner, W.; Rolfes, R. A finite deformation phase-field fracture model for the thermo-viscoelastic analysis of polymer nanocomposites. Comput. Methods Appl. Mech. Eng. 2021, 381, 113821. [Google Scholar] [CrossRef]
- Arash, B.; Wibke, E.; Raimund, R. Effect of moisture on the nonlinear viscoelastic fracture behavior of polymer nanocompsites: A finite deformation phase-field model. Eng. Comput. 2023, 39, 773–790. [Google Scholar] [CrossRef]
- Ullah, A.; ZeinEldin, R.A.; Khalifa, H.A.E.-W. Investigation of the Three-Dimensional Hybrid Casson Nanofluid Flow: A Cattaneo–Christov Theory. ACS Omega 2023, 8, 10991–11002. [Google Scholar] [CrossRef]
- ZeinEldin, R.A.; Ullah, A.; Khalifa, H.A.E.-W.; Ayaz, M. Analytical Study of the Energy Loss Reduction during Three-Dimensional Engine Oil-Based Hybrid Nanofluid Flow by Using Cattaneo–Christov Model. Symmetry 2023, 15, 166. [Google Scholar] [CrossRef]
- Borden, M.J.; Hughes, T.J.; Landis, C.M.; Anvari, A.; Lee, I.J. A phase-field formulation for fracture in ductile materials: Finite deformation balance law derivation, plastic degradation, and stress triaxiality effects. Comput. Methods Appl. Mech. Eng. 2016, 312, 130–166. [Google Scholar] [CrossRef]
- Dunne, F. Introduction to Computational Plasticity; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Amor, H.; Marigo, J.-J.; Maurini, C. Regularized formulation of the variational brittle fracture with unilateral contact: Numerical experiments. J. Mech. Phys. Solids 2009, 57, 1209–1229. [Google Scholar] [CrossRef]
- Liu, G.; Li, Q.; Msekh, M.A.; Zuo, Z. Abaqus implementation of monolithic and staggered schemes for quasi-static and dynamic fracture phase-field model. Comput. Mater. Sci. 2016, 121, 35–47. [Google Scholar] [CrossRef]
- Miehe, C.; Hofacker, M.; Welschinger, F. A phase field model for rate-independent crack propagation: Robust algorithmic implementation based on operator splits. Comput. Methods Appl. Mech. Eng. 2010, 199, 2765–2778. [Google Scholar] [CrossRef]
- Bourdin, B. Numerical implementation of the variational formulation for quasi-static brittle fracture. Interfaces Free Boundaries 2007, 9, 411–430. [Google Scholar] [CrossRef]
- Burke, S.; Ortner, C.; Süli, E. An adaptive finite element approximation of a variational model of brittle fracture. SIAM J. Numer. Anal. 2010, 48, 980–1012. [Google Scholar] [CrossRef]
- Brun, M.K.; Wick, T.; Berre, I.; Nordbotten, J.M.; Radu, F.A. An iterative staggered scheme for phase field brittle fracture propagation with stabilizing parameters. Comput. Methods Appl. Mech. Eng. 2020, 361, 112752. [Google Scholar] [CrossRef]
- Jeong, H.; Signetti, S.; Han, T.-S.; Ryu, S. Phase field modeling of crack propagation under combined shear and tensile loading with hybrid formulation. Comput. Mater. Sci. 2018, 155, 483–492. [Google Scholar] [CrossRef]
- Msekh, M.A.; Sargado, J.M.; Jamshidian, M.; Areias, P.M.; Rabczuk, T. Abaqus implementation of phase-field model for brittle fracture. Comput. Mater. Sci. 2015, 96, 472–484. [Google Scholar] [CrossRef]
- Kang, G.; Kan, Q. Constitutive modeling for uniaxial time-dependent ratcheting of SS304 stainless steel. Mech. Mater. 2007, 39, 488–499. [Google Scholar] [CrossRef]
- Azinpour, E.; Cruz, D.J.; Cesar de Sa, J.M.A.; Santos, A. Phase-field approach in elastoplastic solids: Application of an iterative staggered scheme and its experimental validation. Comput. Mech. 2021, 68, 255–269. [Google Scholar] [CrossRef]
- Verleysen, P.; Peirs, J. Quasi-static and high strain rate fracture behaviour of Ti6Al4V. Int. J. Impact Eng. 2017, 108, 370–388. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).