Abstract
Calcium carbonates are critical in biomineralization processes and as functional materials. For many applications, isotope enrichment in these materials allows researchers to monitor reaction pathways and retrace environmental signatures. When using vibrational spectroscopy, isotopic composition is currently derived by summing the concentration of each isotopologue, assumed to be directly obtainable from the band intensity, divided by the content of the isotope within the different isotopologues (e.g., C16O3, C16O218O, C16O18O2 and C18O3). However, this approach relies on the assumption that each isotopologue band has an equivalent intensity when present at the same concentration within the crystal structure. Here, using a joint experimental and theoretical approach we test the spectral behavior of the O-isotopologues by examining the effect of a key isotopic tracer, 18O, on the vibrational spectra of the calcium carbonate phases calcite and vaterite. We demonstrate that isotopic substitution changes both band positions and band intensities to different extents, depending on the vibrational spectroscopy method used and the bands examined. For calcite, the υ1 symmetrical stretching Raman-active bands related to individual isotopologues are found to have very similar intensities and are not affected by changes in isotopologue distribution within the material. Fitting these bands resulted in a consistent underestimation of the isotopic enrichment of only 1%, thus they are expected to be useful for estimating 18O-enrichment extent in future experimental work. In contrast, vaterite vibrational bands change more extensively and thus cannot be used directly to determine the 18O concentration within the material. These results are expected to contribute to a deeper und less ambiguous understanding of evaluating isotopic enrichment effects in the vibrational spectra of calcium carbonates.
1. Introduction
Calcium carbonates are important biominerals [1] as well as a functional materials [2,3]. Generation of calcium carbonates has been shown to occur via transformation from metastable phases, including vaterite and amorphous calcium carbonate, but the mechanism of transformation is still a matter of debate [4,5]. One method that has been shown to enable tracing the formation of oxyanion-bearing phases, including carbonates, phosphates and silicates, is the use of stable isotopes and vibrational spectroscopy [6,7,8,9,10,11]. These tracer experiments assume that the amount of O-isotope substitution into a material can be determined based on the sum of isotopologue band intensities that have been corrected for the isotope contribution within each isotopologue. However, recent work on C-isotope incorporation in calcite has demonstrated that isotopic enrichment signatures may not be as simply measured using vibrational spectroscopy [12]. Evidence from different amounts of C-isotope enrichment indicate that there is a non-linear relationship for IR band shifts that occur with increasing isotope incorporation. Whether similar effects also occur with O-isotopes is unknown.
The hypothesis that the intensities can be used to derive the isotope concentration also stems from a fundamental assumption, that each of the O-isotopologues formed upon substitution within the carbonate group, i.e., C16O3, C16O218O, C16O18O2 and C18O3, have the same absorption or scattering efficiency in vibrational spectroscopy and thus, when present in equal concentrations should produce the same band intensities. Again, this has not been verified and may not be consistent for all bands within the spectrum as loss of symmetry in the carbonate group upon partial O-isotope substitution has been proposed to lead to splitting of bands that are otherwise degenerate in the fully isotopically substituted calcite [13]. Finally, although some information is available in the literature for isotopic substitution related to the most thermodynamically stable product from calcium carbonate synthesis, calcite, isotopic substitution effects in the vibrational spectrum of the key intermediate phase, vaterite, have not been tested. It is therefore unclear to what extent information can be derived from vibrational spectra of isotopic tracers in the study of transformation mechanisms from metastable phases related to calcite formation.
Probing the effect of isotopic substitution on absorption and scattering properties in vibrational spectroscopy is difficult to achieve experimentally as synthesis of materials with only one, partially substituted isotopologue is extremely complicated. In contrast, these systems can be created and tested with relative ease using computer simulations. In particular, density functional theory (DFT) calculations are an effective method to evaluate the effect of isotope doping on vibrational spectra [14]. For example, the Raman spectrum of calcite generated using DFT in which the 16O atoms have been fully substituted with 18O (i.e., the production of the two end-member isotopologues of the isotopic substitution system) shows excellent agreement with experimental results [15]. However, computational analysis of the partially substituted isotopologues has not yet been reported in the literature. In addition, DFT has been successfully used to evaluate the vibrational spectrum expected from the different structures that vaterite may adopt [16], but again, isotopic substitution has not been considered.
Here, we have employed a joint theoretical and experimental approach to test the hypothesis that the different isotopologues can be used to map the isotopic enrichment in the calcium carbonates calcite and vaterite using techniques of vibrational spectroscopy. The number and placement of the bands related to the carbonate O-isotopologue predicted by the simulations were compared to vibrational spectra obtained from experimentally synthesized material, grown from a solution in which all carbonate O-isotopologues were present. Upon establishing the robustness of the spectra produced in the simulations for the isotopically enriched materials, further calculations were then used to study the effect of isotope distribution and spectral properties related to the different isotopologues, which are difficult to obtain from synthetic materials.
2. Methodological Aspects
Experimental methods. Amorphous calcium carbonate was precipitated by quickly adding a 1 M Na2CO3 solution to 1 M CaCl2 solution at 4 °C, as described in previous work [17]. This amorphous calcium carbonate was then transferred by pipette to a solution that had been equilibrated with calcite for 1 week at room temperature. The amorphous calcium carbonate was then left to transform to vaterite and subsequently calcite, also at room temperature. This transformation was monitored in situ using Raman spectroscopy. When several Raman spectroscopy spot analyses demonstrated that the system had produced vaterite, the solid was removed from solution via evaporation on a glass slide after the application of isopropanol to stabilize the phase for further analysis using infrared (IR) spectroscopy. The rest of the solids were allowed to transform to calcite and dried in a similar manner. To generate vaterite and calcite that were partially substituted with 18O, the same procedure was completed, but this time using a 1 M Na2CO3 that had been allowed to equilibrate with 50% 18O-doped water at 60 °C prior to the synthesis experiment. Raman spectroscopic analysis demonstrated the presence of bands related to the formation of partially and fully 18O-substituted isotopologues of the carbonate ion in solution, consistent with previous work [18].
The samples were analyzed using a WITec 300 alpha Raman spectrometer equipped with an optical microscope. A laser of 488 nm was used in the measurements with a long working distance objective lens of 50× with a numerical aperture of 0.55. This setup provided a spot size of ~1 µm, providing spectra from individual crystals (10–20 µm diameter based on optical images). Full spectra were obtained from the solids with a grating of 2400 grooves/mm to provide the highest Raman scattering efficiency with the best spectral resolution (1.9 cm−1 at 1800 cm−1 based on the full width at half maximum for an inbuilt calibration lamp). Each spectrum was acquired 10 times for 5 s and averaged to provide high signal-to-noise ratios. Infrared spectra of bulk samples with many crystals were obtained using diffuse reflectance infrared Fourier transform spectroscopy (DRIFTS) on a ThermoFisher Scientific Nicolet 6700 infrared spectrometer (Waltham, MA, USA). The background was measured prior to sample measurement and automatically subtracted from the sample spectrum by the ThermoFisher Omnic Spectra program. Each spectrum was acquired 128 times and integrated to achieve sufficient signal to noise ratios. The spacing between data points was 1 cm−1.
Computational details. Density functional theory (DFT) calculations presented in this work were performed using the all-electron code CRYSTAL (2017 release) [19,20], in conjunction with triple-ζ-valence + polarization Gaussian-type basis sets optimized specifically for crystalline calcium carbonate compounds by Valenzano et al. [21]. The hybrid B3LYP exchange-correlation functional [22,23] was used throughout all calculations. Calcite has a R3c structure, described in the simulations using the Graf et al. [24] reference information supplied in the American Mineralogist Crystal Structures Database. In contrast, the true structure of vaterite is still under debate in literature and hard to separate from mixed and hybrid structures [25]. Therefore, we have used the C2 and P3221 space group vaterite structures from previous theoretical simulations [26], that have been shown to reproduce experimentally determined Raman spectra [16] (the initial lattice parameters and atomic positions are freely available at the American Mineralogist Crystal Structures Database as well). The chosen setup has been shown to reproduce the structures as well as the vibrational properties of ionic and semi-ionic compounds in good agreement with experimental data [13,14].
In CRYSTAL, the convergence of the real-space summation of the Coulomb and exchange contributions to the Hamiltonian matrix is controlled by five overlap criteria (TOLINTEG). The values used in this study were 10−7, 10−7, 10−7, 10−7, and 10−14, which were found to ensure converged total energy up to 3 × 10−5 Ha/atom and vibrational frequencies up to 1 cm−1 (tested for TOLINTEG tolerances of 10−9, 10−9, 10−9, 10−9, and 10−22). The threshold of the self-consistent (SCF) energy was set to 10−7 Ha for single-point calculations, while it was set to 10−10 for frequency calculations. For the compounds of interest, the convergence with respect to k-points was checked. Monkhorst-Pack meshes of 7 × 7 × 7 for calcite, 5 × 5 × 5 for vaterite in the C2/c structure, and 5 × 5 × 1 for vaterite in the P3221 crystal structure were used to sample the first Brillouin zone [27]. Infra-red and Raman intensities were computed analytically, based on couple-perturbed Hartree-Fock/Kohn-Sham (CPHF/KS) treatments implemented in the code [28,29,30]. The simulations at present do not provide values for peak widths and concentrate only on the fundamental vibrational modes in the materials studied. Therefore, bands related to more complex interactions within the material, e.g., overtone bands above 1500 cm−1, are not examined in the simulations. Moreover, in contrast to previous work, [12] no approximation of grain geometry was used for the IR spectra, resulting in narrower bands than those observed experimentally.
3. Results and Discussion
3.1. Comparison between Simulated and Experimentally Produced Vibrational Spectra of Isotopically Substituted Calcium Carbonate Phases
Calcite. The measured Raman spectrum of the isotopically doped calcite sample (Figure 1c) were found to be consistent with what has been reported in earlier experimental studies [6,11]. Therefore, the effect of O-isotope enrichment will only be briefly summarized here in relation to the computational simulations. Incorporation of 18O into the calcite structure produced a specific band shift in the majority of the bands present in the spectra of calcite. A comparison between phase pure Raman data and the simulated spectra can be seen in Figure 1b,c and Table S1. The simulated IR spectra are also given (Figure 1a), however, the simulated spectra cannot replicate the broad IR bands found experimentally and therefore we have not attempted to compare between them. A list with estimated band positions can be found in Table S2 and a typical IR spectrum found in Figure S1. Overall, the calculated vibrational frequencies are in good agreement with measured values, having a maximum deviation of 2 cm−1. Furthermore, the changes in the band positions related to the different isotopologues in the 18O-enriched calcite sample are readily traceable in the computed spectra. For example, all the bands occurring between 1020–1090 cm−1 Figure 1b in correlate to the Raman active ν1 symmetrical stretching mode, and the bands found in the frequency range between 670–710 cm−1 are the IR and Raman active ν4 bending modes. These results are comparable to earlier DFT works that examined the fully O-isotope substituted calcite structures [15].
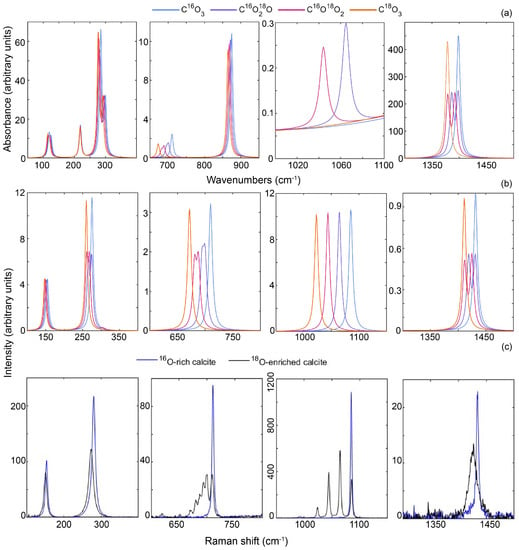
Figure 1.
Calculated vibrational spectrum of calcite with each of the four carbonate O−isotopologues: (a) infrared spectrum, (b) Raman spectrum, where (c) shows the experimentally determined Raman spectrum from a single calcite crystal. The regions outside of the plotted areas have no vibrational bands visible. Note that the individual regions of interest are plotted with different y axes to facilitate visualization.
In addition, our simulations corroborate the hypothesis made in published literature that breaking symmetry within the partially substituted carbonate isotopologues leads to the υ1 becoming IR active [13]. They also demonstrate that the intensity of this band is expected to be low. Gillet and McMillan [13] further predicted that the loss of symmetry upon formation of the C16O218O and C16O18O2 isotopologues results in a splitting of the normally degenerate υ4 band (close to 700 cm−1) to produce six bands (rather than four) in the Raman and IR spectra of calcite upon O-isotope substitution. We confirm this effect in our computed calcite spectra, which showed splitting (Figure 1) due to the change of symmetry from E to A and B when all carbonate groups within the structure were the same partially substituted isotopologue (C16O218O or C16O18O2). The simulations also showed that a similar splitting is predicted for the IR and Raman active υ3 band at 1400 cm−1. However, the broadness of the 1400 cm−1 band in the experimental IR spectrum due to extensive TO-LO (transversal-longitudinal optical mode) splitting [13] meant that this splitting was not resolvable in the spectra of the synthesized material.
Equivalent bands in the Raman spectrum of the synthesized calcite did not show any clear splitting either, but rather, there was a shift of 9 cm−1 and significant broadening of the band, with the full width at half maximum increasing from 6 to 17 cm−1, associated with O-isotope substitution. The calculated spectra indicated that lack of resolution of the individual bands in the experimental data were probably exacerbated by the formation of a Bg band with the same vibrational energy as the Eg bands of the fully substituted isotopologues. This led to a complicated change in the band intensities related to isotopic substitution and, if these bands are broad, significant overlap could have created the broad, but shifted band observed experimentally. The Raman lattice mode band close to 300 cm−1 was also predicted by DFT to be split upon partial substitution within the isotopologues. Yet, in the experimental sample this band also had a shift to lower wavenumbers and was broadened in comparison the 16O-rich calcite Raman spectrum. Although this band did not show any overlap between the Eg and A or B bands in the simulations, the overall band shift expected between the structures with the fully substituted isotopologues was only 20 cm−1 and the differences between individual bands with lower symmetry was only 1–2 cm−1. This is the typical spectral resolution of Raman instruments (1.9 cm−1 in our spectra) and thus, again, there is probably significant overlap of the bands leading to an overall broad and shifted band in this region. A similar effect was also observed for the lattice mode at 150 cm−1 in the simulated Raman spectrum, which was expected to split, but each of the individual, lower symmetry bands only had a shift of 1 cm−1, resulting in a large overlap that again was not experimentally resolvable.
Vaterite. The calculated IR bands for vaterite show a shift to lower wavenumbers upon 18O substitution (Figure 2), which is also observed in the experimental data (Figure S1). However, it was difficult to obtain a phase pure sample for IR analysis and the broad bands made comparisons difficult. A summary of the estimated band positions from an experimentally determined spectrum and their comparison to the simulated spectra can be found in Table S2. In contrast, the experimentally determined Raman spectrum showed clearer distinction between bands and was taken from a vaterite single crystal enabling a more robust comparison to the simulated results. Similar to what was found for calcite, the calculated Raman spectra derived for the C16O3 end-member of vaterite corresponds well to previous works [15]. The overall number and relative intensities of bands in the simulated spectra also corresponded to what has been observed in the current and previous experimental work [31] (Figure 3). However, the two different vaterite input structures used in the calculations produce band positions that deviate from the experimentally determined positions by up to 8 cm−1 (Table S3). The vibrational modes of the C2 vaterite structure are predicted to have no E symmetry. However, there are many bands in P3221 structure that are expected to have E symmetry, including some that are predicted to have a high enough intensity to be discernible in the Raman and IR spectra, e.g., the υ3 modes between 650 and 760 cm−1. Unlike the calcite spectra, these bands are predicted to only experience a band shift upon partial isotope substitution with no loss in the degenerate band nature in the vaterite P3221 structure. Therefore, band splitting due to 18O incorporation cannot be used to distinguish between the two structures.
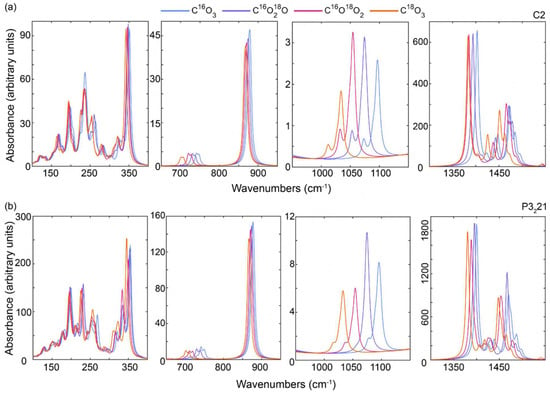
Figure 2.
Calculated IR spectrum of vaterite with each of the four carbonate O−isotopologues: (a) C2 structure, (b) P3221 structure. The regions outside of the plotted areas have no vibrational bands visible. Note that the individual regions of interest are plotted with different y axes to facilitate visualization.
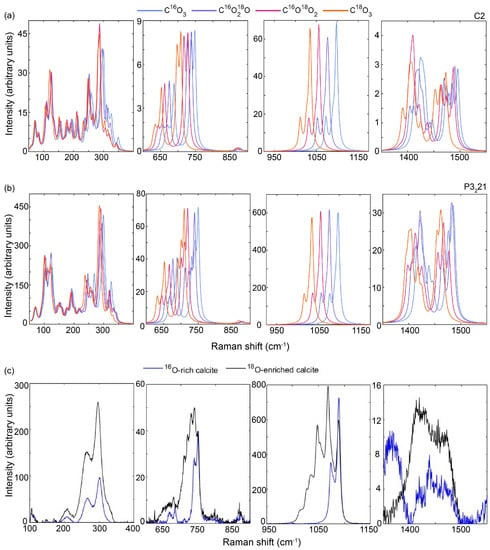
Figure 3.
Calculated Raman spectrum of vaterite with each of the four carbonate O−isotopologues: (a) C2 structure, (b) P3221 structure, (c) experimentally determined Raman spectrum for a single vaterite crystal. The regions outside of the plotted areas have no vibrational bands visible. Note that the individual regions of interest are plotted with different y axes to facilitate visualization.
Isotopic substitution resulted in new bands clearly emerging from the band envelope between 1000 and 1100 cm−1 in the experimental Raman spectrum (Figure 1c, Table S1). In the calculated spectra, the most intense and sharpest bands visible in this envelope at 1048 and 1068 cm−1 fit the shifts of the υ1 symmetric stretching mode, at 1089 cm−1 for the C16O3 isotopologue, estimated based on a harmonic oscillator assumption and the reduced mass of the partially substituted isotopologues and that found in our DFT calculations. The broadening of the entire band envelope in the substituted experimental samples thus occurred due to similar isotope-related splitting of the other υ1 symmetric stretching mode bands, predicted to significantly contribute to this spectral region in the DFT calculations (Figure 3). In our 16O-rich experimental dataset, the structure was best fit with two additional υ1 bands in this region at 1073 and 1079 cm−1, consistent with the majority of the synthetic and biological samples studied previously [31]. The bands in this area showed the highest similarity with the calculated C2 structure of vaterite, as the P3221 structure predicts three bands in addition to the prominent band at 1089 cm−1. Bands related to υ3 modes between 650 and 760 cm−1 were also observed to split from their two doublets in the 16O-rich experiment samples to generate a broad envelope with at least seven bands in the isotopically substituted experiment sample. Again, the production of two doublets in this region for the 16O-rich sample fits best with the C2 vaterite structure in the simulations. An increase in the broadness of the υ4 band envelope was also observed upon isotopic substitution into the vaterite structure. This is consistent and can be traced to the band splitting observed in the calculated spectra. In contrast, only a shift was observed in the lattice mode spectral region below 500 cm−1. Neither structure model accurately replicated the band structure in this region as both predicted a higher number of sharp bands than were observed in the experiment samples.
Similar to what was found for calcite, the calculated Raman spectra derived for the C16O3 end-member of vaterite corresponds well to previous works [15]. These spectra also corresponded well in the overall number and relative intensities of bands observed in the current and previous experimental work [31] (Figure 3). However, the two different vaterite input structures used in the calculations produce band positions that deviate from the experimentally determined positions by up to 8 cm−1 (Table S4). The vibrational modes of the C2 vaterite structure are predicted to have no E symmetry. However, there are many bands in P3221 structure that are expected to have E symmetry, including some that are predicted to have a high enough intensity to be discernible in the Raman and IR spectra, e.g., the υ3 modes between 650 and 760 cm−1. However, unlike the calcite spectra, these bands are predicted to only experience a band shift upon partial isotope substitution with no loss in the degenerate band nature in the vaterite P3221 structure. Therefore, band splitting due to 18O incorporation cannot be used to distinguish between the two structures.
Isotopic substitution resulted in new bands clearly emerging from the band envelope between 1000 and 1100 cm−1 in the experimental Raman spectrum (Figure 1d, Table S1). In the calculated spectra, the most intense and sharpest bands visible in this envelope at 1048 and 1068 cm−1 fit the shifts of the υ1 symmetrical stretching mode, at 1089 cm−1 for the C16O3 isotopologue, estimated based on a harmonic oscillator assumption and the reduced mass of the partially substituted isotopologues and that found in our DFT calculations. The broadening of the entire band envelope in the substituted experimental samples thus occurred due to similar isotope-related splitting of the other υ1 symmetrical stretching mode bands, predicted to significantly contribute to this spectral region in the DFT calculations (Figure 3). In our 16O-rich experimental dataset, the structure was best fit with two additional υ1 bands in this region at 1073 and 1079 cm−1, consistent with the majority of the synthetic and biological samples studied previously [31]. The bands in this area showed the highest similarity with the calculated C2 structure of vaterite, as the P3221 structure predicts three bands in addition to the prominent band at 1089 cm−1. Bands related to υ3 modes between 650 and 760 cm−1 were also observed to split from their two doublets in the 16O-rich experiment samples to generate a broad envelope with at least seven bands in the isotopically substituted experiment sample. Again, the production of two doublets in this region for the 16O-rich sample fits best with the C2 vaterite structure in the simulations. An increase in the broadness of the υ4 band envelope was also observed upon isotopic substitution into the vaterite structure. This is consistent and can be traced to the band splitting observed in the calculated spectra. In contrast, only a shift was observed in the lattice mode spectral region below 500 cm−1. Neither structure model accurately replicated the band structure in this region as both predicted a higher number of sharp bands than were observed in the experiment samples.
3.2. Effect of Isotopologue Distribution on the Vibrational Spectra Characteristics
Preferential incorporation of different isotopologues through equilibrium and kinetic effects is expected within calcite and vaterite, due to changes in the Ca-O bond lengths caused by the presence of heavier isotopes altering the probability of the carbonate groups being incorporated into the crystal structures during growth [31]. Computational simulations of different C-isotope distributions within the calcite crystal structure have been shown to affect the band positions and intensities observed in the vibrational spectra [12]. In this case, nearest neighbor carbonate groups with 13C rather than 12C produced a higher intensity for the 12C-related υ3 and υ4 IR bands. Within a calcium carbonate crystal structure, the carbonate groups are linked together via Ca-O bonds. Thus, the distribution of O-isotope substitution may have an even stronger effect, as substitution into a neighboring group will change the vibrational energy of the Ca-O bonds with consequences for the vibrational modes of the neighboring carbonate groups. Therefore, for both calcite and vaterite, we tested how the different 18O distributions affected the IR and Raman spectra when a single isotopologue was present.
All simulations were carried out with only the partially substituted isotopologue C16O218O. For calcite, there were two different possible configurations for isotopic substitution. Each Ca ion sits in highly symmetrical site surrounded by six O atoms from the carbonate groups, where two O atoms from a carbonate group can interact with one Ca atom. Thus, 18O can be distributed as far apart as possible on opposite sides of the Ca atom, or in positions that lie directly next to each other around the Ca atom, but in a neighboring carbonate group. In contrast, the Ca sites in the two different vaterite structures examined here are less symmetrical and thus have different sizes and shapes. Hence, three different scenarios were tested for the distribution of 18O that can be implemented in both structures. As examined for calcite, in the first configuration the 18O atoms of each carbonate group were placed as far apart as possible. In the second scenario, the 18O substitution was clustered as closely as possible around the Ca atoms. Finally, a midway configuration was chosen, where the 18O was placed in an equivalent position within each carbonate group and in each carbonate layer that is present in the structure, rather than focusing on their specific distribution around the Ca atoms.
Calcite. In the calculated calcite IR spectra the most intense band, i.e., the υ3 asymmetrical stretching at 1400 cm−1, is sensitive to the isotope distribution (Figure 4a), where the splitting described above is observed when the 18O atoms are distributed on the opposite side of the Ca atom. When the isotopes were distributed so that they are closest together, a single strong band was produced at 1391 cm−1 with a weak shoulder at 1418 cm−1. Examination of the symmetry from the simulations demonstrates that the two different configurations resulted in a change from symmetric with respect to the principal symmetry axis (A) in the close configuration, to symmetric with respect to the principal axis and antisymmetric with respect to the center of symmetry (Au) when 18O was situated on opposite sides of the Ca atoms. The other IR bands were more robust with respect to changes in symmetry induced by different distributions. Here, the υ2, υ4 and lattice modes found at 800, 700 and below 500 cm−1, respectively, had the same band distributions with the same intensities or only a small deviation of up to 7% for the lattice bands (Figure 4a).
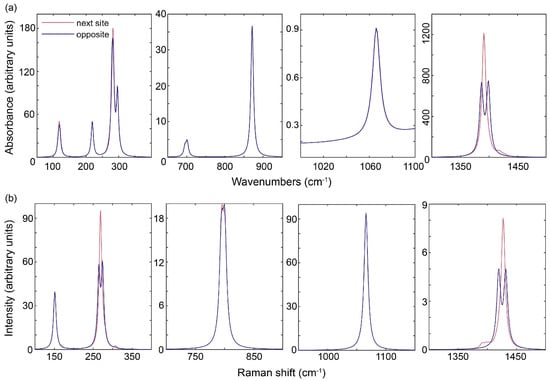
Figure 4.
Calculated band shifts, new band formation, and intensity changes associated with the distribution of 18O in C16O218O in calcite: (a) infrared spectra and (b) Raman spectra. The regions outside of the plotted areas have no vibrational bands visible. Note that the individual spectral regions of interest are plotted with different y axes to facilitate visualization.
Both lattice modes at 150 cm−1 showed no sensitivity to 18O distribution in the Raman spectra as they produced bands at the same location and with the same intensities (Figure 4b). Similarly, the υ1 symmetrical stretching mode at 1065 cm−1 also showed no sensitivity to the isotope distribution. However, the lattice mode close to 270 cm−1, the υ4 bending mode at 700 cm−1 and the υ3 asymmetrical stretching at 1400 cm−1 all show distinct changes based on isotope distribution. When the 18O atoms are distributed closely together around the Ca atom, the lattice mode at the highest wavenumbers is dominated by one band at 269 cm−1 in comparison to the doublet (265 and 274 cm−1) that appears when the 18O atoms are spaced as far apart as possible. The same effect is observed for the υ3 bands, where a single band at 1427 cm−1 was the most intense for the closest configuration, which is split into a doublet (1419 and 1432 cm−1) when the isotopes were distributed as far apart as possible (Figure 4b). Again, these changes could be related to vibrational motions that are symmetrical with respect to both the principal axis and center of symmetry (Ag), rather than possessing A symmetry only when the 18O atoms are located next to each other. In contrast, the two overlapping bands that are found for the υ4 vibration close to 700 cm−1 swap in relative intensities depending on the distribution, although this is a small effect with only a 9% change in intensity for the two bands.
Unfortunately, although the change in splitting for the breaking of the band degeneracy from the fully to partially substituted isotopologues could be observed in the experimental Raman spectrum, the changes related to isotope distribution cannot be resolved as the clearest changes occur within the υ3 bands. However, if these bands could be measured with a higher resolution and intensity, they could provide key information about the isotope distribution within the calcite structure.
Vaterite. The O-isotope distribution played an important role in governing the relative intensities of the different vibrational bands in both of the structures that were used throughout the simulations for vaterite. The most intense bands in the IR spectra, those of the υ4 between 1350 and 1600 cm−1, are significantly altered by the distribution of 18O within both the C2 and P3221 vaterite structures (Figure 5). These bands changed both their positions and their relative intensities when the distribution of 18O was altered, resulting in significantly different spectral features in this region. Fitting the spectra indicated that some υ4 bands were shifted by up to 5 cm−1 and the dominant band intensities changed by up to 24% in some cases. A similar effect was observed for bands in the υ2, υ3, and lattice modes spectral regions. No systematic change in the shift or intensities of the bands was observed related to the distance of the 18O atoms within the crystal structures.
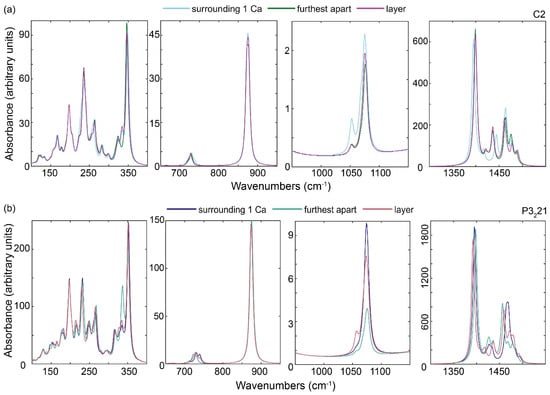
Figure 5.
Calculated band shifts and intensity changes associated with the distribution of 18O in C16O218O vaterite infrared spectra: (a) C2 structure and (b) P3221 structure. The regions outside of the plotted areas have no vibrational bands visible. Note that the individual spectral regions of interest are plotted with different y axes to facilitate visualization.
Critically, the weak IR, but strong Raman, υ1 bands appeared insensitive to changes in 18O distribution, showing only a maximum shift of 1 cm−1 in band positions and a change in intensity of 3% in the Raman spectra for this region within the C2 model (Figure 6a). Similarly, in the P3221 model (Figure 6b), the most intense υ1 Raman band showed a similar change in intensity and <0.5 cm−1 shift with different 18O distributions. In this model the other two bands in this region were more affected by the 18O distribution, with up to 3 cm−1 shift for the band at 1070 cm−1, and up to 30% change in intensity. Again, no systematic change in the intensities was observed in the Raman spectra based on distance between the 18O atoms. As would be expected due to the activity of the bands in both IR and Raman spectra, the υ4, υ3, and lattice modes in the Raman spectrum showed a similar shift as those in the IR spectra. However, there was a larger effect of the 18O on the scattering efficiency of the Raman modes, expressed as band intensity, with the most intense bands in these regions showing shifts of up to 8 cm−1 and changes in intensity of up to 70%, whereas some of the weaker bands disappeared entirely from the spectrum when the 18O distribution was altered. Overall, as a result, these spectral regions expressed a very different band structure dependent on the isotope distribution (Figure 6).
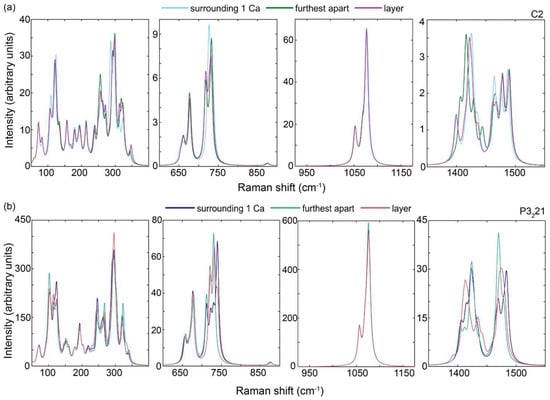
Figure 6.
Calculate band shifts and intensity changes associated with the distribution of 18O in C16O218O vaterite Raman spectra: (a) C2 structure and (b) P3221 structure. The regions outside of the plotted areas have no vibrational bands visible. Note that the individual spectral regions of interest are plotted with different y axes to facilitate visualization.
Given that the typical spectral resolution of Raman instruments is ~1 cm−1 and bands are fitted with different functions to determine their height, the observed differences for the most intense υ1 Raman bands are expected to be within experimental error. In contrast, the other spectral bands will be affected by the isotopic distribution, which may be measurable via vibrational spectroscopy. However, this effect will be difficult to discern in the solid spectra, unless the effects of crystal orientation and chemistry can be disregarded as these can produce similar changes in relative intensities and band shifts [32]. In the calculated spectra, we examined the total Raman and IR spectral signals to negate any orientation effects.
3.3. Evaluation of IR Absorption and Raman Scattering Effects Related to the Presence of Different Isotopologues
It can be seen from the simulations discussed thus far that the increased isotope enrichment leads to the presence of different isotopologues within the crystal structures that are characterized by new or shifted bands in the vibrational spectra. Although the isotope distribution can clearly have an effect on the exact positions and the intensities of specific bands, the differences in the interaction of the different isotopologues with the incoming light may also contribute to the final observed band intensity. This is a critical parameter for tracer experiments because it is the intensity of the different isotopologues that are currently used as a reaction tracer and timer for crystal growth [6,8,9]. We have therefore examined the simulated structures, where all carbonate groups are the same isotopologue. In simulations with the partially substituted isotopologues, the position of the 18O atoms were randomly selected to minimize the effects of distribution on the band intensity.
For calcite, the IR bands showed a decrease in intensity with increasing 18O incorporation into the carbonate group (Figure 1a), where the intensity change between the two isotopologue end members depends on the vibrational mode. The difference between the two fully substituted isotopologues varies from a 5% decrease for the IR υ3 band in the simulated spectra up to a 41% change for the weaker IR υ4 band. When the υ4 and υ3 bands were split due to the partially substituted isotopologues, addition of the two bands resulted in an overall intensity that reflects a linear relationship between the amount of isotope substitution and band intensity. In comparison, the Raman bands (Figure 1b) also produced the same linear dependence of intensity as observed in the IR spectra, which included the addition of the split bands upon symmetry breaking in the partially substituted isotopologues. However, the Raman bands showed a much lower change in intensity, between <1% for the lattice band close to 150 cm−1 and 4% for the υ1 band.
The changes in intensity related to specific isotopologues in the vaterite structure were dependent on the particular structure tested. For example, the C2 structure for vaterite shows a linear trend in band intensities in the simulated IR spectra with increasing 18O substitution into the carbonate groups (Figure 2a), which is evident for both the υ2 bands and most intense υ3 band, which decreased in intensity by 12% and 5%, respectively. In the P3221 structure, however, there was a linear decrease in band intensity with increasing 18O substitution for the υ2 IR bands (−12%), but a much more complex change in intensity that does not appear to be directly correlated with 18O concentration for the most intense υ3 band (Figure 2b). In the Raman spectra, both structures showed that the υ4 bands between 600–800 cm−1 are robust with respect to isotopologue occurrence, with a change in intensity of the strongest band in this region of 2% (Figure 3). However, the vaterite υ1 band is sensitive to the isotopologues present and varies non-linearly in both the C2 and P3221 models. In the C2 model, the intensity decreased by 5% between the two fully substituted isotopologues, but the C16O218O isotopologue shows an anomalously low intensity decrease of 11% in comparison to the C16O3 isotopologue (Figure 3a). In contrast, the intensity of the dominant υ1 band for the fully substituted isotopologue decreased by 2% in the P3221 model (Figure 3b), but the υ1 band increased in intensity for both the partially substituted isotopologues in comparison to the fully substituted isotopologues (up to 4%).
It is clear that the spectral behavior of vaterite bands means that they cannot be used to accurately predict the isotopic enrichment of 18O. However, the calcite υ1 band may be robust enough to measure the amount of isotopic enrichment. We tested this by creating a 2 × 2 × 1 supercell, where each of the lattice parameters was at least 10 Å, and used a random number generator to assign which O atoms were 18O, creating four different, random distributions at 33.3% enrichment or 66.6% enrichment (Figure 7). The distribution of the isotopologues in these configurations can be found in Table 1. Intensities (i) of the different isotopologue bands was estimated using the spectral fitting program Fityk [33] and then used to estimate the isotopic enrichment based on the equation below.
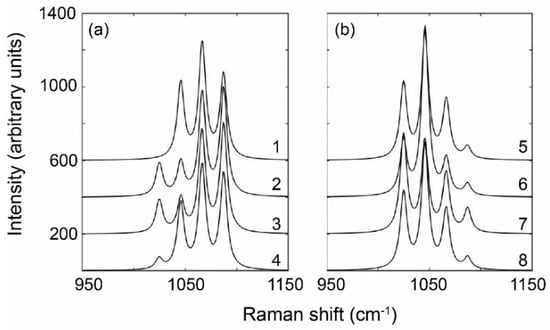
Figure 7.
Focus on the Raman active υ1 region for eight different random distributions of 18O within the calcite structure at either 33% (a) or 66% (b) enrichment. Note, the spectra have been offset by 200 counts to aid visualization of the different isotopologue distributions.

Table 1.
Calculated 18O enrichment from simulated Raman spectra of randomly distributed 18O producing eight different isotopologue distributions at either 33 or 66% enrichment. Total O atoms in the supercell was 72.
As can be seen from the data presented in Table 1, the enrichments estimated from the intensities agrees very well with the modelled system regardless of the configuration of the 18O distributions both between different isotopologues and in space within the supercell. The same approach was then used to estimate the isotopic enrichment of the experimental sample (Table 1). At present, further corroboration of the experimental value cannot be obtained as the standard isotope analytical methods, e.g., secondary ion mass spectrometry techniques, do not have equivalent sampling volumes to the Raman spectrometer and the highly enriched calcite samples are expected to show some heterogeneity. Therefore, a careful approach that considers statistical evaluations of different crystals, methods and spatial resolutions is necessary to tackle this question, which will be the topic of a future study.
4. Conclusions
Our calculations predict that individual isotopologues do not exhibit equivalent spectral behavior. Instead, in both calcite and vaterite, they are expected to differ in the amount of IR absorption or Raman scattering efficiency, as expressed in the band intensities. In addition, the distribution of isotopes within the structures of calcite and vaterite can produce subtle changes in the band positions and intensities in the associated spectra, similar to what has been observed previously with C-isotopes [12].
For vaterite, comparison between the two model structures and the number of bands found upon isotopically doping the experimental samples indicates that the C2 structure is probably the most appropriate representation of the crystal structure. Band intensity changes in the vaterite spectra with increasingly 18O-substituted isotopologues did not follow clear trends. Thus, our findings demonstrate that band intensities cannot be used directly to infer absolute concentration changes of the isotopologues within vaterite from vibrational spectra.
Calcite vibrational spectroscopy of O-isotope substitution appears to be the most robust, with only a 4% loss in intensity expected between the end-member isotopologues. However, band splitting due to loss of symmetry in the partially substituted isotopologues makes the evaluation of the isotopologue-specific intensity difficult for most bands in the calcite spectrum. The exception is the υ1 calcite band, where the isotopologues with increasing 18O substitution show a linear decrease in their intensity that could be corrected for in the future. This band also showed no sensitivity to isotope distribution and reproduced an expected enrichment in the simulated spectra even when different isotopologue distributions are present. Given that the simulations demonstrated that the Raman spectra are less affected by changes in isotopologue distribution or the scattering efficiency than the IR spectra, we recommend that the υ1 symmetric stretching band observable using this technique should be used in the future to evaluate isotopic enrichment in order to obtain the best estimate.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/cryst13010048/s1, Figure: Infrared spectroscopy data of calcite and vaterite that are 16O-rich or 18O-enriched. Tables listing the fitted band positions from experiments and the comparison with those produced during the simulations. Table S1: Comparison between calcite experimental and computationally generated IR spectra. Table S2: Calcite Raman spectra from experiments and simulations. Table S3: Comparison between bands found in experiment and computed IR spectra from vaterite C2 and P3221 structures [34]. Table S4: Bands and assignments from Raman spectra vaterite C2 and P3221 structures and experimentally derived spectra.
Author Contributions
Conceptualization, H.E.K.; methodology, H.E.K. and A.Ž.; validation, H.E.K. and A.Ž.; investigation and data curation, H.E.K. and A.Ž.; writing—original draft preparation, H.E.K.; writing—review and editing, H.E.K., A.Ž. and N.H.d.L.; supervision, H.E.K. and N.H.d.L. All authors have read and agreed to the published version of the manuscript.
Funding
The authors acknowledge the NWO ECHO grant (712.018.005) for funding A.Ž. The Olaf Schuilings Fond at Utrecht University provided funding for the purchase of the 18O-enriched water used to synthesize the calcium carbonates as part of another research project conducted by MSc student L. Hemerijckx.
Acknowledgments
All experiments and analyses were performed within the Faculty of Geoscience laboratory facilities at Utrecht University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Skinner, H.B.C.W. Biominerals. Mineral. Mag. 2005, 69, 621–641. [Google Scholar] [CrossRef]
- Hubbe, M.A.; Gill, R.A. Fillers for Papermaking: A Review of their Properties, Usage Practices, and their Mechanistic Role. Bio. Resources 2016, 11, 2886–2963. [Google Scholar] [CrossRef]
- Holtus, T.; Helmbrecht, L.; Hendrikse, H.C.; Baglai, I.; Meuret, S.; Adhyaksa, G.W.P.; Garnett, E.C.; Noorduin, W.L. Shape-preserving transformation of carbonate minerals into lead halide perovskite semiconductors based on ion exchange/insertion reactions. Nat. Chem. 2018, 10, 740–745. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Navarro, C.; Kudłacz, K.; Cizer, Ö.; Ruiz-Agudo, E. Formation of amorphous calcium carbonate and its transformation into mesostructured calcite. Cryst. Eng. Comm. 2015, 17, 58–72. [Google Scholar] [CrossRef]
- Weiner, S.; Levi-Kalisman, Y.; Raz, S.; Addadi, L. Biologically Formed Amorphous Calcium Carbonate. Connect. Tissue Res. 2003, 44, 214–218. [Google Scholar] [CrossRef]
- Perdikouri, C.; Kasioptas, A.; Geisler, T.; Schmidt, B.C.; Putnis, A. Experimental study of the aragonite to calcite transition in aqueous solution. Geochim. Cosmochim. Acta 2011, 75, 6211–6224. [Google Scholar] [CrossRef]
- King, H.E.; Mattner, D.C.; Plümper, O.; Geisler, T.; Putnis, A. Forming Cohesive Calcium Oxalate Layers on Marble Surfaces for Stone Conservation. Cryst. Growth Des. 2014, 14, 3910–3917. [Google Scholar] [CrossRef]
- Kasioptas, A.; Geisler, T.; Perdikouri, C.; Trepmann, C.; Gussone, N.; Putnis, A. Polycrystalline apatite synthesized by hydrothermal replacement of calcium carbonates. Geochim. Cosmochim. Acta 2011, 75, 3486–3500. [Google Scholar] [CrossRef]
- Jonas, L.; John, T.; King, H.E.; Geisler, T.; Putnis, A. The role of grain boundaries and transient porosity in rocks as fluid pathways for reaction front propagation. Earth Planet. Sci. Lett. 2014, 386, 64–74. [Google Scholar] [CrossRef]
- King, H.E.; Plumper, O.; Geisler, T.; Putnis, A. Experimental investigations into the silicification of olivine: Implications for the reaction mechanism and acid neutralization. Am. Mineral. 2011, 96, 1503–1511. [Google Scholar] [CrossRef]
- Ruiz-Agudo, E.; King, H.E.; Luis, D.; Putnis, C.V.; Geisler, T.; Carlos, R.-N.; Putnis, A. Control of silicate weathering by interface-coupled dissolution-precipitation processes at the mineral-solution interface. Geology 2016, 44, 567–570. [Google Scholar] [CrossRef]
- Xu, B.; Hirsch, A.; Kronik, L.; Poduska, K.M. Vibrational properties of isotopically enriched materials: The case of calcite. RSC Adv. 2018, 8, 33985–33992. [Google Scholar] [CrossRef]
- Gillet, P.; McMillan, P.; Schott, J.; Badro, J.; Grzechnik, A. Thermodynamic properties and isotopic fractionation of calcite from vibrational spectroscopy of 18O-substituted calcite. Geochim. Cosmochim. Acta 1996, 60, 3471–3485. [Google Scholar] [CrossRef]
- Prencipe, M.; Pascale, F.; Zicovich-Wilson, C.M.; Saunders, V.R.; Orlando, R.; Dovesi, R. The vibrational spectrum of calcite (CaCO3): An ab initio quantum-mechanical calculation. Phys. Chem. Miner. 2004, 31, 559–564. [Google Scholar] [CrossRef]
- De La Pierre, M.; Carteret, C.; Maschio, L.; André, E.; Orlando, R.; Dovesi, R. The Raman spectrum of CaCO3 polymorphs calcite and aragonite: A combined experimental and computational study. J. Chem. Phys. 2014, 140, 164509. [Google Scholar] [CrossRef]
- De La Pierre, M.; Demichelis, R.; Wehrmeister, U.; Jacob, D.E.; Raiteri, P.; Gale, J.D.; Orlando, R. Probing the multiple structures of vaterite through combined computational and experimental Raman spectroscopy. J. Phys. Chem. C 2014, 118, 27493–27501. [Google Scholar] [CrossRef]
- Ihli, J.; Wong, W.C.; Noel, E.H.; Kim, Y.-Y.; Kulak, A.N.; Christenson, H.K.; Duer, M.J.; Meldrum, F.C. Dehydration and crystallization of amorphous calcium carbonate in solution and in air. Nat. Commun. 2014, 5, 3169. [Google Scholar] [CrossRef]
- Geisler, T.; Perdikouri, C.; Kasioptas, A.; Dietzel, M. Real-time monitoring of the overall exchange of oxygen isotopes between aqueous and H2O by Raman spectroscopy. Geochim. Cosmochim. Acta 2012, 90, 1–11. [Google Scholar] [CrossRef]
- Dovesi, R.; Saunders, V.R.; Roetti, C.; Orlando, R.; Zicovich-Wilson, C.M.; Pascale, F.; Civalleri, B.; Doll, K.; Harrison, N.M.; Bush, I.J.; et al. CRYSTAL17 User’s Manual; 2017. [Google Scholar]
- Dovesi, R.; Erba, A.; Orlando, R.; Zicovich-Wilson, C.M.; Civalleri, B.; Maschio, L.; Rérat, M.; Casassa, S.; Baima, J.; Salustro, S.; et al. Quantum-mechanical condensed matter simulations with CRYSTAL. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2018, 8, 1–36. [Google Scholar] [CrossRef]
- Valenzano, L.; Torres, F.J.; Doll, K.; Pascale, F.; Zicovich-Wilson, C.M.; Dovesi, R. Ab Initio Study of the Vibrational Spectrum and Related Properties of Crystalline Compounds; the Case of CaCO3 Calcite. Z. Phys. Chem. 2006, 220, 893–912. [Google Scholar] [CrossRef]
- Becke, A.D. A new mixing of Hartree–Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed]
- Graf, D.L. Crystallographic tables for the rhombohedral carbonates. Am. Mineral. J. Earth Planet. Mat 1961, 46, 1283–1316. [Google Scholar]
- Christy, A.G. A Review of the Structures of Vaterite: The Impossible, the Possible, and the Likely. Cryst. Growth Des. 2017, 17, 3567–3578. [Google Scholar] [CrossRef]
- Demichelis, R.; Raiteri, P.; Gale, J.D.; Dovesi, R. The Multiple Structures of Vaterite. Cryst. Growth Des. 2013, 13, 2247–2251. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Maschio, L.; Kirtman, B.; Orlando, R.; Rèrat, M. Ab initio analytical infrared intensities for periodic systems through a coupled perturbed Hartree-Fock/Kohn-Sham method. J. Chem. Phys. 2012, 137, 204113. [Google Scholar] [CrossRef]
- Maschio, L.; Kirtman, B.; Rérat, M.; Orlando, R.; Dovesi, R. Ab initio analytical Raman intensities for periodic systems through a coupled perturbed Hartree-Fock/Kohn-Sham method in an atomic orbital basis. II. Validation and comparison with experiments. J. Chem. Phys. 2013, 139, 164102. [Google Scholar] [CrossRef]
- Maschio, L.; Kirtman, B.; Rérat, M.; Orlando, R.; Dovesi, R. Ab initio analytical Raman intensities for periodic systems through a coupled perturbed Hartree-Fock/Kohn-Sham method in an atomic orbital basis. I. Theory. J. Chem. Phys. 2013, 139, 164101. [Google Scholar] [CrossRef]
- Wehrmeister, U.; Soldati, A.L.; Jacob, D.E.; Häger, T.; Hofmeister, W. Raman spectroscopy of synthetic, geological and biological vaterite: A Raman spectroscopic study. J. Raman Spectrosc. 2010, 41, 193–201. [Google Scholar] [CrossRef]
- Watkins, J.M.; Nielsen, L.C.; Ryerson, F.J.; De Paolo, D.J. The influence of kinetics on the oxygen isotope composition of calcium carbonate. Earth Planet. Sci. Lett. 2013, 375, 349–360. [Google Scholar] [CrossRef]
- Wojdyr, M. Fityk: A general-purpose peak fitting program. J. Appl. Crystallogr. 2010, 43, 1126–1128. [Google Scholar] [CrossRef]
- Andersen, F.A.; Brecevic, L. Infrared spectra of amorphous and crystalline calcium carbonate. Acta Chem. Scand. 1991, 45, 1018–1024. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).