Comparison of Structural, Microstructural, Elastic, and Microplastic Properties of the AAAC (A50) and ACSR (AC50/8) Cables after Various Operation Periods in Power Transmission Lines
Abstract
1. Introduction
2. Materials and Methods
2.1. Samples
2.2. Experimental Details of Measurements and Analysis
2.2.1. Experimental Details of EDX, SEM, and EBSD
2.2.2. Experimental Details of Densitometric Measurements
2.2.3. Experimental Details of XRD Measurements and Analysis
2.2.4. Experimental Details of Acoustic Measurements
3. Results
3.1. SEM and EDX Results
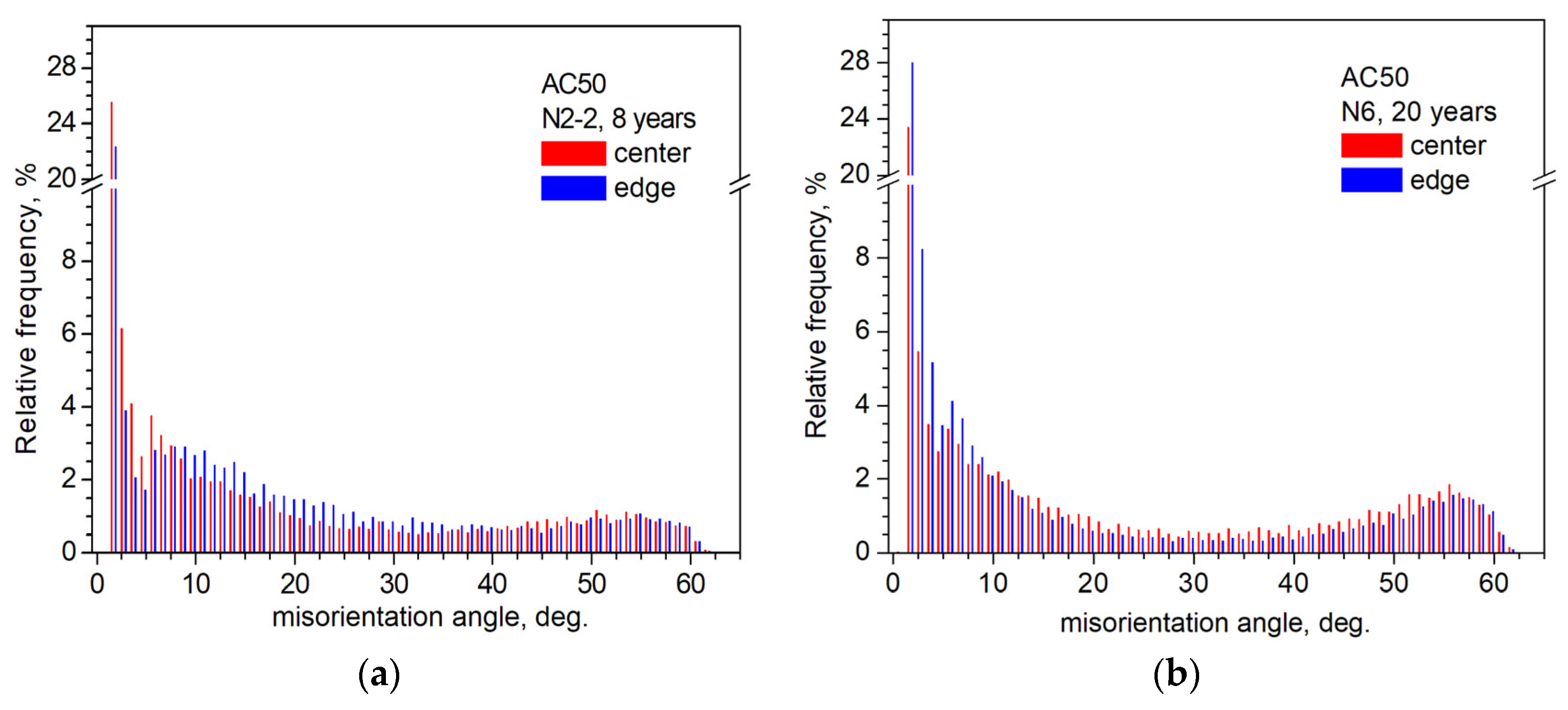
3.2. EBSD Results
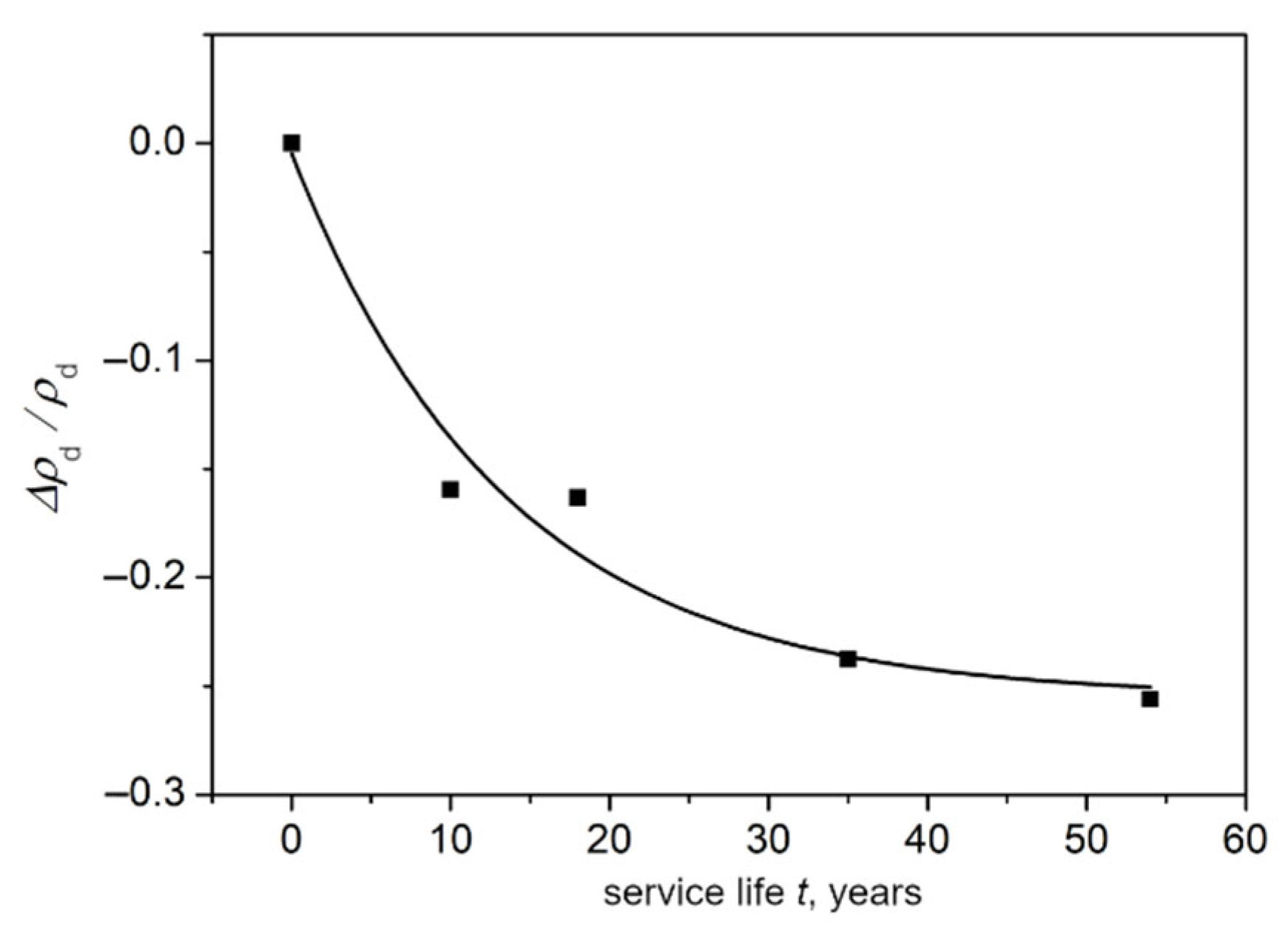
3.3. Results of Densitometric Measurements
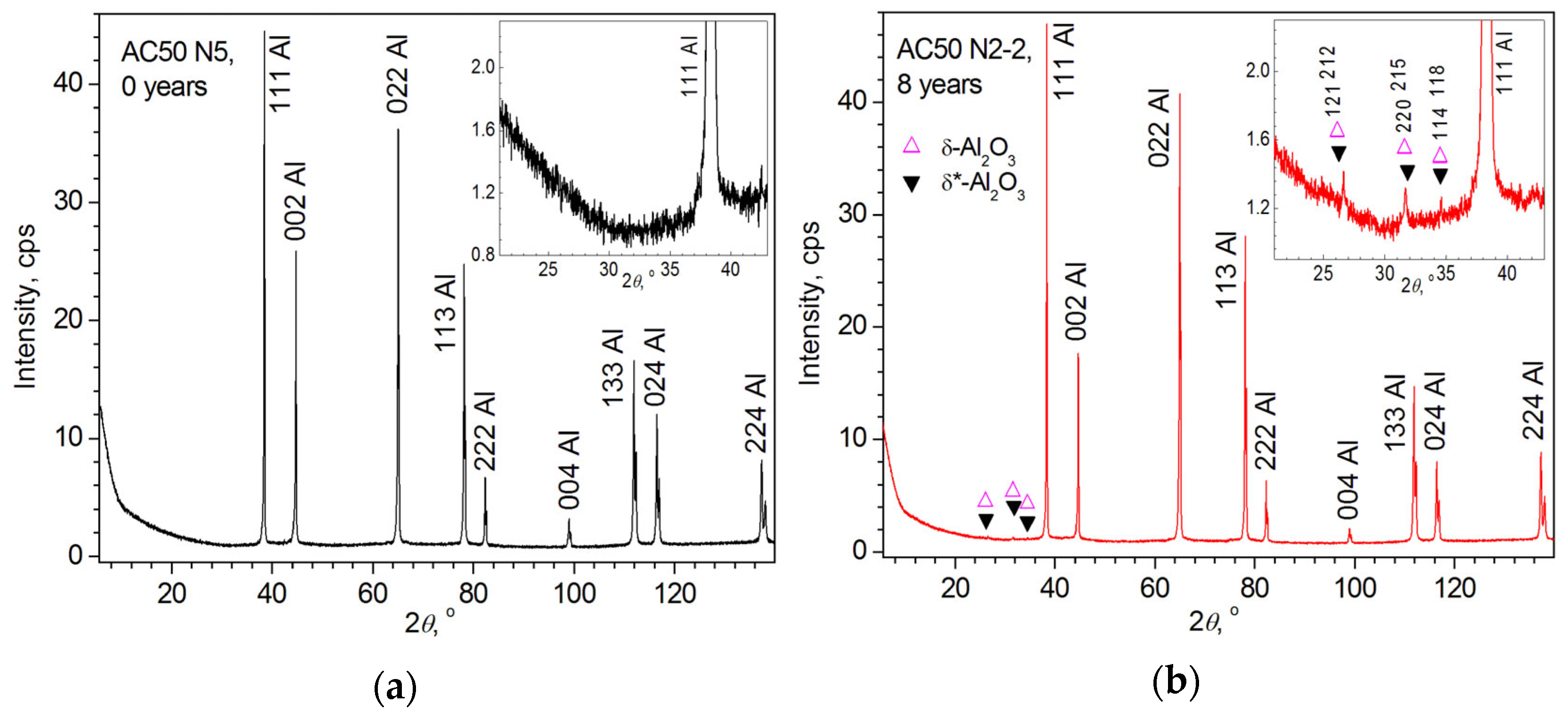
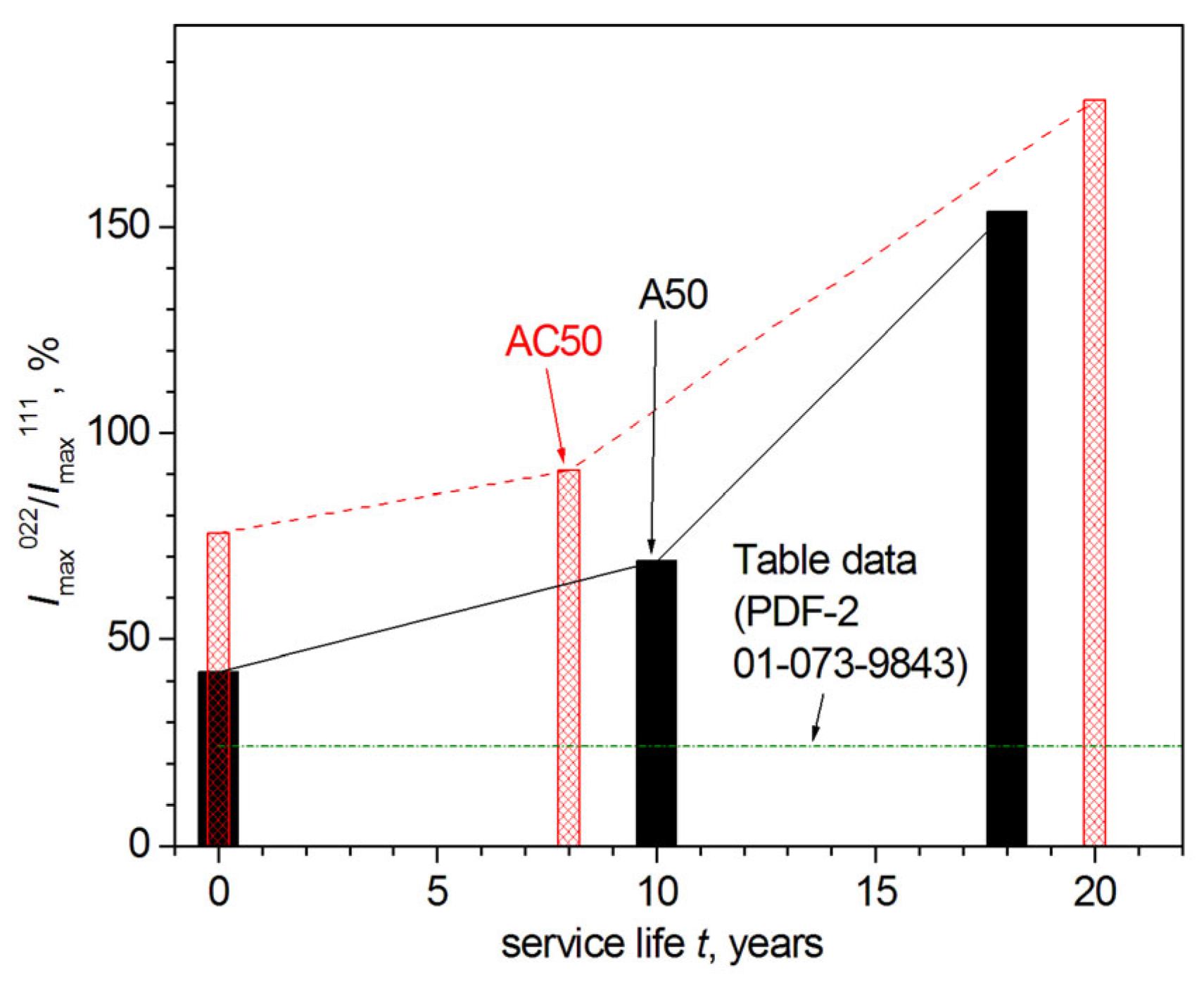
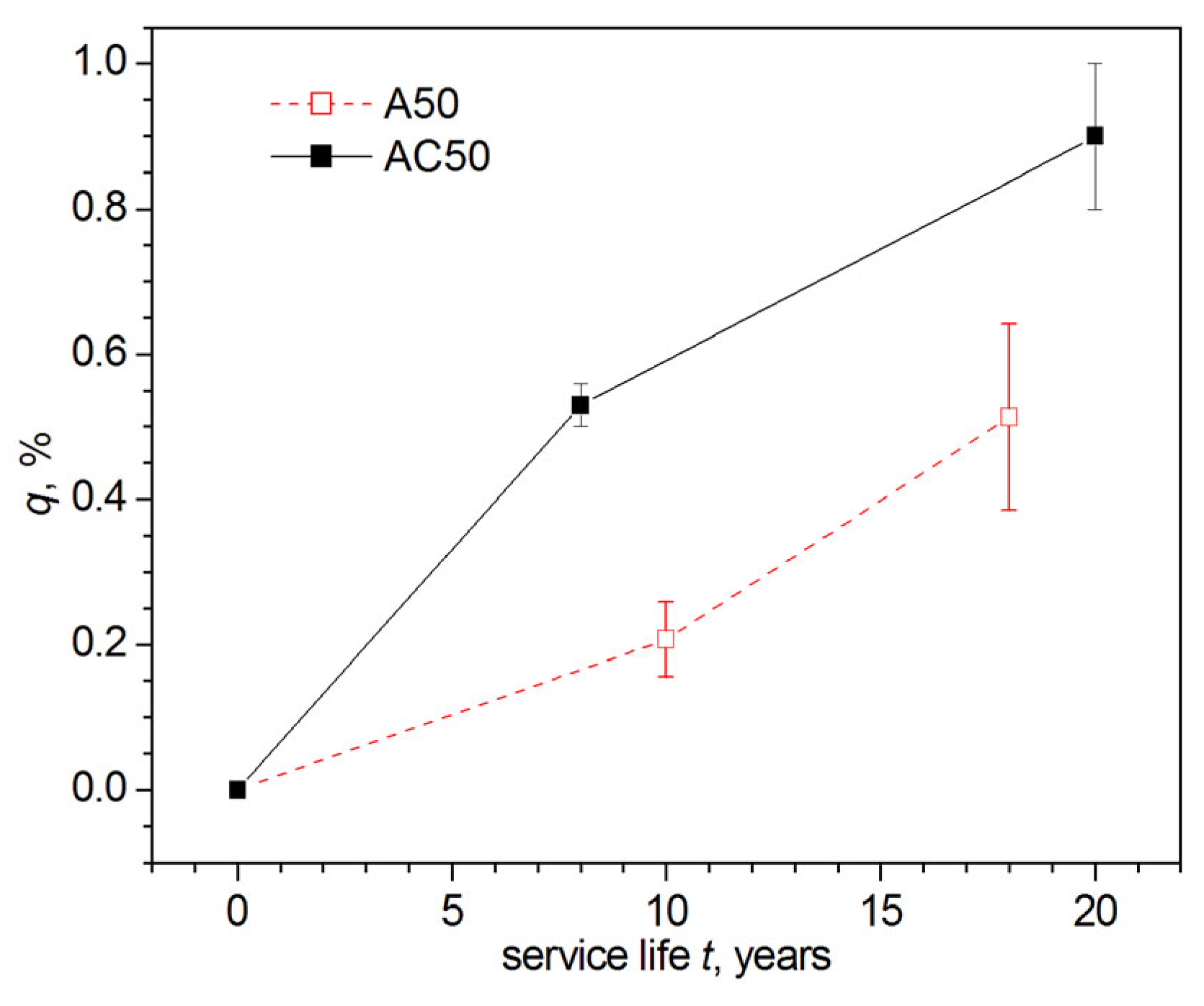
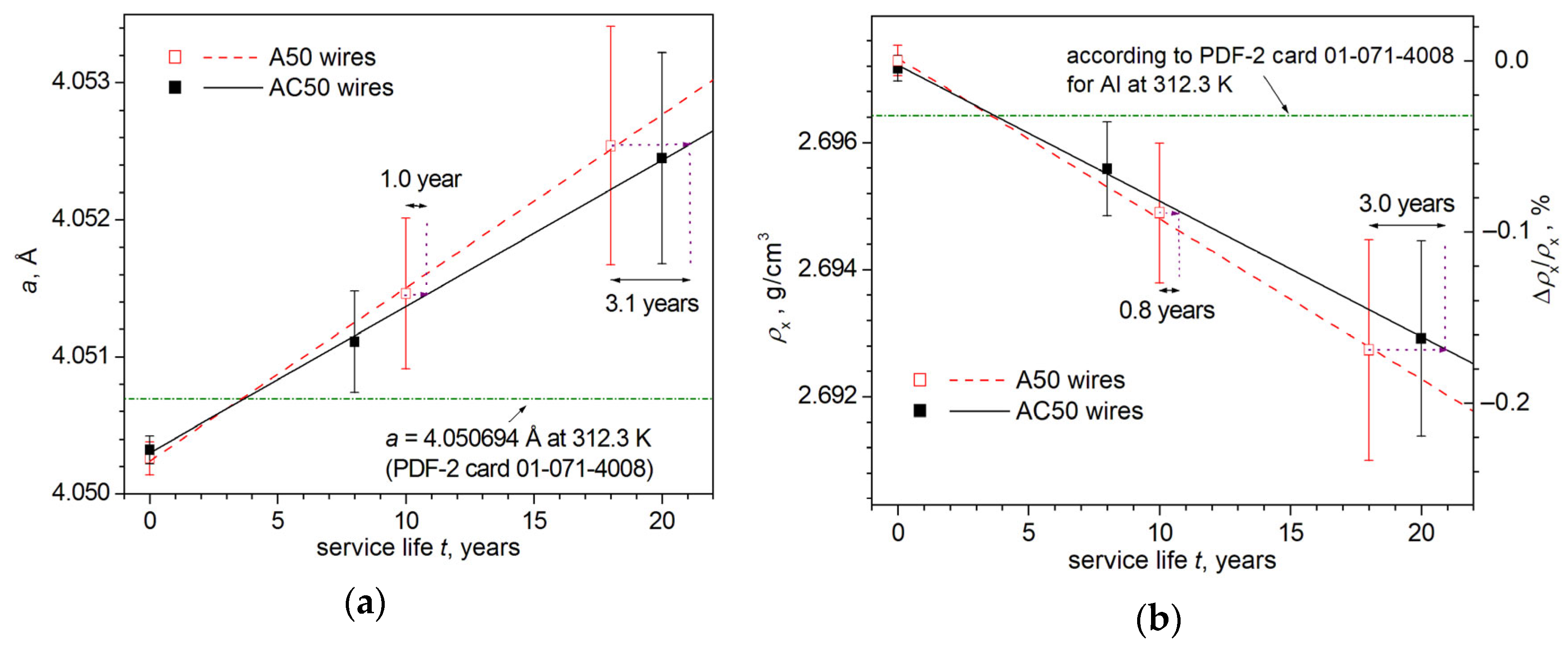
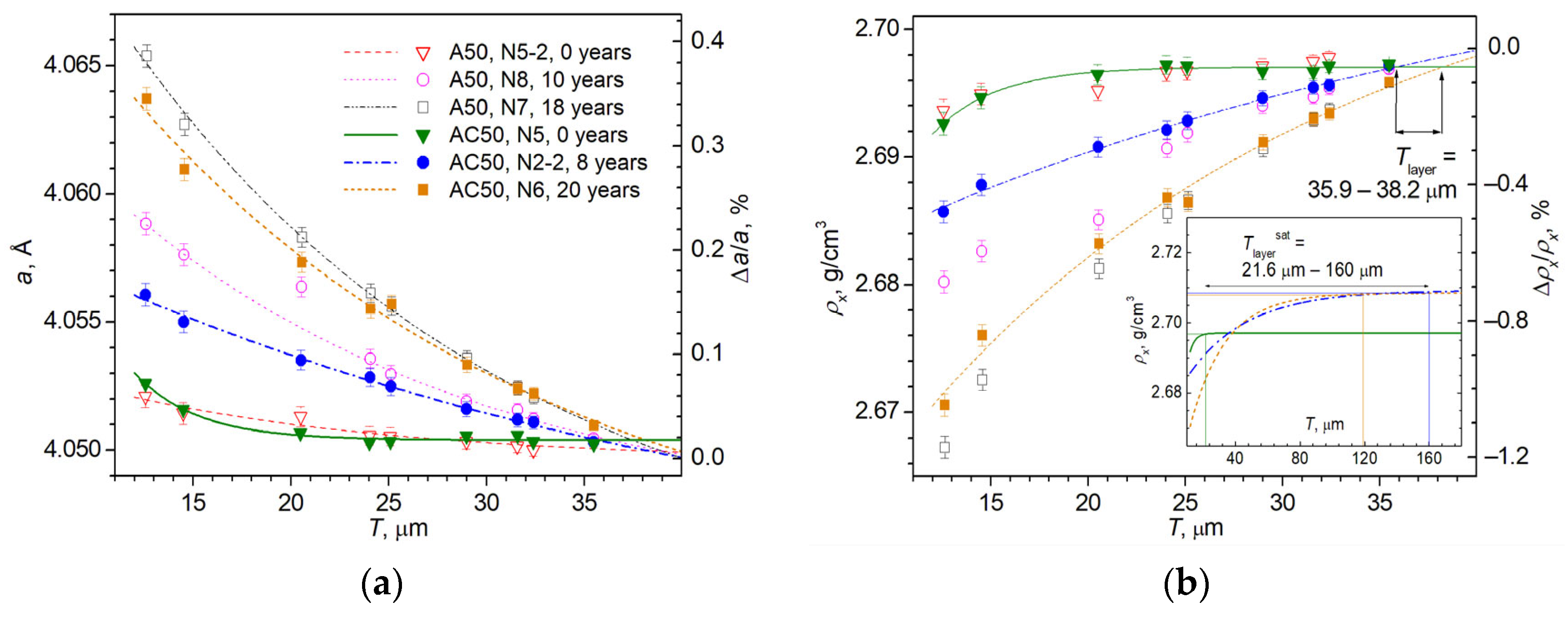
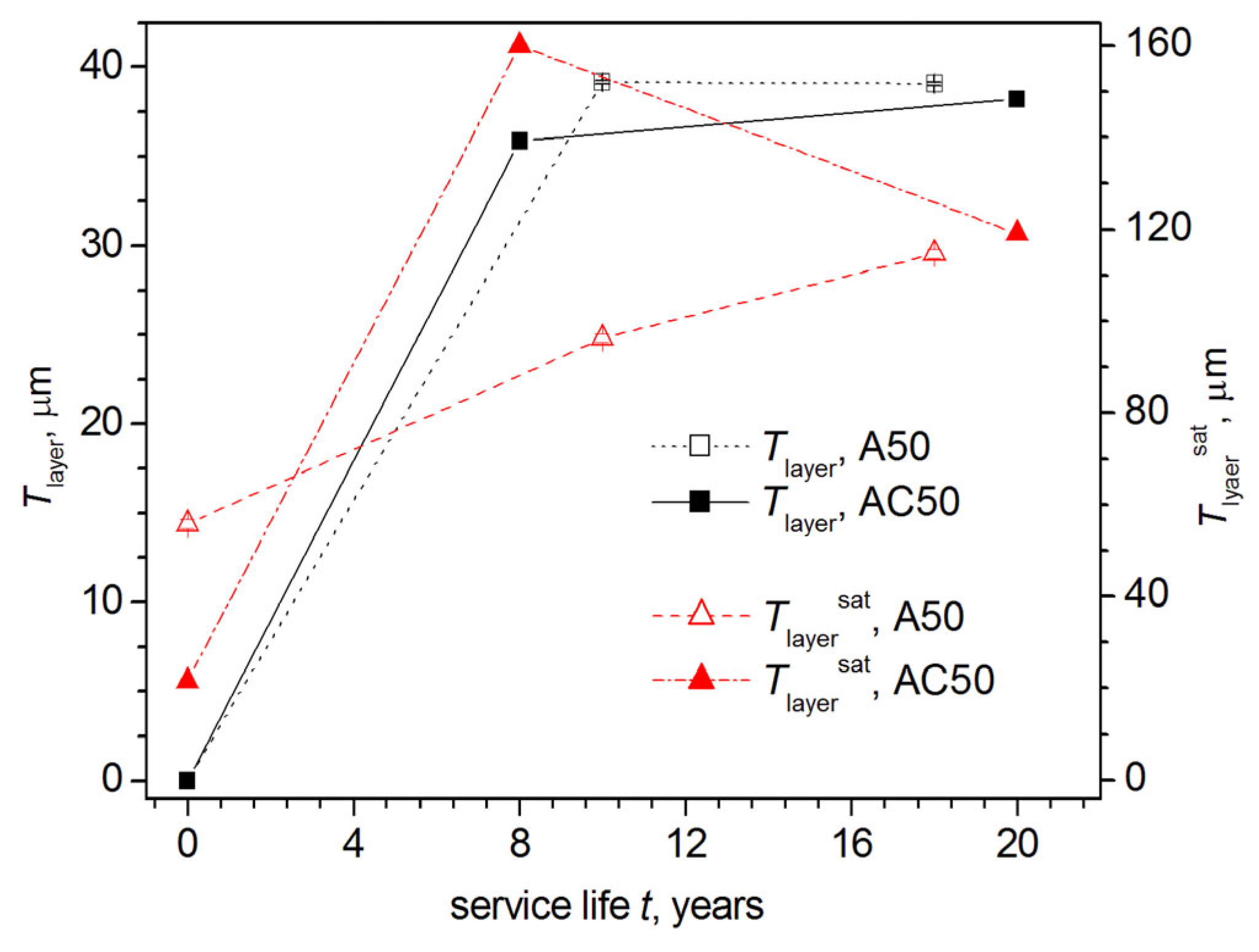
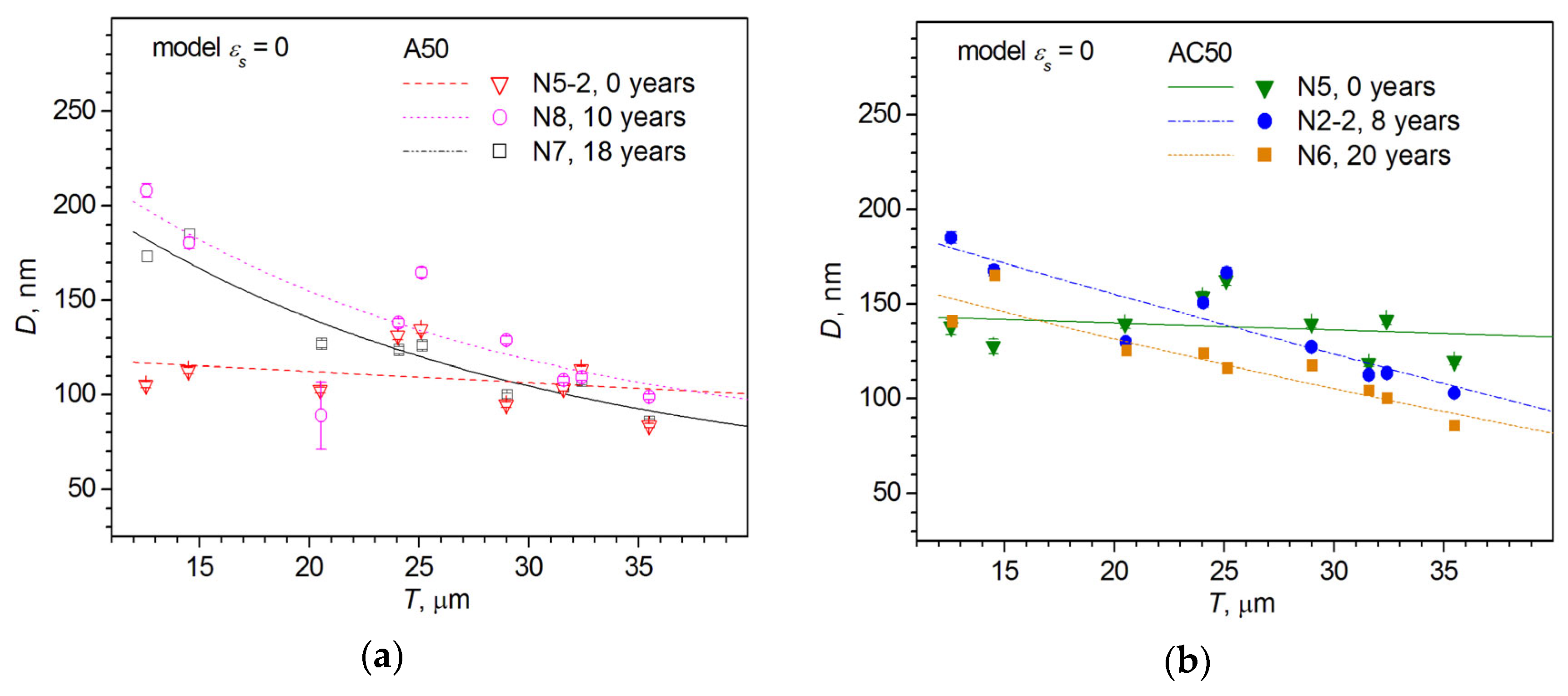
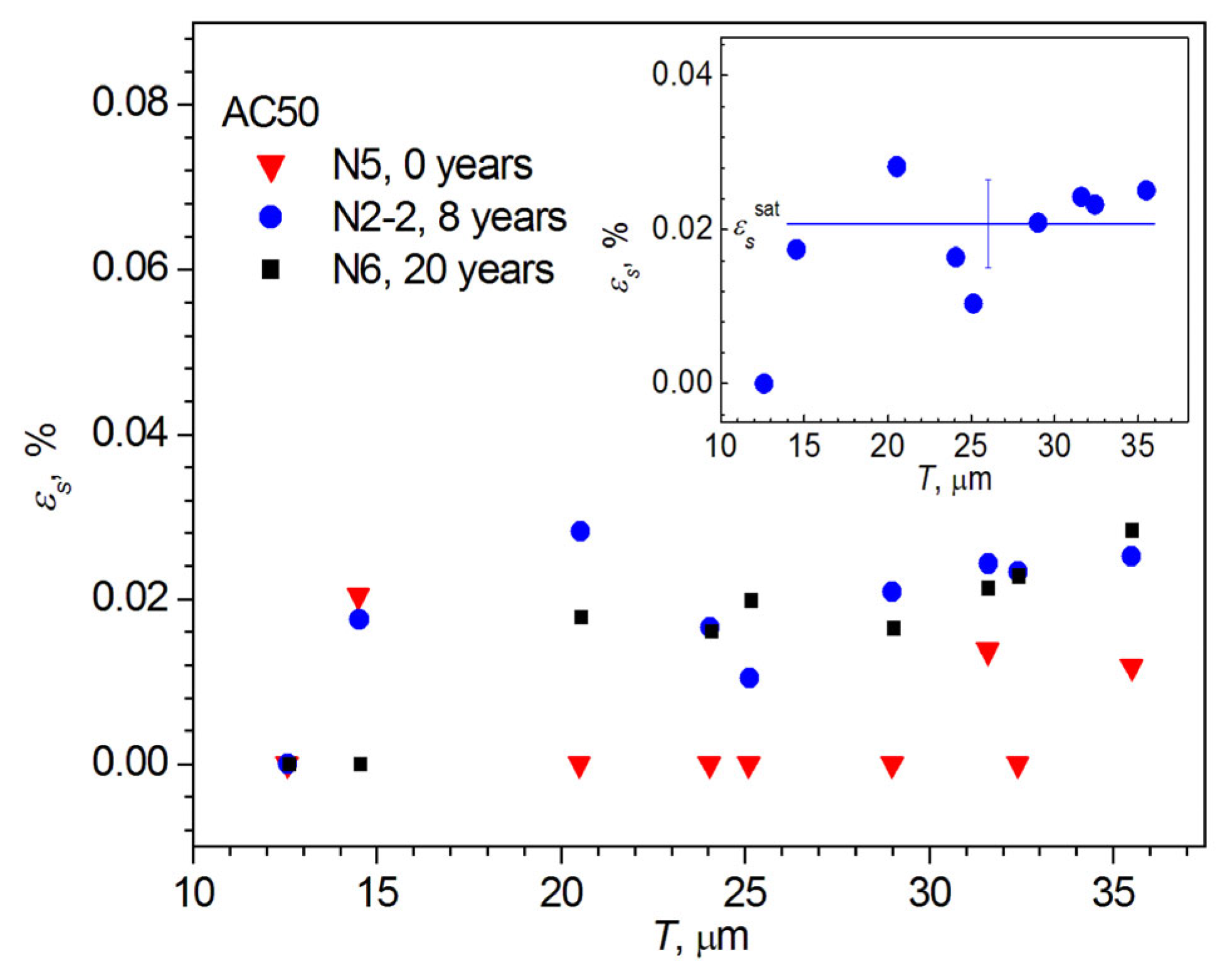
3.4. Results of XRD Investigations
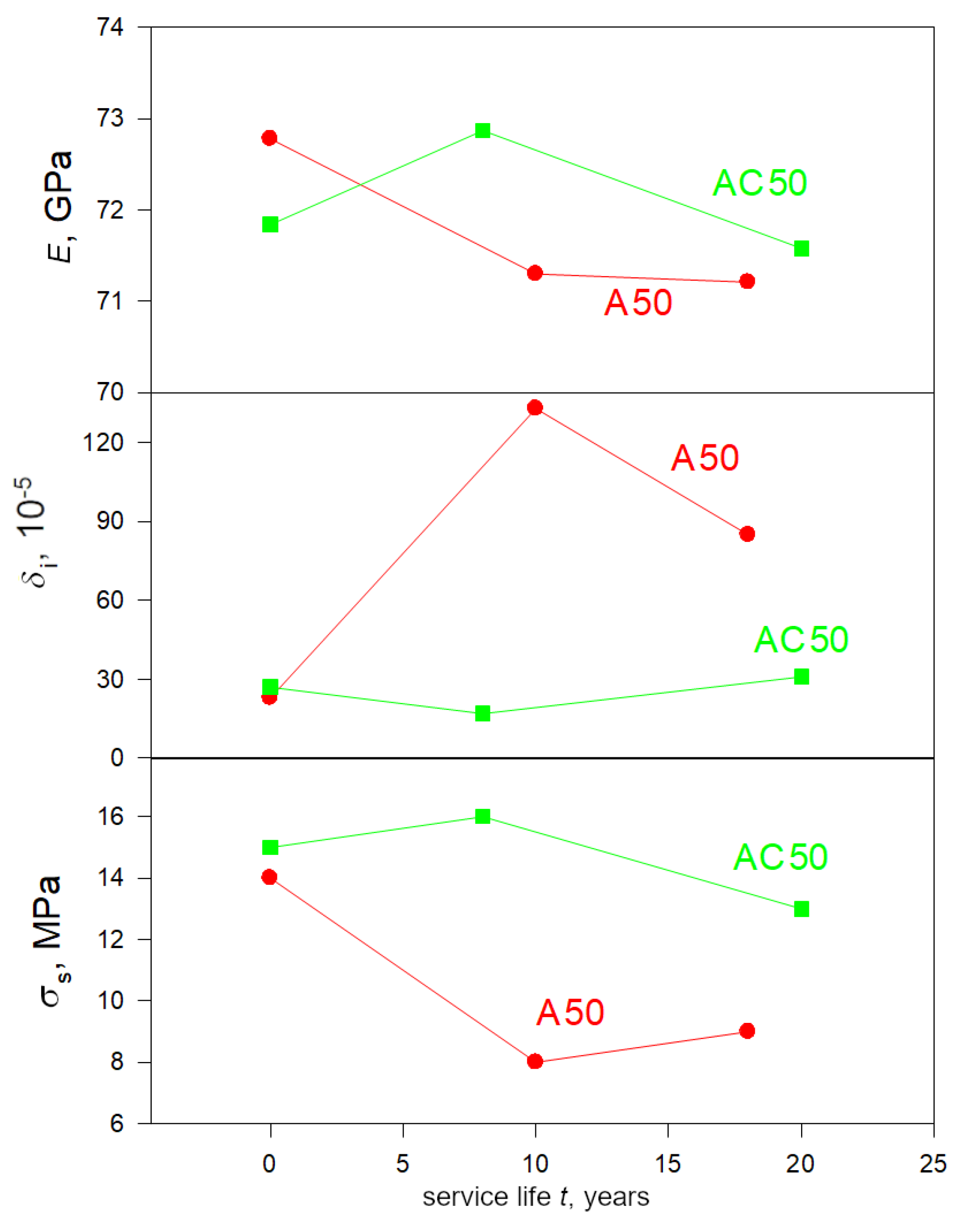
3.5. Results of Acoustic Studies
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| A50 | AAAC cable with an Al conductor cross-section of 49.5 mm2 |
| A7E | grade of cold-drawn aluminum according to GOST |
| AAAC | all aluminum alloy aonductor |
| AC50 (AC50/8) | ACSR cable with Al conductor cross-section of ~50 mm2 and ~8 mm2 cross-section of steel core |
| ACSR | aluminum conductor steel reinforced |
| a.m.u. | atomic mass unit |
| EBSD | electron backscattering diffraction |
| EDX | energy dispersive X-ray microanalysis |
| e.s.d., e.s.d.s. | estimated standard deviation(s) |
| FWHM | full width at half-maximum of XRD reflection |
| GOST | interstate technical standard |
| NSDL, NSDLs | near-surface defect layer(s) |
| PDF-2 | Powder Diffraction File-2 |
| pV | pseudo-Voigt |
| Ref., Refs. | Reference(s) |
| SEM | scanning electron microscopy |
| SSP | size-strain plot |
| SM | Supplementary Materials |
| WHP | Williamson–Hall plot |
| XRD | X-ray diffraction |
| e.g., | Latin” exempli gratia” (for example) |
| i.e., | Latin “id est” (that is) |
| etc. | Latin “et cetera” (and so on) |
| cf. | Latin “confer” (compare) |
| 2θ | diffraction angle |
| 2θB | Bragg angle of XRD reflection corrected to angular corrections (zero shift Δ2θzero and displacement Δ2θdispl) |
| 2θobs | observed Bragg angle of XRD reflection |
| Ar | tabular value of the atomic mass of aluminium |
| a | cubic unit cell parameter of Al |
| a0 | parameter of the Al cubic unit cell in the bulk of a new (0 years of service) wire |
| abulk | parameter of the Al cubic unit cell in the bulk of wire of non-zero service life |
| Bint | integral width of XRD reflection |
| Ca.m.u. | conversion factor of a.m.u. into gram |
| D | average size of crystallites |
| D0 | mean square root value of crystallite size after averaging the Dhkl0 values over all reflections in framework of model with absence of microstrains (εs = 0) |
| Dhkl | size of crystallite corresponding to XRD reflection with Miller indices hkl |
| Dhkl0 | size of crystallite corresponding to XRD reflection with Miller indices hkl in framework of model with absence of microstrains (εs = 0) |
| E | Young’s modulus (modulus of elasticity, elastic modulus) |
| Ei | amplitude-independent Young’s modulus |
| f | oscillation frequency of wire-samples |
| FWHMcorr | FWHMobs corrected for instrumental broadening |
| FWHMobs | observed full width at half-maximum of XRD reflection |
| hkl | Miller indices of XRD reflection |
| [hkl] | Miller indices of crystallographic direction |
| KScherrer | coefficient in Scherrer equation |
| Kstrain | coefficient in Wilson–Stokes equation |
| Imax | maximum intensity of XRD reflection |
| Imax022, Imax111, Imax002 | maximum intensitie of XRD reflection with Miller indices 022, 111, and 002, respectively |
| Iint | integral intensity of XRD reflection |
| IintAl | integral intensity of the strongest Al reflection |
| IintAl2O3 | integral intensity of the 121 δ*-(212 δ-) Al2O3 reflection |
| l | wire-sample length |
| m0 | mass of the sample before polishing (etching) |
| mi | mass of the sample after polishing of the ith layer |
| N5, N5-1, etc. | Number 5, Number 5-1, etc. |
| p | a parameter of wire Al material (unit cell parameter a or X-ray mass density ρx) |
| p0 | a bulk parameter of Al material of a new (0 years of service) wire (unit cell parameter a0 or X-ray mass density ρx) |
| q | fraction of the Al2O3 crystalline phases in wires |
| R0 | radius of the wire-sample in the form of a cylindrical rod (before polishing (etching)) |
| t | service life duration |
| T | depth from the wire surface or or penetratiun depth or temperature (in dependence on context) |
| Tetch | thickness of the layer removed by polishing (etching) |
| Tlayer | layer thickness corresponding to depth where ~70% of the decrease in the mass density ρx occurs in comparison to the ρx200μm value |
| Tlayersat | layer thickness corresponding to depth where ~99% of the decrease in the mass density ρx occurs in comparison to the ρx200μm value |
| penetration depth of X-ray radiation, corresponding to XRD reflection with Miller indices hkl | |
| Vcell | volume of the Al cubic unit cell |
| Z | number of formula units in the Al unit cell |
| Δ2θdispl | displacement correction |
| Δ2θstep | 2θ step of XRD scanning |
| Δ2θzero | correcting shift of the zero of the counter |
| Δa/a | defect (relative change) of the unit cell parameter a |
| (ΔE/E)h | amplitude-dependent Young’s modulus defect (amplitude-dependent variation of E) |
| Δρd/ρd | defect (relative change) of the mass density ρd |
| ΔρdL/ρdL | density defect value of the etched layer |
| Δρx/ρx | defect (relative change) of the mass density ρx |
| δ | (logarithmic) decrement of the sample material ((logarithmic) decrement of elastic vibrations) |
| δ2θB | e.s.d. of Bragg angle 2θB |
| δρd/ρd | relative error of integral density ρd |
| δa | e.s.d. of the Al cubic unit cell parameter a |
| δi | amplitude-independent part of the logarithmic decrement δ (amplitude-independent decrement of elastic vibrations) |
| ε | vibrational strain amplitude (vibrational deformation) |
| εd | non-linear inelastic strain (non-linear inelastic deformation) |
| εs | absolute value of average magnitude of microstrains |
| εshkl | absolute value of microstrain corresponding to XRD reflection with Miller inices hkl |
| εssat | average microstrain εssat in the NSDL at depths T ≥ 15 μm if the crystallite size is fixed and equal to the crystallite size at a depth of T ~12.5 μm |
| θ | half a diffraction angle |
| θB | half a Bragg angle of XRD reflection 2θB |
| λ | wavelength of Cu-Kα1 radiation (after correction of Cu-Kα2 contribution) |
| μl | the linear mass absorption coefficient of material |
| ρ | mass density |
| ρd | mass density of material measured by densitometry technique (‘densitometric density‘, ’integral density’) |
| ρd0 | density of a sample before polishing (etching) measured by densitometry technique |
| ρdi | density of a sample after polishing (etching) of the ith layer measured by densitometry technique |
| ρdL | mass density of the etched layer obtained by densitometry technique |
| ρx | mass density of material calculated according to XRD structural data (‘XRD density’, ‘X-ray density’) |
| ρx12.5μm | XRD mass density at depth of 12.5 μm from the surface |
| ρx200μm | XRD mass density at depth of 200 μm from the surface |
| ρxbulk | XRD mass density in the bulk of the wire-sample |
| ρxTlayer | XRD mass density of Al material at a depth of Tlayer |
| ρxsat | XRD mass density of Al material at a depth of Tlayersat |
| ρx0 | XRD density in the bulk of a new (0 years of service) Al wire |
| ρx 0 years | mean density of the A50 wire N5-2 (service life of 0 years) |
| σ | amplitude of vibrational stress (microplastic deformation, microplastic stress) |
| σs | microplastic flow stress (microplastic stress, micro-flow stress) equal to σ at inelastic strain εd = 5.0 × 10−8 |
| Φ | Euler angle (angle of nutation) |
| φ1 | Euler angle (angle of intrinsic rotation) |
| φ2 | Euler angle (angle of precession) |
References
- Nakhimova, L.I. (Ed.) GOST 839-2019. Non-Insulated Conductors for Overhead Power Lines. Specifications; Strojizdat: Moscow, Russia, 2019. (In Russian) [Google Scholar]
- Karabay, S.; Ertürk, A.T.; Zeren, M.; Yamanoğlu, R.; Karakulak, E. Failure analysis of wire-breaks in aluminum conductor production and investigation of early failure reasons for transmission lines. Eng. Fail. Anal. 2018, 83, 47–56. [Google Scholar] [CrossRef]
- Karabay, S.; Feyzullahoğlu, E. Determination of early failure sources and mechanisms for Al 99.7% and Al–Mg–Si alloy bare conductors used in aerial transmission line. Eng. Fail. Anal. 2014, 38, 1–15. [Google Scholar] [CrossRef]
- Betekhtin, V.I.; Sklenicka, V.; Kadomtsev, A.G.; Kolobov, Y.R.; Narykova, M.V. Defect Structure and Thermomechanical Stability of Nano- and Microcrystalline Titanium Obtained by Different Methods of Intense Plastic Deformation. Phys. Solid State 2017, 59, 960–966. [Google Scholar] [CrossRef]
- Betekhtin, V.I.; Kadomtsev, A.G.; Narykova, M.V. Evolution of a Defect Structure during Creep Tests of Ultrafine-Grained Metals and Alloys Produced by Severe Plastic Deformation. Phys. Solid State 2020, 62, 318–324. [Google Scholar] [CrossRef]
- Brettschneider, S.; Fofana, I. Evolution of Countermeasures against Atmospheric Icing of Power Lines over the Past Four Decades and Their Applications into Field Operations. Energies 2021, 14, 6291. [Google Scholar] [CrossRef]
- Lu, J.; Hu, J.; Fang, Z.; Qiao, X.; Zhang, Z. Electric Field Distribution and AC Breakdown Characteristics of Polluted Novel Lightning Protection Insulator under Icing Conditions. Energies 2021, 14, 7493. [Google Scholar] [CrossRef]
- Zhou, Z.R.; Cardou, A.; Goudreau, S.; Fiset, M. Fundamental investigations of electrical conductor fretting fatigue. Tribol. Int. 1996, 29, 221–232. [Google Scholar] [CrossRef]
- Azevedo, C.R.F.; Cescon, T. Failure analysis of aluminum cable steel reinforced (ACSR) conductor of the transmission line 1232 crossing the Parana River. Eng. Fail. Anal. 2002, 9, 645–664. [Google Scholar] [CrossRef]
- Narykova, M.V.; Levin, A.A.; Prasolov, N.D.; Lihachev, A.I.; Kardashev, B.K.; Kadomtsev, A.G.; Panfilov, A.G.; Sokolov, R.V.; Brunkov, P.N.; Sultanov, M.M.; et al. The structure of the near-surface layer of the AAAC overhead power line wires after operation and its effect on their elastic, microplastic, and electroresistance properties. Crystals 2022, 12, 166. [Google Scholar] [CrossRef]
- Kalombo, R.B.; Araujo, J.A.; Ferreira, J.L.A.; da Silva, C.R.M.; Alencar, R.; Capra, A.R. Assessment of the fatigue failure of an All Aluminium Alloy Cable (AAAC) for a 230 kV transmission line in the Center-West of Brazil. Eng. Fail. Anal. 2015, 61, 77–87. [Google Scholar] [CrossRef]
- Matos, I.M.; Rocha, P.H.C.; Kalombo, R.B.; Veloso, L.A.C.M.; Araujo, J.A.; Castro, F.C. Fretting fatigue of 6201 aluminum alloy wires of overhead conductors. Int. J. Fatique 2020, 141, 105884. [Google Scholar] [CrossRef]
- Kalombo, R.B.; Martínez, J.M.G.; Ferreira, J.L.A.; da Silva, C.R.M.; Araújo, J.A. Comparative fatigue resistance of overhead 1222 conductors made of aluminium and aluminium alloy: Tests and analysis. Proc. Eng. 2015, 133, 223–232. [Google Scholar] [CrossRef]
- Kalombo, R.B.; Pestana, M.S.; Freire, R.C.S.; Ferreira, J.L.A.; da Silva, C.R.M.; Veloso, L.A.C.M.; Camara, E.C.B.; Araujo, J.A. Fatigue life estimation of an all aluminium alloy 1055 MCM conductor for different mean stresses using an artificial neural network. Int. J. Fatique 2020, 140, 105814. [Google Scholar] [CrossRef]
- Lévesque, F.; Goudreau, S.; Cardou, A.; Cloutier, L. Strain Measurements on ACSR Conductors During Fatigue Tests I—Experimental Method and Data. IEEE Trans. Power Deliv. 2010, 25, 2825–2834. [Google Scholar] [CrossRef]
- Rocha, P.H.C.; Díaz, J.I.M.; Silva, C.R.M.; Araújo, J.A.; Castro. F., C. Fatigue of two contacting wires of the ACSR Ibis 397.5 MCM conductor: Experiments and life prediction. Int. J. Fatique 2019, 127, 25–35. [Google Scholar] [CrossRef]
- Kreislova, K.; Jaglova, M.; Turek, L.; Koukalova, A. Evaluation of corrosion of long-term exposed aluminium conductor. Koroze a Ochrana Materiálu 2013, 57, 25–34. [Google Scholar] [CrossRef][Green Version]
- De Araujo, M.M.; Manheimmer, W.A.; Serra, E. Corrosion aspects in aluminum electrical conductors. Mater. Sci. 1988, 8, 175–197. [Google Scholar] [CrossRef]
- De la Fuente, D.; Otero-Huerta, E.; Morcillo, M. Studies of long-term weathering of aluminium in the atmosphere. Corros. Sci. 2007, 49, 3134–3148. [Google Scholar] [CrossRef]
- Vargel, C. Corrosion of Aluminium, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar] [CrossRef]
- Sawada, S. Corrosion and overhead aluminum conductors and the prevention of it. Smitomo Electr. Tech. Rev. 1968, 11, 22–32. [Google Scholar]
- Graedel, E. Corrosion mechanism for aluminum exposed to the atmosphere. J. Electrochem. Soc. 1989, 136, 204C–212C. [Google Scholar] [CrossRef]
- Isozaki, M.; Adachi, K.; Hita, T.; Asano, Y. Study of corrosion resistance improvement by metallic coating for overhead transmission line conductor. Electr. Eng. Jpn. 2008, 163, 41–47. [Google Scholar] [CrossRef]
- Harvard, D.G.; Bellamy, G.; Buchan, P.G.; Ewing, H.A.; Horrocks, D.J.; Krishnasamy, S.G.; Motlis, J.; Yoshiki-Gravelsins, K.S. Aged ACSR conductors. I. Testing procedures for conductors and line items. IEEE Trans. Power Deliv. 1992, 7, 581–587. [Google Scholar] [CrossRef]
- Deng, Y.J.; Yu, J.C.; Xia, K.Q.; Yang, L. Corrosion Conditions Analysis of In-service ACSR Overhead Lines. Appl. Mech. Mater. 2013, 446–447, 753–758. [Google Scholar] [CrossRef]
- Havard, D.G.; Bissada, M.K.; Fajardo, C.G.; Horrocks, D.J.; Meale, J.R.; Motlis, J.Y.; Tabatabai, M.; Yoshiki-Gravelsins K., S. Aged ACSR conductors. II. Prediction of remaining life. IEEE Trans. Power Deliv. 1992, 7, 588–595. [Google Scholar] [CrossRef]
- Chen, G.H.; Wang, X.; Wang, J.Q.; Liu, J.J.; Zhang, T.; Tang, W.M. Damage investigation of the aged aluminium cable steel reinforced (ACSR) conductors in a high-voltage transmission line. Eng. Fail. Anal. 2012, 19, 13–21. [Google Scholar] [CrossRef]
- Lequien, F.; Auzoux, Q.; Moine, G.; Rousseau, M.; Pasquier-Tilliette, S.; Holande, A.; Ammi, S.; Heurtault, S.; Prieur, P. Characterization of an aluminum conductor steel reinforced (ACSR) after 60 years of operation. Eng. Fail. Anal. 2021, 120, 105039. [Google Scholar] [CrossRef]
- Kim, S.D.; Morcos, M.M. Mechanical deterioration of ACSR conductors due to forest fires. IEEE Trans. Power Deliv. 2003, 18, 271–276. [Google Scholar] [CrossRef]
- Hakansson, E.; Predecki, P.; Kumosa, M.S. Galvanic Corrosion of High Temperature Low Sag Aluminum Conductor Composite Core and Conventional Aluminum Conductor Steel Reinforced Overhead High Voltage Conductors. IEEE Trans. Realib. 2015, 64, 928–934. [Google Scholar] [CrossRef]
- Achiriloaiei, D.; Medeleanu, M. Studies on the Effects of Environmental Pollution on ACSR Conductors. Rev. Chim. 2019, 70, 3984–3986. [Google Scholar] [CrossRef]
- Jaffrey, N.A.; Hettiwatte, S. Corrosion Detection in Steel Reinforced Aluminium Conductor Cables. In Proceedings of the Australasian Universities Power Engineering Conference (AUPEC), Perth, Australia, 28 September–1 October 2014. [Google Scholar] [CrossRef]
- Karabay, S.; Önder, F.K. An approach for analysis in refurbishment of existing conventional HV–ACSR transmission lines with AAAC. Electr. Power Syst. Res. 2004, 72, 179–185. [Google Scholar] [CrossRef]
- Kopsidas, K.; Rowland, S.M. A Performance Analysis of Reconductoring an Overhead Line Structure. IEEE Trans. Power Deliv. 2009, 24, 2248–2256. [Google Scholar] [CrossRef]
- Kalombo, R.B.; Pestana, M.S.; Ferreira, J.L.A.; da Silva, C.R.M.; Araujo, J.A. Influence of the catenary parameter (H/w) on the fatigue life of overhead conductors. Tribol. Int. 2017, 108, 141–149. [Google Scholar] [CrossRef]
- Ma, X.C.; Gao, L.; Zhang, J.X.; Zhang, L.C. Fretting Wear Behaviors of Aluminum Cable Steel Reinforced (ACSR) Conductors in High-Voltage Transmission Line. Metals 2017, 7, 373. [Google Scholar] [CrossRef]
- Levin, A.A.; Narykova, M.V.; Lihachev, A.I.; Kardashev, B.K.; Kadomtsev, A.G.; Brunkov, P.N.; Panfilov, A.G.; Prasolov, N.D.; Sultanov, M.M.; Kuryanov, V.N.; et al. Modification of the structural, microstructural, and elastoplastic properties of aluminum wires after operation. Metals 2021, 11, 1955. [Google Scholar] [CrossRef]
- Kul’kov, V.G.; Tyshkevich, V.N.; Kuryanov, V.N.; Sultanov, M.M.; Norov, D.S.; Narykova, M.V.; Kadomtsev, A.G.; Prasolov, N.D.; Brunkov, P.N.; Likhachev, A.I.; et al. Experimental studies of fatigue strength and surface electrical resistance of aluminum wire of overhead power transmission lines. Saf. Reliab. Power Ind. 2021, 14, 189–195. (In Russian) [Google Scholar] [CrossRef]
- Nakhimova, L.I. (Ed.) GOST 11069-2001. Primary Aluminium. Grades; IPK Izdatel. Standartov: Moscow, Russia, 2004. (In Russian) [Google Scholar]
- Bruker AXS. Karlsruhe, Diffrac. Suite Eva, Version 5.1.0.5. DIFFRAC.SUITE User Manual. Bruker AXS GmbH: Karlsruhe, Germany, 2019.
- International Centre for Diffraction Data (ICDD). Powder Diffraction File-2 Release 2014; ICDD: Newton Square, PA, USA, 2014. [Google Scholar]
- Maunders, C.; Etheridge, J.; Wright, N.; Whitfield, H.J. Structure and microstructure of hexagonal Ba3Ti2RuO9 by electron diffraction and microscopy. Acta Crystallogr. Sect. B Struct. Sci. 2005, 61, 154–159. [Google Scholar] [CrossRef]
- Levin, A.A. Program SizeCr for Calculation of the Microstructure Parameters from X-ray Diffraction Data. Preprint. 2022. Available online: https://www.researchgate.net/profile/Alexander-Levin-6/research (accessed on 5 June 2022).
- Terlan, B.; Levin, A.A.; Börrnert, F.; Simon, F.; Oschatz, M.; Schmidt, M.; Cardoso-Gil, R.; Lorenz, T.; Baburin, I.A.; Joswig, J.-O.; et al. Effect of Surface Properties on the Microstructure, Thermal, and Colloidal Stability of VB2 Nanoparticles. Chem. Mater. 2015, 27, 5106–5115. [Google Scholar] [CrossRef]
- Terlan, B.; Levin, A.A.; Börrnert, F.; Zeisner, J.; Kataev, V.; Schmidt, M.; Eychmüller, A. A Size-Dependent Analysis of the Structural, Surface, Colloidal, and Thermal Properties of Ti1–xB2 (x = 0.03–0.08) Nanoparticles. Eur. J. Inorg. Chem. 2016, 2016, 3460–3468. [Google Scholar] [CrossRef]
- Welzel, U.; Ligot, J.; Lamparter, P.; Vermeulen, A.C.; Mittemeijer, E.J. Stress analysis of polycrystalline thin films and surface regions by X-ray diffraction. J. Appl. Crystallogr. 2005, 38, 1–29. [Google Scholar] [CrossRef]
- Nikanorov, S.P.; Kardashev, B.K. Elasticity and Dislocation Inelasticity of Crystals; Moscow Izdatel. Nauka: Moscow, Russia, 1985. (In Russian) [Google Scholar]
- Mason, J.K.; Schuh, C.A. Representation of Texture. In Electron Backscatter Diffraction in Material Science, 2nd ed.; Schwartz, A.I., Kumar, M., Adams, B.L., Field, D.P., Eds.; Springer: Boston, MA, USA, 2009; pp. 45–46. [Google Scholar] [CrossRef]
- Miller Jr, P.H.; DuMond, J.W.M. Tests for the Validity of the X-Ray Crystal Method for Determining N and e with Aluminum, Silver and Quartz. Phys. Rev. 1940, 57, 198–206. [Google Scholar] [CrossRef]
- Otte, H.M.; Montague, W.G.; Welch, D.O. X-ray diffractometer determination of the thermal expansion coefficient of aluminum near room temperature. J. Appl. Phys. 1963, 34, 3149–3150. [Google Scholar] [CrossRef]
- Tsybulya, S.; Kryukova, G. New X-ray powder diffraction data on δ-Al2O3. Powder Diffr. 2003, 18, 309–311. [Google Scholar] [CrossRef]
- Fargeot, D.; Mercurio, D.; Dauger, A. Structural characterization of alumina metastable phases in plasma sprayed deposits. Mater. Chem. Phys. 1990, 24, 299. [Google Scholar] [CrossRef]
- Kaibyshev, O.A.; Valiev, R.Z. Grain Boundaries and Properties of Metals; Metallurgiya: Moscow, Russia, 1987; pp. 156–157. (In Russian) [Google Scholar]
- Tromans, D. Elastic anisotropy of HCP metal crystals and polycrystals. Int. J. Res. Rev. Appl. Sci. 2011, 6, 462–483. [Google Scholar]
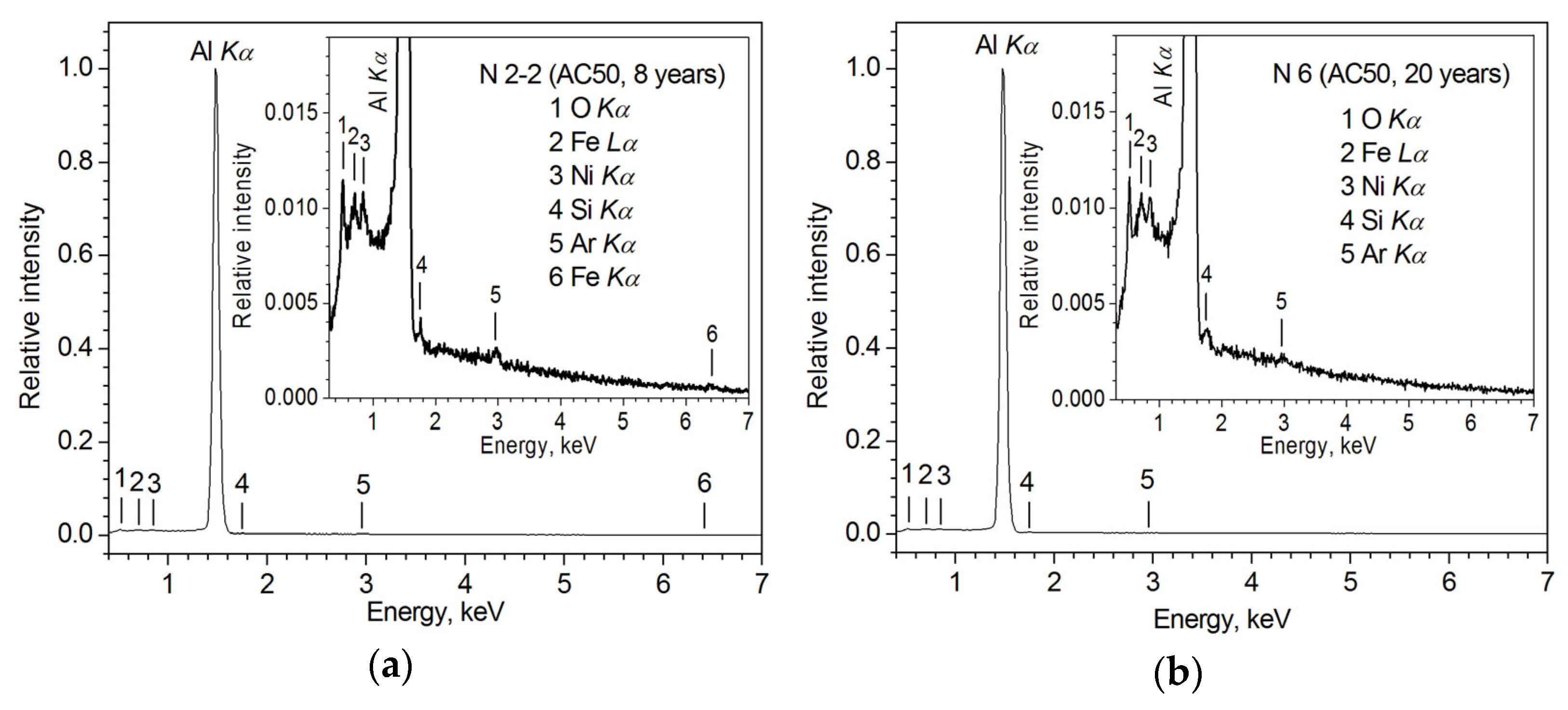

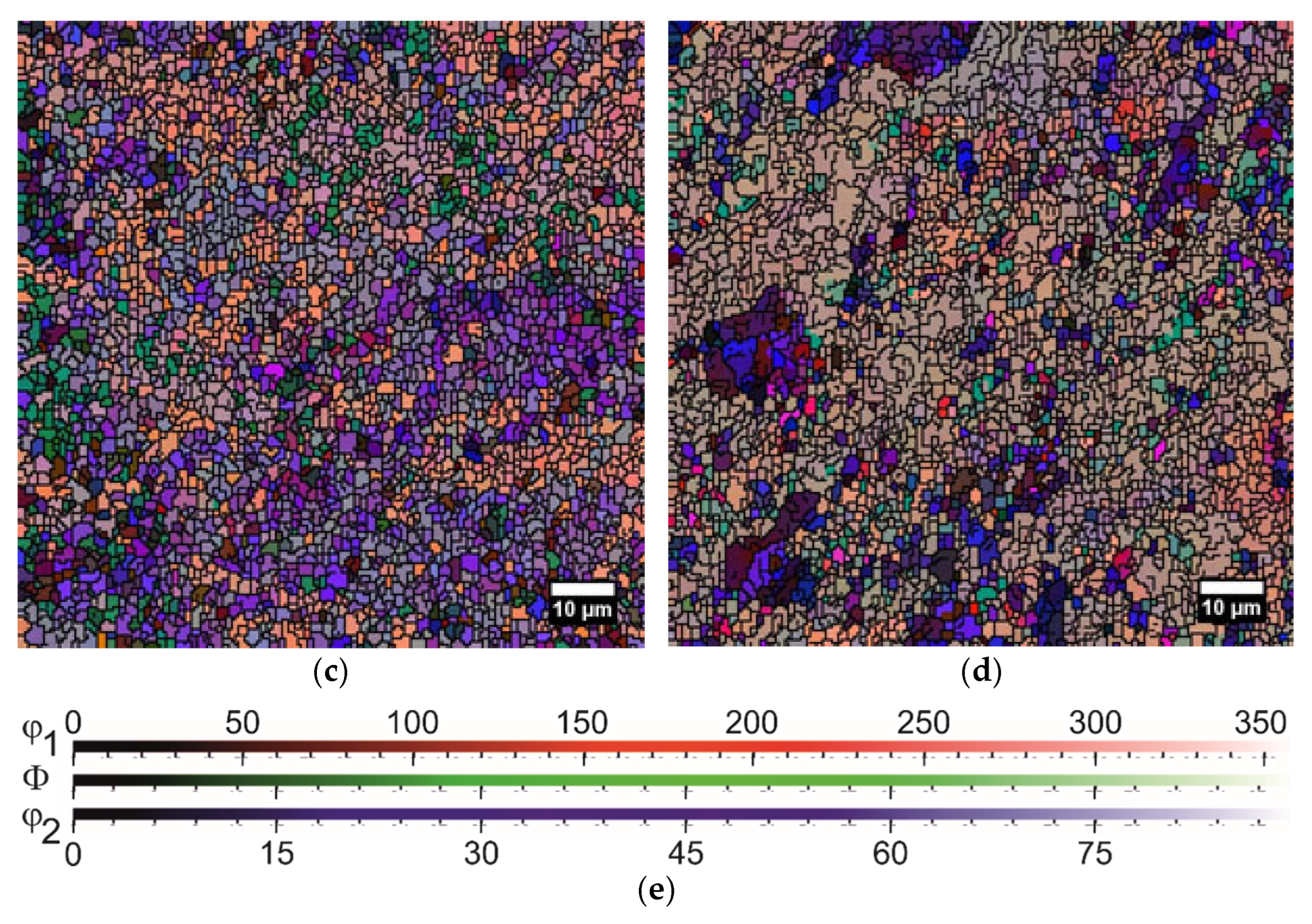
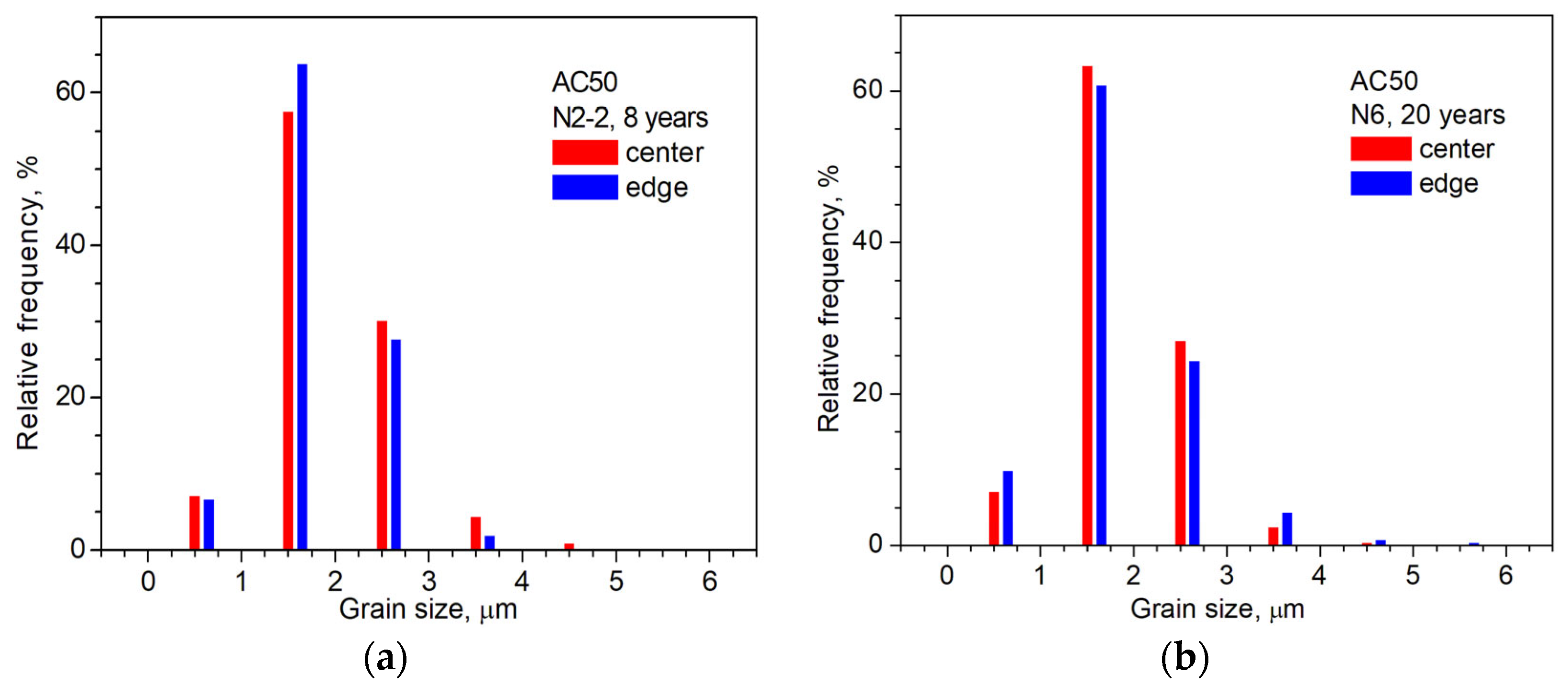
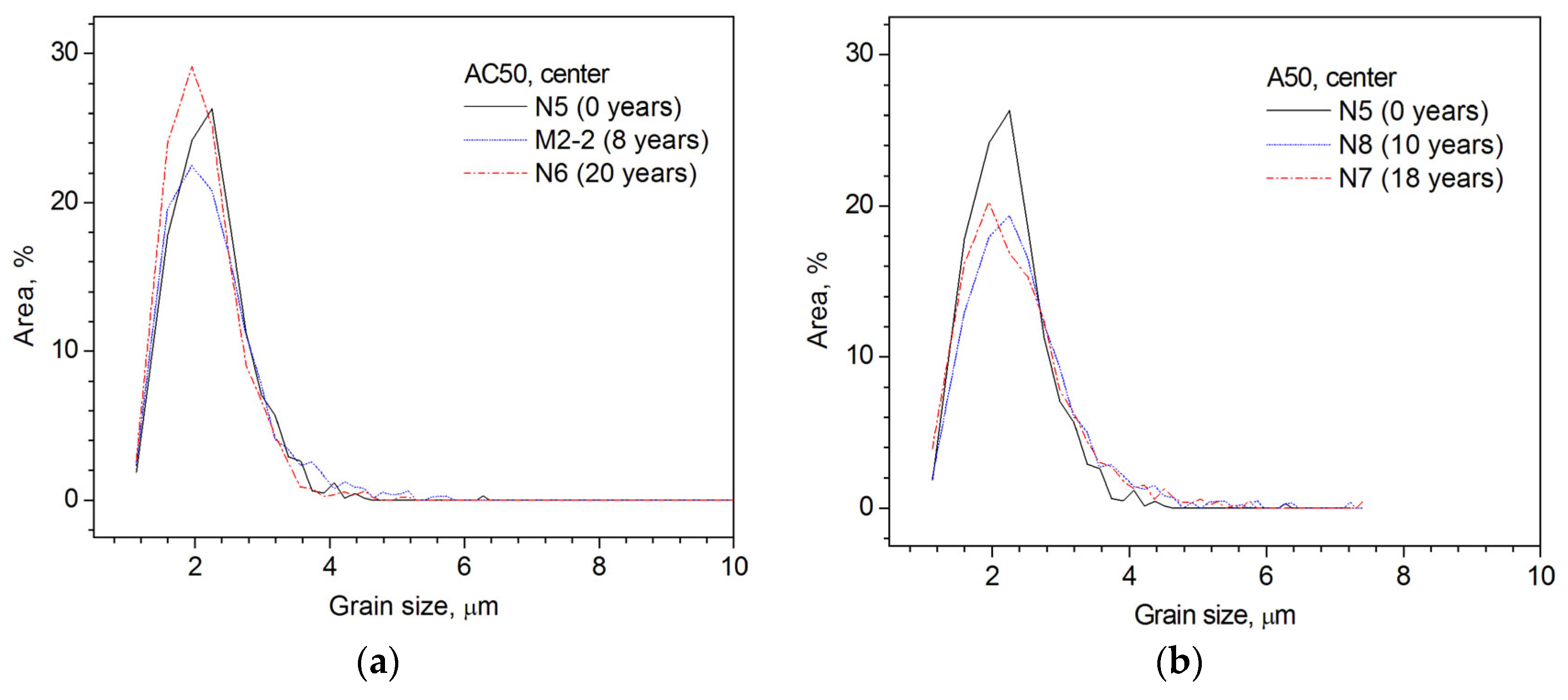









| Cable Type | Number of Al Wires in Cable | Number of Steel Wires in Cable | Individual Wire Diameter, mm | Cable Section, mm2 | Estimated Cable Weight, kg/km | Cable Breaking Strength (≤), N |
|---|---|---|---|---|---|---|
| A50 | 7 | 0 | 3.0 | 49.5 | 135 | 8198 |
| AC50 | 6 | 1 | 3.2 | 56.24 a | 195 | 17,112 |
| Sample, N | 5-2 | 5 | 8 | 2-2 | 7 | 6 |
|---|---|---|---|---|---|---|
| Type | A50 | AC50 | A50 | AC50 | A50 | AC50 |
| Service life t, years | 0 | 0 | 10 | 8 | 18 | 20 |
| Wire diameter d, mm | 3.02 | 3.20 | 2.85 | 3.24 | 3.03 | 3.07 |
| Al | Fe | Si | Zn | Ga | Mg | Cu | Ti + V + Cr + Mn | Other |
|---|---|---|---|---|---|---|---|---|
| 99.59 | 0.20 | 0.08 | 0.04 | 0.03 | 0.02 | 0.01 | 0.01 | 0.02 |
| Observed Preferential Orientation | WHP | SSP | |||
|---|---|---|---|---|---|
| Sample N/Years | [hkl] | Imax022/Imax111, % Imax002/Imax022, % | a, Å/ρx, g/cm3 D0, nm (εs = 0) | D, nm εs, % | D, nm εs, % |
| A50 type | |||||
| 5-2/0 | [011] | 42.0(3) 76.4(7) | 4.05026(12)/2.6973(2) 109(16) | 111(14) 0.010(14) | 109(16)0 |
| 8/10 | [011] | 69.0(4) 66.1(4) | 4.0515(5)/2.6949(11) 139(16) | 302(54) 0.031(2) | 298(26) 0.031(2) |
| 7/18 | [011] | 153.8(1.6) 55.6(6) | 4.0525(9)/2.6927(17) 126(33) | 246(55) 0.033(3) | 252(32) 0.034(3) |
| AC50 type | |||||
| 5/0 | [011] | 75.8(9) 68.4(9) | 4.05032(10)/2.6972(2) 138(16) | 141(17) 0.007(11) | 138(16) 0 |
| 2-2/8 | [011] | 90.9(6) 38.8(4) | 4.0511(4)/2.6956(7) 136(29) | 212(28) 0.026(3) | 219(19) 0.026(3) |
| 6/20 | [011] | 180.7(2.0) 42.7(5) | 4.0525(8)/2.6929(15) 120(23) | 187(27) 0.029(3) | 167(13) 0.025(3) |
| Table data for crystalline Al powder | |||||
| PDF-2 card 01-071-4008, [50] T = 312.3 K | no | - - | 4.050694/2.69642 - | - | - |
| PDF-2 card 01-073-9843, [49] T = 298 K | no | 24.0 191.7 | 4.04932(2)/2.6992(4) - | - - | - - |
| Sample N | Type | Service Life t, Years | E, GPa | δi · 105 | σs, MPa at εd = 4 ∙ 10−8 |
|---|---|---|---|---|---|
| 5-2 (3) | A50 | 0 | 72.78 | 23 | 14 |
| 5 (1) | AC50 | 0 | 71.84 | 27 | 15 |
| 8 (3) | A50 | 10 | 71.30 | 133 | 8.0 |
| 2-2 (3) | AC50 | 8 | 72.87 | 17 | 16 |
| 7 (1) | A50 | 18 | 71.21 | 85 | 9.0 |
| 6 (3) | AC50 | 20 | 71.58 | 31 | 13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Levin, A.A.; Narykova, M.V.; Lihachev, A.I.; Kardashev, B.K.; Kadomtsev, A.G.; Prasolov, N.D.; Panfilov, A.G.; Sokolov, R.V.; Brunkov, P.N.; Sultanov, M.M.; et al. Comparison of Structural, Microstructural, Elastic, and Microplastic Properties of the AAAC (A50) and ACSR (AC50/8) Cables after Various Operation Periods in Power Transmission Lines. Crystals 2022, 12, 1267. https://doi.org/10.3390/cryst12091267
Levin AA, Narykova MV, Lihachev AI, Kardashev BK, Kadomtsev AG, Prasolov ND, Panfilov AG, Sokolov RV, Brunkov PN, Sultanov MM, et al. Comparison of Structural, Microstructural, Elastic, and Microplastic Properties of the AAAC (A50) and ACSR (AC50/8) Cables after Various Operation Periods in Power Transmission Lines. Crystals. 2022; 12(9):1267. https://doi.org/10.3390/cryst12091267
Chicago/Turabian StyleLevin, Aleksandr A., Maria V. Narykova, Alexey I. Lihachev, Boris K. Kardashev, Andrej G. Kadomtsev, Nikita D. Prasolov, Andrei G. Panfilov, Roman V. Sokolov, Pavel N. Brunkov, Makhsud M. Sultanov, and et al. 2022. "Comparison of Structural, Microstructural, Elastic, and Microplastic Properties of the AAAC (A50) and ACSR (AC50/8) Cables after Various Operation Periods in Power Transmission Lines" Crystals 12, no. 9: 1267. https://doi.org/10.3390/cryst12091267
APA StyleLevin, A. A., Narykova, M. V., Lihachev, A. I., Kardashev, B. K., Kadomtsev, A. G., Prasolov, N. D., Panfilov, A. G., Sokolov, R. V., Brunkov, P. N., Sultanov, M. M., Strizhichenko, A. V., & Boldyrev, I. A. (2022). Comparison of Structural, Microstructural, Elastic, and Microplastic Properties of the AAAC (A50) and ACSR (AC50/8) Cables after Various Operation Periods in Power Transmission Lines. Crystals, 12(9), 1267. https://doi.org/10.3390/cryst12091267









