An Analysis Method of Symplectic Dual System for Decagonal Quasicrystal Plane Elasticity and Application
Abstract
:1. Introduction
2. Theoretical Formulation
2.1. Basic Equations
2.2. Variational Principle and Hamiltonian Dual Equation
2.3. Symplectic Analysis and Eigenvectors
2.3.1. The First-Order Jordan Form Eigen-Solutions
2.3.2. The SecondOrder Jordan Form Eigen-Solutions
2.3.3. The Third-Order Jordan Form Eigen-Solutions
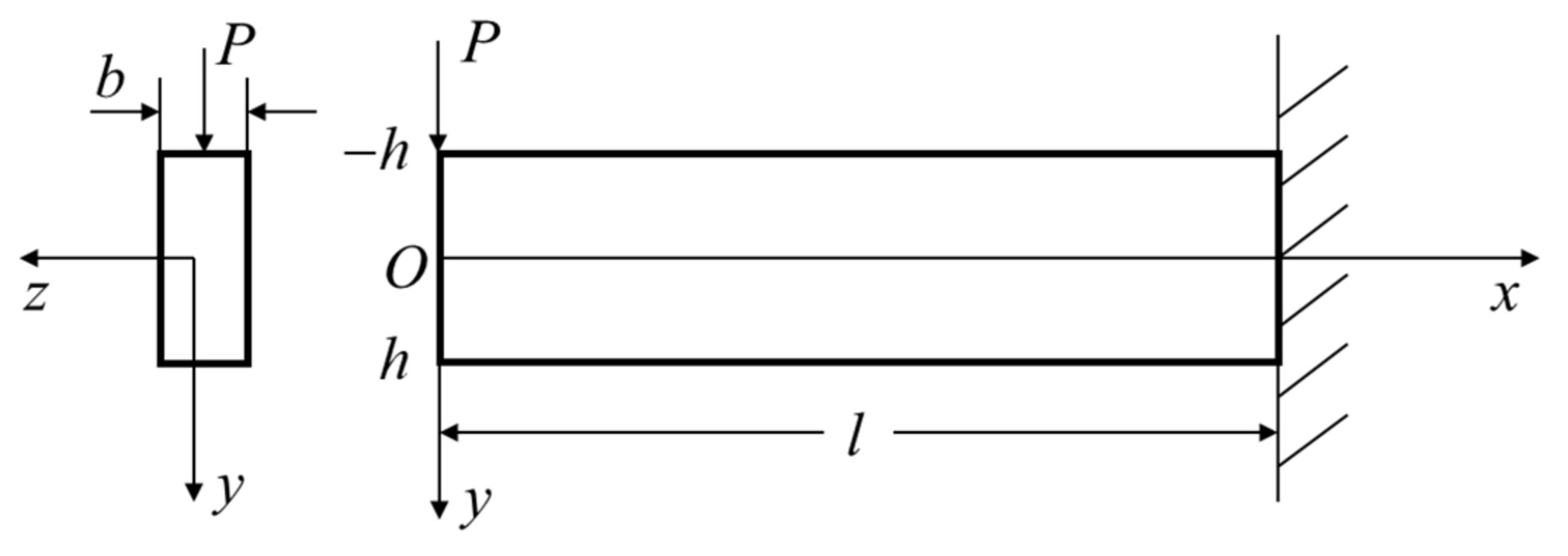
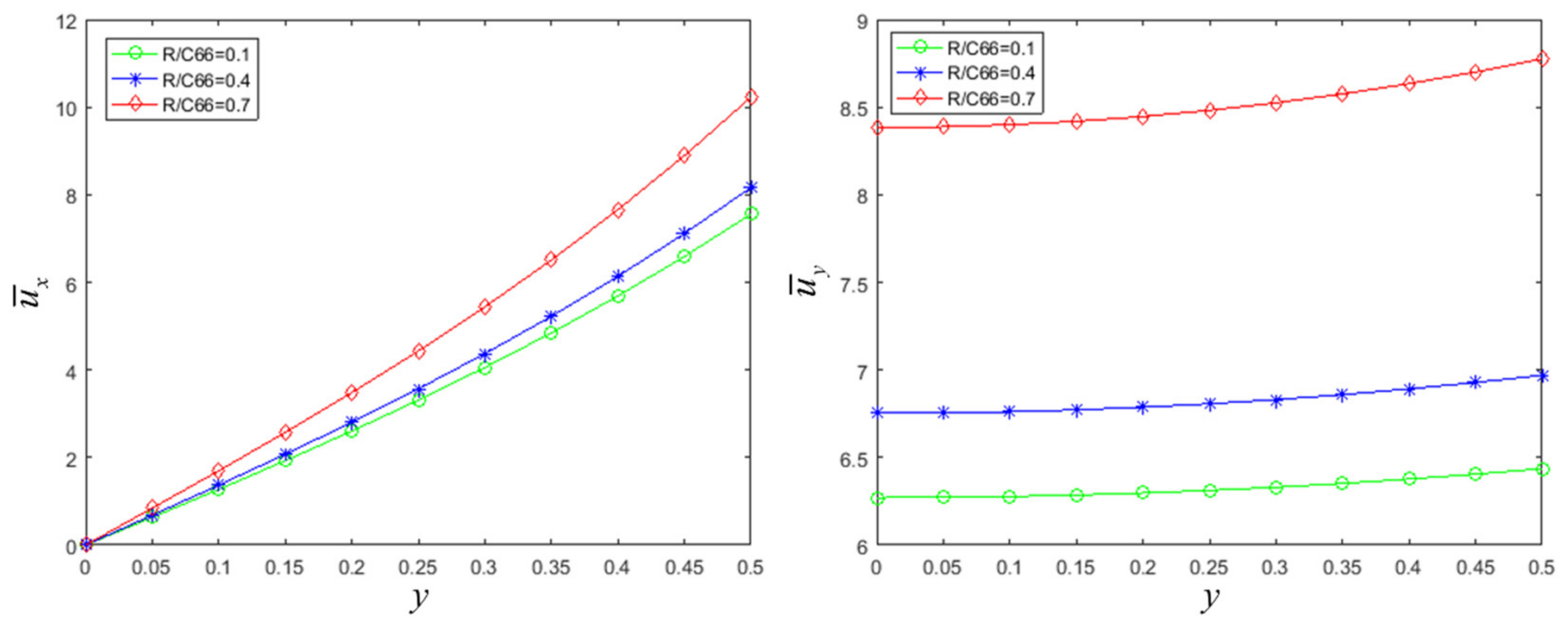
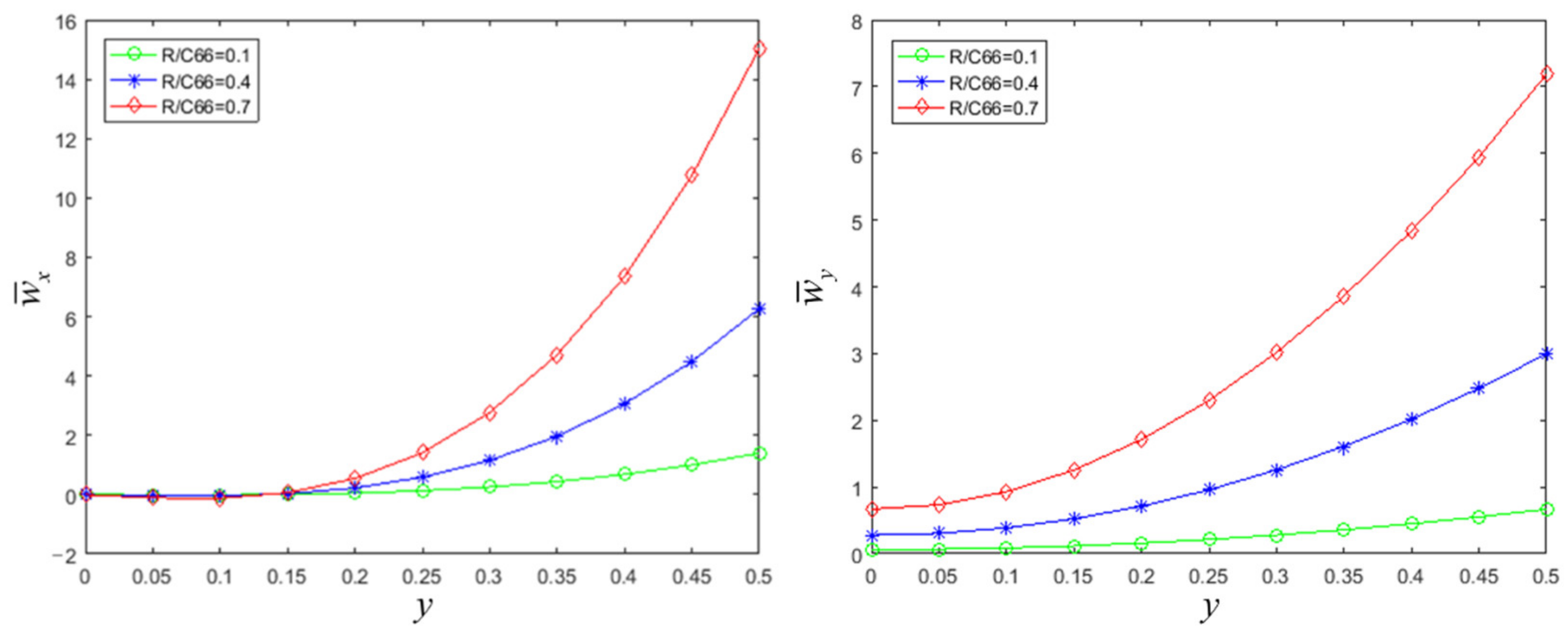
3. Bending of Decagonal Quasicrystal Cantilever Beam with Concentrated Load
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Shechtman, D.; Blech, I.; Gratias, D.; Cahn, J.W. Metallic phase with long-range orientational order and no translational symmetry. Phys. Rev. Lett. 1984, 53, 1951–1953. [Google Scholar] [CrossRef] [Green Version]
- Hu, C.Z.; Wang, R.H.; Ding, D.H. Symmetry groups, physical property tensors, elasticity and dislocations in quasicrystals. Rep. Prog. Phys. 2000, 63, 1–39. [Google Scholar] [CrossRef]
- Suck, J.B.; Schreiber, M.; Häussler, P. Quasicrystals: An Introduction to Structure, Physical Properties and Applications; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Li, X.F.; Fan, T.Y. Elastic analysis of a mode II crack in a decagonal quasi-crystal. Chin. Phys. B 2002, 11, 266–271. [Google Scholar]
- Gao, Y.; Ricoeur, A.; Zhang, L.L. Plane problems of cubic quasicrystal media with an elliptic hole or a crack. Phys. Lett. A 2011, 375, 2775–2781. [Google Scholar] [CrossRef]
- Radi, E.; Mariano, P.M. Stationary straight cracks in quasicrystals. Int. J. Fract. 2010, 166, 105–120. [Google Scholar] [CrossRef]
- Yang, L.Z.; Gao, Y.; Pan, E.; Waksmanski, N. An exact solution for a multilayered two-dimensional decagonal quasicrystal plate. Int. J. Solids Struct. 2014, 51, 1737–1749. [Google Scholar] [CrossRef] [Green Version]
- Li, X.Y. Elastic field in an infinite medium of one-dimensional hexagonal quasicrystal with a planar crack. Int. J. Solids Struct. 2014, 51, 1442–1455. [Google Scholar] [CrossRef] [Green Version]
- Li, L.H.; Liu, T.G. Decagonal quasicrystal plate with elliptic holes subjected to out-of-plane bending moments. Phys. Lett. A 2014, 378, 839–844. [Google Scholar] [CrossRef]
- Lazar, M.; Agiasofitou, E. Fundamentals generalized elasticity and dislocation theory of quasicrystals: Green tenser, dislocation key-formulas ang dislocation loops. Philos. Mag. 2014, 94, 4080–4101. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.F.; Li, X.; Ding, S.H. Two kinds of contact problems in three-dimensional icosahedral quasicrystals. Appl. Math. Mech. 2015, 36, 1569–1580. [Google Scholar] [CrossRef]
- Lazar, M.; Agiasofitou, E. Eshelbian mechanics of novel materials: Quasicrystals. J. Micromech. Mol. Phys. 2016, 1, 1640008. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Schiavone, P. Elastic field near the tip of an anticrack in a decagonal quasicrystalline material. Appl. Math. Mech. 2020, 41, 401–408. [Google Scholar] [CrossRef]
- Sun, T.Y.; Guo, J.H.; Pan, E. Nonlocal vibration and buckling of two-dimensional layered quasicrystal nanoplates embedded in an elastic medium. Appl. Math. Mech. 2021, 42, 1077–1094. [Google Scholar] [CrossRef]
- Zhong, W.X. A New Systematic Methodology for Theory of Elasticity; Dalian University of Technology Press: Dalian, China, 1995. (In Chinese) [Google Scholar]
- Feng, K. On difference scheme and symplectic geometry. In Proceedings of the Beijing Symposium Differential Geometry and Differential Equations; Science Press: Beijing, China, 1985; pp. 42–58. [Google Scholar]
- Zhong, W.X. Plane elasticity problem in strip domain and Hamiltonian system. J. Dalian Univ. Technol. 1991, 31, 373–384. (In Chinese) [Google Scholar]
- Yao, W.A.; Zhong, W.X. Symplectic Elasticity; Higher Education Press: Beijing, China, 2002. (In Chinese) [Google Scholar]
- Leung, A.Y.T.; Xu, X.S.; Zhou, Z.H.; Wu, Y.F. Analytic stress intensity factors for finite elastic disk using symplectic expansion. Eng. Fract. Mech. 2009, 76, 1866–1882. [Google Scholar] [CrossRef]
- Liu, Y.M.; Li, R. Accurate bending analysis of rectangular plates with two adjacent edges free and the others clamped or simply supported based on new symplectic approach. Appl. Math. Model. 2010, 34, 856–865. [Google Scholar] [CrossRef]
- Leung, A.Y.T.; Zheng, J.J.; Lim, C.W.; Zhang, X.C.; Xu, X.S.; Gu, Q. A new symplectic approach for piezoelectric cantilever composite plates. Comput. Struct. 2008, 86, 1865–1874. [Google Scholar] [CrossRef]
- Xu, X.S.; Gu, Q.; Leung, A.Y.T.; Zheng, J.J. A symplectic eigensolution method in transversely isotropic piezoelectric cylindrical media. J. Zhejiang Univ.-Sci. A 2005, 6, 922–927. [Google Scholar]
- Zhao, L.; Chen, W.Q. Symplectic analysis of plane problems of functionally graded piezoelectric materials. Mech. Mater. 2009, 41, 1330–1339. [Google Scholar] [CrossRef]
- Jiménez, F.; Ober-Blöbaum, S. Fractional Damping through Restricted Calculus of Variations. J. Nonlinear Sci. 2021, 31, 46. [Google Scholar] [CrossRef]
- Xu, C.H.; Leng, S.; Zhou, Z.H.; Xu, X.S.; Deng, Z.C. Accurate and straightforward symplectic approach for fracture analysis of fractional viscoelastic media. Appl. Math. Mech. 2022, 43, 403–416. [Google Scholar] [CrossRef]
- Koyunbakan, H. The Transmutation Method and Schrödinger Equation with Perturbed Exactly Solvable Potential. J. Comput. Acoust. 2009, 17, 1–10. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Goodier, J.N. Theory of EIasticity; Higher Education Press: Beijing, China, 2013. (In Chinese) [Google Scholar]
- Fan, T.Y. Mathematical theory and methods of mechanics of quasicrystalline materials. Engineering 2013, 5, 407–448. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Li, L. An Analysis Method of Symplectic Dual System for Decagonal Quasicrystal Plane Elasticity and Application. Crystals 2022, 12, 636. https://doi.org/10.3390/cryst12050636
Li G, Li L. An Analysis Method of Symplectic Dual System for Decagonal Quasicrystal Plane Elasticity and Application. Crystals. 2022; 12(5):636. https://doi.org/10.3390/cryst12050636
Chicago/Turabian StyleLi, Guangfang, and Lianhe Li. 2022. "An Analysis Method of Symplectic Dual System for Decagonal Quasicrystal Plane Elasticity and Application" Crystals 12, no. 5: 636. https://doi.org/10.3390/cryst12050636
APA StyleLi, G., & Li, L. (2022). An Analysis Method of Symplectic Dual System for Decagonal Quasicrystal Plane Elasticity and Application. Crystals, 12(5), 636. https://doi.org/10.3390/cryst12050636




