Grain Knowledge Graph Representation Learning: A New Paradigm for Microstructure-Property Prediction
Abstract
:1. Introduction
2. Materials and Methods
2.1. Dataset
2.1.1. Polycrystal Sample Preparation
2.1.2. Dataset Preparation
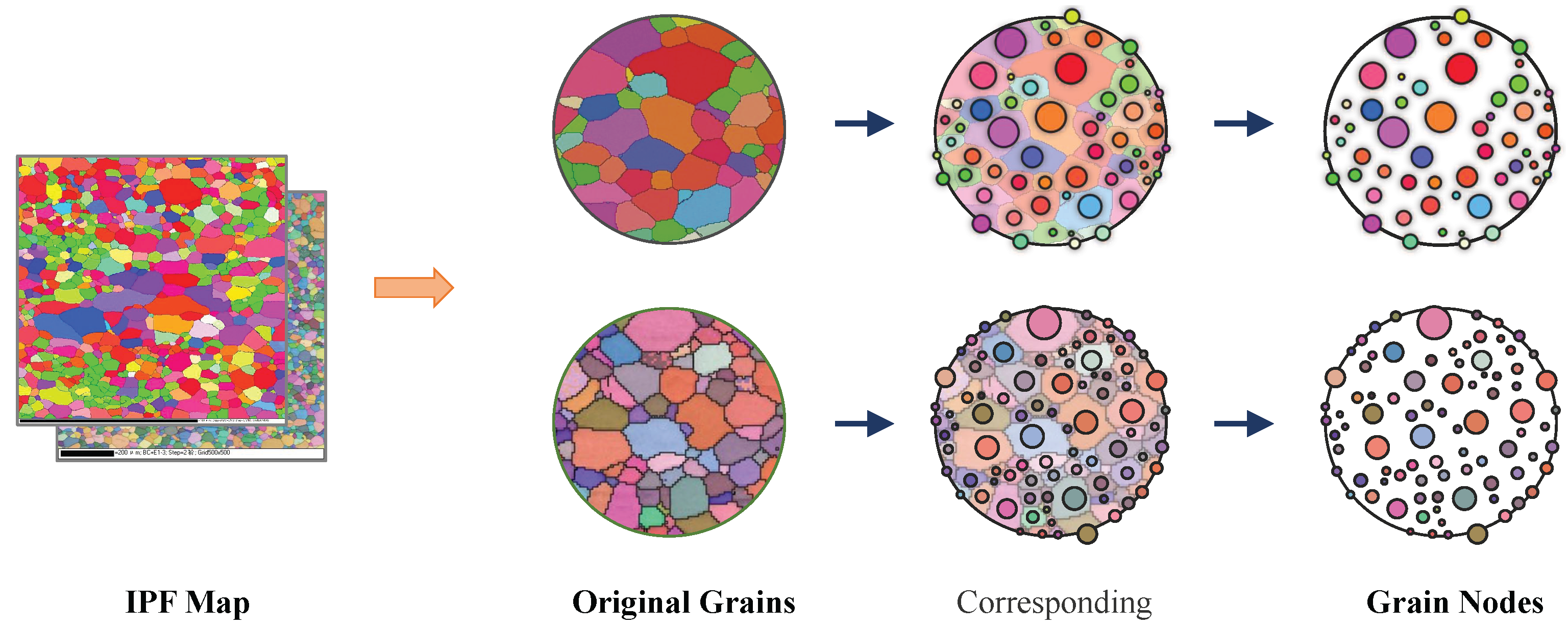
2.2. Representation of the Grain Knowledge Graph
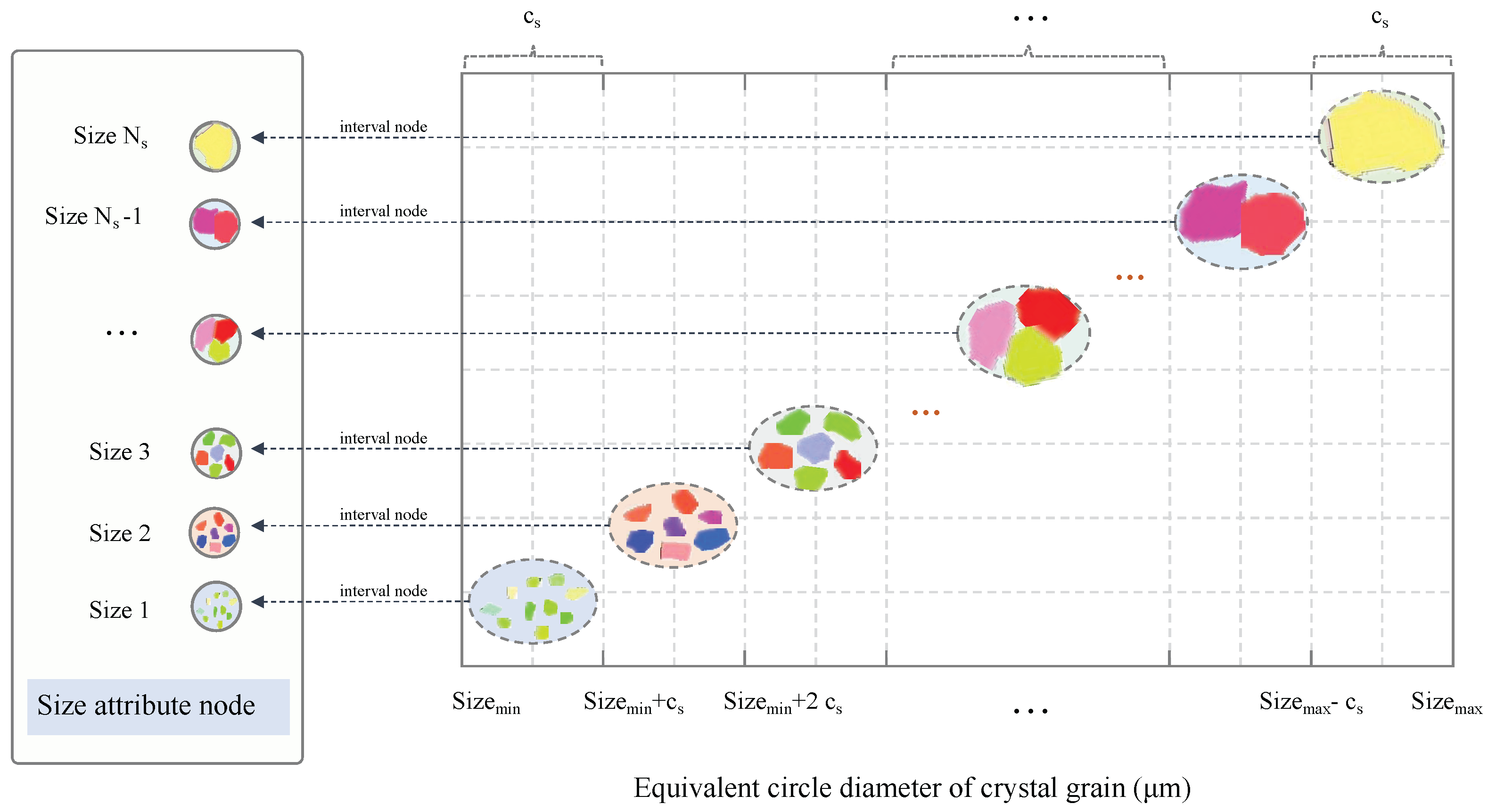
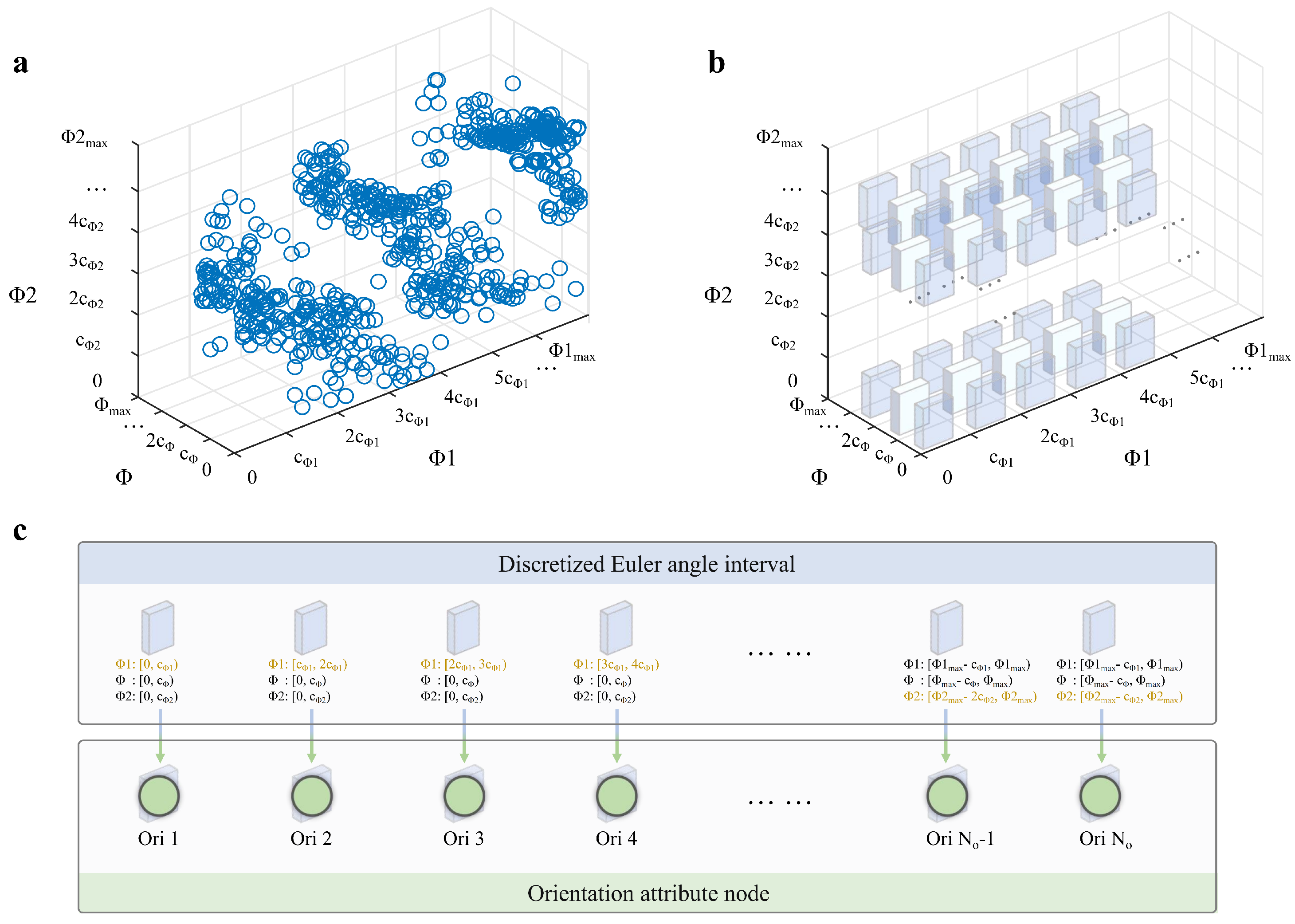
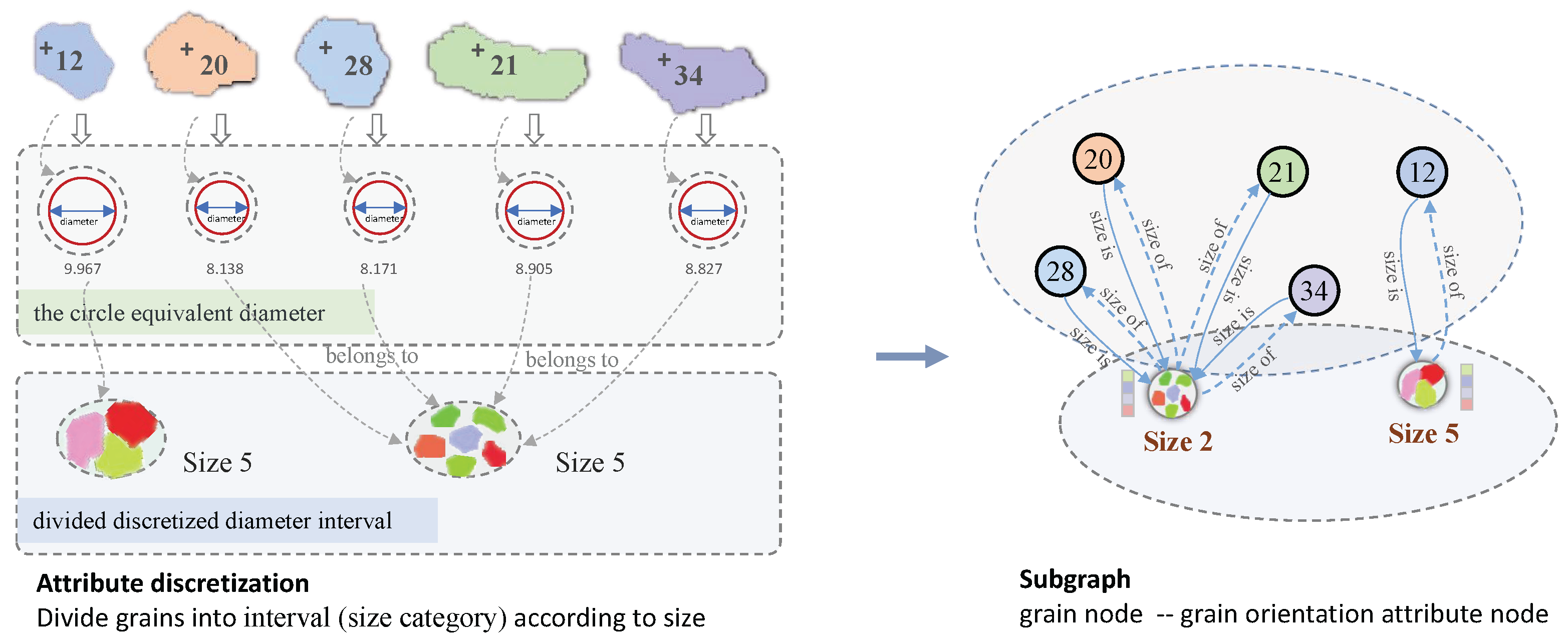
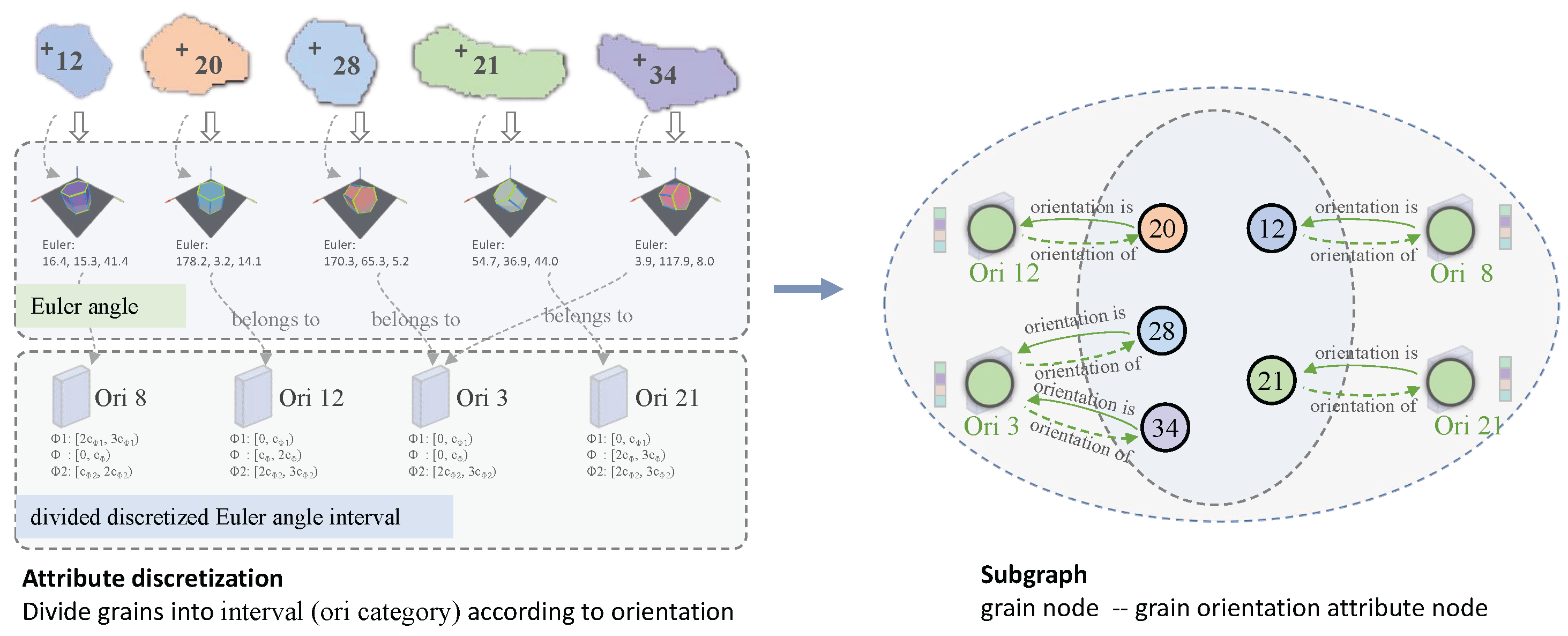
2.2.1. Node Representation
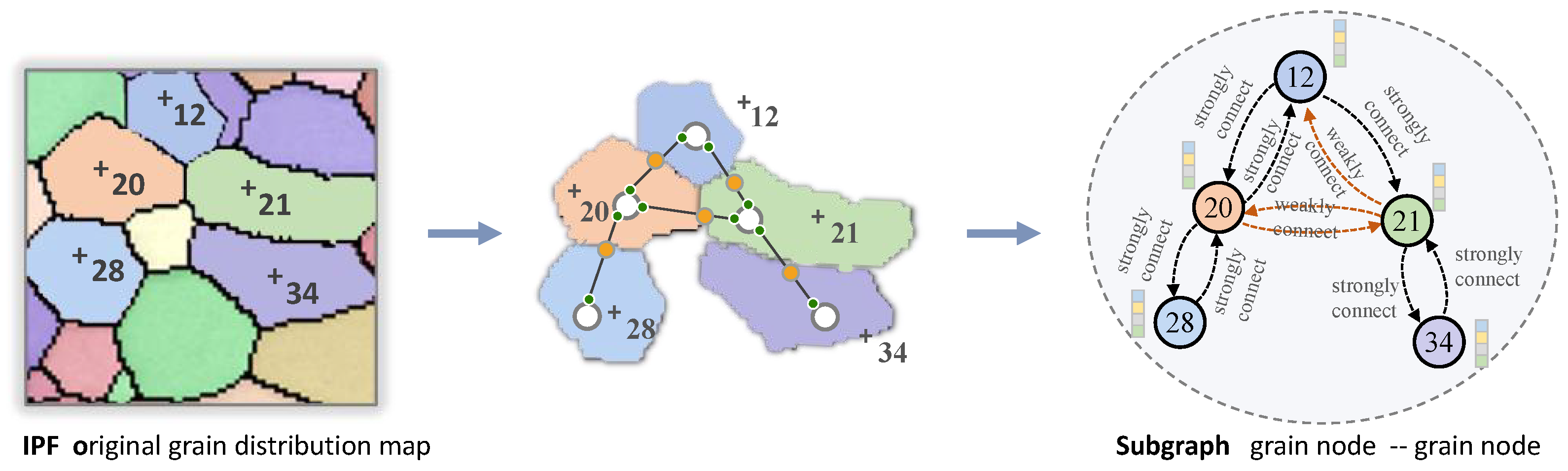
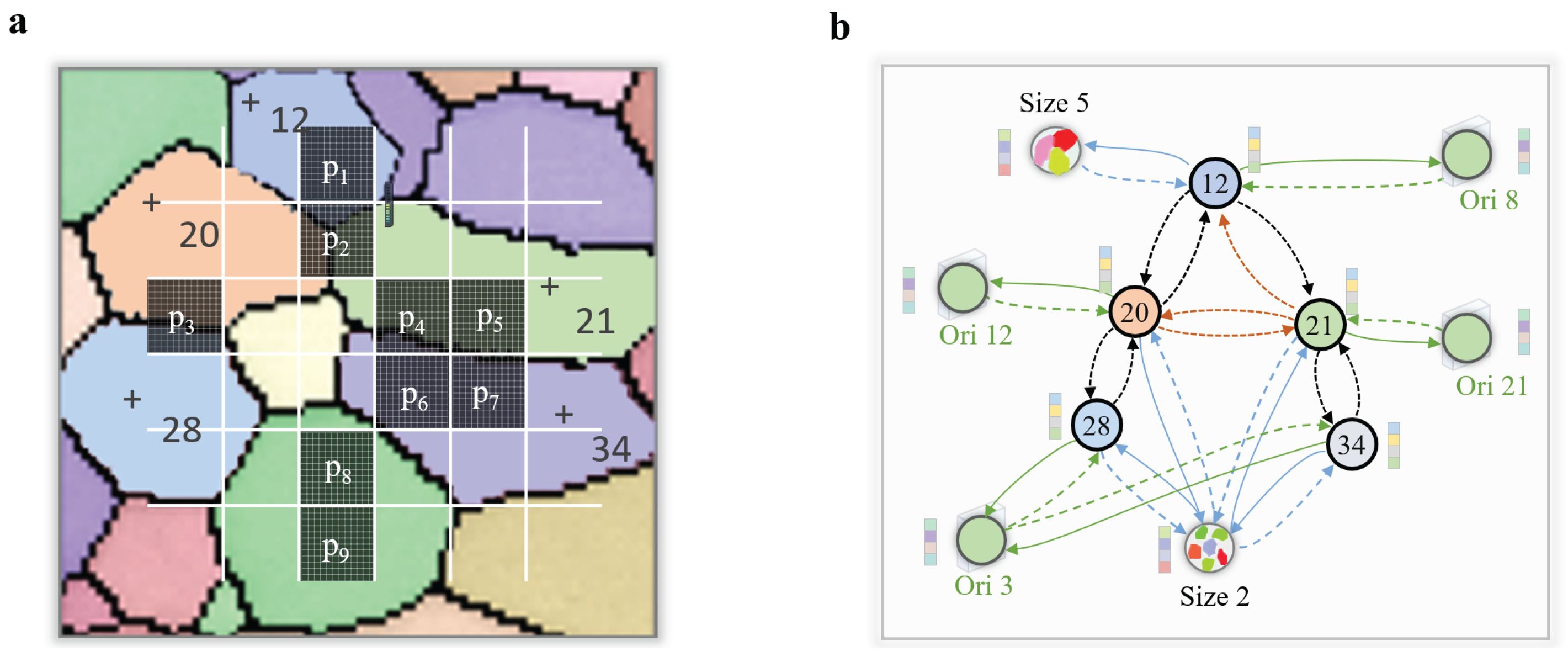
2.2.2. Edge Representation
2.2.3. Representation Structure Analysis
2.3. Grain Knowledge Graph Representation Calculation
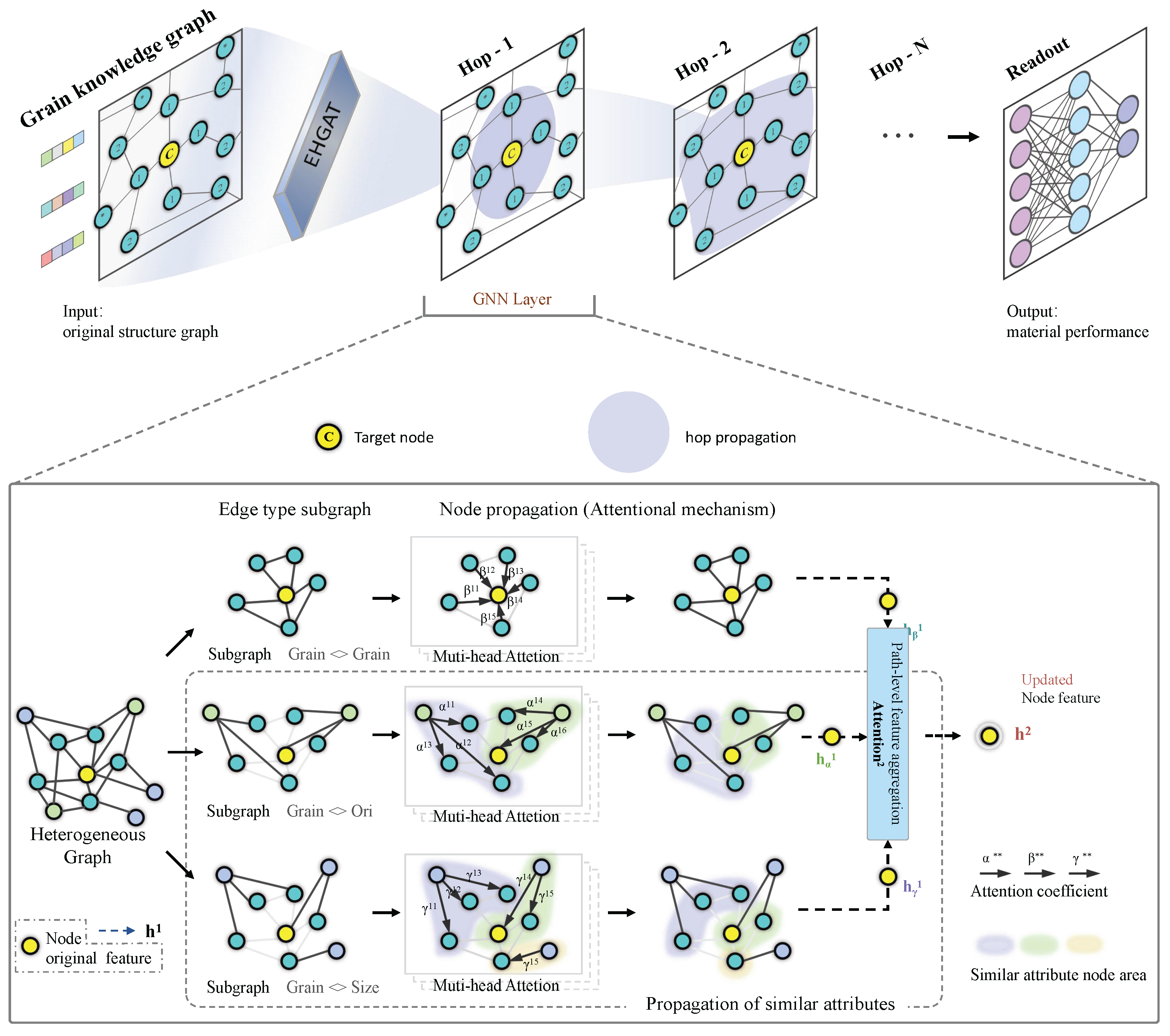
2.3.1. Overview of the HGGAT
2.3.2. The Propagation Process of HGGAT
3. Results
3.1. Experiment Settings
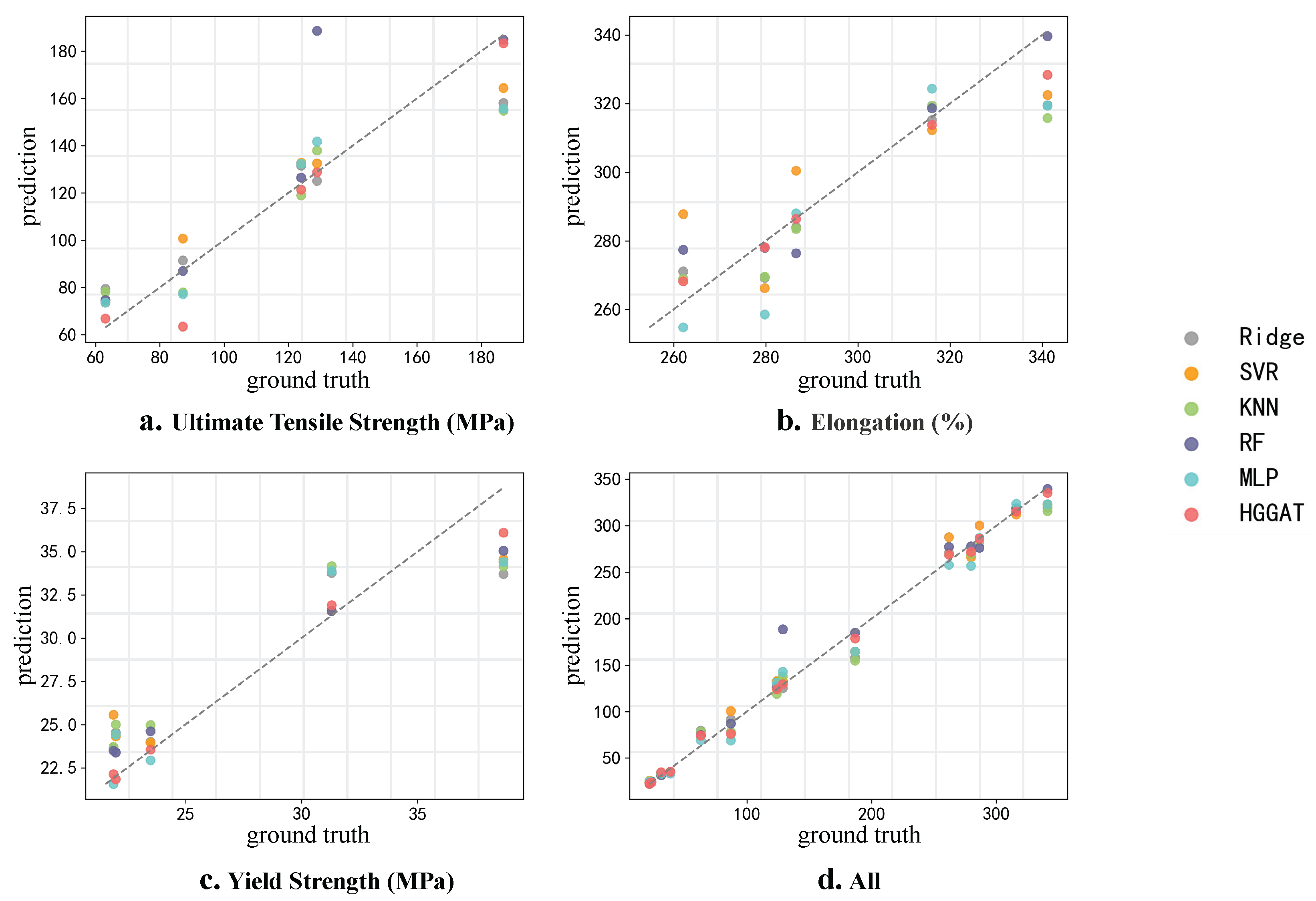
3.2. Prediction Results
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Oganov, A.R.; Pickard, C.J.; Zhu, Q.; Needs, R.J. Structure prediction drives materials discovery. Nat. Rev. Mater. 2019, 4, 331–348. [Google Scholar] [CrossRef]
- Rekha, S.; Raja, V.B. Review on Microstructure Analysis of Metals and Alloys Using Image Analysis Techniques. IOP Conf. Ser. Mater. Sci. Eng. 2017, 197, 012010. [Google Scholar] [CrossRef] [Green Version]
- Jain, A.; Ong, S.P.; Hautier, G.; Chen, W.; Persson, K.A. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 011002. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Lu, L.; Li, J.; Zhang, X.; Gao, H. Mechanical properties and deformation mechanisms of gradient nanostructured metals and alloys. Nat. Rev. Mater. 2020, 5, 706–723. [Google Scholar] [CrossRef]
- Liu, R.; Tian, Y.; Zhang, Z.; An, X.; Zhang, P.; Zhang, Z. Exceptional high fatigue strength in Cu-15at.% Al alloy with moderate grain size. Sci. Rep. 2016, 6, 27433. [Google Scholar] [CrossRef] [Green Version]
- Chai, Y.; Jiang, B.; Song, J.; Wang, Q.; He, J.; Zhao, J.; Huang, G.; Jiang, Z.; Pan, F. Role of Al content on the microstructure, texture and mechanical properties of Mg-3.5 Ca based alloys. Mater. Sci. Eng. A 2018, 730, 303–316. [Google Scholar] [CrossRef]
- He, J.; Mao, Y.; Fu, Y.; Jiang, B.; Xiong, K.; Zhang, S.; Pan, F. Improving the room-temperature formability of Mg-3Al-1Zn alloy sheet by introducing an orthogonal four-peak texture. J. Alloys Compd. 2019, 797, 443–455. [Google Scholar] [CrossRef]
- Kang, L.; Yang, C. A review on high-strength titanium alloys: Microstructure, strengthening, and properties. Adv. Eng. Mater. 2019, 21, 1801359. [Google Scholar] [CrossRef]
- Ahmad, R.; Yin, B.; Wu, Z.; Curtin, W. Designing high ductility in magnesium alloys. Acta Mater. 2019, 172, 161–184. [Google Scholar] [CrossRef]
- Joost, W.J.; Krajewski, P.E. Towards magnesium alloys for high-volume automotive applications. Scr. Mater. 2017, 128, 107–112. [Google Scholar] [CrossRef]
- Shao, C.; Zhang, P.; Zhu, Y.; Zhang, Z.; Pang, J.; Zhang, Z. Improvement of low-cycle fatigue resistance in TWIP steel by regulating the grain size and distribution. Acta Mater. 2017, 134, 128–142. [Google Scholar] [CrossRef]
- Białobrzeska, B.; Konat, Ł.; Jasiński, R. The influence of austenite grain size on the mechanical properties of low-alloy steel with boron. Metals 2017, 7, 26. [Google Scholar] [CrossRef] [Green Version]
- Carneiro, Í.; Simões, S. Recent advances in EBSD characterization of metals. Metals 2020, 10, 1097. [Google Scholar] [CrossRef]
- Alian, A.; Meguid, S. Hybrid molecular dynamics–finite element simulations of the elastic behavior of polycrystalline graphene. Int. J. Mech. Mater. Des. 2018, 14, 551–563. [Google Scholar] [CrossRef]
- Knezevic, M.; Beyerlein, I.J. Multiscale modeling of microstructure-property relationships of polycrystalline metals during thermo-mechanical deformation. Adv. Eng. Mater. 2018, 20, 1700956. [Google Scholar] [CrossRef]
- Smith, B.; Shih, D.; McDowell, D. Cyclic plasticity experiments and polycrystal plasticity modeling of three distinct Ti alloy microstructures. Int. J. Plast. 2018, 101, 1–23. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, J.; Xu, Z.; Zhang, J.; ul Hassan, H.; Li, G.; Zhang, H.; Hartmaier, A.; Fang, F.; Yan, Y.; et al. Crystal plasticity finite element modeling and simulation of diamond cutting of polycrystalline copper. J. Manuf. Process. 2019, 38, 187–195. [Google Scholar] [CrossRef]
- Sharma, B.B.; Parashar, A. A review on thermo-mechanical properties of bi-crystalline and polycrystalline 2D nanomaterials. Crit. Rev. Solid State Mater. Sci. 2020, 45, 134–170. [Google Scholar] [CrossRef]
- Sahoo, S.K.; Dhinwal, S.S.; Vu, V.Q.; Toth, L.S. A new macroscopic strain hardening function based on microscale crystal plasticity and its application in polycrystal modeling. Mater. Sci. Eng. A 2021, 823, 141634. [Google Scholar] [CrossRef]
- Hart, G.L.; Mueller, T.; Toher, C.; Curtarolo, S. Machine learning for alloys. Nat. Rev. Mater. 2021, 6, 730–755. [Google Scholar] [CrossRef]
- Zhou, Q.; Lu, S.; Wu, Y.; Wang, J. Property-Oriented Material Design Based on a Data-Driven Machine Learning Technique. J. Phys. Chem. Lett. 2020, 11, 3920–3927. [Google Scholar] [CrossRef] [PubMed]
- Kondo, R.; Yamakawa, S.; Masuoka, Y.; Tajima, S.; Asahi, R. Microstructure recognition using convolutional neural networks for prediction of ionic conductivity in ceramics. Acta Mater. 2017, 141, 29–38. [Google Scholar] [CrossRef]
- Wang, Z.L.; Adachi, Y. Property prediction and properties-to-microstructure inverse analysis of steels by a machine-learning approach. Mater. Sci. Eng. A 2019, 744, 661–670. [Google Scholar] [CrossRef]
- Pokuri, B.S.S.; Ghosal, S.; Kokate, A.; Sarkar, S.; Ganapathysubramanian, B. Interpretable deep learning for guided microstructure-property explorations in photovoltaics. NPJ Comput. Mater. 2019, 5, 95. [Google Scholar] [CrossRef] [Green Version]
- Khosravani, A.; Cecen, A.; Kalidindi, S.R. Development of high throughput assays for establishing process-structure-property linkages in multiphase polycrystalline metals: Application to dual-phase steels. Acta Mater. 2017, 123, 55–69. [Google Scholar] [CrossRef] [Green Version]
- Yabansu, Y.C.; Patel, D.K.; Kalidindi, S.R. Calibrated localization relationships for elastic response of polycrystalline aggregates. Acta Mater. 2014, 81, 151–160. [Google Scholar] [CrossRef]
- Yabansu, Y.C.; Kalidindi, S.R. Representation and calibration of elastic localization kernels for a broad class of cubic polycrystals. Acta Mater. 2015, 94, 26–35. [Google Scholar] [CrossRef] [Green Version]
- Latypov, M.I.; Kühbach, M.; Beyerlein, I.J.; Stinville, J.C.; Toth, L.S.; Pollock, T.M.; Kalidindi, S.R. Application of chord length distributions and principal component analysis for quantification and representation of diverse polycrystalline microstructures. Mater. Charact. 2018, 145, 671–685. [Google Scholar] [CrossRef]
- Cang, R.; Li, H.; Yao, H.; Jiao, Y.; Ren, Y. Improving direct physical properties prediction of heterogeneous materials from imaging data via convolutional neural network and a morphology-aware generative model. Comput. Mater. Sci. 2018, 150, 212–221. [Google Scholar] [CrossRef] [Green Version]
- Rong, Q.; Wei, H.; Huang, X.; Bao, H. Predicting the effective thermal conductivity of composites from cross sections images using deep learning methods. Compos. Sci. Technol. 2019, 184, 107861. [Google Scholar] [CrossRef]
- Chan, H.; Cherukara, M.; Loeffler, T.D.; Narayanan, B.; Sankaranarayanan, S.K. Machine learning enabled autonomous microstructural characterization in 3D samples. NPJ Comput. Mater. 2020, 6, 1. [Google Scholar] [CrossRef]
- Herriott, C.; Spear, A.D. Predicting microstructure-dependent mechanical properties in additively manufactured metals with machine-and deep-learning methods. Comput. Mater. Sci. 2020, 175, 109599. [Google Scholar] [CrossRef]
- Yang, C.; Kim, Y.; Ryu, S.; Gu, G.X. Prediction of composite microstructure stress-strain curves using convolutional neural networks. Mater. Des. 2020, 189, 108509. [Google Scholar] [CrossRef]
- Albawi, S.; Mohammed, T.A.; Al-Zawi, S. Understanding of a convolutional neural network. In Proceedings of the 2017 International Conference on Engineering and Technology (ICET), Antalya, Turkey, 21–24 August 2017; pp. 1–6. [Google Scholar]
- Sateesan, A.; Sinha, S.; Smitha, K.; Vinod, A. A Survey of Algorithmic and Hardware Optimization Techniques for Vision Convolutional Neural Networks on FPGAs. Neural Process. Lett. 2021, 53, 2331–2377. [Google Scholar] [CrossRef]
- Sainath, T.N.; Vinyals, O.; Senior, A.; Sak, H. Convolutional, long short-term memory, fully connected deep neural networks. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brisbane, Australia, 19–24 April 2015; pp. 4580–4584. [Google Scholar]
- Yuan, B. Efficient hardware architecture of softmax layer in deep neural network. In Proceedings of the 2016 29th IEEE International System-on-Chip Conference (SOCC), Seattle, WA, USA, 6–9 September 2016; pp. 323–326. [Google Scholar]
- Zhou, J.; Cui, G.; Hu, S.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph neural networks: A review of methods and applications. AI Open 2020, 1, 57–81. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Philip, S.Y. A comprehensive survey on graph neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4–24. [Google Scholar] [CrossRef] [Green Version]
- Dai, M.; Demirel, M.F.; Liang, Y.; Hu, J.M. Graph neural networks for an accurate and interpretable prediction of the properties of polycrystalline materials. NPJ Comput. Mater. 2021, 7, 103. [Google Scholar] [CrossRef]
- Zhang, S.; Tong, H.; Xu, J.; Maciejewski, R. Graph convolutional networks: Algorithms, applications and open challenges. In International Conference on Computational Social Networks; Springer: Berlin/Heidelberg, Germany, 2018; pp. 79–91. [Google Scholar]
- Zhang, S.; Tong, H.; Xu, J.; Maciejewski, R. Graph convolutional networks: A comprehensive review. Comput. Soc. Netw. 2019, 6, 11. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Hussain, F.; Tan, C.L.; Dash, M. Discretization: An enabling technique. Data Min. Knowl. Discov. 2002, 6, 393–423. [Google Scholar] [CrossRef]
- Wang, Q.; Mao, Z.; Wang, B.; Guo, L. Knowledge graph embedding: A survey of approaches and applications. IEEE Trans. Knowl. Data Eng. 2017, 29, 2724–2743. [Google Scholar] [CrossRef]
- Ji, S.; Pan, S.; Cambria, E.; Marttinen, P.; Philip, S.Y. A survey on knowledge graphs: Representation, acquisition, and applications. arXiv 2021, arXiv:2002.00388. [Google Scholar] [CrossRef]
- Hamilton, W.L. Graph representation learning. Synth. Lect. Artifical Intell. Mach. Learn. 2020, 14, 1–159. [Google Scholar] [CrossRef]
- Trang, T.; Zhang, J.; Kim, J.; Zargaran, A.; Hwang, J.; Suh, B.C.; Kim, N. Designing a magnesium alloy with high strength and high formability. Nat. Commun. 2018, 9, 2522. [Google Scholar] [CrossRef]
- Zhang, J.; Tan, T. Brief review of invariant texture analysis methods. Pattern Recognit. 2002, 35, 735–747. [Google Scholar] [CrossRef] [Green Version]
- Wang, N.; Wang, Z.; Aust, K.; Erb, U. Effect of grain size on mechanical properties of nanocrystalline materials. Acta Metall. Mater. 1995, 43, 519–528. [Google Scholar] [CrossRef]
- Wang, X.; Shi, T.; Jiang, Z.; Chen, W.; Guo, M.; Zhang, J.; Zhuang, L.; Wang, Y. Relationship among grain size, texture and mechanical properties of aluminums with different particle distributions. Mater. Sci. Eng. A 2019, 753, 122–134. [Google Scholar] [CrossRef]
- Jeh, G.; Widom, J. Simrank: A measure of structural-context similarity. In Proceedings of the Eighth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Edmonton, AB, Canada, 23–26 July 2002; pp. 538–543. [Google Scholar]
- Yu, W.; Lin, X.; Zhang, W.; Pei, J.; McCann, J.A. SimRank*: Effective and scalable pairwise similarity search based on graph topology. VLDB J. 2019, 28, 401–426. [Google Scholar] [CrossRef] [Green Version]
- Beausir, B.; Fundenberger, J.J. Analysis Tools for Electron and X-ray Diffraction; Université de Lorraine: Mace, France, 2017. [Google Scholar]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Wang, X.; Ji, H.; Shi, C.; Wang, B.; Ye, Y.; Cui, P.; Yu, P.S. Heterogeneous graph attention network. In Proceedings of the World Wide Web Conference, San Francisco, CA, USA, 13–17 May 2019; pp. 2022–2032. [Google Scholar]
- Gurney, K. An Introduction to Neural Networks; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]

| Alloy | Mg | Zn | Li | Al |
|---|---|---|---|---|
| Mg-2Zn | Bal | 1.99 | - | - |
| Mg-2Zn-1Li | Bal | 1.67 | 1.11 | - |
| Mg-2Zn-3Li | Bal | 1.82 | 3.08 | - |
| Mg-2Zn-1Gd | Bal | 1.74 | 0.97 | - |
| AZ31 | Bal | 2.98 | - | 0.99 |
| Model | MSE ↓ | MAE ↓ | EV ↑ | ↑ |
|---|---|---|---|---|
| Ridge | 0.139 | 0.299 | 0.850 | 0.836 |
| SVR | 0.176 | 0.351 | 0.796 | 0.792 |
| KNN | 0.160 | 0.336 | 0.834 | 0.810 |
| RF | 0.157 | 0.250 | 0.841 | 0.802 |
| MLP | 0.153 | 0.305 | 0.844 | 0.819 |
| GGAT | 0.116 | 0.234 | 0.873 | 0.865 |
| HGGAT(Our) | 0.051 | 0.164 | 0.943 | 0.941 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shu, C.; He, J.; Xue, G.; Xie, C. Grain Knowledge Graph Representation Learning: A New Paradigm for Microstructure-Property Prediction. Crystals 2022, 12, 280. https://doi.org/10.3390/cryst12020280
Shu C, He J, Xue G, Xie C. Grain Knowledge Graph Representation Learning: A New Paradigm for Microstructure-Property Prediction. Crystals. 2022; 12(2):280. https://doi.org/10.3390/cryst12020280
Chicago/Turabian StyleShu, Chao, Junjie He, Guangjie Xue, and Cheng Xie. 2022. "Grain Knowledge Graph Representation Learning: A New Paradigm for Microstructure-Property Prediction" Crystals 12, no. 2: 280. https://doi.org/10.3390/cryst12020280
APA StyleShu, C., He, J., Xue, G., & Xie, C. (2022). Grain Knowledge Graph Representation Learning: A New Paradigm for Microstructure-Property Prediction. Crystals, 12(2), 280. https://doi.org/10.3390/cryst12020280






