Investigating the β-Mg17Al12 Alloy under Pressure Using First-Principles Methods: Structure, Elastic Properties, and Mechanical Properties
Abstract
:1. Introduction
2. Calculation Details
3. Results and Discussion
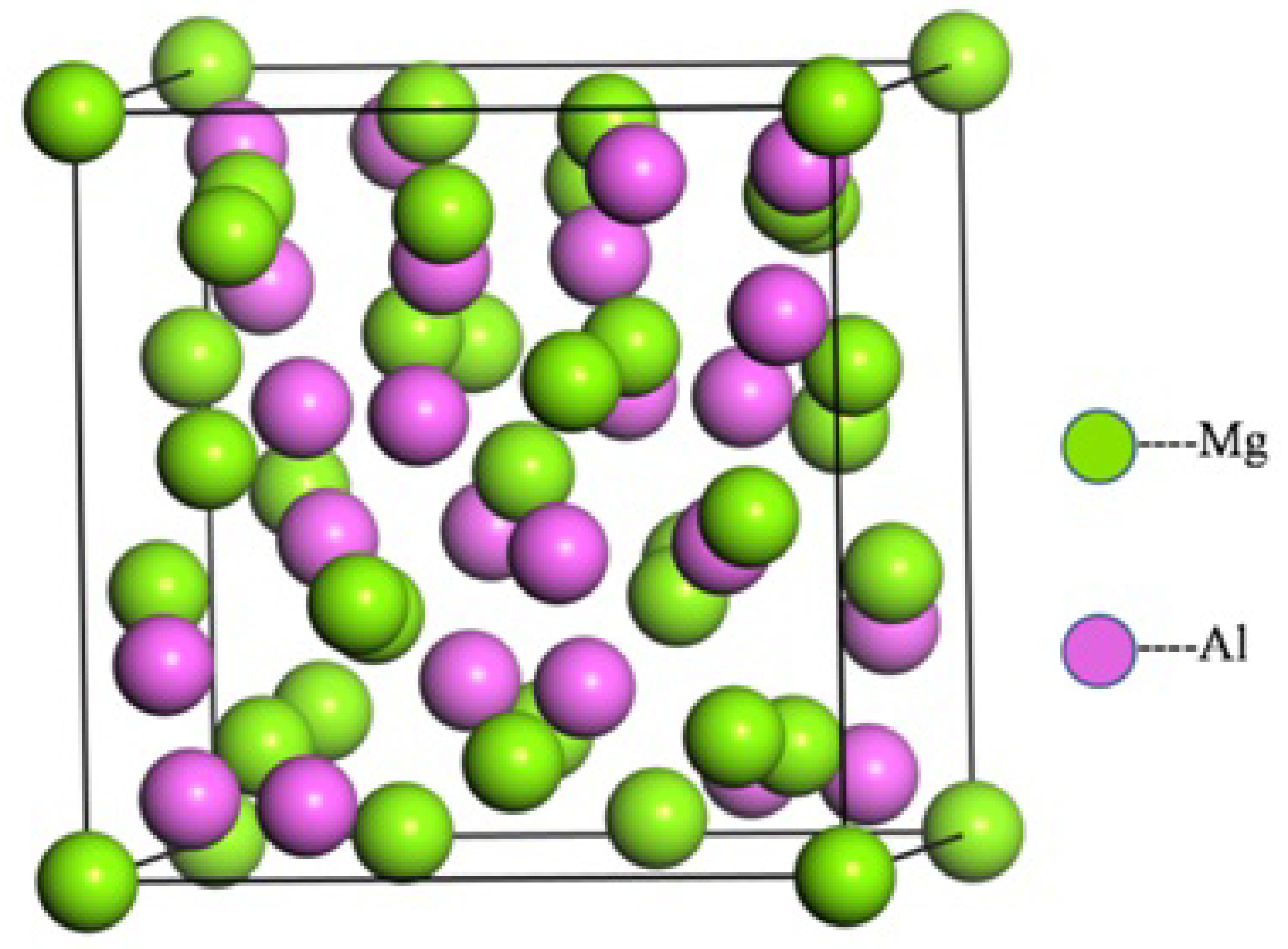
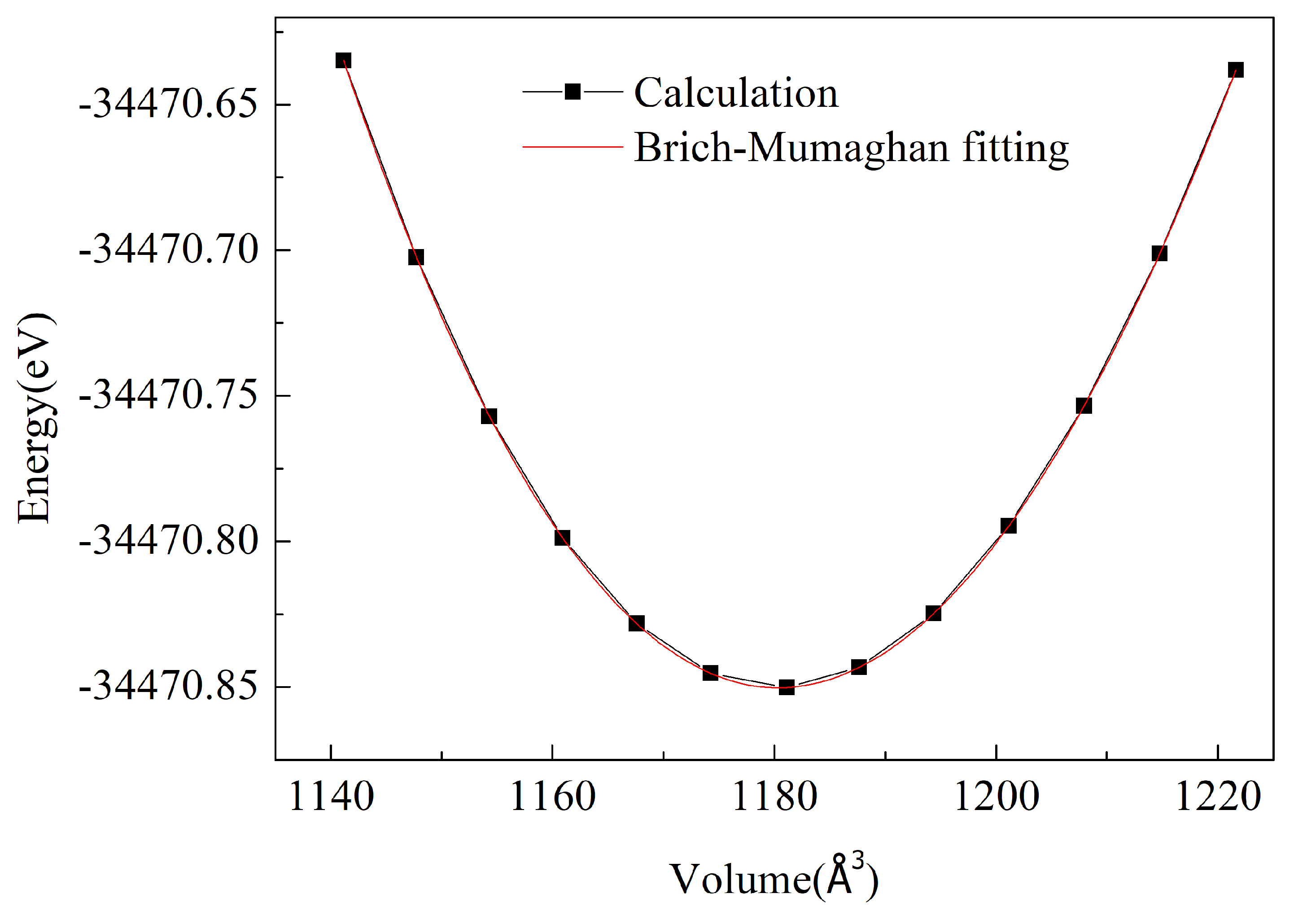
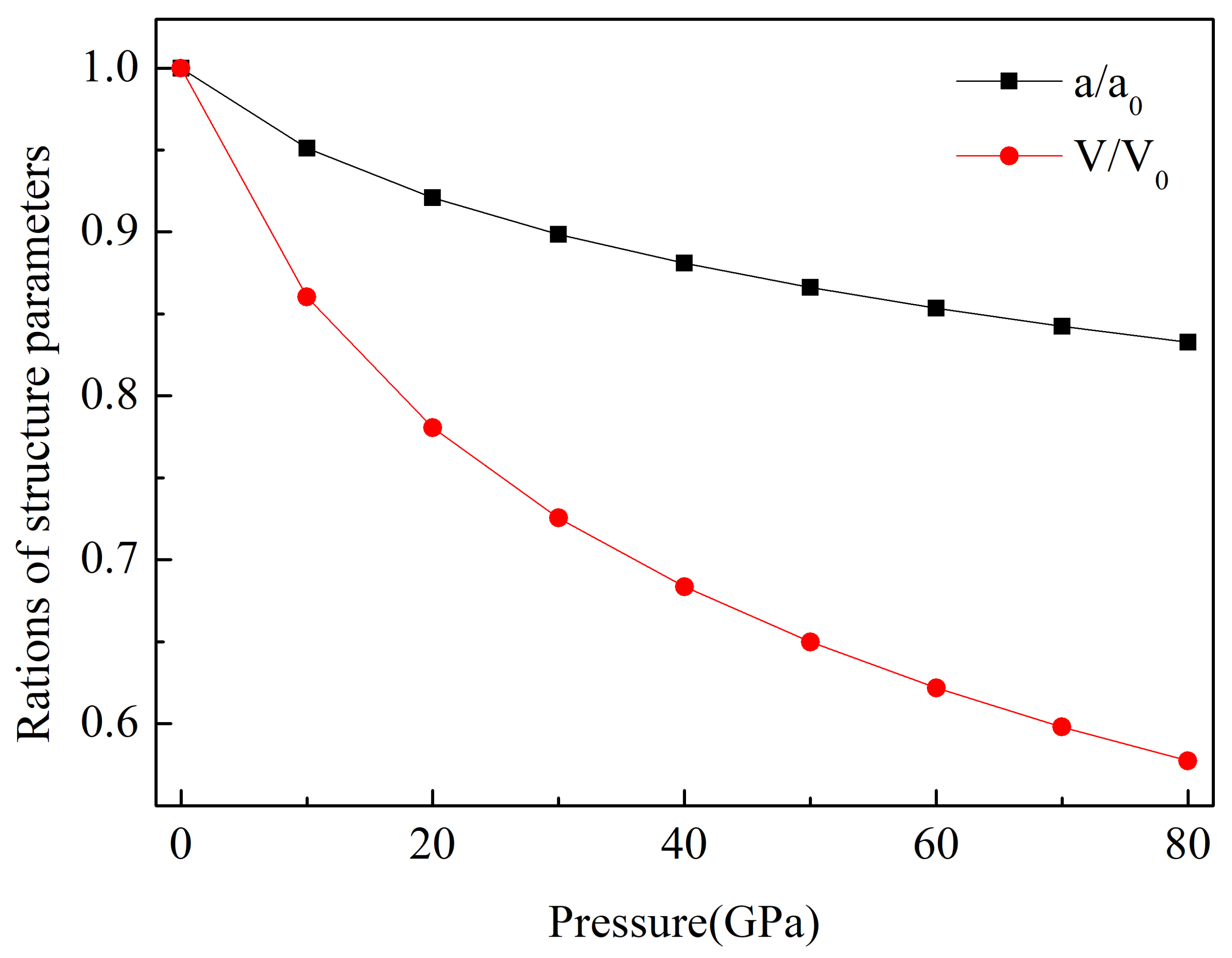
3.1. Structural Properties and Stability
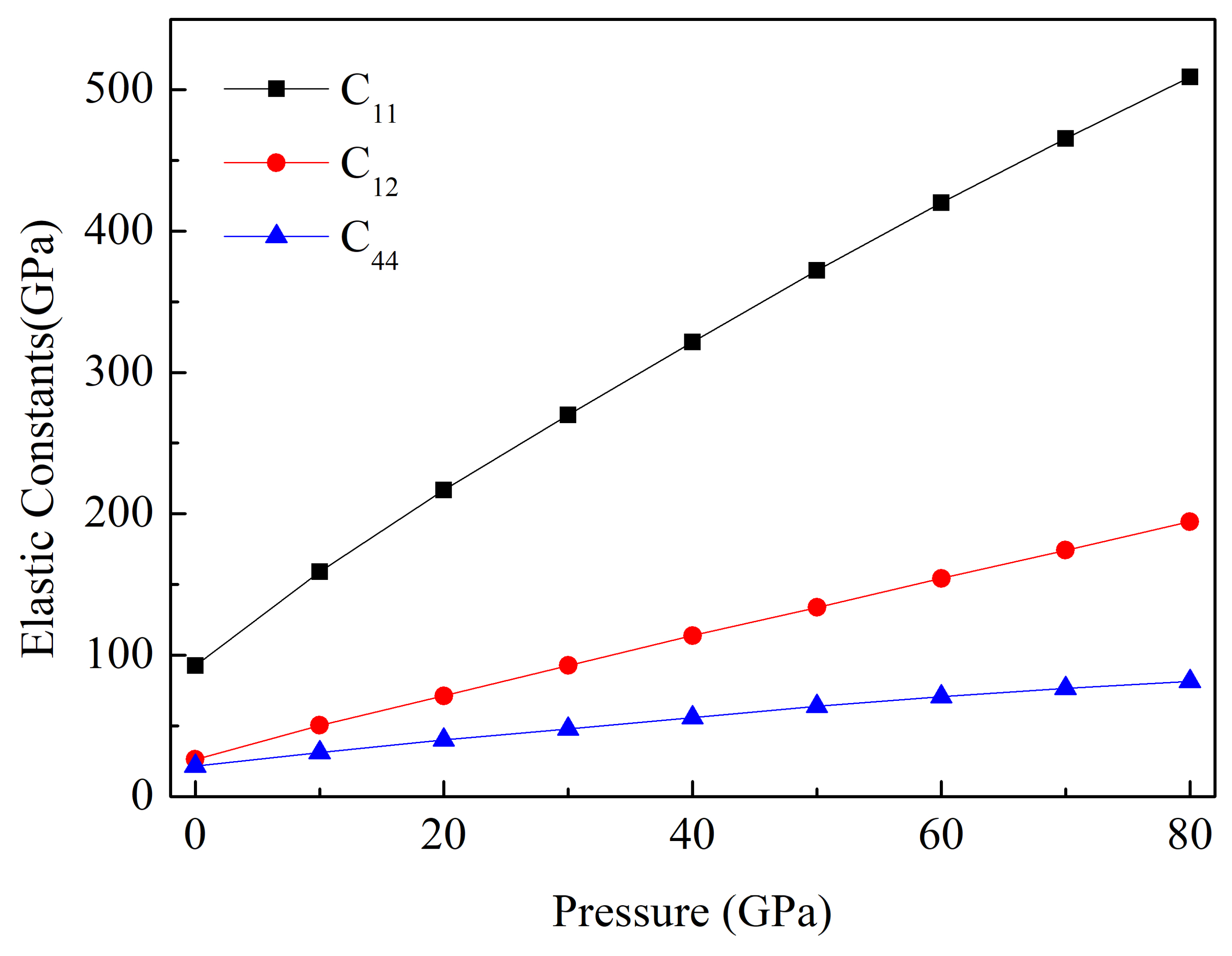
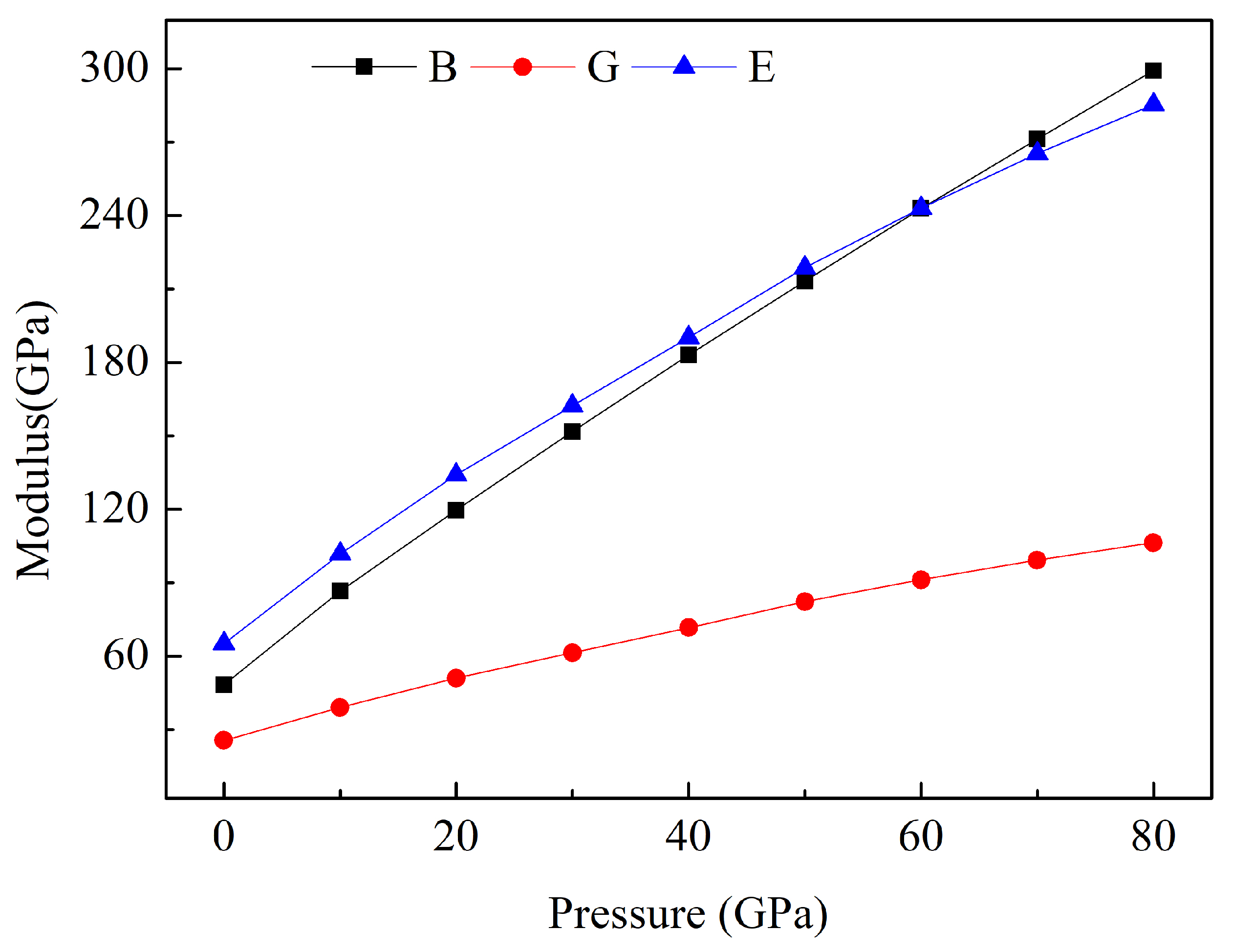
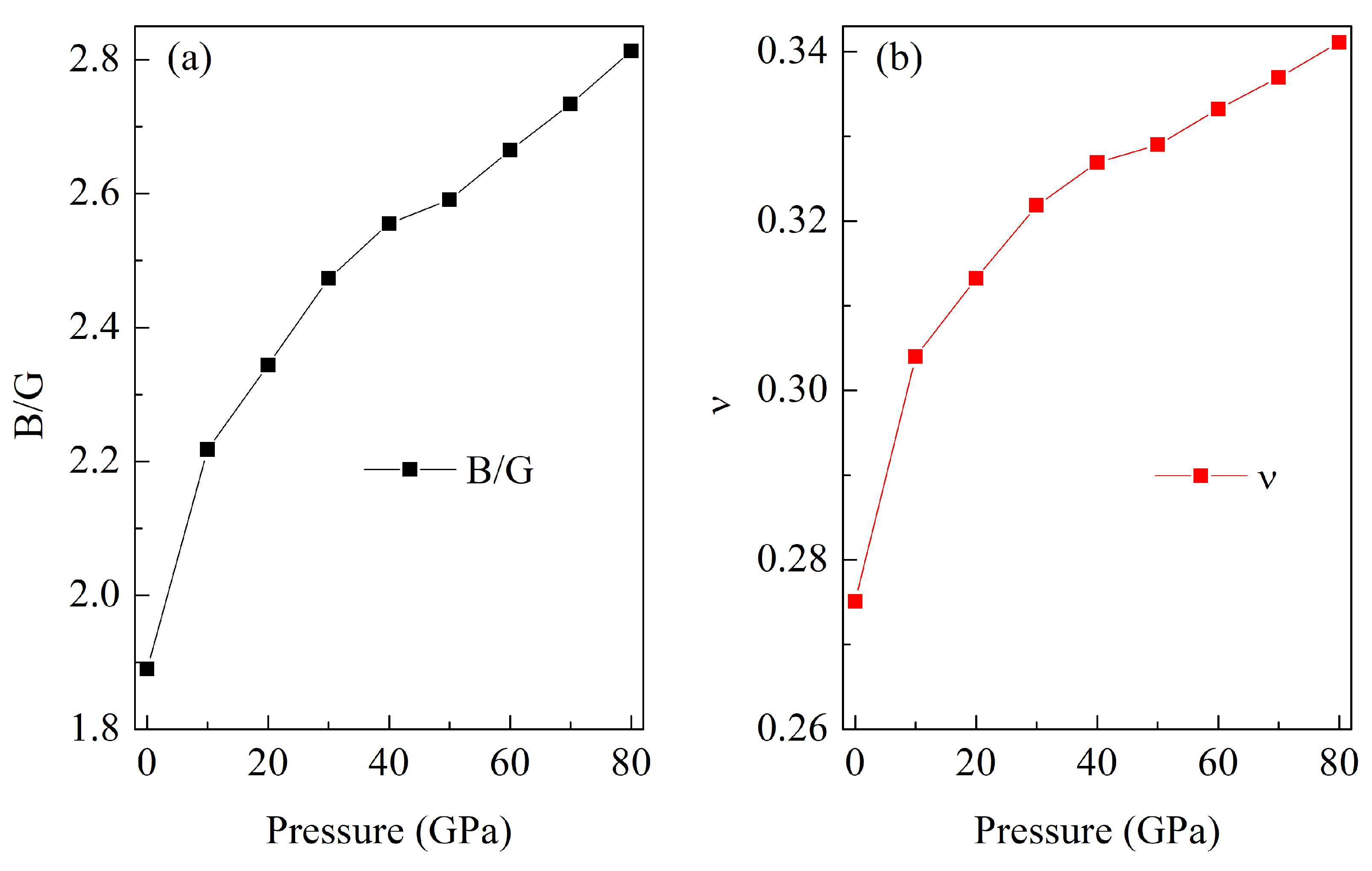
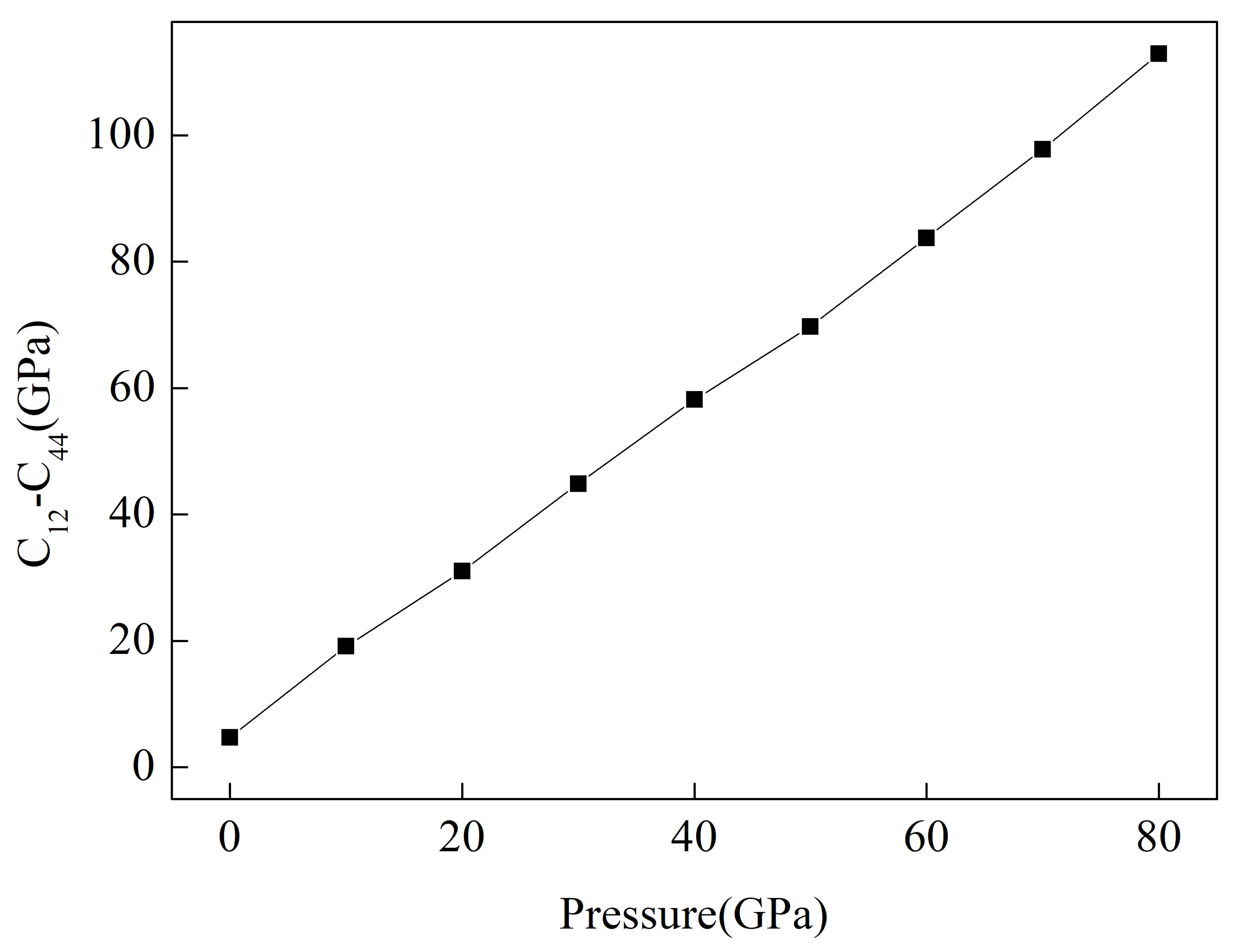
3.2. Mechanical Properties
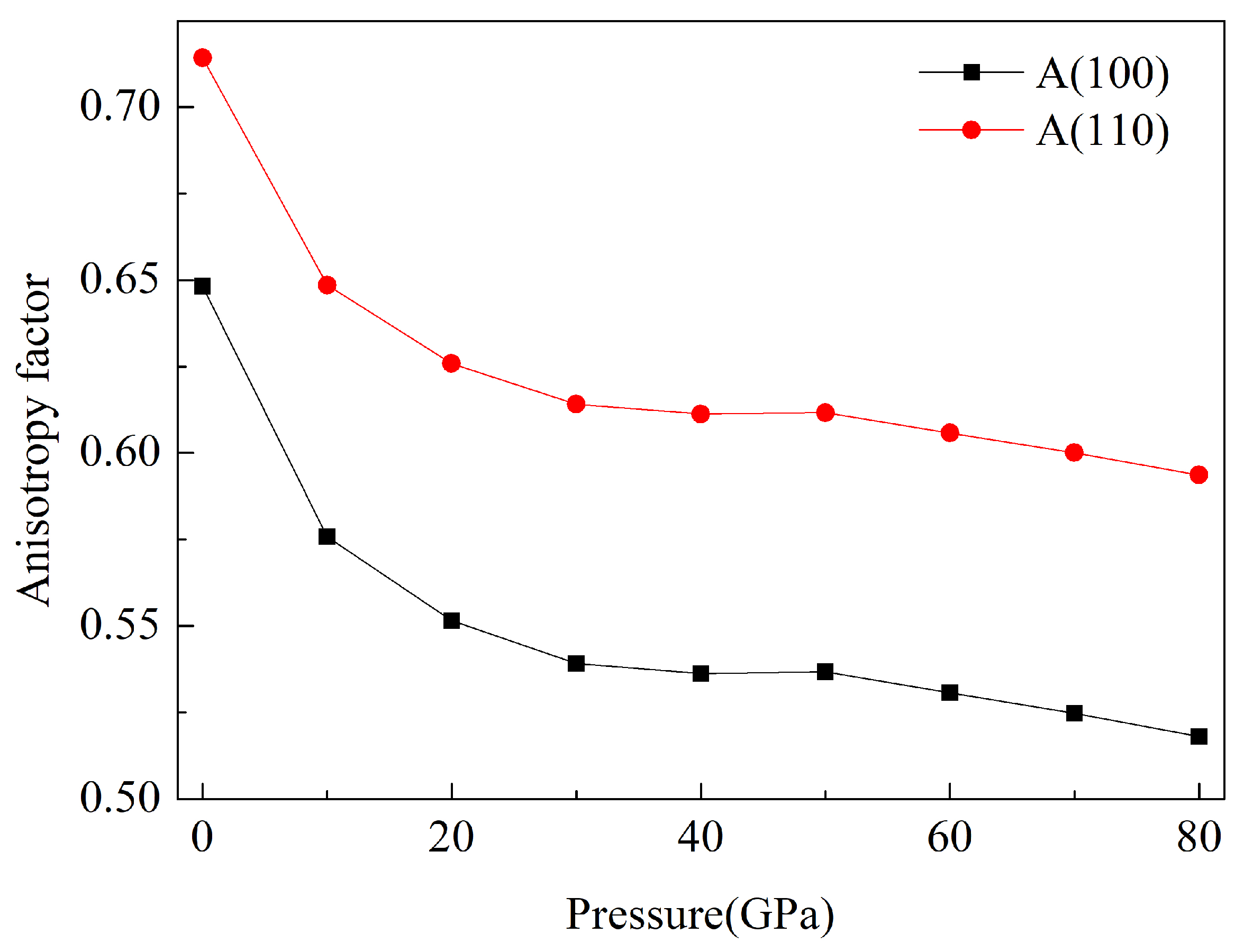
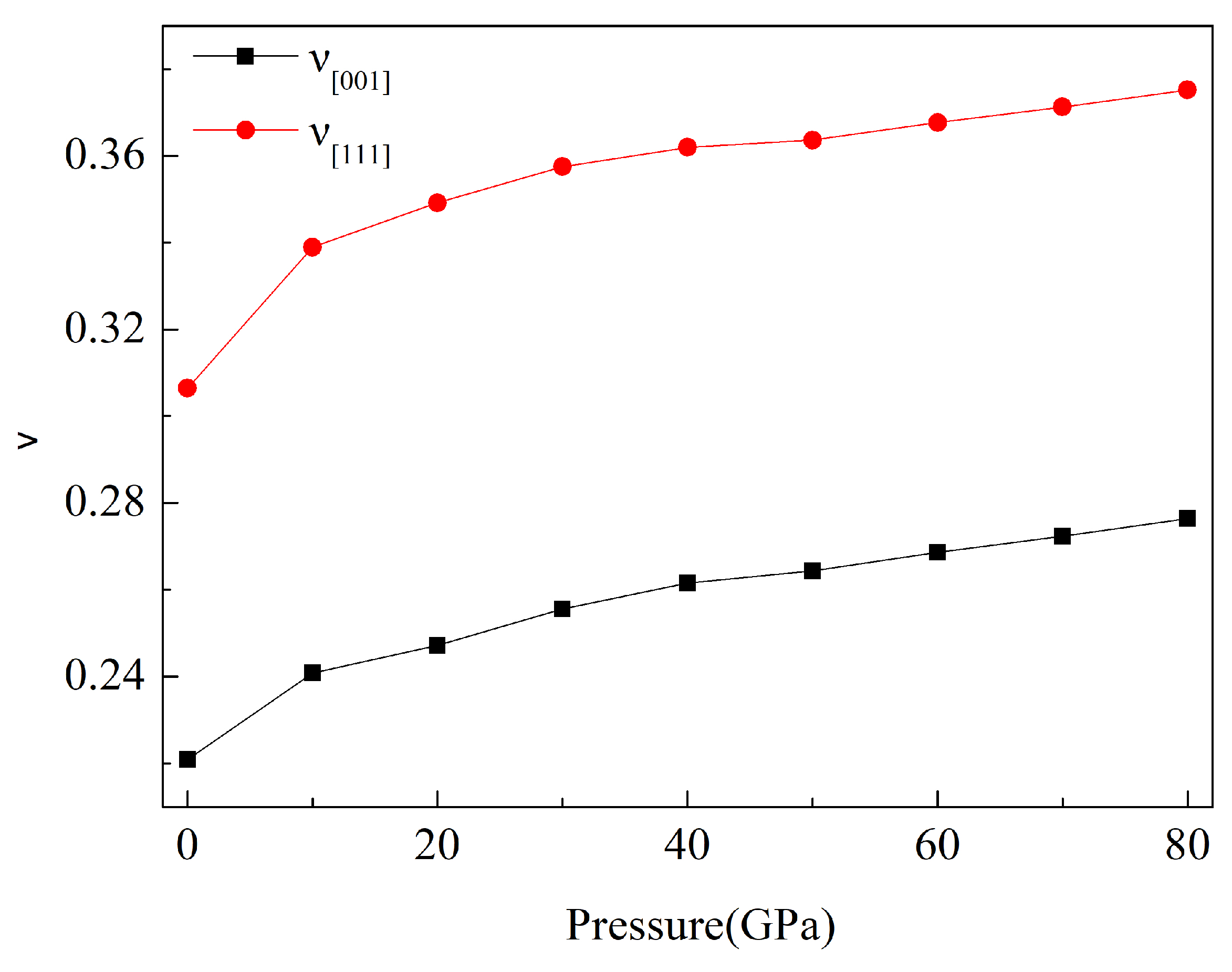
3.3. Anisotropy
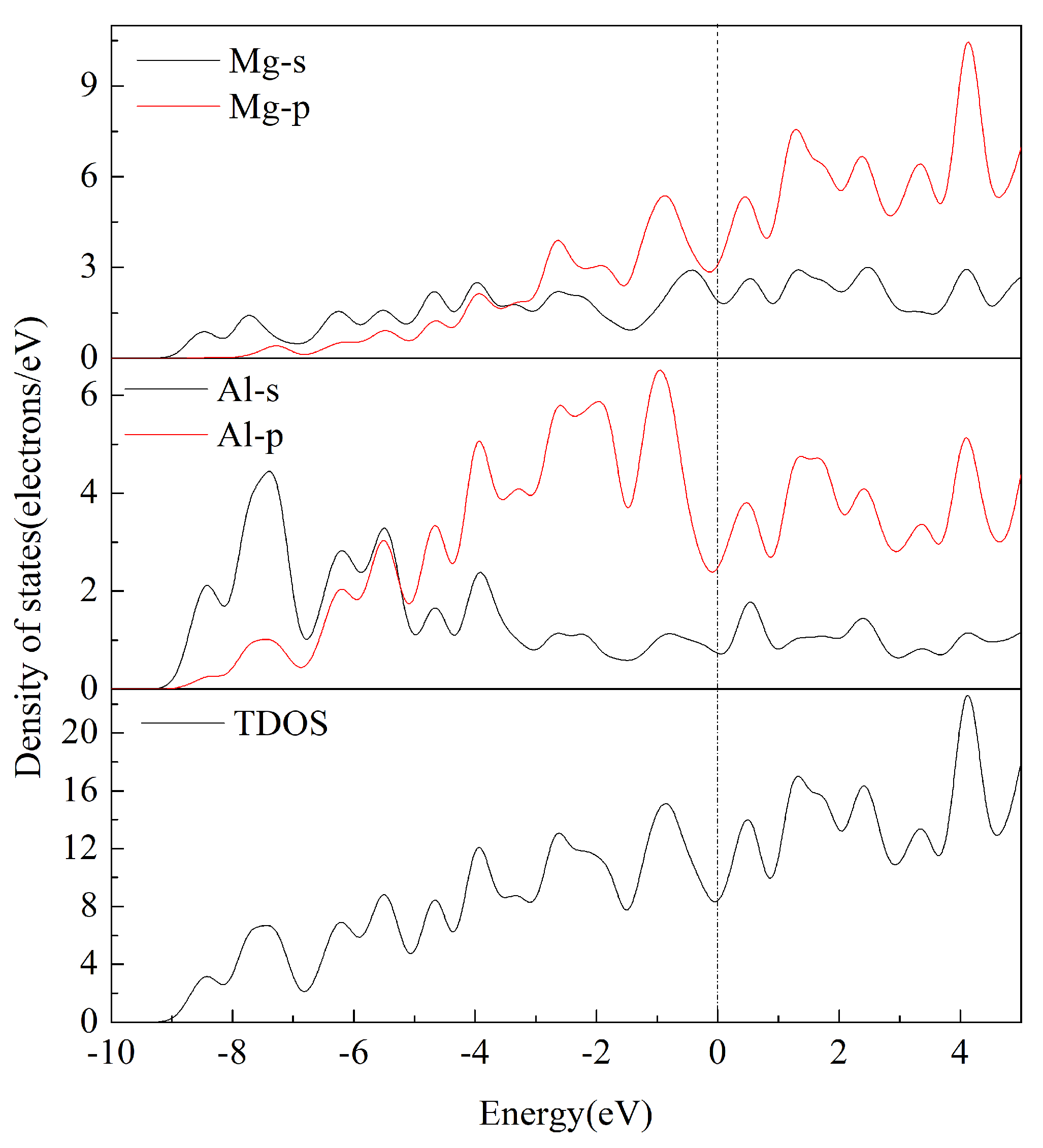
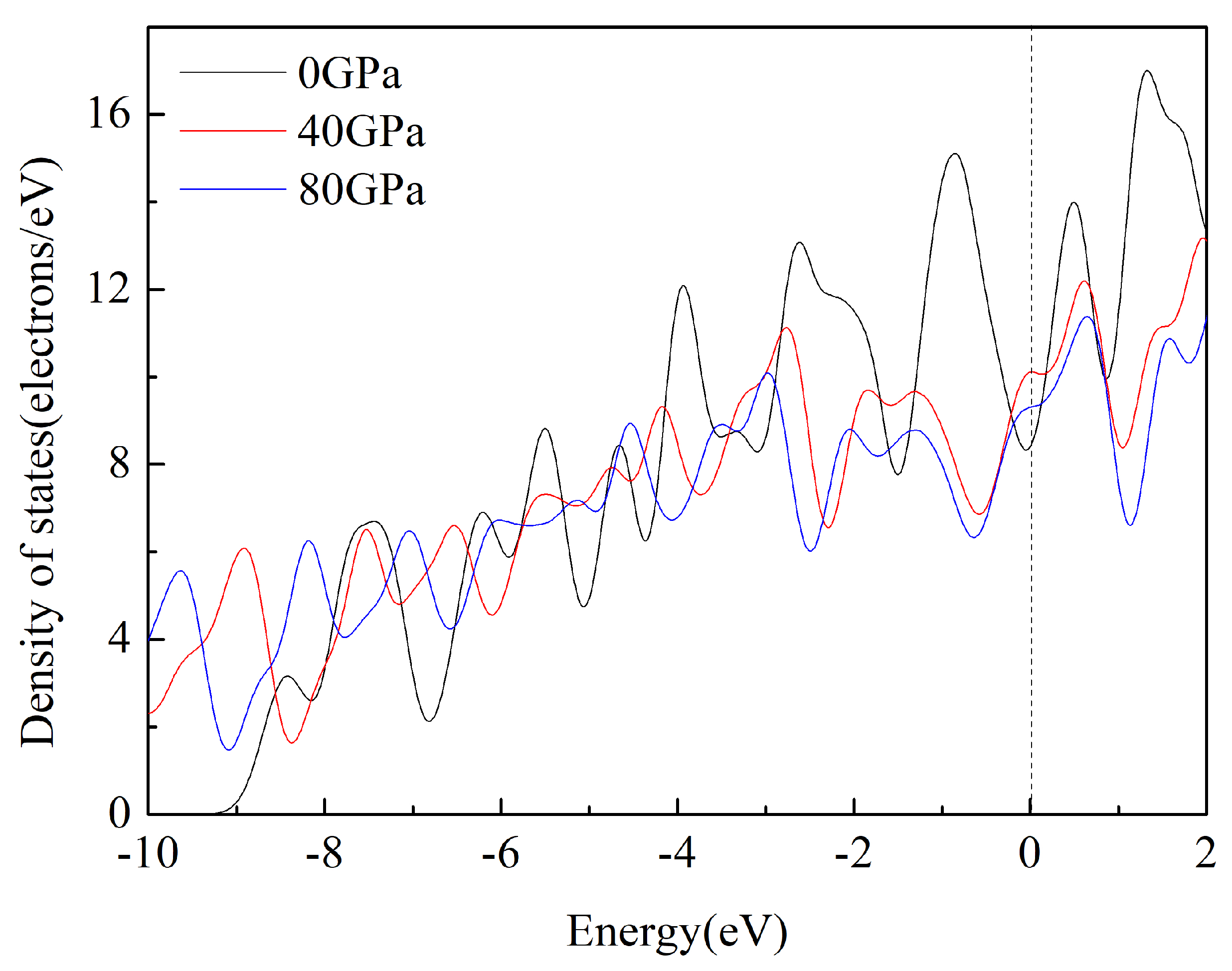
3.4. Electronic Properties
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sevvel, P.; Jaiganesh, V. Impact of process parameters during friction stir welding of AZ80A Mg alloy. Sci. Technol. Weld. Join. 2016, 21, 83–90. [Google Scholar] [CrossRef]
- Ji, S.; Huang, R.; Meng, X.; Zhang, L.; Huang, Y. Enhancing friction stir weldability of 6061-T6 Al and AZ31B Mg alloys assisted by external non-rotational shoulder. J. Mater. Eng. Perform. 2017, 26, 2359–2367. [Google Scholar] [CrossRef]
- Potzies, C.; Kainer, K.U. Fatigue of magnesium alloys. Adv. Eng. Mater. 2004, 6, 281–289. [Google Scholar] [CrossRef]
- Bettles, C.J.; Gibson, M. Microstructural Design for Enhanced Elevated Temperature Properties in Sand-Castable Magnesium Alloys. Adv. Eng. Mater. 2003, 5, 859–865. [Google Scholar] [CrossRef]
- Mordike, B. Creep-resistant magnesium alloys. Mater. Sci. Eng. A 2002, 324, 103–112. [Google Scholar] [CrossRef]
- Suzuki, A.; Saddock, N.; Jones, J.; Pollock, T. Solidification paths and eutectic intermetallic phases in Mg–Al–Ca ternary alloys. Acta Mater. 2005, 53, 2823–2834. [Google Scholar] [CrossRef]
- Mordike, B.; Ebert, T. Magnesium: Properties—Applications—Potential. Mater. Sci. Eng. A 2001, 302, 37–45. [Google Scholar] [CrossRef]
- Liu, L. Welding and Joining of Magnesium Alloys; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Luo, A.; Pekguleryuz, M. Cast magnesium alloys for elevated temperature applications. J. Mater. Sci. 1994, 29, 5259–5271. [Google Scholar] [CrossRef]
- Luo, A.A. Recent magnesium alloy development for elevated temperature applications. Int. Mater. Rev. 2004, 49, 13–30. [Google Scholar] [CrossRef]
- Jia, J.; Xu, Y.; Yang, Y.; Chen, C.; Liu, W.; Hu, L.; Luo, J. Microstructure evolution of an AZ91D magnesium alloy subjected to intense plastic straining. J. Alloys Compd. 2017, 721, 347–362. [Google Scholar] [CrossRef]
- Wang, N.; Yu, W.Y.; Tang, B.Y.; Peng, L.M.; Ding, W.J. Structural and mechanical properties of Mg17Al12 and Mg24Y5 from first-principles calculations. J. Phys. D Appl. Phys. 2008, 41, 195408. [Google Scholar] [CrossRef]
- Yu, F.; Sun, J.X.; Yang, W.; Tian, R.G.; Ji, G.F. A study of the phase transitions, electronic structures and optical properties of Mg2Si under high pressure. Solid State Commun. 2010, 150, 620–624. [Google Scholar] [CrossRef]
- Wang, Z.L.; Wei, Z.J.; Wang, H.W.; Cao, L. Effects of high pressure on microstructure and phase of Al–Mg–Zn alloy. Int. J. Cast Met. Res. 2006, 19, 269–273. [Google Scholar] [CrossRef]
- Milman, V.; Winkler, B.; White, J.A.; Pickard, C.J.; Payne, M.C.; Akhmatskaya, E.V.; Nobes, R.H. Electronic structure, properties, and phase stability of inorganic crystals: A pseudopotential plane-wave study. Int. J. Quantum Chem. 2000, 77, 895–910. [Google Scholar] [CrossRef]
- Segall, M.D.; Lindan, P.J.D.; Probert, M.J.; Pickard, C.J.; Hasnip, P.J.; Clark, S.J.; Payne, M.C. First-principles simulation: Ideas, illustrations and the CASTEP code. J. Phys. Condens. Matter 2002, 14, 2717–2744. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.J.; Refson, K.; Payne, M.C. First Principles Methods Using CASTEP. Z. fur Krist. 2005, 220, 567–570. [Google Scholar] [CrossRef] [Green Version]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef] [Green Version]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Hamann, D.R. Optimized norm-conserving Vanderbilt pseudopotentials. Phys. Rev. B 2013, 88, 085117. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Mull, B.T.; Baumeister, M.M.; Freund, H. Bimodal velocity distributions after ultraviolet-laser-induced desorption of NO from oxide surfaces. Experiments and results of model calculations. J. Chem. Phys. 1992, 96, 7108–7116. [Google Scholar] [CrossRef]
- Birch, F. Finite Elastic Strain of Cubic Crystals. Phys. Rev. 1947, 71, 809–824. [Google Scholar] [CrossRef]
- Zhuang, H.; Chen, M.; Carter, E.A. Elastic and thermodynamic properties of complex Mg-Al intermetallic compounds via orbital-free density functional theory. Phys. Rev. Appl. 2016, 5, 064021. [Google Scholar] [CrossRef] [Green Version]
- First-principles calculations of the elastic, phonon and thermodynamic properties of Al12Mg17. Acta Mater. 2010, 58, 4012–4018. [CrossRef]
- Hu, W.C.; Liu, Y.; Hu, X.W.; Li, D.J.; Zeng, X.Q.; Yang, X.; Xu, Y.X.; Zeng, X.S.; Wang, K.G.; Huang, B.L. Predictions of mechanical and thermodynamic properties of Mg17Al12 and Mg2Sn from first-principles calculations. Philos. Mag. 2015, 95, 1626–1645. [Google Scholar] [CrossRef]
- Zhou, Y.; Dang, M.; Sun, L.; Zhai, W.; Dong, H.; Gao, Q.; Zhao, F.; Peng, J. First–principle studies on the electronic structural, thermodynamics and elastic properties of Mg17Al12 intermediate phase under high pressure. Mater. Res. Express 2019, 6, 0865e1. [Google Scholar] [CrossRef]
- Wang, J.; Yip, S.; Phillpot, S.; Wolf, D. Crystal instabilities at finite strain. Phys. Rev. Lett. 1993, 71, 4182. [Google Scholar] [CrossRef]
- Huang, Z.; Zhao, Y.; Hou, H.; Han, P. Electronic structural, elastic properties and thermodynamics of Mg17Al12, Mg2Si and Al2Y phases from first-principles calculations. Phys. B Condens. Matter 2012, 407, 1075–1081. [Google Scholar] [CrossRef]
- Zhou, D.; Liu, J.; Xu, S.; Peng, P. Thermal stability and elastic properties of Mg3Sb2 and Mg3Bi2 phases from first-principles calculations. Phys. B Condens. Matter 2010, 405, 2863–2868. [Google Scholar] [CrossRef]
- Pugh, S. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Nong, Z.S.; Zhu, J.C.; Yang, X.W.; Cao, Y.; Lai, Z.H.; Liu, Y.; Sun, W. First-principles calculations of the stability and hydrogen storage behavior of C14 Laves phase compound TiCrMn. Solid State Sci. 2014, 32, 1–7. [Google Scholar] [CrossRef]
- Pettifor, D. Theoretical predictions of structure and related properties of intermetallics. Mater. Sci. Technol. 1992, 8, 345–349. [Google Scholar] [CrossRef]
- Fu, H.; Li, D.; Peng, F.; Gao, T.; Cheng, X. Ab initio calculations of elastic constants and thermodynamic properties of NiAl under high pressures. Comput. Mater. Sci. 2008, 44, 774–778. [Google Scholar] [CrossRef]
- Johnson, R.A. Analytic nearest-neighbor model for fcc metals. Phys. Rev. B 1988, 37, 3924–3931. [Google Scholar] [CrossRef]
- Mattesini, M.; Ahuja, R.; Johansson, B. Cubic Hf3N4 and Zr3N4: A class of hard materials. Phys. Rev. B 2003, 68, 184108. [Google Scholar] [CrossRef]
- Fu, H.; Li, D.; Peng, F.; Gao, T.; Cheng, X. Structural and elastic properties of γTiAl under high pressure from electronic structure calculations. J. Alloys Compd. 2009, 473, 255–261. [Google Scholar] [CrossRef]
- Yoo, M. On the theory of anomalous yield behavior of Ni3 Al-Effect of elastic anisotropy. Scr. Metall. 1986, 20, 915–920. [Google Scholar] [CrossRef]
- Lau, K.; McCurdy, A. Elastic anisotropy factors for orthorhombic, tetragonal, and hexagonal crystals. Phys. Rev. B 1998, 58, 8980. [Google Scholar] [CrossRef]
- Fu, H.; Li, X.F.; Liu, W.cF.; Ma, Y.; Tao, G.; Hong, X. Electronic and dynamical properties of NiAl studied from first principles. Intermetallics 2011, 19, 1959–1967. [Google Scholar] [CrossRef]
- Reed, R.P.; Clark, A.F. Materials at Low Temperatures; American Society of Metals: Metals Park, OH, USA, 1983. [Google Scholar] [CrossRef]
- Friák, M.; Šob, M.; Vitek, V. Ab initio calculation of tensile strength in iron. Philos. Mag. 2003, 83, 3529–3537. [Google Scholar] [CrossRef]
| B | G | E | |||||
|---|---|---|---|---|---|---|---|
| Present | 92.52 | 26.24 | 21.48 | 48.33 | 25.57 | 65.21 | 0.27 |
| Literature [28] | 116.90 | 18.01 | 35.15 | 50.97 | 40.31 | 95.69 | 0.18 |
| Literature [26] | 98.00 | 28.00 | 31.00 | 51.55 | 32.54 | 80.60 | 0.24 |
| Literature [27] | 90.50 | 26.70 | 29.70 | 48.02 | 30.56 | 76.30 | 0.24 |
| Literature [12] | 87.00 | 29.00 | 20.00 | 48.33 | 23.22 | 60.04 | 0.29 |
| Literature [30] | 88.38 | 23.54 | 26.95 | 45.15 | 29.14 | 71.94 | 0.23 |
| Literature [31] | 89.86 | 27.21 | 33.32 | 48.09 | 32.49 | 79.62 | 0.23 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, C.; Tu, Z.; Liao, L.; Liu, Z.; Wen, Y.; Zeng, X. Investigating the β-Mg17Al12 Alloy under Pressure Using First-Principles Methods: Structure, Elastic Properties, and Mechanical Properties. Crystals 2022, 12, 1741. https://doi.org/10.3390/cryst12121741
Xiao C, Tu Z, Liao L, Liu Z, Wen Y, Zeng X. Investigating the β-Mg17Al12 Alloy under Pressure Using First-Principles Methods: Structure, Elastic Properties, and Mechanical Properties. Crystals. 2022; 12(12):1741. https://doi.org/10.3390/cryst12121741
Chicago/Turabian StyleXiao, Chuncai, Zongxing Tu, Luliang Liao, Zhiwen Liu, Yufeng Wen, and Xianshi Zeng. 2022. "Investigating the β-Mg17Al12 Alloy under Pressure Using First-Principles Methods: Structure, Elastic Properties, and Mechanical Properties" Crystals 12, no. 12: 1741. https://doi.org/10.3390/cryst12121741
APA StyleXiao, C., Tu, Z., Liao, L., Liu, Z., Wen, Y., & Zeng, X. (2022). Investigating the β-Mg17Al12 Alloy under Pressure Using First-Principles Methods: Structure, Elastic Properties, and Mechanical Properties. Crystals, 12(12), 1741. https://doi.org/10.3390/cryst12121741






