On the Theory of Unsteady-State Operation of Bulk Continuous Crystallization
Abstract
1. Introduction
2. The Integro-Differential Model and Its Analytical Solution
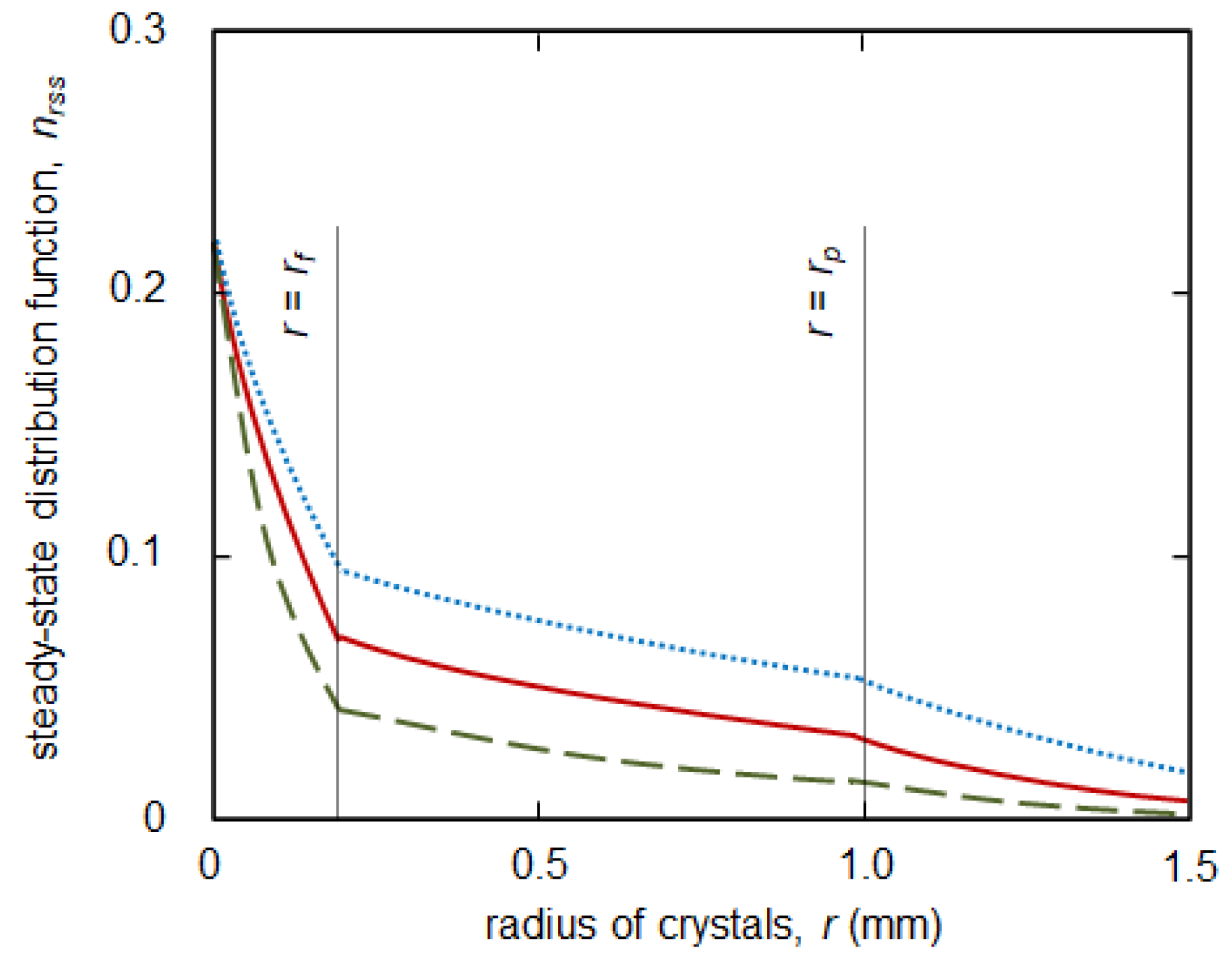
2.1. The Steady-State Solutions
2.2. The Unsteady-State Solutions
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kelton, K.F.; Greer, A.L. Nucleation in Condensed Matter: Applications in Materials and Biology; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Dubrovskii, V.G. Nucleation Theory and Growth of Nanostructures; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Vekilov, P.G. Nucleation. Cryst. Growth Des. 2010, 10, 5007–5019. [Google Scholar] [CrossRef] [PubMed]
- Rosenberger, F.; Vekilov, P.G.; Muschol, M.; Thomas, B.R. Nucleation and crystallization of globular proteins—What we know and what is missing. J. Cryst. Growth 1996, 168, 1–27. [Google Scholar] [CrossRef]
- Toropova, L.V.; Makoveeva, E.V.; Osipov, S.I.; Malygin, A.P.; Yang, Y.; Alexandrov, D.V. Nucleation and growth of an ensemble of crystals during the intermediate stage of a phase transition in metastable liquids. Crystals 2022, 12, 895. [Google Scholar] [CrossRef]
- Mullin, J.W. Crystallization; Butterworths: London, UK, 1972. [Google Scholar]
- Buyevich, Y.A.; Mansurov, V.V. Kinetics of the intermediate stage of phase transition in batch crystallization. J. Cryst. Growth 1990, 104, 861–867. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Nizovtseva, I.G. On the theory of crystal growth in metastable systems with biomedical applications: Protein and insulin crystallization. Philos. Trans. R. Soc. A 2019, 377, 20180214. [Google Scholar] [CrossRef]
- Buyevich, Y.A.; Goldobin, Y.M.; Yasnikov, G.P. Evolution of a particulate system governed by exchange with its environment. Int. J. Heat Mass Trans. 1994, 37, 3003–3014. [Google Scholar] [CrossRef]
- Barlow, D.A. Theory of the intermediate stage of crystal growth with applications to protein crystallization. J. Cryst. Growth 2009, 311, 2480–2483. [Google Scholar] [CrossRef]
- Barlow, D.A. Theory of the intermediate stage of crystal growth with applications to insulin crystallization. J. Cryst. Growth 2017, 470, 8–14. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Alexandrova, I.V.; Ivanov, A.A.; Malygin, A.P.; Starodumov, I.O.; Toropova, L.V. On the theory of the nonstationary spherical crystal growth in supercooled melts and supersaturated solutions. Russ. Metall. (Metally) 2019, 2019, 787–794. [Google Scholar] [CrossRef]
- Alexandrova, I.V.; Ivanov, A.A.; Malygin, A.P.; Alexandrov, D.V.; Nikishina, M.A. Growth of spherical and ellipsoidal crystals in a metastable liquid. Eur. Phys. J. Spec. Top. 2022, 231, 1089–1100. [Google Scholar] [CrossRef]
- Alexandrova, I.V.; Alexandrov, D.V. Dynamics of particulate assemblages in metastable liquids: A test of theory with nucleation and growth kinetics. Philos. Trans. R. Soc. A 2020, 378, 20190245. [Google Scholar] [CrossRef] [PubMed]
- Prieler, R.; Hubert, J.; Li, D.; Verleye, B.; Haberkern, R.; Emmerich, H. An anisotropic phase-field crystal model for heterogeneous nucleation of ellipsoidal colloids. J. Phys. Condens. Matter 2009, 21, 464110. [Google Scholar] [CrossRef] [PubMed]
- Kertis, F.; Khurshid, S.; Okman, O.; Kysar, J.W.; Govada, L.; Chayen, N.; Erlebacher, J. Heterogeneous nucleation of protein crystals using nanoporous gold nucleants. J. Mater. Chem. 2012, 22, 21928–21934. [Google Scholar] [CrossRef]
- Ocaña, M.; Morales, M.P.; Serna, C.J. The growth mechanism of α-Fe2O3 ellipsoidal particles in solution. J. Colloid Int. Sci. 1995, 171, 85–91. [Google Scholar] [CrossRef]
- Shepilov, M.P.; Baik, D.S. Computer simulation of crystallization kinetics for the model with simultaneous nucleation of randomly-oriented ellipsoidal crystals. J. Non-Crystall. Solids 1994, 171, 141–156. [Google Scholar] [CrossRef]
- Nikishina, M.A.; Alexandrov, D.V. Nucleation and growth dynamics of ellipsoidal crystals in metastable liquids. Philos. Trans. R. Soc. A 2021, 379, 20200306. [Google Scholar] [CrossRef]
- Nikishina, M.A.; Alexandrov, D.V. Nucleation and growth of ellipsoidal crystals in a supercooled binary melt. J. Phys. A Math. Theor. 2022, 55, 255701. [Google Scholar] [CrossRef]
- Buyevich, Y.A.; Mansurov, V.V.; Natalukha, I.A. Instability and unsteady processes of the bulk continuous crystallization-I. Linear stability analysis. Chem. Eng. Sci. 1991, 46, 2573–2578. [Google Scholar] [CrossRef]
- Vollmer, U.; Raisch, J. H∞-Control of a continuous crystallizer. Control Eng. Pract. 2001, 9, 837–845. [Google Scholar] [CrossRef]
- Rachah, A.; Noll, D.; Espitalier, F.; Baillon, F. A mathematical model for continuous crystallization. Math. Methods Appl. Sci. 2015, 39, 1101–1120. [Google Scholar] [CrossRef]
- Makoveeva, E.V.; Alexandrov, D.V. Mathematical simulation of the crystal nucleation and growth at the intermediate stage of a phase transition. Russ. Metall. (Metally) 2018, 2018, 707–715. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Ivanov, A.A.; Nizovtseva, I.G.; Lippmann, S.; Alexandrova, I.V.; Makoveeva, E.V. Evolution of a polydisperse ensemble of spherical particles in a metastable medium with allowance for heat and mass exchange with the environment. Crystals 2022, 12, 949. [Google Scholar] [CrossRef]
- Janse, A.H. Nucleation and Crystal Growth in Batch Crystallizers; Delft University of Technology: Delft, The Netherlands, 1977. [Google Scholar]
- Pot, A. Industrial Sucrose Crystallization; Delft University of Technology: Delft, The Netherlands, 1980. [Google Scholar]
- Kouchi, A.; Tsuchiyama, A.; Sunagawa, I. Effect of stirring on crystallization kinetics of basalt: Texture and element partitioning. Contr. Mineral. Petrol. 1986, 93, 429–438. [Google Scholar] [CrossRef]
- Adachi, H.; Matsumura, H.; Niino, A.; Takano, K.; Kinoshita, T.; Warizaya, M.; Inoue, T.; Mori, Y.; Sasaki, T. Improving the quality of protein crystals using stirring crystallization. Jpn. J. Appl. Phys. 2004, 43, L522. [Google Scholar] [CrossRef]
- Alexandrov, D.V. Nucleation and crystal growth kinetics during solidification: The role of crystallite withdrawal rate and external heat and mass sources. Chem. Eng. Sci. 2014, 117, 156–160. [Google Scholar] [CrossRef]
- Buyevich, Y.A.; Natalukha, I. Unsteady processes of combined polymerization and crystallization in continuous apparatuses. Chem. Eng. Sci. 1994, 49, 3241–3247. [Google Scholar] [CrossRef]
- Lifshitz, E.M.; Pitaevskii, L.P. Physical Kinetics; Pergamon Press: Oxford, UK, 1981. [Google Scholar]
- Slezov, V.V. Kinetics of First-Order Phase Transitions; Wiley, VCH: Hoboken, NJ, USA, 2009. [Google Scholar]
- Alyab’eva, A.V.; Buyevich, Y.A.; Mansurov, V.V. Evolution of a particulate assemblage due to coalescence combined with coagulation. J. Phys. II Fr. 1994, 4, 951–957. [Google Scholar] [CrossRef]
- Alexandrov, D.V. Kinetics of particle coarsening with allowance for Ostwald ripening and coagulation. J. Phys. Condens. Matter 2016, 28, 035102. [Google Scholar] [CrossRef]
- Hunt, J.R. Self-similar particle-size distributions during coagulation: Theory and experimental verification. J. Fluid Mech. 1982, 122, 169–185. [Google Scholar] [CrossRef]
- Alexandrova, I.V.; Alexandrov, D.V.; Makoveeva, E.V. Ostwald ripening in the presence of simultaneous occurrence of various mass transfer mechanisms: An extension of the Lifshitz–Slyozov theory. Philos. Trans. R. Soc. A 2021, 379, 20200308. [Google Scholar] [CrossRef]
- Alexandrova, I.V.; Alexandrov, D.V. A complete analytical solution of unsteady coagulation equations and transition between the intermediate and concluding stages of a phase transformation. Eur. Phys. J. Spec. Top. 2022, 231, 1115–1121. [Google Scholar] [CrossRef]
- Toropova, L.V.; Alexandrov, D.V. Dynamical law of the phase interface motion in the presence of crystals nucleation. Sci. Rep. 2022, 12, 10997. [Google Scholar] [CrossRef] [PubMed]
- Alexandrov, D.V.; Toropova, L.V. The role of incoming flow on crystallization of undercooled liquids with a two-phase layer. Sci. Rep. 2022, 12, 17857. [Google Scholar] [CrossRef] [PubMed]
- Ivanov, A.A.; Alexandrova, I.V.; Alexandrov, D.V. Phase transformations in metastable liquids combined with polymerization. Philos. Trans. R. Soc. A 2019, 377, 20180215. [Google Scholar] [CrossRef] [PubMed]
- Buyevich, Y.A.; Mansurov, V.V.; Natalukha, I.A. Instability and unsteady processes of the bulk continuous crystallization-II. Non-linear periodic regimes. Chem. Eng. Sci. 1991, 46, 2579–2588. [Google Scholar] [CrossRef]
- Natalukha, I.A. Unstable regimes of continuous crystallization in a cascade of well-mixed vessels. Chem. Eng. Sci. 1996, 51, 1181–1185. [Google Scholar] [CrossRef]
- Ivanov, A.A.; Alexandrova, I.V.; Alexandrov, D.V. Towards the theory of phase transformations in metastable liquids. Analytical solutions and stability analysis. Eur. Phys. J. Spec. Top. 2020, 229, 365–373. [Google Scholar] [CrossRef]
- Makoveeva, E.V.; Alexandrov, D.V. How the shift in the phase transition temperature influences the evolution of crystals during the intermediate stage of phase transformations. Eur. Phys. J. Spec. Top. 2020, 229, 2923–2935. [Google Scholar] [CrossRef]
- Ditkin, V.A.; Prudnikov, A.P. Integral Transforms and Operational Calculus; Pergamon Press: Oxford, UK, 1965. [Google Scholar]
- von Doetsch, G. Anleitung zum Praktischen Gebrauch der Laplace-Transformation und der Z-Transformation; R. Oldenbourg: Munich, Germany, 1967. [Google Scholar]
- McGinty, J.; Yazdanpanah, N.; Price, C.; ter Horst, J.H.; Sefcik, J. Nucleation and crystal growth in continuous crystallization. In The Handbook of Continuous Crystallization; Yazdanpanah, N., Nagy, Z.K., Eds.; Royal Society of Chemistry: London, UK, 2020; pp. 1–50. [Google Scholar]
- Alexandrov, D.V. A nonlinear instability analysis of crystallization processes with a two-phase zone. J. Metast. Nanocrystalline Mater. 2004, 20–21, 468–473. [Google Scholar] [CrossRef]
- Alexandrov, D.V. Absolute morphological stability of the self-similar solidification with a planar front. J. Metast. Nanocrystalline Mater. 2004, 20–21, 476–481. [Google Scholar] [CrossRef]
- Feltham, D.L.; Worster, M.G. Flow-induced morphological instability of a mushy layer. J. Fluid Mech. 1999, 391, 337–357. [Google Scholar] [CrossRef]
- Anderson, D.M.; Worster, M.G. A new oscillatory instability in a mushy layer during the solidification of binary alloys. J. Fluid Mech. 1996, 307, 245–267. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Malygin, A.P. Flow-induced morphological instability and solidification with the slurry and mushy layers in the presence of convection. Int. J. Heat Mass Trans. 2012, 55, 3196–3204. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Ivanov, A.O. Dynamic stability analysis of the solidification of binary melts in the presence of a mushy region: Changeover of instability. J. Cryst. Growth 2000, 210, 797–810. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Makoveeva, E.V.; Alexandrov, D.V.; Ivanov, A.A. On the Theory of Unsteady-State Operation of Bulk Continuous Crystallization. Crystals 2022, 12, 1634. https://doi.org/10.3390/cryst12111634
Makoveeva EV, Alexandrov DV, Ivanov AA. On the Theory of Unsteady-State Operation of Bulk Continuous Crystallization. Crystals. 2022; 12(11):1634. https://doi.org/10.3390/cryst12111634
Chicago/Turabian StyleMakoveeva, Eugenya V., Dmitri V. Alexandrov, and Alexander A. Ivanov. 2022. "On the Theory of Unsteady-State Operation of Bulk Continuous Crystallization" Crystals 12, no. 11: 1634. https://doi.org/10.3390/cryst12111634
APA StyleMakoveeva, E. V., Alexandrov, D. V., & Ivanov, A. A. (2022). On the Theory of Unsteady-State Operation of Bulk Continuous Crystallization. Crystals, 12(11), 1634. https://doi.org/10.3390/cryst12111634






