Mathematical Modeling of the Solid–Liquid Interface Propagation by the Boundary Integral Method with Nonlinear Liquidus Equation and Atomic Kinetics
Abstract
1. Introduction
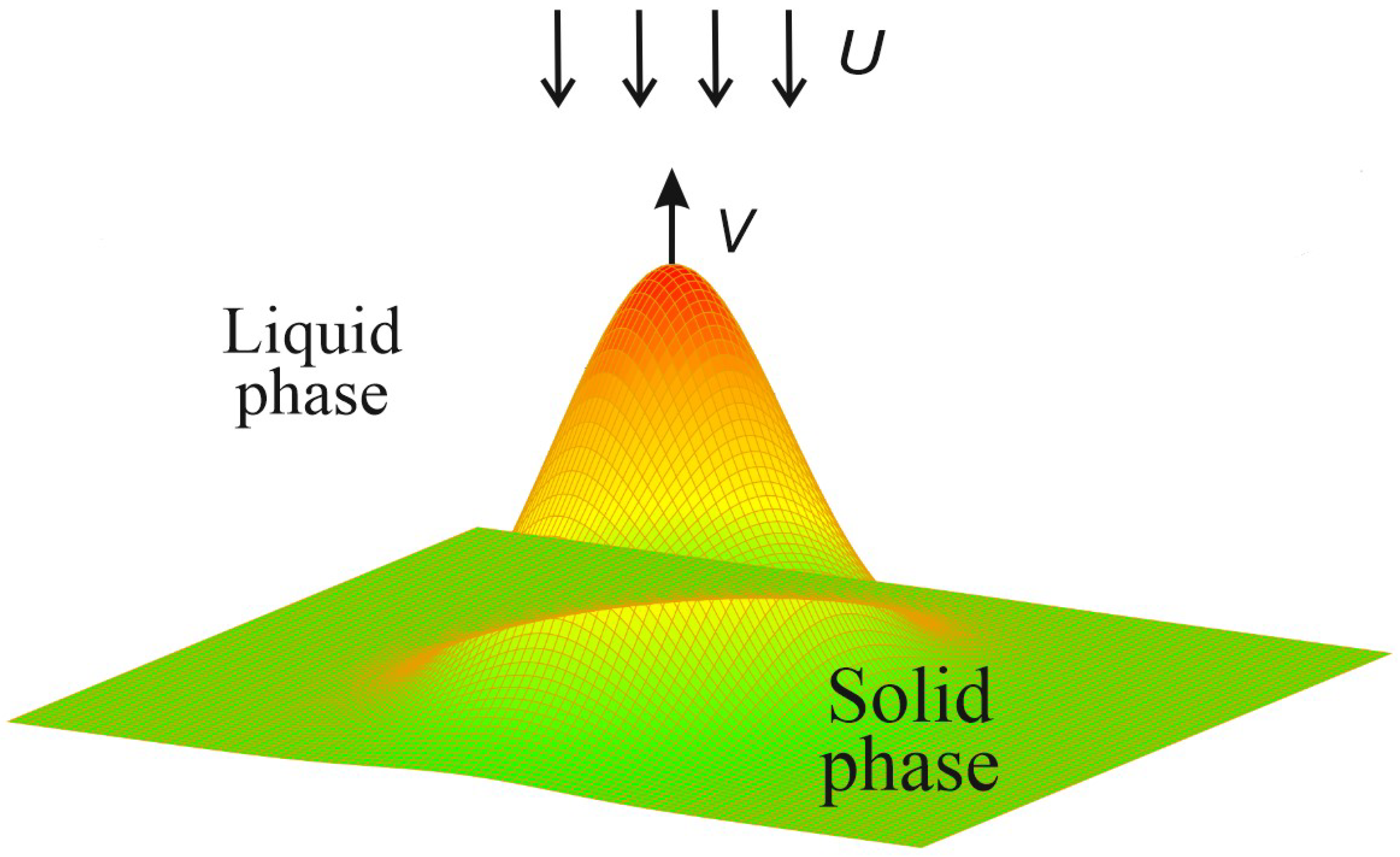
2. The Model and BIE for the Interface Function
2.1. The Heat and Mass Transfer Model
2.2. The Green’s Function Technique
2.3. Stationary Growth
2.4. The Parabolic Cylinder Reference Frame
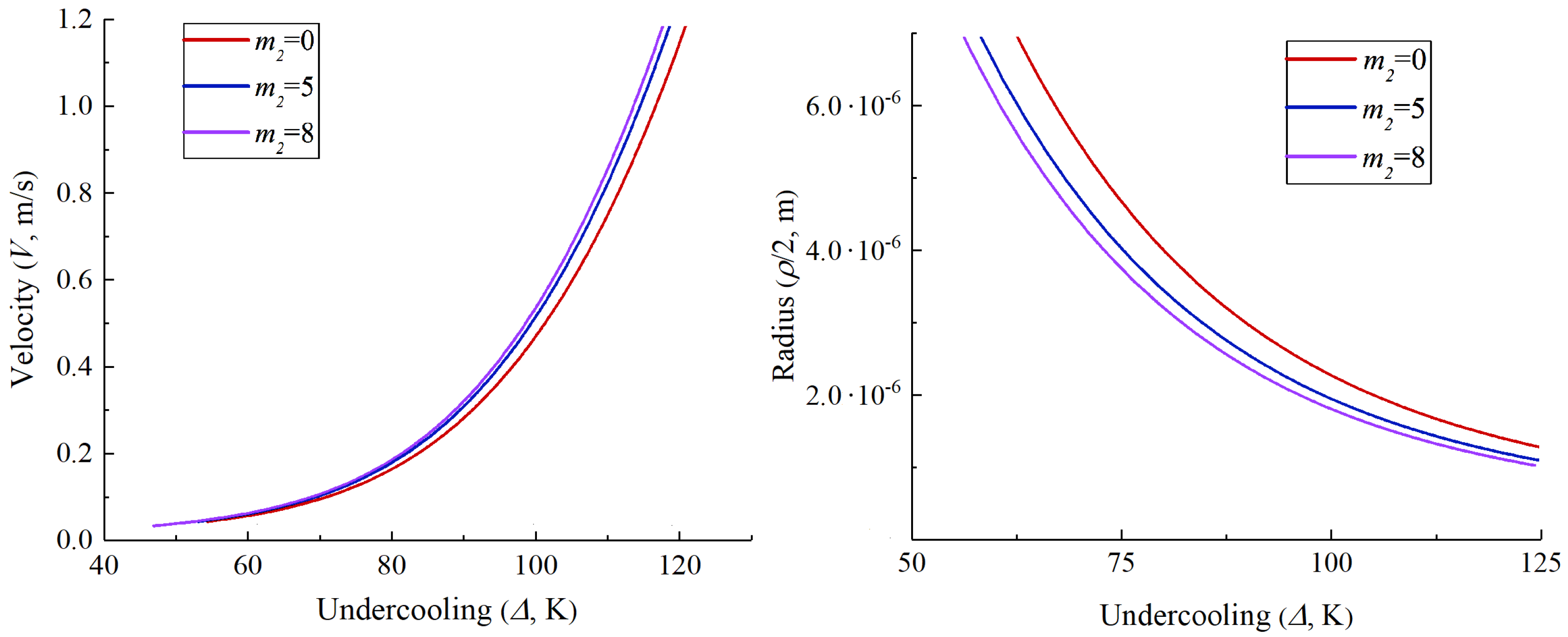
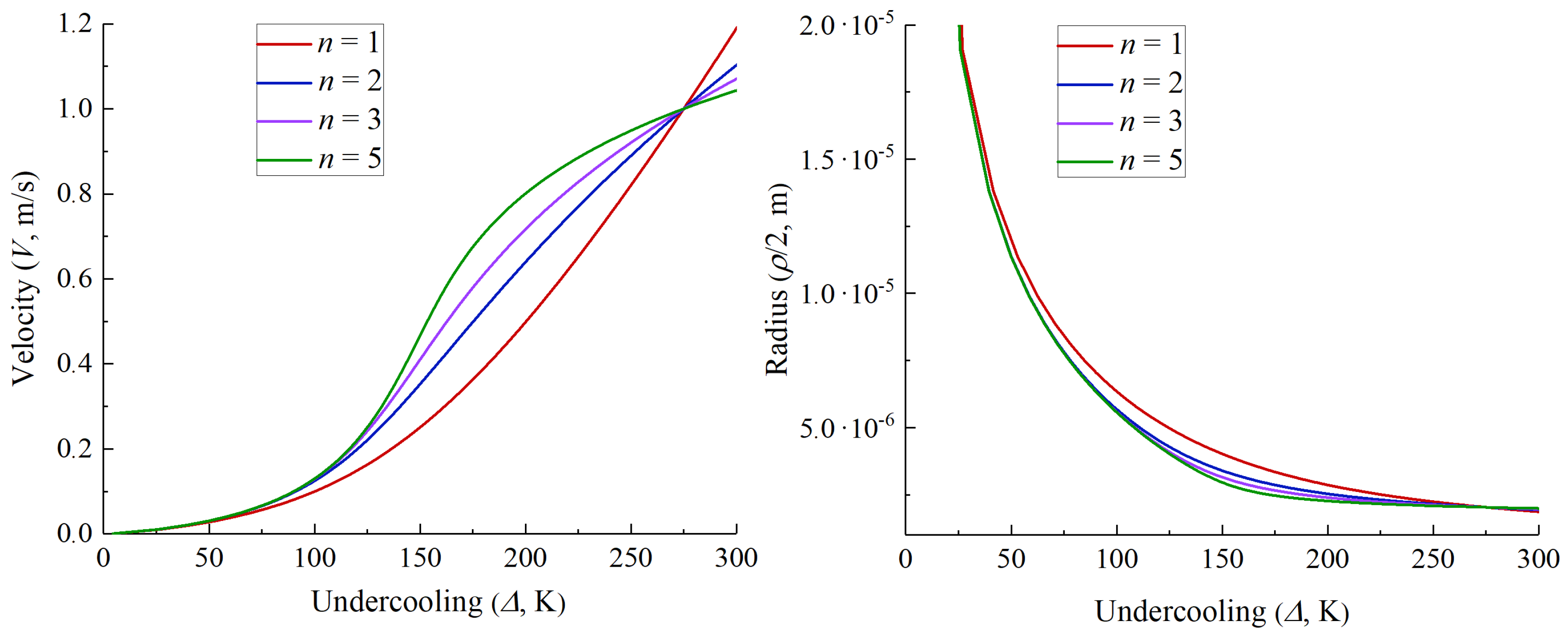
3. Numerical Examples
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pelcé, P. Dynamics of Curved Fronts; Academic Press: Boston, MA, USA, 1988. [Google Scholar]
- Kessler, D.A.; Koplik, J.; Levine, H. Pattern selection in fingered growth phenomena. Adv. Phys. 1988, 37, 255–339. [Google Scholar] [CrossRef]
- Almgren, R.; Dai, W.-S.; Hakim, V. Scaling behavior in anisotropic Hele–Shaw flow. Phys. Rev. Lett. 1993, 71, 3461–3464. [Google Scholar] [CrossRef] [PubMed]
- Alexandrov, D.V. Self-similar solidification: Morphological stability of the regime. Int. J. Heat Mass Trans. 2004, 47, 1383–1389. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Ivanov, A.A. Solidification of a ternary melt from a cooled boundary, or nonlinear dynamics of mushy layers. Int. J. Heat Mass Trans. 2009, 52, 4807–4811. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Nizovtseva, I.G.; Malygin, A.P.; Huang, H.-N.; Lee, D. Unidirectional solidification of binary melts from a cooled boundary: Analytical solutions of a nonlinear diffusion-limited problem. J. Phys. Condens. Matter 2008, 20, 114105. [Google Scholar] [CrossRef]
- Nash, G.E. Capillary-limited, steady state dendritic growth. Part I. Theoretical development. NRL Rep. 1974, 7679. [Google Scholar]
- Nash, G.E.; Glicksman, M.E. Capillary-limited steady-state dendritic growth: I. Theoretical development. Acta Metall. 1974, 22, 1283–1290. [Google Scholar] [CrossRef]
- Langer, J.S.; Turski, L.A. Studies in the theory of interfacial stability: I. Stationary symmetric model. Acta Metall. 1977, 25, 1113–1119. [Google Scholar] [CrossRef]
- Langer, J.S. Studies in the theory of interfacial stability: II. Moving symmetric model. Acta Metall. 1977, 25, 1121–1137. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Galenko, P.K. Boundary integral approach for propagating interfaces in a binary non-isothermal mixture. Phys. A 2017, 469, 420–428. [Google Scholar] [CrossRef]
- Galenko, P.K.; Alexandrov, D.V.; Titova, E.A. The boundary integral theory for slow and rapid curved solid–liquid interfaces propagating into binary systems. Philos. Trans. R. Soc. A 2018, 376, 20170218. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Galenko, P.K. Selected mode for rapidly growing needle-like dendrite controlled by heat and mass transport. Acta Mater. 2017, 137, 64–70. [Google Scholar] [CrossRef]
- Saville, D.A.; Beaghton, P.J. Growth of needle-shaped crystals in the presence of convection. Phys. Rev. A 1988, 37, 3423–3430. [Google Scholar] [CrossRef]
- Titova, E.A.; Alexandrov, D.V. The boundary integral equation for curved solid–liquid interfaces propagating into a binary liquid with convection. J. Phys. A Math. Theor. 2022, 55, 055701. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Bashkirtseva, I.A.; Ryashko, L.B. Nonlinear dynamics of mushy layers induced by external stochastic fluctuations. Philos. Trans. R. Soc. A 2018, 376, 20170216. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Rakhmatullina, I.V.; Malygin, A.P. On the theory of solidification with a two phase concentration supercooling zone. Russ. Metall. (Met.) 2010, 2010, 745–750. [Google Scholar] [CrossRef]
- Morse, P.M.; Feshbach, H. Methods of Theoretical Physics; Academic Press: Boston, MA, USA, 1953. [Google Scholar]
- Korn, G.A.; Korn, T.M. Mathematical Handbook for Scientists and Engineers: Definitions, Theorems, and Formulas for Reference and Review; McGraw-Hill Book Company: New York, NY, USA, 1968. [Google Scholar]
- Dash, S.K.; Gill, W.N. Foced convection heat and momentum transfer to dendritic structures (parabolic cylinders and paraboloids of revolution). Int. J. Heat Mass Transf. 1984, 27, 1345–1356. [Google Scholar]
- Alexandrov, D.V.; Galenko, P.K. A review on the theory of stable dendritic growth. Philos. Trans. R. Soc. A 2021, 379, 20200325. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Galenko, P.K. Selection criterion of stable mode of dendritic growth with n-fold symmetry at arbitrary Péclet numbers with a forced convection. In IUTAM Symposium on Recent Advances in Moving Boundary Problems in Mechanics; Springer: Cham, Switzerland, 2019; pp. 203–215. [Google Scholar]
- Deguen, R.; Alboussière, T.; Brito, D. On the existence and structure of a mush at the inner core boundary of the Earth. Phys. Earth Planet. Inter. 2007, 164, 36–49. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Britousova, A.V. Interdendritic spacing in growth processes with a mushy layer. AIP Conf. Proc. 2014, 1648, 850101. [Google Scholar]
- Toropova, L.V.; Alexandrov, D.V.; Rettenmayr, M.; Liu, D. Microstructure and morphology of Si crystals grown in pure Si and Al-Si melts. J. Phys. Condens. Matter 2022, 34, 094002. [Google Scholar] [CrossRef] [PubMed]
- Alexandrov, D.V.; Galenko, P.K. The shape of dendritic tips. Philos. Trans. R. Soc. A 2020, 378, 20190243. [Google Scholar] [CrossRef] [PubMed]
- Galenko, P.K.; Danilov, D.A. Model for free dendritic alloy growth under interfacial and bulk phase nonequilibrium conditions. J. Cryst. Growth 1999, 197, 992–1002. [Google Scholar] [CrossRef]
- Galenko, P.K.; Danilov, D.A. Selection of the dynamically stable regime of rapid solidification front motion in an isothermal binary alloy. J. Cryst. Growth 2000, 216, 512–526. [Google Scholar] [CrossRef]
- Starodumov, I.O.; Titova, E.A.; Pavlyuk, E.V.; Alexandrov, D.V. The tip of dendritic crystal in an inclined viscous flow. Crystals 2022, 12, 1590. [Google Scholar] [CrossRef]
- Brener, E.A.; Mel’nikov, V.A. Pattern selection in two-dimensional dendritic growth. Adv. Phys. 1991, 40, 53–97. [Google Scholar] [CrossRef]
- Buyevich, Y.A.; Mansurov, V.V.; Natalukha, I.A. Instability and unsteady processes of the bulk continuous crystallization. Chem. Eng. Sci. 1991, 46, 2573–2588. [Google Scholar] [CrossRef]
- Makoveeva, E.V.; Alexandrov, D.V. Mathematical simulation of the crystal nucleation and growth at the intermediate stage of a phase transition. Russ. Metall. (Met.) 2018, 2018, 707–715. [Google Scholar] [CrossRef]
- Makoveeva, E.V.; Alexandrov, D.V. On the theory of phase transformation process in a binary supercooled melt. Eur. Phys. J. Spec. Top. 2020, 229, 375–382. [Google Scholar] [CrossRef]
- Makoveeva, E.; Alexandrov, D.; Ivanov, A. Mathematical modeling of crystallization process from a supercooled binary melt. Math. Methods Appl. Sci. 2021, 44, 12244–12251. [Google Scholar] [CrossRef]
- Barlow, D.A.; LaVoie-Ingram, E.; Bayat, J. Population-balance study of protein crystal growth from solution using a hyperbolic rate law. J. Cryst. Growth 2022, 578, 126417. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Ivanov, A.A.; Nizovtseva, I.G.; Lippmann, S.; Alexandrova, I.V.; Makoveeva, E.V. Evolution of a polydisperse ensemble of spherical particles in a metastable medium with allowance for heat and mass exchange with the environment. Crystals 2022, 12, 949. [Google Scholar] [CrossRef]
- Toropova, L.V.; Alexandrov, D.V. Dynamical law of the phase interface motion in the presence of crystals nucleation. Sci. Rep. 2022, 12, 10997. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Toropova, L.V. The role of incoming flow on crystallization of undercooled liquids with a two-phase layer. Sci. Rep. 2022, 12, 17857. [Google Scholar] [CrossRef]
- Peppin, S.S.L.; Aussillous, P.; Huppert, H.E.; Worster, M.G. Steady-state mushy layers: Experiments and theory. J. Fluid Mech. 2007, 570, 69–77. [Google Scholar] [CrossRef]
- Alexandrov, D.V. Solidification with a quasiequilibrium two phase zone. Acta Mater. 2001, 49, 759–764. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Aseev, D.L. One-dimensional solidification of an alloy with a mushy zone: Thermodiffusion and temperature-dependent diffusivity. J. Fluid Mech. 2005, 527, 57–66. [Google Scholar] [CrossRef]
- Kerr, R.C.; Woods, A.W.; Worster, M.G.; Huppert, H.E. Solidification of an alloy cooled from above Part 1. Equilibrium growth. J. Fluid Mech. 1990, 216, 323–342. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Aseev, D.L.; Nizovtseva, I.G.; Huang, H.-N.; Lee, D. Nonlinear dynamics of directional solidification with a mushy layer. Analytic solutions of the problem. Int. J. Heat Mass Transf. 2007, 50, 3616–3623. [Google Scholar] [CrossRef]
- Nizovtseva, I.G.; Starodumov, I.O.; Pavlyuk, E.V.; Ivanov, A.A. Mathematical modeling of binary compounds with the presence of a phase transition layer. Math. Methods Appl. Sci. 2021, 44, 12260–12270. [Google Scholar] [CrossRef]
- Saeed, T.; Abbas, I. Finite element analyses of nonlinear DPL bioheat model in spherical tissues using experimental data. Mech. Based Des. Struct. Mach. 2022, 50, 1287–1297. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Zubarev, A.Y. Patterns in soft and biological matters. Philos. Trans. R. Soc. A 2020, 378, 20200002. [Google Scholar] [CrossRef] [PubMed]
- Abbas, I.A.; Abdalla, A.E.N.N.; Alzahrani, F.S.; Spagnuolo, M. Wave propagation in a generalized thermoelastic plate using eigenvalue approach. J. Therm. Stress. 2016, 39, 1367–1377. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Zubarev, A.Y. Heterogeneous materials: Metastable and non-ergodic internal structures. Philos. Trans. R. Soc. A 2019, 377, 20180353. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Titova, E.A.; Alexandrov, D.V.; Toropova, L.V. Mathematical Modeling of the Solid–Liquid Interface Propagation by the Boundary Integral Method with Nonlinear Liquidus Equation and Atomic Kinetics. Crystals 2022, 12, 1657. https://doi.org/10.3390/cryst12111657
Titova EA, Alexandrov DV, Toropova LV. Mathematical Modeling of the Solid–Liquid Interface Propagation by the Boundary Integral Method with Nonlinear Liquidus Equation and Atomic Kinetics. Crystals. 2022; 12(11):1657. https://doi.org/10.3390/cryst12111657
Chicago/Turabian StyleTitova, Ekaterina A., Dmitri V. Alexandrov, and Liubov V. Toropova. 2022. "Mathematical Modeling of the Solid–Liquid Interface Propagation by the Boundary Integral Method with Nonlinear Liquidus Equation and Atomic Kinetics" Crystals 12, no. 11: 1657. https://doi.org/10.3390/cryst12111657
APA StyleTitova, E. A., Alexandrov, D. V., & Toropova, L. V. (2022). Mathematical Modeling of the Solid–Liquid Interface Propagation by the Boundary Integral Method with Nonlinear Liquidus Equation and Atomic Kinetics. Crystals, 12(11), 1657. https://doi.org/10.3390/cryst12111657






