Abstract
Layered organic superconductors motivate intense investigations because they provide various unexpected issues associated with their low dimensionality and the strong electron correlation. Since layered organic superconductors possess simple Fermi surface geometry and they often share similarities to the high temperature oxide superconductors and heavy fermion compounds, research on layered organic superconductors is suitable for understanding the essence and nature of strongly correlated electron systems. In strongly correlated electron systems, one of the central problems concerning the superconducting (SC) state is the symmetry of the SC gap, which is closely related to the paring mechanism. Thus, experimental determination of the SC gap structure is of essential importance. In this review, we present the experimental results for the in-plane angular variation of the flux-flow resistance in layered organic superconductors k-(ET)2Cu(NCS)2, β″-(ET)2SF5CH2CF2SO3, and λ-(BETS)2GaCl4. The interplay between the vortex dynamics and nodal structures is discussed for these superconductors.
1. Introduction
Physics of organic conductors has provided the fascinating and rich issues associated with the low dimensionality and effect of electron correlation [1]. One of the most interesting systems are the layered organic conductors composed of the ET donor molecule, where ET denotes bis(ethylenedithio)tetrathiafulvalene. The ET donor molecules form two-dimensional (2D) conducting layers that are separated by insulating anion layers with a monovalent ion X−. Figure 1a shows schematic structure of ET (or BETS) donor conducting layers and anion insulating layers in a layered organic conductor, where BETS denotes bis(ethylenedithio)tetraselenafulvalene. The molecular structures of ET and BETS are shown in the upper right side of Figure 1a. In layered organic superconductors, there are several types (labeled by Greek letters) in packed ET donor layers. The k-, β″-, and λ-type arrangements in donor layers are shown in Figure 1b–d. In the k type compounds, k-(ET)2X, the measurements of Shubnikov-de Haas (SdH) and de Haas-van Alphen (dHvA) oscillations have elucidated the presence of a well-defined Fermi surface (FS) with simple structures [2]. Moreover. the moderately heavy effective mass revealed by SdH and dHvA experiments suggests that electron correlation plays a significant role on determining the physical properties of the normal state as well as superconducting (SC) state. It was suggested that superconductivity appears in proximity to the antiferromagnetic insulating state in the electronic phase diagram [3,4]. Since some of these unusual physical properties suggest similarities with high-Tc cuprates, many researchers have pointed out that the spin fluctuations play a vital role for the appearance of SC state [5,6,7,8].
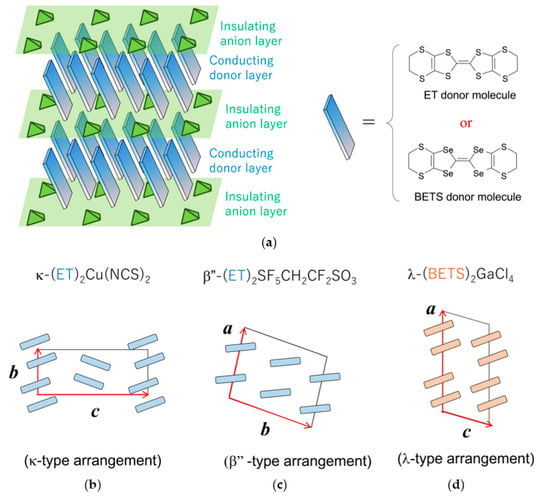
Figure 1.
(a) (Upper left side) Schematic structure of donor conducting layers and anion insulating layers in a layered organic conductor. (Upper right side) Structures of ET and BETS donor molecules. (Lower side) Three patterns within packed donor conducting layers for (b) k-, (c) β″-, and (d) λ-type arrangements.
For layered organic superconductors, many experimental studies have pointed out the existence of nodes in the SC gap [9,10,11,12,13,14,15]. The SC gap structure in unconventional superconductors mostly have nodes parallel to certain orientations in the momentum space. The confirmation of point or line nodes is often discussed from power-law temperature (T) dependences in physical quantities such as the heat capacity or the nuclear spin relaxation rate. However, determination of the SC gap structure is a harder task. For example, the SC gap symmetry of dxy (with nodes along vertical and horizontal directions) differs from dx2−y2 (diagonal direction) only in the location of the line nodes (π/4 rotation of the latter becomes identical with the former). Therefore, direction-sensitive experimental methods are highly needed to distinguish between these gap structures. Since the SC gap structure is intimately associated with the pairing mechanism [16], it is of fundamental importance to elucidate the SC gap structure.
In the vortex state of d-wave superconductors, gapless quasiparticles (QPs) extending outside the vortex core play an important role for determining their physical properties at magnetic fields [17,18]. As an effect of applied magnetic field on d-wave superconductors, Volovik [17] theoretically introduced a “Doppler shifted state” in the energy spectrum of the QP which is induced by superfluid flow around the vortices. The QPs with low energy are induced by the application of magnetic field, mainly around the nodes where the QP velocity is perpendicular to the magnetic field orientation. The QP density depends on the relative direction of the magnetic field with respect to the nodes. Derived from the Doppler sifted state that depend on the magnetic field orientation, the dependence of the heat capacity and the thermal conductivity on applied field orientation was demonstrated to be a useful probe for detecting the nodal directions in a SC gap structure [14,15,19].
Up to now, we have focused on the interplay between vortex dynamics and the SC gap structure in layered organic superconductors because the flux-flow resistivity is a measure of QP dissipation in the vortex dynamics [20,21,22,23,24]. To investigate the correlation between vortex dynamics and the SC gap structure, we measured the in-plane anisotropy of the flux-flow resistivity for the layered organic superconductors k-(ET)2Cu(NCS)2, β″-(ET)2SF5CH2CF2SO3, and λ-(BETS)2GaCl4 [25,26,27]. SC parameters for these superconductors are listed in Table 1. As shown below, we clearly observed the flux-flow resistivity with fourfold-symmetric anisotropy, owning to the d-wave SC gap symmetry in k-(ET)2Cu(NCS)2 and β″-(ET)2SF5CH2CF2SO3. On the other hand, twofold symmetric anisotropy was found in λ-(BETS)2GaCl4 although λ-(BETS)2GaCl4 possesses the similar FS and SC gap structures in the former two superconductors. Interplay between in-plane anisotropy of vortex dynamics and nodal SC gap structures for these superconductors are discussed below.

Table 1.
Superconducting parameters for k-(ET)2Cu(NCS)2 [2], β″-(ET)2SF5CH2CF2SO3 [2,28,29,30] and λ-(BETS)2GaCl4 [2,31,32].
2. Experimental Methods
Single crystals of k-(ET)2Cu(NCS)2, β″-(ET)2SF5CH2CF2SO3, and λ-(BETS)2GaCl4 were synthesized electrochemically. The interlayer resistance was measured by a four-terminal ac method, where the electric current is parallel to the least conducting direction. To investigate the in-plane angular variation of the flux-flow resistance for layered organic superconductors, it is crucial to rotate applied field parallel to the conducting layers with high accuracy because a slight field-angle misalignment gives rise to twofold anisotropy of the magnetoresistance related to the huge Hc2 anisotropy [33]. To check the reproducibility, four samples were simultaneously mounted on a two-axis rotator in a 4He cryostat with a 17-T SC magnet. By using the rotator, it is possible to sweep the θ angle with a resolution of ∆θ = 0.1°, where θ is the polar angle between the least conducting axis and magnetic field direction. In addition, we can discretely control the plane of rotation, which is represented by the azimuthal angle ϕ with intervals of ∆ϕ = 5° or 10 within the conducting layers.
To investigate the in-plane anisotropy of the flux-flow resistance at a constant magnetic field, the resistivity as a function of the angle θ at various fixed ϕ was measured because we can easily find the position of the H parallel to the conducting plane at any ϕ. For example, the interlayer resistivity of k-(ET)2Cu(NCS)2 is shown in Figure 2a [25]. For the magnetic field exactly applied parallel to the conducting plane, the ρ(θ) curve shows a sharp drop due to the SC transition at the lowest current density of 0.5 mA/cm2. It is remarkable that the resistivity at θ = 90° depends strongly on the current density. A sharp peak is clearly observed at θ = 90° for highest current density of 100 mA/cm2. The resistivity for |θ − 90°| > 5° is independent of current density of up to 100 mA/cm2. Thus, the effect of Joule heating is negligibly small. Instead, the sharp peaks are due to the vortex dynamics [25,33,34,35,36,37,38]. Similar features are found for β″-(ET)2SF5CH2CF2SO3 in Figure 2b and λ-(BETS)2GaCl4 in Figure 2c [26,27].
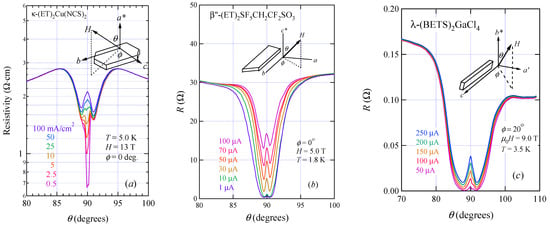
Figure 2.
Interlayer resistance as a function of polar angle θ for κ-(ET)2Cu(NCS)2 (a), β”-(ET)2SF5CH2SF2SO3 (b), and λ-(BETS)2GaCl4 (c). The insets show the definition of θ and ϕ. Adapted from refs. [25,26,27].
3. Results and Discussion
3.1. κ-(ET)2Cu(NCS)2
The nature of the k-type organic superconductor k-(ET)2X possesses similar features to that of high-Tc cuprates, such as quasi-2D electronic structure and the competition of its SC phase with the antiferromagnetic insulating phase [2,3,4]. To elucidate the pairing mechanism in the k-(ET)2X system, its SC gap symmetry has been extensively investigated from both experimental and theoretical points of view [9,10,11,12,13,14]. Various experiments such as NMR [9], heat capacity [10,11], and mm-wave transmission measurements [12] suggested presence of d-wave SC gap in k-(ET)2Cu(NCS)2. As for the nodal direction, scanning tunneling microscopy (STM) [13] and thermal conductivity experiments [14] suggested the line node gap rotated 45° relative to the b and c axes (dx2−y2 symmetry). Malone et al. [15] argued in favor of dxy symmetry (the line nodes along the b and c axes) from the heat capacity measurement. These results have demonstrated the d-wave superconductivity in the k-(ET)2X system, but the location of gap nodes is still controversial. In this section, we present in-plane anisotropy of upper critical field and vortex flow resistivity for k-(ET)2Cu(NCS)2 and discuss the nodal structure.
3.1.1. In-Plane Anisotropy of Upper Critical Field in k-(ET)2Cu(NCS)2
To discuss the in-plane anisotropy of upper critical field, measurements of the interlayer resistance were performed for ϕ = 0° (H // c), ϕ = 45°, ϕ = 90° (H // b). Figure 3a presents the temperature dependence of interlayer resistance for various values of magnetic field applied along the b-axis (ϕ = 90°) up to 14.8 T. Due to a broad transition into the SC state, the following four criteria are used here to extract the SC transition temperature at each magnetic field. These are shown in Figure 3a, where the four criteria of the SC transition temperature: a “junction” TJ, a “midpoint” TM, “a zero resistance extrapolation” TX (ignoring the tail near R = 0), and “zero resistance point” TZ are defined. A similar fashion was confirmed for ϕ = 45° and ϕ = 0° (H // c).
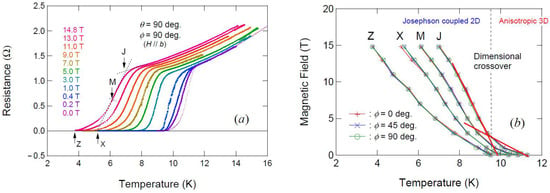
Figure 3.
(a) Temperature dependence of interlayer resistance for various magnetic fields H // b (ϕ = 90°) in κ-(ET)2Cu(NCS)2. (b) H–T phase diagram derived from (a), where four criteria, J (junction), M (midpoint), X (R → 0), and Z (R = 0) are plotted for Tc(H).
Figure 2b presents a T–H phase diagram for three magnetic field directions, using the four criteria. All criteria clearly show highly isotropic behavior within our experimental error, suggesting the lack of in-plane anisotropy of Hc2 in spite of many suggestions of d-wave pairing symmetry in k-(ET)2Cu(NCS)2. This is consistent with previous magnetoresistance study by Nam et al. [39]. Lower temperatures will be needed for confirmation of an expected d-wave nature in Hc2. In addition, we find change of slope in Hc2 line near Tc, suggesting the dimensional crossover from anisotropic 3D SC to Josephson coupled 2D SC state [40,41,42]. It means that despite short coherence length along the interlayer direction, the SC state can be regarded as anisotropic 3D SC state only near Hc2 line.
3.1.2. In-Plane Anisotropy of Vortex Dynamics in k-(ET)2Cu(NCS)2
Figure 4a presents the interlayer resistivity as a function of polar angle θ at various ϕ values with an interval of ∆ϕ = 5°. As seen in Figure 4a, there is the peak structure at θ = 90° at all ϕ values, which confirms the vortex motion for all in-plane field directions. The peak structure gradually changes with ϕ. To discuss the in-plane anisotropic effect in flux-flow resistance, we display the ϕ dependence of the interlayer resistivity at θ = 90° at various temperatures in Figure 4b. In the entire temperature range measured, the ρ(ϕ,T) curves show minima at ϕ = 0° (H // c) and 90° (H // b). At temperatures beyond 7.8 K, a sinusoidal angular variation was observed. At elevated temperature, the amplitude of oscillatory behavior is weakened but survives even at 18 K, where the SC phase is vanished. At temperatures below 7.8 K, we find a non-sinusoidal fourfold angular-variation: cusp-like minima are found at ϕ = 0° and 90° that are independent of temperature.
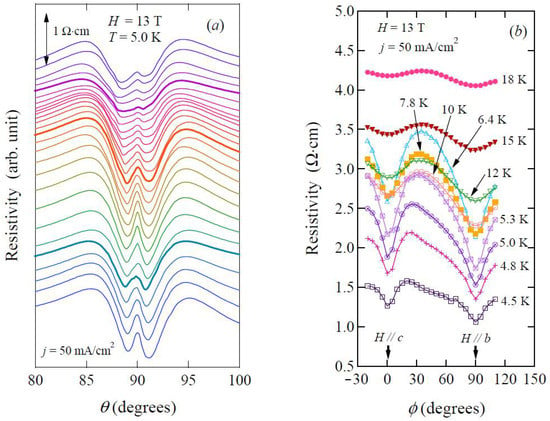
Figure 4.
(a) Polar angle dependence of interlayer resistance at 5.0 K under a magnetic field of 13 T for various values of ϕ. The curves are measured in intervals of ∆ϕ = 5° between 120° (top curve) and −20° (bottom). (b) Dependence of resistivity at θ = 90° at various temperatures. (Reprinted from [25]. Copyright 2013 The Physical Society of Japan.)
As seen in Figure 4b, the ρ(ϕ) curves seem to be described by a fourfold symmetric origin. Takanaka and Kuboya theoretically showed that the angular variation of the upper critical field is described as Hc2(ϕ) ∝ cos4ϕ in the d-wave superconductivity [43,44,45]. The ρ(ϕ) curves are naively consistent with this theory; the maximum and minimum of Hc2 give the minimum and maximum resistivities, respectively. When dx2−y2 pairing is assumed, Hc2(ϕ) has maxima at ϕ = 0° (H // c) and ϕ = 90° (H // b), and a minimum at ϕ = 45°, whereas dxy pairing leads to Hc2 with maxima and minima reversed with respect to dx2−y2 pairing. Thus, the fourfold symmetry in Figure 3b is not inconsistent with the Hc2 anisotropy originating from the dx2−y2 pairing state. However, detailed magnetoresistance studies at 1.5 and 4.2 K [39] as well as Figure 3 showed the lack of in-plane anisotropy of Hc2. In addition, the cusp-like minima that appear below 7.8 K cannot be represented by a simple cos4ϕ dependence. Thus, another mechanism to describe these oscillation patterns is necessary.
As seen in Figure 4b, we observe sharp peaks related to dissipative feature arising from the vortex dynamics at any azimuth direction within the conducting plane. Therefore, the origin of the cusp-like minima is discussed in terms of the anisotropic vortex dynamics. Since the Josephson vortex essentially does not have a normal core, the pinning effect arising from lattice defects and/or impurities is negligibly small for vortex motion parallel to the conducting layers. In this situation, the friction force is largely affected by the damping viscosity, which depends on the energy dissipation processes of QPs. In the simple description of flux-flow behavior, the Lorentz force on a vortex is balanced by a viscous drag force. Since the Lorentz force keeps constant during the field direction changed, the anisotropic flux-flow resistivity observed here suggests a remarkable variation of the QP excitations by the applied field rotating within the conducting layers because flux-flow resistance can be regarded as a measure of QP dissipation in the vortex dynamics [20,21,22,23,24].
Let us discuss the mechanism of the observed fourfold oscillation in terms of the Doppler effect originally proposed by Volovik [17,18]. In the d-wave paring state, a nonzero QP density-of-state (DOS) is generated on the Fermi surface by the effect of Doppler shifted state. Theoretical studies [18] clearly show that the DOS possesses a broad maximum for the field parallel to the antinodal direction and sharp minimum for the field along the node. When an applied field is parallel to the antinodal orientation, all four nodes affect the DOS. On the other hand, when the field is parallel to a nodal orientation, QPs at that node do not affect the DOS. Since a damping of the Josephson vortex motion by QPs is expected, the stronger damping will occur when the magnetic field is applied parallel to the antinodal orientations, leading to the suppression of the flux-flow resistivity for the antinodal orientation. When the dx2−y2 pairing is assumed, ρ(ϕ) should become minima at ϕ = 0° (H // c) and ϕ = 90° (H // b) and maximum at ϕ = 45°, which agrees with Figure 4b. Thus, we consider that our result concerned with flux-flow resistance is consistent with dx2−y2 pairing state, as suggested by STM [13] and thermal conductivity experiments [14].
The above consideration is essentially based on the semiclassical theory [17,18]. Unfortunately, this semiclassical treatment is valid only at low temperatures and low fields and does not consider the scattering effect between the QPs and moving vortices. For wider temperature and field ranges, Vorontsov and Vekhter [46,47] developed a microscopic theory for the angular dependent properties of thermal conductivity and heat capacity in d-wave SC state. They found that application of the magnetic field parallel to the SC gap nodes may result in maxima or minima in their angular dependence, depending upon the location in the T–H plane. This variation is attributable to the scattering of the QPs on vortices. Such sign reversal oscillation was observed and discussed in the heavy fermion superconductor CeCoIn5 [48]. A similar problem between the thermal conductivity and heat capacity measurements was discussed for k-(ET)2Cu(NCS)2 [14,15]. According to the T–H diagrams in [46,47], field-angle dependences of heat capacity and thermal conductivity do not show sign reversal pattern at H/Hc2 ~ 0.43 and T/Tc > 0.48, where our experimental study was done. Although our results are not inconsistent with no sign reversal oscillation for a wide temperature region, further experimental study such as confirmation of sign reversal pattern at lower fields will be needed to elucidate the effect of the Doppler shifted state on the vortex dynamics.
3.2. β″-(ET)2SF5CH2CF2SO3
The crystal structure of β″-(ET)2SF5CH2CF2SO3 (Tc = 5.2 K) has triclinic symmetry and the ET donor molecules form 2D conduction layers parallel to the a-b plane [49]. The insulating SF5CH2CF2SO3− layer is intercalated between the ET donor layers, which makes the c*-axis the least conducting direction. Both a 2D Fermi pocket and a pair of quasi-1D Fermi sheets is predicted from the band-structure calculation [50]. The SdH effect and AMRO (angular-dependent magnetoresistance oscillation) studies clearly show one small 2D FS with an area of 5% of the first Brillouin zone [50,51]. Reflecting the layered structure, its GL coherence length perpendicular to the conducting layers, ξ⊥(0) (~ 7.9 ± 1.5 Å), is shorter than the interlayer spacing d of 17.5 Å [28].
There are three intriguing properties in β″-(ET)2SF5CH2CF2SO3. First, high field AMRO showed the nature of incoherent interlayer transport. This means that the FS of β″-(ET)2SF5CH2CF2SO3 is regarded as the highly 2D confined electron system [52]. Second, the FS structure is very similar to that of k-(ET)2Cu(NCS)2 [49]. Third and most importantly, the SC state of β″-(ET)2SF5CH2CF2SO3 may be mediated by charge fluctuations because a pressure-induced charge ordering state is observed at around 1 GPa [53]. For β″ type organic conductors, a large intersite Coulomb repulsion has been theoretically predicted [6,8,54]. Moreover, d-wave superconductivity mediated by charge fluctuations has been proposed based on above theoretical study [8,55], but not confirmed experimentally. In this section, we discuss the relationship between in-plane angular variation of Hc2 and vortex dynamics in β″-(ET)2SF5CH2CF2SO3.
3.2.1. Anisotropy of Upper Critical Field in β″-(ET)2SF5CH2CF2SO3
To study the upper critical field, Hc2(ϕ), within the conducting a-b plane, the interlayer resistance as a function of magnetic field at various fixed ϕ was investigated as shown by Figure 5a. The resistance curves were taken in intervals of ∆ϕ = 10°. At around the SC transition, the resistance gradually reaches zero with decreasing magnetic field. Figure 5b presents the in-plane angular variation of Hc2. We define Hc2, when R/Rn = 0.9, 0.7, and 0.5, where Rn is the normal state resistance given by extrapolating R(H) in the higher field region of 13 ≦ μ0H ≦ 14 T. It is clear that the angular variation of Hc2 exhibits maxima at around ϕ = ±90° and ϕ = 0°. Although the values of Hc2 are changed by the different criteria, the fourfold oscillation pattern of Hc2 itself remains.
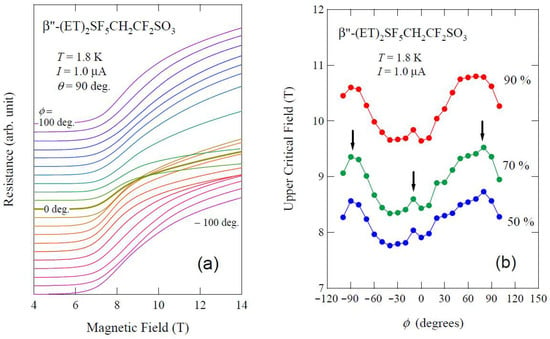
Figure 5.
(a) Magnetic field dependence of interlayer resistance at various fixed ϕ in the ohmic regime, where applied field is parallel to the conducting plane. The curves are taken from ϕ = 100° (top curve) to −100° (bottom) with intervals of Δϕ = 10°. (b) In-plane angular variation of Hc2 determined from the resistive transition. The Hc2 values are defined as the fields at which the resistance of the measured sample has reached 90%, 70%, and 50% of its normal-state value. (Reprinted from [27]. Copyright 2015 The Physical Society of Japan.)
For an unconventional superconductor, Hc2(ϕ) minima occur for applied field parallel to the nodal directions. Thus, it is considered that the SC gap possesses its node (or minimum) at approximately π/4 from the b-axis. This result is in favor of a dx2−y2 gap symmetry [38].
3.2.2. In-Plane Anisotropy of Vortex Dynamics in β″-(ET)2SF5CH2CF2SO3
To further discuss observed d-wave like anisotropy of Hc2, the in-plane anisotropy of the vortex dynamics is next shown. Figure 6 presents the polar angle dependence of the interlayer resistance at various ϕ values. The structures around θ = 90° (i.e., dip or peak) depend on ϕ, showing the anisotropic vortex dynamics within the conducting layers. To see the anisotropic field effect, the ϕ-dependence of the interlayer resistance at θ = 90° for various currents is shown in Figure 7a. At 100 μA, we observe a fourfold angular oscillation: cusp-like minima are observed at ϕ = 20° and ±90°. With increasing current, the amplitude increases, showing the remarkable non-ohmic transport phenomena. Figure 7b presents ϕ-dependence of the interlayer resistance at θ = 90° for several magnetic fields. As shown by Figure 7b, the effect of magnetic field on the flux-flow resistance is very similar to Figure 7a. With increasing magnetic field, a non-sinusoidal fourfold angular pattern is found. The cusp-like minima are observed at ϕ = 20° and ±90° that are the same as Figure 7a. The current dependence of the flux-flow resistance at a fixed field strength (Figure 7a) is very similar to the field dependence of that at a fixed current (Figure 7b), suggesting that combination of high magnetic field and large current, that is, Lorentz force plays an important role for appearance of the fourfold pattern in the flux-flow resistance. Similar fourfold pattern has been found in the flux-flow resistance in k-(ET)2Cu(NCS)2 [25].
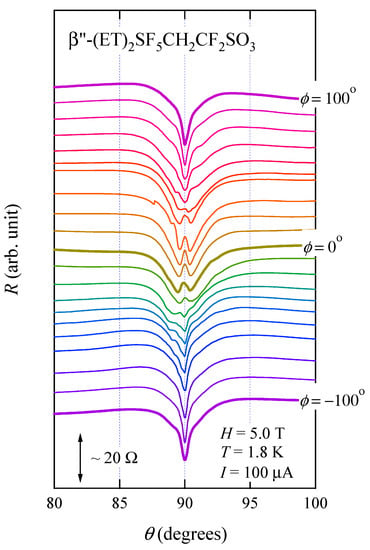
Figure 6.
Polar angle dependence of interlayer resistance for various fixed ϕ values. The curves are taken in intervals of ∆ϕ = 10° between ϕ = 100° (top curve) and −100° (bottom). (Reprinted from [27]. Copyright 2015 The Physical Society of Japan.).
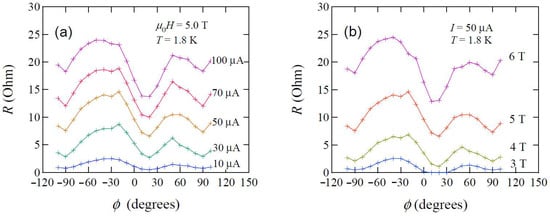
Figure 7.
Azimuth angle dependence of the flux-flow resistance for several values of current (a) and of magnetic field (b). (Reprinted from [27]. Copyright 2015 The Physical Society of Japan.)
According to theoretical studies [18,46,47], the Doppler effect in the d-wave paring state gives rise to remarkable response of QP generation on the Fermi surface at low temperatures. It is known that as a field is parallel to the antinodal orientation, QPs are excited at four nodes that contribute to the DOS. On the other hand, when the field is directed along a nodal orientation, QPs at that node do not contribute to the DOS, and therefore the Doppler shift vanishes at these points. Since the QPs are expected to dampen the vortex motion, the flux-flow resistance associated with the vortex motion will be suppressed for the magnetic field applied parallel to the antinodal directions, giving rise to the weaker FFR for the antinodal orientation. For β″-(ET)2SF5CH2CF2SO3, when dx2−y2 pairing, as discussed in Figure 4b, is assumed, R(ϕ) should have minima at around ϕ = ±90° and ϕ = 0° and it should have maxima at around ϕ = ±45° orientations, and therefore this is consistent with Figure 7a,b.
Finally, a comment is given on the paring mechanism for the SC state in β″-(ET)2SF5CH2CF2SO3. The nodal orientations discussed here are far from the orientations of most effective nesting vector on the Fermi surface predicted from the band-structure calculation, as well as determined from the AMRO experiments [26,50,51]. If a spin fluctuation scenario is assumed, it is natural to expect the nodes that are parallel to the antiferromagnetic nesting vector, to be along the b* and a* (or a) orientations. It is intriguing to point out that superconductivity with another d-wave symmetry is theoretically suggested based on the charge fluctuation scenario [55]. Further investigation is needed to elucidate which mechanism (i.e., spin fluctuations versus charge fluctuations) is more likely.
3.3. λ-(BETS)2GaCl4
The layered organic conductor λ-(BETS)2GaCl4 undergoes a SC transition at Tc of ~8 K [56]. The BETS donor molecules are stacked along the a- and c-axes. The insulating GaCl4− anion layers are inserted between the BETS conducting layers. Thus, the 2D conducting layers are formed in λ-(BETS)2GaCl4. Reflecting the layered structure, its GL coherence length perpendicular to the layers is shorter than the interlayer spacing of 18.6 Å [57]. λ-(BETS)2GaCl4 is known as a good candidate for realizing the Fulde–Ferrell–Larkin–Ovchinnikov state [57,58]. Another intriguing point is that its isostructural compound λ-(BETS)2FeCl4 shows a field-induced SC transition [59]. Band-structure calculation [56] predicts the existence of one closed 2D Fermi pocket and two 1D Fermi sheets that are topologically the same as k-(ET)2Cu(NCS)2 [50,51]. Measurements of the SdH and AMROs are qualitatively consistent with the band calculation [60].
As for the SC gap structure, a STM experiment suggested dxy–wave symmetry with the line nodes along the a*- and c*-axes [61]. From systematic investigations by chemical substitution in the anions [62,63] or by selecting different donor molecules [64], the SC phase is suggested to exist next to the Mott insulating phase, which is similar to the k-(ET)2X system [65]. An NMR study showed the development of spin fluctuations beyond the SC phase transition temperature [66]. A heat capacity study showed a d-wave pairing state [67], whereas a μSR study clamed a mixture of the extended s- and d-wave SC gap [68]. In this section, we discuss the interplay between in-plane anisotropy of vortex dynamics and the SC gap structure for λ-(BETS)2GaCl4 [26].
In-Plane Anisotropy of Vortex Dynamics in λ-(BETS)2GaCl4
Figure 8 shows the polar angle dependence of the interlayer resistance at various fixed ϕ values. The sharp peak is clearly observed at θ = 90° at all ϕ values, which shows the vortex dynamics for all ϕ-directions. Figure 9 shows the azimuth angle dependence of the interlayer resistance at θ = 90° for various currents. The in-plane angular dependence is mainly represented by the twofold symmetry with the sharp dip at ϕ = 0° (H // c). This feature differs from the cases of k-(ET)2Cu(NCS)2 [25] and β″-(ET)2SF5CH2CF2SO3 [27] even though the FS geometry of λ-(BETS)2GaCl4 [56] is similar to that of k-(ET)2Cu(NCS)2 [60] and β″-(ET)2SF5CH2CF2SO3 [50,51].
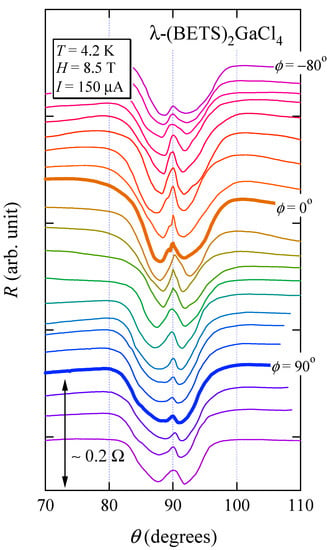
Figure 8.
Polar angle dependence of interlayer resistance under rotating field of 8.5 T for various fixed ϕ. The curves are taken in intervals of ∆ϕ = 10° between −80° (top curve) and 120° (bottom). (Reprinted from [26]. Copyright 2014 The Physical Society of Japan.)
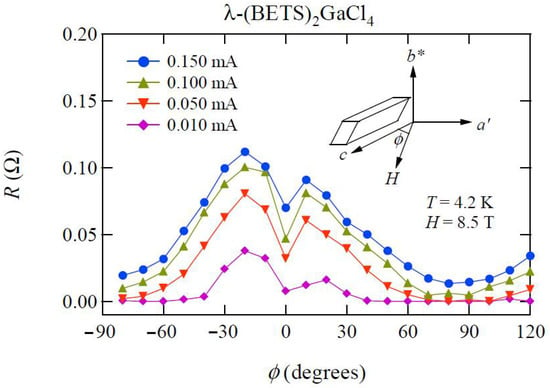
Figure 9.
Azimuth angle dependence of flux-flow resistance in λ−(BETS)2GaCl4 at various currents. A sharp minimum is observed at ϕ = 0° (H // c). (Reprinted from [26]. Copyright 2014 The Physical Society of Japan.)
In spite of the similar FS geometry, we found an in-plane twofold flux-flow resistance anisotropy in λ-(BETS)2GaCl4 while fourfold-symmetric flux-flow resistance for β″-(ET)2SF5CH2CF2SO3 and k-(ET)2Cu(NCS)2. As a possible explanation, we consider that the different anisotropic feature may be related to the difference of the interlayer coupling strength [31]. The anisotropy parameter Γ, given by (ξ///ξ⊥)2, for β″-(ET)2SF5CH2CF2SO3 is Γ ~ 330 that is larger the those of k-(ET)2Cu(NCS)2 (Γ ~ 100) and λ-(BETS)2GaCl4 (Γ ~ 60) [27]. Since λ-(BETS)2GaCl4 is more three dimensional than k-(ET)2Cu(NCS)2 and β″-(ET)2SF5CH2CF2SO3, an orbital pair breaking effect in λ-(BETS)2GaCl4 is stronger than in k-(ET)2Cu(NCS)2 and β″-(ET)2SF5CH2CF2SO3.
Due to the orbital pair breaking effect in λ-(BETS)2GaCl4, the superposition of the normal-state magnetoresistance cannot be avoided in the in-plane anisotropy of the flux-flow resistance. Figure 10 presents the in-plane angular dependence of normal-state magnetoresistance in the magnetic field of 14.8 T [26]. The normal-state magnetoresistance possesses the twofold symmetry with broad maximum at around ϕ = −20°. The result is consistent with Tanatar et al. [57]. The twofold symmetric normal-state magnetoresistance can be understood in terms of Fermi-surface anisotropy if it mainly originates from the ellipsoidal 2D pocket elongated along the c-axis. In the small Γ system, the large twofold component in the normal-state magnetoresistance may mask the fourfold ones.
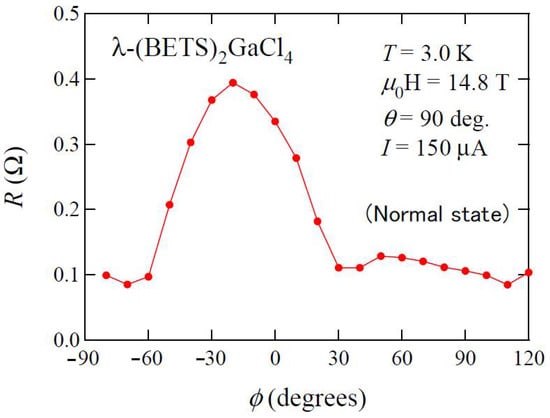
Figure 10.
Azimuth angle dependence of normal-state magnetoresistance in λ−(BETS)2GaCl4 within the conducting plane. (Reprinted from [26]. Copyright 2014 The Physical Society of Japan.)
The origins of the sharp dip (ϕ = −20°) and the broad minimum (around ϕ = 90°) in Figure 9 are next discussed. Similar dip structures are found in k-(ET)2Cu(NCS)2 and β″-(ET)2SF5CH2CF2SO3. The origin of the dip in λ-(BETS)2GaCl4 should be the same as that in k-(ET)2Cu(NCS)2 and β″-(ET)2SF5CH2CF2SO3. To theoretically discuss the SC gap structure for λ-(BETS)2GaCl4, Aizawa et al. [69] performed first-principles band calculation. Considering the spin-fluctuation-mediated mechanism, they discussed the SC gap function by applying the random phase approximation. They showed that the obtained SC gap changes its sign four times along the Fermi surface, suggesting a d-wave SC gap in λ-(BETS)2GaCl4. Reflecting the low symmetry of the crystal structure in λ-(BETS)2GaCl4, however, the SC gap has only twofold symmetry. It means that the predicted SC gap has a large gap between narrow opening nodes with an acute angle (around the steep node structure) and a small gap between wide opening nodes with an obtuse angle. Recent magnetic-field-angle-resolved heat capacity study [70] is consistent with theoretically predicted SC gap function. The large gap is located along the c-axis [69] which agrees with the position of sharp dip [26]. The small gap exists at around a-axis [69], where we observed broad minimum in flux-flow resistance [26]. Thus, experimental results of flux-flow resistance in λ-(BETS)2GaCl4 [26] are consistent with the d-wave gap structure theoretically discussed by Aizawa [69].
4. Summary
In order to discuss the relationship between vortex dynamics and the SC gap structure with d-wave paring symmetry, we investigated in-plane angular variation of vortex dynamics for the layered organic superconductors k-(ET)2Cu(NCS)2, β″-(ET)2SF5CH2CF2SO3, and λ-(BETS)2GaCl4. We observed clear fourfold-symmetric anisotropy in the interlayer flux-flow resistance for k-(ET)2Cu(NCS)2 and β″-(ET)2SF5CH2CF2SO3, while only twofold symmetry in λ-(BETS)2GaCl4. For k-(ET)2Cu(NCS)2 and β″-(ET)2SF5CH2CF2SO3, flux-flow resistivity showing fourfold oscillation can be consistently explained by assuming the enhanced viscous motion of vortices by QPs arising from the Doppler effect. Absence of the fourfold anisotropy in λ-(BETS)2GaCl4 is discussed in the two regimes. The first regime is related to the stronger interlayer coupling in the λ-(BETS)2GaCl4 system as compared with k-(ET)2Cu(NCS)2 and β″-(ET)2SF5CH2CF2SO3. The second regime is discussed in terms of recent theoretical study by Aizawa et al. In this scenario, flux-flow resistivity with twofold anisotropy may be associated with the crystal structure with low symmetry, which is rather different from those of k-(ET)2Cu(NCS)2 and β″-(ET)2SF5CH2CF2SO3.
For these three organic superconductors, the origin of the in-plane anisotropy of flux-flow resistance with sharp minima is discussed in terms of the effect of Doppler shifted state. Based on these results, we claim that angular dependence of the vortex dynamics strongly depends on the SC gap structure. We hope that further understanding of the vortex dynamics presented here leads to clarifying the mechanism of the unconventional superconductors in various strongly correlated electron systems.
Funding
These works were partly supported by Grants-in-Aid for Scientific Research on Innovative Areas (Grant No. 20110004) from the Ministry of Education, Culture, Sports, Science, and Technology (MEXT) of Japan, and Grants-in-Aid for Scientific Research (C) (Grant No. 25400383) from the Japan Society for the Promotion of Science (JSPS).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available within the article.
Acknowledgments
The author thanks Shinya Uji, Taichi Terashima, Takako Konoike, Satoshi Tsuchiya, Kaori Sugii, Takayuki Isono, Yoritsugu Iida, Kazuya Saito, Yasuhisa Yamamura, Motoi Kimata, Hidetaka Satsukawa, Jun-ichi Yamada, Biao Zhou, Akiko Kobayashi, Hayao Kobayashi, John A. Schlueter, Hirohito Aizawa, Kazuhiko Kuroki, Nobuhiko Hayashi, and Yoichi Higashi for useful discussions and suggestions.
Conflicts of Interest
The author declares no conflict of interest.
References
- Ardavan, A.; Brown, S.; Kagoshima, S.; Kanoda, K.; Kuroki, K.; Mori, H.; Ogata, M.; Uji, S.; Wosnitza, J. Recent Topics of Organic Superconductors. J. Phys. Soc. Jpn. 2012, 81, 011012. [Google Scholar] [CrossRef]
- Lang, M.; Muller, J. Organic Superconductors. In Superconductivity; Bennemann, K.H., Ketterson, J.B., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume II, pp. 1155–1223. [Google Scholar]
- Kanoda, K. Electron correlation, metal-insulator transition and superconductivity in quasi-2D organic systems, (ET)2X. Physica C 1997, 282–287, 299–302. [Google Scholar] [CrossRef]
- Sasaki, T.; Yoneyama, N.; Matsuyama, A.; Kobayashi, N. Magnetic and electronic phase diagram and superconductivity in the organic superconductors κ-(ET)2X. Phys. Rev. B 2002, 65, 060505. [Google Scholar] [CrossRef]
- Clay, R.T.; Li, H.; Mazumdar, S. Absence of Superconductivity in the Half-Filled Band Hubbard Model on the Anisotropic Triangular Lattice. Phys. Rev. Lett. 2008, 101, 166403. [Google Scholar] [CrossRef] [PubMed]
- Dayal, S.; Clay, R.T.; Li, H.; Mazumdar, S. Paired electron crystal: Order from frustration in the quarter-filled band. Phys. Rev. B 2011, 83, 245106. [Google Scholar] [CrossRef]
- Dayal, S.; Clay, R.T.; Mazumdar, S. Absence of long-range superconducting correlations in the frustrated half-filled-band Hubbard model. Phys. Rev. B 2012, 85, 165141. [Google Scholar] [CrossRef]
- Qin, M.; Chung, C.-M.; Shi, H.; Vitali, E.; Hubig, C.; Schollwöck, U.; White, S.R.; Zhang, S. Absence of Superconductivity in the Pure Two-Dimensional Hubbard Model. Phys. Rev. X 2020, 10, 031016. [Google Scholar] [CrossRef]
- Mayaffre, H.; Wzietek, P.; Jérome, D.; Batail, P. Superconducting State of κ-(ET)2Cu[N(CN)2]Br Studied by 13C NMR: Evidence for Vortex-Core-Induced Nuclear Relaxation and Unconventional Pairing. Phys. Rev. Lett. 1995, 75, 4122–4125. [Google Scholar] [CrossRef] [PubMed]
- Nakazawa, Y.; Kanoda, K. Low-temperature specific heat of κ-(BEDT-TTF)2Cu[N(CN)2]Br in the superconducting state. Phys. Rev. B 1986, 55, R8670–R8673. [Google Scholar] [CrossRef]
- Taylor, O.J.; Carrington, A.; Schlueter, J.A. Specific-Heat Measurements of the Gap Structure of the Organic Superconductors κ-(ET)2Cu[N(CN)2]Br and κ-(ET)2Cu(NCS)2. Phys. Rev. Lett. 2007, 99, 057001. [Google Scholar] [CrossRef] [PubMed]
- Schrama, J.M.; Rzepniewski, E.; Edwards, R.S.; Singleton, J.; Ardvan, A.; Kurmoo, M.; Day, P. Millimeter-Wave Magneto-optical Determination of the Anisotropy of the Superconducting Order Parameter in the Molecular Superconductor κ-(BEDT-TTF)2Cu(NCS)2. Phys. Rev. Lett. 1999, 83, 3041–3044. [Google Scholar] [CrossRef]
- Arai, T.; Ichimura, K.; Nomura, K.; Takasaki, S.; Yamada, J.; Nakatsuji, S.; Anzai, H. Tunneling spectroscopy on the organic superconductor κ-(BEDT-TTF)2Cu(NCS)2 using STM. Phys. Rev. B 2001, 63, 104518. [Google Scholar] [CrossRef]
- Izawa, K.; Yamaguchi, H.; Sasaki, T.; Matsuda, Y. Superconducting Gap Structure of κ-(BEDT-TTF)2Cu(NCS)2 Probed by Thermal Conductivity Tensor. Phys. Rev. Lett. 2001, 88, 027002. [Google Scholar] [CrossRef]
- Malone, L.; Taylor, O.J.; Schlueter, J.A.; Carrington, A. Location of gap nodes in the organic superconductors κ-(ET)2Cu(NCS)2 and κ-(ET)2Cu[N(CN)2]Br determined by magnetocalorimetry. Phys. Rev. B 2010, 82, 014522. [Google Scholar] [CrossRef]
- Sigrist, M.; Ueda, K. Phenomenological theory of unconventional superconductivity. Rev. Mod. Phys. 1991, 63, 239–311. [Google Scholar] [CrossRef]
- Volovik, G.E. Superconductivity with lines of gap nodes: Density of states in the vortex. JETP Lett. 1993, 58, 469–473. [Google Scholar]
- Vekhter, I.; Hirschfeld, P.J.; Carbotte, J.P.; Nicol, E.J. Anisotropic thermodynamics of d-wave superconductors in the vortex state. Phys. Rev. B 1999, 59, R9023–R9026. [Google Scholar] [CrossRef]
- Deguchi, K.; Mao, Z.Q.; Yaguchi, H.; Maeno, Y. Gap Structure of the Spin-Triplet Superconductor Sr2RuO4 Determined from the Field-Orientation Dependence of the Specific Heat. Phys. Rev. Lett. 2004, 92, 047002. [Google Scholar] [CrossRef]
- Higashi, Y.; Nagai, Y.; Machida, M.; Hayashi, N. Field-angle dependence of the quasiparticle scattering inside a vortex core in unconventional superconductors. Physica C 2011, 471, 828–830. [Google Scholar] [CrossRef][Green Version]
- Higashi, Y.; Nagai, Y.; Machida, M.; Hayashi, N. Effect of uniaxially anisotropic Fermi surface on the quasiparticle scattering inside a vortex core in unconventional superconductors. Physica C 2013, 484, 97–99. [Google Scholar] [CrossRef][Green Version]
- Higashi, Y.; Nagai, Y.; Machida, M.; Hayashi, N. Field-angle resolved flux-flow resistivity as a phase-sensitive probe of unconventional Cooper pairing. Phys. Rev. B 2013, 88, 224511. [Google Scholar] [CrossRef]
- Clem, J.R.; Coffey, M.W. Viscous flux motion in a Josephson-coupled layer model of high-Tc superconductors. Phys. Rev. B 1990, 42, 6209–6216. [Google Scholar] [CrossRef]
- Koshelev, A.E. Role of in-plane dissipation in dynamics of a Josephson vortex lattice in high-temperature superconductors. Phys. Rev. B 2000, 62, R3616–R3619. [Google Scholar] [CrossRef]
- Yasuzuka, S.; Saito, K.; Uji, S.; Kimata, M.; Satsukawa, H.; Terashima, T.; Yamada, J.-I. Anisotropic Josephson-Vortex Dynamics in Layered Organic Superconductor with d-Wave Pairing Symmetry. J. Phys. Soc. Jpn. 2013, 82, 064716. [Google Scholar] [CrossRef]
- Yasuzuka, S.; Uji, S.; Terashima, T.; Tsuchiya, S.; Sugii, K.; Zhou, B.; Kobayashi, A.; Kobayashi, H. In-Plane Anisotropy of Flux-Flow Resistivity in Layered Organic Superconductor λ-(BETS)2GaCl4. J. Phys. Soc. Jpn. 2014, 83, 013705. [Google Scholar] [CrossRef]
- Yasuzuka, S.; Uji, S.; Terashima, T.; Sugii, K.; Isono, T.; Iida, Y.; Schlueter, J.A. In-Plane Anisotropy of Upper Critical Field and Flux-Flow Resistivity in Layered Organic Superconductor β″-(ET)2SF5CH2CF2SO3. J. Phys. Soc. Jpn. 2015, 84, 094709. [Google Scholar] [CrossRef]
- Müller, J.; Lang, M.; Steglich, F.; Schlueter, J.A.; Kini, A.M.; Geiser, U.; Mohtasham, J.; Winter, R.W.; Gard, G.L.; Sasaki, T.; et al. Comparative thermal-expansion study of β”-(ET)2SF5CH2CF2SO3 and κ-(ET)2Cu(NCS)2: Uniaxial pressure coefficients of Tc and upper critical fields. Phys. Rev. B 2000, 61, 11739–11744. [Google Scholar] [CrossRef]
- Wanka, S.; Hagel, J.; Beckmann, D.; Wosnitza, J.; Schlueter, J.A.; Williams, J.M.; Nixon, P.G.; Winter, R.W.; Garal, G.L. Specific heat and critical field of the organic superconductor β”-(ET)2SF5CH2CF2SO3. Phys. Rev. B 1997, 57, 3084–3088. [Google Scholar] [CrossRef]
- Prozorov, R.; Giannetta, R.W.; Schlueter, J.A.; Kini, A.M.; Mohtasham, J.; Winter, R.W.; Gard, G.L. Unusual temperature dependence of the London penetration depth in all-organic β”-(ET)2SF5CH2SF2SO3 single crystals. Phys. Rev. B 2001, 63, 052506. [Google Scholar] [CrossRef]
- Mielke, C.; Singleton, J.; Nam, M.-S.; Harrison, N.; Agosta, C.C.; Fravel, B.; Montgomery, L.K. Superconducting properties and Fermi-surface topology of the quasi-two-dimensional organic superconductor λ-(BETS)2GaCl4. J. Phys. Condens. Matter 2001, 13, 8325–8345. [Google Scholar] [CrossRef]
- Sari, D.P.; Naito, R.; Hiraki, K.; Nakano, T.; Hagiwara, M.; Nozue, Y.; Kusakawa, T.; Hori, A.; Watanabe, I.; Ishii, Y. Anisotropy of Lower Critical Field in Organic Layered Superconductor λ-(BETS)2GaCl4. Key Eng. Mater. 2020, 860, 137–141. [Google Scholar] [CrossRef]
- Saito, G.; Yamochi, H.; Nakamura, T.; Komatsu, T.; Ishiguro, T.; Nogami, Y.; Ito, Y.; Mori, H.; Oshima, K.; Nakashima, M.; et al. Overview of organic superconductor κ-(BEDT-TTF)2[Cu(NCS)2] and its related materials. Synth. Met. 1991, 42, 1993–1998. [Google Scholar] [CrossRef]
- Chaparala, M.; Chung, O.H.; Ren, Z.F.; White, M.; Coppens, P.; Wang, J.H.; Hope, A.P.; Naughton, M.J. Vortex-state resistance near parallel orientation in layered superconductors. Phys. Rev. B 1996, 53, 5818. [Google Scholar] [CrossRef] [PubMed]
- Uji, S.; Terashima, T.; Nishimura, M.; Konoike, T.; Enomoto, K.; Cui, H.; Kobayashi, H.; Kobayashi, A.; Tanaka, H.; Tokumoto, M.; et al. Vortex Dynamics and the Fulde-Ferrell-Larkin-Ovchinnikov State in a Magnetic-Field-Induced Organic Superconductor. Phys. Rev. Lett. 2006, 97, 157001. [Google Scholar] [CrossRef]
- Yasuzuka, S.; Uji, S.; Satsukawa, H.; Kimata, M.; Terashima, T.; Koga, H.; Yamamura, Y.; Saito, K.; Akutsu, H.; Yamada, J. Anisotropic Josephson-vortex dynamics in layered organic superconductors. Physica B 2010, 405, S288–S290. [Google Scholar] [CrossRef]
- Feinberg, D.; Villard, C. Intrinsic pinning and lock-in transition of flux lines in layered type-II superconductors. Phys. Rev. Lett. 1990, 65, 919–922. [Google Scholar] [CrossRef] [PubMed]
- Mansky, P.A.; Chaikin, P.M.; Haddon, R.C. Vortex lock-in state in a layered superconductor. Phys. Rev. Lett. 1993, 70, 1323–1326. [Google Scholar] [CrossRef]
- Nam, M.-S.; Symington, J.A.; Singleton, J.; Blundell, S.; Ardavan, A.; Perenboom, J.A.A.J.; Kurmoo, M.; Day, P. Angle dependence of the upper critical field in the layered organic superconductor κ-(BEDT-TTF)2Cu(NCS)2 (BEDT-TTF ≡ bis(ethylene-dithio)tetrathiafulvalene). J. Phys. Condens. Matter. 1999, 11, L477–L484. [Google Scholar] [CrossRef]
- Klemm, R.A.; Luther, A.; Beasley, M.R. Theory of the upper critical field in layered superconductors. Phys. Rev. B 1975, 12, 877–891. [Google Scholar] [CrossRef]
- Schneider, T.; Schmidt, A. Dimensional crossover in the upper critical field of layered superconductors. Phys. Rev. B 1993, 47, 5915–5921. [Google Scholar] [CrossRef]
- Oshima, K.; Urayama, H.; Yamochi, H.; Saito, G. Peculiar Critical Field Behaviour in the Recectly Discovered Ambient Pressure Organic Superconductor (BEDT-TTF)2Cu (NCS)2 (Tc = 10.4 K). J. Phys. Soc. Jpn. 1988, 57, 730–733. [Google Scholar] [CrossRef]
- Takanaka, K.; Kuboya, K. Anisotropy of Upper Critical Field and Pairing Symmetry. Phys. Rev. Lett. 1995, 75, 323–325. [Google Scholar] [CrossRef]
- Yasuzuka, S.; Koga, H.; Yamamura, Y.; Saito, K.; Uji, S.; Terashima, T.; Akutsu, H.; Yamada, J.-I. Dimensional Crossover and Its Interplay with In-Plane Anisotropy of Upper Critical Field in β-(BDA-TTP)2SbF6. J. Phys. Soc. Jpn. 2017, 86, 084704. [Google Scholar] [CrossRef]
- Yasuzuka, S.; Uji, S.; Sugiura, S.; Terashima, T.; Nogami, Y.; Ichimura, K.; Tanda, S. Highly Isotropic In-plane Upper Critical Field in the Anisotropic s-Wave Superconductor 2H-NbSe2. J. Supercond. Nov. Magn. 2020, 33, 953–958. [Google Scholar] [CrossRef]
- Vorontsov, A.B.; Vekhter, I. Unconventional superconductors under a rotating magnetic field. I. Density of states and specific heat. Phys. Rev. B 2007, 75, 224501. [Google Scholar] [CrossRef]
- Vorontsov, A.B.; Vekhter, I. Unconventional superconductors under a rotating magnetic field. II. Thermal transport. Phys. Rev. B 2007, 75, 224502. [Google Scholar] [CrossRef]
- An, K.; Sakakibara, T.; Settai, R.; Onuki, Y.; Hiragi, M.; Ichioka, M.; Machida, K. Sign Reversal of Field-Angle Resolved Heat Capacity Oscillations in a Heavy Fermion Superconductor CeCoIn5 and dx2−y2 Pairing Symmetry. Phys. Rev. Lett. 2010, 104, 037002. [Google Scholar] [CrossRef]
- Geiser, U.; Schlueter, J.A.; Wang, H.H.; Kini, A.M.; Williams, J.M.; Sche, P.P.; Zakowicz, H.I.; VanZile, M.L.; Dudek, J.D.; Nixon, P.G.; et al. Superconductivity at 5.2 K in an Electron Donor Radical Salt of Bis(ethylenedithio)tetrathiafulvalene (BEDT-TTF) with the Novel Polyfluorinated Organic Anion SF5CH2CF2SO3−. J. Am. Chem. Soc. 1996, 118, 9996–9997. [Google Scholar] [CrossRef]
- Beckmann, D.; Wanka, S.; Wosnitza, J.; Schlueter, J.A.; Williams, J.M.; Nixon, P.G.; Winter, R.W.; Gard, G.L.; Ren, J.; Whangbo, M.-H. Characterization of the Fermi surface of the organic superconductor β”-(ET)2SF5CH2CF2SO3 by measurements of Shubnikov-de Haas and angle-dependent magnetoresistance oscillations and by electronic band-structure calculations. Eur. Phys. J. B 1998, 1, 295–300. [Google Scholar] [CrossRef]
- Brooks, J.S.; Williams, V.; Choi, E.S.; Graf, D.; Tokumoto, M.; Uji, S.; Zou, F.; Wosnitza, J.; Schlueter, J.A.; Davis, H.; et al. Fermiology and superconductivity at high magnetic fields in a completely organic cation radical salt. New J. Phys. 2006, 8, 255. [Google Scholar] [CrossRef]
- Wosnitza, J.; Hagel, J.; Qualls, J.S.; Brooks, J.S.; Balthes, E.; Schweitaer, D.; Schlueter, J.A.; Geiser, U.; Mohtasham, J.; Winter, R.W.; et al. Coherent versus incoherent interlayer transport in layered metals. Phys. Rev. B 2000, 65, R180506. [Google Scholar] [CrossRef]
- Hagel, J.; Wosnitza, J.; Pfleiderer, C.; Schlueter, J.A.; Mohtasham, J.; Gard, G.L. Pressure-induced insulating state in an organic superconductor. Phys. Rev. B 2003, 68, 104504. [Google Scholar] [CrossRef]
- Calandra, M.; Merino, J.; Mckenzie, R.H. Metal-insulator transition and charge ordering in the extended Hubbard model at one-quarter filling. Phys. Rev. B 2002, 66, 195102. [Google Scholar] [CrossRef]
- Merino, J.; Mckenzie, R.H. Superconductivity Mediated by Charge Fluctuations in Layered Molecular Crystals. Phys. Rev. Lett. 2001, 87, 237002. [Google Scholar] [CrossRef]
- Kobayashi, H.; Udagawa, T.; Tomita, H.; Bun, K.; Naito, T.; Kobayashi, A. A New Organic Superconductor, λ-(BEDT-TSF)2GaCl4. Chem. Lett. 1993, 22, 1559–1562. [Google Scholar] [CrossRef]
- Tanatar, M.A.; Ishiguro, T.; Tanaka, H.; Kobayashi, H. Magnetic field–temperature phase diagram of the quasi-two-dimensional organic superconductor λ-(BETS)2GaCl4 studied via thermal conductivity. Phys. Rev. B 2002, 66, 134503. [Google Scholar] [CrossRef]
- Uji, S.; Kodama, K.; Sugii, K.; Terashima, T.; Yamaguchi, T.; Kurita, N.; Tsuchiya, S.; Konoike, T.; Kimata, M.; Kobayashi, A.; et al. Vortex Dynamics and Diamagnetic Torque Signals in Two Dimensional Organic Superconductor λ-(BETS)2GaCl4. J. Phys. Soc. Jpn. 2015, 84, 104709. [Google Scholar] [CrossRef]
- Uji, S.; Shinagawa, H.; Terashima, T.; Yakabe, T.; Terai, Y.; Tokumoto, M.; Kobayashi, A.; Tanaka, H.; Kobayashi, H. Magnetic-field-induced superconductivity in a two-dimensional organic conductor. Nature 2001, 410, 908–910. [Google Scholar] [CrossRef]
- Goddard, P.A.; Blundell, S.J.; Singleton, J.; McDonald, R.D.; Ardavan, A.; Narduzzo, A.; Schlueter, J.A.; Kini, A.M.; Sasaki, T. Angle-dependent magnetoresistance of the layered organic superconductor κ-ET2Cu(NCS)2: Simulation and experiment. Phys. Rev. B 2004, 69, 174509. [Google Scholar] [CrossRef]
- Clark, K.; Hassanien, A.; Khan, S.; Braun, K.-F.; Tanaka, H.; Hla, S.-W. Superconductivity in just four pairs of (BETS)2GaCl4 molecules. Nat. Nanotechnol. 2010, 5, 261–265. [Google Scholar] [CrossRef]
- Kobayashi, H.; Akutsu, H.; Arai, E.; Tanaka, H.; Kobayashi, A. Electric and magnetic properties and phase diagram of a series of organic superconductors λ−BETS2GaXzY4−z [BETS = bis(ethylenedithiotetraselenafulvalene; X, Y = F, Cl, Br; 0 < z < 2)]. Phys. Rev. B 1997, 56, R8526–R8529. [Google Scholar]
- Tanaka, H.; Kobayashi, A.; Sato, A.; Akutsu, H.; Kobayashi, H. Chemical Control of Electrical Properties and Phase Diagram of a Series of λ-Type BETS Superconductors, λ-(BETS)2GaBrxCl4−x. J. Am. Chem. Soc. 1999, 121, 760–768. [Google Scholar] [CrossRef]
- Mori, H.; Okano, T.; Kamiya, M.; Haemori, M.; Suzuki, H.; Tanaka, S.; Nishio, Y.; Kajita, K.; Moriyama, H. Bandwidth and band filling control in organic conductors. Physica C 2001, 357–360, 103–107. [Google Scholar] [CrossRef]
- Kanoda, K. Metal–Insulator Transition in κ-(ET)2X and (DCNQI)2M: Two Contrasting Manifestation of Electron Correlation. J. Phys. Soc. Jpn. 2006, 75, 051007. [Google Scholar] [CrossRef]
- Kobayashi, T.; Kawamoto, A. Evidence of antiferromagnetic fluctuation in the unconventional superconductor λ-(BETS)2GaCl4 by 13C NMR. Phys. Rev. B 2017, 96, 125115. [Google Scholar] [CrossRef]
- Imajo, S.; Kanda, N.; Yamashita, S.; Akutsu, H.; Nakazawa, Y.; Kumagai, H.; Kobayashi, T.; Kawamoto, A. Thermodynamic Evidence of d-Wave Superconductivity of the Organic Superconductor λ-(BETS)2GaCl4. J. Phys. Soc. Jpn. 2016, 85, 043705. [Google Scholar] [CrossRef]
- Sari, D.P.; Asih, R.; Mohm-Tajudin, S.S.; Adam, N.; Hiraki, K.; Ishii, Y.; Takahashi, T.; Nakano, T.; Nozue, Y.; Sulaiman, S.; et al. μSR Study of Organic Superconductor λ-(BETS)2GaCl4. IOP Conf. Ser. Mater. Sci. Eng. 2017, 196, 012047. [Google Scholar] [CrossRef]
- Aizawa, H.; Koretsune, T.; Kuroki, K.; Seo, H. Electronic Structure Calculation and Superconductivity in λ-(BETS)2GaCl4. J. Phys. Soc. Jpn. 2018, 87, 093701. [Google Scholar] [CrossRef]
- Imajo, S.; Yamashita, S.; Akutsu, H.; Kumagai, H.; Kobayashi, T.; Kawamoto, A.; Nakazawa, Y. Gap Symmetry of the Organic Superconductor λ-(BETS)2GaCl4 Determined by Magnetic-Field-Angle-Resolved Heat Capacity. J. Phys. Soc. Jpn. 2019, 88, 023702. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).