Abstract
In the most studied family of organic superconductors -(BEDT-TTF)X, the BEDT-TTF molecules that make up the conducting planes are coupled as dimers. For some anions X, an antiferromagnetic insulator is found at low temperatures adjacent to superconductivity. With an average of one hole carrier per dimer, the BEDT-TTF band is effectively -filled. Numerous theories have suggested that fluctuations of the magnetic order can drive superconducting pairing in these models, even as direct calculations of superconducting pairing in monomer -filled band models find no superconductivity. Here, we present accurate zero-temperature Density Matrix Renormalization Group (DMRG) calculations of a dimerized lattice with one hole per dimer. While we do find an antiferromagnetic state in our results, we find no evidence for superconducting pairing. This further demonstrates that magnetic fluctuations in the effective -filled band approach do not drive superconductivity in these and related materials.
1. Introduction
Correlated-electron superconductivity (SC) continues to be one of the most challenging problems in condensed matter physics. Even as the large majority of investigators in this research area have focused on cuprates and iron-based superconductors (and more recently, ruthenates), it is now widely recognized that there exist many other unconventional or correlated-electron superconductors, although with lower superconducting critical temperature T [1,2,3,4,5,6,7,8,9]. Superconducting organic charge-transfer (CT) solids hold a special place in this context, as SC in CT solids was discovered significantly prior to the discovery of the phenomenon in the cuprates [10]. Despite intensive investigations over the past four decades, however, the mechanism of SC in CT solids remains a mystery, and organic SC continues to be an active research area, as illustrated by the appearance of many review articles on the subject over the past decade [11,12,13,14,15]. In the present paper, we report the results of our latest calculations that have probed a key question in the field of organic SC.
The common theme among many (though not all, see below) correlated-electron superconductors is the proximity of SC to spin-density wave (SDW) or antiferromagnetism (AFM). This property is shared by organic superconductors based on the cation TMTSF as well as some -phase BEDT-TTF compounds. Unlike in the cuprates, though, transition from the insulating magnetic phase to the superconducting phase is driven by the application of moderate pressure as opposed to doping. Both TMTSF and BEDT-TTF based superconductors (hereafter (TMTSF)X and (BEDT-TTF)X) are characterized by cation:anion ratio of 2:1, with closed-shell monovalent anions X, the implication being that each individual cation monomer has charge +. In both families, the cation lattice is highly dimerized, such that the overall charge on a dimer of cations is exactly +1. This has led to various effective half-filled band theories of organic CT superconductors, within which the dimer of cations is considered as a single site in a lattice described within anisotropic triangular lattice Hubbard models (we emphasize that these theories are therefore not applicable to nondimerized (BEDT-TTF)X families, such as those belonging to the -family, which also exhibit SC; we revisit this issue later). Within mean-field and dynamic mean field theory (DMFT) calculations on the half-filled band anisotropic triangular lattice Hubbard model, pressure increases the lattice frustration, causing thereby a bandwidth-driven transition from the AFM insulator to the superconducting state (or in the case of a lattice that is already strongly frustrated, as in -(BEDT-TTF)Cu(CN), from a quantum spin liquid (QSL) to SC) [16,17,18,19,20,21,22,23,24,25,26,27,28]. Direct numerical calculations of superconducting pair-pair correlations within the -filled Hubbard band on triangular lattices have, however, consistently found absence of SC [29,30,31,32,33]. Taken together with the very recent convincing demonstration of the absence of SC within the weakly doped square lattice two-dimensional (2D) Hubbard Hamiltonian [34], numerical calculations then cast serious doubt on the existing approximate spin fluctuation mechanisms of AFM-to-SC transition.
Conceivably, one possible origin of disagreement between the mean-field theories of organic SC and numerical calculations is that retention of the explicit dimeric structure of the Hubbard lattice sites is essential for superconducting correlations to dominate. That is, even as intra-dimer charge fluctuations are precluded within the effective -filled band models (since that would make the effective -filled description invalid and can even destroy the AFM in the weakly frustrated region of the Hamiltonian), the superconducting singlets should be defined such that they span over a pair of dimers, as opposed to a pair of effective single sites. Needless to say such a numerical calculation is far more involved than where dimers are replaced with single sites, as the required lattice sizes needed are twice that in the previous calculations [29,30,33]. We report precisely such a calculation here, which again finds absence of SC in such a dimer lattice.
2. Methods
We consider the Hubbard Hamiltonian,
In Equation (1) creates an electron of spin on molecule i and . U is the onsite Hubbard interaction. It is important to note that this U is the Coulomb repulsion between carriers on each monomer site and is not the same as the effective dimer . The lattice we consider is a rectangular lattice of dimers (see Figure 1). In this lattice there are three hopping integrals : is the intra-dimer hopping, t the inter-dimer hopping, and a frustrating hopping (see Figure 1). We take the system to be -filled with an average electron density of per monomer site. This lattice is expected to show Néel AFM order in the unfrustrated limit of small .
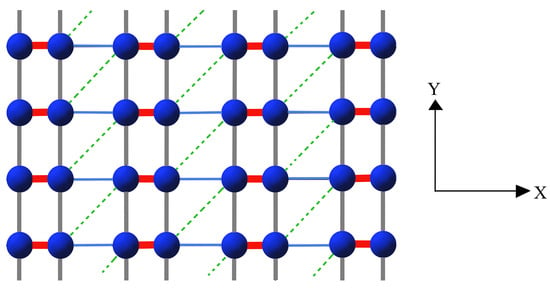
Figure 1.
The dimer lattice we consider. Thick lines are the intra-dimer hopping , thin lines are the inter-dimer hopping t, and dashed lines are the frustrating bond . Boundary conditions in our DMRG calculations are open in x and periodic in y.
To solve for the ground state of Equation (1) we employ the Density Matrix Renormalization Group (DMRG) method [35] using the ITensor library [36] with real-space parallelization [37]. DMRG can calculate essentially numerically exact correlation functions in quasi-one-dimensional systems. However, its primary limitation is an exponential scaling in the transverse size of systems that can be studied. Here, we consider lattices of dimension 4 sites in y and up to 32 sites in x (see Figure 1), corresponding to a 16 × 4 lattice in terms of dimers. We choose = 1.5 and t = 0.5 such that the average hopping along the x axis is 1.0; our choice of is comparable to the dimerization found in the CT solid superconductors [14]. We take boundary conditions that are open (periodic) in x (y). The same boundary condition has been successfully used in several recent calculations on the Hubbard model [34,38], and has been tested against other approaches. We used a DMRG bond dimension m of up to 15,000 with minimum truncation error of 10–10; all results we show are extrapolated to zero truncation error.
3. Results
We measure dimer spin–spin and pair–pair correlation functions. The dimer spin operator is
where the sites and make up the dimer i. We calculate the dimer spin–spin correlation function . In Figure 2 for a 16 × 4 lattice we plot where dimer 1 is on the first chain and dimer j is on the nearest neighbor chain for and 0.4.
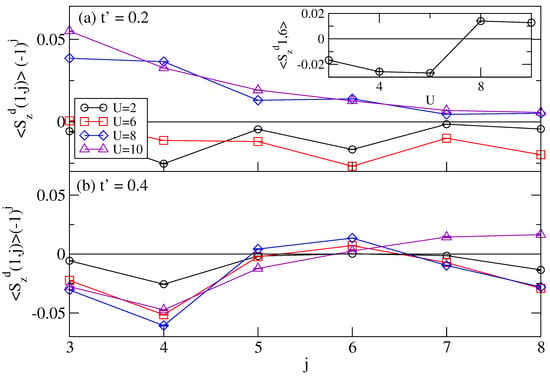
Figure 2.
Dimer spin-spin correlations for a 16 × 4 lattice between the first dimer on chain 1 and dimer j on chain 2, multiplied by , the expected sign for Néel AFM. (a) . The inset shows the U dependence of a single spin-spin correlation at long distance. Néel AFM order is present at for . (b) . Here, we find no AFM order.
As shown in Figure 2a, for and this quantity is positive for all spin correlations, indicating the presence of Néel AFM order. For (Figure 2b) we do not find Néel AFM order up to at least . These results show that Néel AFM order is only present in this system when the frustration is low, and for realistic U values AFM will not be present when .
To define superconducting pair–pair correlations in the effective -filled representation, we first define an operator creating an effective particle on dimer i with equal monomer populations, as required within effective -filled band theories,
The operator creates a singlet pair between nearest-neighbor (n.n.) dimers separated by :
Note that Equation (3) involves four different lattice sites. We consider two kinds of n.n. pairs with taken as the n.n. distance between dimers in the x and y directions,
In the effective dimer model pairing is expected to have d-wave symmetry. Because of the small transverse dimensions of our lattice we do not define full pairs involving four n.n. singlets, but instead calculate only single singlet-singlet correlations. To check if the pairing has the expected d-wave sign structure we calculate two different correlation functions, and . corresponds to correlations between two singlets both oriented along x, while corresponds to one singlet oriented along x and one along y. For pairing should be negative.
In a 2D superconductor long-range order should be present in at zero temperature. Because of the quasi-one-dimensional nature of cylindrical geometry of the lattice that we can solve in DMRG long-range order in is not possible even in the limit . If such a quasi-one-dimensional system showed a tendency to SC however, the system would behave as a Luther-Emery liquid [39] with decaying as a power law with . In addition to long-range order in , if SC in the system is driven by Coulomb interactions, one expects that [29].
In Figure 3 we plot as a function of r. In Figure 3a the indices i and j in Equation (4) are taken on the same chain, in Figure 3b they are on nearest neighbor chains, and in Figure 3c they are on second neighbor chains. In each panel r is the center-to-center distance between pairs in units of the dimer-dimer spacing. In Figure 3a we also plot the function . While the distances we have on the lattice are limited and we cannot determine if decays with r as a power law or as an exponential, we find that on each chain decays significantly faster than . We discuss the distance decay of further below.
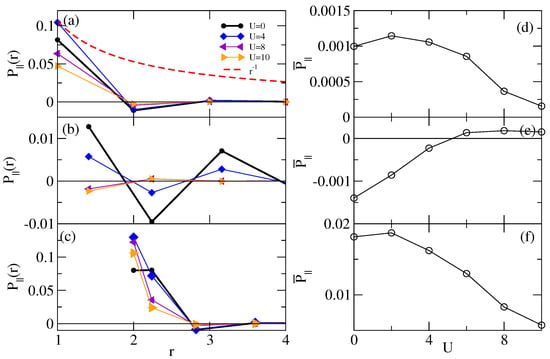
Figure 3.
Pair–pair correlation for for parallel-oriented n.n. pairs on a 16 × 4 lattice. (a) Pair-pair correlation for n.n. x-axis pairs on chain 1 (b) for n.n. x-axis pairs on chains 1 and 2 (c) for n.n. x-axis pairs on chains 1 and 3. In (a–c), r is the center-to-center pair distance. In (a) we show the function for comparison as the dashed curve. In panels (d) we plot the U dependence of the average long-range correlation (see text) for the chain 1—chain 1 correlations in (a); panels (e,f) are similar for chain 1—chain 2 and chain 1—chain 3 correlations, respectively.
As seen in Figure 3a,c, only at very short range () we find that is enhanced very slightly over its value at . Similar enhancement at the shortest pair separations was previously found in calculations in the monomer -filled Hubbard model on an anisotropic triangular lattice [29,30]. As noted in [40], at the pair-pair correlation can be written as a linear combination of charge-charge and spin-spin correlations; the latter are enhanced by U [40]. To measure the effect of correlations on pairing we define the average long-range pair-pair correlation [41],
In Equation (5) is the number of terms in the sum, and the sum is over r greater than 2 in dimer-dimer units but less than a maximum distance . The upper cutoff is necessary because of the open boundary conditions along x in our lattice and is chosen so that the maximum pair-pair distance along the chain is 4 (one half of the lattice length of 8 dimers). Figure 3d–f show as a function of U. In each case the magnitude of decreases with U apart from an insignificant increase at very small U. A large decrease in also takes place for upon entering the AFM insulating phase. A similar decrease is seen in calculations within the monomer -filled band [29,30].
Figure 4a–c shows perpendicular correlations as a function of r. Like , we find that along the chain direction decays faster than . These are negative in many cases (Figure 4a,c), which would be consistent with a type pairing symmetry. However, some correlations are positive rather than negative (see Figure 4b). This apparent sign inconsistency with order may be a finite-size effect related to the small transverse dimensions of our lattice. It may also indicate that another type of pair symmetry besides is relevant, as found in other 4-chain calculations [38]. Figure 4d shows a clear decrease in magnitude of with increasing U. The U dependence of Figure 4e,f are harder to interpret. We believe that the unusual U dependence here is due to shorter range correlations, for example as in Figure 4b where changes discontinuously at small U at [42]. As in Reference [41], as distances are excluded, we again find a continuous decrease of with increasing U.
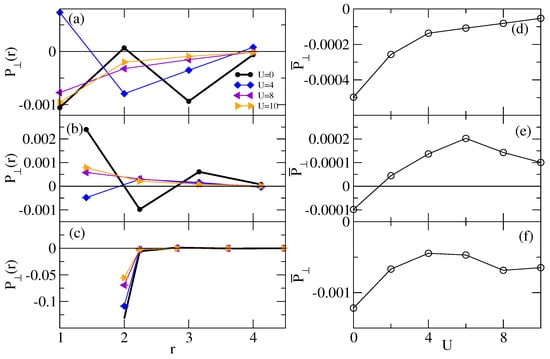
Figure 4.
Panels (a–f) are the same as in Figure 3 except that the pair-pair correlation is for the perpendicular orientation of pairs. Note that in (d–f), is negative, with decreasing magnitude as U increases. in (e) is strongly affected by shorter-range correlations which lead to the unusual U dependence (see text).
Figure 5 and Figure 6 show the pair–pair correlations at . Here AFM order is absent over the whole range of U we studied. We again find that decreases faster than (see Figure 5a). As at smaller we again find that some pair-pair correlations are enhanced by U at short range (). However, here both and decrease continuously with U, again with the exception of one point at shorter r where there is a discontinuous change at small U (see Figure 6b,e).
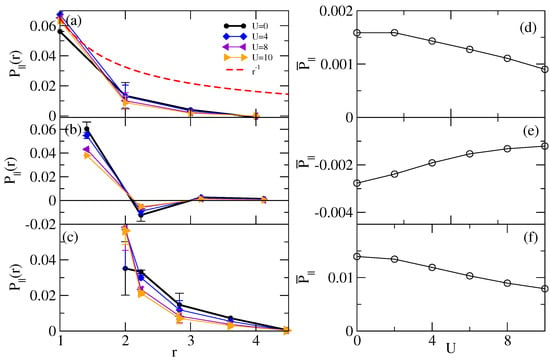
Figure 5.
Panels (a–f) are the same as Figure 3 but with .
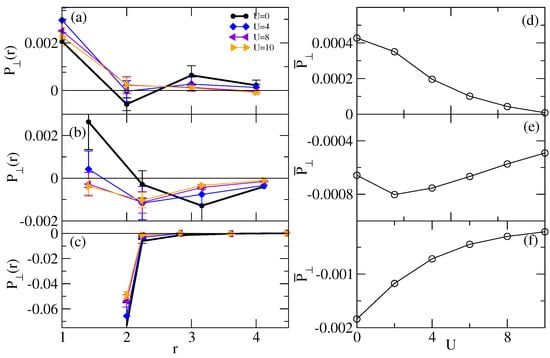
Figure 6.
Panels (a–f) are the same as Figure 4 but with .
A critical question is whether decays as an exponential or power law with r [34]. In Figure 7 we compare for the 16 × 4 lattice and the 32 × 4 lattice for intermediate where AFM order is not present. Figure 7a shows the distance dependence of for pairs on the first chain of the lattice. We cannot definitively distinguish between a power law and an exponential decay with the system lengths available to us. However, as shown in Figure 7a, we find that if decays with distance as , then . This decay is significantly faster with distance than found in quasi-1D superconducting systems like the weakly doped two-leg Hubbard ladder, where [43]. Additionally, in the 32 × 4 lattice we find that the magnitude of decreases with U at long range (Figure 7a), which is also seen in DMRG calculations on the doped single-band Hubbard model (see [Reference [34], Figure 11]). Finally, in the larger lattice the average long-range pairing also decreases monotonically with increasing U (see Figure 7b), which would preclude AFM-driven SC.
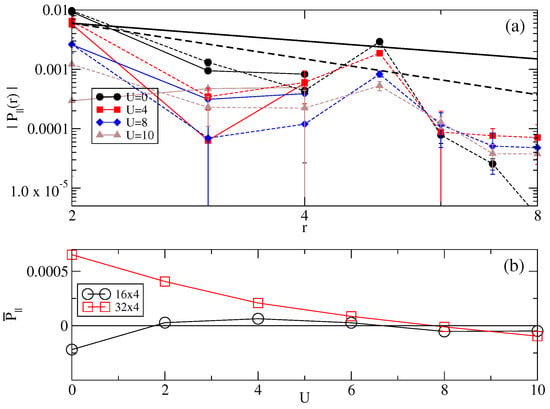
Figure 7.
Pair–pair correlations for = 0.4 for parallel-oriented n.n. pairs on chain 1. In (a) points connected with solid (dashed) lines are for a 16 × 4 (32 × 4) lattice. For comparison we show the power law functions and . In (b), the U dependence of the average long-range correlation for both lattices.
Summarizing our data, while we cannot prove the presence of long range AFM order without undertaking a full finite-size scaling, we do find strong AFM correlations for weak frustration and moderately strong U. We find no evidence that within the effective -filled picture that the superconducting pair-pair correlations are enhanced over their value for non-interacting electrons, and on our cylindrical lattice the distance dependence of in the x direction does not support the presence of long-range order.
4. Discussion
The conclusions of our work are: (i) SC is absent within the model; and (ii) the presence or absence of AFM order is not related to the tendency towards SC.
In -(BEDT-TTF)X with X = Cu[N(CN)]Cl where AFM order is found under ambient pressure, estimates for vary between 0.44 and 0.53 [14]. Similarly, no AFM order is found for X = Cu(CN) where 0.80 ⪅ ⪅ 0.99 [14]. In our present results, we find AFM order at () but no AFM order at , which is roughly consistent with what is observed experimentally. SC is however found in both X = Cu[N(CN)]Cl and X = Cu(CN), under pressures of 0.03 and 0.6 GPa, respectively. Moreover, there is no obvious connection between the superconducting in -(BEDT-TTF)X and the value of [14]. For example SC is also found for ( in X = CFSO [44]). This suggests that SC in -(BEDT-TTF)X is not related to the proximity to an AFM or QSL phase. This is also consistent with our present results, where we find little difference in the pair–pair correlations between where AFM is present and where AFM is absent.
Our results on the absence of SC in the effective -filled Hubbard dimer model is in complete agreement with our previous results on the -filled Hubbard monomer model [29,30,33]. Independent of whether one considers the dimers of BEDT-TTF molecules as effective single sites with charge occupancy +1 (previous calculations) or as dimers with monomer charge occupancies of each (present calculations), the superconducting pair correlations are found to be suppressed by Hubbard U continuously from . This fundamental observation was arrived at from exact diagonalization [29,33], Path Integral Renormalization Group [30] and now DMRG on completely different lattices, thereby confirming that the result is not an artifact of the choice of a specific lattice or a particular computational technique. Taken together, these results very clearly indicate that spin fluctuations are not driving organic SC. With hindsight, this conclusion should not be surprising: as already pointed out in the above, AFM occurs in only three -(BEDT-TTF)X, X = Cu[N(CN)Cl, deuterated X = Cu[N(CN)Br and CFSO. Whether or not X = Cu(CN) and Ag(CN) are true QSLs continue to be debated, and both claims of a CO phase below 6 K [45] as well its absence [46] exist in the literature. What is perhaps very relevant in this context is that transition from CO to SC is far more common in CT solids, including in the , , and -families [14]. Even among the -phase materials, CO has been detected in X = Hg(SCN)Cl [47,48,49] while in the related material X = Hg(SCN)Br there occurs a dipolar liquid phase [50] the formation of which is related to the mechanism of CO formation [51,52]. While these latter materials are also strongly correlated, CO requires an effective -filled (or -filled) description of CT solids, within which intra-dimer charge dimer degrees of freedom are explicitly taken into account [14,53,54,55,56]. The charge-charge correlations in the CO phase in these systems are different from that in Wigner crystals. The CO phase is a paired-electron crystal, with nearest neighbor spin-singlet charge-rich molecules separated by pairs of charge-poor molecules. Pressure increases frustration, causing the spin singlets to be mobile. Calculations on an anisotropic triangular lattice [41] as well as on -lattices [42,57] have indeed found that superconducting pair correlations are enhanced by the Hubbard U uniquely at -filling. DMRG calculations on a width-three triangular lattice found evidence for p-wave and d-wave SC in the density range 0.40∼0.65 [58], which would appear to agree with the conclusion from the previous work [41]. Additionally, electron-electron and electron-bond phonon interactions act co-operatively at this bandfilling to enhance superconducting pair correlations, even as they compete with one another at all other fillings [59]. These results are encouraging and suggest further research along this direction.
Author Contributions
Conceptualization and methodology, R.T.C. and S.M.; software, R.T.C.; Validation, formal analysis, investigation, visualization, D.R., R.T.C. and S.M.; data curation, D.R. and R.T.C.; writing, R.T.C. and S.M.; Supervision, project administration, R.T.C. and S.M.; funding acquisition, S.M. All authors have read and agreed to the published version of the manuscript.
Funding
S.M. acknowledges support by the National Science Foundation grant NSF-CHE-1764152.
Data Availability Statements
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mazumdar, S. A unified theoretical approach to superconductors with strong Coulomb correlations: The organics, LiTi2O4, electron- and hole-doped copper oxides and doped BaBiO3. In Interacting Electrons in Reduced Dimensions. Proceedings of a NATO Advanced Research Workshop; Baeriswyl, D., Campbell, D.K., Eds.; Plenum: New York, NY, USA, 1989; pp. 315–329.BaBiO3. In Interacting Electrons in Reduced Dimensions. Proceedings of a NATO Advanced Research Workshop; Baeriswyl, D., Campbell, D.K., Baeriswyl, D., Campbell, D.K., Eds.; Plenum: New York, NY, USA, 1989; pp. 315–329. [Google Scholar]
- Uemura, Y.J.; Le, L.P.; Luke, G.M.; Sternlieb, B.J.; Wu, W.D.; Brewer, J.H.; Riseman, T.M.; Seaman, C.L.; Maple, M.B.; Ishikawa, M.; et al. Basic similarities among cuprate, bismuthate, organic, Chevrel-phase, and heavy-fermion superconductors shown by penetration-depth measurements. Phys. Rev. Lett. 1991, 66, 2665–2668. [Google Scholar] [CrossRef]
- Fukuyama, H.; Hasegawa, Y. Superconductivity in organics and oxides: Similarity and dissimilarity. Physica B+C 1987, 148, 204–211. [Google Scholar] [CrossRef]
- Fukuyama, H. On some organic conductors in the light of oxide superconductors. In Physics and Chemistry of Organic Superconductors. Proceedings of the ISSP International Symposium; Saito, G., Kagoshima, S., Eds.; Springer: Berlin, Germany, 1990; pp. 15–20. [Google Scholar]
- McKenzie, R.H. Similarities between organic and cuprate superconductors. Science 1997, 278, 820–821. [Google Scholar] [CrossRef]
- Iwasa, Y.; Takenobu, T. Superconductivity, Mott-Hubbard states, and molecular orbital order in intercalated fullerides. J. Phys. Condens. Matter 2003, 15, R495. [Google Scholar] [CrossRef]
- Capone, M.; Fabrizio, M.; Castellani, C.; Tosatti, E. Colloquium: Modeling the unconventional superconducting properties of expanded A3C60 fullerides. Rev. Mod. Phys. 2009, 81, 943–958. [Google Scholar] [CrossRef]
- Mazumdar, S.; Clay, R.T. Is there a common theme behind the correlated-electron superconductivity in organic charge-transfer solids, cobaltates, spinels and fullerides? Phys. Stat. Solidi 2012, 249, 995–998. [Google Scholar] [CrossRef]
- Baskaran, G. RVB states in doped band insulators from Coulomb forces: Theory and a case study of superconductivity in BiS2 layers. Supercond. Sci. Technol. 2016, 29, 124002. [Google Scholar] [CrossRef]
- Jérome, D.; Mazaud, A.; Ribault, M.; Bechgaard, K. Superconductivity in a synthetic organic conductor (TMTSF)2PF6. J. Phys. (Paris) Lett. 1980, 41, L95–L98. [Google Scholar] [CrossRef]
- Kanoda, K.; Kato, R. Mott physics in organic conductors with triangular lattices. Annu. Rev. Condens. Matter Phys. 2011, 2, 167–188. [Google Scholar] [CrossRef]
- Kato, R. Special issue: Molecular conductors. Crystals 2012, 2012, 56–1482. [Google Scholar]
- Brown, S.E. Organic superconductors: The Bechgaard salts and relatives. Physica C 2015, 514, 279–289. [Google Scholar] [CrossRef]
- Clay, R.T.; Mazumdar, S. From charge- and spin-ordering to superconductivity in the organic charge-transfer solids. Phys. Rep. 2019, 788, 1–89. [Google Scholar] [CrossRef]
- Dressel, M.; Tomić, S. Molecular quantum materials: Electronic phases and charge dynamics in two-dimensional organic solids. Adv. Phys. 2020, 69, 1–120. [Google Scholar] [CrossRef]
- Kino, H.; Kontani, H. Phase diagram of superconductivity on the anisotropic triangular lattice Hubbard model: An effective model of κ-(BEDT-TTF) salts. J. Phys. Soc. Jpn. 1998, 67, 3691–3694. [Google Scholar] [CrossRef]
- Schmalian, J. Pairing due to spin fluctuations in layered organic superconductors. Phys. Rev. Lett. 1998, 81, 4232–4235. [Google Scholar] [CrossRef]
- Kondo, H.; Moriya, T. Spin Fluctuation-Induced Superconductivity in Organic Compounds. J. Phys. Soc. Jpn. 1998, 67, 3695–3698. [Google Scholar] [CrossRef]
- Vojta, M.; Dagotto, E. Indications of unconventional superconductivity in doped and undoped triangular antiferromagnets. Phys. Rev. B 1999, 59, R713–R716. [Google Scholar] [CrossRef]
- Baskaran, G. Mott Insulator to High Tc Superconductor via Pressure: Resonating Valence Bond Theory and Prediction of New Systems. Phys. Rev. Lett. 2003, 90, 197007. [Google Scholar] [CrossRef]
- Liu, J.; Schmalian, J.; Trivedi, N. Pairing and Superconductivity Driven by Strong Quasiparticle Renormalization in Two-Dimensional Organic Charge Transfer Salts. Phys. Rev. Lett. 2005, 94, 127003. [Google Scholar] [CrossRef]
- Kyung, B.; Tremblay, A.M.S. Mott transition, antiferromagnetism, and d-wave superconductivity in two-dimensional organic conductors. Phys. Rev. Lett. 2006, 97, 046402. [Google Scholar] [CrossRef]
- Yokoyama, H.; Ogata, M.; Tanaka, Y. Mott Transitions and d-Wave Superconductivity in Half-Filled-Band Hubbard Model on Square Lattice with Geometric Frustration. J. Phys. Soc. Jpn. 2006, 75, 114706. [Google Scholar] [CrossRef]
- Watanabe, T.; Yokoyama, H.; Tanaka, Y.; Inoue, J. Superconductivity and a Mott Transition in a Hubbard Model on an Anisotropic Triangular Lattice. J. Phys. Soc. Jpn. 2006, 75, 074707. [Google Scholar] [CrossRef]
- Sahebsara, P.; Sénéchal, D. Antiferromagnetism and Superconductivity in Layered Organic Conductors: Variational Cluster Approach. Phys. Rev. Lett. 2006, 97, 257004. [Google Scholar] [CrossRef] [PubMed]
- Nevidomskyy, A.H.; Scheiber, C.; Sénéchal, D.; Tremblay, A.M.S. Magnetism and d-wave superconductivity on the half-filled square lattice with frustration. Phys. Rev. B 2008, 77, 064427. [Google Scholar] [CrossRef]
- Sentef, M.; Werner, P.; Gull, E.; Kampf, A.P. Superconducting Phase and Pairing Fluctuations in the Half-Filled Two-Dimensional Hubbard Model. Phys. Rev. Lett. 2011, 107, 126401. [Google Scholar] [CrossRef]
- Hebert, C.D.; Semon, P.; Tremblay, A.M.S. Superconducting dome in doped quasi-two-dimensional organic Mott insulators: A paradigm for strongly correlated superconductivity. Phys. Rev. B 2015, 92, 195112. [Google Scholar] [CrossRef]
- Clay, R.T.; Li, H.; Mazumdar, S. Absence of superconductivity in the half-filled band Hubbard model on the anisotropic triangular lattice. Phys. Rev. Lett. 2008, 101, 166403. [Google Scholar] [CrossRef]
- Dayal, S.; Clay, R.T.; Mazumdar, S. Absence of long-range superconducting correlations in the frustrated -filled band Hubbard model. Phys. Rev. B 2012, 85, 165141. [Google Scholar] [CrossRef]
- Watanabe, T.; Yokoyama, H.; Tanaka, Y.; Inoue, J. Predominant magnetic states in the Hubbard model on anisotropic triangular lattices. Phys. Rev. B 2008, 77, 214505. [Google Scholar] [CrossRef]
- Tocchio, L.F.; Parola, A.; Gros, C.; Becca, F. Spin-liquid and magnetic phases in the anisotropic triangular lattice: The case of κ-(ET)2X. Phys. Rev. B 2009, 80, 064419. [Google Scholar] [CrossRef]
- Gomes, N.; Clay, R.T.; Mazumdar, S. Absence of superconductivity and valence bond order in the Hubbard-Heisenberg model for organic charge-transfer solids. J. Phys. Condens. Matter 2013, 25, 385603. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Qin, M.; Chung, C.M.; Shi, H.; Vitali, E.; Hubig, C.; Schollwöck, U.; White, S.R.; Zhang, S. Absence of superconductivity in the pure two-dimensional Hubbard model. Phys. Rev. X 2020, 10, 031016. [Google Scholar] [CrossRef]
- White, S.R. Density matrix formulation for quantum renormalization groups. Phys. Rev. Lett. 1992, 69, 2863–2866. [Google Scholar] [CrossRef]
- Fishman, M.; White, S.R.; Stoudenmire, E.M. The ITensor Software Library for Tensor Network Calculations. arXiv 2020, arXiv:2007.14822. [Google Scholar]
- Stoudenmire, E.M.; White, S.R. Real-space parallel density matrix renormalization group. Phys. Rev. B 2013, 87, 155137. [Google Scholar] [CrossRef]
- Chung, C.M.; Qin, M.; Zhang, S.; Schollwöck, U.; White, S.R. Plaquette versus ordinary d-wave pairing in the t′-Hubbard model on a width 4 cylinder. Phys. Rev. B 2020, 102, 041106. [Google Scholar] [CrossRef]
- Luther, A.; Emery, V.J. Backward Scattering in the One-Dimensional Electron Gas. Phys. Rev. Lett. 1974, 33, 589–592. [Google Scholar] [CrossRef]
- Aimi, T.; Imada, M. Does Simple Two-Dimensional Hubbard Model Account for High-Tc Superconductivity in Copper Oxides? J. Phys. Soc. Jpn. 2007, 76, 113708. [Google Scholar] [CrossRef]
- Gomes, N.; De Silva, W.W.; Dutta, T.; Clay, R.T.; Mazumdar, S. Coulomb Enhanced Superconducting Pair Correlations in the Frustrated Quarter-Filled Band. Phys. Rev. B 2016, 93, 165110. [Google Scholar] [CrossRef]
- Clay, R.T.; Gomes, N.; Mazumdar, S. Theory of triangular lattice quasi-one-dimensional charge-transfer-solids. Phys. Rev. B 2019, 100, 115158. [Google Scholar] [CrossRef]
- Dolfi, M.; Bauer, B.; Keller, S.; Troyer, M. Pair correlations in doped Hubbard ladders. Phys. Rev. B 2015, 92, 195139. [Google Scholar] [CrossRef]
- Ito, H.; Asai, T.; Shimizu, Y.; Hayama, H.; Yoshida, Y.; Saito, G. Pressure-induced superconductivity in the antiferromagnet κ-(ET)2CF2(SO)3. Phys. Rev. B 2016, 94, 020503(R). [Google Scholar] [CrossRef]
- Kobayashi, T.; Ding, Q.P.; Taniguchi, H.; Satoh, K.; Kawamoto, A.; Furukawa, Y. Charge disproportionation in the spin-liquid candidate κ-(ET)2Cu2(CN)3 at 6 K revealed by 63Cu NQR measurements. Phys. Rev. Res. 2020, 2, 042023(R). [Google Scholar] [CrossRef]
- Sedlmeier, K.; Elsässer, S.; Neubauer, D.; Beyer, R.; Wu, D.; Ivek, T.; Tomic, S.; Schlueter, J.A.; Dressel, M. Absence of charge order in the dimerized κ-phase BEDT-TTF salts. Phys. Rev. B 2012, 86, 245103. [Google Scholar] [CrossRef]
- Drichko, N.; Beyer, R.; Rose, E.; Dressel, M.; Schlueter, J.A.; Turunova, S.A.; Zhilyaeva, E.I.; Lyubovskaya, R.N. Metallic state and charge-order metal-insulator transition in the quasi-two-dimensional conductor κ-(BEDT-TTF)2Hg(SCN)2Cl. Phys. Rev. B 2014, 89, 075133. [Google Scholar] [CrossRef]
- Hassan, N.M.; Thirunavukkuarasu, K.; Lu, Z.; Smirnov, D.; Zhilyaeva, E.I.; Torunova, S.; Lyubovskaya, R.N.; Drichko, N. Melting of charge order in the low-temperature state of an electronic ferroelectric-like system. NPJ Quant. Mater. 2020, 5, 15. [Google Scholar] [CrossRef]
- Gati, E.; Fischer, J.K.; Lunkenheimer, P.; Zielke, D.; Köhler, S.; Kolb, F.; von Nidda, H.A.K.; Winter, S.M.; Schubert, H.; Schlueter, J.A.; et al. Evidence for Electronically Driven Ferroelectricity in a Strongly Correlated Dimerized BEDT-TTF Molecular Conductor. Phys. Rev. Lett. 2018, 120, 247601. [Google Scholar] [CrossRef]
- Hassan, N.; Cunningham, S.; Mourigal, M.; Zhilyaeva, E.I.; Torunova, S.A.; Lyubovskaya, R.N.; Schlueter, J.A.; Drichko, N. Evidence for a quantum dipole liquid state in an organic quasi–two-dimensional material. Science 2018, 360, 1101–1104. [Google Scholar] [CrossRef]
- Hotta, C. Quantum electric dipoles in spin-liquid dimer Mott insulator κ-(ET)2Cu2(CN)3. Phys. Rev. B 2010, 82, 241104(R). [Google Scholar] [CrossRef]
- Naka, M.; Ishihara, S. Electronic Ferroelectricity in a Dimer Mott Insulator. J. Phys. Soc. Jpn. 2010, 79, 063707. [Google Scholar] [CrossRef]
- Li, H.; Clay, R.T.; Mazumdar, S. The paired-electron crystal in the two-dimensional frustrated quarter-filled band. J. Phys. Condens. Matter 2010, 22, 272201. [Google Scholar] [CrossRef] [PubMed]
- Dayal, S.; Clay, R.T.; Li, H.; Mazumdar, S. Paired electron crystal: Order from frustration in the quarter-filled band. Phys. Rev. B 2011, 83, 245106. [Google Scholar] [CrossRef]
- Seo, H. Charge Ordering in Organic ET Compounds. J. Phys. Soc. Jpn. 2000, 69, 805–820. [Google Scholar] [CrossRef]
- Kaneko, R.; Tocchio, L.F.; Valentí, R.; Becca, F. Charge orders in organic charge-transfer salts. New J. Phys. 2017, 19, 103033. [Google Scholar] [CrossRef]
- De Silva, W.W.; Gomes, N.; Mazumdar, S.; Clay, R.T. Coulomb enhancement of superconducting pair-pair correlations in a -filled model for κ-(BEDT-TTF)2X. Phys. Rev. B 2016, 93, 205111. [Google Scholar] [CrossRef]
- Venderley, J.; Kim, E.A. Density matrix renormalization group study of superconductivity in the triangular lattice Hubbard model. Phys. Rev. B 2019, 100, 060506. [Google Scholar] [CrossRef]
- Clay, R.T.; Roy, D. Superconductivity due to cooperation of electron-electron and electron-phonon interactions at quarter-filling. Phys. Rev. Res. 2020, 2, 023006. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).