Observation of Backflow during the Anihilation of Topologocal Defects in Freely Suspended Smectic Films
Abstract
1. Introduction
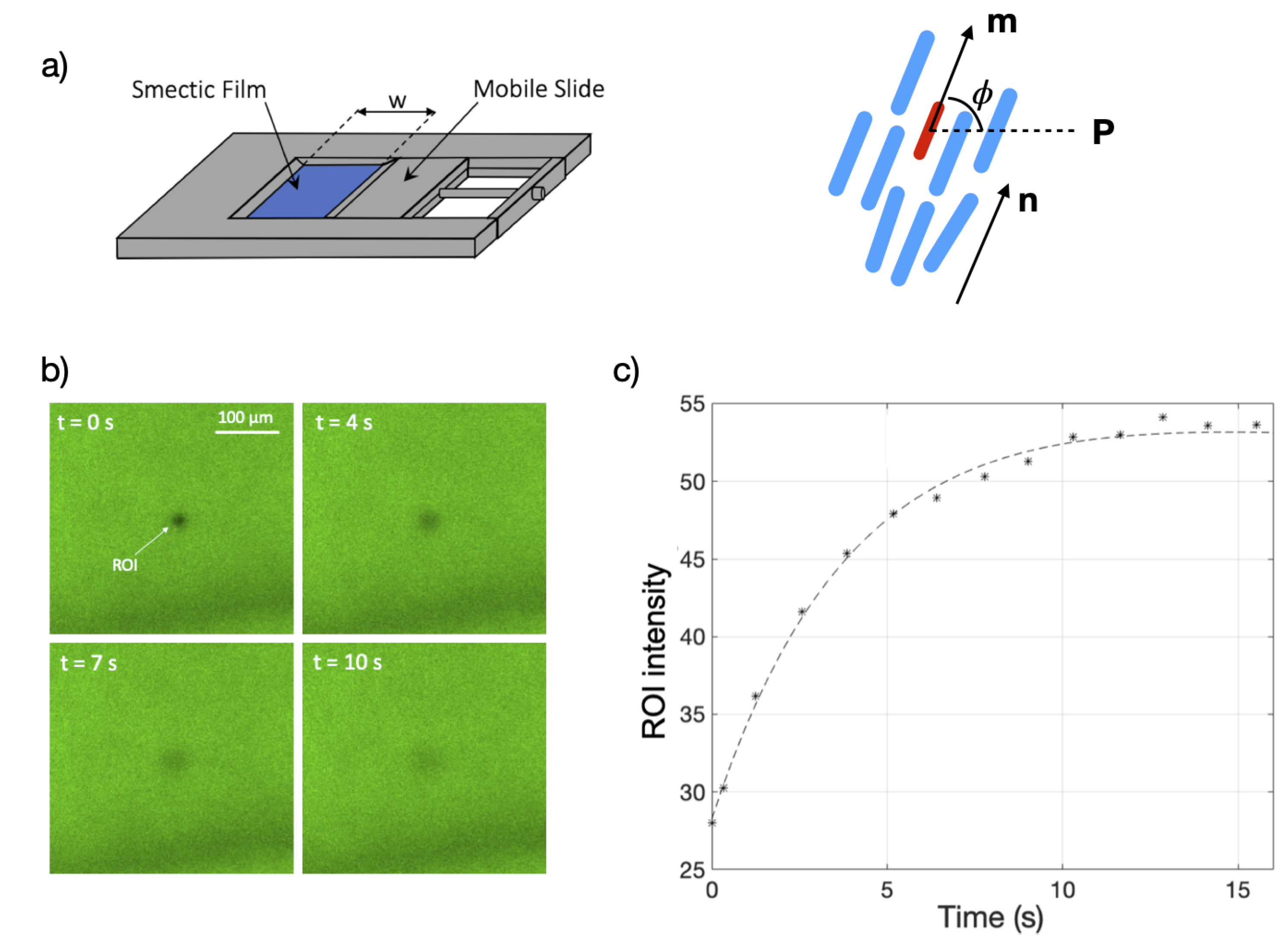
2. Materials and Methods
3. Results and Discussion
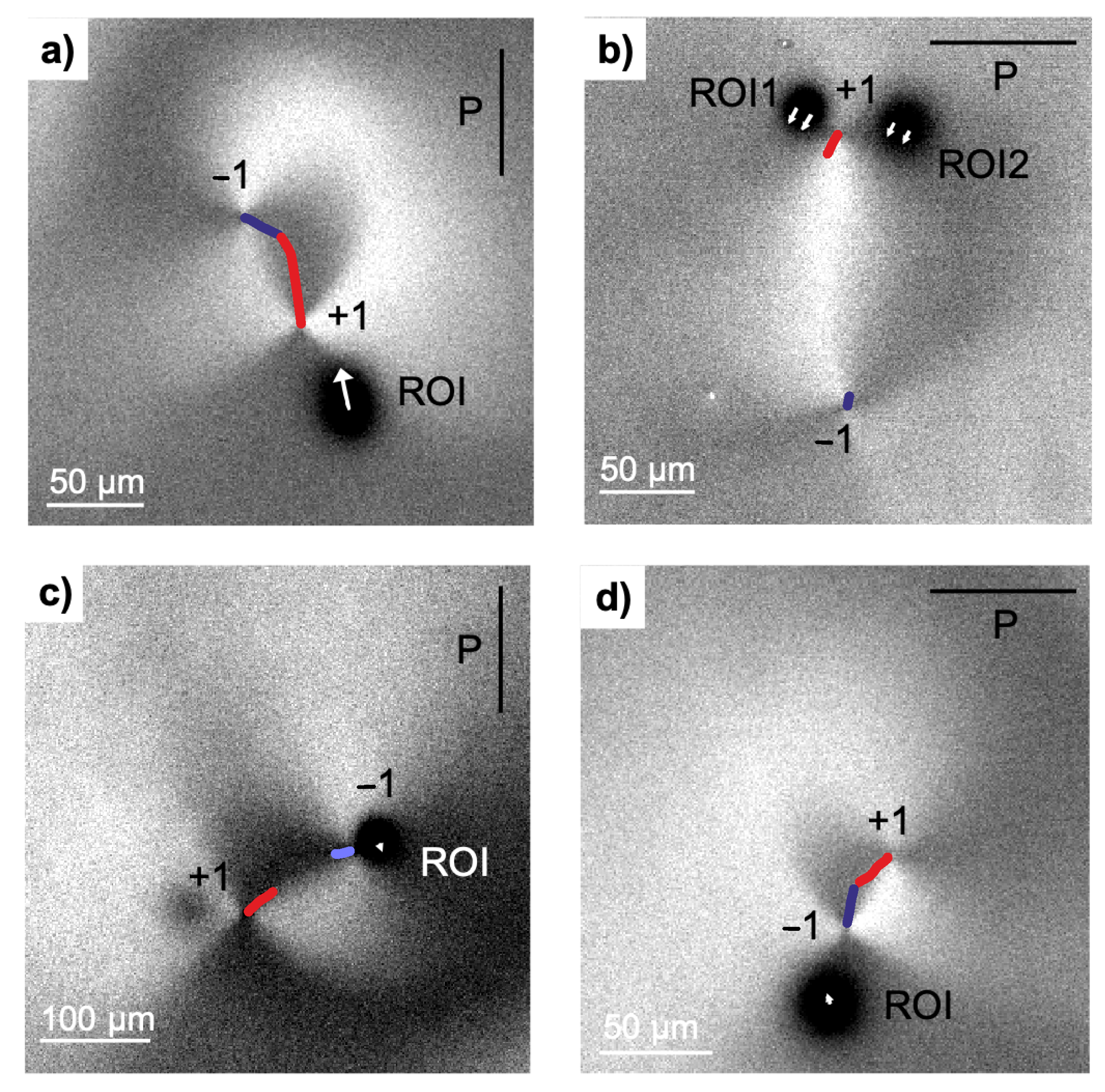
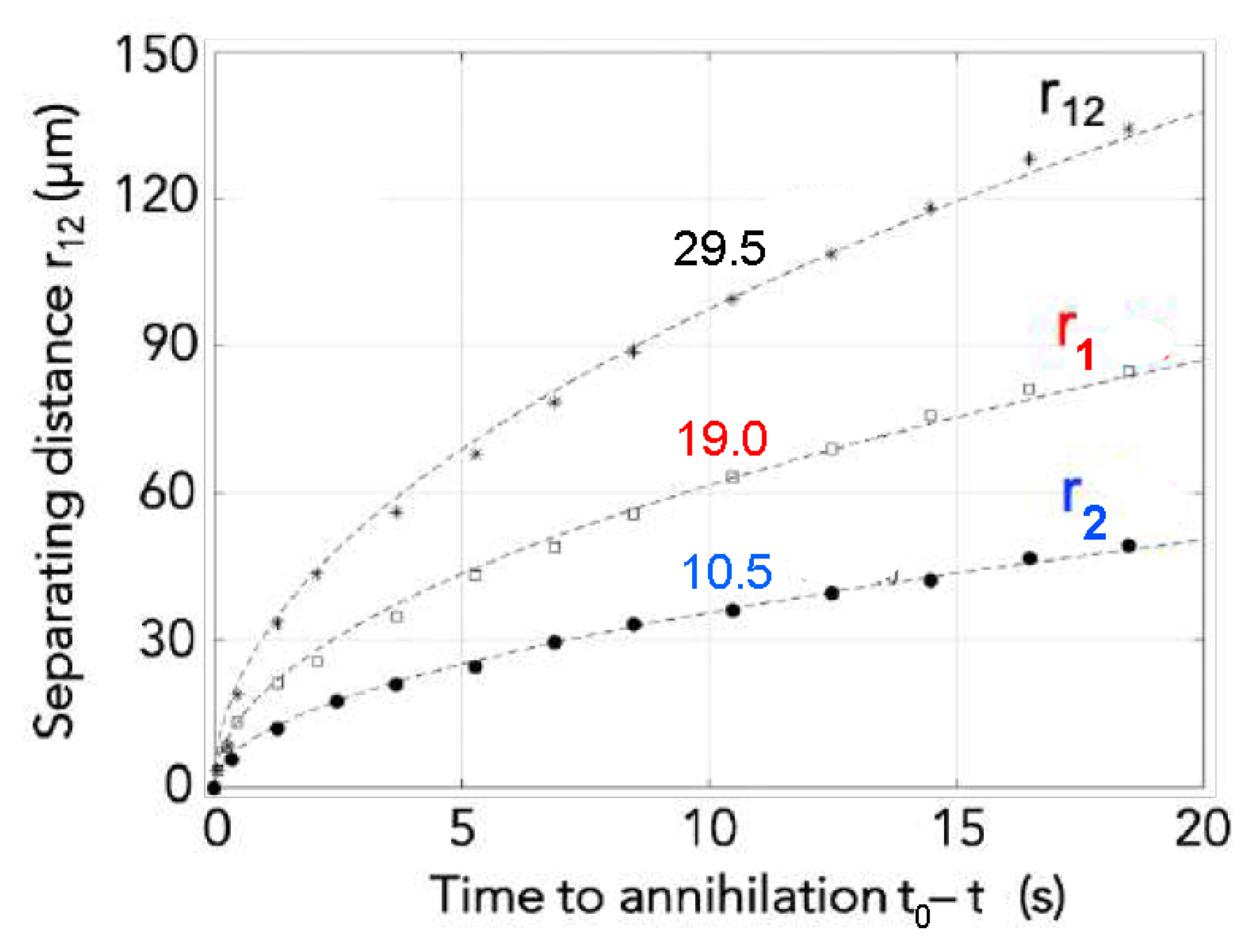
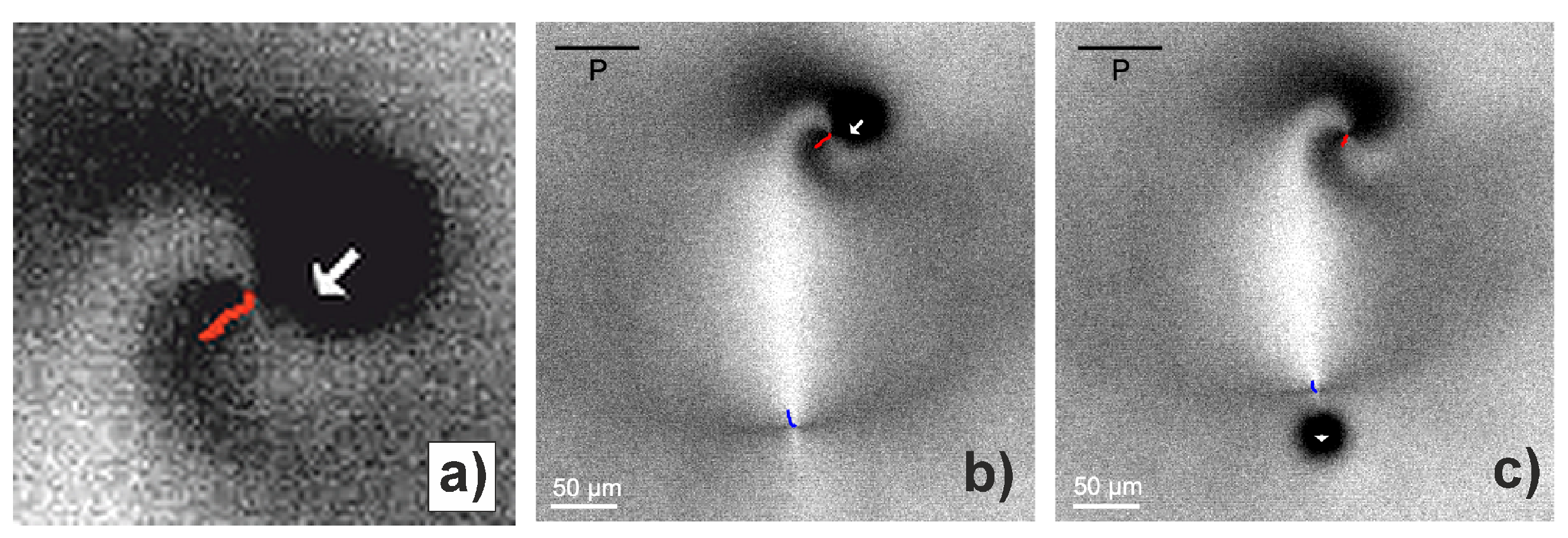
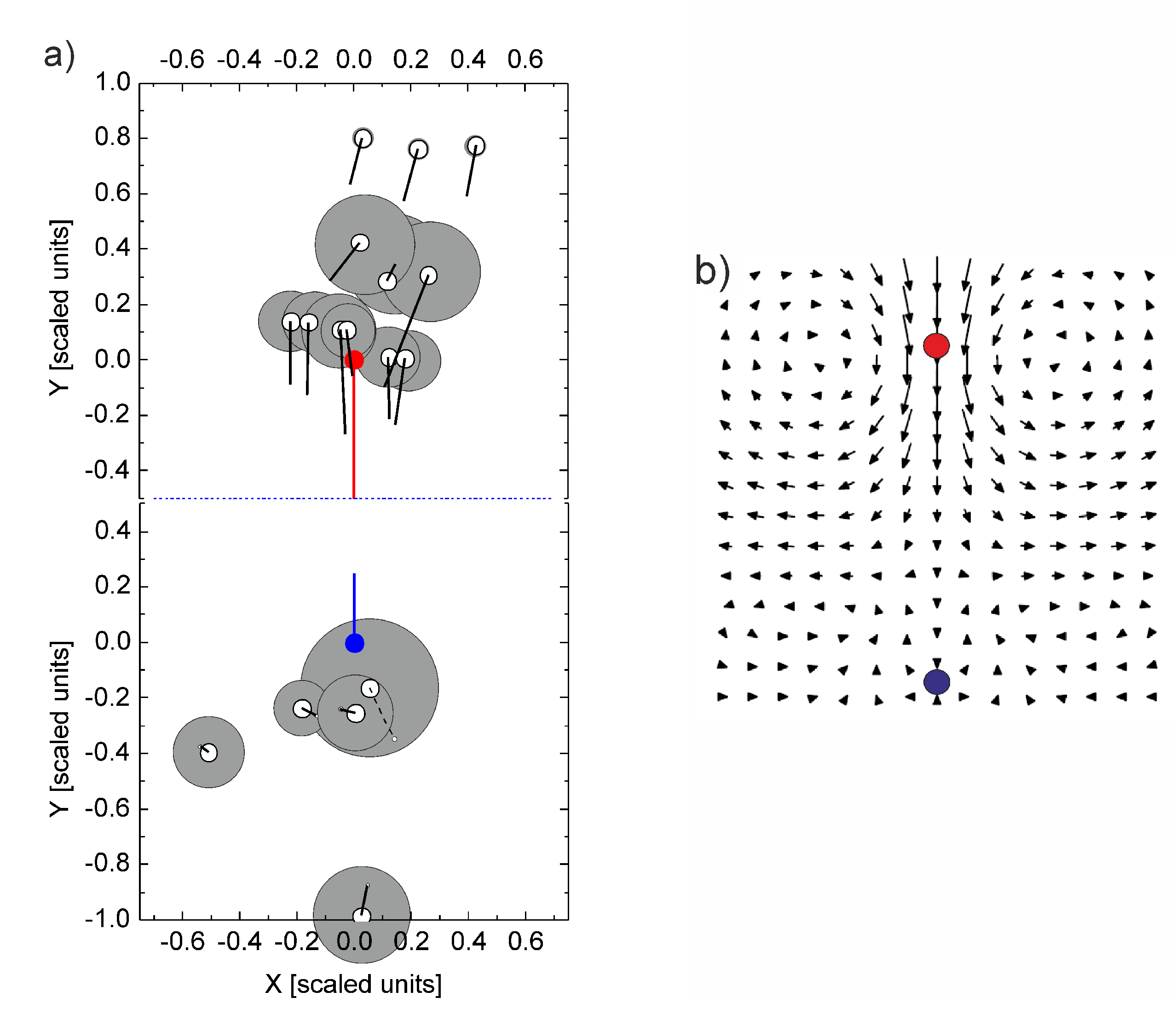
3.1. Experimental Results
3.2. Discussion and Theoretical Background
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
Abbreviations
| FSF | freely suspended smectic film |
| ROI | region of interest |
| SmC | smectic C |
References
- Mermin, N.D. The topological theory of defects in ordered media. Rev. Mod. Phys. 1979, 51, 591–648. [Google Scholar] [CrossRef]
- Roessler, U.K.; Bogdanov, A.N.; Pfleiderer, C. Spontaneous skyrmion ground states in magnetic metals. Nature 2006, 442, 797–801. [Google Scholar] [CrossRef] [PubMed]
- Woods, C.R.; Britnell, L.; Eckmann, A.; Ma, R.S.; Lu, J.C.; Guo, H.M.; Lin, X.; Yu, G.L.; Cao, Y.; Gorbachev, R.V.; et al. Commensurate-incommensurate transition in graphene on hexagonal boron nitride. Nat. Phys. 2014, 10, 451–456. [Google Scholar] [CrossRef]
- Vasudevan, R.K.; Neumayer, S.M.; Susner, M.A.; McGuire, M.A.; Pantelides, S.T.; Maksymovych, P.; Leonard, D.N.; Balke, N.; Borisevich, A.Y. Domains and Topological Defects in Layered Ferrielectric Materials: Implications for Nanoelectronics. ACS Appl. Nano Mater. 2020, 3, 8161–8166. [Google Scholar] [CrossRef]
- Bauerle, C.; Bunkov, Y.M.; Fisher, S.N.; Godfrin, H.; Pickett, G.R. Laboratory simulation of cosmic string formation in the early Universe using superfluid 3He. Nature 1996, 382, 332–334. [Google Scholar] [CrossRef]
- Ruutu, V.M.H.; Eltsov, V.B.; Gill, A.J.; Kibble, T.W.B.; Krusius, M.; Makhlin, Y.G.; Placais, B.; Volovik, G.E.; Xu, W. Vortex formation in neutron-irradiated superfluid 3He as an analogue of cosmological defect formation. Nature 1996, 382, 334–336. [Google Scholar] [CrossRef]
- Bowick, M.J.; Giomi, L. Two-dimensional matter: Order, curvature and defects. Adv. Phys. 2009, 58, 449–563. [Google Scholar] [CrossRef]
- Irvine, W.T.M.; Vitelli, V.; Chaikin, P.M. Pleats in crystals on curved surfaces. Nature 2010, 468, 947–951. [Google Scholar] [CrossRef]
- Irvine, W.T.M.; Hollingsworth, A.D.; Grier, D.G.; Chaikin, P.M. Dislocation reactions, grain boundaries, and irreversibility in two-dimensional lattices using topological tweezers. Proc. Natl. Acad. Sci. USA 2013, 110, 15544–15548. [Google Scholar] [CrossRef]
- Musevic, I.; Skarabot, M.; Tkalec, U.; Ravnik, M.; Zumer, S. Two-dimensional nematic colloidal crystals self-assembled by topological defects. Science 2006, 313, 954–958. [Google Scholar] [CrossRef]
- Tkalec, U.; Ravnik, M.; Copar, S.; Zumer, S.; Musevic, I. Reconfigurable Knots and Links in Chiral Nematic Colloids. Science 2011, 333, 62–65. [Google Scholar] [CrossRef]
- Muzny, C.; Clark, N. Direct observation of the Brownian-motion of a liquid-crystal topological defect. Phys. Rev. Lett. 1992, 68, 804–807. [Google Scholar] [CrossRef]
- Alexander, G.P.; Chen, B.G.G.; Matsumoto, E.A.; Kamien, R.D. Colloquium: Disclination loops, point defects, and all that in nematic liquid crystals. Rev. Mod. Phys. 2012, 84, 497–514. [Google Scholar] [CrossRef]
- Harth, K.; Stannarius, R. Topological Point Defects of Liquid Crystals in Quasi-Two-Dimensional Geometries. Front. Phys. 2020, 8, 112. [Google Scholar] [CrossRef]
- Beliaev, M.; Zoellner, D.; Pacureanu, A.; Zaslansky, P.; Zlotnikov, I. Dynamics of topological defects and structural synchronization in a forming periodic tissue. Nat. Phys. 2021. [Google Scholar] [CrossRef]
- Fardin, M.A.; Ladoux, B. Living proof of effective defects. Nature 2021, 17, 172. [Google Scholar]
- Kleman, M.; Friedel, J. Disclinations, dislocations, and continuous defects: A reappraisal. Rev. Mod. Phys. 2008, 80, 61–115. [Google Scholar] [CrossRef]
- Chuang, I.; Durrer, R.; Turok, N.; Yurke, B. Cosmology in the Laboratory: Defect Dynamics in Liquid Crystals. Science 1991, 251, 1336–1342. [Google Scholar] [CrossRef]
- Wright, D.C.; Mermin, N.D. Crystalline liquids—The blue phases. Rev. Mod. Phys. 1989, 61, 385–432. [Google Scholar] [CrossRef]
- Dafermos, C.M. Disinclinations in Liquid Crystals. Q. J. Mech. Appl. Math. 1970, 23, S49. [Google Scholar] [CrossRef]
- Imura, H.; Okano, K. Friction coefficient for a moving disclination in a nematic liquid crystal. Phys. Lett. 1973, A42, 403. [Google Scholar] [CrossRef]
- Pleiner, H. Dynamics of a disclination point in smectic-C and -C* liquid-crystal films. Phys. Rev. A 1988, 37, 3986. [Google Scholar] [CrossRef] [PubMed]
- Kleman, M.; Lavrentovich, O.D. Soft Matter Physics: An Introduction; Springer: Berlin, Germany, 2003. [Google Scholar]
- Svenšek, D.; Žumer, S. Hydrodynamics of Pair-Annihilating Disclinations in SmC Films. Phys. Rev. Lett. 2003, 90, 155501, Erratum in 2003, 90, 219901. [Google Scholar] [CrossRef]
- Vromans, A.J.; Giomi, L. Orientational properties of nematic disclinations. Soft Matter 2016, 12, 6490–6495. [Google Scholar] [CrossRef] [PubMed]
- Tang, X.; Selinger, J.V. Orientation of topological defects in 2D nematic liquid crystals. Soft Matter 2017, 13, 5481. [Google Scholar] [CrossRef] [PubMed]
- Tang, X.; Selinger, J.V. Theory of defect motion in 2D passive and active nematic liquid crystals. Soft Matter 2019, 15, 587. [Google Scholar] [CrossRef] [PubMed]
- Tang, X.; Selinger, J.V. Annihilation trajectory of defects in smectic-C films. Phys. Rev. E 2020, 102, 012702. [Google Scholar] [CrossRef]
- Pargellis, A.N.; Finn, P.; Goodby, J.W.; Panizza, P.; Yurke, B.; Cladis, P.E. Defect dynamics and coarsening dynamics in smectic-C films. Phys. Rev. A 1992, 46, 7765. [Google Scholar] [CrossRef] [PubMed]
- Blanc, C.; Svenšek, D.; Žumer, S.; Nobili, M. Dynamics of Nematic Liquid Crystal Disclinations: The Role of the Backflow. Phys. Rev. Lett. 2005, 95, 097802. [Google Scholar] [CrossRef]
- Dierking, I.; Marshall, O.; Wright, J.; Bulleid, N. Annihilation dynamics of umbilical defects in nematic liquid crystals under applied electric fields. Phys. Rev. E 2005, 71, 061709. [Google Scholar] [CrossRef]
- Oswald, P.; Ignes-Mullol, J. Backflow-Induced Asymmetric Collapse of Disclination Lines in Liquid Crystals. Phys. Rev. Lett. 2006, 95, 027801. [Google Scholar] [CrossRef] [PubMed]
- Dierking, I.; Ravnik, M.; Lark, E.; Healey, J.; Alexander, G.P.; Yeomans, J.M. Anisotropy in the annihilation dynamics of umbilic defects in nematic liquid crystals. Phys. Rev. E 2012, 85, 021703. [Google Scholar] [CrossRef]
- Missaoui, A.; Harth, K.; Salamon, P.; Stannarius, R. Annihilation of point defect pairs in freely suspended liquid crystal films. Phys. Rev. Res. 2020, 2, 013080. [Google Scholar] [CrossRef]
- Muzny, C. Properties of Defects in Freely Suspended Smectic C Thin Films. Ph.D. Thesis, University of Colorado, Boulder, CO, USA, 1994. [Google Scholar]
- Stannarius, R.; Harth, K. Defect Interactions in Anisotropic Two-Dimensional Fluids. Phys. Rev. Lett 2016, 117, 157801. [Google Scholar] [CrossRef] [PubMed]
- Pettey, D.; Lubensky, T.C.; Link, D.R. Topological Inclusions in 2D Smectic-C Films. Liq. Cryst. 1998, 25, 579. [Google Scholar] [CrossRef]
- Silvestre, N.M.; Patricio, P.; Telo da Gama, M.M.; Pattanaporkratana, A.; Park, C.S.; Maclennan, J.E.; Clark, N.A. Modeling dipolar and quadrupolar defect structures generated by chiral islands in freely suspended liquid crystal films. Phys. Rev. E 2009, 80, 041708. [Google Scholar] [CrossRef]
- Bohley, C.; Stannarius, R. Inclusions in free standing smectic liquid crystal films. Soft Matter 2008, 4, 683. [Google Scholar] [CrossRef]
- Dolganov, P.V.; Cluzeau, P.; Dolganov, V.K. Interaction and self-organization of inclusions in two-dimensional free-standing smectic films. Liq. Cryst. Rev. 2019, 7, 1. [Google Scholar] [CrossRef]
- Cheung, C.; Hwang, Y.; Wu, X.; Choi, H. Diffusion of particles in free-standing liquid films. Phys. Rev. Lett. 1996, 76, 2531–2534. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, Z.H.; Atkinson, M.; Park, C.S.; Maclennan, J.; Glaser, M.; Clark, N. Crossover between 2D and 3D Fluid Dynamics in the Diffusion of Islands in Ultrathin Freely Suspended Smectic Films. Phys. Rew. Lett. 2010, 105, 268304. [Google Scholar] [CrossRef]
- Eremin, A.; Baumgarten, S.; Harth, K.; Stannarius, R.; Nguyen, Z.H.; Goldfain, A.; Park, C.S.; Maclennan, J.E.; Glaser, M.A.; Clark, N.A. Two-dimensional microrheology of freely suspended liquid crystal films. Phys. Rev. Lett. 2011, 107, 268301. [Google Scholar] [CrossRef]
- Qi, Z.; Nguyen, Z.H.; Park, C.S.; Glaser, M.A.; Maclennan, J.E.; Clark, N.A.; Kuriabova, T.; Powers, T.R. Mutual Diffusion of Inclusions in Freely Suspended Smectic Liquid Crystal Films. Phys. Rev. Lett. 2014, 113, 128304. [Google Scholar] [CrossRef]
- Ishikawa-Ankerhold, H.C.; Ankerhold, R.; Drummen, G.P.C. Advanced Fluorescence Microscopy Techniques-FRAP, FLIP, FLAP, FRET and FLIM. Molecules 2012, 17, 4047–4132. [Google Scholar] [PubMed]
- Clark, N.A.; Eremin, A.; Glaser, M.A.; Hall, N.R.; Harth, K.; Klopp, C.; Maclennan, J.E.; Park, C.S.; Stannarius, R.; Tin, P.; et al. Realization of hydrodynamic experiments on quasi-2D liquid crystal films in microgravity. Adv. Space Res. 2017, 60, 737. [Google Scholar] [CrossRef][Green Version]
- Harth, K. Otto von Guericke University, Magdeburg. Personal communication, 2009. [Google Scholar]
- Smalyukh, I.I. Confocal Microscopy of Director Structures in Strongly Confined and Composite Systems. Mol. Cryst. Liq. Cryst. 2007, 477, 23–41. [Google Scholar] [CrossRef]
- Yoshioka, J.; Ito, F.; Suzuki, Y.; Takahashi, H.; Takizawa, H.; Tabe, Y. Director/barycentric rotation in cholesteric droplets under temperature gradient. Soft Matter 2014, 10, 5869. [Google Scholar] [CrossRef] [PubMed]
- Poy, G.; Oswald, P. Do Lehmann cholesteric droplets subjected to a temperature gradient rotate as rigid bodies? Soft Matter 2016, 12, 2604. [Google Scholar] [CrossRef]
- Ryskin, G.; Kremenetsky, M. Drag Force on a Line Defect Moving through an Otherwise Undisturbed Field: Disclination Line in a Nematic Liquid Crystal. Phys. Rev. Lett. 1991, 67, 1574. [Google Scholar] [CrossRef]
- Missaoui, A. Dynamics of Topological Defects in Freely Suspended Smectic Liquid Crystal Films and Bubbles. Ph.D. Thesis, Otto von Guericke University, Magdeburg and Sorbonne University, Paris, France, 2021. [Google Scholar]
- Eremin, A.; Bohley, C.; Stannarius, R. Stick-slip dynamics around a topological defect in free standing smectic films. Phys. Rev. E 2006, 74, 040701(R). [Google Scholar] [CrossRef]
- Stewart, I.W. The Static and Dynamic Continuum Theory of Liquid Crystals; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar] [CrossRef]
- Tóth, G.; Denniston, C.; Yeomans, J.M. Hydrodynamics of Topological Defects in Nematic Liquid Crystals. Phys. Rev. Lett. 2002, 88, 105504. [Google Scholar] [CrossRef]
- Brugués, J.; Ignés-Mullol, J.; Casademunt, J.; Sagués, F. Probing Elastic Anisotropy from Defect Dynamics in Langmuir Monolayers. Phys. Rev. Lett. 2008, 100, 037801. [Google Scholar] [CrossRef] [PubMed]

| Figure | ||||
|---|---|---|---|---|
| Figure 3a | 6.0 | 2.6 | 2.6 | - |
| Figure 3b | 2.6 | 1.7 | 1.2 | - |
| Figure 3c | 4.0 | 2.2 | - | <0.2 |
| Figure 3d | 4.5 | 3.2 | - | 0.5 |
| Figure 5a,b | 1.9 | 1.7 | 1.2 | - |
| Figure 5c | 1.2 | 1.2 | - | <0.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Missaoui, A.; Lacaze, E.; Eremin, A.; Stannarius, R. Observation of Backflow during the Anihilation of Topologocal Defects in Freely Suspended Smectic Films. Crystals 2021, 11, 430. https://doi.org/10.3390/cryst11040430
Missaoui A, Lacaze E, Eremin A, Stannarius R. Observation of Backflow during the Anihilation of Topologocal Defects in Freely Suspended Smectic Films. Crystals. 2021; 11(4):430. https://doi.org/10.3390/cryst11040430
Chicago/Turabian StyleMissaoui, Amine, Emmanuelle Lacaze, Alexey Eremin, and Ralf Stannarius. 2021. "Observation of Backflow during the Anihilation of Topologocal Defects in Freely Suspended Smectic Films" Crystals 11, no. 4: 430. https://doi.org/10.3390/cryst11040430
APA StyleMissaoui, A., Lacaze, E., Eremin, A., & Stannarius, R. (2021). Observation of Backflow during the Anihilation of Topologocal Defects in Freely Suspended Smectic Films. Crystals, 11(4), 430. https://doi.org/10.3390/cryst11040430







