Fractional Power-Law Intraband Optical Conductivity in the Low-Dimensional Dirac Material CaMnBi2
Abstract
1. Introduction
2. Materials and Methods
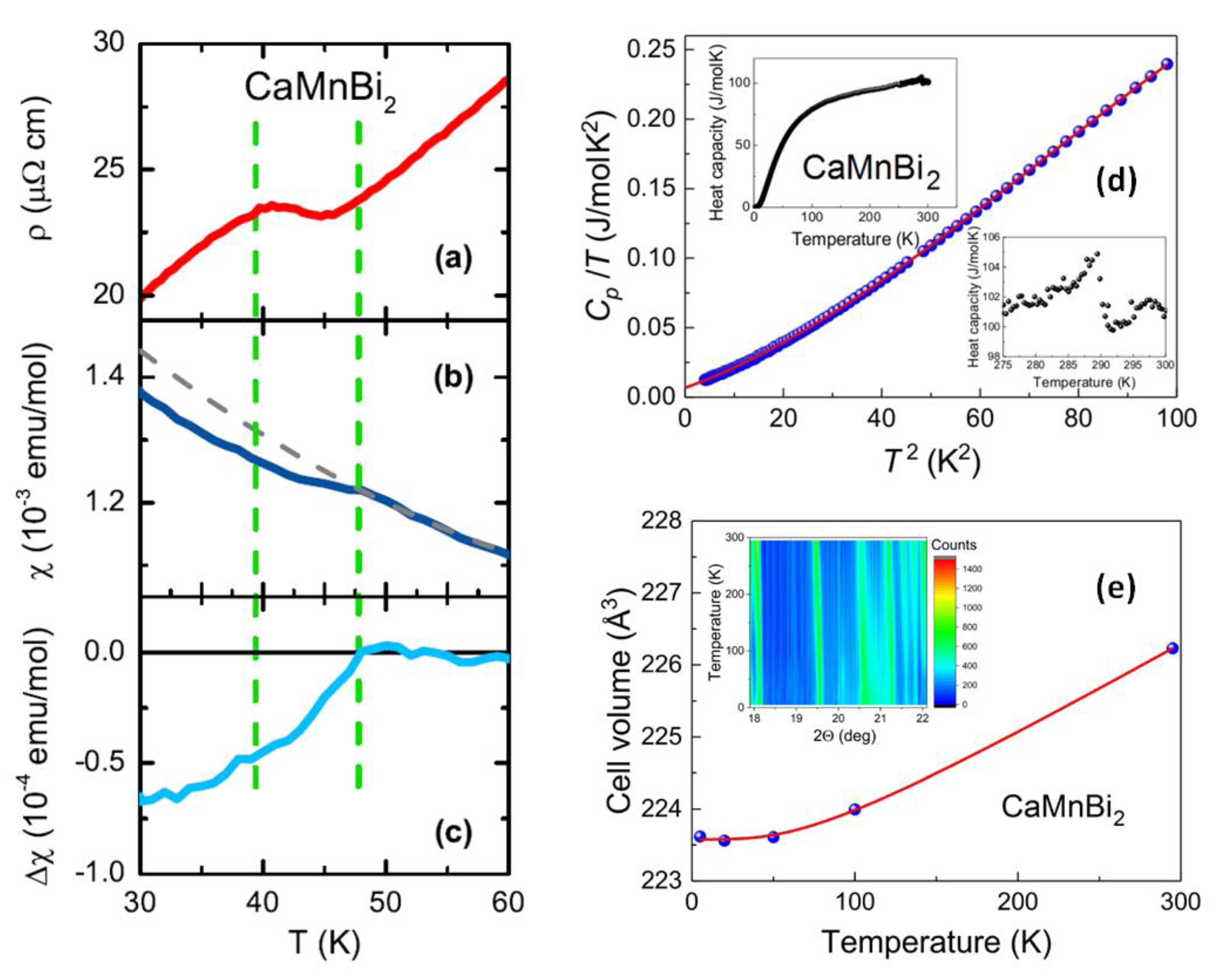
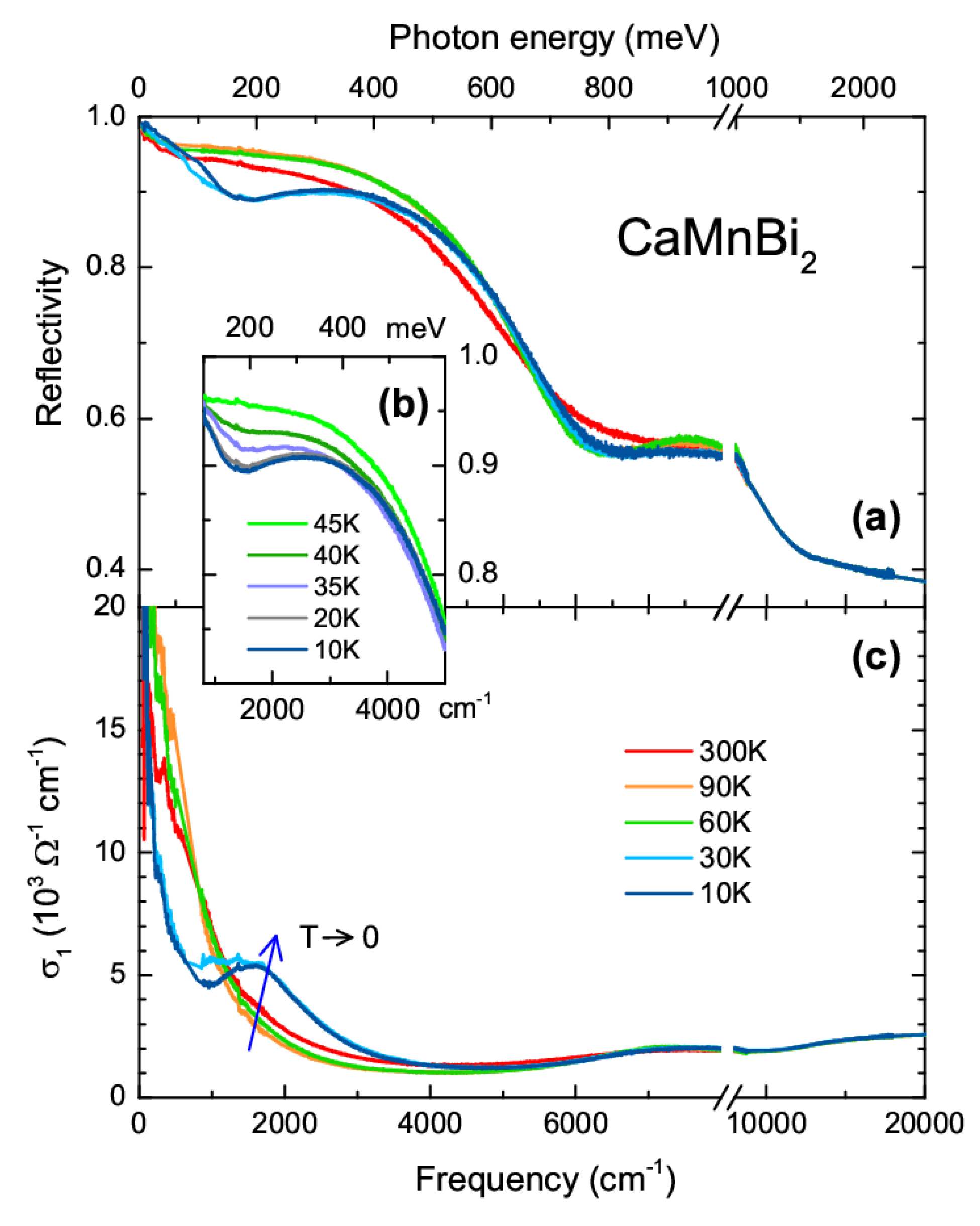
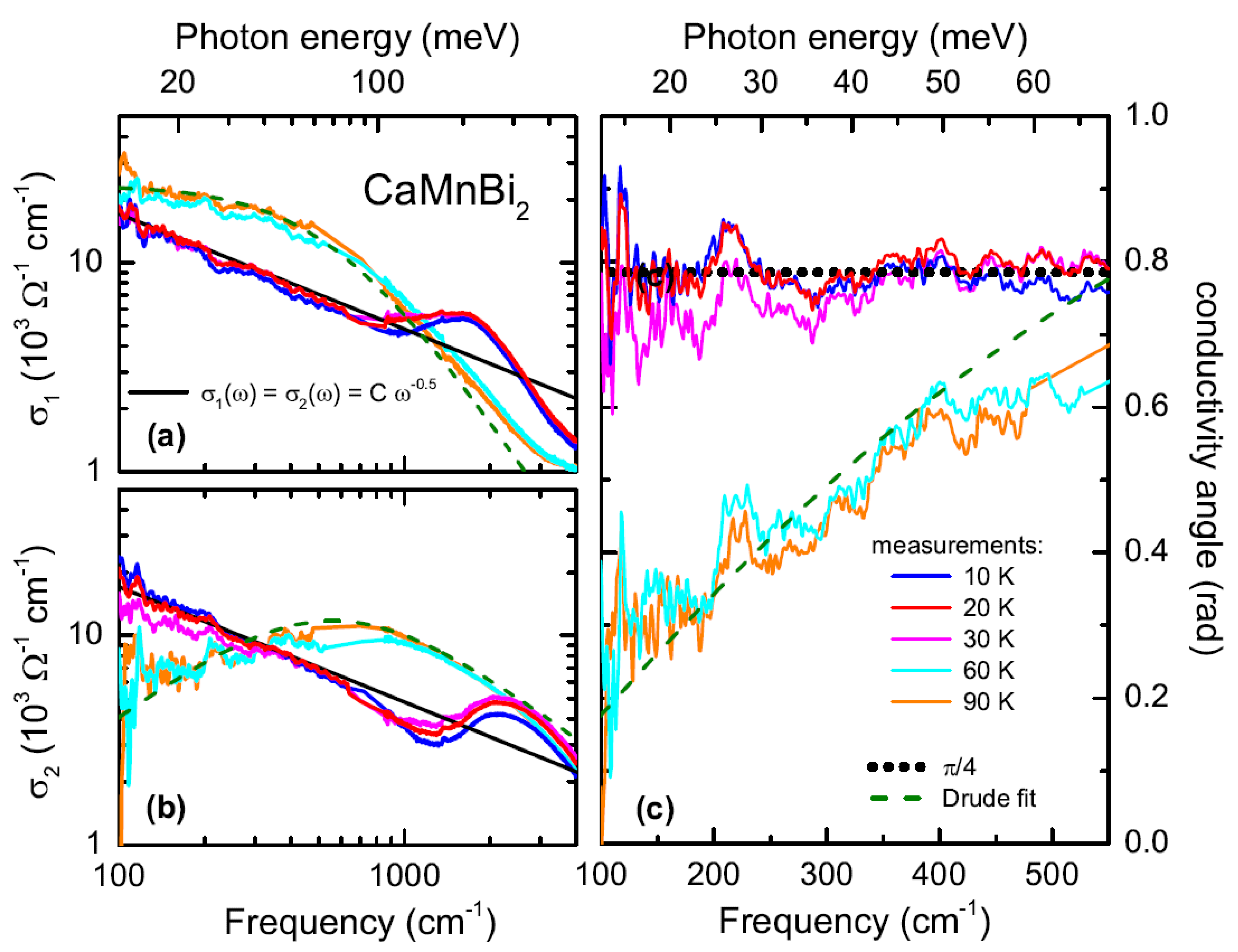
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Park, J.; Lee, G.; Wolff-Fabris, F.; Koh, Y.Y.; Eom, M.J.; Kim, Y.K.; Farhan, M.A.; Jo, Y.J.; Kim, C.; Shim, J.H.; et al. Anisotropic Dirac Fermions in a Bi Square Net of SrMnBi2. Phys. Rev. Lett. 2011, 107, 126402. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Graf, D.; Wang, L.; Lei, H.; Tozer, S.W.; Petrovic, C. Two-dimensional Dirac fermions and quantum magnetoresistance in CaMnBi2. Phys. Rev. B 2012, 85, 041101(R). [Google Scholar] [CrossRef]
- He, J.B.; Wang, D.M.; Chen, G.F. Giant magnetoresistance in layered manganese pnictide CaMnBi2. Appl. Phys. Lett. 2012, 100, 112405. [Google Scholar] [CrossRef]
- Lee, G.; Farhan, M.A.; Kim, J.S.; Shim, J.H. Anisotropic Dirac electronic structures of AMnBi2 (A = Sr, Ca). Phys. Rev. B 2013, 87, 245104. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, Z.; Chen, C.; Shi, Y.; Xie, Z.; Yi, H.; Liang, A.; He, S.; He, J.; Peng, Y.; et al. Strong Anisotropy of Dirac Cones in SrMnBi2 and CaMnBi2 Revealed by Angle-Resolved Photoemission Spectroscopy. Sci. Rep. 2014, 4, 5385. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.F.; Princep, A.J.; Zhang, X.; Manuel, P.; Khalyavin, D.; Mazin, I.I.; Shi, Y.G.; Boothroyd, A.T. Coupling of magnetic order to planar Bi electrons in the anisotropic Dirac metals AMnBi2 (A = Sr, Ca). Phys. Rev. B 2014, 90, 075120. [Google Scholar] [CrossRef]
- Rahn, M.C.; Princep, A.J.; Piovano, A.; Kulda, J.; Guo, Y.F.; Shi, Y.G.; Boothroyd, A.T. Spin dynamics in the antiferromagnetic phases of the Dirac metals AMnBi2 (A = Sr, Ca). Phys. Rev. B 2017, 95, 134405. [Google Scholar] [CrossRef]
- Wang, K.; Wang, L.; Petrovic, C. Large magnetothermopower effect in Dirac materials (Sr/Ca)MnBi2. Appl. Phys. Lett. 2012, 100, 112111. [Google Scholar]
- Wang, A.; Graf, D.; Wu, L.; Wang, K.; Bozin, E.; Zhu, Y.; Petrovic, C. Interlayer electronic transport in CaMnBi2 antiferromagnet. Phys. Rev. B 2016, 94, 125118. [Google Scholar] [CrossRef]
- Corasaniti, M.; Yang, R.; Pal, A.; Chinotti, M.; Degiorgi, L.; Wang, A.; Petrovic, C. Fermi surface gapping in the Dirac material Ca1−xNaxMnBi2. Phys. Rev. B 2019, 100, 041107. [Google Scholar] [CrossRef]
- Yang, R.; Corasaniti, M.; Le, C.C.; Liao, Z.Y.; Wang, A.F.; Du, Q.; Petrovic, C.; Qiu, X.G.; Hu, J.P.; Degiorgi, L. Spin-Canting-Induced Band Reconstruction in the Dirac Material Ca1−xNaxMnBi2. Phys. Rev. Lett. 2020, 124, 137201. [Google Scholar] [CrossRef]
- Tanner, D.B. Use of x-ray scattering functions in Kramers-Kronig analysis of reflectance. Phys. Rev. B 2015, 91, 035123. [Google Scholar] [CrossRef]
- Hosur, P.; Parameswaran, S.A.; Vishwanath, A. Charge Transport in Weyl Semimetals. Phys. Rev. Lett. 2012, 108, 046602. [Google Scholar] [CrossRef] [PubMed]
- Bácsi, Á.; Virosztek, A. Low-frequency optical conductivity in graphene and in other scale-invariant two-band systems. Phys. Rev. B 2013, 87, 125425. [Google Scholar] [CrossRef]
- Ashby, P.E.C.; Carbotte, J.P. Chiral anomaly and optical absorption in Weyl semimetals. Phys. Rev. B 2014, 89, 245121. [Google Scholar] [CrossRef]
- Ahn, S.; Mele, E.J.; Min, H. Electrodynamics on Fermi Cyclides in Nodal Line Semimetals. Phys. Rev. Lett. 2017, 119, 147402. [Google Scholar] [CrossRef]
- Carbotte, J.P. Optical response of a line node semimetal. J. Phys. Condens. Matter 2017, 29, 045301. [Google Scholar] [CrossRef]
- Schilling, M.B.; Löhle, A.; Neubauer, D.; Shekhar, C.; Felser, C.; Dressel, M.; Pronin, A.V. Two-channel conduction in YbPtBi. Phys. Rev. B 2017, 95, 155201. [Google Scholar] [CrossRef]
- Chaudhuri, D.; Cheng, B.; Yaresko, A.; Gibson, Q.D.; Cava, R.J.; Armitage, N.P. Optical investigation of the strong spin-orbit-coupled magnetic semimetal YbMnBi2. Phys. Rev. B 2017, 96, 075151. [Google Scholar] [CrossRef]
- Neubauer, D.; Yaresko, A.; Li, W.; Löhle, A.; Hübner, R.; Schilling, M.B.; Shekhar, C.; Felser, C.; Dressel, M.; Pronin, A.V. Optical conductivity of the Weyl semimetal NbP. Phys. Rev. B 2018, 98, 195203. [Google Scholar] [CrossRef]
- Kemmler, R.; Hübner, R.; Löhle, A.; Neubauer, D.; Voloshenko, I.; Schoop, L.M.; Dressel, M.; Pronin, A.V. Free-carrier dynamics in Au2Pb probed by optical conductivity measurements. J. Phys.: Condens. Matter 2018, 30, 485403. [Google Scholar] [CrossRef] [PubMed]
- Maulana, L.Z.; Manna, K.; Uykur, E.; Felser, C.; Dressel, M.; Pronin, A.V. Optical conductivity of multifold fermions: The case of RhSi. Phys. Rev. Research 2020, 2, 023018. [Google Scholar] [CrossRef]
- Maulana, L.Z.; Li, Z.; Uykur, E.; Manna, K.; Polatkan, S.; Felser, C.; Dressel, M.; Pronin, A.V. Broadband optical conductivity of the chiral multifold semimetal PdGa. Phys. Rev. B 2021, 103, 115206. [Google Scholar] [CrossRef]
- Dressel, M.; Gürner, G. Electrodynamics of Solids; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Sachdev, S. Quantum Phase Transitions; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Van der Marel, D.; Molegraaf, H.J.A.; Zaanen, J.; Nussinov, Z.; Carbone, F.; Damascelli, A.; Eisaki, H.; Greven, M.; Kes, P.H.; Li, M. Quantum critical behaviour in a high-Tc superconductor. Nature 2003, 425, 271–274. [Google Scholar] [CrossRef] [PubMed]
- Ioffe, L.B.; Millis, A.J. Zone-diagonal-dominated transport in high-Tc cuprates. Phys. Rev. B 1998, 58, 11631–11637. [Google Scholar] [CrossRef]
- Van der Marel, D. Anisotropy of the optical conductivity of high-Tc cuprates. Phys. Rev. B 1999, 60, R765. [Google Scholar] [CrossRef]
- Anderson, P.W. Infrared conductivity of cuprate metals: Detailed fit using Luttinger-liquid theory. Phys. Rev. B 1997, 55, 11785–11788. [Google Scholar] [CrossRef]
- Schilling, M.B.; Schoop, L.M.; Lotsch, B.V.; Dressel, M.; Pronin, A.V. Flat Optical Conductivity in ZrSiS due to Two-Dimensional Dirac Bands. Phys. Rev. Lett. 2017, 119, 187401. [Google Scholar] [CrossRef]
- Brechtel, E.; Cordier, G.; Schäfer, H. Zur Darstellung und Struktur von CaMnBi2. Z. Naturforsch. B 1980, 35, 1–3. [Google Scholar] [CrossRef]
- Sayetat, F.; Fertey, P.; Kessler, M. An Easy Method for the Determination of Debye Temperature from Thermal Expansion Analyses. J. Appl. Cryst. 1998, 31, 121–127. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schilling, M.B.; Wang, C.X.; Shi, Y.G.; Kremer, R.K.; Dressel, M.; Pronin, A.V. Fractional Power-Law Intraband Optical Conductivity in the Low-Dimensional Dirac Material CaMnBi2. Crystals 2021, 11, 428. https://doi.org/10.3390/cryst11040428
Schilling MB, Wang CX, Shi YG, Kremer RK, Dressel M, Pronin AV. Fractional Power-Law Intraband Optical Conductivity in the Low-Dimensional Dirac Material CaMnBi2. Crystals. 2021; 11(4):428. https://doi.org/10.3390/cryst11040428
Chicago/Turabian StyleSchilling, M. B., C. X. Wang, Y. G. Shi, R. K. Kremer, M. Dressel, and A. V. Pronin. 2021. "Fractional Power-Law Intraband Optical Conductivity in the Low-Dimensional Dirac Material CaMnBi2" Crystals 11, no. 4: 428. https://doi.org/10.3390/cryst11040428
APA StyleSchilling, M. B., Wang, C. X., Shi, Y. G., Kremer, R. K., Dressel, M., & Pronin, A. V. (2021). Fractional Power-Law Intraband Optical Conductivity in the Low-Dimensional Dirac Material CaMnBi2. Crystals, 11(4), 428. https://doi.org/10.3390/cryst11040428








