Modeling of the Resonant X-ray Response of a Chiral Cubic Phase
Abstract
1. Introduction
2. Methods
3. Results
3.1. Tensor Form Factor
3.2. Resonant and Resonantly Enhanced Peaks
3.3. Intensities of the Peaks
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dolan, J.A.; Wilts, B.D.; Vignolini, S.; Baumberg, J.J.; Steiner, U.; Wilkinson, T.D. Optical properties of gyroid structured materials: From photonic crystals to metamaterials. Adv. Opt. Mater. 2015, 3, 12–32. [Google Scholar] [CrossRef]
- Pelanconi, M.; Ortona, A. Nature-inspired, ultra-lightweight structures with gyroid cores produced by additive manufacturing and reinforced by unidirectional carbon fiber ribs. Materials 2019, 12, 4134. [Google Scholar] [CrossRef]
- Crossland, E.J.; Kamperman, M.; Nedelcu, M.; Ducati, C.; Wiesner, U.; Smilgies, D.-M.; Toombes, G.E.; Hillmyer, M.A.; Ludwigs, S.; Steiner, U.; et al. A bicontinuous double gyroid hybrid solar cell. Nano Lett. 2009, 9, 2807–2812. [Google Scholar] [CrossRef] [PubMed]
- Kutsumizu, S.; Ichikawa, T.; Nojima, S.; Yano, S. A cubic–cubic phase transition of 4A-n-hexacosyloxy-3A-nitrobiphenyl-4-carboxylic acid (ANBC-26). Chem. Commun. 1999, 1181–1182. [Google Scholar] [CrossRef]
- Imperor-Clerc, M.; Sotta, P.; Veber, M. Crystal shapes of cubic mesophases in pure and mixed carboxylic acids observed by optical microscopy. Liq. Cryst. 2000, 27, 1001–1009. [Google Scholar] [CrossRef]
- Zeng, X.; Ungar, G.; Impéror-Clerc, M. A triple-network tricontinuous cubicliquid crystal. Nat. Mater. 2005, 4, 562–567. [Google Scholar] [CrossRef]
- Ozawa, K.; Yamamura, Y.; Yasuzuka, S.; Mori, H.; Kutsumizu, S.; Saito, K. Coexistence of Two Aggregation Modes in Exotic Liquid-Crystalline Superstructure: Systematic Maximum Entropy Analysis for Cubic Mesogen, 1,2-Bis (4′-n-alkoxybenzoyl) hydrazine [BABH (n)]. J. Phys. Chem. B 2008, 112, 12179–12181. [Google Scholar] [CrossRef] [PubMed]
- Dressel, C.; Liu, F.; Prehm, M.; Zeng, X.; Ungar, G.; Tschierske, C. Dynamic mirror-symmetry breaking in bicontinuous cubic phases. Angew. Chem. Int. Ed. 2014, 53, 13115–13120. [Google Scholar] [CrossRef] [PubMed]
- Saito, K.; Yamamura, Y.; Miwa, Y.; Kutsumizu, S. A structural model of the chiral “Im 3 m” cubic phase. Angew. Chem. Int. Ed. 2016, 18, 3280–3284. [Google Scholar]
- Zeng, X.; Ungar, G. Spontaneously chiral cubic liquid crystal: Three interpenetrating networks with a twist. J. Mater. Chem. C 2020, 8, 5389–5398. [Google Scholar] [CrossRef]
- Vaupotič, N.; Salamończyk, M.; Matraszek, J.; Vogrin, M.; Pociecha, D.; Gorecka, E. New structural model of a chiral cubic liquid crystalline phase. Phys. Chem. Chem. Phys. 2020, 22, 12814–12820. [Google Scholar] [CrossRef] [PubMed]
- Guillon, D.; Skoulios, A. Molecular model for the “smectic D” mesophase. Europhys. Lett. 1987, 3, 79–85. [Google Scholar] [CrossRef]
- Nakazawa, Y.; Yamamura, Y.; Kutsumizu, S.; Saito, K. Molecular mechanism responsible for reentrance to Ia3d gyroid phase in cubic mesogen BABH (n). J. Phys. Soc. Jap. 2012, 81, 094601. [Google Scholar] [CrossRef]
- Tschierske, C.; Ungar, G. Mirror symmetry breaking by chirality synchronisation in liquids and liquid crystals of achiral molecules. ChemPhysChem 2016, 17, 9–26. [Google Scholar] [CrossRef]
- Cao, Y.; Alaasar, M.; Nallapaneni, A.; Salamończyk, M.; Marinko, P.; Gorecka, E.; Tschierske, C.; Liu, F.; Vaupotič, N.; Zhu, C. Molecular Packing in Double Gyroid Cubic Phases Revealed via Resonant Soft X-ray Scattering. Phys. Rev. Lett. E 2020, 125, 027801. [Google Scholar] [CrossRef]
- Matraszek, J.; Pociecha, D.; Vaupotič, N.; Salamończyk, M.; Vogrin, M.; Gorecka, E. Bi-continuous orthorhombic soft matter phase made of polycatenar molecules. Soft Matter 2020, 16, 3882–3885. [Google Scholar] [CrossRef]
- Dmitrienko, V.E. Forbidden reflections due to anisotropic X-ray susceptibility of crystals. Acta Cryst. A 1983, 39, 29–35. [Google Scholar] [CrossRef]
- Dmitrienko, V.E. Anisotropy of X-ray susceptibility and Bragg reflections in cubic crystals. Sect. A Found. Crystallogr. 1984, 40, 89–95. [Google Scholar] [CrossRef]
- Templeton, D.H.; Templeton, L.K. Polarized X-ray absorption and double refraction in vanadyl bisacetylacetonate. Acta Cryst. A 1980, 36, 237–241. [Google Scholar] [CrossRef]
- Templeton, D.H.; Templeton, L.K. X-ray dichroism and polarized anomalous scattering of the uranyl ion. Acta Cryst. A 1982, 38, 62–67. [Google Scholar] [CrossRef]
- Templeton, L.K.; Templeton, D.H.; Phizackerley, R.P.; Hodgson, K.O. L3-edge anomalous scattering by gadolinium and samarium measured at high resolution with synchrotron radiation. Acta Cryst. A 1982, 38, 74–78. [Google Scholar] [CrossRef]
- Levelut, A.-M.; Pansu, B. Tensorial X-ray structure factor in smectic liquid crystals. Phys. Rev. Lett. E 1999, 60, 6803–6815. [Google Scholar] [CrossRef] [PubMed]

| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 |
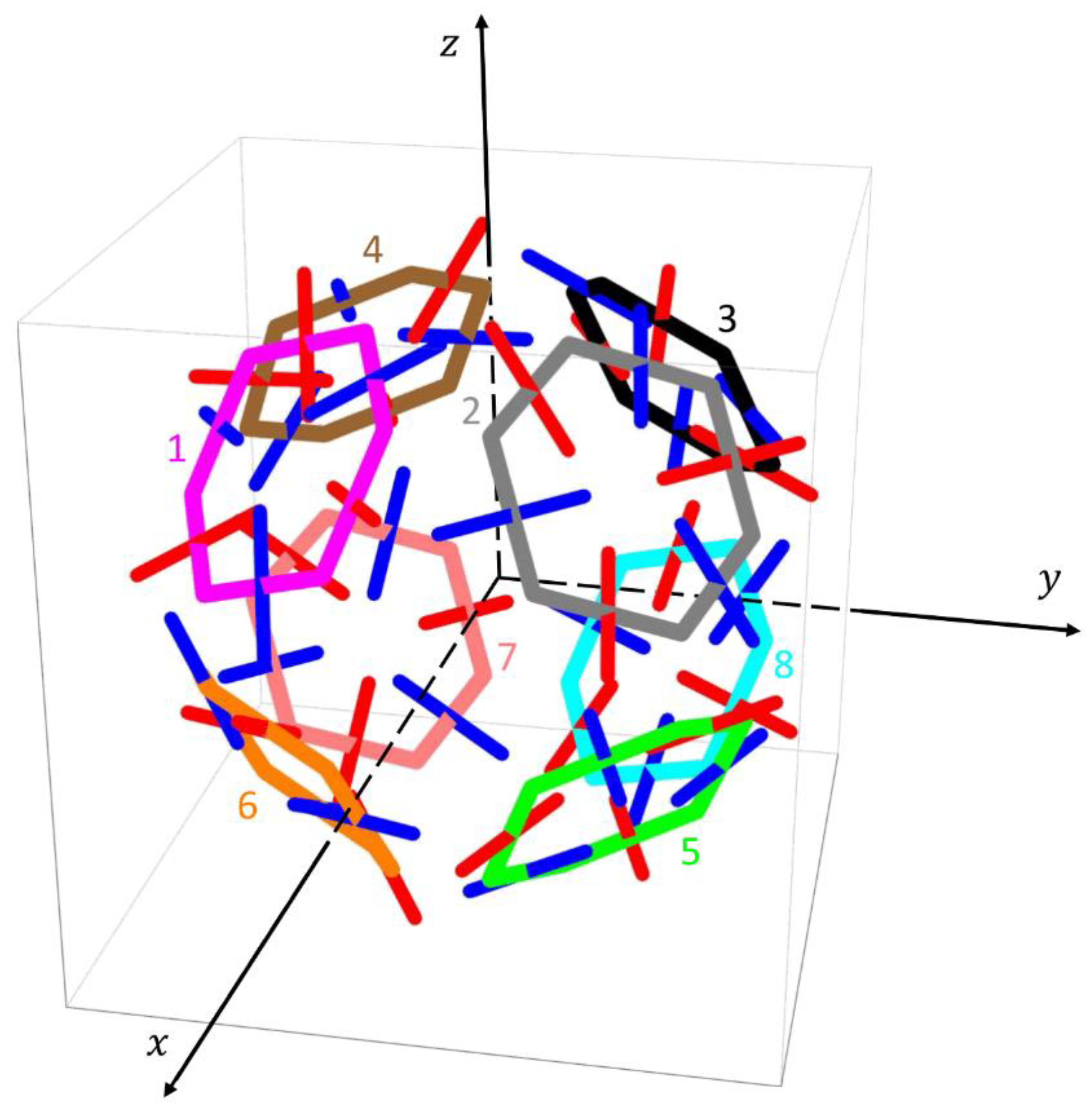
| (Color on Figure 3) | |||
|---|---|---|---|
| 1 (magenta) | |||
| 2 (gray) | |||
| 3 (black) | |||
| 4 (brown) | |||
| 5 (green) | |||
| 6 (orange) | |||
| 7 (pink) | |||
| 8 (cyan) |
| (011) | ||
| 12 | (011) | RSoXS | ||
| 6 | (002) | |||
| 24 | (012) | |||
| 24 | (012) | TReXS | ||
| 24 | (113) | |||
| 24 | (023) | |||
| 24 | (014) | |||
| 24 | (223) | |||
| 48 | (124) | |||
| 24 | (233) | |||
| 24 | (034) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grabovac, T.; Gorecka, E.; Pociecha, D.; Vaupotič, N. Modeling of the Resonant X-ray Response of a Chiral Cubic Phase. Crystals 2021, 11, 214. https://doi.org/10.3390/cryst11020214
Grabovac T, Gorecka E, Pociecha D, Vaupotič N. Modeling of the Resonant X-ray Response of a Chiral Cubic Phase. Crystals. 2021; 11(2):214. https://doi.org/10.3390/cryst11020214
Chicago/Turabian StyleGrabovac, Timon, Ewa Gorecka, Damian Pociecha, and Nataša Vaupotič. 2021. "Modeling of the Resonant X-ray Response of a Chiral Cubic Phase" Crystals 11, no. 2: 214. https://doi.org/10.3390/cryst11020214
APA StyleGrabovac, T., Gorecka, E., Pociecha, D., & Vaupotič, N. (2021). Modeling of the Resonant X-ray Response of a Chiral Cubic Phase. Crystals, 11(2), 214. https://doi.org/10.3390/cryst11020214






