Abstract
High-level quantum-chemical computations (G4MP2) are carried out in the study of complexes featuring tetrel bonding between the carbon atom in the carbenoid CB11H11—obtained by hydride removal in the C-H bond of the known closo-monocarbadodecaborate anion CB11H12(−) and acting as Lewis acid (LA)—and Lewis bases (LB) of different type; the electron donor groups in the tetrel bond feature carbon, nitrogen, oxygen, fluorine, silicon, phosphorus, sulfur, and chlorine atomic centres in neutral molecules as well as anions H(−), OH(−), and F(−). The empty radial 2pr vacant orbital on the carbon centre in CB11H11, which corresponds to the LUMO, acts as a Lewis acid or electron attractor, as shown by the molecular electrostatic potential (MEP) and electron localization function (ELF). The thermochemistry and topological analysis of the complexes {CB11H11:LB} are comprehensively analysed and classified according to shared or closed-shell interactions. ELF analysis shows that the tetrel C⋯X bond ranges from very polarised bonds, as in H11B11C:F(−) to very weak interactions as in H11B11C⋯FH and H11B11C⋯O=C=O.
Keywords:
Lewis acid; carborane; carbonium ylide; tetrel bond; quantum chemistry; electron density; ELF 1. Introduction
The very stable B12H12(2−) dianion and its neutral dicarbon counterparts ortho-(1,2-C2B10H12), meta-(1,7-C2B10H12), and para-carborane (1,12-C2B10H12) are icosahedral systems that are closely related to elemental boron. Their isoelectronic analogue, closo-monocarbadodecaborate anion CB11H12(−), first prepared in 1967 [1] and further with other synthesis methods [2,3], is similarly resistant to cage degradation, and many derivatives have been synthesized as described in the literature [4]. The stability and three-dimensional aromaticity of CB11H12(−) has also been explained using quantum-chemical computations [5]. Extraction of hydride H(−) in the C-H bond from CB11H12(−) leads to a carbocation ylide or carbenoid (1) with a vacant radial 2pr orbital on the cage carbon atom as shown in Figure 1. On the other hand, reaction mechanisms of polyhedral (car)boranes and their derivatives are scarce in the literature and further research is needed in this respect [6,7,8]. Thus, the permethylated carbenoid analogue CB11Me11 has been postulated as a reaction intermediate during the extraction of the L substituent from L-CB11Me11 carboranes (L = BrCH2CH2 or (CF3)2CHO) by electrophiles [6,7], further reacting with arenes in the presence of (CF3)2CHOH to generate 1-aryl-CB11Me11 products [6,7,8]. The methyl groups in the permethylated anion CB11Me12(−) have substantial CH3(−) (methide) character according to DFT computations [6,7,8] and can easily bind to transition metal and main group elements.
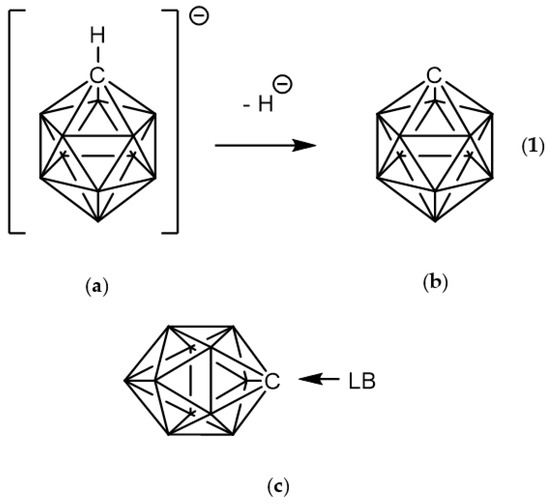
Figure 1.
Removal of hydride from the C-H bond in (a) closo-monocarbadodecaborate anion CB11H12(−) leads to (b) carbocation ylide or carbenoid CB11H11 (1). (c) Complex formation between (1) and a Lewis base (LB). All vertices correspond to B-H moieties except for the carbon vertex.
On the other hand, in recent years, tetrel bonding—defined as an interaction between any electron donating system (ED) and a group 14 element acting as Lewis acid—has called the attention of both experimentalists [9] and theoreticians [10,11,12]. Here the carbon centre in (1) is clearly an acceptor of electrons or Lewis acid; hence, we can define a tetrel bonding interaction with an electron donor (ED) or Lewis base, as shown in Figure 1c.
The goal of this work is to study the electronic interaction between the naked carbon vertex in the carbenoid (1) with a series of electron donor molecules and anions leading to tetrel C-X bonds. The chosen 18 LB systems, including the anions H(−), F(−), and OH(−), are displayed below in Scheme 1 with the corresponding label.
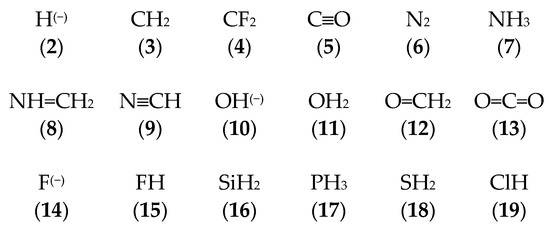
Scheme 1.
The chosen set of molecules acting as Lewis base (LB) and forming a tetrel bond with the C atom from carbenoid (1) according to Figure 1c.
2. Computational Methods
Electronic structure quantum-chemical computations were carried out using the G4MP2 model [13], which is a fourth-generation method available in the Gaussian16 scientific software [14]. This method combines density-functional theory [15,16] and second-order perturbation theory [17] and provides an accurate and economical method for thermochemical predictions. The G4(MP2) model works as follows: The geometries of the molecules are optimized at the B3LYP/6-31G(2df,p) level of theory, and then a series of single point energy calculations at higher levels of theory are computed. The zero-point energy, E(ZPE), is based on B3LYP/6-31G(2df,p) frequencies scaled by 0.9854, the same as in G4 theory. The first energy calculation is at the triples-augmented coupled cluster level of theory, CCSD(T), with the 6-31G(d) basis set, i.e., CCSD(T)/6-31G(d). This energy is then modified by a series of energy corrections to obtain a total energy E0. For more details on the G4(MP2) method, the reader is referred to Reference [13]. In the particular case of the 1:LB complexes, we computed the enthalpy and free energy differences between the complex and separated systems 1 and LB at room temperature as indication of stability of the complex. All complexes included in this work correspond to energy minimum structures, checked with frequency computations. The quantum theory of atoms-in-molecules (QTAIM) [18,19] was used in the topological analysis of the electron density of the 1:LB complexes with the scientific software AIMAll [20]. This method is based on the analysis of the electron density ρ, its gradient ∇ρ, and the corresponding Laplacian ∇2ρ. For further aspects of this methodology, the reader is referred to the above References [17,18] and Section 3.3.1 below. The electron localisation function (ELF) [21,22] was also used in the topological analysis of the complexes. The ELF is a distribution function which measures the probability of finding two electrons with the same spin, as further described in Section 3.3.2 below. The TopMod09 package [23] was used for the ELF calculations.
3. Results
3.1. Geometries of Complexes (1:n), n = 2–19
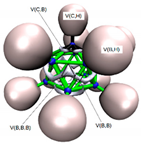
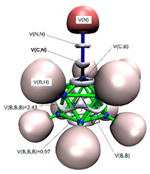
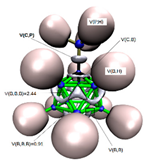
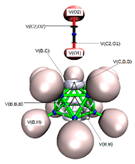
In Figure 2a,b we display the G4MP2 optimized geometries of CB11H12(−) with C5v symmetry—the (1:2) complex and the carbonium ylide CB11H11 (1), with the different tetrel complexes (1:n), n = 2–19 and structural parameters when necessary, in order to highlight the atomic rearrangements undergone due to the complexation process. The loss of H(−) in the C-H leads also to a structure with C5v symmetry—with a geometrical change which involves a considerable flattening of the CB5 pentagonal pyramid with expansion of the corresponding B5 pentagon, since there is an increase of the B-B bond distance of Δ = +0.022 Å. As we proceed down the cage from the top (C atom), the B-B bond differences are +0.022 Å, +0.022 Å, and −0.015 Å. Quite noticeable is the shortening of the apical intracage C⋯B distance (Δ∼−0.3 Å). The B-H bond distances hardly change at all, with a very slight shortening upon loss of H(−) with Δ = −0.007 Å, −0.008 Å, and −0.001 Å, from top to bottom, respectively. If we take the C and B cage nuclei as point charges and define a distorted C5v icosahedron, the corresponding volumes are V(CB11H12(−)) = 12.03 Å3 and V(CB11H11) = 11.90 Å3, and therefore there is a shrinkage of the cage by ΔV = −0.13 Å3 (1%). In summary, the extraction of hydride in the C-H bond from CB11H12(−) implies a minor change in the cage volume with a flattening of the top CB5 pentagonal pyramid and minor changes as we proceed down the cage from the top C atom. In Figure 2c–s, we display the optimised geometries for the remaining complexes with the coordinates gathered in the Supplementary Material (SI, Tables S1–S10). The shortest and longest C⋯X tetrel interactions correspond to the original anion CB11H12(−) or complex (1:2) and the CB11H11⋯O=C=O tetrel complex (1:13), respectively. In the latter case, the interaction is clearly non-covalent in origin with d(C⋯O) = 2.693 Å, as will be discussed later on. We should also emphasize the C⋯X interaction of the CH2 and SiH2 complexes (1:3) and (1:16), respectively, with the LB groups tilted from the C5 axis of rotation. In all other systems, including the CF2 complex (1:4), the C⋯X bond is aligned with the C5 axis of rotation.
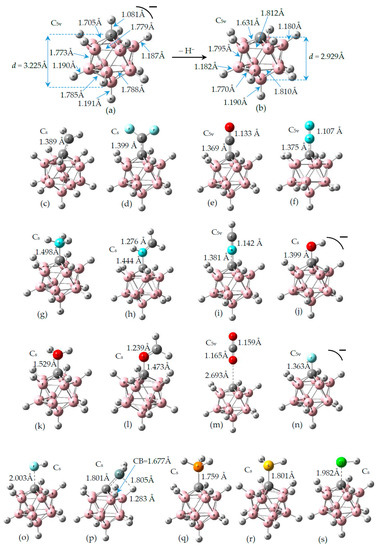
Figure 2.
Structures of the G4MP2 optimized geometries for the 18 tetrel complexes (1:n)—with n = 2–19—considered in this work, following Scheme 1: (a) The known anion CB11H12(−) corresponding to complex (1:2), (b) carbenoid CB11H11 (1), (c) (1:3), (d) (1:4), (e) (1:5), (f) (1:6), (g) (1:7), (h) (1:8), (i) (1:9), (j) (1:10), (k) (1:11), (l) (1:12), (m) (1:13), (n) (1:14), (o) (1:15), (p) (1:16), (q) (1:17), (r) (1:18), and (s) (1:19).
In Figure 3, we display the d(C⋯X) distances in the tetrel bonding complexes, ordered from shortest to longest. Clearly, we can classify five groups according to the C⋯X distances, in increasing order: (i) The original anion CB11H12(−) or (1:2) complex; (ii) complexes with d∼1.4–1.5 Å including complexes (1:k2), with k2 = (3–12, 14); (iii) complexes with d∼1.8 Å, including complexes (1:k3), with k3 = 16–18; (iv) complexes with d∼2.0 Å, including complexes (1:15) and (1:19); and finally (v) the (1:13) complex with d∼2.7 Å.
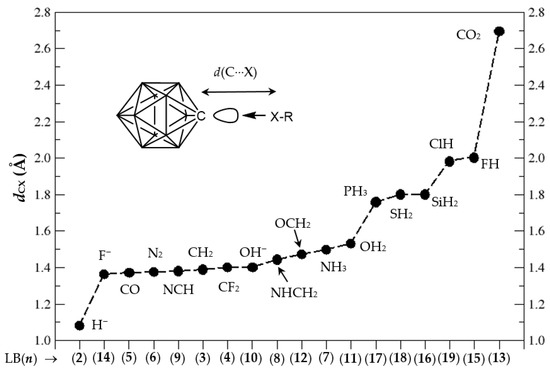
Figure 3.
C⋯X distances dCX (Å) in the tetrel complexes (1:n), n = 2–19, from Figure 2, in increasing order; x axis corresponds to Lewis base (LB) n and y axis to dCX distances (Å), respectively.
3.2. Thermochemistry of Complexes (1:n), n = 2–19
In this subsection, we predict the ΔH and ΔG of the tetrel bonding complexes (1:n), n = 2–19. In Table 1, we gather the computed enthalpies and free energies at the G4MP2 level of theory.

Table 1.
Enthalpy (ΔH) and free energy (ΔG) of formation for complexes (1:n), n = 2–19, in kJ·mol−1. LB: Lewis base.
The free energy of formation for complexes (1:n) is always negative except for (1:13) and (1:15) complexes, namely the O=C=O and FH complexes, respectively. Small negative values (|ΔG| < 10 kJ·mol−1) are obtained for complexes (1:6) and (1:19) with Lewis bases N2 and ClH, respectively. Therefore, all complexes with negative ΔG should be formed at room temperature spontaneously, provided an isolated Lewis acid (1) approaches an isolated Lewis base. On the other hand, the enthalpies of formation are negative for all complexes, an indication that the bond energies of a given complex (1:n) have a lower value than the bond energies of separated systems (1) and (n). In order to better visualize the similarities and differences of the thermochemical aspects of complexes (1:n), we plot ΔG and ΔH vs. n in increasing order of each state function.
As shown in Figure 4 from left to right in the abscissa, the ΔG (black) and ΔH (blue) in complex formation follow the same order as function of Lewis base number except for ClH (1:19) and N2 (1:6), where the order is inverted in the ΔH tendency as compared to ΔG. Hence, the formation of anionic complexes are the most energetic and favourable ones in the order (1:2), (1:10), (1:14) corresponding to Lewis bases H(−), OH(−), and F(−), respectively; then follow complexes (1:3), (1:16), and (1:4) corresponding to Lewis bases CH2, SiH2 and CF2, respectively, namely the carbene series. A plateau with complexes (1:8), (1:17), and (1:7) follows with Lewis bases NH=CH2, PH3, and NH3, respectively. A smaller (positive) slope of ΔG/ΔH vs. n appears with complexes (1:5), (1:18), (1:9), (1:12), and (1:11) always in increasing order, which correspond to Lewis bases C≡O, SH2, N≡CH, O=CH2, and OH2, respectively. The weakest bound complexes with ΔG < 0 correspond to (1:19) and (1:6) with Lewis bases ClH and N2, respectively. Finally, complexes (1:13) and (1:15) with Lewis bases O=C=O and FH, respectively, show a predicted quantum-chemical value of ΔG > 0, and therefore one should not expect a spontaneous formation of these complexes at room temperature. It is noteworthy to mention the tiny value ΔH(1:15) = −0.7 kJ·mol−1 for FH attachment to (1); this number is within the accuracy of the method and therefore a heat of formation for complex (1:15) or the bond energy on both sides of the equation remains unaltered.
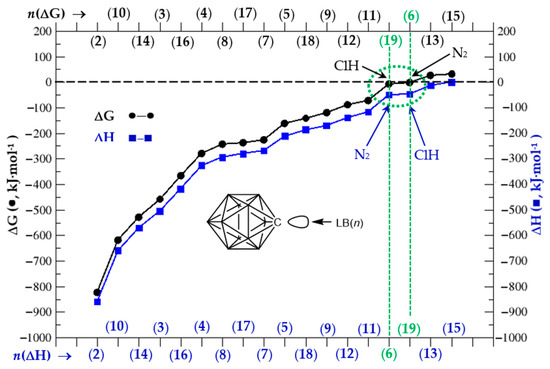
Figure 4.
ΔG and ΔH vs. Lewis base n in respective increasing order, all in kJ·mol−1.
3.3. Electronic Structure of Complexes (1:n), n = 2–19
In Figure 5, we show for (1) the molecular electrostatic potential (MEP) and the electron localization function (ELF). These electronic structure features are computed using the optimized geometry of the system with the G4MP2 method—B3LYP/6-31G(2df,p) model chemistry for structure optimization. As noticed in Figure 5a, the shape of the MEP and the corresponding π-hole just on top of the C ylide centre shows the electron-attraction nature of this region of the molecule. In the ELF from Figure 5b, we show disynaptic V(B,H) yellow basins corresponding to the B-H bonds; the ELF distribution around the CB11 icosahedral cage can be partitioned into green disynaptic and trisynaptic basins, as we will describe below in Section 3.3.2.
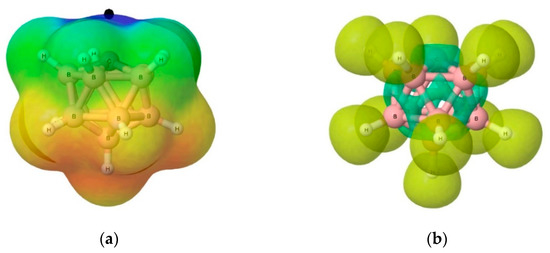
Figure 5.
Electronic structure of carbonium ylide (1) CB11H11: (a) Molecular electrostatic potential V(r). Red colour for V(r) < −0.015 au, Blue colour for V(r) > 0.03 au. The black dot indicates the localization of the π-hole (0.061 au), and (b) Electron Localization Function (ELF) with an isosurface of ELF = 0.75. Computations with the G4MP2 level of theory.
The molecular electrostatic potential (MEP) is the potential energy of a proton at a particular location near a molecule. Negative electrostatic potential corresponds to an attraction of the proton by the concentrated electron density in the molecules. The MEP of (1)—Figure 5b—shows that the potential energy of a proton is most positive above the C atom with a π-hole of +0.061 au, hence a repulsive region for a proton approaching (1), or electron acceptor region. The MEP is smoothly changing from positive to negative values of the potential energy as the proton moves from the C atom down to the B skeleton cage region. A proton would then be attached more favourably to the lower region of the carbonium ylide (1). In other words, Lewis bases, electron donors, and nucleophiles should then tend to bind through the C atom of the ylide, hence the study of the tetrel bonding in the complexes (1:n).
3.3.1. Atoms-in-Molecules (AIM) Topological Analysis of Complexes (1:n), n = 2–19
The Quantum Theory of Atoms in Molecules (QTAIM) [18,19] is a useful tool for analysing the electronic structure of a polyatomic many-electron system, with the electron density ρ(r) as the central function. The topological properties of ρ(r) are analysed with the gradient of ∇ρ(r), the Laplacian of ρ(r), ∇2ρ(r), and the eigenvalues of the Hessian matrix of the electron density λ1, λ2, λ3. The critical points are those with and a bond critical point (BCP) has λ3 > 0 associated with the bond path direction, and λ1 < 0, λ2 < 0 the two latter associated to two directions where is a maximum; the BCP (−,−,+) appears at the intersection of the bond path with the interatomic surface S. Other critical points are classified according to the signs of λi: Nuclei positions with (−, −, −); ring critical points with (−,+,+); cage critical points with (+,+,+). We should also introduce the local electron kinetic (G > 0), potential (V < 0), and total (H) energy densities, with H = G + V, also useful parameters at the BCP for the description of the type of bonding interaction between atoms in a many-electron system [24]. In the SI (Table S11), we provide the computed values of ρ(r), ∇ρ(r), ∇2ρ(r), G, V, and H for the BCP found between the X atom of the Lewis base in contact with the C ylide centre in (1), for all complexes (1:n), n = 2–19.
In Figure 6a, we plot the electron density at the BCP for the C⋯X interaction vs. d(CX) distance. The largest values of ρBCP correspond to CH2 (ρBCP(CH2) = 0.32 e/a03), CF2, and CO, followed by H(−), OH(−), NHCH2, N2, and F(−). Another group follows with lower values, NH3, OCH2, PH3, OH2, SH2, and further down, SiH2 and ClH with similar values. Finally, the lowest ρBCP correspond to FH and CO2, the latter with ρBCP(CO2) = 0.01 e/a03. We should emphasize that the ratio ρBCP,max(CH2)/ρBCP,min(CO2) = 32 gives an idea of the topological differences in these BCPs. Given the different type of C⋯X interactions in the complexes, the ρBCP vs. d(CX) can be fit to an approximate negative exponential curve with ρBCP (dCX) = a + b·exp(−c·dCX), with a = −0.022, b = +3.222, and c = −1.751, and a correlation factor of R2 = 0.99 for closed-shell interacting complexes: CO2, FH, SiH2, N2, and NCH. This curve is displayed in the SI (Figure S1). In general, very good correlations appear if we fix the two interacting atoms both belonging to the same row of the Periodic Table [25,26,27].
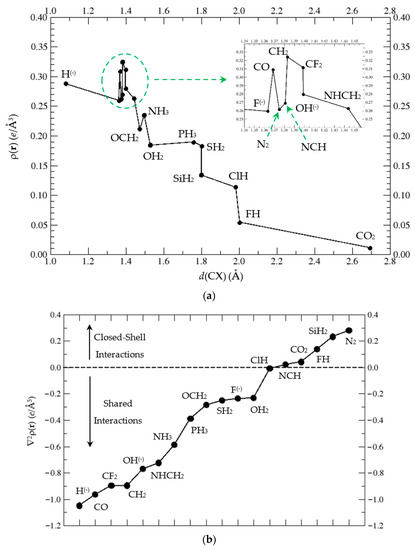
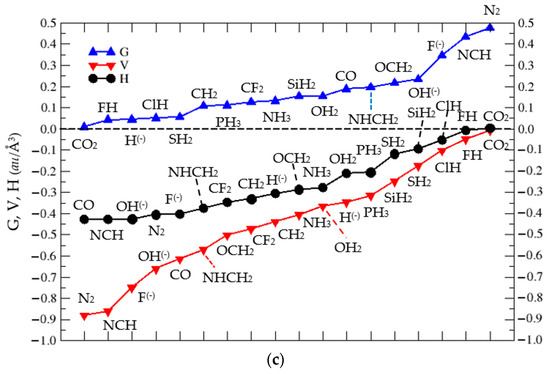
Figure 6.
(a). ρ(r) at the BCP of the C⋯X interaction in complexes (1:n) vs. d(CX), with n = 2–19. We label each point with the corresponding LB. (b) ∇2ρ(r) at the C⋯X BCP for complexes (1:n), n = 2–19. (c) Plot of G (▲), V (▼), and H (●) vs. Lewis base LB(n) in increasing order of G, V, and H, respectively, at the Bond Critical Point (BCP) in the C⋯X interaction of complexes (1:n), n = 2–19, as described in Scheme 1.
In order to estimate the type of interaction we need to go beyond the electron density at the BCP and analyse the second derivative, the Laplacian ∇2ρ, and the kinetic, potential, and total energy, G, V, and H respectively, of the BCPs in complexes (1:n). In Figure 6b, the Laplacian is plotted vs. LB(n) in increasing order. Clearly, we can distinguish the shared interactions for ∇2ρ < 0 in the lower left corner and closed-shell interactions for ∇2ρ > 0 in the upper right corner of Figure 6b. The two-electron sharing in complexes with H(−), CO, CF2, and CH2 is large, and it is diminished up to OH2. For the complex with HCl, ∇2ρ = −0.0067 e/Å5, namely in the limit between shared and closed-shell interactions. For positive Laplacians, in increasing order, the LB in the (1:n) complexes correspond to: NCH, CO2, FH, SiH2, and N2; in these systems, the closed-shell interactions are important.
A further analysis of the BCP in the C⋯X interactions of the (1:n) complexes can be found in the values of G, V, and H—with H = G + V being the total energy—as displayed in Figure 6c. The kinetic energy G is associated with repulsion in the bonding region, and the local potential energy density or local virial field V is a measure of the average effective potential field experienced by a single electron in a many-particle system. Thus, according to Figure 6c, the G and V profiles are inverted for N2, NCH, F(−), and OH(−), but due to the nature of different nuclei in the C-X interactions, this is not always the case, as seen when we follow the profiles as function of LB(n).
3.3.2. Electron Localisation Function (ELF) Analysis of Complexes (1:n), n = 2–19
We should emphasize that ELF is a function which reports the probability of finding an electron pair with opposite spins in a region of space. Using a certain isovalue, we are able to define regions of space, basins, with a certain probability to find an electron pair. For example, in the plots of the ELF, we used an isovalue of 0.83; in other words, we plot regions of space where we have a high probability to find a pair of electrons. Once the basins are defined, we can integrate the electronic density into those basins, which are the values reported above in Table 2 and correspond to the number of electrons in that basin. In ELF analysis, the partition of space is not based on the electron density, as in AIM, but on the ELF probability function. In order to better understand from the electronic structure point of view the tetrel bonding in the (1:n) complexes, we further computed the electron localisation function (ELF) [21,22,28], a measure of the likelihood of finding an electron in the neighborhood space of a reference electron located at a given point and with the same spin; therefore, ELF is a measure of the Pauli repulsion or exchange interaction [29,30]. The ELF for the carbonium ylidene CB11H11 (1) is shown in Figure 4. ELF values ranges from zero to one (normalized and without units). In the SI file we provide the ELF for all complexes (1:n) not shown here (Table S12), and below we have selected four cases with short, medium, long, and very long C⋯X distances, according to Figure 3 above: (i) LB = H(−), complex (1:2), (ii) LB = N2, complex (1:6), (iii) LB = PH3, complex (1:17), and (iv) LB = CO2, complex (1:13). In Table 2, we gather the ELF function for these four complexes.

Table 2.
Electron localisation function (ELF) (isovalue 0.83 au) for complexes H11B11C:H(−) → (1:2), H11B11C:N≡N → (1:6), H11B11C:PH3 → (1:17), and H11B11C:O=C=O → (1:13). Basin labels are depicted for each complex. Population of ELF disynaptic basins V(C, X) in bold.
Below each ELF function of a given complex (1:n), we also report the function value and average population for the different types of basins. A threshold of 0.2 electrons is considered as to include or not a basin in a group. Below each ELF function of a given complex (1:n), we report the population of the different basins. In order to avoid dealing with a long list of populations and after observing that basins involving the same elements have similar populations, we decided to report only for each type of basins the average population. A threshold of 0.2 electrons was chosen to decide if two basins belong to the same group or not. For instance, if we consider basins V(B1,B2) and V(B1,B3) with populations of 0.8 and 1.5 electrons, respectively, they belong to different groups. In bold letters, we report the value of the disynaptic basin corresponding to the tetrel C⋯X interaction.
In Table 2 we use the following notation:
- C: core basin
- V(X): monosynaptic basin, which can be associated to a lone pair
- V(X,X): disynaptic basin
- V(X,X,X): trisynaptic basin
- 5 V(B,B) = 0.42: There are 5 disynaptic basins involving two boron atoms with an average population of 0.42 electrons.
In the ELF representation, the following colours are used:
- Blue: core basin
- Red: monosynaptic basin
- Grey: polysynaptic basin
- Beige: V(X,H) basin
- Atoms: Boron (green), Carbon (black), Hydrogen (silver), Oxygen (red), and Phosphorus (tan).
Thus, according to Table 2, in the complex (1:2), the existing anion CB11H12(−), the 11 core electrons from the boron cage, the 1s2(B) ones, are gathered in the C(B) core basins, which have an average population of 2.07 electrons; the same description applies for the single C atom and the C(C) = 2.11 basin. The 11 B-H bonds on each non-naked B vertex of the icosahedron correspond to the 11 V(B,H) = 2.05, basically a two-electron covalent B-H bond. Then the distribution of the remaining valence cage electrons (corresponding to 2s and 2p electrons from B and C, plus the surplus electron or negative charge of the anion) are distributed in the 10 V(B,B,B) trisynaptic basins with an average population of 0.81 electrons, the 15 V(B,B) disynaptic basins with a population of 0.76 electrons, and the 5 V(C,B) disynaptic basins with ∼1 electron in them. The V(C,H) disynaptic basin, with a population of 2.05, corresponds to the C⋯X = C-H bond in (1:2), a two-centre two-electron bond. Addition of the values of all basins leads to the number of electrons in CB11H12(−): 74.
As reported in Table 2, the C⋯X interaction in the selected complexes can be described by the presence or absence of V(C,X) valence basins and its population. For the complexes (1:6) and (1:17), these values are V(1:6)(C,N) = 2.62 and V(1:17)(C,P) = 2.21, respectively. Therefore, ELF describes the C⋯X for the N2 complex as a bond, with a multiplicity close to 1.5, between the C(ylide) and N nuclei and for the PH3 complex a C(ylide)P single bond, with additional 0.2 electrons. As regard to the (1:13) complex with CO2, the ELF does not localize a basin between the C(ylide) and the O=C=O molecule; the absence of ELF basins indicate that electron pairs are not shared, and therefore, the interaction is not covalent. However, other interactions such as ionic or non-covalent are possible even in the absence of ELF basins. The lone pairs from N2 and CO2 appear as red monosynaptic basins, as displayed in Table 2.
4. Discussion
The presence of a filled or empty lone pair on the C atom in the known anion CB11H12(−), complex (1:2), depends on whether we remove a proton or a hydride from the C-H bond, leading to a dianion [CB11H11](2−) (1b) or a carbonium ylide CB11H11 (1), respectively; the latter process is shown in Figure 1. The tetrel complexes (1:n) presented in the previous section show a rich variety of thermochemical and electronic structure features with tetrel C⋯X interactions from different nuclei: X = {H, C, N, O, F, Si, P, Cl}. The C(ylide) centre in (1) confers to this particular molecule with a Lewis acid (LA) character, hence the tetrel denomination. The strength for electronic attachment in (1) is given by the computed free energy of formation (1) + (n) → (1:n). The strongest complexes correspond to those formed with anions H(−), OH(−), and F(−), and the weakest complexes to those formed with FH, CO2, N2, and ClH. The C⋯X distance varies considerably in all complexes, ranging from 1.081 Å for (1:2), LB = H(−), to 2.694 Å for (1:13), LB = CO2. The complex strength is not related to the C⋯X distance; namely, complexes with similar C⋯X distances may have different free energy of formation, e.g., the free energy of formation for complexes (1:14) LB = F(−) and (1:6) LB = N2 is −530 kJ·mol−1 and −3 kJ·mol−1, respectively, with very similar d(C-X) distances, 1.364 Å and 1.375 Å.
Examples of recent related systems is the 3D analogue of phenyllithium, the lithiacarborane CB11H11:Li(−), studied in solution as a solid and by quantum-chemical computations [31]. Indeed, Li(−) is a very poor Lewis base but certainly attaches to (1), as recently shown, and defined as the lithiated mono-anion [Li−CB11H11](−). On the other hand, this process can also be seen as a carborane dianion [CB11H11](2−)—a very reactive species—attached to Li(+), as described in Reference [31]. Table 8-1 from the book by Grimes, Carboranes [4], reports hundreds of compounds derived from CB11H12(−), and therefore this is a rich field not only from a synthetic point of view but also for studying the electronic structure of tetrel C⋯X bonds in these compounds, and especially if the isolated tetrel complexes (1:n) could ever be synthesized, taking into account that this work is purely theoretical with predictive quantum-chemical computations.
The electronic structure of the complexes has been analysed thoroughly with AIM and ELF methods, showing the C⋯X sharing and closed-shell interactions in the complexes according to the values of the Laplacian of the electron density. In Table 3, we gather the ELF values for disynaptic basins V(C, X) in the C⋯X region showing values of ELF: we can find very polarised C-F bonds in (1:14)—only one electron in the C⋯X region—single C-X bonds for H(−) and NH=CH2 and intermediate cases, such as in complex (1:5) with a 1.5 multiplicity C-C bond for the CO complex. No V(C,X) disynaptic basins are found for CO2 and FH, an indication of the poor electron-donating ability of these Lewis bases (LB) with indeed long d(C-X) distances and positive free energies of formation ΔG > 0, hence confirming the unlikely formation of these two complexes.

Table 3.
Population of ELF disynaptic basins V(C, X) in tetrel complexes (1:n), n = 2–19, describing the C⋯X interaction. LB = Lewis base.
According to the Cambridge structural database(CSD) [32], several tetrel complexes derived from (1) have been characterised [33,34,35,36,37,38,39] where the C(ylide) centre interacts with a nitrogen atom from neutral aminoderivatives including pyridine. These structures are shown in the SI file as Table S13. The shortest C(ylide)⋯N distance, d(C⋯N) = 1.477 Å, corresponds to the pyridine complex 1-(4-methoxypyridinium)-1-carba-closo-dodecaborane [33]. The longest C(ylide)⋯N distance, d(C⋯N) = 1.554 Å, corresponds to the complex 12-iodo-1-(4-pentylquinuclidine)-1-carba-closo-dodecaborane [34]. There is a tetrel complex of (1) with NH3, 1-amino-2-fluorocarba-closo-dodecaborane [35], where one B-H vertex hydrogen atom on position 2 has been substituted by a fluorine atom with d(C⋯N) = 1.486 Å. Our (1:7) tetrel complex H11B11C ←:NH3 has a predicted d(C⋯N) = 1.498 Å according to the G4MP2 computational model.
5. Conclusions
The results presented in this work show that by means of quantum-chemical computations we should expect the formation of tetrel complexes between the icosahedral carbonium ylide CB11H11—derived from extraction of H(−) in the known anion CB11H12(−)—and a set of simple molecules and anions. The driving force of formation for these complexes can be accounted for from thermochemical quantum-chemical computations using statistical mechanics implemented in the scientific software Gaussian16 [14], and the results indicate that all the complexes should be formed with the exception of the FH and CO2 molecules, with N2 and ClH complexes with indeed very low, though negative, free energies of formation.
The tetrel C⋯X interactions in all complexes have been thoroughly studied by means of AIM and ELF methods, hence defining the type of bond and interaction, ranging from very polarised bonds, with one electron in the C⋯X moiety, to intermediate cases as in the carbenes CH2 and CF2 and silane SiH2, with one and a half electrons in the C⋯X region.
The existence of known tetrel complexes of the carbonium ylide CB11H11 with amino derivatives, including pyridine, opens the door toward further experimental and theoretical studies in the electronic structure of unusual bonds and interactions between C(ylide) centres in carboranes and other atoms.
We hope that the results from this work can be used for the isolation of reactive species, such as the recently found dianion derived from proton extraction in the well-known carborane anion CB11H12(−), a key molecule in the description of 3D aromaticity within boron chemistry.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/cryst11040391/s1, Tables S1–S10. G4MP2 optimised geometries of complexes (1:n). Table S11. AIM data for complexes (1:n). Table S12. ELF data for complexes (1:n) not displayed in the main text.
Author Contributions
Writing-original draft preparation, computations, and data curation: J.M.O.-E., M.F., I.A., and J.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Spanish MICINN, grant number CTQ2018-094644-B-C22 and Comunidad de Madrid, grant number P2018/EMT-4329 AIRTEC-CM.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Knoth, W.H. 1-B9H9CH− and B11H11CH−. J. Am. Chem. Soc. 1967, 89, 1274–1275. [Google Scholar] [CrossRef]
- Plešek, J.; Jelínek, T.; Drdáková, E.; Heřmánek, S.; Štíbr, B. A convenient preparation of 1-CB11H12− and its C-amino derivatives. Collect. Czechoslov. Chem. Commun. 1984, 49, 1559–1562. [Google Scholar] [CrossRef]
- Franken, A.; King, B.T.; Rudolph, J.; Rao, P.; Noll, B.C.; Michl, J. Preparation of [closo-CB11H12]− by dichlorocarbene insertion into [nido-B11H14]. Collect. Czechoslov. Chem. Commun. 2001, 66, 1238–1249. [Google Scholar] [CrossRef]
- Grimes, R.N. Carboranes, 3rd ed.; Academic Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Schleyer, P.v.R.; Najafian, K. Stability and three-dimensional aromaticity of closo-monocarbaborane anions, CBn-1Hn−,and closo-dicarboranes, C2Bn-2Hn. Inorg. Chem. 1998, 37, 3454–3470. [Google Scholar] [CrossRef] [PubMed]
- Michl, J. Chemistry of the three-dimensionally aromatic CB11 cage. Pure Appl. Chem. 2008, 80, 429–446. [Google Scholar] [CrossRef]
- Vyakaranam, K.; Körbe, S.; Divišová, H.; Michl, J. A new type of intermediate, C+(BCH3)11− ↔ C(BCH3)11, in a Grob fragmentation coupled with intramolecular hydride transfer. A nonclassical carbocation ylide or a carbenoid? J. Am. Chem. Soc. 2004, 126, 15795–15801. [Google Scholar] [CrossRef] [PubMed]
- Vyanakaram, K.; Havlas, Z.; Michl, J. Aromatic substitution with hypercloso C(BCH3)11: A new mechanism. J. Am. Chem. Soc. 2007, 129, 4172–4174. [Google Scholar] [CrossRef] [PubMed]
- Thomas, S.P.; Pavan, M.S.; Guru Row, T.N. Experimental evidence for ‘carbon bonding’ in the solid state from charge density analysis. Chem. Commun. 2014, 50, 49–51. [Google Scholar] [CrossRef]
- Alkorta, I.; Rozas, I.; Elguero, J. Molecular complexes between silicon derivatives and electron-rich groups. J. Phys. Chem. A 2001, 105, 743–749. [Google Scholar] [CrossRef]
- Bauzá, A.; Mooibroek, T.J.; Frontera, A. Tetrel-bonding interaction: Rediscovered supramolecular force? Angew. Chem. Int. Ed. 2013, 52, 12317–12321. [Google Scholar] [CrossRef] [PubMed]
- Grabowski, S.J. Tetrel bond–σ-hole bond as a preliminary stage of the SN2 reaction. Phys. Chem. Chem. Phys. 2014, 16, 1824–1834. [Google Scholar] [CrossRef]
- Curtiss, L.A.; Redfern, P.C.; Raghavachari, K. Gaussian-4 theory using reduced order perturbation theory. J. Chem. Phys. 2007, 127, 124105. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16; Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Møller, C.; Plesset, M.S. Note on an approximation treatment for many-electron systems. Phys. Rev. 1934, 46, 618–622. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Clarendon Press: Oxford, UK, 1990. [Google Scholar]
- Popelier, P.L.A. Atoms in Molecules. An Introduction; Prentice Hall: Harlow, UK, 2000. [Google Scholar]
- Keith, T.A. AIMAll; Version 19.10.12; TK Gristmill Software: Overland Park, KS, USA, 2017. [Google Scholar]
- Silvi, B.; Savin, A. Classification of chemical bonds based on topological analysis of electron localization functions. Nature 1994, 371, 683–686. [Google Scholar] [CrossRef]
- Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
- Noury, S.; Krokidis, X.; Fuster, F.; Silvi, B. TopMod Package; Universite Pierre et Marie Curie: Paris, France, 1997. [Google Scholar]
- Mata, I.; Alkorta, I.; Molins, E.; Espinosa, E. Universal features of the electron density distribution in hydrogen-bonding regions: A comprehensive study involving H···X (X=H, C, N, O, F, S, Cl, π) interactions. Chem. Eur. J. 2010, 16, 2442–2452. [Google Scholar] [CrossRef]
- Alkorta, I.; Solimannejad, M.; Provasi, P.F.; Elguero, J. Theoretical study of complexes and fluoride cation transfer between N2F+ and electron donors. J. Phys. Chem. A 2007, 111, 7154–7161. [Google Scholar] [CrossRef] [PubMed]
- Sánchez-Sanz, G.; Trujillo, C.; Alkorta, I.; Elguero, J. Intermolecular weak interactions in HTexH dimers (X=O, S, Se, Te): Hydrogen bonds, chalcogen-chalcogen contacts and chiral discrimination. ChemPhysChem 2012, 13, 496–503. [Google Scholar] [CrossRef] [PubMed]
- Alkorta, I.; Mata, I.; Molins, E.; Espinosa, E. Charged versus neutral hydrogen-bonded complexes: Is there a difference in the nature of the hydrogen bonds? Chem. Eur. J. 2016, 22, 9226–9234. [Google Scholar] [CrossRef] [PubMed]
- Savin, A.; Jepsen, O.; Flad, J.; Andersen, O.K.; Preuss, H.; Von Schnering, H.G. Electron localization in solid-state structures of the elements: The diamond structure. Angew. Chem. Int. Ed. 1992, 31, 187–188. [Google Scholar] [CrossRef]
- Heisenberg, W. Mehrkörperproblem und Resonanz in der Quantenmechanik. Zeit. Phys. 1985, 38, 456–471. [Google Scholar] [CrossRef]
- Dirac, P.A.M. On the theory of quantum mechanics. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1926, 112, 661–677. [Google Scholar] [CrossRef]
- Dontha, R.; Zhu, T.-C.; Shen, Y.; Wörle, M.; Hong, X.; Duttwyler, S. A 3D Analogue of phenyllithium: Solution-phase, solid-state, and computational study of the lithiacarborane [Li−CB11H11]. Angew. Chem. Int. Ed. Engl. 2019, 58, 19007–19013. [Google Scholar] [CrossRef] [PubMed]
- Groom, C.R.; Bruno, I.J.; Lightfoot, M.P.; Ward, S.C. The Cambridge structural database. Acta Crystallogr. B Struct. Sci. Cryst. Eng. Mater. 2016, B72, 171–179. [Google Scholar] [CrossRef] [PubMed]
- Pecyna, J.; Ringstrand, B.; Domagała, S.; Kaszyński, P.; Woźniak, K. Synthesis and characterization of 12-pyridinium derivatives of the [closo-1-CB11H12]− anion. Inorg. Chem. 2014, 53, 12617–12626. [Google Scholar] [CrossRef]
- Douglass, A.G.; Janousek, Z.; Kaszynski, P.; Young, V.G., Jr. Synthesis and molecular structure of 12-iodo-1-(4-pentylquinuclidin-1-yl)-1-carba-closo-dodecaborane. Inorg. Chem. 1998, 37, 6361–6365. [Google Scholar] [CrossRef]
- Finze, M.; Sprenger, J.A.P. 1-amino-2-fluoromonocarba-closo-dodecaborates: K[1-H2N-2-F-closo-1-CB11H10] and [Et4N][1-H2N-2-F-closo-1-CB11I10]. Z. Anorg. Allg. Chem. 2010, 636, 1538–1542. [Google Scholar] [CrossRef]
- Pecyna, J.; Kaszynski, P.; Ringstrand, B.; Pociecha, D.; Pakhomov, S.; Douglass, A.G.; Young, V.G., Jr. Synthesis and characterization of quinuclidinium derivatives of the [closo-1-CB11H12]− anion as potential polar components of liquid crystal materials. Inorg. Chem. 2016, 55, 4016–4025. [Google Scholar] [CrossRef]
- Maly, K.; Subrtova, V.; Petricek, V. Structure of 1-trimethylamine-1-carba-closo-dodecaborane(11). Acta Crystallogr. Sect. C Cryst. Struct. Commun. 1987, C43, 593–594. [Google Scholar] [CrossRef]
- Hailmann, M.; Herkert, L.; Himmelspach, A.; Finze, M. Difunctionalized {closo-1-CB11} clusters: 1- and 2-amino-12-ethynylcarba-closo-dodecaborates. Chem. Eur. J. 2013, 19, 15745–15758. [Google Scholar] [CrossRef] [PubMed]
- Morris, J.H.; Peters, G.S.; Spicer, M.D. 1-Me2NH-2-CH2Cl-closo-l-CB11H10. An unusual product from the insertion reaction of Me2NBCl2 with Li2[7-Me3N-nido-7-CB10H10]. J. Organomet. Chem. 1995, 494, 195–198. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).