Isotropic Nature of the Metallic Kagome Ferromagnet Fe3Sn2 at High Temperatures
Abstract
1. Introduction
2. Materials and Methods
3. Results
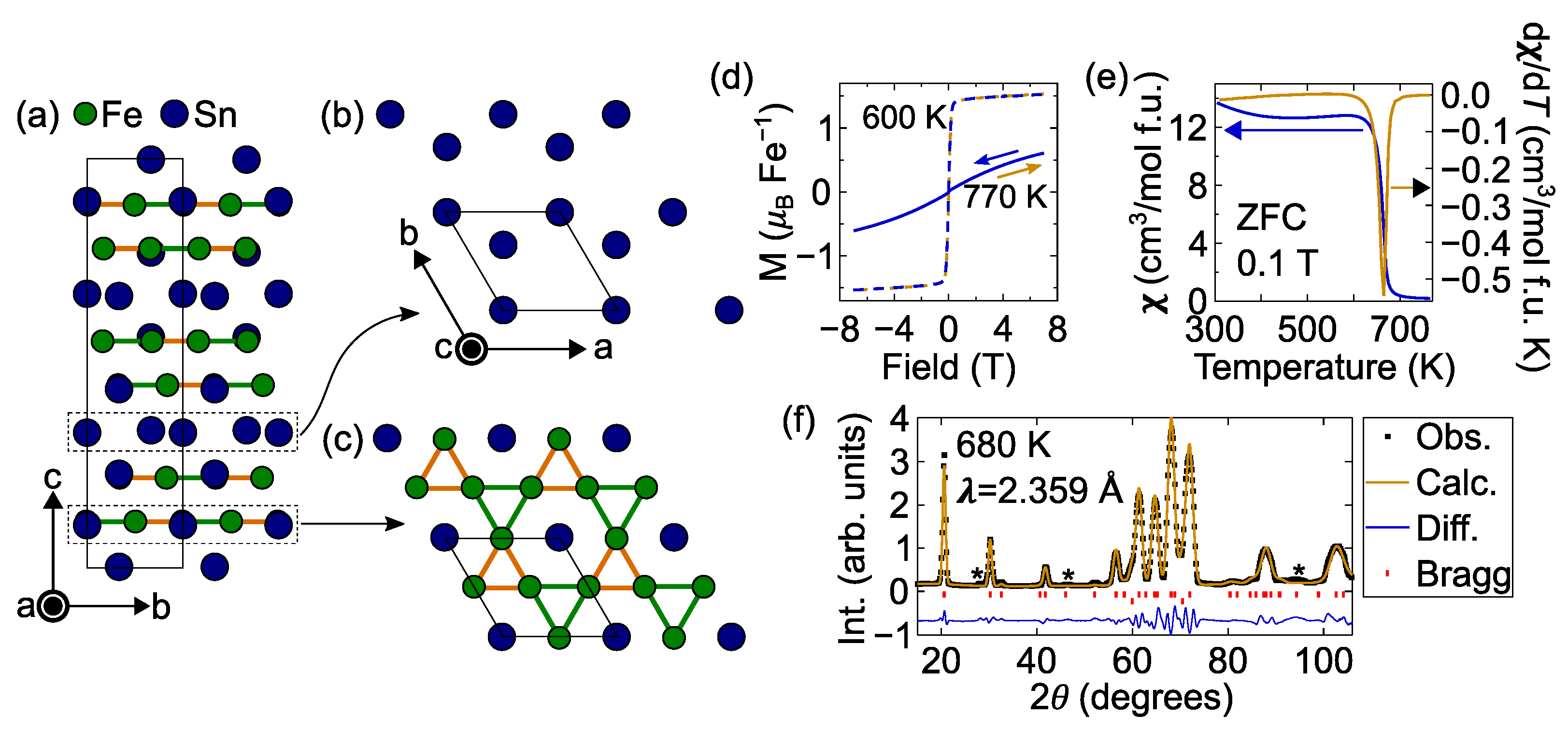
3.1. Characterization
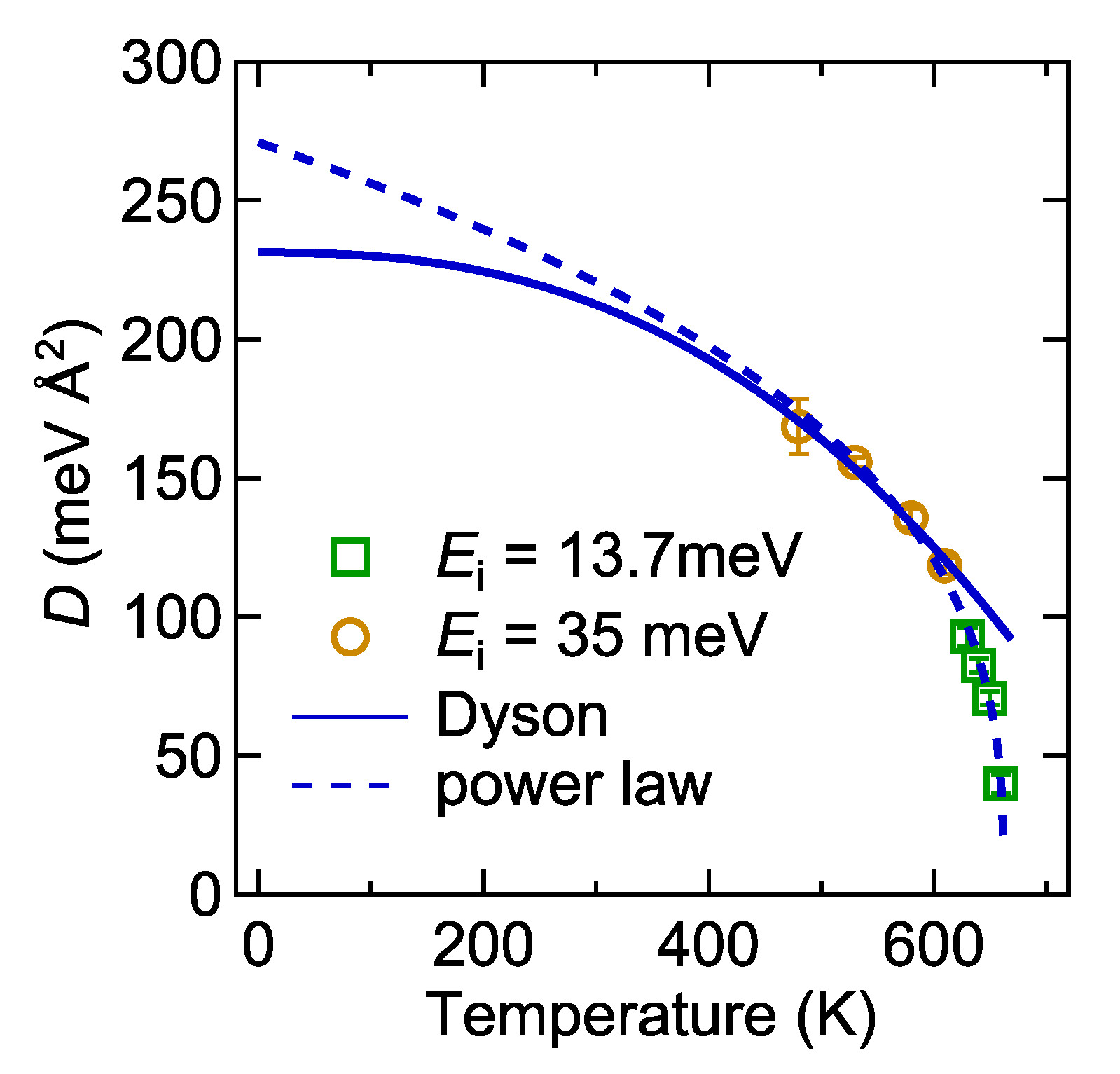
3.2. Inelastic Neutron Scattering
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guo, H.M.; Franz, M. Topological insulator on the kagome lattice. Phys. Rev. B 2009, 80, 113102. [Google Scholar] [CrossRef]
- Mazin, I.; Jeschke, H.O.; Lechermann, F.; Lee, H.; Fink, M.; Thomale, R.; Valentí, R. Theoretical prediction of a strongly correlated Dirac metal. Nat. Commun. 2014, 5, 1–7. [Google Scholar] [CrossRef]
- Kang, M.; Ye, L.; Fang, S.; You, J.S.; Levitan, A.; Han, M.; Facio, J.I.; Jozwiak, C.; Bostwick, A.; Rotenberg, E.; et al. Dirac fermions and flat bands in the ideal kagome metal FeSn. Nat. Mater. 2020, 19, 163–169. [Google Scholar] [CrossRef]
- Ye, L.; Kang, M.; Liu, J.; Von Cube, F.; Wicker, C.R.; Suzuki, T.; Jozwiak, C.; Bostwick, A.; Rotenberg, E.; Bell, D.C.; et al. Massive Dirac fermions in a ferromagnetic kagome metal. Nature 2018, 555, 638–642. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Sun, S.; Zhang, X.; Pang, F.; Lei, H. Anomalous Hall effect in a ferromagnetic Fe3Sn2 single crystal with a geometrically frustrated Fe bilayer kagome lattice. Phys. Rev. B 2016, 94, 075135. [Google Scholar] [CrossRef]
- Karplus, R.; Luttinger, J.M. Hall Effect in Ferromagnetics. Phys. Rev. 1954, 95, 1154–1160. [Google Scholar] [CrossRef]
- Lin, Z.; Choi, J.H.; Zhang, Q.; Qin, W.; Yi, S.; Wang, P.; Li, L.; Wang, Y.; Zhang, H.; Sun, Z.; et al. Flatbands and Emergent Ferromagnetic Ordering in Fe3Sn2 Kagome Lattices. Phys. Rev. Lett. 2018, 121, 096401. [Google Scholar] [CrossRef]
- Malaman, B.; Roques, B.; Courtois, A.; Protas, J. Structure cristalline du stannure de fer Fe3Sn2. Acta Crystallogr. Sect. B 1976, 32, 1348–1351. [Google Scholar] [CrossRef]
- Vaqueiro, P.; Sobany, G.G. A powder neutron diffraction study of the metallic ferromagnet Co3Sn2S2. Solid State Sci. 2009, 11, 513–518. [Google Scholar] [CrossRef]
- Hou, Z.; Ren, W.; Ding, B.; Xu, G.; Wang, Y.; Yang, B.; Zhang, Q.; Zhang, Y.; Liu, E.; Xu, F.; et al. Observation of Various and Spontaneous Magnetic Skyrmionic Bubbles at Room Temperature in a Frustrated Kagome Magnet with Uniaxial Magnetic Anisotropy. Adv. Mater. 2017, 29, 1–8. [Google Scholar] [CrossRef]
- Tang, J.; Kong, L.; Wu, Y.; Wang, W.; Chen, Y.; Wang, Y.; Li, J.; Soh, Y.; Xiong, Y.; Tian, M.; et al. Target Bubbles in Fe3Sn2 Nanodisks at Zero Magnetic Field. ACS Nano 2020, 14, 10986–10992. [Google Scholar] [CrossRef]
- Hou, Z.; Zhang, Q.; Xu, G.; Zhang, S.; Gong, C.; Ding, B.; Li, H.; Xu, F.; Yao, Y.; Liu, E.; et al. Manipulating the Topology of Nanoscale Skyrmion Bubbles by Spatially Geometric Confinement. ACS Nano 2019, 13, 922–929. [Google Scholar] [CrossRef]
- Hou, Z.; Zhang, Q.; Zhang, X.; Xu, G.; Xia, J.; Ding, B.; Li, H.; Zhang, S.; Batra, N.M.; Costa, P.M.F.J.; et al. Current-Induced Helicity Reversal of a Single Skyrmionic Bubble Chain in a Nanostructured Frustrated Magnet. Adv. Mater. 2020, 32, 1904815. [Google Scholar] [CrossRef]
- Hou, Z.; Zhang, Q.; Xu, G.; Gong, C.; Ding, B.; Wang, Y.; Li, H.; Liu, E.; Xu, F.; Zhang, H.; et al. Creation of Single Chain of Nanoscale Skyrmion Bubbles with Record-High Temperature Stability in a Geometrically Confined Nanostripe. Nano Lett. 2018, 18, 1274–1279. [Google Scholar] [CrossRef]
- Li, H.; Ding, B.; Chen, J.; Li, Z.; Hou, Z.; Liu, E.; Zhang, H.; Xi, X.; Wu, G.; Wang, W. Large topological Hall effect in a geometrically frustrated kagome magnet Fe3Sn2. Appl. Phys. Lett. 2019, 114, 192408. [Google Scholar] [CrossRef]
- O’Neill, C.D.; Wills, A.S.; Huxley, A.D. Possible topological contribution to the anomalous Hall effect of the noncollinear ferromagnet Fe3Sn2. Phys. Rev. B 2019, 100, 174420. [Google Scholar] [CrossRef]
- Wang, Q.; Yin, Q.; Lei, H. Giant topological Hall effect of ferromagnetic kagome metal Fe3Sn2. Chin. Phys. B 2020, 29, 017101. [Google Scholar] [CrossRef]
- Du, Q.; Han, M.G.; Liu, Y.; Ren, W.; Zhu, Y.; Petrovic, C. Room-Temperature Skyrmion Thermopower in Fe3Sn2. Adv. Quantum Technol. 2020, 3, 2000058. [Google Scholar] [CrossRef]
- Okubo, T.; Chung, S.; Kawamura, H. Multiple-q States and the Skyrmion Lattice of the Triangular-Lattice Heisenberg Antiferromagnet under Magnetic Fields. Phys. Rev. Lett. 2012, 108, 017206. [Google Scholar] [CrossRef] [PubMed]
- Hayami, S.; Lin, S.Z.; Batista, C.D. Bubble and skyrmion crystals in frustrated magnets with easy-axis anisotropy. Phys. Rev. B 2016, 93, 184413. [Google Scholar] [CrossRef]
- Leonov, A.; Mostovoy, M. Multiply periodic states and isolated skyrmions in an anisotropic frustrated magnet. Nat. Commun. 2015, 6, 1–8. [Google Scholar] [CrossRef]
- Lin, S.Z.; Hayami, S. Ginzburg-Landau theory for skyrmions in inversion-symmetric magnets with competing interactions. Phys. Rev. B 2016, 93, 064430. [Google Scholar] [CrossRef]
- Malaman, B.; Fruchart, D.; Caer, G.L. Magnetic properties of Fe3Sn2. II. Neutron diffraction study (and Mossbauer effect). J. Phys. Met. Phys. 1978, 8, 2389–2399. [Google Scholar] [CrossRef]
- Fenner, L.A.; Dee, A.A.; Wills, A.S. Non-collinearity and spin frustration in the itinerant kagome ferromagnet Fe3Sn2. J. Phys. Condens. Matter 2009, 21, 452202. [Google Scholar] [CrossRef]
- Kumar, N.; Soh, Y.; Wang, Y.; Xiong, Y. Magnetotransport as a diagnostic of spin reorientation: Kagome ferromagnet as a case study. Phys. Rev. B 2019, 100, 214420. [Google Scholar] [CrossRef]
- Heritage, K.; Bryant, B.; Fenner, L.A.; Wills, A.S.; Aeppli, G.; Soh, Y.A. Images of a First-Order Spin-Reorientation Phase Transition in a Metallic Kagome Ferromagnet. Adv. Funct. Mater. 2020, 30, 1909163. [Google Scholar] [CrossRef]
- Kida, T.; Fenner, L.A.; Dee, A.A.; Terasaki, I.; Hagiwara, M.; Wills, A.S. The giant anomalous Hall effect in the ferromagnet Fe3Sn2—A frustrated kagome metal. J. Physics: Condens. Matter 2011, 23, 112205. [Google Scholar] [CrossRef] [PubMed]
- Lynn, J.; Chen, Y.; Chang, S.; Zhao, Y.; Chi, S.; Ratcliff, W. Double-focusing thermal triple-axis spectrometer at the NCNR. J. Res. NIST 2012, 117, 61. [Google Scholar] [CrossRef]
- Rodríguez-Carvajal, J. Recent advances in magnetic structure determination by neutron powder diffraction. Phys. B 1993, 192, 55–69. [Google Scholar] [CrossRef]
- Lynn, J.W.; Fernandez-Baca, J.A. Neutron Scattering Studies of the Spin Dynamics of Amorphous Alloys. In The Magnetism of Amorphous Metals And Alloys; Ching, W.Y., Fernandez-Baca, J.A., Eds.; World Scientific Publishing Company: Singapore, 1995; Chapter 5; pp. 221–260. [Google Scholar]
- Lynn, J.W.; Erwin, R.W.; Borchers, J.A.; Huang, Q.; Santoro, A.; Peng, J.L.; Li, Z.Y. Unconventional Ferromagnetic Transition in La1-xCaxMnO3. Phys. Rev. Lett. 1996, 76, 4046–4049. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, P.W.; Cowley, R.A.; Higgins, S.A. The resolution function of triple-axis neutron spectrometers in the limit of small scattering angles. Acta Crystallogr. Sect. A 1984, 40, 152–160. [Google Scholar] [CrossRef]
- Zheludev, A. ResLib v3.4c. 2009. Available online: https://neutron.ethz.ch/Methods/reslib.html (accessed on 15 January 2021).
- Harris, A.B. Energy Width of Spin Waves in the Heisenberg Ferromagnet. Phys. Rev. 1968, 175, 674–679, Erratum in 1969, 184, 606–606.. [Google Scholar] [CrossRef]
- Mattis, D.C. The Theory of Magnetism I: Statics and Dynamics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 17. [Google Scholar]
- Collins, M.F. Magnetic Critical Scattering; Oxford University Press: Oxford, UK, 1989. [Google Scholar]
- Collins, M.F.; Minkiewicz, V.J.; Nathans, R.; Passell, L.; Shirane, G. Critical and Spin-Wave Scattering of Neutrons from Iron. Phys. Rev. 1969, 179, 417–430. [Google Scholar] [CrossRef]
- Minkiewicz, V.J.; Collins, M.F.; Nathans, R.; Shirane, G. Critical and Spin-Wave Fluctuations in Nickel by Neutron Scattering. Phys. Rev. 1969, 182, 624–631. [Google Scholar] [CrossRef]
- Lynn, J.; Mook, H. Temperature dependence of the dynamic susceptibility of nickel. Phys. Rev. B 1981, 23, 198. [Google Scholar] [CrossRef]
- Holstein, T.; Primakoff, H. Field Dependence of the Intrinsic Domain Magnetization of a Ferromagnet. Phys. Rev. 1940, 58, 1098–1113. [Google Scholar] [CrossRef]
- Lin, Z.Z.; Chen, X. Tunable Massive Dirac Fermions in Ferromagnetic Fe3Sn2 Kagome Lattice. Phys. Status Solidi-(Rrl) Rapid Res. Lett. 2020, 14, 1900705. [Google Scholar] [CrossRef]
- Skomski, R.; Coey, J. Magnetic anisotropy—How much is enough for a permanent magnet? Scr. Mater. 2016, 112, 3–8. [Google Scholar] [CrossRef]
- Xiao, Y.; Morvan, F.J.; He, A.N.; Wang, M.K.; Luo, H.B.; Jiao, R.B.; Xia, W.X.; Zhao, G.P.; Liu, J.P. Spin-reorientation transition induced magnetic skyrmion in Nd2Fe14B magnet. Appl. Phys. Lett. 2020, 117, 132402. [Google Scholar] [CrossRef]
- Hirschberger, M.; Nakajima, T.; Gao, S.; Peng, L.; Kikkawa, A.; Kurumaji, T.; Kriener, M.; Yamasaki, Y.; Sagayama, H.; Nakao, H.; et al. Skyrmion phase and competing magnetic orders on a breathing kagomé lattice. Nat. Commun. 2019, 10, 1–9. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dally, R.L.; Phelan, D.; Bishop, N.; Ghimire, N.J.; Lynn, J.W. Isotropic Nature of the Metallic Kagome Ferromagnet Fe3Sn2 at High Temperatures. Crystals 2021, 11, 307. https://doi.org/10.3390/cryst11030307
Dally RL, Phelan D, Bishop N, Ghimire NJ, Lynn JW. Isotropic Nature of the Metallic Kagome Ferromagnet Fe3Sn2 at High Temperatures. Crystals. 2021; 11(3):307. https://doi.org/10.3390/cryst11030307
Chicago/Turabian StyleDally, Rebecca L., Daniel Phelan, Nicholas Bishop, Nirmal J. Ghimire, and Jeffrey W. Lynn. 2021. "Isotropic Nature of the Metallic Kagome Ferromagnet Fe3Sn2 at High Temperatures" Crystals 11, no. 3: 307. https://doi.org/10.3390/cryst11030307
APA StyleDally, R. L., Phelan, D., Bishop, N., Ghimire, N. J., & Lynn, J. W. (2021). Isotropic Nature of the Metallic Kagome Ferromagnet Fe3Sn2 at High Temperatures. Crystals, 11(3), 307. https://doi.org/10.3390/cryst11030307





