1. Introduction
This paper is in memoriam of Ortwin Schirmer who throughout his long career pioneered the study of lithium niobate. Lithium niobate (LiNbO
, LN) is widely employed in electro-, acousto- and nonlinear optical applications. In addition, since free and trapped charge carriers of both positive and negative signs are known to form small polarons in LN, this material serves as an elegant and robust model system to study fundamental physical properties [
1].
An electronic charge carrier becomes self-trapped when it is bound within the potential well produced by its displacements of the equilibrium positions of the atoms that surround it. The composite quasiparticle comprising a self-trapped electronic charge carrier taken together with the displaced atomic equilibrium positions is termed polaron [
1]. This name polaron was adopted in recognition of their prevalence in polar (i.e., ionic) materials.
Lithium niobate is a perovskite-like oxide ferroelectric with especially displaceable ions [
2,
3]. The dependence of the energy of an electronic carrier on displacements of surrounding atoms produces both long-range and short-range electron–phonon interactions. The long-range electron–phonon interaction results from the Coulomb energy of an electronic carrier depending on displacements of distant ions. It is proportional to (1/
), where
and
respectively designate a material’s static and high-frequency constant. Values of this parameter in LN (
,
[
4]) are comparable to those of other ionic materials (e.g., alkali halides) whose charge carriers form polarons. Short-range electron–phonon interactions result from the energies and covalency of bonds between neighboring atoms changing with their separations. Short-range electron–lattice interactions as well as disorder foster the collapse of self-trapped electronic carriers to single sites thereby forming small polarons [
1,
5].
In addition to free small-polarons in LN [
6], defects are sites for defect-related electron and hole polarons as well as bipolarons [
7,
8]. Small-polarons govern many of the linear and non-linear optical properties of LN [
9,
10,
11] that include the bulk photovoltaic effect [
12], green-induced infrared absorption (GRIIRA), optical damage and photoconductivity (PC) [
8,
11,
13,
14]. The transient broad-band small-polaron absorptions and index changes in LN [
9,
10] provide a clear link between small-polaron absorption and their hopping motion. For instance, the stretched-exponential relaxation of the transient absorption is attributed to small-polarons’ hopping [
15,
16,
17].
Small polarons exhibit distinctive optical and electronic transport properties [
1]. In particular, phonon-broadened absorption bands result from photon-assisted inter-site transfers of small-polarons’ self-trapped electronic carriers. In addition, small polarons generally move with extremely low mobilities via phonon-assisted hopping. A small-polaron absorption band disappears as its small polarons are eliminated by their recombination with oppositely charged carriers. Recombination is facilitated by both photon-assisted and phonon-assisted hopping. In the former case, increasing the intensity of absorption within a small-polaron band fosters its elimination. In this manner, small-polaron absorptions are bleached. In the latter case, increasing temperature fosters disappearance of small-polaron absorptions.
Essential features of a small-polaron’s phonon-assisted hopping are well established [
1]. Self-trapped electronic carriers usually move fast enough to adiabatically adjust to the relatively slow vibrations of atoms. Adiabatic small-polaron hopping has been addressed at high enough temperatures for atoms’ vibrations to be classical. The small-polaron jump rate is then Arrhenius both for uncorrelated hops [
18,
19] and when the slow transfer of vibrational energy between atoms causes hops to occur in flurries with enhanced pre-exponential factors [
1,
20,
21]. Nonetheless, for computational simplicity, almost all calculations of phonon-assisted hopping are performed in the non-adiabatic limit in which an electronic carrier’s inter-site motion is assumed to be arbitrarily slow. In particular, the elemental non-adiabatic small-polaron jump rate has been calculated for its self-trapped carrier interacting with acoustic [
22], optical [
23] and both acoustic and optical phonons [
24].
All studies of small-polaron hopping report three distinct temperature regimes [
1]. At the highest temperatures, atoms’ vibrations are classical with a self-trapped carrier moving between initial and final sites when its electronic energy at these sites become coincident with each other. The jump rate’s primary temperature dependence is then Arrhenius and independent of phonon energies:
, where
denotes the energy difference between final and initial sites with
being the activation energy for equivalent sites,
. At the lowest temperatures, a self-trapped carrier hops when atoms quantum-mechanically tunnel between the configurations they assume when the self-trapped carrier occupies initial and final sites. The jump rate’s primary temperature dependence is then also Arrhenius and independent of phonon energies:
. Then a hop upward in energy,
, is Arrhenius,
, while a hop downward in energy,
, is temperature independent. Distinctively, the small-polaron jump rate between these high-temperature and low-temperature limits is non-Arrhenius and dependent on phonon energies. The primary temperature dependence of the small polaron jump rate is
for
, where
represents the characteristic phonon energy. Thus, measuring the temperature dependence in the high-temperature and intermediate regimes provides an estimate of this characteristic phonon energy. The reasonableness of this estimate tests the small-polaron approach.
Sufficiently separated oppositely charged small polarons will experience a mutual Coulomb attraction [
1]. Recombination between oppositely charged small polarons can occur once a series of small-polaron hops enables them to move close enough to one another. These hops will tend to be downward in energy,
, since small-polaron jump rates are proportional to
. The rate-limiting hop, the slowest of this sequence, occurs at its beginning where
tends to be smallest. Since the oppositely charged small polarons generated by our experiment’s pump will have a distribution of initial separations, their recombination will be characterized by a distribution of recombination times. Thus, as observed [
15], the time-dependent relaxation of the pump-induced transient absorption will be a stretched exponential.
We utilize a two-photon pump to produce electron and hole small-polarons whose recombination is then monitored by their absorption’s temporal decay. To generate free small-polarons, we study an LN crystal that was congruently grown from a melt with 6.5 % Mg since it contains a negligible concentration of antisite defects. Our optical excitation then primarily produces free Nb
n-type small polarons and O
–V
sites, p-type polarons bound to lithium vacancies [
25,
26]. We thereby avoid the profusion of other types of polaron states that occur in materials such as Fe:LN [
17,
27]. The transient near infra-red absorption in LN is primarily due to small polarons [
6,
28]. Other optical phenomena are also associated with self-trapped charge carriers and excitons [
29,
30,
31,
32,
33]
We explore the transient absorption from to s for temperatures between 45 K and 225 K. A simple model enables us to relate the observed decay rate of the absorption to the temperature-dependent small-polaron jump rate. Analysis of the small-polaron jump rate through the observed temperature range yields plausible estimates of the activation energy for small-polaron hopping and distinctively, the characteristic atomic-vibration frequency.
2. Methods
The lithium niobate sample (thickness d = 2 mm, Mg-doping of 6.5 mol% in the melt, z-cut) was grown, cut and polished by Kovács et al. at the WIGNER Research Centre for Physics, Budapest. The crystal was mounted in a closed-cycle cryostat which operates between 40 K and room temperature.
Optical windows on the cryostat enable nanosecond-pump and continuous-wave-probe measurements for probing small-polarons’ transient absorption (TA). Small polarons were generated in Mg:LN via two-photon absorption from an ordinarily polarized, frequency-doubled Nd:YAG pulse laser ( nm, = 8 ns, MW/cm). Transmitted polarized light of a continuous wave probe laser ( nm) was split and detected (1) by a Si-PIN photo diode connected to a fast digital storage oscilloscope and (2) by a photometer. Thus, the TA signal was recorded (1) in a time range from nanoseconds up to five seconds and (2) in a time range from one second up to several thousands of seconds, respectively. The power of the probe laser was kept below 1 mW to minimize its effect on the transient absorption. For this purpose, a fast electronic shutter was also introduced into the probe beam’s path so that the transient absorption at long times was only affected intermittently. The transient absorption is determined from the ratio of the intensity of the transmitted probe light after the pulse was applied to that prior to the pulse event , giving: .
3. Decay of Photo-Induced Absorption
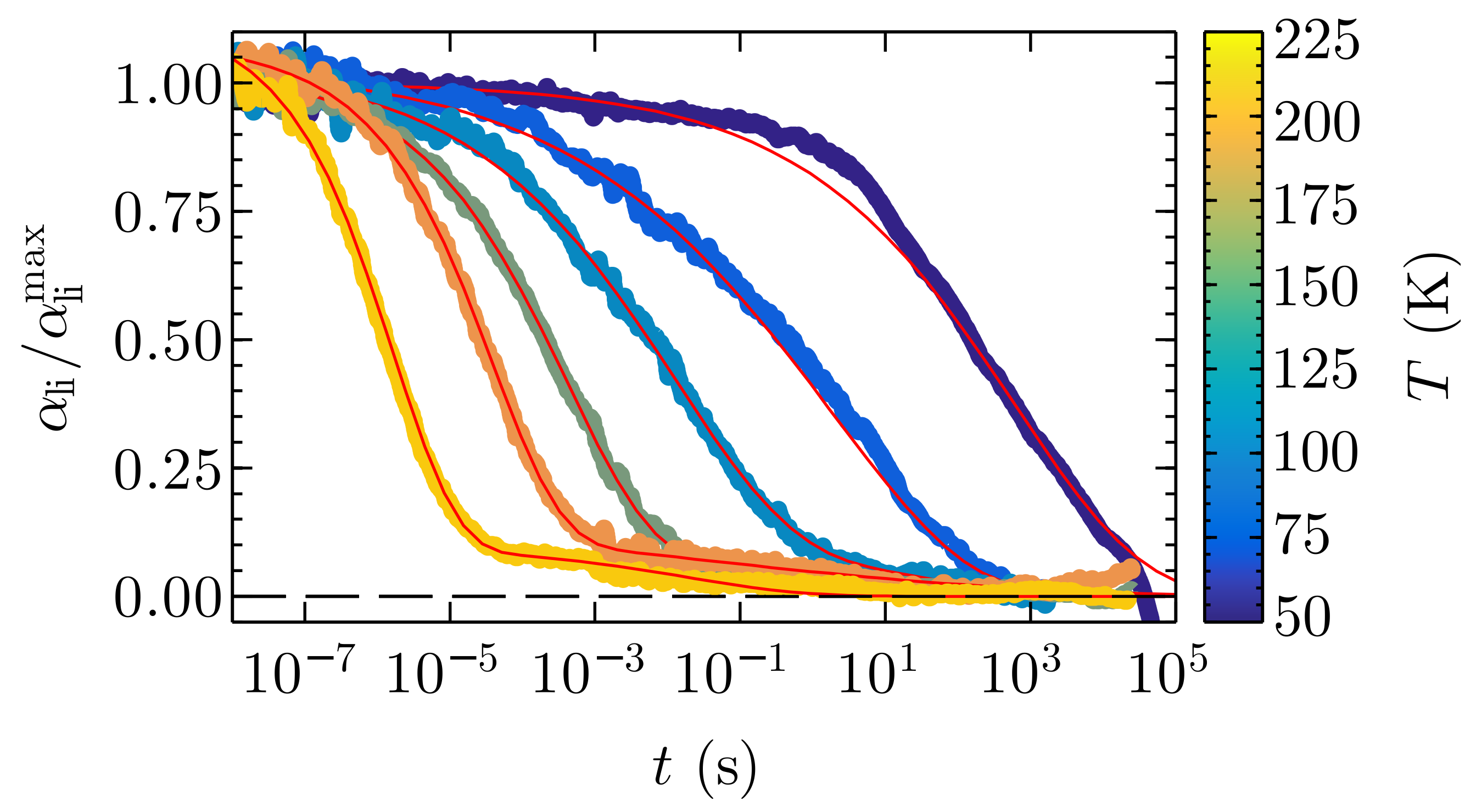
Figure 1 shows the normalized temperature-dependent results of transient absorption measurements at the probe wavelength
nm for Mg:LN. Obviously, these data are not well described as simple temporal decays,
. However, our data are well fitted with the two temperature-dependent parameters [
and
] of Kohlrausch–Williams–Watts (KWW) stretched-exponentials,
. The red curve accompanying the lowest-temperature data shows such a fit. The red curve accompanying the highest-temperature data illustrates that the fitting result is only slightly improved upon employing six adjustable parameters of a sum of two KWW stretched exponentials,
. We note that we used the fit parameter for the starting amplitude
to account for the elevation of the measured data above the value 1, that was caused by the noise in the experimental data. We therefore illustrate our results in terms of a single KWW stretched exponential with its two temperature dependent parameters,
and
.
KWW stretched-exponentials are phenomenological representations of processes with distributions of relaxation times. The mean relaxation time for a KWW stretched exponential is , where denotes the mathematical gamma function. is found from the values of and obtained from stretched-exponential fits to our transient-absorption data.
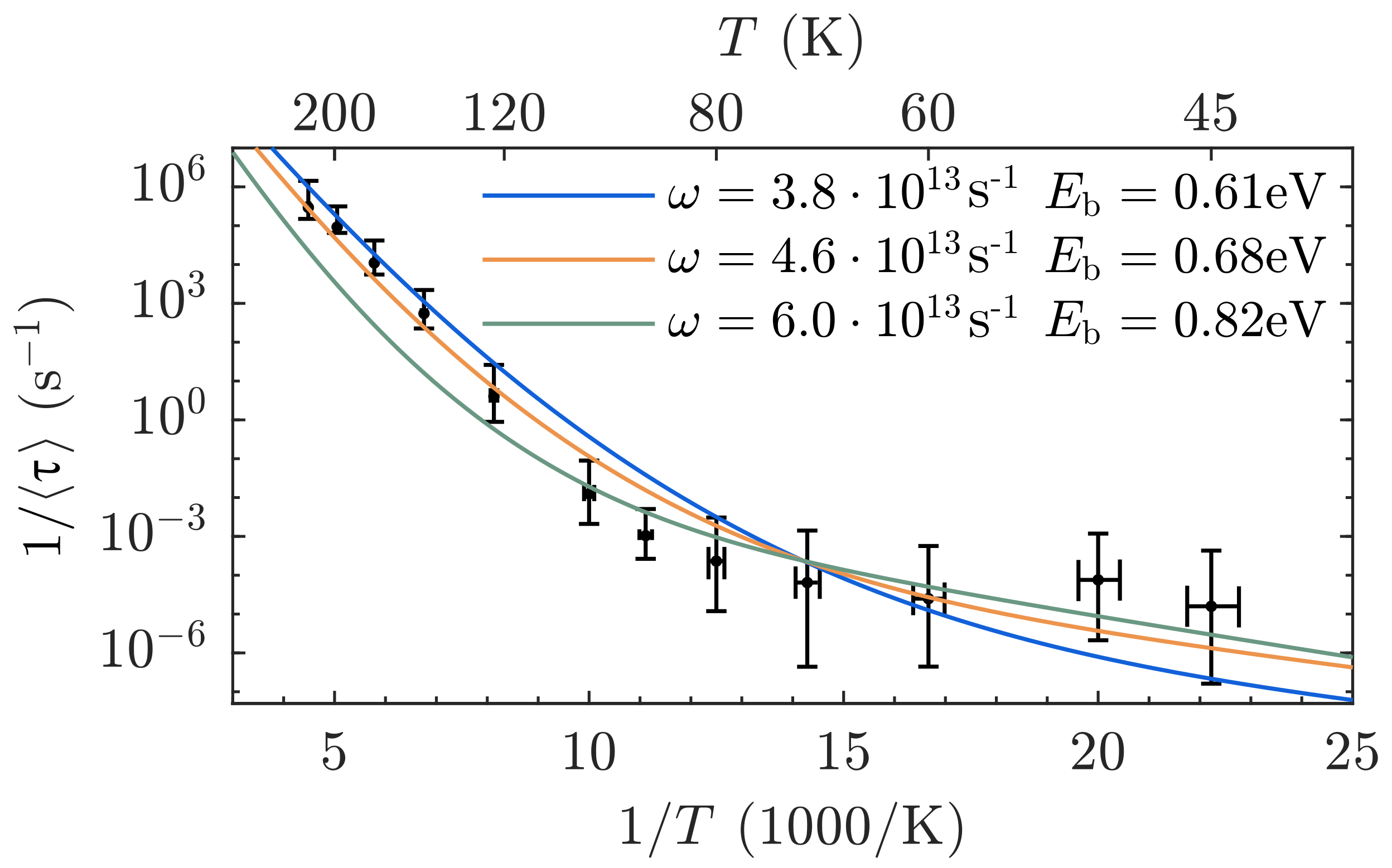
The resulting values of
plotted against reciprocal temperature in units of 1000/T are the experimental points shown in
Figure 2. Distinctively, the photo-induced decay rate
appears Arrhenius above 100 K and becomes non-Arrhenius below 100 K.
4. Small-Polaron Recombination and Phonon-Assisted Hopping
Well-separated oppositely charged small polarons attract each other through their mutual Coulomb attraction,
when separated by distance
s. Oppositely charged small polarons only recombine once they are close enough to one another to overlap significantly. Small polarons move toward recombination via a series of phonon-assisted hops. The rate for each phonon-assisted jump increases as the energy of its final state falls increasingly below that of its initial state except when this energy disparity is exceptionally large [
1,
22,
23,
24]. Thus, the recombination of well-separated oppositely charged small polarons tends to occur via a series of jumps in which each hop is progressively faster. The rate-limiting jump is the initial hop of this series, a jump with minimal energy disparity. The recombination rate of oppositely charged small polarons therefore is determined by the hop between sites of nearly equal energy.
A phonon-assisted hop occurs when an electronic carrier transfers between sites in response to atoms assuming favorable configurations [
1]. A hop is termed non-adiabatic when the inter-site transfer energy of the electronic charge carrier is so small that it rarely avails itself of the opportunity to move [
18,
19]. Alternatively, adiabatic hopping occurs when the electronic carriers are able to adjust to changing atomic configurations. Small-polaron hopping is generally adiabatic [
1]. Nonetheless, phonon-assisted jump rates are usually computed for the non-adiabatic limit, where they are perturbative to lowest-order in the hop’s electronic transfer-energy.
The non-adiabatic small-polaron jump rate has been calculated exactly for the Holstein Molecular-Crystal-Model (MCM), where the electronic carrier is assumed to interact with a single vibrational mode of frequency
, only [
23]. To enable small-polaron formation in this idealized model, its small-polaron binding energy
is taken to exceed both the phonon energy
and the inter-site electronic transfer energy
J. An approximate formula for the adiabatic small-polaron jump rate is obtained at all but very low temperatures when dividing this non-adiabatic rate by the high-temperature probability of the electronic carrier transferring in response to an appropriate atomic configuration [
1,
19]. In particular, the approximate formula for the adiabatic rate for a hop between equivalent sites is found by dividing the right-hand-side of Equation (59) of Ref. [
23] by
:
where
denotes the zeroth-order modified Bessel function. At high and intermediate temperatures relative to
, this expression becomes
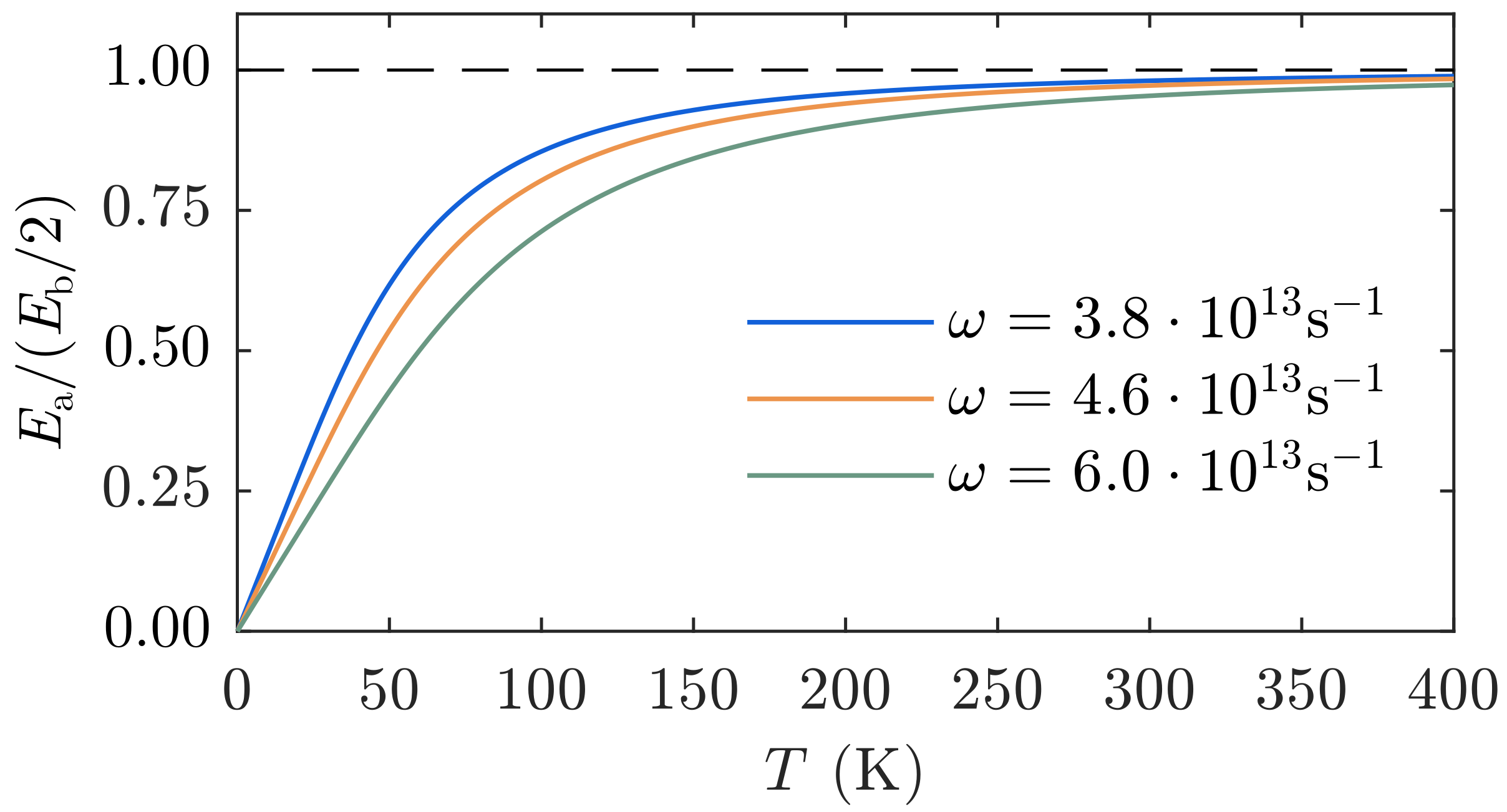
Distinctively, the Arrhenius behavior with activation energy
progressively disappears as
is lowered relative to
. In other words, as shown in
Figure 3, the activation energy progressively shrinks from
as the temperature is reduced.
Beyond the simple MCM, a small-polaron’s phonon-assisted hop is primarily associated with movements of the atoms in the immediate vicinity of its self-trapped electronic carrier [
1]. As such, a small-polaron hop generally involves interactions with short-wavelength phonons from both acoustic and optic vibration modes. The activation energy for an Arrhenius small-polaron jump is the sum of contributions from these modes. The pre-exponential factor of the adiabatic jump rate of Equation (
2) is then the square-root of the sum of the squares of these zone edge phonons weighted by their relative contributions to the jump’s activation energy [
19].
5. Combining the Decay of Lithium Niobate’s Induced Absorption with Small-Polaron Recombination
We ascribe the observed photo-induced absorption mainly to photo-generated Nb
n-type free small polarons. The decay of this photo-induced absorption is attributed to their recombination with p-type small polarons that are bound to lithium vacancies, O
−V
. This attribution is supported by evidence of only negligible Fe and Nb
contamination in these crystals [
17]. Indeed, room-temperature transient absorption measurements on a series of Mg-doped and nominally pure LN samples by Conradi et al. [
26] also concluded that the primary signal at 785 nm stems from Nb
free small polarons. Furthermore, subsequent work only found a secondary relatively weak and slow decay that most likely results from the recombination of self-trapped excitons pinned at various defects [
29,
31]. As shown in
Figure 1, a single KWW function provides a satisfactory fit to our low-temperature data.
Distinctively, we measure the decay of the photo-induced absorption in Mg:LN over a wide temperature range. As a result, we observe the shift from Arrhenius behavior at highest temperatures to a relatively weak temperature-dependence at lowest temperatures. This fundamental feature of small-polarons’ hopping is sensitive to the phonon energies with which their self-trapped electrons interact [
1,
22,
23,
24]. As shown in
Figure 2, the mean decay time of the photo-induced absorption is well fitted by our model for small-polaron recombination. Best fit’s are obtained for
eV and
s
. Both of these values are typical of small-polaron hopping.
6. Discussion
Polarons are generally characterized by broad asymmetric absorption bands. These absorptions arise from exciting polarons’ self-trapped electronic carriers from the potential wells that bind them [
1,
34]. As shown in Figures 5 and 6 of Ref. [
34], small-polaron absorption bands tend to be higher on the low-frequency side of their peaks. By contrast, large-polaron absorptions tend to be higher on the high-frequency side of their peaks [
34]. This distinction can be used to differentiate between small-polaron and large-polaron absorption bands. As illustrated in Figure 7 of Ref. [
23], the peak of the small-polaron absorption in the MCM occurs at
, twice the small-polaron binding energy. This figure shows that the absorption becomes broader and less symmetric with increasing temperature. An early calculation of a small-polaron absorption band [
35] did not adequately describe its width and inherent asymmetry.
In the non-adiabatic limit of the MCM, the activation energy for Arrhenius small-polaron hopping
is simply half the small-polaron binding energy
. However, the MCM only envisions a short-range component of the electron–phonon interaction. As noted in this paper’s introduction, LN is an ionic material with a significant long-range component of its electron–phonon interaction. As the long-range component of the electron–phonon interaction increases,
decreases as a fraction of the small-polaron binding energy [
1]. Furthermore, the small-polaron hopping activation energy decreases upon progressing from the non-adiabatic limit into the adiabatic regime [
1,
18]. Thus, a small-polaron’s binding energy
will tend to be somewhat larger than twice the activation energy of its high-temperature Arrhenius hopping
.
A polaron becomes small when its self-trapped electronic carrier collapses to a single site, e.g., a single Nb cation in LN. Its self-trapped electronic carrier then hops between adjacent sites by primarily interacting with short-wavelength phonons. The characteristic phonon frequency for small-polaron hopping will then be comparable to those of these short-wavelength modes. In LN these modes have wavenumbers of about 250 cm
[
36,
37,
38,
39]. The inverse of the frequencies of these modes also corresponds to the time determined for atoms to shift their equilibrium positions in response to the addition of a severely localized electronic charge carrier [
40,
41]. Thus, the frequencies of these short-wavelength phonons are comparable to what we measure to be the characteristic phonon frequency associated with n-type small-polaron hopping in LN,
s
.
7. Summary
In summary, we measured the temporal decay of the photo-induced absorption of Mg:LN from 45 K to 225 K. The time dependencies of decays of the induced absorption at 785 nm fit well with the phenomenological Kohlrausch–Williams–Watts (KWW) stretched-exponentials, . The effective decay rate, the inverse of the mean decay time of each KWW curve, a function of and , is a function of temperature. At the highest temperatures, the decay rate for the photo-induced absorption manifests an Arrhenius temperature dependence. This temperature dependence weakens and becomes non-Arrhenius as the temperature is lowered.
These decays are ascribed to the hopping of Nb n-type small polarons leading to their eventual recombination with O p-type small polarons bound to Li vacancies. The n-type and p-type small polarons are attracted to one another by their mutual Coulomb attraction reduced by the static dielectric constant of LN. We model this hopping sequence as a series of jumps that are increasingly downward in energy. The rate-limiting step in this sequence of small-polaron hops, its slowest jump, is then its first step since its energy disparity is smallest. We take the energy disparity of well-separated oppositely charged small polarons to be minimal. As such, we compare the adiabatic jump rate of small polarons between sites of equal energy with the inverse of the mean decay time for KWW decays.
The rate for adiabatic small-polaron hops between equivalent sites is Arrhenius at high temperatures. As the temperature is reduced the temperature dependence of this adiabatic small-polaron jump rate weakens as it becomes non-Arrhenius [
1,
22,
23,
24]. The transition between these two behaviors occurs at the temperature corresponding to a significant fraction of that characterizing the principal phonons with which a small-polaron’s self-trapped electronic carrier interacts. This feature yields a more precise value for the characteristic phonon frequency than can be obtained from only fitting data from the high-temperature Arrhenius region. Fitting the decay rate of photo-induced decay in Mg:LN to the adiabatic small-polaron jump rate between equivalent states yields reasonable values of the small-polaron binding energy and the characteristic frequency of the phonons with which its self-trapped electron interacts:
eV and
s
.