Abstract
In the paper, a phononic crystal plate composed of a magnetorheological elastomer with adjustable band gaps in the low frequency range is constructed. The dispersion relations of Lamb waves are studied by the supercell plane wave expansion method. The transmission responses as well as the displacement fields of Lamb waves are calculated by the finite element method. The influence of geometric parameters on the band gaps, the regulation effect of the volume ratio of Fe particles and the bias magnetic field on the band gaps are analyzed. Based on the numerical results, we find that the volume ratio of Fe particles and the magnetic field affect the band gap effectively. The location and width of the band gaps can be adjusted within a broad frequency range by varying the geometric parameters and magnetic field. We can control the band gap, achieve an appropriate and wide low band gap by selecting proper geometric parameters and applying an external contactless magnetic field to deal with complicated and changeable engineering environment. The results are useful for understanding and optimizing the design of composite vibration isolation plates.
1. Introduction
Plates are extensively used as the containment structures in many areas such as transport, aerospace engineering, marine and civil engineering [1,2]. As the direct bearing and disseminator of vibration in engineering, the vibration control of plates will directly affect the precision of the instrument and equipment, normal operation of instrument and the durability of the building. However, there are few measures to control the vibration of plates in practical engineering. Reducing the impact of vibration is a hot topic in current scientific research. The appearance of phononic crystals (PCs) provides a new idea for vibration reduction. PCs, as a kind of periodic artificial structure, has been widely studied with regard to the unique frequency characteristics called the phononic band gap, in which the elastic/acoustic waves cannot propagate [3,4,5,6]. The amazing feature of the band gap is valuable for noise control, elastic/acoustic filters, vibration shield and acoustic wave guides [7,8,9].
Unlike the infinite PC for bulk wave, the Lamb wave [10,11,12,13] in the PC plate is taken to be a finite size system in one direction. It has attracted increased attention due to the coupling of the longitudinal and the transversal waves, which makes the elastic wave propagation in a plate more complicated. Chen and Han [14] investigated the band structures of Lamb waves in one-dimensional PC plates. From numerical results, they concluded that when a thin PC plate is bordered with the silicon loading layers, both the midgap frequencies of the first band gaps of S0 and A0 modes change approximately linearly with the thickness of the silicon loading layers. Later, they [15,16] discussed the propagation properties of Lamb waves in different configurations of the plate and found that the band gaps can be effectively shifted by changing the geometrical parameters of the plate. Zhu et al. [17] analyzed different transmission modes in a 1D piezoelectric PC plate, in which one important piezoelectric-sensitive mode was defined and revealed. Wang et al. [18] presented an experimental Lamb wave propagation in coupled-resonator elastic waveguides formed by a chain of cavities in a two-dimensional PC plate with cross holes, and observed the transmission of strongly confined Lamb waves along a straight waveguide and in a wave splitter circuit. This research provides a solid foundation for people to understand the band gap characteristic of Lamb waves in PC plates. However, the studies of Lamb waves for vibration control in low frequencies need to be further studied.
The band structure of PCs depends on the physical and geometrical properties of the unit cell. Once the physical and geometric parameters are confirmed, most traditional PCs manipulate at fixed frequency ranges, which inevitably limit their applications in practical engineering. To deal with a complex and changeable engineering environment, the study of tunable band gaps in PCs has turned into a research focus in recent years. The rise of intelligent materials gives new ideas to tune band gaps. A significant effort has been made to design intelligent PCs whose band gap can be tuned by adjusting the geometry or physical parameters of constituent materials through external stimuli [19,20,21,22]. A magnetorheological elastomer (MRE) is one of these smart materials [23,24,25]. Generally, MREs consist of an elastomeric matrix interspersed with micron sized ferromagnetic particles and hence combine the functionality of a highly elastic polymer matrix with the magnetic field-responsive properties. As a multiphase composite intelligent material, MRE has the giant deformational effects, high elasticity, and quick response to magnetic fields. The mechanical properties of MRE (such as Young’s modulus) can be adjusted reversibly by magnetic fields. Due to them having the advantages of an adjustable rigidity, strong reversibility, rapid response and excellent mechanical properties [26,27,28], MREs present huge potential applications in civil engineering, automobiles and aviation. Recently, MRE has been introduced into PCs. Xu et al. [29] analyzed shear-wave band gaps tuned in two-dimensional PCs with magnetorheological material, they concluded that S-wave band gaps can be obtained and tuned as frequency-selective filters by the application of an external contactless magnetic field. Later, they [30] investigated the MRE vibration isolation of tunable three-dimensional locally resonant acoustic metamaterials. The MRE was used as cladding. It was found that, when applying an external magnetic field to the structure, the central position and width of the elastic band gap can be modulated. Wen et al. [31] designed a two-dimensional PC isolator based on MREs. They reported that in a definite magnetic field, the position of the band gap moves up while the width is basically unchanged by an increasing volume fraction of iron particles. Liu et al. [32] proposed two types of acoustic metamaterials with MREs by the finite element method. It was found that the frequency and width of band gap, the maximum attenuation frequency and transmission loss of transmission spectrum increase with the increase in the externally applied magnetic field intensity. From the above literature, it can be seen that the studies on the propagation of elastic waves in the MRE PCs plate are few—the application of MREs to PCs needs to be further studied.
To promote the application of PC plates in engineering and satisfy the needs of vibration control in complex engineering environments, the acquisition of tunable band gaps with large bandwidths in the low frequency range is of great importance. Herein, a PC plate constituted of MRE, steel, concrete and rubber is proposed. The regulation effect of the bias magnetic field on the band gap characteristics is analyzed. The band structures and propagation properties of Lamb wave are calculated by the supercell plane wave expansion method and validated by the finite element method. The proposed composite plate with a certain extent of strength can bear load, furthermore, its vibration isolation frequency can be adjusted by applying an external contactless magnetic field. The investigation of this paper offers a good reference for the design of tunable band gaps in PC plates.
2. Formulation of the Problem
In this paper, a PC plate is constructed by periodically embed steel (material C) to increase the intensity of the periodic structure as shown in Figure 1. In order to obtain a higher bearing capacity, material A is assumed as concrete, material B is MRE, and material D is rubber. The lattice constant a = a1 + a2 + a3, and the filling ratio of each part is defined as f1 = a1/a, f2 = a2/a, f3 = a3/a. The thickness of the steel is h2, and the upper and lower layer of the MRE are h1 and h3, respectively. The total thickness of a unit cell is h = h1 + h2 + h3. z = h is the upper free boundary of the plate, while z = 0 is the lower free boundary of the plate. The Lamb wave propagates along the x-direction, and all field components are assumed to be independent of the y-direction.
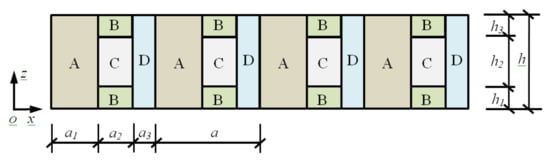
Figure 1.
A phononic crystal plate.
The band structures of the Lamb wave in the PC plate are computed by the supercell plane wave expansion method, which has been proven to be an efficient method [14,15]. Two vacuum layers with a thickness tv (tv = a/2) are added on the upper and lower surfaces of the plate to form the supercell as shown in Figure 2. These two alternate vacuum layers are used for designing the imaginary periodic system, which can resolve Lamb wave modes in 1D PC plates, and the stress-free boundary condition of Lamb waves is satisfied.
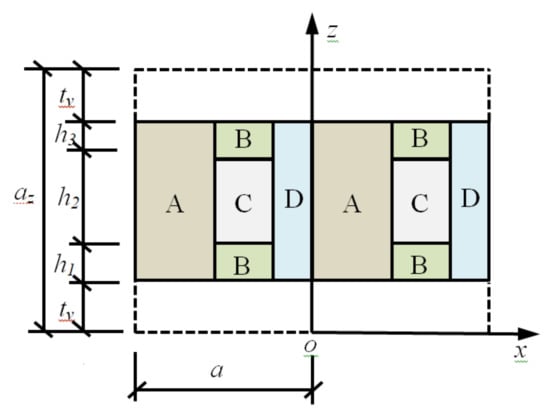
Figure 2.
Supercell structure.
The wave equation of the xz mode can be expressed as follows
where is the density, u is displacement,, and are the elastic constants.
Due to the spatial periodicity, the material constants (, , , and ) can be expanded in the Fourier series as follows
where are the 2D reciprocal lattice vectors. Furthermore, the Fourier expansion coefficients in Equation (3) can be expressed as
where is the area of supercell, and the integral area is the whole supercell.
Utilizing the Bloch theorem and expanding the displacement vector in Fourier series, one obtains
where is the reduced wave vector in the x direction, is circular frequency and . Substituting Equations (3) and (5) into (1) and (2), Equations (1) and (2) can be simplified as
where , and are reciprocal vectors with the relation , and are
Because of the periodicity and symmetry, sweeping the wave vector in the first Brillouin zone, we can obtain the dispersion relation of the total structure.
The MRE is composed of Fe particles dispersed in silicone rubber with a volume ratio . The Fe particle density is , and the density of silicone rubber is . They have the relationship
where is the density of the MRE.
The tensile and shear properties of MREs are similar, and the Poisson’s ratio is 0.47 [33]. The shear modulus of MREs is calculated by the magnetic dipole model [34,35]. The relationship between the change of shear modulus and the external magnetic field is
where is the volume ratio of Fe, is the relative permeability of silicone rubber, is the permeability of the vacuum, H is external magnetic field strength, R is the radius of Fe particles, and d is the distance between two adjacent particles. In this paper, we assume: d/R=2.5, , , where is the relative permeability of Fe particles.
Under the action of an external magnetic field, the shear modulus of the MRE is
where is the shear modulus of the MRE without a magnetic field, and is the shear modulus of silicone rubber.
Figure 3 shows that the external magnetic field can effectively control the shear modulus of the MRE. The change of the shear modulus is increased with the volume ratio of Fe particles and magnetic field. We can use this change to adjust the band gap of Lamb waves in the composite plate.
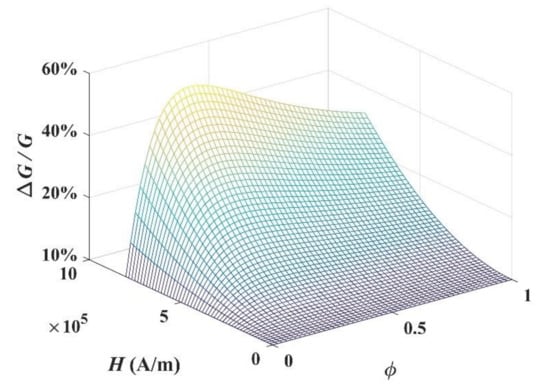
Figure 3.
Effect of volume ratio of Fe particles and magnetic field on shear modulus of magnetorheological elastomers (MREs).
3. Numerical Results
In order to illustrate the accuracy of the results, we compared the result that calculated in this study with Ref. [15] by the supercell plane wave expansion method. The computational model which consists of embedded elastic square cylinders (vacuum) and a matrix material (tungsten), the material parameters and geometric parameters are the same as Ref. [15]. Figure 4 shows the results obtained by two papers. The solid line represents the calculation results of this paper, and the circle represents the calculation results of Ref. [15]. The shade area between the black lines represents the band gap, which is from 1.372 to 1.745 MHz between the third and the fourth transmission band. It is quite clear that the two calculation results are in good agreement, which testifies the derivation and program used in this study are valid.
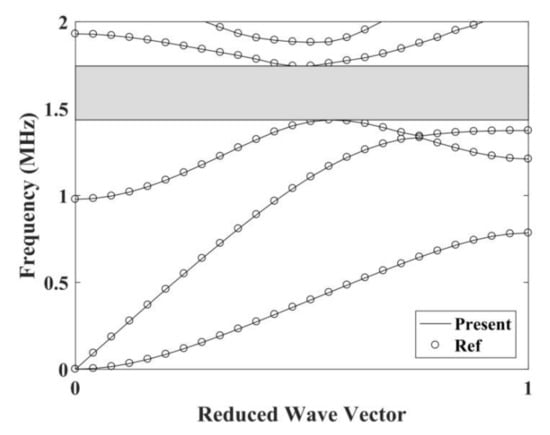
Figure 4.
Dispersion curve.
Unless stated otherwise, we assume that the material and geometric parameters of the periodic composite plate are as shown in Table 1 and Table 2.

Table 1.
Material parameters of the plate.

Table 2.
Geometric parameters of the plate.
3.1. Influence of Geometric Parameters on Band Gaps
The dispersion curve of the Lamb wave strongly depends on the characteristics of materials and the geometry of the periodic PC structure. When the periodic structure is designed reasonably, the appropriate band gap can be generated to prevent the wave propagation. First, we give the dispersion curve when the periodic composite plate is simply composed of steel and concrete as shown in Figure 5a, where a = 300 mm, f1 = 0.375, f2 = 0.625, i.e., a1: a2 = 3:5, as same as the next calculation. The yellow shade area between the black lines represents the band gap, which is from 4128.27 to 9571.44 Hz. The lower boundary of the band gap is higher than 4000 Hz, despite the width of the band gap being wider than 5000 Hz, however, the band gap of this PC plate is too high to satisfy the requirement of a low frequency in engineering. Therefore, we append rubber and MRE into the plate to obtain a low frequency of the band gap and try to control the band gap for an effective reduction vibration.
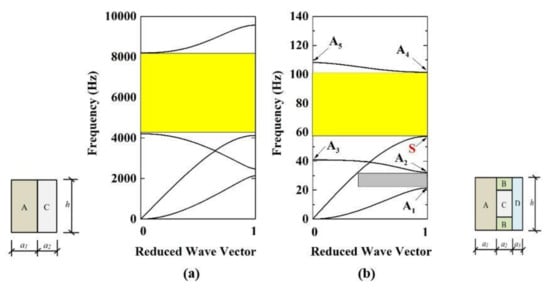
Figure 5.
Dispersion curve. (a) The two-element PC plate; (b) The proposed PC plate.
Figure 5b shows the dispersion curve of the designed PC plate. The geometric parameters are shown in the above table. It is easy to find that there are two band gaps in the figure: the gray shade area and yellow shade area. The gray shade area (from 22.1 to 36.1 Hz) is a partial band gap, it prohibited some modes of Lamb wave propagation, the detail of which we will discuss in the following. The yellow shade area (from 57.21 to 101.41 Hz) is a complete band gap, it prohibited any modes of Lamb wave propagation. Comparing Figure 5a,b, it is noticed that the upper and lower boundary of the complete band gap are significantly shifted to lower frequencies. Although the width of the complete band gap in Figure 5b is only about 44.2 Hz, much smaller than that in Figure 5a, the low frequency of this band gap satisfies the requirement of vibration isolation in engineering. Therefore, the propositional PC plate is very meaningful to practical engineering for vibration suppression in a low frequency range.
The band gap of Lamb waves strongly depends on the characteristics of the geometry of the periodic structure. The influences of the filling rate on band gaps are shown in Figure 6, Figure 7 and Figure 8. The filling ratio of the plate can be divided into three cases. The first case is that f2:f3 = 5:2 remains unchanged, we consider the influence of f1 = a1/a on the band gap; the second case is that f1:f3 = 3:2, we discuss the influence of f2 = a2/a on the band gap; the third case is that f1:f2 = 3:5, we give the influence of f3 = a3/a on the band gap. It can be seen from Figure 6 that with the increase in the filling rate f1 for the concrete layer, the upper and lower boundary of the band gaps gradually increase, and the width of the band gap increases by 109%, from 41.6 to 87.12 Hz. However, the lower and upper boundary of the band gap reach up to 97.96 and 185.08 Hz when f1 = 0.7. This band gap is a little higher to isolate low frequency vibrations. Therefore, we chose f1 = 0.3 as the next calculation.
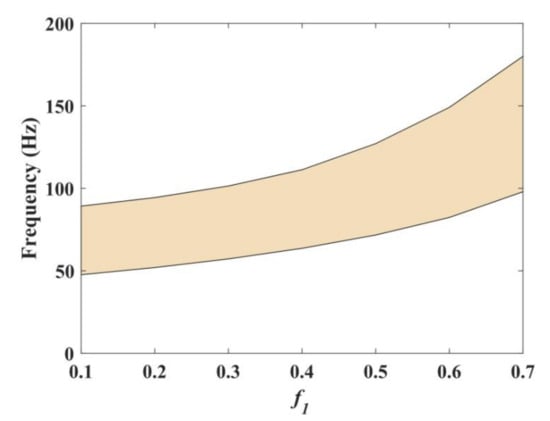
Figure 6.
The influence of f1 on the band gap.
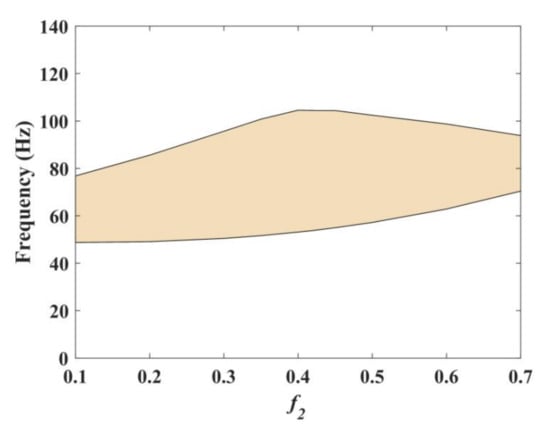
Figure 7.
The influence of f2 on the band gap.
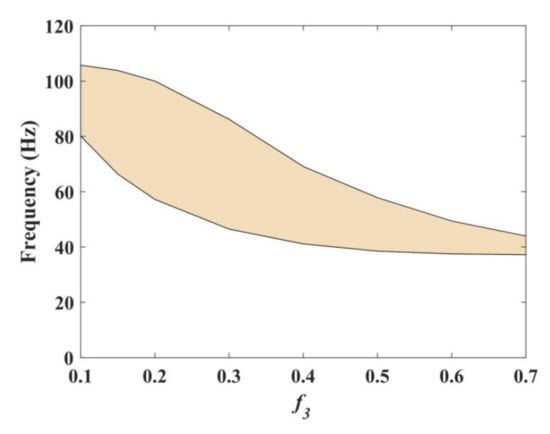
Figure 8.
The influence of f3 on the band gap.
The middle part of unit cell consists of an MRE and steel. The influence of the filling rate f2 on band gaps is given as Figure 7. From Figure 7, we can find that the lower boundary of the band gap gradually increased, while the upper boundary of the band gap was not a monotone increase, it increased at first and then decreased, and the maximum band gap occurred at f2 = 0.4. Additionally, the width of the band gap was not a monotone increase—it varied with the upper boundary. When f2 = 0.4, the maximum width was reached at 51.43 Hz. Compared to the band gap width at f2 = 0.7, the width of the band gap increased by 219%. This change is very meaningful to obtain broadband gaps, and furthermore, increasing the size of the steel section can improve the bearing capacity of plate. Considering the effect of the MRE, we chose f2 = 0.5 as the calculation.
As shown in Figure 8, with the increase in the filling rate f3 for the rubber layer, the upper and lower boundaries of the band gap all decrease. However, the width of the band gap increased before f3 = 0.2, and then decreased. The effect of rubber is the reduction in the frequency of band gap and it acting as a local resonance of steel. Therefore, if one wants to obtain a low and broadband gap, regulating f3 is an effective approach.
Let f1: f2: f3 = 3:5:2 and the total height h = 200 mm. When we consider the change of h1 for the MRE, the h2 of the steel remained unchanged. The influence of h1 on the band gap is obtained in Figure 9. We can find that the change of the band gap width is not a monotone increase. When the height of the MRE h1 = 75 mm, the width of the band gap was the largest, up to 44.2 Hz; when h1 = 150 mm, namely, the steel was at the top of the middle unit cell, MRE was at the bottom, and the width decreased to 29.83 Hz. On the other hand, when h1 = 0 mm, MRE was only at the top, steel was at the bottom, and the band gap structure was the same as h1 = 150 mm. That is to say, in order to obtain a wide band gap, it is better to cover the MRE on the two sides of the steel. Then, we consider the change of h2, and the h1, h3 synchronous change, i.e., h1 = h3 at this point. From Figure 10, it can be seen that with the increase in h2, the lower boundary remained unchanged, but the upper boundary and the width of the band gap increased gradually. The steel in the composite plate increased both the strength and the band gap—this phenomenon is very beneficial to the composite PC plate.
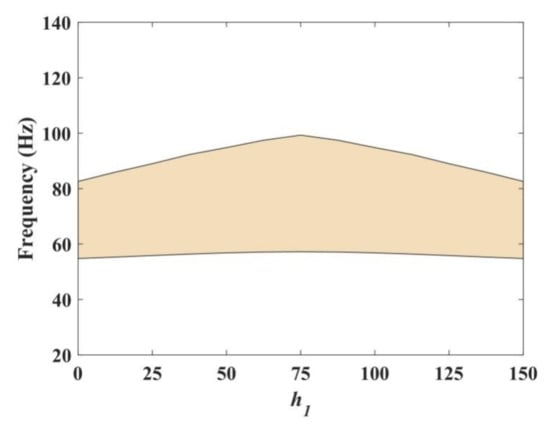
Figure 9.
The influence of h1 on the band gap.
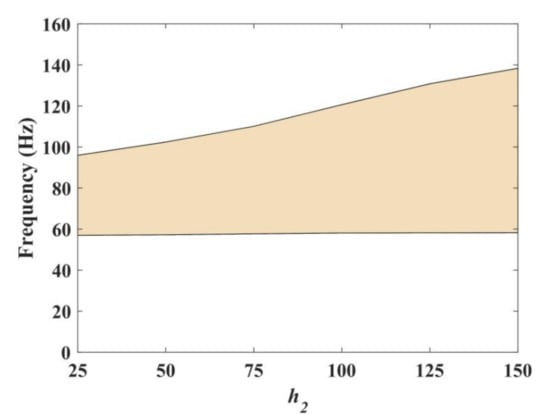
Figure 10.
The influence of h2 on the band gap.
The total height h of the unit cell is another important parameter of the composite plates. It can be seen from Figure 11 that the frequencies of band gaps change from 52.47–124.57 to 59.92–81.01 Hz with the increase in h, and the width of band gap decreased from 72.1 to 21.09 Hz. That is to say, thin plates are more likely to generate wide band gaps.
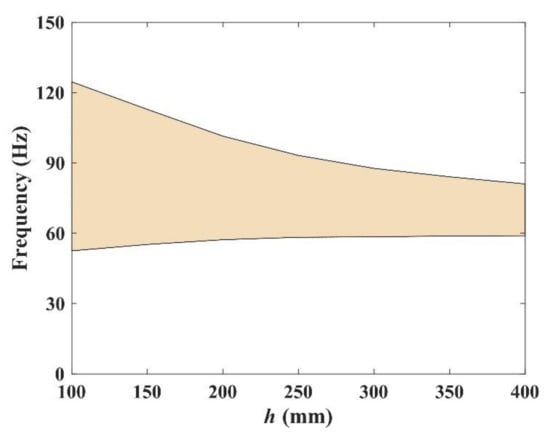
Figure 11.
The influence of h on the band gap.
The influence of lattice constant a on the band gap is plotted in Figure 12. The figure shows that the upper and lower boundary of the band gap are all decreased with the increase in a; the reason for this phenomenon is Bragg scattering [3]. We also found that the widths of the band gaps basically remain the same regardless of whether a = 200 mm or a = 500 mm. Hence, if a low frequency vibration isolation is required, appropriately increasing a is an option.
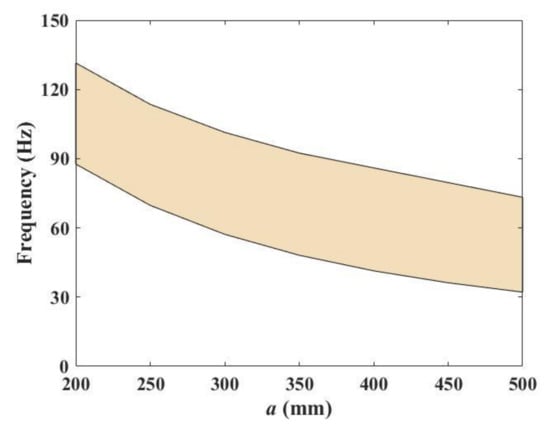
Figure 12.
The influence of a on the band gap.
3.2. Influence of Magnetic Field on Band Gaps
The MRE was composed of Fe particles with a volume ratio , so, the volume ratio may affect the band gap of the Lamb wave. Next, we discuss the influence of the volume ratio on the band gap. From Figure 13, it can be found that with the increase in the volume ratio, the lower and upper boundary of the band gap gradually increased. However, the upper boundary of the band gap increased faster than the lower boundary, so the width of the band gap increased with the upper boundary, which extends from 40.84 to 64.23 Hz—about a 57% increase. This result indicates that the MRE had a significant effect on the band gap. We can use MREs to regulate the band gap without changing the structure and obtain an appropriate band gap for vibration isolation.
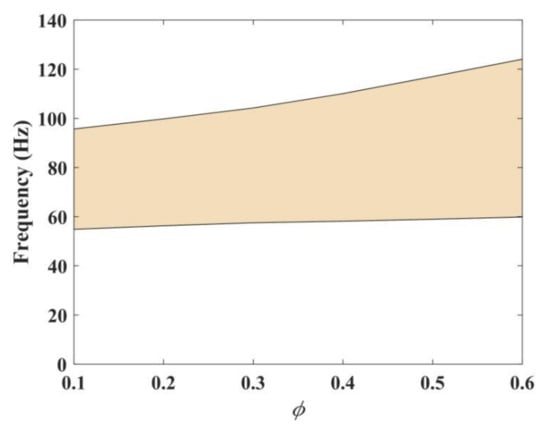
Figure 13.
The effect of the volume ratio of Fe particles on the band gap.
Figure 14 presents the effect of the magnetic field intensity H on the band gap. It can be seen that with the increase in magnetic field intensity, the lower boundary of the band gap increased a little, while the upper boundary increased more obviously. When H increased from 0 A/m to A/m, the upper boundary of the band gap increased from 101.41 to 120.81 Hz, the lower boundary only increased by 3.45 Hz, from 57.21 to 60.66 Hz. The total width increased by 36%, from 44.2 to 60.15 Hz. Therefore, we can conclude that the magnetic field plays a significant role in regulating the band gap of composite plates.
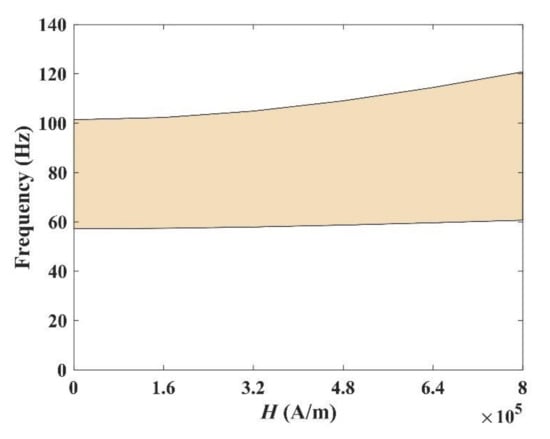
Figure 14.
The influence of magnetic field intensity H on the band gap.
3.3. Influence of Period Number n and Magnetic Field Intensity H on Attenuation Properties
In order to verify the correctness of the previous calculation and the analysis, we calculated the attenuation properties and transmission response curves of Lamb wave by finite element method (FEM). In view of the fact that there is no infinite periodic structure in actual engineering, we used a finite period in the calculation. In fact, like the experimental method used to obtain the transmission energy loss, the calculation results by FEM can be used as an important reference for the application of periodic composite plates in practical engineering and can partly replace experiments. We use COMSOL Multiphysics to solve the current work. The computational transmission FEM model is shown in Figure 15, in which the unit cell is the same as Figure 1. The excitor is on the left side, and the receiver is on the right side. The length of the PC plate was assumed as S, matrix as L, and L = S/2. The external boundaries were surrounded with perfect match layers (PMLs) which simulate the infinite region by suppressing any reflection. The effect of viscoelastic properties on the attenuation is not considered in the paper for it has little effect on the low frequency [36].
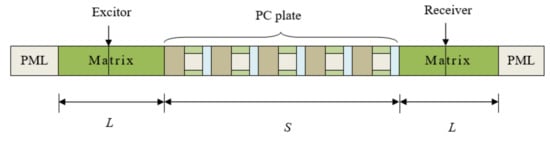
Figure 15.
The transmission finite element method (FEM) model.
Figure 16 shows the transmission response curves of the Lamb wave when the period number n was 3, 5 and 7, respectively. From Figure 16, it can be seen that there was an obvious attenuation domain, from 58.1 to 102.3 Hz, which is in good agreement with the band gap (yellow shade area) in Figure 5b. In addition, we can find that the attenuation coefficient and amplitude apparently increase as the periods increase, the attenuation with period numbers n = 3, 5 and 7 were measured to be greater than −171, −263 and −366 dB, respectively, which indicates that vibration decays quickly when period number increases. This result also means that the proposed PC plate can isolate Lamb waves effectively when the number of the unit cell is more than three. When the lattice constant a = 300 mm, the lengths of 3~5 cycles are 0.9 m~1.5 m. It is feasible to apply a uniform magnetic field to the plate within two meters in engineering. Therefore, we can use this composite PC plate with tunable band gaps in the place where it is needed to deal with a variable low frequency engineering environment.
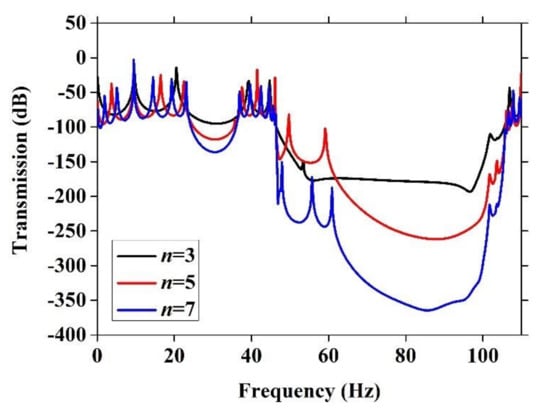
Figure 16.
The transmission response curves with different period number n.
Besides the attenuation domain corresponding to this complete band gap, a lower frequency attenuation domain with the range 23.1–36.1 Hz appears; this band gap corresponds to the partial band gap (gray shade area) in Figure 5b. The reason for this phenomenon is that the Lamb wave has multimode characteristics. When an excitation is applied to the periodic composite plate, at least two Lamb wave modes, symmetric and antisymmetric, will be generated. To better understand this phenomenon, we give the band edge modes of points A1–A5 and S in Figure 17a–f (corresponding to the points in Figure 5b). From Figure 17, it can be found that the modes A1–A5 are antisymmetric Lamb waves, and modes S represents the symmetric Lamb waves. In the attenuation domain of 23.1–36.1 Hz, only the symmetrical Lamb wave modes can pass, while the antisymmetric Lamb wave modes are prohibited.
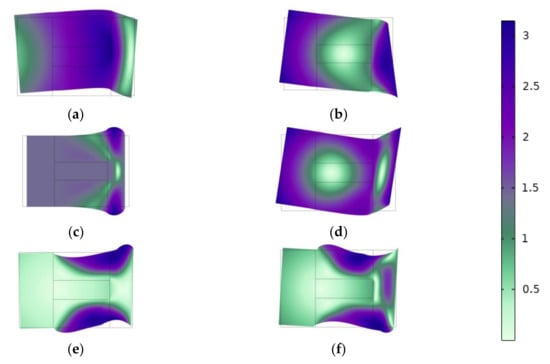
Figure 17.
Band edge modes of points A1-A5 and S, (a) Mode A1, (b) Mode A2, (c) Mode S, (d) Mode A3, (e) Mode A4, (f) Mode A5.
In order to further study the regulating effect of magnetic fields on the band gap, we calculated the transmission response curves with the period number n = 5 when the magnetic field intensity H = 0 A/m A/m, respectively. The results are shown in Figure 18. It can be seen that when the magnetic field intensity H changed from 0 A/m to A/m, the lower and upper boundary of the band gap increased simultaneously. The lower boundary changes were small, from 58.1 to 62.1 Hz, while the upper boundary increase was very remarkable, from 101.7 to 126.8 Hz. These results are in good agreement with Figure 14. In addition, we can find that with the increase in magnetic field intensity H, the maximum attenuation amplitudes reached −263 and −281 dB, respectively. This result means that the effect of the period number on the attenuation has a greater effect than the magnetic field intensity.
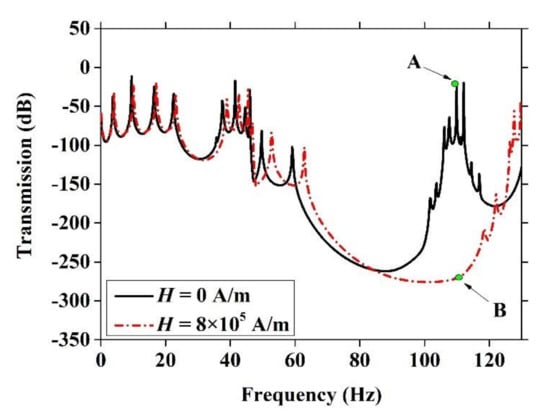
Figure 18.
The transmission response curves with different magnetic field intensity H.
There are two points: A and B in Figure 18 when the frequency was 108.1 Hz. We show their displacement fields in Figure 19. Point A represents the displacement field in the pass band, and point B represents the displacement field in the band gap. From Figure 19a, when the frequency falls outside the band gap, as shown in Figure 19a, the Lamb wave can propagate without any obvious attenuation. However, when the frequency fell within the band gap, as shown in Figure 19b, the Lamb wave decayed rapidly, and its energy seemed to be locked by the plate. This result shows that the designed PC plate has a good vibration isolation effect.
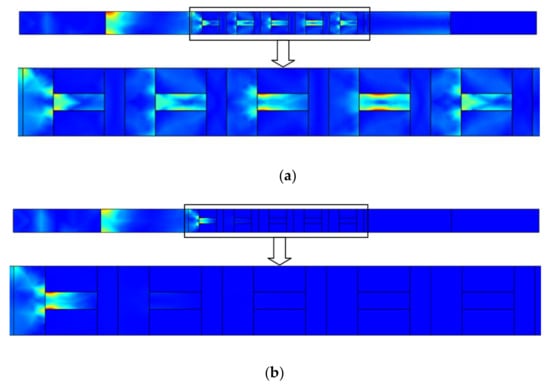
Figure 19.
A and B displacement field, (a) point A, (b) point B.
4. Conclusions
In this paper, we have investigated the propagation of Lamb waves in a PC plate composed of an MRE, concrete, rubber and steel. The dispersion relation of Lamb wave was obtained by the supercell plane wave expansion method. The transmission responses and the displacement fields of the eigenmodes for Lamb wave were calculated by the finite element method. Numerical results are presented to illustrate the band structures and wave propagation characteristics of the periodic composite plate.
Based on the numerical results, we can find that the volume ratio of Fe particles, filling rate, height, lattice constant and period number of the PC plate have a significant effect on the band gap. The band gap of Lamb wave can be effectively modulated by applying a magnetic field. MREs play a significant role in the regulation of the band gap. Moreover, the attenuation frequency ranges of the transmission responses and the band structures show good agreement. The proposed PC plate is demonstrated to possess a large band gap in the low frequency range, resulting in a low frequency broadband Lamb wave attenuation and vibration suppression. The study opens new possibilities to broaden band gaps of PC plate at lower frequency, and the results can provide a theoretical basis for reducing the vibration of composite plates.
Author Contributions
Conceptualization, P.Z. and L.Y.; methodology, P.Z. and L.Y.; software, P.Z.; validation, L.Y. and Y.D.; formal analysis, J.D.; investigation, T.M.; resources, L.Y. and B.D.; data curation, P.Z.; writing—original draft preparation, L.Y.; writing—review and editing, P.Z. and L.Y.; visualization, Y.D.; supervision, J.W.; project administration, L.Y.; funding acquisition, L.Y. and Y.D.; All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by [Natural Science Foundation of Ningbo City] grant number [202002N3118], [Natural Science Foundation of Zhejiang Province] grant number [LY19A020003, LY19E080009 and LGG19A020001], [National Natural Science Foundation of China] grant number [11772163] And the K. C. Wong Magana Fund was funded by Ningbo University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sun, Y.-J.; Yu, Y.-J.; Zuo, Y.-Y.; Qiu, L.-L.; Dong, M.-M.; Ye, J.-T.; Yang, J. Band gap and experimental study in phononic crystals with super-cell structure. Results Phys. 2019, 13, 102200. [Google Scholar] [CrossRef]
- Lu, K.; Zhou, G.-J.; Gao, N.-S.; Li, L.-Z.; Lei, H.-X.; Yu, M.-R. Flexural vibration bandgaps of the multiple local resonance elastic metamaterial plates with irregular resonators. Appl. Acoust. 2020, 159, 107115. [Google Scholar] [CrossRef]
- Kushwaha, M.-S.; Halevi, P.; Dobrzynsi, L. Acoustic band structure of periodic elastic composites. Phys. Rev. Lett. 1993, 71, 2022–2025. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.-Y.; Zhang, X.; Mao, Y. Locally resonant sonic materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef] [PubMed]
- Guo, T.; Yang, X.-W.; Geng, Q.; Li, Z.; Li, Y.-M.; Wang, X.; Zhang, H. Anisotropic phononic crystal structure with low-frequency bandgap and heat flux manipulation. Sci. China Phys. Mech. Astron. 2020, 63, 224711. [Google Scholar] [CrossRef]
- Graczykowski, B.; EI Sachat, A.; Reparaz, J.-S.; Sledzinska, M.; Wagner, M.-R.; Chavez-Angel, E.; Wu, Y.; Volz, S.; Wu, Y.; Alzina, F.; et al. Thermal conductivity and air-mediated losses in periodic porous silicon membranes at high temperatures. Nat. Commun. 2017, 8, 415. [Google Scholar] [CrossRef]
- An, X.-Y.; Fan, H.-L.; Zhang, C.-Z. Elastic wave and vibration bandgaps in two-dimensional acoustic metamaterials with resonators and disorders. Wave Motion 2018, 80, 69–81. [Google Scholar] [CrossRef]
- Oudich, M.; Yong, L.; Assouar, B.-M. A sonic band gap based on the locally resonant phononic plates with stubs. New J. Phys. 2010, 12, 1–10. [Google Scholar] [CrossRef]
- Sukhovich, A.; Merheb, B.; Muralidharan, K.; Vasseur, J.-O.; Pennec, Y.; Deymier, P.-A.; Page, J.-H. Experimental and theoretical evidence for subwavelength imaging in phononic crystals. Phys. Rev. Lett. 2019, 102, 154301. [Google Scholar] [CrossRef]
- Hou, Z.-L.; Assouar, B.-M. Modeling of Lamb wave propagation in plate with two-dimensional phononic crystal layer coated on uniform substrate using plane-wave-expansion method. Phys. Lett. A 2008, 372, 2091–2097. [Google Scholar] [CrossRef]
- Graczykowski, B.; Vogel, N.; Bley, K.; Butt, H.-J.; Fytas, G. Multiband hypersound filtering in two-dimensional colloidal crystals: Adhesion, resonances, and periodicity. Nano Lett. 2020, 20, 1883–1889. [Google Scholar] [CrossRef] [PubMed]
- Yao, Y.-W.; Wu, F.-G.; Zhang, X.; Hou, Z.-L. Lamb wave band gaps in locally resonant phononic crystal strip waveguides. Phys. Lett. A 2012, 376, 579–583. [Google Scholar] [CrossRef]
- Hedayatrasa, S.; Abhary, K.; Uddin, M. Numerical study and topology optimization of 1D periodic biomaterial phononic crystal plates for bandgaps of low order Lamb waves. Ultrasonics 2015, 57, 104–124. [Google Scholar] [CrossRef]
- Chen, J.-J.; Han, X. The propagation of Lamb waves in one-dimensional phononic crystal plates bordered with symmetric uniform layers. Phys. Lett. A 2010, 374, 3243–3246. [Google Scholar] [CrossRef]
- Chen, J.-J.; Xia, Y.-J.; Han, X.; Zhang, H.-B. Lamb waves in phononic crystal slabs: Truncated plane parallels to the axis of periodicity. Ultrasonics 2012, 52, 920–924. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.-B.; Chen, J.-J.; Han, X. Lamb wave band gaps in a homogenous plate with periodic tapered surface. J. Appl. Phys. 2012, 112, 054503. [Google Scholar] [CrossRef]
- Zhu, Y.-F.; Yuan, Y.; Zou, X.-Y.; Cheng, J.-C. Piezoelectric-sensitive mode of lamb wave in one-dimensional piezoelectric phononic crystal plate. Wave Motion 2015, 54, 66–75. [Google Scholar] [CrossRef]
- Wang, Y.-F.; Wang, T.-T.; Liu, J.-P.; Wang, Y.-S.; Laude, V. Guiding and splitting Lamb waves in coupled-resonator elastic waveguides. Compos. Struct. 2018, 206, 588–593. [Google Scholar] [CrossRef]
- Zhou, W.-J.; Wu, B.; Su, Y.-P.; Liu, D.-Y.; Chen, W.-Q.; Bao, R.-H. Tunable flexural wave band gaps in a prestressed elastic beam with periodic smart resonators. Mech. Adv. Mater. Struct. 2019, 1–8. [Google Scholar] [CrossRef]
- Zhu, J.; Chen, H.-Y.; Wu, B.; Chen, W.-Q.; Balogun, O. Tunable band gaps and transmission behavior of SH waves with oblique incident angle in periodic dielectric elastomer laminates. Int. J. Mech. Sci. 2018, 146, 81–90. [Google Scholar] [CrossRef]
- Gao, N.-S.; Hou, H.; Mu, Y.-H. Low frequency acoustic properties of bilayer membrane acoustic metamaterial with magnetic oscillator. Theor. Appl. Mech. Lett. 2017, 7, 252–257. [Google Scholar] [CrossRef]
- Chen, Q.-L.; Elbanna, A. Tension-induced tunable corrugation in two-phase soft composites: Mechanisms and implications. Extreme Mech. Lett. 2015, 4, 26–37. [Google Scholar] [CrossRef]
- Farshad, M.; Benine, A. Magnetoactive elastomer composites. Polym. Test. 2004, 23, 347–353. [Google Scholar] [CrossRef]
- Elhajjar, R.; Law, C.-T.; Pegoretti, A. Magnetostrictive polymer composites: Recent advances in materials, structures and properties. Progr. Mater. Sci. 2018, 97, 204–229. [Google Scholar] [CrossRef]
- Perales-Martínez, I.-A.; Palacios-Pineda, L.-M.; Lozano-Sánchez, L.-M. Enhancement of a magnetorheological PDMS elastomer with carbonyl iron particles. Polym. Test. 2017, 57, 78–86. [Google Scholar] [CrossRef]
- Winger, J.; Schümann, M.; Kupka, A.; Odenbach, S. Influence of the particle size on the magnetorheological effect of magnetorheological elastomers. J. Magn. Magn. Mater. 2019, 481, 176–182. [Google Scholar] [CrossRef]
- Sun, S.-S.; Yang, J.; Yildirim, T.-J.; Ning, D.-H.; Zhu, X.-J.; Du, H.-P.; Zhang, S.-W.; Nakano, M.; Li, W.-H. A magnetorheological elastomer rail damper for wideband attenuation of rail noise and vibration. J. Intell. Mater. Syst. Struct. 2020, 31, 220–228. [Google Scholar] [CrossRef]
- Mikhailov, V.-P.; Bazinenkov, A.-M. Active vibration isolation platform on base of magnetorheological elastomers. J. Magn. Magn. Mater. 2017, 431, 266–268. [Google Scholar] [CrossRef]
- Xu, Z.-L.; Wu, F.-G.; Guo, Z.-N. Shear-wave band gaps tuned in two-dimensional phononic crystals with magnetorheological material. Solid State Commun. 2013, 154, 43–45. [Google Scholar] [CrossRef]
- Xu, Z.-L.; Tong, J.; Wu, F.-G. Magnetorheological elastomer vibration isolation of tunable three-dimensional locally resonant acoustic metamaterial. Solid State Commun. 2018, 271, 51–55. [Google Scholar] [CrossRef]
- Wen, X.-X.; Yu, G.-J.; Wang, L.-Y.; Zhu, S.-J. Band Gap Vibration Isolation of Phononic Crystals Based on Magnetorheological Elastomers. J. Synth. Cryst. 2018, 47, 102–108. [Google Scholar]
- Liu, S.-G.; Zhao, Y.-C.; Zhao, D. Bandgap and transmission spectrum characteristics of multilayered acoustic metamaterials with magnetorheological elastomer. Acta Phys. Sin. 2019, 68, 234301. [Google Scholar]
- Bellan, C.; Bossis, G. Field dependence of viscoelastic properties of mr elastomers. Int. J. Mod. Phys. B 2002, 16, 2447–2453. [Google Scholar] [CrossRef]
- Davis, L.-C. Model of magnetorheological elastomers. J. Appl. Phys. 1999, 85, 3348–3351. [Google Scholar] [CrossRef]
- Jolly, M.-R.; Carlson, J.-D.; Munoz, B.-C. The magnetoviscoelastic response of elastomer composites consisting of ferrous particles embedded in a polymer matrix. J. Intell. Mater. Syst. Struct. 1996, 7, 613–622. [Google Scholar] [CrossRef]
- Wang, G.; Wen, J.-h.; Liu, Y.-Z.; Yu, D.-L.; Zhao, H.-G. Research on the vibration band gaps of one dimensional viscoelastic periodic structure. Chin. J. Mech. Eng. 2004, 40, 47–50. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).