Next Article in Journal
Effect of Overheating Temperature on Thermal Cycling Creep Properties of K465 Superalloy
Next Article in Special Issue
Linking Time-Domain Vibration Behaviors to Spatial-Domain Propagating Waves in a Leaf-like Gradient-Index Phononic Crystal Lens
Previous Article in Journal
Investigation of TiO2 Nanoparticles Synthesized by Sol-Gel Method for Effectual Photodegradation, Oxidation and Reduction Reaction
Previous Article in Special Issue
Study on Lamb Waves in a Composite Phononic Crystal Plate
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 11
Issue 12
10.3390/cryst11121457
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Two-Dimensional Composite Acoustic Metamaterials of Rectangular Unit Cell from Pentamode to Band Gap

by
Qi Li
1,2,*,
Ke Wu
1 and
Mingquan Zhang
1
1
Department of Mechanical Engineering, Naval Architecture and Ocean Engineering College, Dalian Maritime University, Dalian 116026, China
2
Polar Shipping and Safety Institute, Dalian Maritime University, Dalian 116026, China
*
Author to whom correspondence should be addressed.
Crystals 2021, 11(12), 1457; https://doi.org/10.3390/cryst11121457
Submission received: 7 October 2021 / Revised: 19 November 2021 / Accepted: 22 November 2021 / Published: 25 November 2021
(This article belongs to the Special Issue Recent Advances in Phononic Crystals and Acoustic Metamaterials)
Browse Figures
Versions Notes

Abstract

:
Pentamode metamaterials have been receiving an increasing amount of interest due to their water-like properties. In this paper, a two-dimensional composite pentamode metamaterial of rectangular unit cell is proposed. The unit cells can be classified into two groups, one with uniform arms and the other with non-uniform arms. Phononic band structures of the unit cells were calculated to derive their properties. The unit cells can be pentamode metamaterials that permit acoustic wave travelling or have a total band gap that impedes acoustic wave propagation by varying the structures. The influences of geometric parameters and materials of the composed elements on the effective velocities and anisotropy were analyzed. The metamaterials can be used for acoustic wave control under water. Simulations of materials with different unit cells were conducted to verify the calculated properties of the unit cells. The research provides theoretical support for applications of the pentamode metamaterials.

1. Introduction

Acoustic metamaterials (AMs) [1] are rationally designed materials that can manipulate and control acoustic waves in ways that are impossible for conventional materials. Pentamode metamaterials (PMs) [2] are characterized by five eigenvalues of zero, which means that they can only withstand compressional stresses. PMs behave like fluids, although they have solid structures. They have attracted lots of attention after Norris [3] analyzed theoretically the feasibility of acoustic cloaks with PMs.
The original PMs proposed by Milton and Cherkaev [2] are three-dimensional (3D) face-centered-cubic (FCC) unit cells. The 3D PMs have been studied theoretically and experimentally for their effective properties and fabrications. The phonon band structures [4] of the FCC cells were calculated to show the existence of pentamode bands. Anisotropic properties [5,6] were studied by varying their structures. Besides the original model, the PMs with different unit cells [7,8,9], different cross-section shapes [10], asymmetric arms [11,12], composite materials [13,14,15], or structures [16,17] were studied for their improved properties. Due to the complicated structures, 3D PMs can be fabricated by selective laser melting (SLM), [18] 3D printer [19], dip-in direct-laser-writing optical lithography [20], etc.
Two-dimensional (2D) PMs are 2D equivalents to PMs with similar properties but are easier for fabrication and application. The 2D PMs, also named bimode materials, were first presented by Milton and Cherkaev [2]. They have honeycomb structures. The unit cells were studied with different structure parameters for their effective properties and water-like characteristics [21,22,23]. An oblique honeycomb lattice [24] was also studied for high anisotropy. Properties of single-material PMs were customized by bottom-up topology optimization [25]. PMs with triple-phase microstructure [26] were designed and studied for their effective properties and transmission performance. The properties of specific unit cells were verified with models fabricated by waterjet [27] or selective laser melting [28]. The 2D PMs can be used in various applications. They were used to manipulate acoustic wavefronts [29,30], design an underwater acoustic carpet cloak [31] and 2D latticed pentamode cloak [32], bend acoustic waves [33,34], communicate with acoustic orbital angular momentum [35] and focus underwater sound with gradient index lens [27] or with negative refraction [36].
Compared with conventional materials, AMs are ideal materials in controlling acoustic waves because their properties can be designed according to their applications. PMs have water-like properties that permit broadband propagation of acoustic waves without scattering. Additionally, acoustic transmission can be suppressed by AMs with negative effective density [37] or negative effective bulk modulus [38]. It can also be realized by embedding spherical cavities [39] or hard spheres [40] in soft medium. PMs also have total band gaps in 2D [41] or 3D [12,42,43]. The band structures of phononic crystals can be calculated with a finite element method (FEM) [44,45] or with other methods [46,47,48]. The calculation of phononic bands with FEM software is also popular due to the convenience and accuracy. The formation mechanism of the band gaps is due to bragg scattering, local resonance, or both. The band width of the gap can be tailored by its parameters.
In this paper, a new composite 2D PM unit cell is proposed. The phononic band structures of the unit cell show that the unit cells can have pentamode band gaps within which only compressional modes exist or have total band gaps where no mode is supported. The influences of geometric parameters and materials on the effective properties were analyzed. High variation of effective properties and high anisotropy can be derived for some cells. Broadband total band gaps can be obtained by varying the structures. Simulations in acoustic field with different models are conducted to verify their properties.
The paper is structured as follows. Section 2 deals with the geometric model, which will be used in the following sections. The models of rectangular unit cells can be classified as two groups according to the identity of the arms composed of the unit cells. Section 3 deals with the effective properties (pentamode bands, effective velocities, anisotropy) of the model with uniform arms. Section 4 deals with effective properties and total band gaps of the models with non-uniform arms. Section 5 is the conclusion that was drawn from the study.

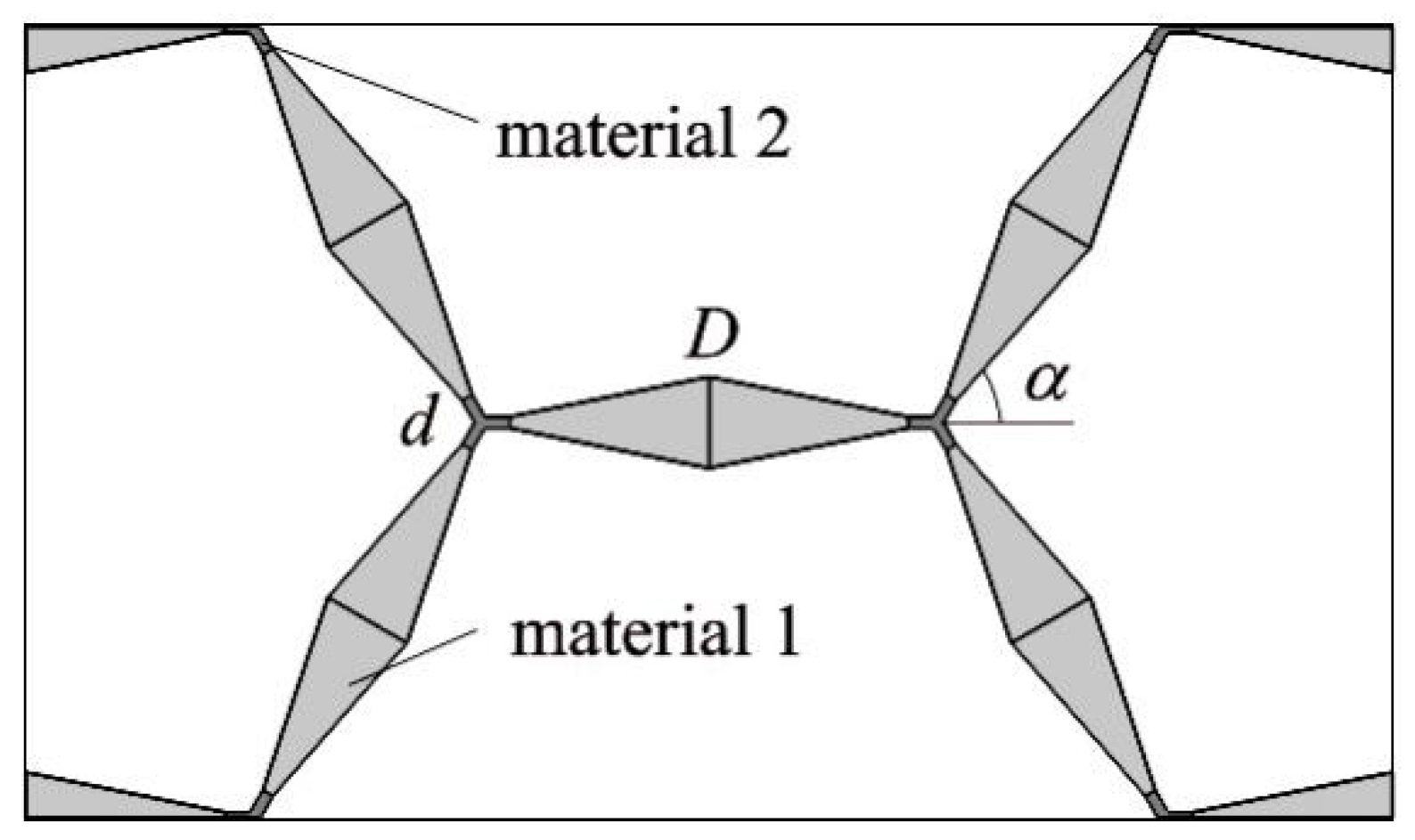
2. Geometric Models

Traditional 2D PMs are usually of honeycomb structures with specific arms. Inspired by the honeycomb structures, a rectangular unit cell was designed, as shown in Figure 1.
The unit cell consists of composite arms connected together. All the arms in the unit cell are the same. Throughout Section 3, the lengths of all the arms in a unit cell are the same. Since metamaterial is scalable, the dimensions are normalized by the length of the arm L. Each arm consists of two small rectangles with width d and two trapezoids with top width d and bottom width D. Three arms connect each other by their rectangles at the intersection point of the extended lines of the trapezoid. The trapezoid is made of material 1 and the rectangle is made of material 2, which means the unit cell is a composite structure. The angle of the oblique arm from the horizontal direction is denoted as α. All the angles between each two arms are the same when α is 60° and are different when α changes. The advantage of the unit cell is that it is mirror symmetrical in both horizontal and vertical directions and the extreme velocities lie in these directions. It is convenient to tailor the extreme properties of the unit cells. The rectangular shape of the unit cell is suitable for composing large materials along their extreme directions. The study of the model is described in Section 3.
The uniformity of the arms can be broken to increase the ways of tailoring the effective properties of the unit cells. The dimensions of the center arm can be different to tailor the effective properties slightly. Another way is to move the connection points within the unit cell along the vertical direction. The two connection points can move in the same direction, as shown in Figure 2a, or in the opposite directions, as shown in Figure 2b. The study of the models with non-uniform arms is described in Section 4.

3. Properties of Models with Uniform Arms

The typical characteristics of PMs reflect on their phononic band structures. There is a pentamode band gap where only a compressional wave exists. All the shear waves are not supported. The PMs are sometimes called metafluid due to their water-like properties. However, compared with real fluids, their properties can be tailored by their geometric parameters and anisotropy can be obtained by changing the structures. For the composite structures proposed in this paper, the material couples used to build the unit cell can also affect its properties. The properties of the unit cell were derived within its first Brillouin zone. The analyses were conducted with finite element software COMSOL Multiphysics. The Solid Mechanics in the physics part was utilized. Two groups of periodic boundary conditions were set as floquet periodic, as shown in Figure 3. The k-vector was along specific routines in the Brillouin zone with a parametric sweep, which was set in the Study part. The Eigenfrequency study was chosen, and the solver was ARPACK. Free Triangular method with Extra-fine size was used to mesh all the domain. There were 1274 domain elements for a specific model. Other settings and results are described in the following sections.

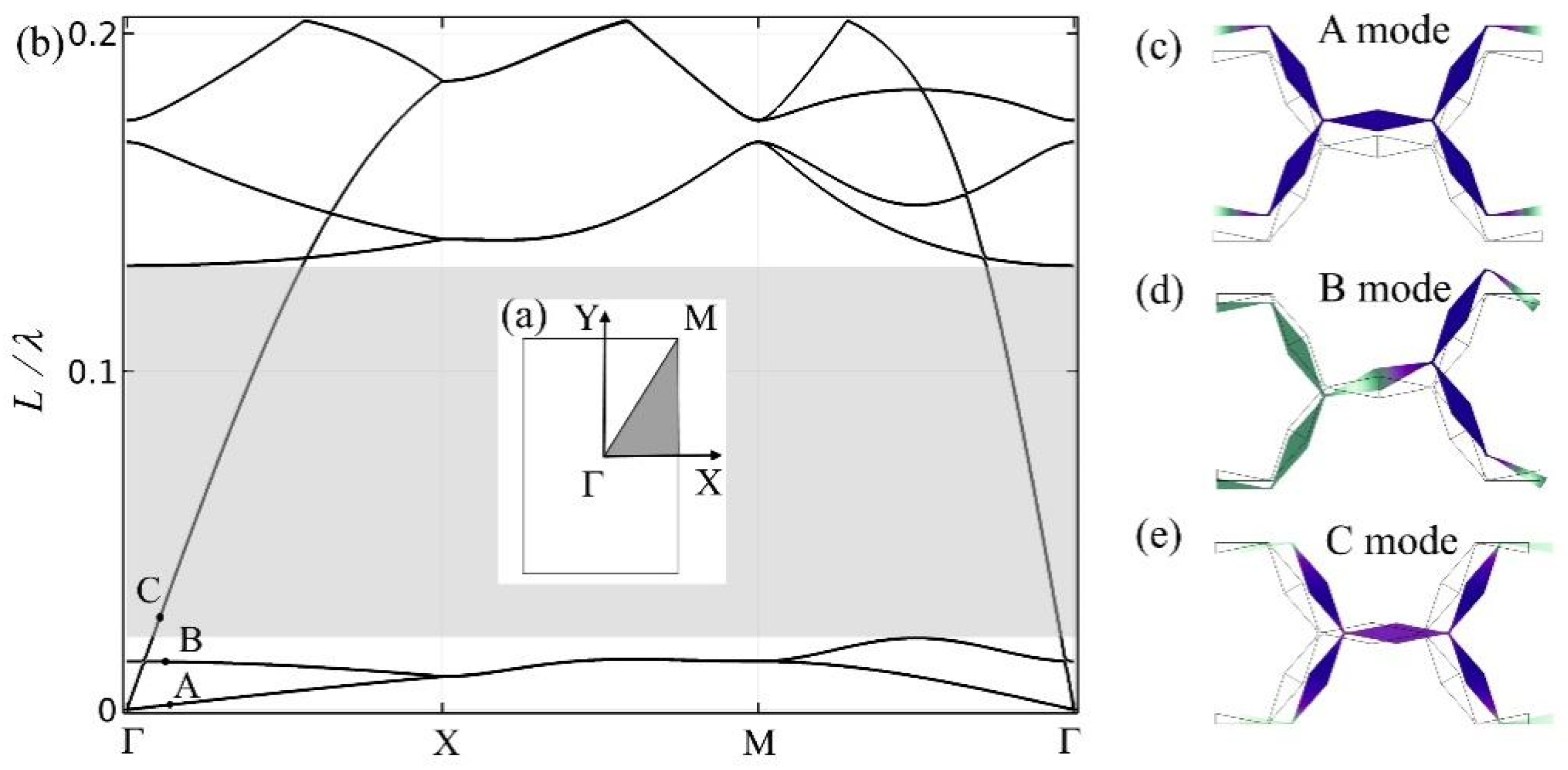
3.1. Phononic Band Structures

Pentamode characteristics can be discovered from the phononic band structures along the edges of the irreducible Brillouin zone. The phononic bands for the model with D = 0.2L, d = 0.025L, and α = 60° are shown in Figure 4. Material 1 was aluminum (E = 76 GPa, r = 2700 kg/m3, Poisson’s ratio = 0.33) and material 2 was steel (E = 200 GPa, r = 7870 kg/m3, Poisson’s ratio = 0.29).
The Brillouin zone of the unit cell was a rectangle, as shown in Figure 4a. The band structures were calculated along Γ-X-M-Γ. The result is shown in Figure 4b. The modes at the labeled points of the three lower bands are shown in Figure 4c–e. The mode at Point C was compressional mode, while the other two were shear modes. The shaded part in Figure 4b illustrates the band gap for shear waves, meaning that only compressional waves existed.
The pentamode bands were different for different unit cells. From previous studies, the pentamode bands varied with the parameter d. When d approached zero, the models were ideal PMs. However, the thin ends could not be zero for the mechanical stability of the structure. Better stability resulted with an increase of d but led to stronger shear modes. The dimension of the unit cell changed with the angle α. The pentamode bands of the unit cells with variation of α are plotted in Figure 5. The upper limit of the band was noted as fu, and the lower limit was noted as fl.
The band width changed little when α was between 20° and 75°. When α exceeded 75°, the band width decreased significantly due to the sharp decrease of the upper limit. When α approached 90°, the arms were almost in perpendicular directions, which caused the arms to easily deform. If a large pentamode band width is required, α should be around 20° and 75°.

3.2. Effective Velocities and Pentamode Bands with d and D

Effective velocities can be calculated by the slopes of the phononic band branches starting from the center of the Brillouin zone to that direction. Effective compressional wave velocities are key parameters of the material in controlling acoustic waves. The shear wave velocities of the PMs are negligible compared with those of compressional waves. Thus, the effects of the geometric parameters, d and D, on effective compressional wave velocities were analyzed, and their effects on pentamode bands were also explored.
The compressional wave velocity in the horizontal direction was denoted as vx, while the velocity along vertical direction was denoted as vy. The effects of d and D on effective properties were analyzed for aluminum–steel models. The variation of the effective compressional wave velocities and pentamode bands with d is shown in Figure 6a when D = 0.2L and α = 60°. The velocities increased with the increase of d when the other parameters remained unchanged. For the pentamode bands, both the upper limit and the lower limit increased steadily with the increase of d, and the band width changed little. The variation of the effective velocities with D is shown in Figure 6b when d = 0.025L and α = 60°. The velocities decreased with the increase of D when the other parameters remained unchanged. For pentamode bands, the upper band limit was affected greatly when D was relatively small while the lower limit changed little all the time. These results were as expected since increasing d increases effective stiffness and leads to a large velocity, while increasing D increases the effective density and leads to a low velocity. From the figures, it can also be seen that vx and vy were close to each other when α = 60° no matter what d and D were. That means the materials may have been isotropic when α = 60°.

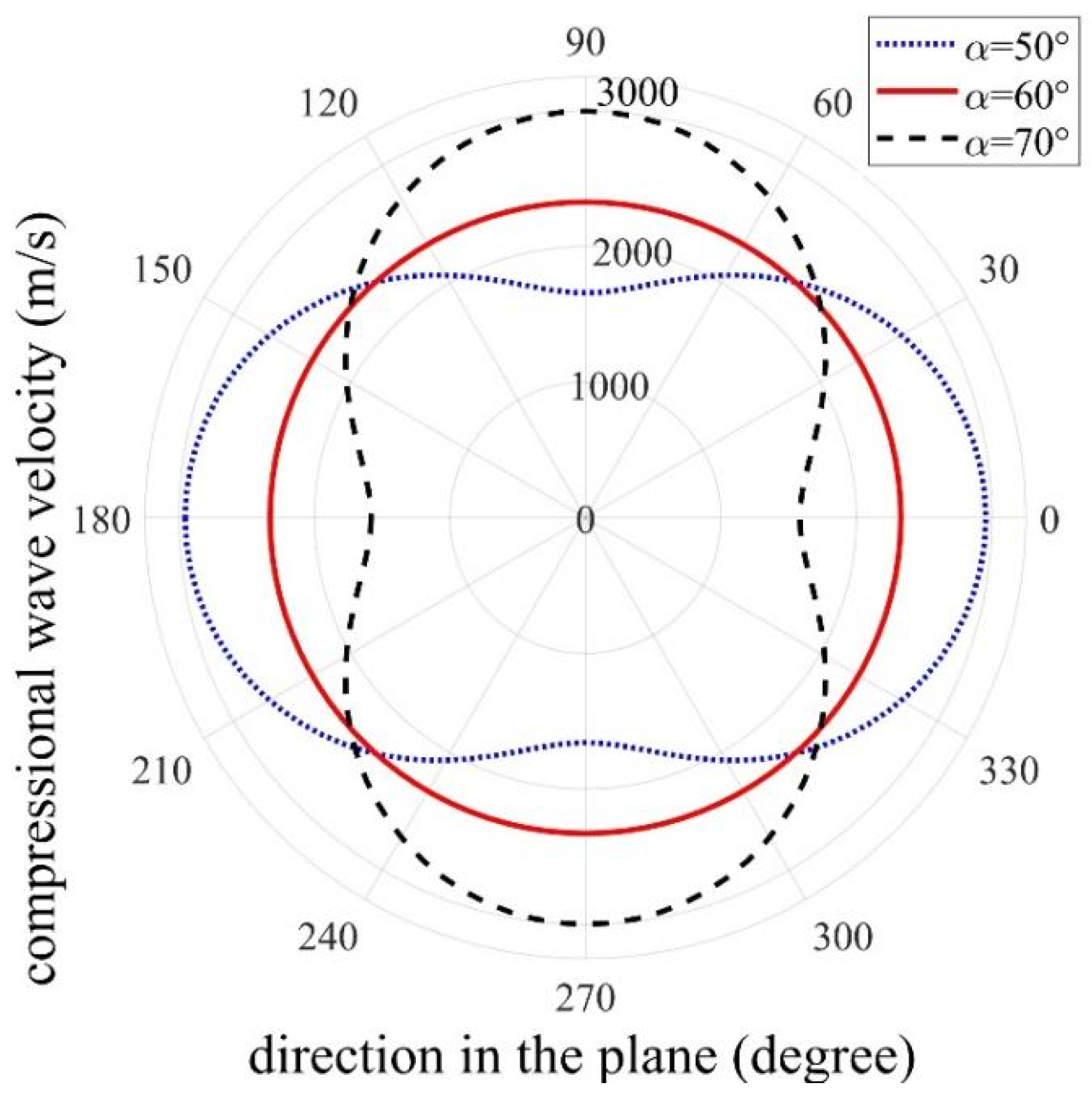
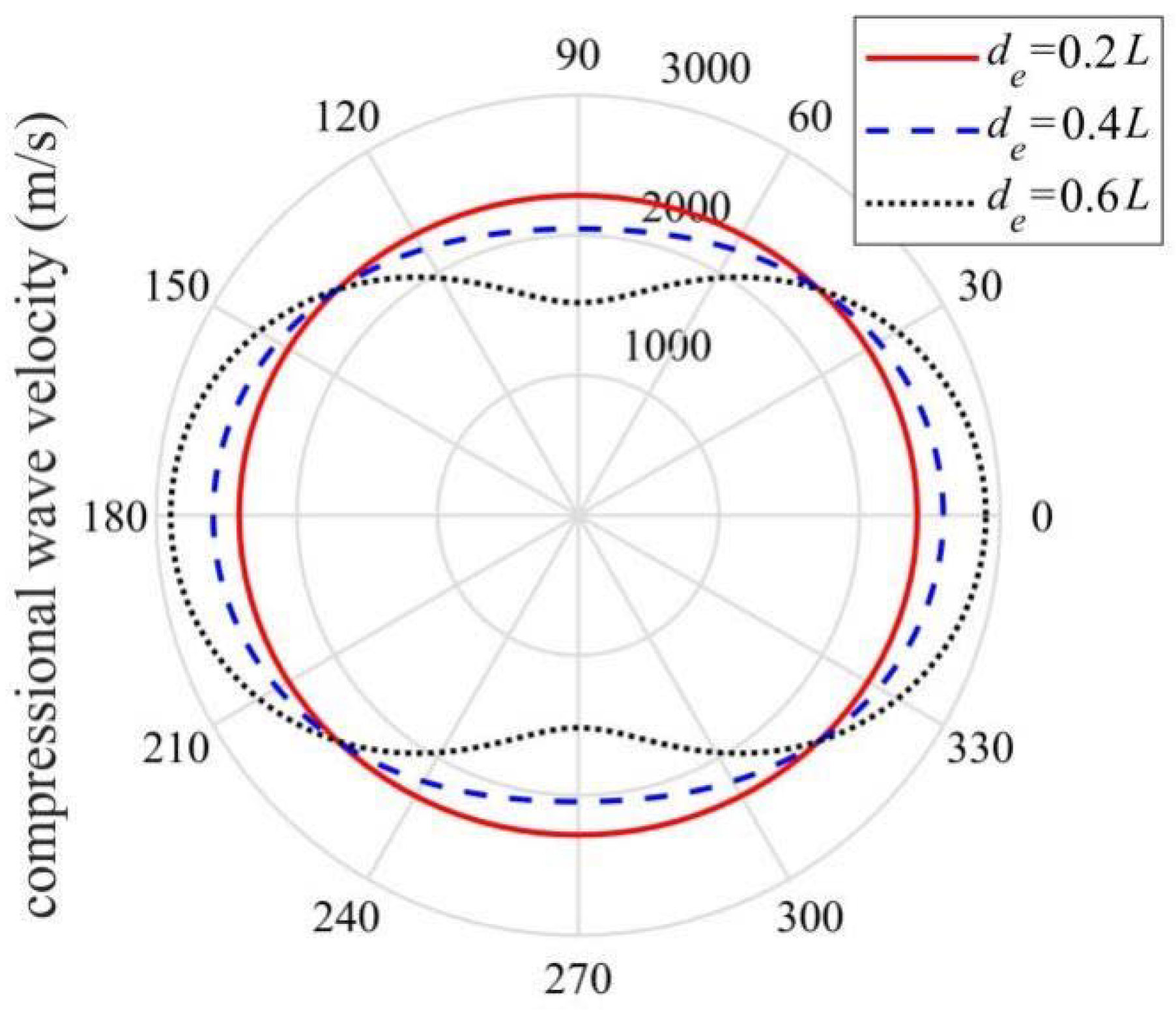
3.3. Anisotropy

The unit cell was isotropic when α = 60°, as seen in Section 3.2. Anisotropy was introduced when α deviated from 60°. To show it clearly, the compressional wave velocities along all directions in the plane were calculated for the aluminum–steel unit cells with D = 0.2L and d = 0.025L. Three models with α = 50°, 60°, and 70° were studied. The results are shown in Figure 7. The velocity map was a perfect circle when α = 60°, which means the unit cell was isotropic. The unit cells with α = 50° and 70° were anisotropic. When α = 50°, the maximum was in a horizontal direction and the minimum was in a vertical direction. When α = 70°, the maximum was in a vertical direction and the minimum was in a horizontal direction.
In order to explore the effect of α on the anisotropy, more values were taken to analyze it. Since extreme velocities were in horizontal and vertical directions, the velocities vx and vy were plotted only. The variation of compressional wave velocities vx and vy with α is shown in Figure 8. The velocity decreased in the horizontal direction and increased in the vertical direction with the increase of α. The two curves intersected at 60° where the unit cell was isotropic. Anisotropy was introduced when α deviated from 60°. High anisotropy was derived when α approached 0° or 90°. Due to the structure requirements, too-small values were not available. The anisotropy can be as large as 35 times when α = 13°.
The results agreed with the ideal bimode metamaterials with honeycomb structures [2]. When α = 60°, the effective compressional wave velocities in horizontal and vertical directions were the same. It was in accordance with the fact that the stress matrix of ideal bimode metamaterial with α = 60° was an identity matrix. The stress element of the ideal bimode metamaterial in the horizontal direction was larger when α < 60°, and the stress element in the vertical direction was larger when α > 60°. It conformed with the variation of the compressional wave velocities of the proposed unit cell. From a physical point of view, it can be explained that the unit cell was easier to deform in the vertical direction when α < 60° and it was easier to deform in the horizontal direction when α > 60°.

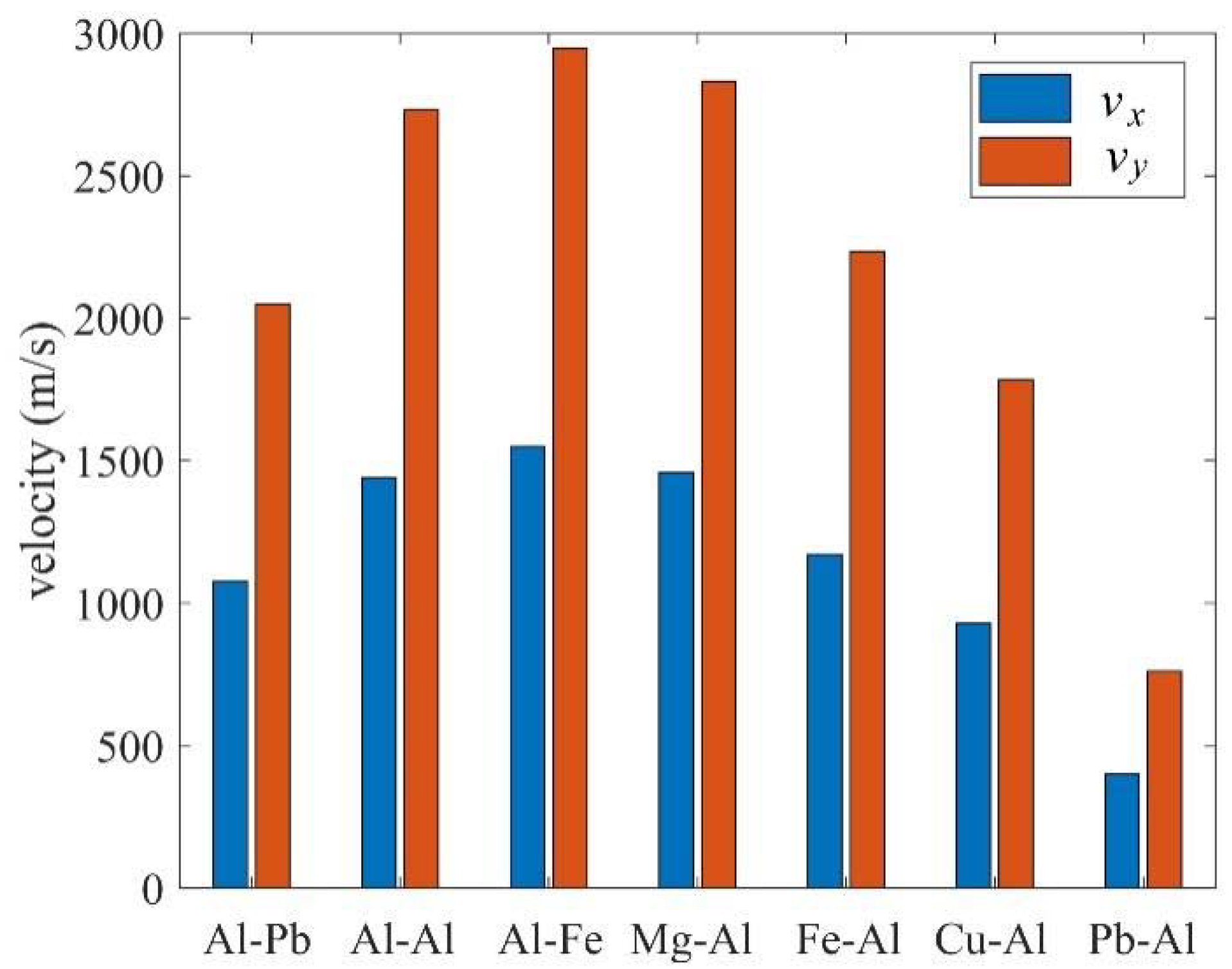
3.4. Effects of Materials

The models proposed in this paper were made of material 1 and material 2. In the above analyses, aluminum–steel models were adopted as examples. However, the composite model can be made of other materials.
Different material couples were used in the model with the parameters d = 0.04L, D = 0.35L, and α = 70°. The results are shown in Figure 9. It can be seen from the figure that the materials also had a great influence on the effective compressional wave velocities. When material 1 was aluminum, the processional wave velocities were larger and material 2 had a higher Young’s modulus. When material 2 was aluminum, the compressional velocities were smaller and material 1 had a larger density. Thus, it can be concluded that the velocity was larger if material 1 had a lighter density and material 2 had a larger Young’s modulus. Although anisotropy existed when α = 70°, the velocities in both directions varied in the same way.

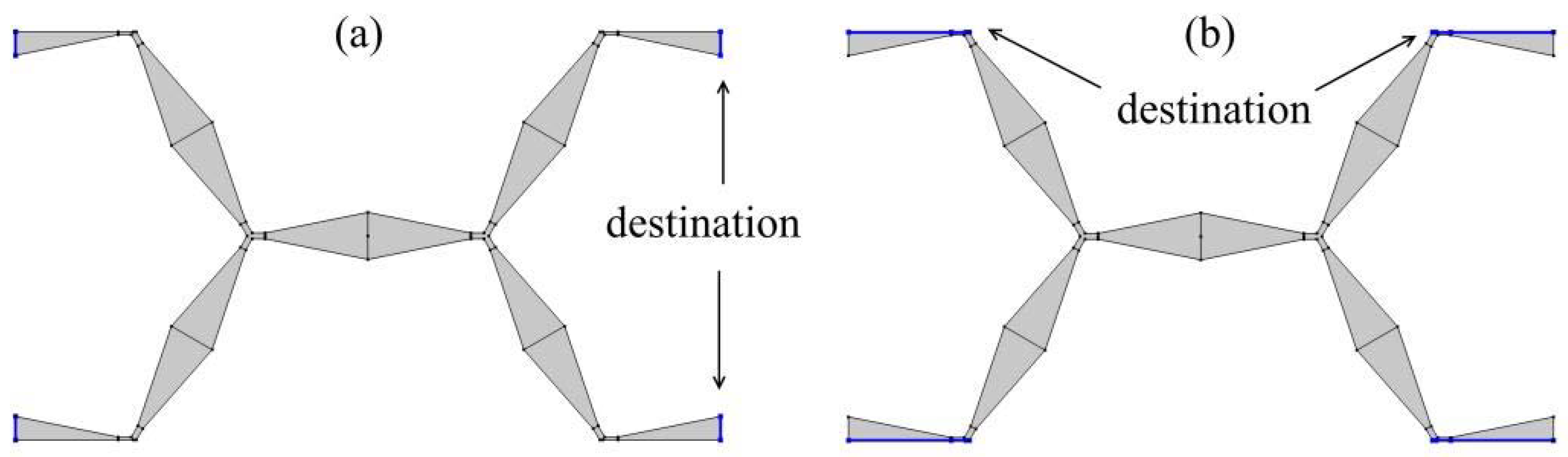
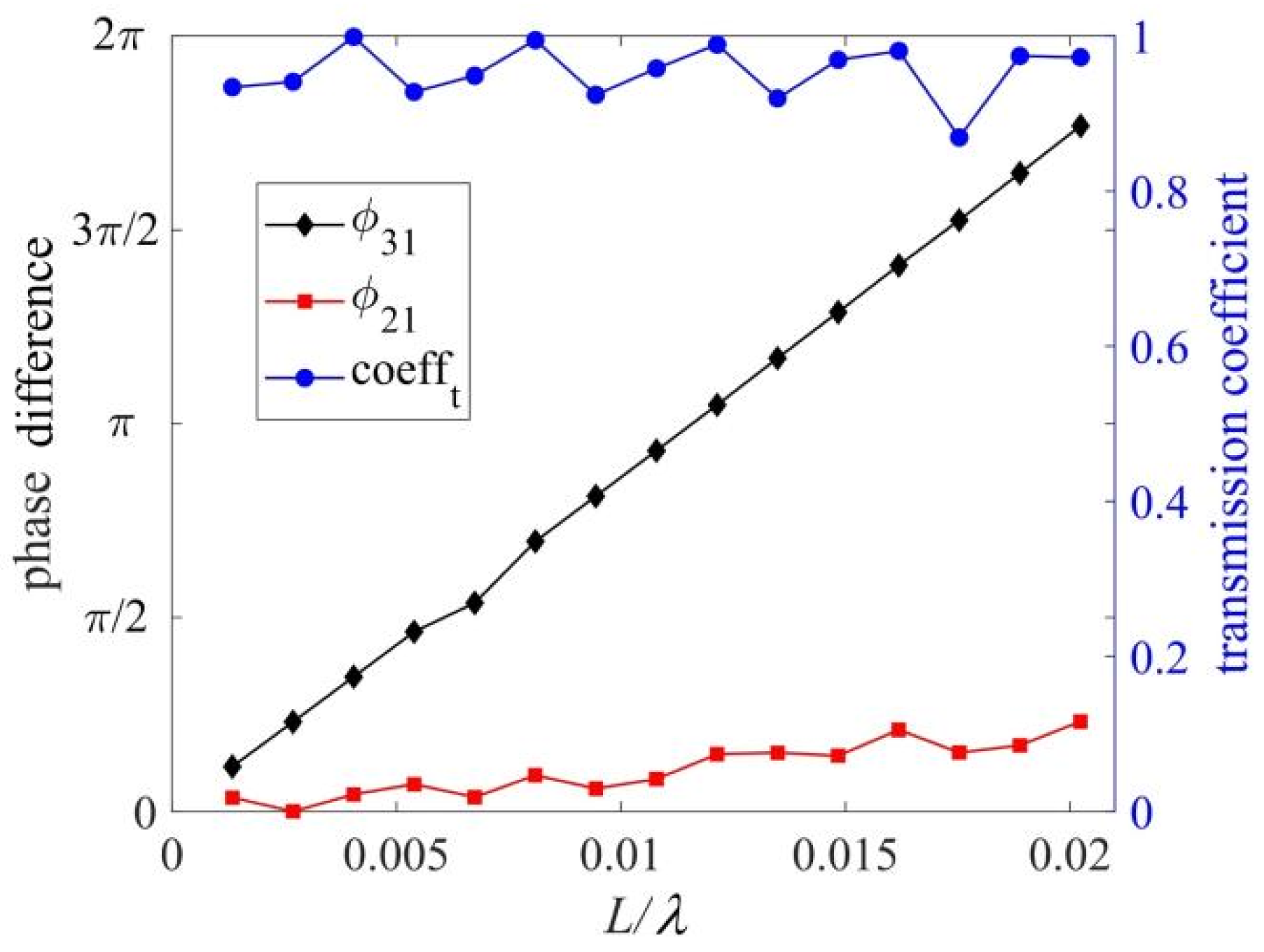
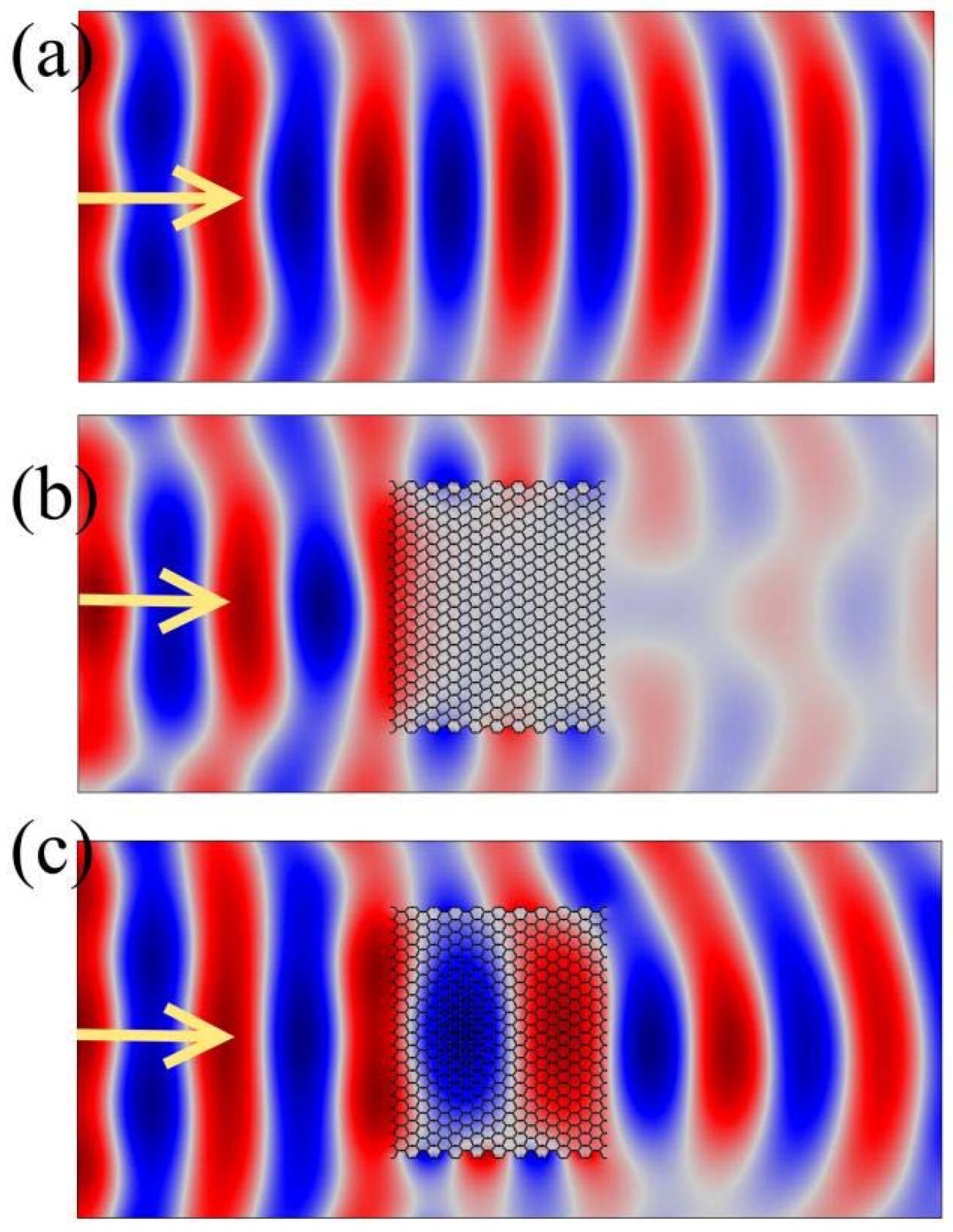
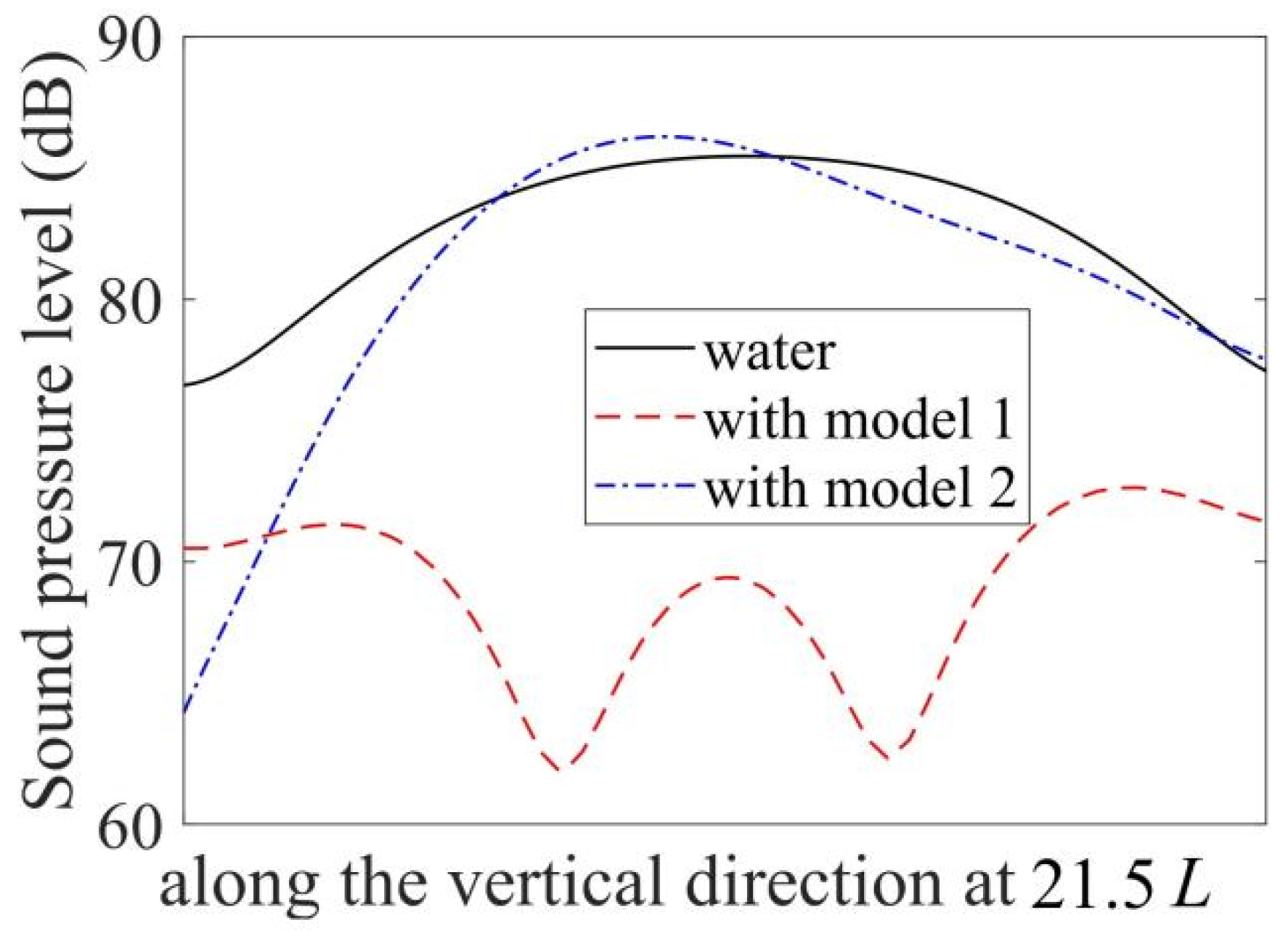
3.5. Simulation of an Application Example

The PMs have water-like properties and the effective compressional wave velocity can be tailored by geometric parameters and composed materials. The unit cells can be used for many applications where specific velocities or anisotropy are required.
A phase compensator was designed with the proposed unit cells as an example. When wavelength is much larger than tube dimensions, an acoustic wave can propagate as a plane wave even in curved tubes. However, as the routine is elongated, the phase at the outlet changes. If a material with velocity eliminates the effect of the elongation of the routine, the phases at the outlets are the same. A curved water tube with an area consisting of aluminum–steel unit cells was simulated for acoustic waves compared with a straight one and a curved one, as shown in Figure 10. The widths of the tubes were 15L. The PMs counteracted the effect of the elongated path so that the wave at the end of the curved tube had the same phase as that of the straight one. The effective velocity of the unit cell along the horizontal direction was determined by the difference of the two paths, and acoustic impedance was required to be matched to reduce transmission loss. That means both the effective density and compressional wave velocity were required to be satisfied at the same time. Since the effective properties can be tailored by geometric parameters and materials, the parameters of the unit cell can be determined by varying all the parameters to satisfy the requirements. The parameters of the unit cell were d = 0.04L, D = 0.4606L, α = 60°, material 1 was aluminum, and material 2 was steel. The effective compressional wave velocity in the horizontal direction was calculated to be 2110 m/s, and the effective density was 740 kg/m3. It can be seen from the results that the curved tube with the PMs mimicked the acoustic waves in a straight tube. The two tubes could not be differentiated only from the inlets and outlets. The wave at the outlet of the curved tubes without PMs obviously had a phase difference.
The performance of the phase compensator was analyzed for a broad frequency range. The results are shown in Figure 11. The symbol φ21 was the outlet phase difference of channel 2 to channel 1, and φ31 was the outlet phase difference of channel 3 to channel 1. With the increase of frequency, the phase difference φ31 increased while φ21 remained at low values. It means the phase compensator worked at a broadband range. The transmission coefficient (the ratio of the transmitted pressure to the incident pressure) was mainly larger than 0.9. That means acoustic waves transmitted well through the material with low energy loss. These corresponded to the aim of the design. The effective velocity of the materials eliminated the effect of the elongated routine, and the impedance matching reduced the transmission loss. The performance could be improved if the unit cell was adjusted to approximate the effective properties better.

4. Properties of Models with Non-Uniform Arms

The structures of the rectangular unit cell can be modified by breaking the identity of the composed arms. There is an arm lying in the center. The dimensions of the center arm can be varied to change the unit cell. The two connection points within the unit cell can move in the vertical direction to greatly change the inner structure.

4.1. Changing Dimensions of the Centre Arm

The center arm lies totally within the unit cell. The dimensions of the center arm can be varied independently to change the effective properties of the materials. The aluminum–steel models with D = 0.2L, dc = d = 0.025L, and α = 60° were studied while the dimensions of the center arm were varied. The modified unit cell is shown in Figure 12a.
The modified unit cells still had pentamode band gaps by calculating their band structures. It means that they were still pentamode metamaterials. The effective properties could be modified only by changing the dimensions and materials of the center arm. The effective compressional wave velocities and pentamode band limits were calculated with different Dc. The results are shown in Figure 12b. It can be seen that the lower limit of the pentamode band changed little while the upper limit increased slowly with Dc. The effective density increased slowly and the effective compressional wave velocity decreased slowly with Dc.
As was known, compressional wave velocity was proportional to the reciprocal of the square root of density. The decrease of the compressional wave velocity was mainly due to the increase of density by calculation. The materials of the center arm also had great impact on the effective properties. It provides another way to vary the effective properties slightly.

4.2. Moving the Two Connection Points in the Same Direction

There were two connection points within the unit cell. When the two connection points moved in the same direction vertically, as Figure 2a shows, the structures of the unit cell changed greatly. The unit cell lost central symmetry and mirror symmetry about x direction. The irreducible Brillouin zone was a rectangle instead of a triangle, as shown within the Figure 13.
The band structures of the modified unit cells were calculated along the boundaries of the irreducible Brillouin zone. The unit cells were obtained by moving the two connection points in the same direction vertically with the aluminum–steel model of D = 0.2L, d = 0.025L, and α = 60°. The results of the model with de = 0.2L are shown in Figure 13. The unit cell was still PMs because there was a pentamode band, which is shaded in Figure 13.
To study the effect of de on pentamode bands, the above cell was modified with different de. The band structures of the unit cells were calculated. The results are shown in Figure 14. With the increase of de, the lower limit increased and the upper limit decreased, which led to the decrease of the pentamode band width. The unit cell with de = 0 had the widest pentamode band width when other parameters were the same.
With the introduction of de, the inner structure of the unit cell changed. The compressional wave velocities of three models with de = 0.2L, 0.4L, and 0.6L were calculated. The other parameters were the same as above. The results along all the directions in the plane are shown in Figure 15.
With the increase of de, the compressional wave velocity in the horizontal direction increased while the compressional wave velocity in the vertical direction decreased, leading to higher anisotropy. It can be explained that when de increased, the angle between the two oblique arms at one connection point decreased, which caused the unit cell to easily deform in the vertical direction and to difficulty deform in the horizontal direction.

4.3. Moving the Two Connection Points in Opposite Directions

In Section 4.2, the two connection points moved in the same direction vertically. If the two connection points move in opposite directions vertically, it is the model as shown in Figure 2b. The model is central symmetric without any mirror symmetry. The irreducible Brillouin zone is also a rectangle, as shown within Figure 16.
The band structures of the modified unit cells along the boundaries of the irreducible Brillouin zone were calculated. The models were obtained by moving the two connection points in opposite directions vertically with the aluminum–steel unit cell of D = 0.2L, d = 0.025L, and α = 60°. The band structure of the model with de = 0.2L is shown in Figure 16. Different from the above models, there was a total band gap in the band structure where pentamode band gap was supposed to be for other models. The total band gap means any wave is not supported at these frequencies. Only by varying de are the limits of the total band gap studied. The results are shown in Figure 17.
The upper limit (bu) of the total band gap changed dramatically with de while the lower limit (bl) changed gently with de. When de was larger than 0.05L, total band gap occurred. After that, the width of the total band gap increased and reached the maximum around 0.3L (the model is shown in Figure 17b). The band gap started from 0.026L/λ to 0.105L/λ. Then, the band width decreased and almost disappeared at 0.6L (the model is shown in Figure 17c). There was still a total band gap when de was larger than 0.6L.
The total band gap mainly depended on the structures of the unit cells. Models with the geometric structures also had total band gaps if other material couples or a single material were applied. However, the band width changed accordingly with materials.

4.4. Simulation of Examples

It can be drawn from Section 4.2 and Section 4.3 that the properties of the unit cells with the same parameters were different only by moving the two connection points in the same direction or in opposite directions vertically. Acoustic waves through an area with two models were simulated compared with water. Acoustic waves entered from the left edge and exited from the right edge. All the boundaries were set as plane wave radiation so that no reflections at boundaries were caused. Model 1 was composed of 10 layers of the unit cells of Figure 13 and Model 2 was composed of 10 layers of the unit cells of Figure 16. The results are shown in Figure 18. At the same frequency (L/λ = 0.05), Model 1 blocked and Model 2 permitted the propagation of the acoustic waves.
To quantitatively evaluate the performance of the two models, sound pressure levels at the cross line of 21.5L behind the end of the models were calculated compared with that of water. The results are shown in Figure 19. It can be seen that Model 1 suppressed the acoustic waves greatly, by more than 10 dB, while Model 2 permitted the passed waves to have a similar level with that of water. The results are in accordance with the calculated properties of the unit cells.

5. Conclusions

In this work, a 2D composite pentamode metamaterial with rectangular unit cell was proposed. The phononic band structures of some unit cells revealed that there exist pentamode bands where only compressional waves are supported. By moving the two connection points within the unit cell in opposite directions vertically, total band gap was obtained where no wave was supported to propagate.
Pentamode bands exist for unit cells with uniform arms, varied center arm, or moving the two connection points in the same direction vertically. Geometric parameters, composed materials, and connection moving displacement all have effects on the effective properties and pentamode bands. Anisotropy can be derived with various ways. The anisotropy can be as large as 35 times in a model with uniform arms by decreasing the angles of arms.
The total band gap of the unit cells by moving the two connection points in opposite directions depends on the displacement of the movement. The width of the total band gap reached its maximum around the displacement of 0.3L, where the band gap started from 0.026L/λ to 0.105L/λ. The total band gap almost disappeared around the displacement of 0.6L.
Simulations in an underwater acoustic field with different unit cells were conducted to verify their calculated properties. A phase compensator composed of unit cells with uniform arms can counteract the effect of the elongated path with little energy loss. Moving the two connection points within the unit cell in the same direction or in opposite directions based on the same unit cell leads to totally different properties. Simulation shows one permits acoustic waves travelling through without energy loss and another impedes acoustic waves’ propagating.
The materials have interesting properties and the properties can be tailored greatly by parameters. They are promising in applications for acoustic wave control.

Author Contributions

Conceptualization, Q.L.; methodology, Q.L.; writing—original draft preparation, Q.L.; software-properties, K.W.; data curation, K.W.; software-simulation, M.Z.; validation, Q.L.; writing—review and editing, Q.L.; supervision, Q.L.; project administration, Q.L.; funding acquisition, Q.L. All authors have read and agreed to the published version of the manuscript.

Funding

The research was funded by National Natural Science Foundation of China, grant number 52001046 and the Fundamental Research Funds for the Central Universities, grant number, DMU: 3132021112, 3132019308.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Acknowledgments

We acknowledge the support given by the Naval Architecture and Ocean Engineering College, Dalian Maritime University.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Cummer, S.A.; Christensen, J.; Alù, A. Controlling sound with acoustic metamaterials. Nat. Rev. Mater. 2016, 1, 1–13. [Google Scholar] [CrossRef] [Green Version]
  2. Milton, G.W.; Cherkaev, A.V. Which elasticity tensors are realizable? J. Eng. Mater. Technol. 1995, 117, 483–493. [Google Scholar] [CrossRef]
  3. Norris, A.N. Acoustic cloaking theory. Proc. R. Soc. A Math. Phys. Eng. Sci. 2008, 464, 2411–2434. [Google Scholar] [CrossRef]
  4. Martin, A.; Kadic, M.; Schittny, R.; Bückmann, T.; Wegener, M. Phonon band structures of three-dimensional pentamode metamaterials. Phys. Rev. B 2012, 86, 155116. [Google Scholar] [CrossRef] [Green Version]
  5. Kadic, M.; Bückmann, T.; Schittny, R.; Wegener, M. On anisotropic versions of three-dimensional pentamode metamaterials. New J. Phys. 2013, 15, 023029. [Google Scholar] [CrossRef]
  6. Cai, C.; Guo, R.; Wang, X.; Sun, F.; Wang, Z.; Xu, Z. Effect of anisotropy on phononic band structure and figure of merit of pentamode metamaterials. J. Appl. Phys. 2020, 127, 124903. [Google Scholar] [CrossRef]
  7. Huang, Y.; Lu, X.; Liang, G.; Xu, Z. Comparative study of the pentamodal property of four potential pentamode microstructures. J. Appl. Phys. 2017, 121, 125110. [Google Scholar] [CrossRef]
  8. Li, Q.; Vipperman, J. Three-dimensional pentamode acoustic metamaterials with hexagonal unit cells. J. Acoust. Soc. Am. 2019, 145, 1372–1377. [Google Scholar] [CrossRef]
  9. Wang, G.; Jin, L.; Zhang, L.; Xu, Z. Phonon band structures of the three dimensional latticed pentamode metamaterials. AIP Adv. 2017, 7, 025309. [Google Scholar] [CrossRef]
  10. Huang, Y.; Lu, X.; Liang, G.; Xu, Z. Pentamodal property and acoustic band gaps of pentamode metamaterials with different cross-section shapes. Phys. Lett. A 2016, 380, 1334–1338. [Google Scholar] [CrossRef]
  11. Cai, C.; Wang, Z.; Li, Q.; Xu, Z.; Tian, X. Pentamode metamaterials with asymmetric double-cone elements. J. Phys. D Appl. Phys. 2015, 48, 175103. [Google Scholar] [CrossRef]
  12. Wang, Z.; Cai, C.; Li, Q.; Li, J.; Xu, Z. Pentamode metamaterials with tunable acoustics band gaps and large figures of merit. J. Appl. Phys. 2016, 120, 024903. [Google Scholar] [CrossRef]
  13. Wang, Z.; Chu, Y.; Cai, C.; Liu, G.; Wang, M.R. Composite pentamode metamaterials with low frequency locally resonant Characteristics. J. Appl. Phys. 2017, 122, 025114. [Google Scholar] [CrossRef]
  14. Li, Q.; Zhang, M. Composite hexagonal pentamode acoustic metamaterials with tailored properties. J. Phys. Condes. Matter 2020, 32, 475701. [Google Scholar] [CrossRef]
  15. Kadic, M.; Bückmann, T.; Schittny, R.; Gumbsch, P.; Wegener, M. Pentamode metamaterials with independently tailored bulk modulus and mass density. Phys. Rev. Appl. 2014, 2, 054007. [Google Scholar] [CrossRef] [Green Version]
  16. Amendola, A.; Carpentieri, G.; Feo, L.; Fraternali, F. Bending dominated response of layered mechanical metamaterials alternating pentamode lattices and confinement plates. Compos. Struct. 2016, 157, 71–77. [Google Scholar] [CrossRef] [Green Version]
  17. Krushynska, A.O.; Galich, P.; Bosia, F.; Pugno, N.M.; Rudykh, S. Hybrid metamaterials combining pentamode lattices and phononic plates. Appl. Phys. Lett. 2018, 113, 201901. [Google Scholar] [CrossRef] [Green Version]
  18. Hedayati, R.; Leeflang, A.M.; Zadpoor, A.A. Additively manufactured metallic pentamode meta-materials. Appl. Phys. Lett. 2017, 110, 091905. [Google Scholar] [CrossRef] [Green Version]
  19. Mohammadi, K.; Movahhedy, M.R.; Shishkovsky, I.; Hedayati, R. Hybrid anisotropic pentamode mechanical metamaterial produced by additive manufacturing technique. Appl. Phys. Lett. 2020, 117, 061901. [Google Scholar] [CrossRef]
  20. Kadic, M.; Bückmann, T.; Stenger, N.; Thiel, M.; Wegener, M. On the practicability of pentamode mechanical metamaterials. Appl. Phys. Lett. 2012, 100, 191901. [Google Scholar] [CrossRef] [Green Version]
  21. Cai, X.; Wang, L.; Zhao, Z.; Zhao, A.; Zhang, X.; Wu, T.; Chen, H. The mechanical and acoustic properties of two-dimensional pentamode metamaterials with different structural parameters. Appl. Phys. Lett. 2016, 109, 131904. [Google Scholar] [CrossRef]
  22. Zhang, L.; Song, B.; Zhao, A.; Liu, R.; Yang, L.; Shi, Y. Study on mechanical properties of honeycomb pentamode structures fabricated by laser additive manufacturing: Numerical simulation and experimental verification. Compos. Struct. 2019, 226, 111199. [Google Scholar] [CrossRef]
  23. Zhao, A.; Zhao, Z.; Zhang, X.; Cai, X.; Wang, L.; Wu, T.; Chen, H. Design and experimental verification of a water-like pentamode material. Appl. Phys. Lett. 2017, 110, 011907. [Google Scholar] [CrossRef]
  24. Layman, C.N.; Naify, C.J.; Martin, T.P.; Calvo, D.C.; Orris, G.J. Highly anisotropic elements for acoustic pentamode applications. Phys. Rev. Lett. 2013, 111, 024302. [Google Scholar] [CrossRef] [PubMed]
  25. Dong, H.W.; Zhao, S.D.; Miao, X.B.; Shen, C.; Zhang, X.; Zhao, Z.; Zhang, C.; Wang, Y.S.; Cheng, L. Customized broadband pentamode metamaterials by topology optimization. J. Mech. Phys. Solids 2021, 152, 104407. [Google Scholar] [CrossRef]
  26. Zhao, A.; Zhang, X.; Yu, W.; Zhao, Z.; Cai, X.; Chen, H. Design and simulation of broadband multiphase pentamode metamaterials. Appl. Phys. Lett. 2021, 118, 224103. [Google Scholar] [CrossRef]
  27. Su, X.; Norris, A.N.; Cushing, C.W.; Haberman, M.R.; Wilson, P.S. Broadband focusing of underwater sound using a transparent pentamode lens. J. Acoust. Soc. Am. 2017, 141, 4408–4417. [Google Scholar] [CrossRef] [Green Version]
  28. Zhang, L.; Song, B.; Liu, R.; Zhao, A.; Zhang, J.; Zhuo, L.; Tang, G.; Shi, Y. Effects of structural parameters on the Poisson’s ratio and compressive modulus of 2D pentamode structures fabricated by selective laser melting. Engineering 2020, 6, 56–67. [Google Scholar] [CrossRef]
  29. Tian, Y.; Wei, Q.; Cheng, Y.; Xu, Z.; Liu, X. Broadband manipulation of acoustic wavefronts by pentamode metasurface. Appl. Phys. Lett. 2015, 107, 221906. [Google Scholar] [CrossRef]
  30. Chu, Y.; Wang, Z.; Xu, Z. Broadband high-efficiency controllable asymmetric propagation by pentamode acoustic metasurface. Phys. Lett. A 2020, 384, 126230. [Google Scholar] [CrossRef]
  31. Chen, J.; Liu, J.; Liu, X. Broadband underwater acoustic carpet cloak based on pentamode materials under normal incidence. AIP Adv. 2018, 8, 085024. [Google Scholar] [CrossRef]
  32. Chen, Y.; Liu, X.; Hu, G. Latticed pentamode acoustic cloak. Sci. Rep. 2015, 5, 15745. [Google Scholar] [CrossRef] [PubMed]
  33. Sun, Z.; Jia, H.; Chen, Y.; Wang, Z.; Yang, J. Design of an underwater acoustic bend by pentamode metafluid. J. Acoust. Soc. Am. 2018, 143, 1029–1034. [Google Scholar] [CrossRef] [Green Version]
  34. Lu, Z.M.; Cai, L.; Wen, J.H.; Chen, X. Physically realizable broadband acoustic metamaterials with anisotropic density. Chin. Phys. Lett. 2019, 36, 024301. [Google Scholar] [CrossRef]
  35. Sun, Z.; Shi, Y.; Sun, X.; Jia, H.; Jin, Z.; Deng, K.; Yang, J. Underwater acoustic multiplexing communication by pentamode metasurface. J. Phys. D Appl. Phys. 2021, 54, 205303. [Google Scholar] [CrossRef]
  36. Hladky-Hennion, A.C.; Vasseur, J.O.; Haw, G.; Croënne, C.; Haumesser, L.; Norris, A.N. Negative refraction of acoustic waves using a foam-like metallic structure. Appl. Phys. Lett. 2013, 102, 144103. [Google Scholar] [CrossRef] [Green Version]
  37. Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally resonant sonic materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef]
  38. Fang, N.; Xi, D.; Xu, J.; Ambati, M.; Srituravanich, W.; Sun, C.; Zhang, X. Ultrasonic metamaterials with negative modulus. Nat. Mater. 2006, 5, 452–456. [Google Scholar] [CrossRef]
  39. Sharma, G.S.; Skvortsov, A.; MacGillivray, I.; Kessissoglou, N. Sound scattering by a bubble metasurface. Phys. Rev. B 2020, 102, 214308. [Google Scholar] [CrossRef]
  40. Skvortsov, A.; Sharma, G.S.; MacGillivray, I.; Kessissoglou, N. Sound absorption by a metasurface comprising hard spheres in a soft medium. J. Acoust. Soc. Am. 2021, 150, 1448–1452. [Google Scholar] [CrossRef]
  41. Huang, Z.-G.; Su, C.-F. Band gap effects in a two-dimensional regular polygonal graphene-like structure. Cryst. Struct. Theory Appl. 2014, 3, 10–21. [Google Scholar] [CrossRef] [Green Version]
  42. Cai, C.; Wang, Z.; Chu, Y.; Liu, G.; Xu, Z. The phononic band gaps of Bragg scattering and locally resonant pentamode metamaterials. J. Phys. D Appl. Phys. 2017, 50, 415105. [Google Scholar] [CrossRef] [Green Version]
  43. Cai, C.; Han, C.; Wu, J.; Wang, Z.; Zhang, Q. Tuning method of phononic band gaps of locally resonant pentamode metamaterials. J. Phys. D Appl. Phys. 2018, 52, 045601. [Google Scholar] [CrossRef]
  44. Axmann, W.; Kuchment, P. An efficient finite element method for computing spectra of photonic and acoustic band-gap materials—I. Scalar case. J. Comput. Phys. 1999, 150, 468–481. [Google Scholar] [CrossRef]
  45. Li, J.-B.; Wang, Y.-S.; Zhang, C. Dispersion relations of a periodic array of fluid-filled holes embedded in an elastic solid. J. Comput. Acoust. 2012, 20, 525–541. [Google Scholar] [CrossRef]
  46. Zheng, H.; Yang, Z.; Zhang, C.; Tyrer, M. A local radial basis function collocation method for band structure computation of phononic crystals with scatterers of arbitrary geometry. Appl. Math. Model. 2018, 60, 447–459. [Google Scholar] [CrossRef]
  47. Zheng, H.; Zhang, C.; Yang, Z. A local radial basis function collocation method for band structure computation of 3D phononic crystals. Appl. Math. Model. 2020, 77, 1954–1964. [Google Scholar] [CrossRef]
  48. Zheng, H.; Zhou, C.; Yan, D.-J.; Wang, Y.-S.; Zhang, C. A meshless collocation method for band structure simulation of nanoscale phononic crystals based on nonlocal elasticity theory. J. Comput. Phys. 2020, 408, 109268. [Google Scholar] [CrossRef]
Crystals 11 01457 g001 550
Figure 1. Rectangular unit cell with uniform composite arms.
Figure 1. Rectangular unit cell with uniform composite arms.
Crystals 11 01457 g001
Crystals 11 01457 g002 550
Figure 2. Rectangular unit cell with non-uniform composite arms (a) two inner connections move in the same direction vertically (b) two inner connections move in opposite directions vertically.
Figure 2. Rectangular unit cell with non-uniform composite arms (a) two inner connections move in the same direction vertically (b) two inner connections move in opposite directions vertically.
Crystals 11 01457 g002
Crystals 11 01457 g003 550
Figure 3. Periodic boundary conditions’ setting of the unit cell of (a) group 1 and (b) group 2.
Figure 3. Periodic boundary conditions’ setting of the unit cell of (a) group 1 and (b) group 2.
Crystals 11 01457 g003
Crystals 11 01457 g004 550
Figure 4. Band structures of the unit cell with D = 0.2L, d = 0.025L, α = 60°, material 1 of aluminum, and material 2 of steel for (a) Brillouin zone, (b) phononic band, (c) mode at A, (d) mode at B, and (e) mode at C.
Figure 4. Band structures of the unit cell with D = 0.2L, d = 0.025L, α = 60°, material 1 of aluminum, and material 2 of steel for (a) Brillouin zone, (b) phononic band, (c) mode at A, (d) mode at B, and (e) mode at C.
Crystals 11 01457 g004
Crystals 11 01457 g005 550
Figure 5. The pentamode bands of the unit cell with variation of α while D = 0.2L, d = 0.025L, material 1 of aluminum, and material 2 of steel.
Figure 5. The pentamode bands of the unit cell with variation of α while D = 0.2L, d = 0.025L, material 1 of aluminum, and material 2 of steel.
Crystals 11 01457 g005
Crystals 11 01457 g006 550
Figure 6. Variation of compressional wave velocities and pentamode bands of the aluminum–steel unit cell with geometric parameters when α = 60° of (a) effects of d and (b) effects of D.
Figure 6. Variation of compressional wave velocities and pentamode bands of the aluminum–steel unit cell with geometric parameters when α = 60° of (a) effects of d and (b) effects of D.
Crystals 11 01457 g006
Crystals 11 01457 g007 550
Figure 7. The compressional wave velocities along all directions for aluminum–steel models with α = 50°, 60°, and 70° when D = 0.2L and d = 0.025L.
Figure 7. The compressional wave velocities along all directions for aluminum–steel models with α = 50°, 60°, and 70° when D = 0.2L and d = 0.025L.
Crystals 11 01457 g007
Crystals 11 01457 g008 550
Figure 8. Variation of the compressional wave velocities with α when D = 0.2L and d = 0.025L.
Figure 8. Variation of the compressional wave velocities with α when D = 0.2L and d = 0.025L.
Crystals 11 01457 g008
Crystals 11 01457 g009 550
Figure 9. The effects of different material couples on the compressional wave velocities with d = 0.04L, D = 0.35L, and α = 70°.
Figure 9. The effects of different material couples on the compressional wave velocities with d = 0.04L, D = 0.35L, and α = 70°.
Crystals 11 01457 g009
Crystals 11 01457 g010 550
Figure 10. The simulation of acoustic waves in three water tubes to show the effects of the pentamode materials.
Figure 10. The simulation of acoustic waves in three water tubes to show the effects of the pentamode materials.
Crystals 11 01457 g010
Crystals 11 01457 g011 550
Figure 11. The performance of the phase compensator compared with curved water tube without phase compensator.
Figure 11. The performance of the phase compensator compared with curved water tube without phase compensator.
Crystals 11 01457 g011
Crystals 11 01457 g012 550
Figure 12. Modified unit cell by changing the dimensions of the center arm and the effective properties of (a) the modified unit cell and (b) the effective properties with Dc.
Figure 12. Modified unit cell by changing the dimensions of the center arm and the effective properties of (a) the modified unit cell and (b) the effective properties with Dc.
Crystals 11 01457 g012
Crystals 11 01457 g013 550
Figure 13. The band structures of the modified aluminum–steel unit cell with D = 0.2L, d = 0.025L, α = 60°, and de = 0.2L in the same direction.
Figure 13. The band structures of the modified aluminum–steel unit cell with D = 0.2L, d = 0.025L, α = 60°, and de = 0.2L in the same direction.
Crystals 11 01457 g013
Crystals 11 01457 g014 550
Figure 14. The pentamode band limits of the modified aluminum–steel unit cell with D = 0.2L, d = 0.025L, α = 60°, and different de in the same direction.
Figure 14. The pentamode band limits of the modified aluminum–steel unit cell with D = 0.2L, d = 0.025L, α = 60°, and different de in the same direction.
Crystals 11 01457 g014
Crystals 11 01457 g015 550
Figure 15. Compressional wave velocities in all the directions of the plane for three models with de = 0.2L, 0.4L, and 0.6L.
Figure 15. Compressional wave velocities in all the directions of the plane for three models with de = 0.2L, 0.4L, and 0.6L.
Crystals 11 01457 g015
Crystals 11 01457 g016 550
Figure 16. The band structures of the modified aluminum–steel unit cell with D = 0.2L, d = 0.025L, α = 60°, and de = 0.2L in opposite directions.
Figure 16. The band structures of the modified aluminum–steel unit cell with D = 0.2L, d = 0.025L, α = 60°, and de = 0.2L in opposite directions.
Crystals 11 01457 g016
Crystals 11 01457 g017 550
Figure 17. The limits of total band gap with de and specific unit cells of (a) total band gap limits with de and (b) unit cell with de = 0.3L and (c) de = 0.6L.
Figure 17. The limits of total band gap with de and specific unit cells of (a) total band gap limits with de and (b) unit cell with de = 0.3L and (c) de = 0.6L.
Crystals 11 01457 g017
Crystals 11 01457 g018 550
Figure 18. The propagation of acoustic waves through three media: (a) water, (b) water with Model 1, and (c) water with Model 2.
Figure 18. The propagation of acoustic waves through three media: (a) water, (b) water with Model 1, and (c) water with Model 2.
Crystals 11 01457 g018
Crystals 11 01457 g019 550
Figure 19. Sound pressure levels of the three cases along the vertical direction at 21.5L behind the end of the models.
Figure 19. Sound pressure levels of the three cases along the vertical direction at 21.5L behind the end of the models.
Crystals 11 01457 g019
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Li, Q.; Wu, K.; Zhang, M. Two-Dimensional Composite Acoustic Metamaterials of Rectangular Unit Cell from Pentamode to Band Gap. Crystals 2021, 11, 1457. https://doi.org/10.3390/cryst11121457

AMA Style

Li Q, Wu K, Zhang M. Two-Dimensional Composite Acoustic Metamaterials of Rectangular Unit Cell from Pentamode to Band Gap. Crystals. 2021; 11(12):1457. https://doi.org/10.3390/cryst11121457

Chicago/Turabian Style

Li, Qi, Ke Wu, and Mingquan Zhang. 2021. "Two-Dimensional Composite Acoustic Metamaterials of Rectangular Unit Cell from Pentamode to Band Gap" Crystals 11, no. 12: 1457. https://doi.org/10.3390/cryst11121457

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop