Narrow/Broad-Band Absorption Based on Water-Hybrid Metamaterial
Abstract
1. Introduction
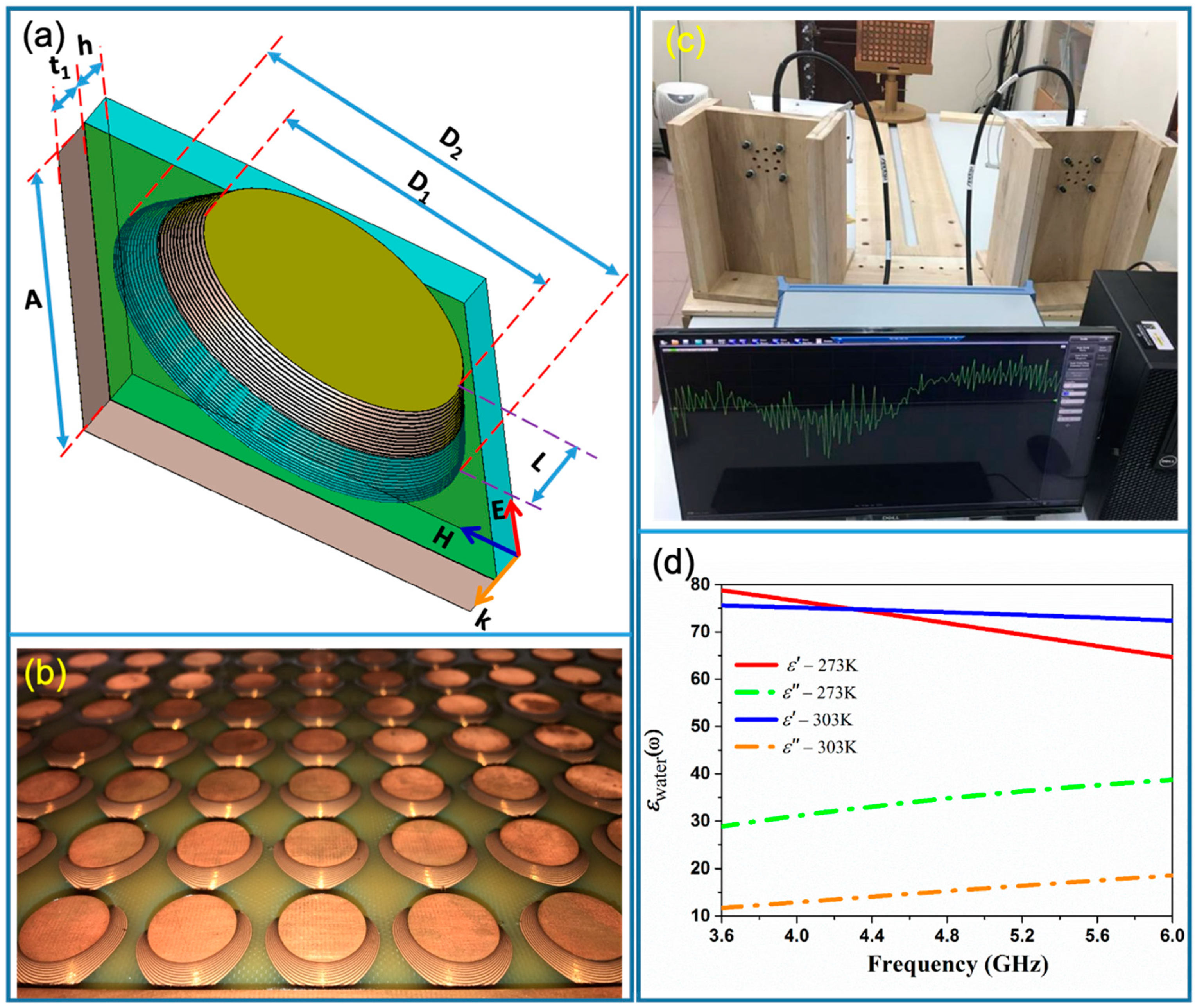
2. Materials and Methods
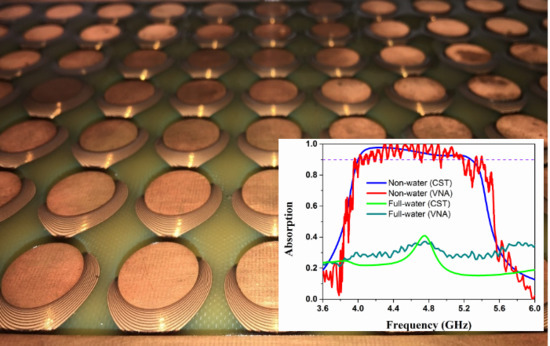
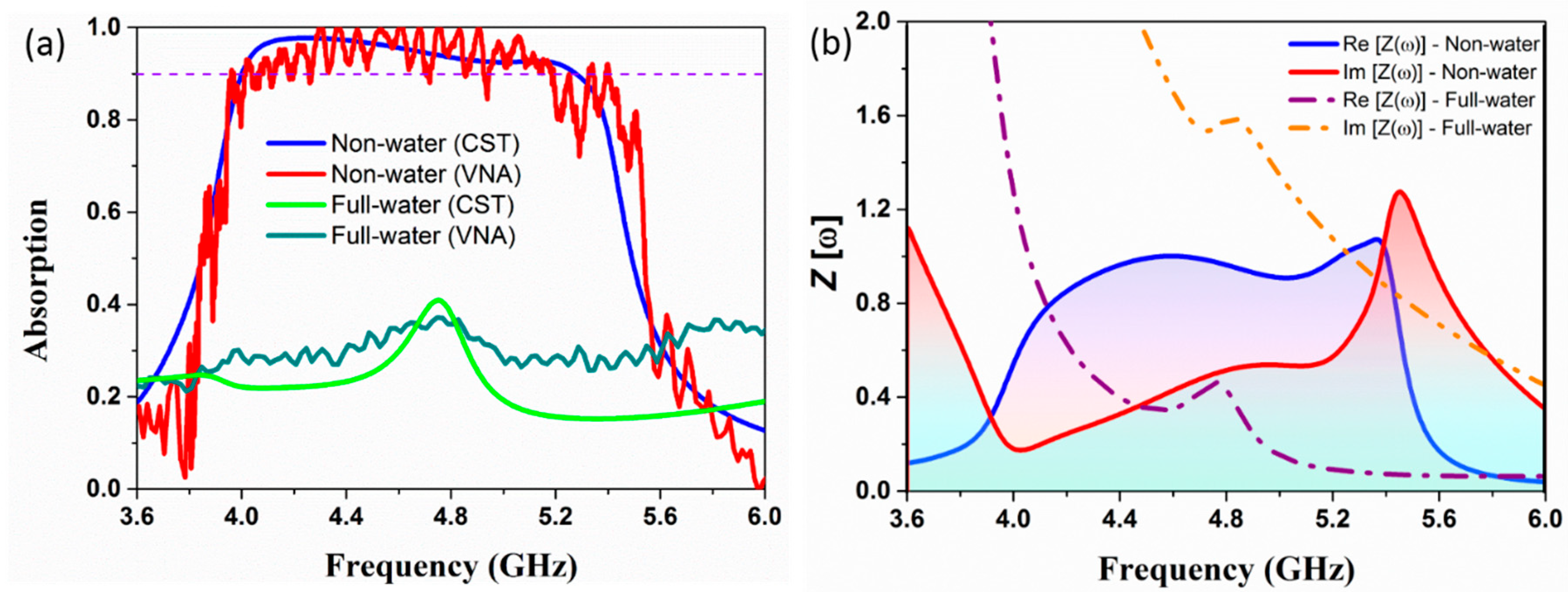
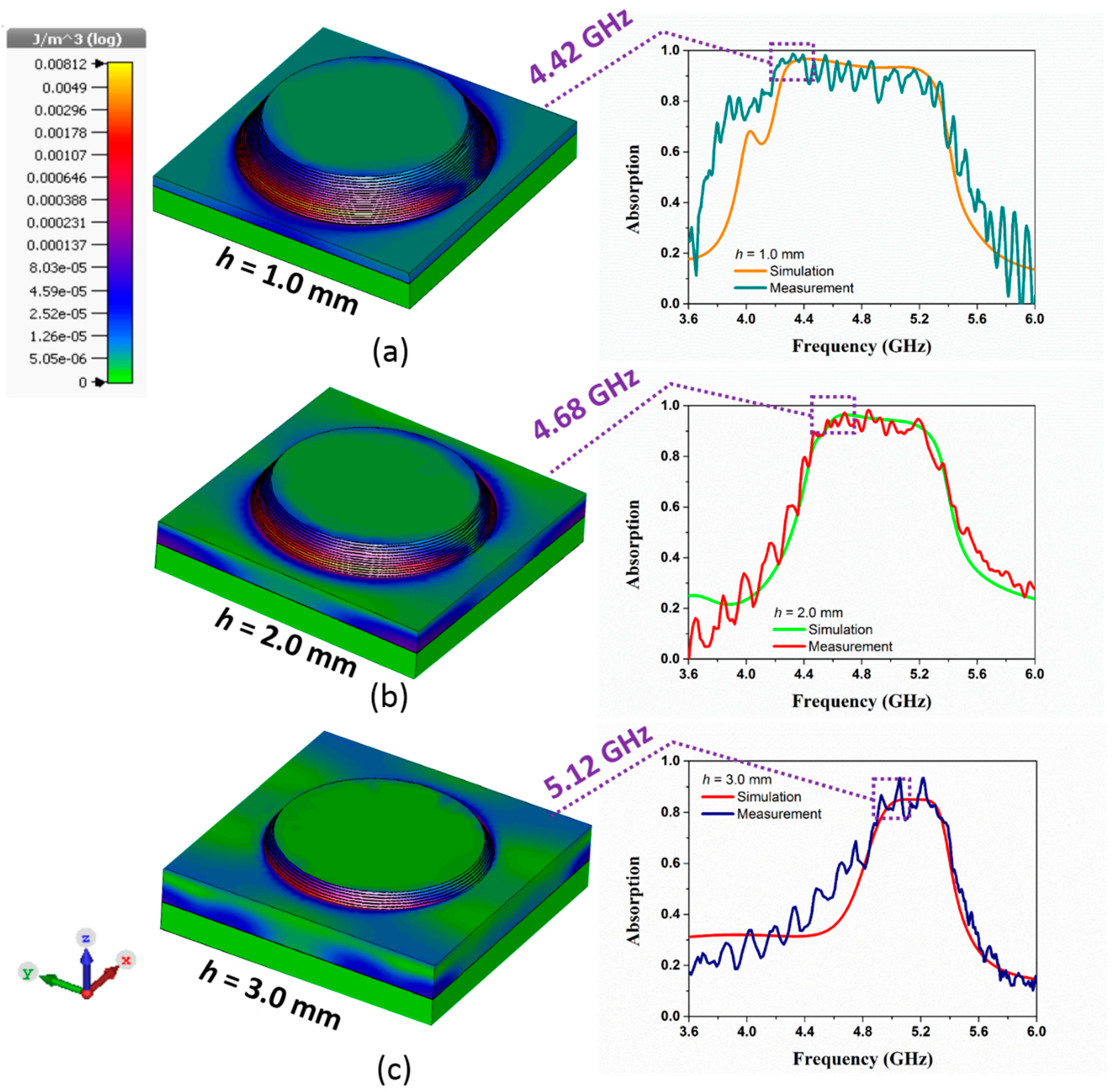
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Koschny, T.; Soukoulis, C.M.; Wegener, M. Metamaterials in microwaves, optics, mechanics, thermodynamics, and transport. J. Opt. 2017, 19, 084005. [Google Scholar] [CrossRef]
- Landy, N.I.; Sajuyigbe, S.; Mock, J.J.; Smith, D.R.; Padilla, W.J. Perfect Metamaterial Absorber. Phys. Rev. Lett. 2008, 100, 207402. [Google Scholar] [CrossRef] [PubMed]
- Knott, E.F.; Shaeffer, J.F.; Tuley, M.T. Radar Cross Section, 2nd ed.; SciTech Publishing, Inc.: NC, USA, 2004. [Google Scholar]
- Paul, C.R. Introduction to Electromagnetic Compatibility; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Khuyen, B.X.; Tung, B.S.; Tung, N.T.; Hien, N.; Kim, Y.J.; Chen, L.-Y.; Lee, Y.P.; Linh, P.T.; Lam, V.D. Realization for dual-band high-order perfect absorption, based on metamaterial. J. Phys. D: Appl. Phys. 2019, 53, 105502. [Google Scholar] [CrossRef]
- Tran, C.M.; Pham, H.V.; Nguyen, H.T.; Nguyen, T.T.; Vu, L.D.; Do, T.H. Creating Multiband and Broadband Metamaterial Absorber by Multiporous Square Layer Structure. Plasmonics 2019, 14, 1587–1592. [Google Scholar] [CrossRef]
- Wu, P.; Chen, Z.; Jile, H.; Zhang, C.; Xu, D.; Lv, L. An infrared perfect absorber based on metal-dielectric-metal multi-layerfilms with nanocircle holes arrays. Results Phys. 2020, 16, 1029522. [Google Scholar] [CrossRef]
- Park, H.; Lee, S.-Y.; Kim, J. Near-infrared coherent perfect absorption in plasmonic metal-insulator-metal waveguide. Opt. Express 2015, 23, 24464. [Google Scholar] [CrossRef]
- Li, W.; Guler, U.; Kinsey, N.; Naik, G.V.; Boltasseva, A.; Guan, J.; Shalaev, V.M.; Kildishev, A.V. Refractory Plasmonics with Titanium Nitride: Broadband Metamaterial Absorber. Adv. Mater. 2014, 26, 7959–7965. [Google Scholar] [CrossRef]
- Hedayati, M.K.; Javaherirahim, M.; Mozooni, B.; Abdelaziz, R.; Tavassolizadeh, A.; Chakravadhanula, V.S.K.; Zaporojtchenko, V.; Strunkus, T.; Faupel, F.; Elbahri, M.; et al. Design of a Perfect Black Absorber at Visible Frequencies Using Plasmonic Metamaterials. Adv. Mater. 2011, 23, 5410–5414. [Google Scholar] [CrossRef]
- Ding, F.; Cui, Y.; Ge, X.; Jin, Y.; He, S. Ultra-broadband microwave metamaterial absorber. Appl. Phys. Lett. 2012, 100, 103506. [Google Scholar] [CrossRef]
- Yu, P.; Besteiro, L.V.; Huang, Y.; Wu, J.; Fu, L.; Tan, H.H.; Jagadish, C.; Wiederrecht, G.P.; Govorov, A.O.; Wang, Z. Broadband Metamaterial Absorbers. Adv. Opt. Mater. 2018, 7, 1800995. [Google Scholar] [CrossRef]
- Deng, T.; Li, Z.-W.; Chua, M.-J.; Chen, Z.N. Broadband and Ultrathin Frequency-Dispersive Metamaterial Screen for Reflectivity Reduction. IEEE Trans. Antennas Propag. 2015, 63, 4156. [Google Scholar] [CrossRef]
- Zhu, J.; Ma, Z.; Sun, W.; Ding, F.; He, Q.; Zhou, L.; Ma, Y. Ultra-broadband terahertz metamaterial absorber. Appl. Phys. Lett. 2014, 105, 021102. [Google Scholar] [CrossRef]
- Yin, S.; Zhu, J.; Xu, W.; Jiang, W.; Yuan, J.; Yin, G.; Xie, L.; Ying, Y.; Ma, Y. High-performance terahertz wave absorbers made of silicon-based metamaterials. Appl. Phys. Lett. 2015, 107, 073903. [Google Scholar] [CrossRef]
- Cong, L.L.; Cao, X.Y.; Song, T.; Gao, J.; Lan, J.X. Angular- and Polarization-insensitive Ultrathin Double-layered Metamaterial Absorber for Ultra-wideband Application. Sci. Rep. 2018, 8, 9627. [Google Scholar] [CrossRef]
- Liu, H.; Wang, Z.-H.; Li, L.; Fan, Y.-X.; Tao, Z.-Y. Vanadium Dioxide-assisted Broadband Tunable Terahertz Metamaterial Absorber. Sci. Rep. 2019, 9, 5751. [Google Scholar] [CrossRef]
- Chen, L.; Sun, L.; Dong, H.; Mou, N.; Zhang, Y.; Li, Q.; Jiang, X.; Zhang, L. Near-field imaging of the multi-resonant mode induced broadband tunable metamaterial absorber. RSC Adv. 2020, 10, 5146–5151. [Google Scholar] [CrossRef]
- Zhang, H.; Ling, F.; Wang, H.; Zhang, Y.; Zhang, B. A water hybrid graphene metamaterial absorber with broadband absorption. Opt. Commun. 2020, 463, 125394. [Google Scholar] [CrossRef]
- Huynh, T.V.; Tung, B.S.; Khuyen, B.X.; Tung, N.T.; Lam, V.D. Electrically tunable graphene-based metamaterials: A brief review. Mod. Phys. Lett. B 2019, 33, 1950404. [Google Scholar] [CrossRef]
- Buchner, R.; Barthel, J.; Stauber, J. The dielectric relaxation of water between 0°C and 35°C. Chem. Phys. Lett. 1999, 306, 57–63. [Google Scholar] [CrossRef]
- Andryieuski, A.; Kuznetsova, S.M.; Zhukovsky, S.V.; Kivshar, Y.S.; Lavrinenko, A.V. Water: Promising Opportunities for Tunable All-dielectric Electromagnetic Metamaterials. Sci. Rep. 2015, 5, 13535. [Google Scholar] [CrossRef]
- Shen, Y.; Zhang, J.; Pang, Y.; Zheng, L.; Wang, J.; Ma, H.; Qu, S. Thermally Tunable Ultra-wideband Metamaterial Absorbers based on Three-dimensional Water-substrate Construction. Sci. Rep. 2018, 8, 4423. [Google Scholar] [CrossRef] [PubMed]
- Pang, Y.; Wang, J.; Cheng, Q.; Xia, S.; Zhou, X.-Y.; Xu, Z.; Cui, T.J.; Qu, S. Thermally tunable water-substrate broadband metamaterial absorbers. Appl. Phys. Lett. 2017, 110, 104103. [Google Scholar] [CrossRef]
- Wu, Z.; Chen, X.; Zhang, Z.; Heng, L.; Wang, S.; Zou, Y. Design and optimization of a flexible water-based microwave absorbing metamaterial. Appl. Phys. Express 2019, 12, 057003. [Google Scholar] [CrossRef]
- Zhou, Y.; Shen, Z.; Huang, X.; Wu, J.; Li, Y.; Huang, S.; Yang, H. Ultra-wideband water-based metamaterial absorber with temperature insensitivity. Phys. Lett. A 2019, 383, 2739–2743. [Google Scholar] [CrossRef]
- Zhou, Y.; Shen, Z.; Wu, J.; Zhang, Y.; Huang, S.; Yang, H. Design of ultra-wideband and near-unity absorption water-based metamaterial absorber. Appl. Phys. A 2020, 126, 1–5. [Google Scholar] [CrossRef]
- Yoo, Y.J.; Ju, S.; Park, S.Y.; Kim, Y.J.; Bong, J.; Lim, T.; Kim, K.W.; Rhee, J.Y.; Lee, Y.P. Metamaterial Absorber for Electromagnetic Waves in Periodic Water Droplets. Sci. Rep. 2015, 5, 14018. [Google Scholar] [CrossRef]
- Song, Q.; Zhang, W.; Wu, P.C.; Zhu, W.; Shen, Z.X.; Chong, P.H.; Liang, Q.X.; Yang, Z.C.; Hao, Y.L.; Cai, H.; et al. Water-Resonator-Based Metasurface: An Ultrabroadband and Near-Unity Absorption. Adv. Opt. Mater. 2017, 5, 1601103. [Google Scholar] [CrossRef]
- Pang, Y.; Shen, Y.; Li, Y.; Wang, J.; Xu, Z.; Qu, S. Water-based metamaterial absorbers for optical transparency and broadband microwave absorption. J. Appl. Phys. 2018, 123, 155106. [Google Scholar] [CrossRef]
- Rybin, M.; Samusev, K.B.; Kapitanova, P.; Filonov, D.S.; Belov, P.A.; Kivshar, Y.S.; Limonov, M. Switchable invisibility of dielectric resonators. Phys. Rev. B 2017, 95, 165119. [Google Scholar] [CrossRef]
- Ellison, W. Permittivity of pure water, at standard atmospheric pressure, over the frequency range 0–25 THz and the temperature range 0–100◦C. J. Phys. Chem. Ref. Data 2007, 36, 1–18. [Google Scholar] [CrossRef]
- Liebe, H.J.; Hufford, G.A.; Manabe, T. A model for the complex permittivity of water at frequencies below 1 THz. Int. J. Infrared Millim. Waves 1991, 12, 659–675. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Srivastava, K.V. Triple band polarization-independent ultra-thin metamaterial absorber using electric field-driven LC resonator. J. Appl. Phys. 2014, 115, 64508. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M.; Pitaevskii, L.P. Electrodynamics of Continuous Media, 2nd ed.; Section 87, 301; Pergamon Press: New York, NY, USA, 1984. [Google Scholar]
- Kim, Y.J.; Yoo, Y.J.; Kim, K.W.; Rhee, J.Y.; Kim, Y.H.; Lee, Y.P. Dual broadband metamaterial absorber. Opt. Express 2015, 23, 3861–3868. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Wei, S.; Wang, C.; Chen, K.; Zhu, B.; Jiang, T.; Feng, Y.-J. Broadband microwave absorption utilizing water-based metamaterial structures. Opt. Express 2018, 26, 8522–8531. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khuyen, B.X.; Hanh, V.T.H.; Tung, B.S.; Lam, V.D.; Kim, Y.J.; Lee, Y.; Tu, H.-T.; Chen, L.Y. Narrow/Broad-Band Absorption Based on Water-Hybrid Metamaterial. Crystals 2020, 10, 415. https://doi.org/10.3390/cryst10050415
Khuyen BX, Hanh VTH, Tung BS, Lam VD, Kim YJ, Lee Y, Tu H-T, Chen LY. Narrow/Broad-Band Absorption Based on Water-Hybrid Metamaterial. Crystals. 2020; 10(5):415. https://doi.org/10.3390/cryst10050415
Chicago/Turabian StyleKhuyen, Bui Xuan, Vu Thi Hong Hanh, Bui Son Tung, Vu Dinh Lam, Young Ju Kim, YoungPak Lee, Hua-Tian Tu, and Liang Yao Chen. 2020. "Narrow/Broad-Band Absorption Based on Water-Hybrid Metamaterial" Crystals 10, no. 5: 415. https://doi.org/10.3390/cryst10050415
APA StyleKhuyen, B. X., Hanh, V. T. H., Tung, B. S., Lam, V. D., Kim, Y. J., Lee, Y., Tu, H.-T., & Chen, L. Y. (2020). Narrow/Broad-Band Absorption Based on Water-Hybrid Metamaterial. Crystals, 10(5), 415. https://doi.org/10.3390/cryst10050415