A Review of Acoustic Metamaterials and Phononic Crystals
Abstract
1. Research Background
2. Basic Concept of Acoustic Metamaterials and Phononic Crystals
2.1. Proposals for Acoustic Metamaterials and Phononic Crystals
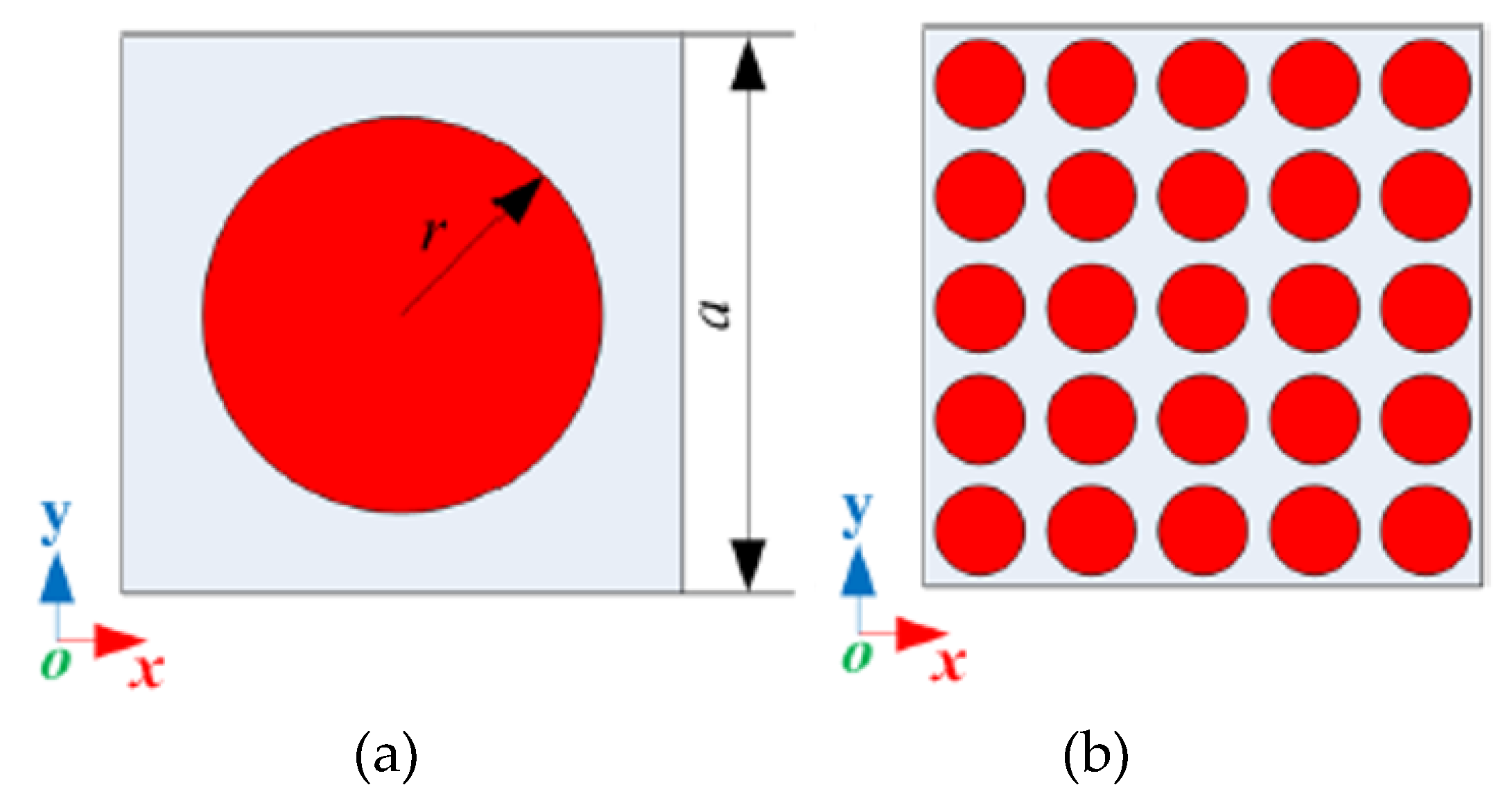
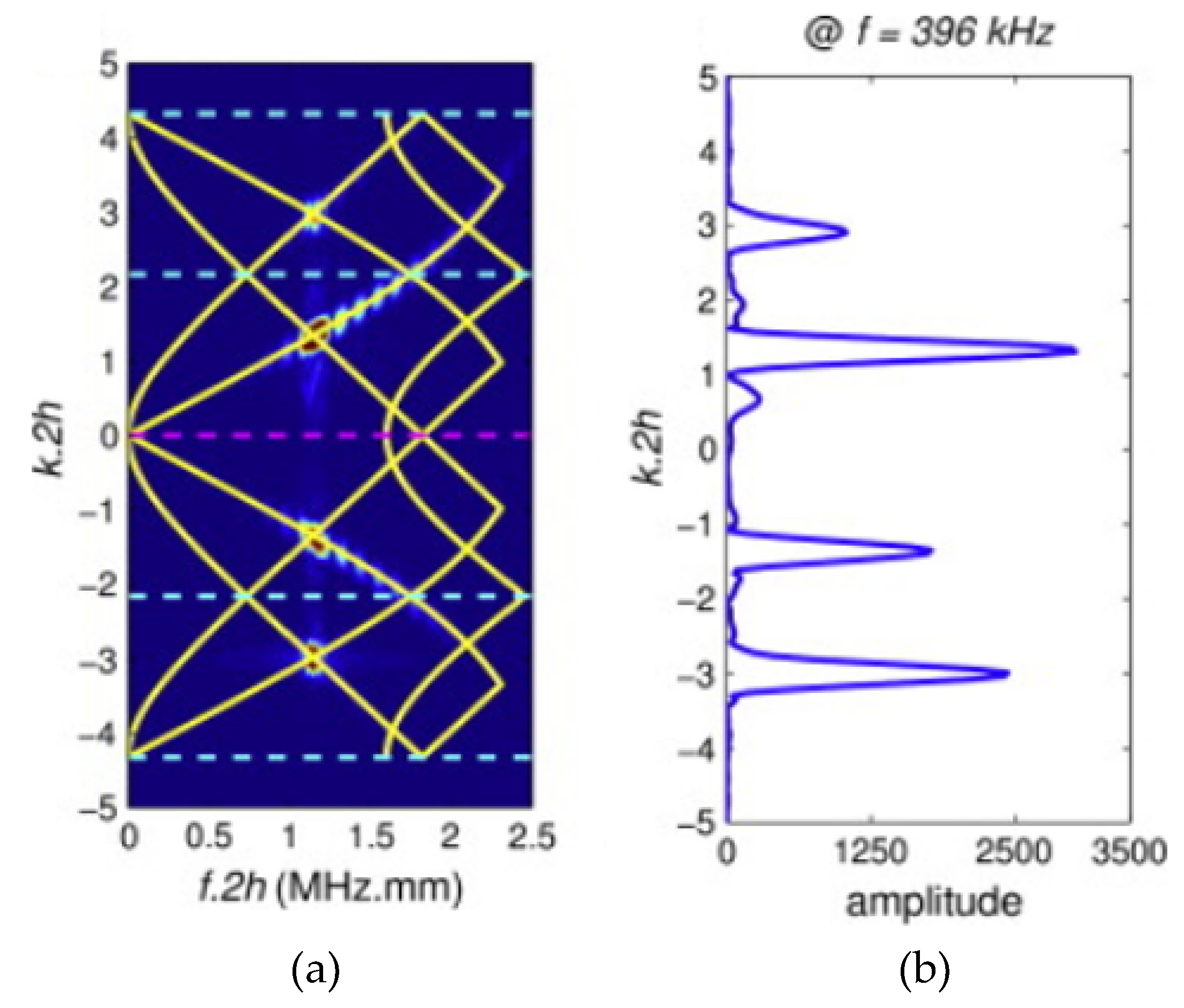
2.2. Band Structure Calculation Method of Phononic Crystal and Acoustic Metamaterials
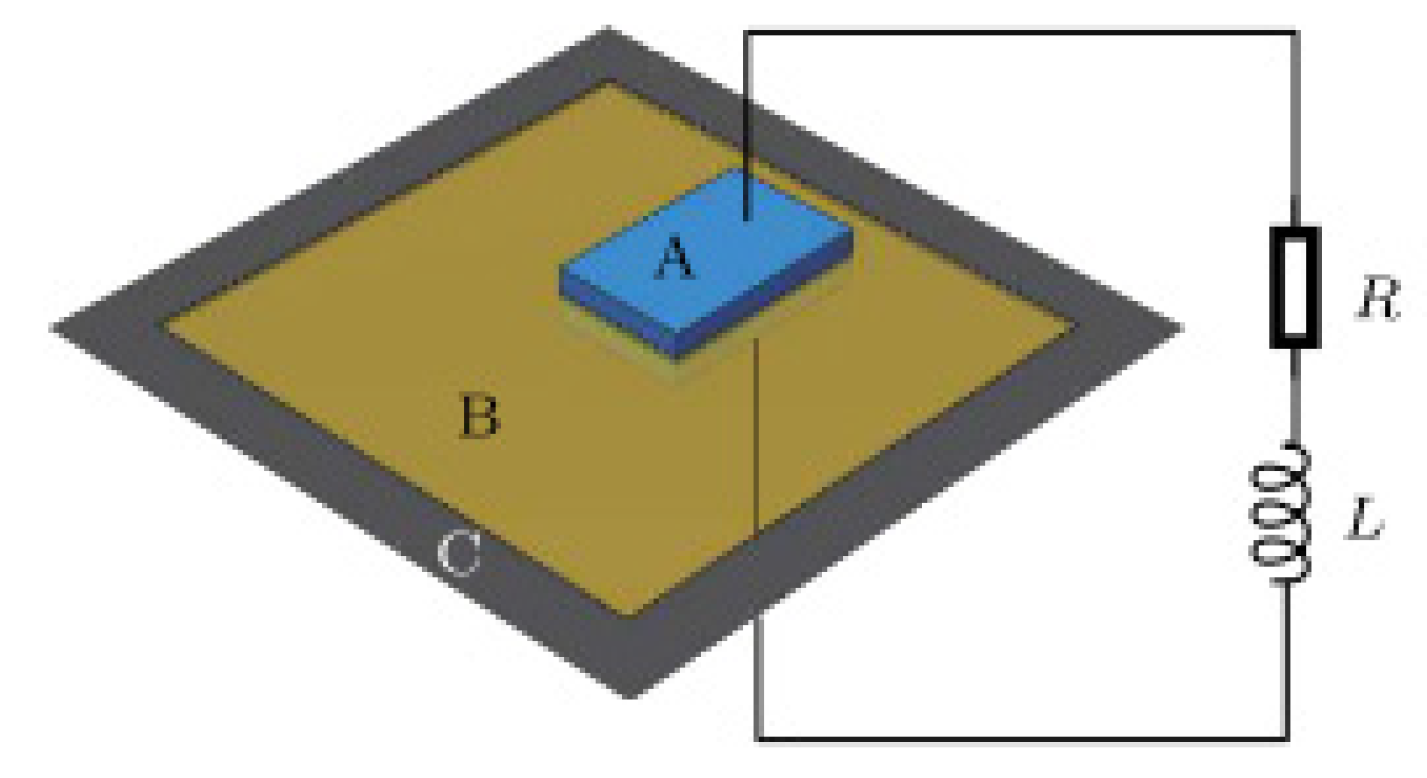
3. Equivalent Acoustic Parameters of Acoustic Metamaterials
4. Typical Types of Acoustic Metamaterials and Phononic Crystals
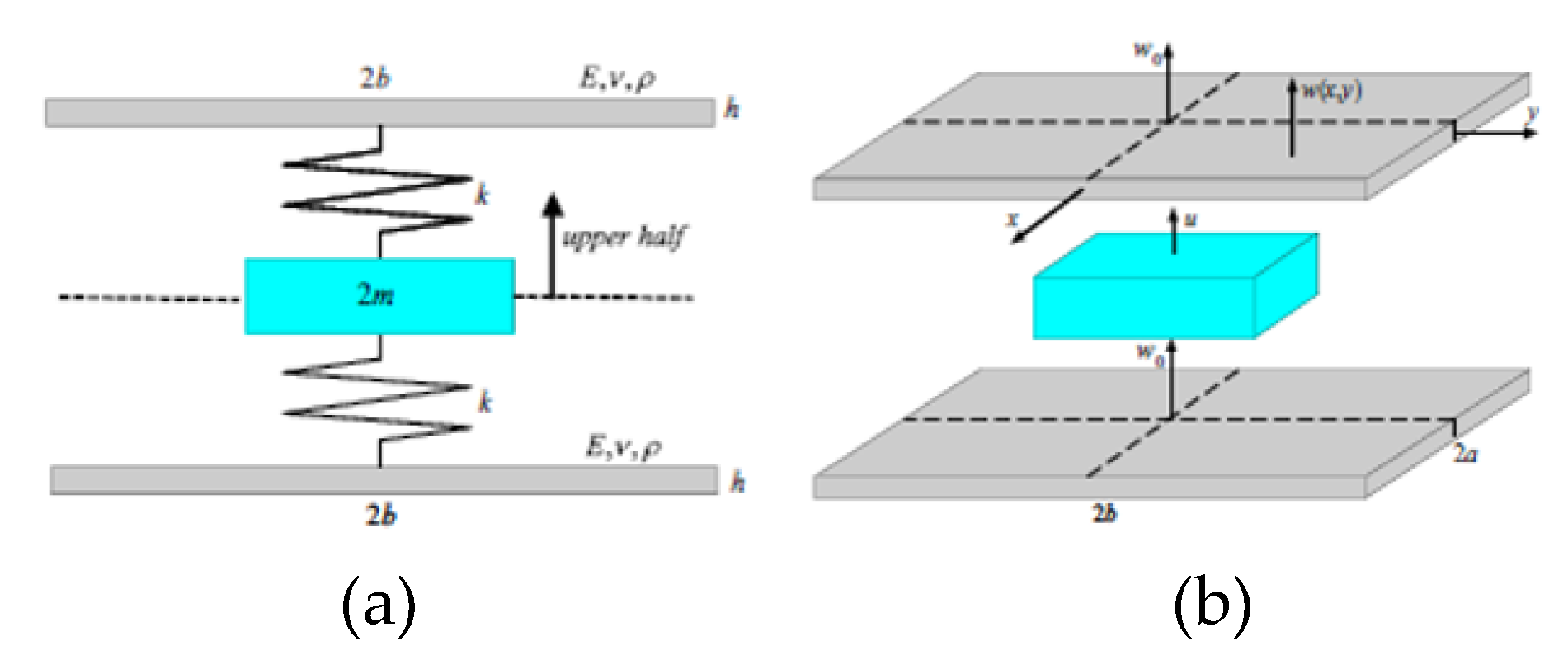
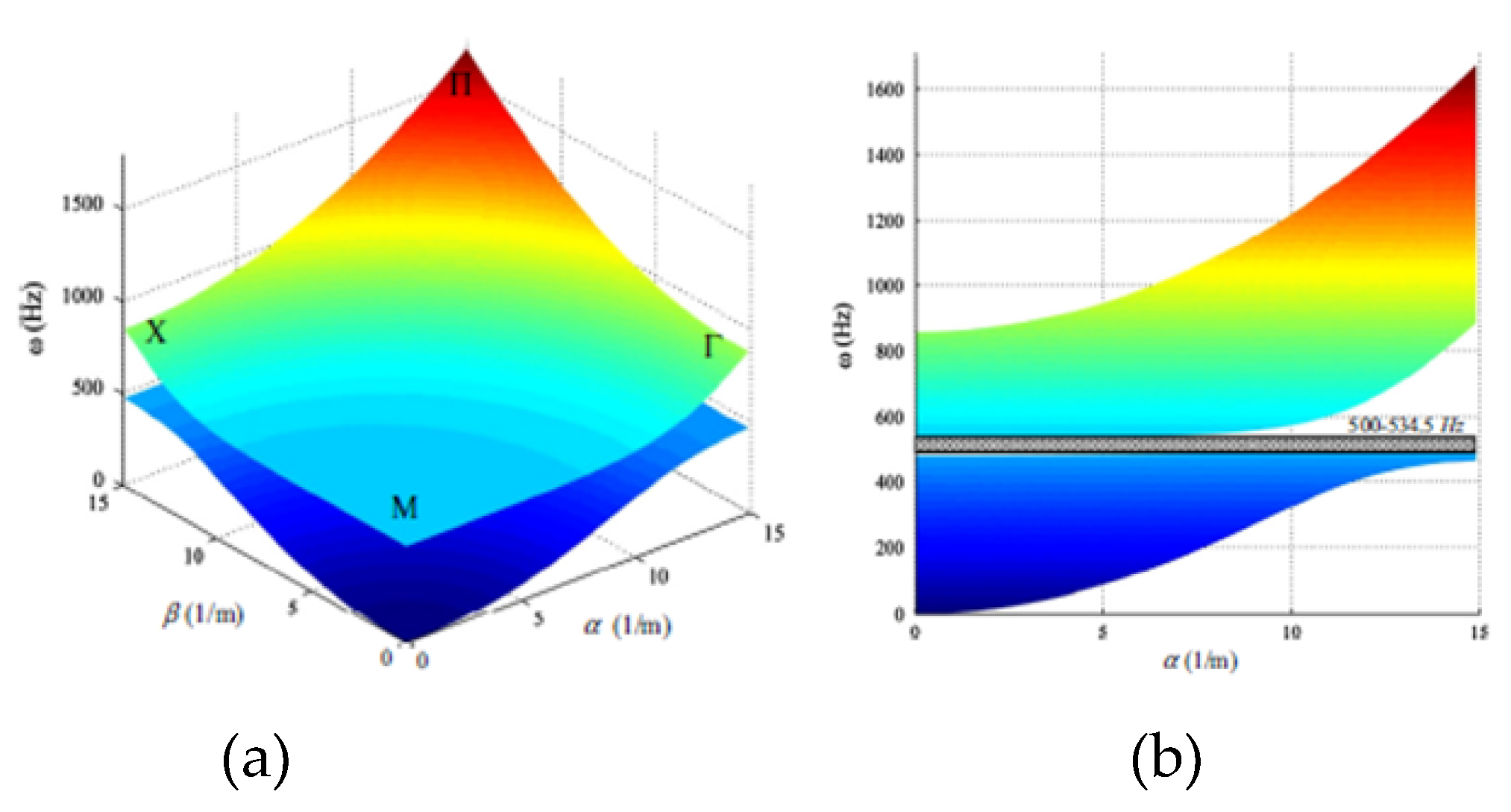
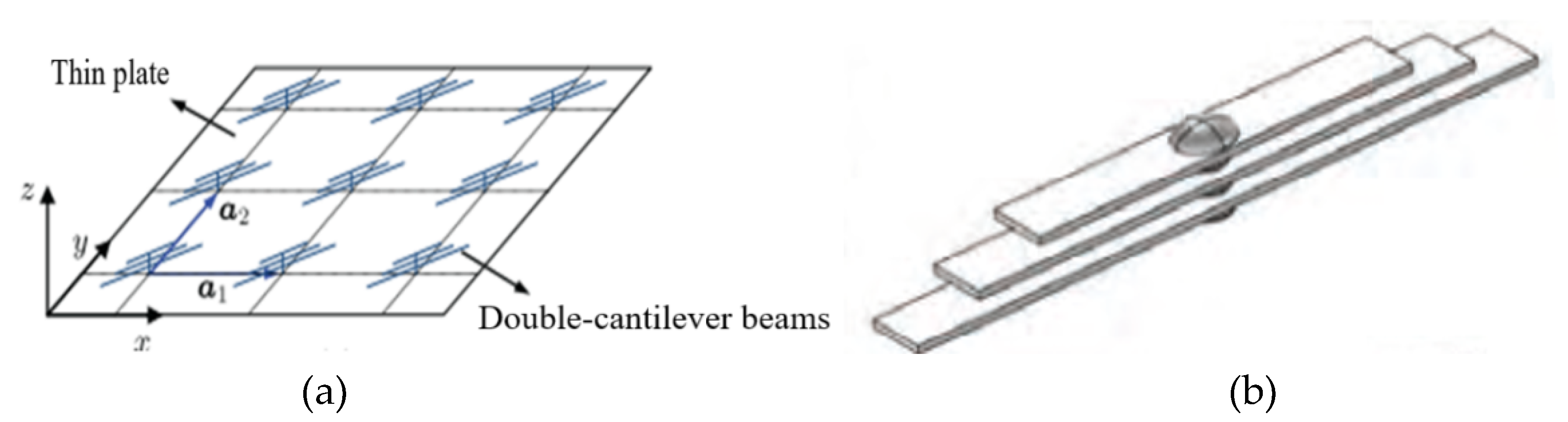
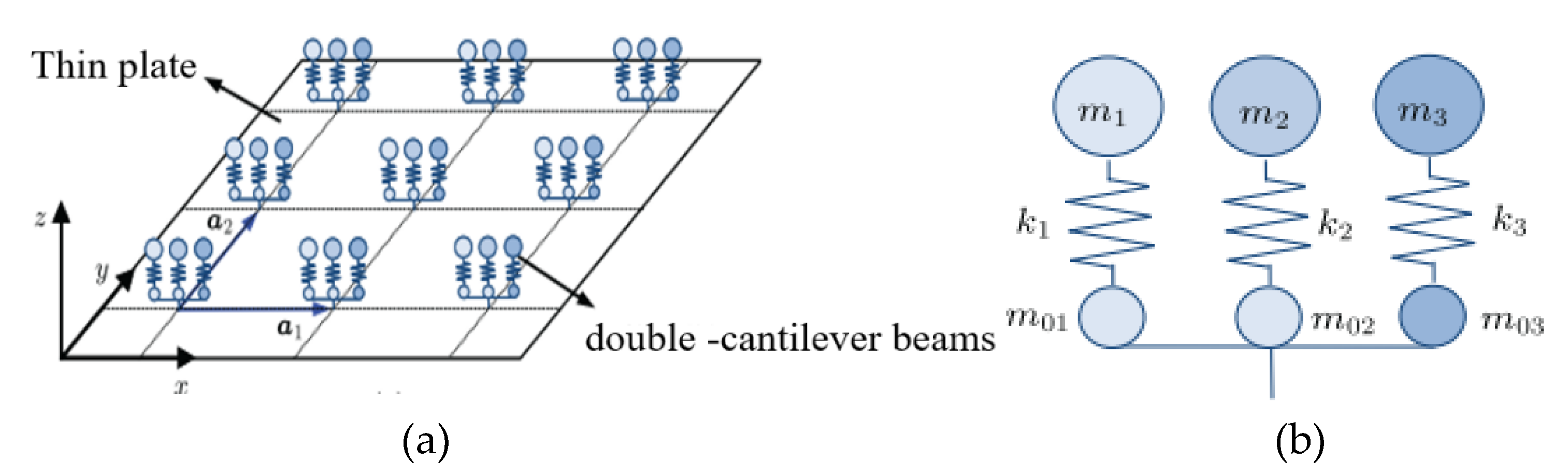
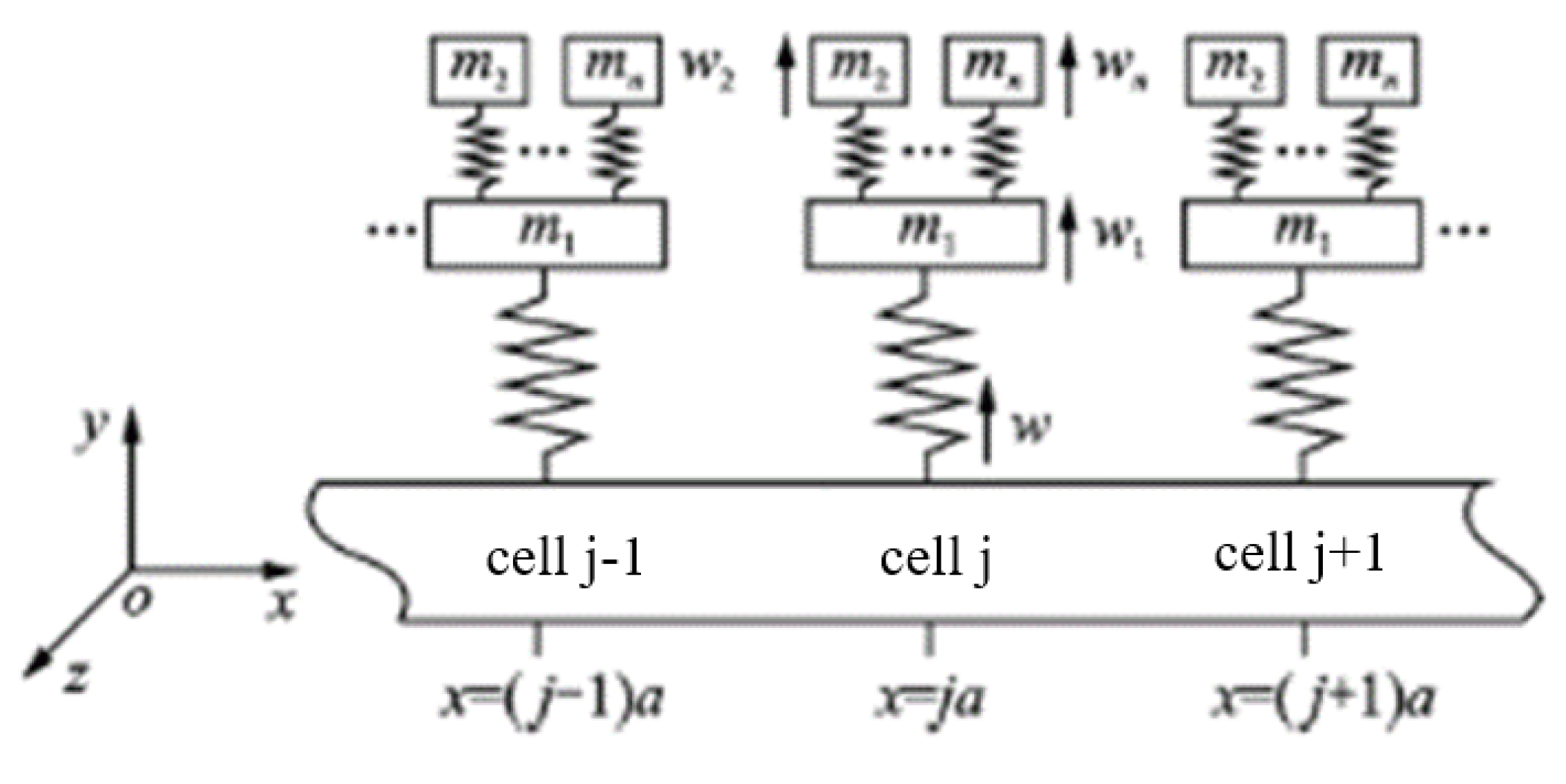
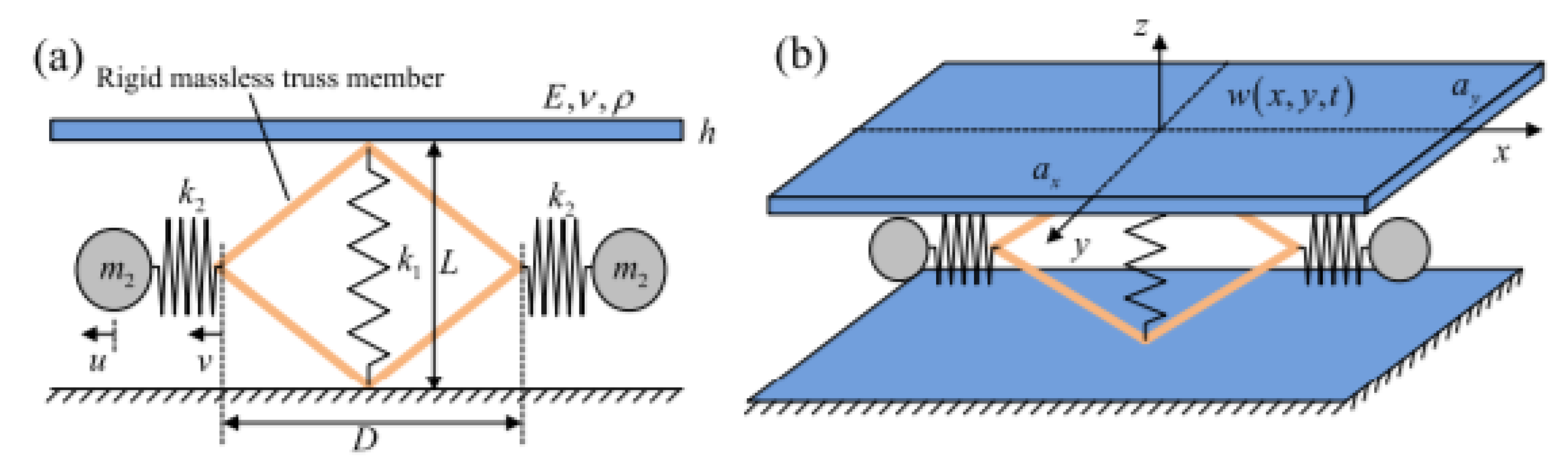
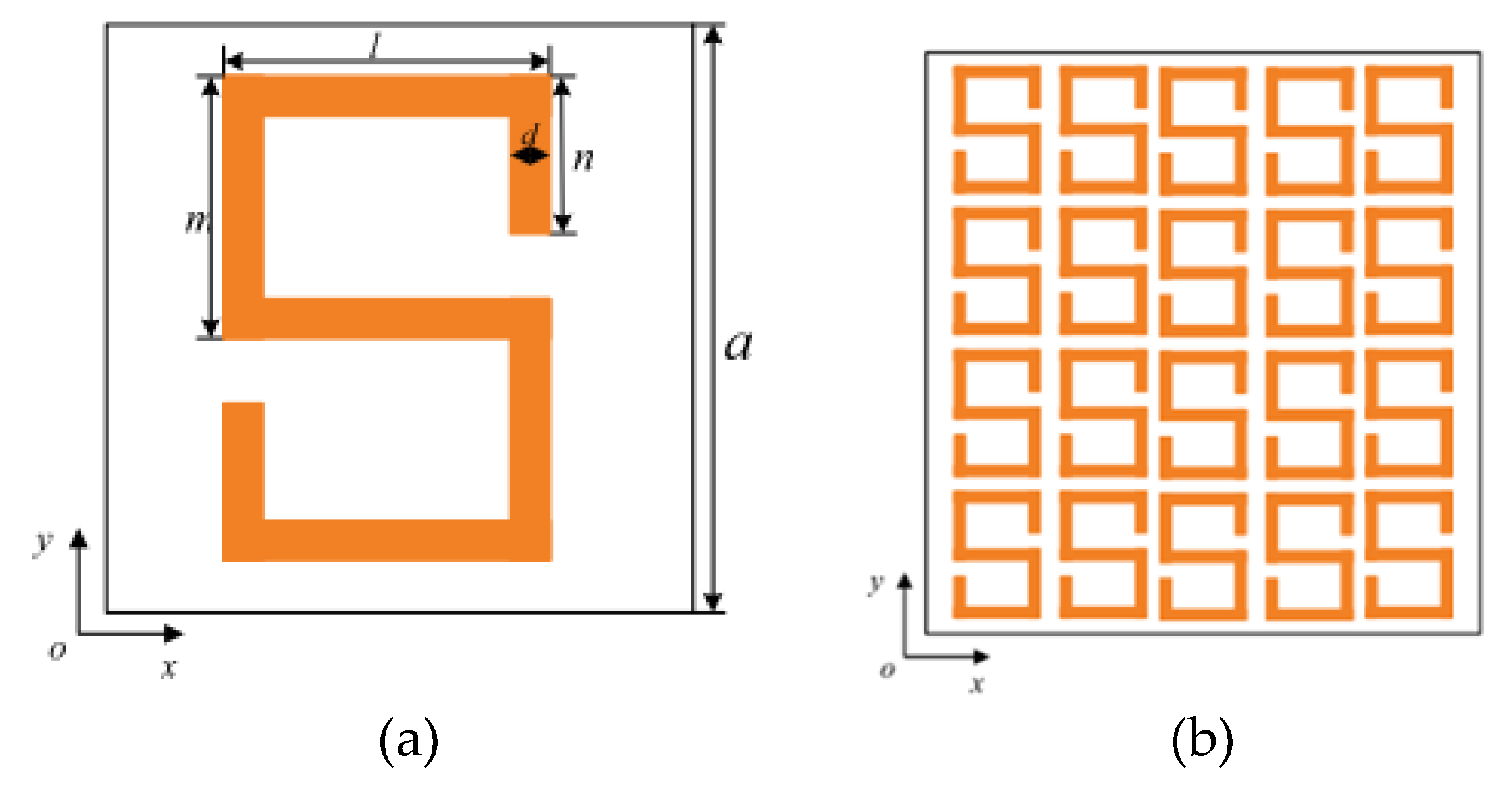
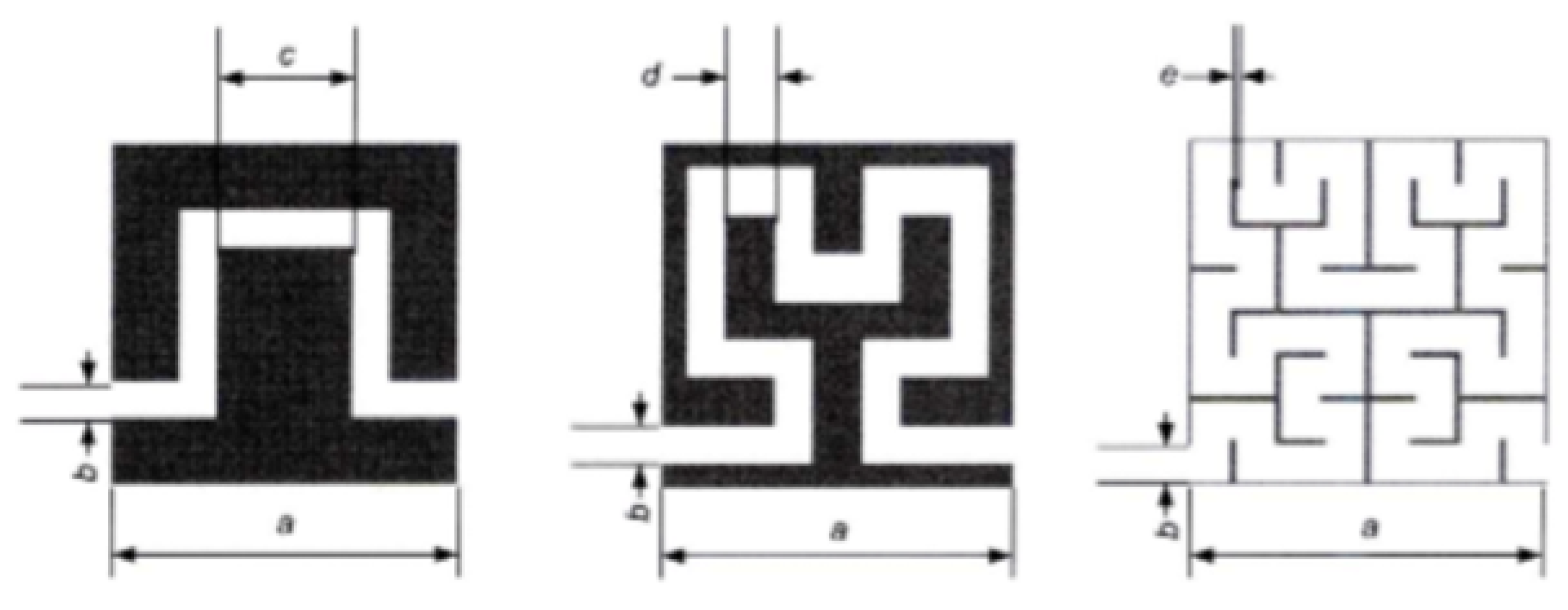
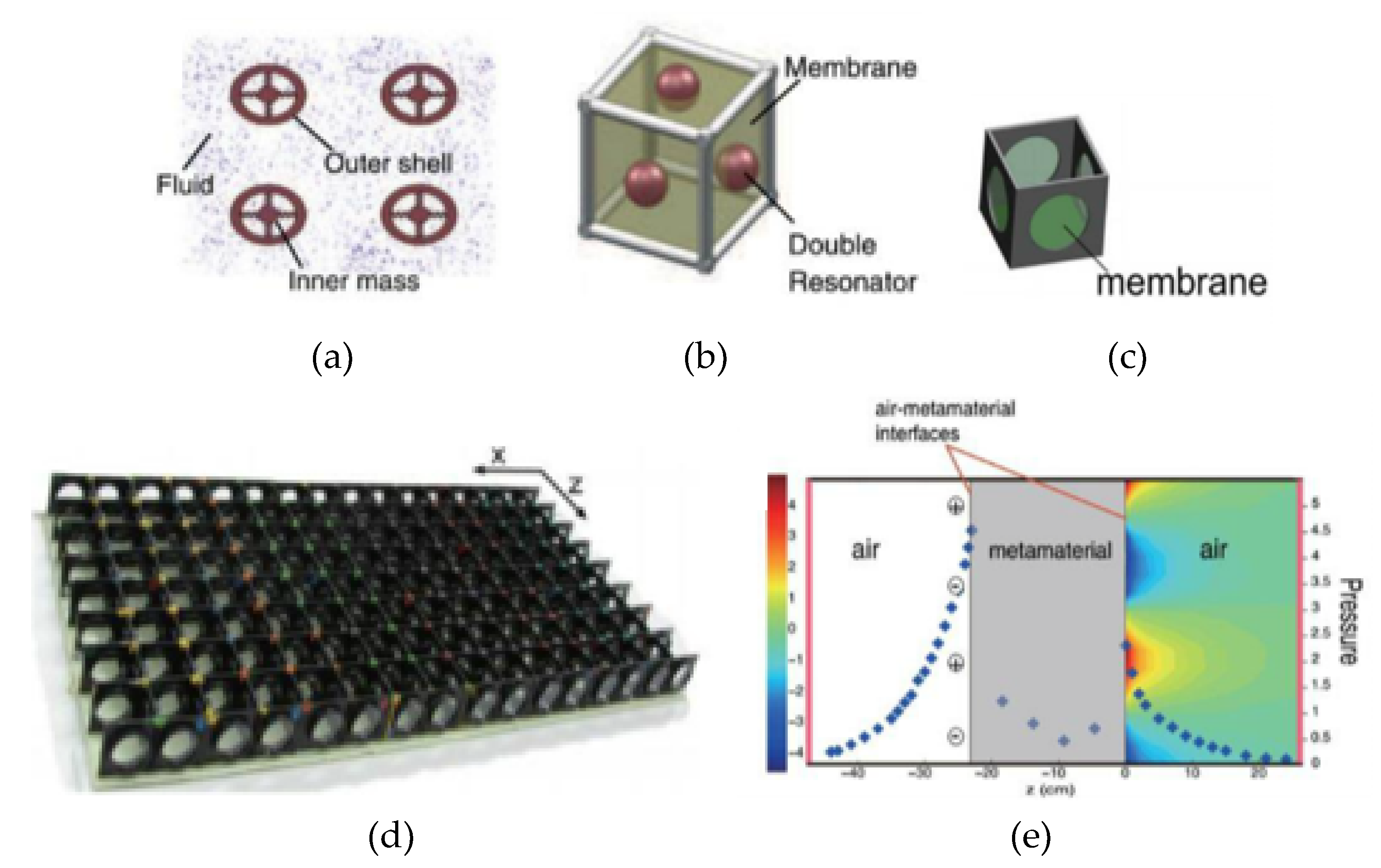
4.1. Structures Composed of Functional Units with Certain Mechanical Characteristics
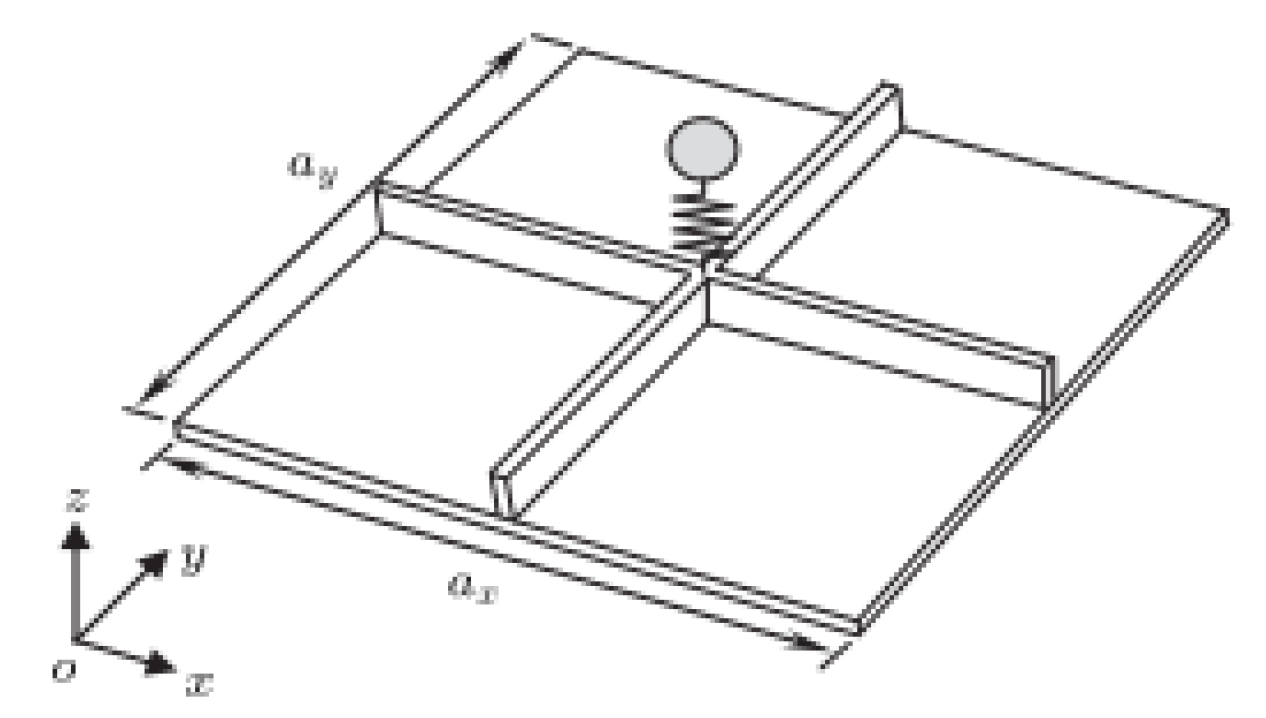
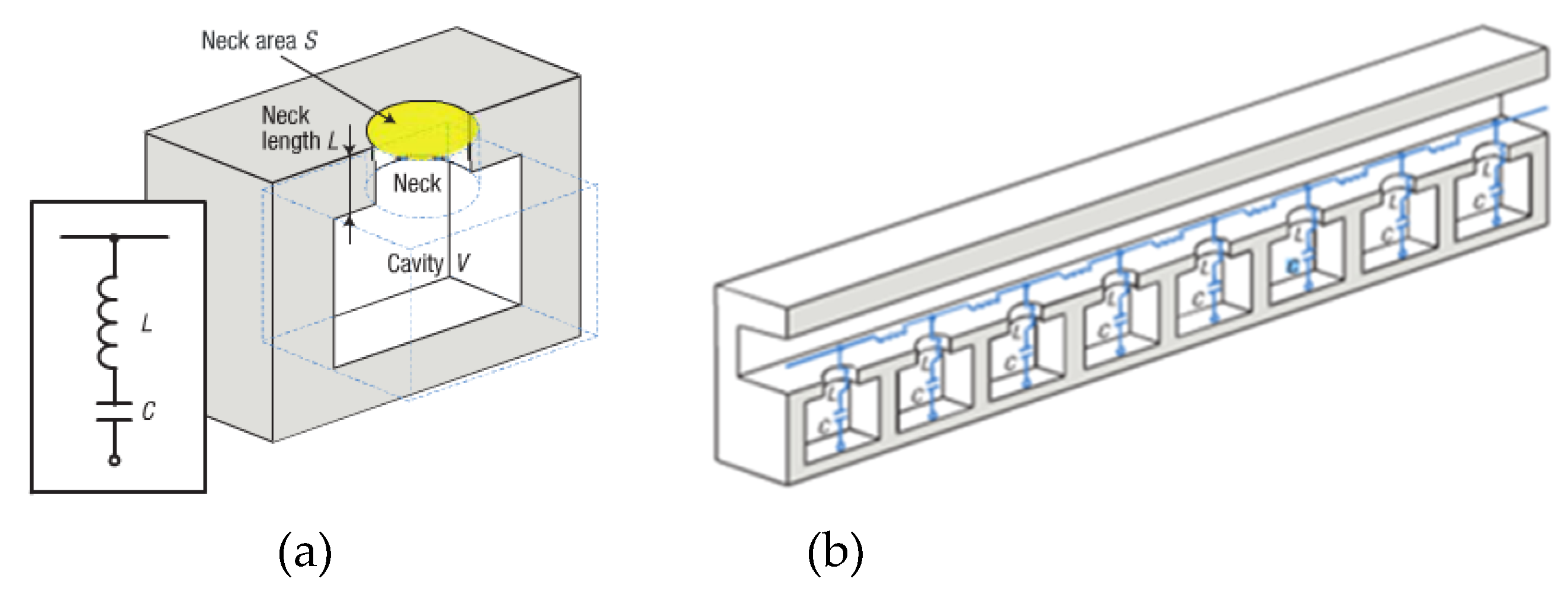
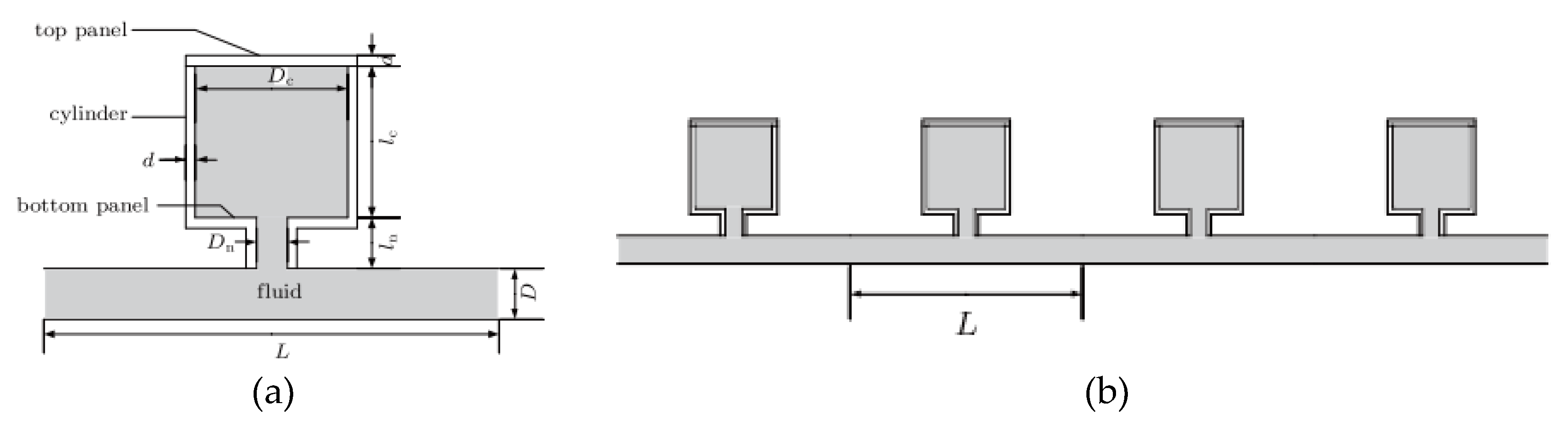
4.2. Helmholtz Resonator Periodic Arrangement Structures
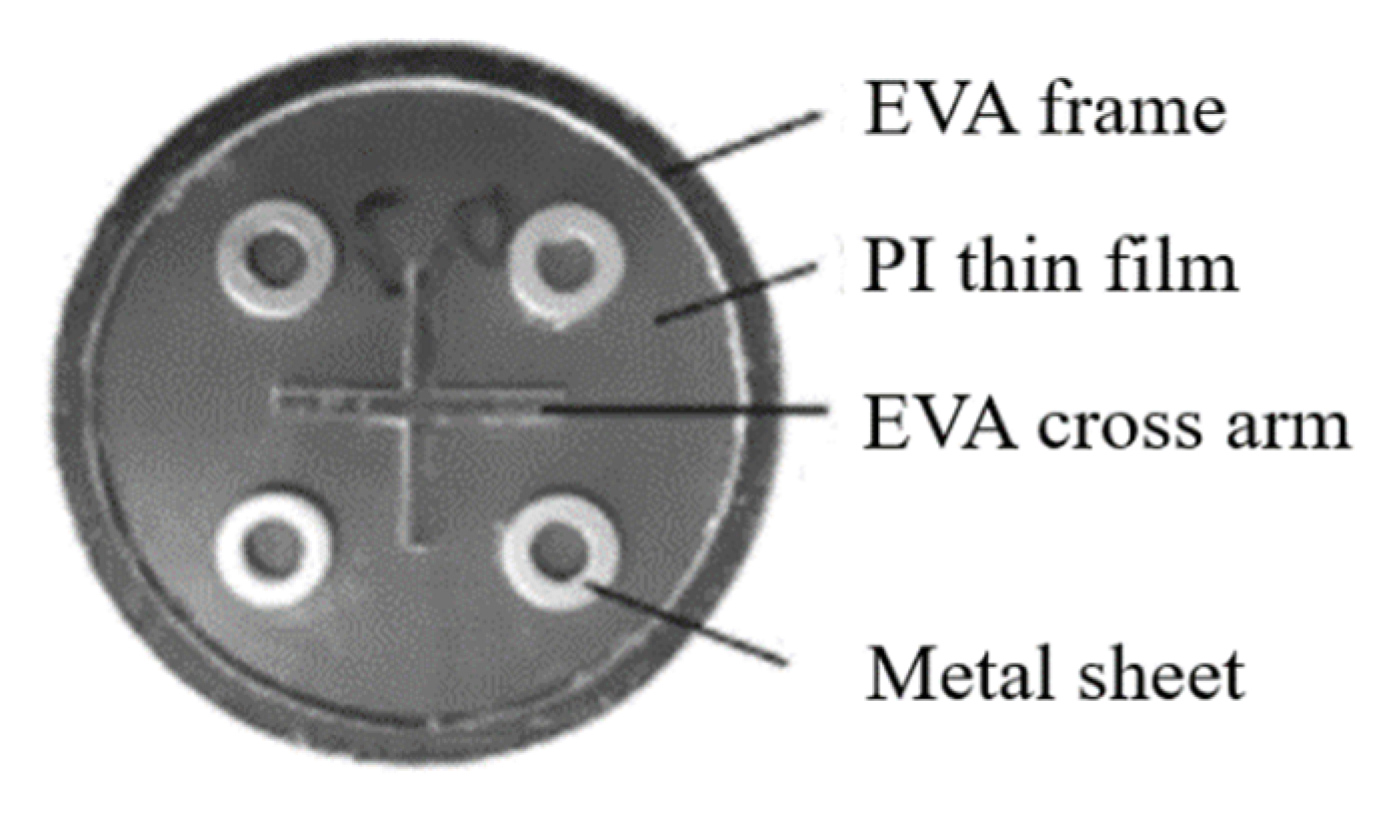
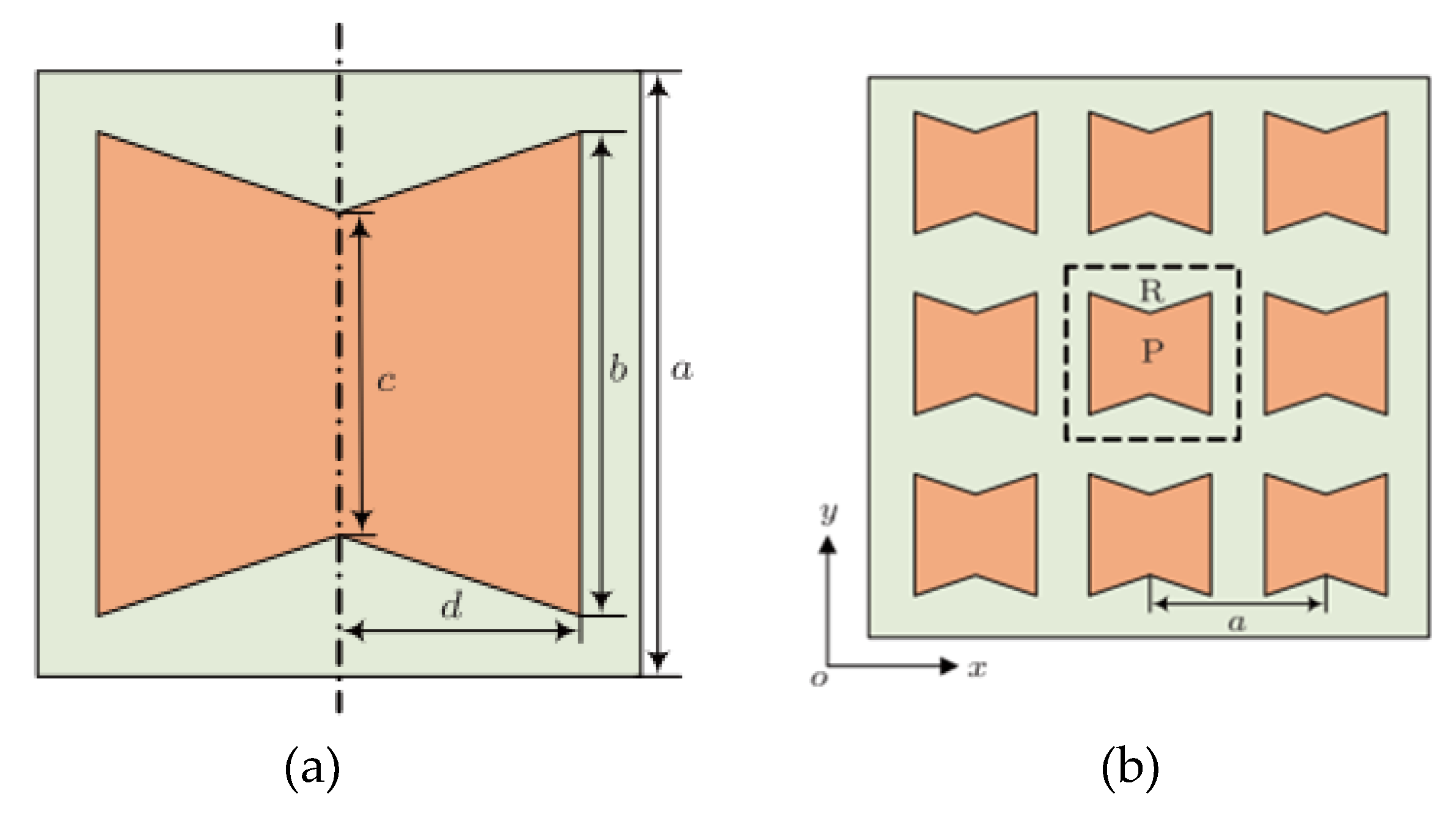
4.3. Thin Film Acoustic Metamaterials
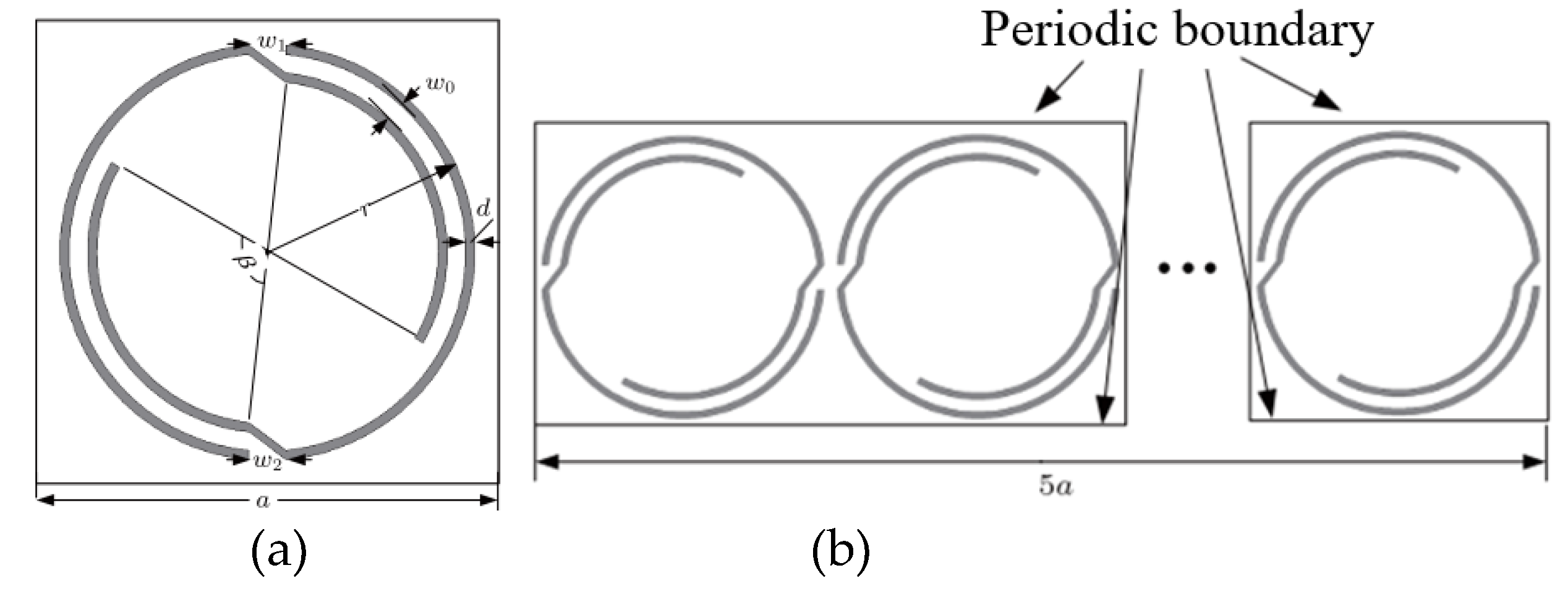
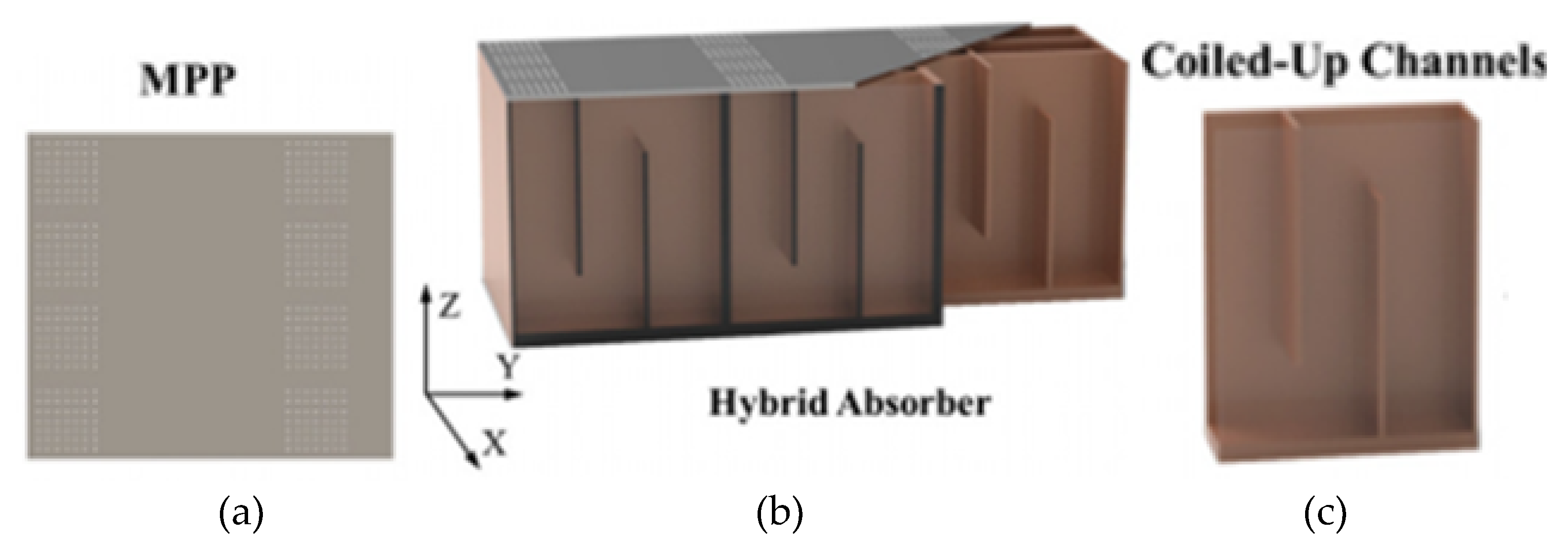
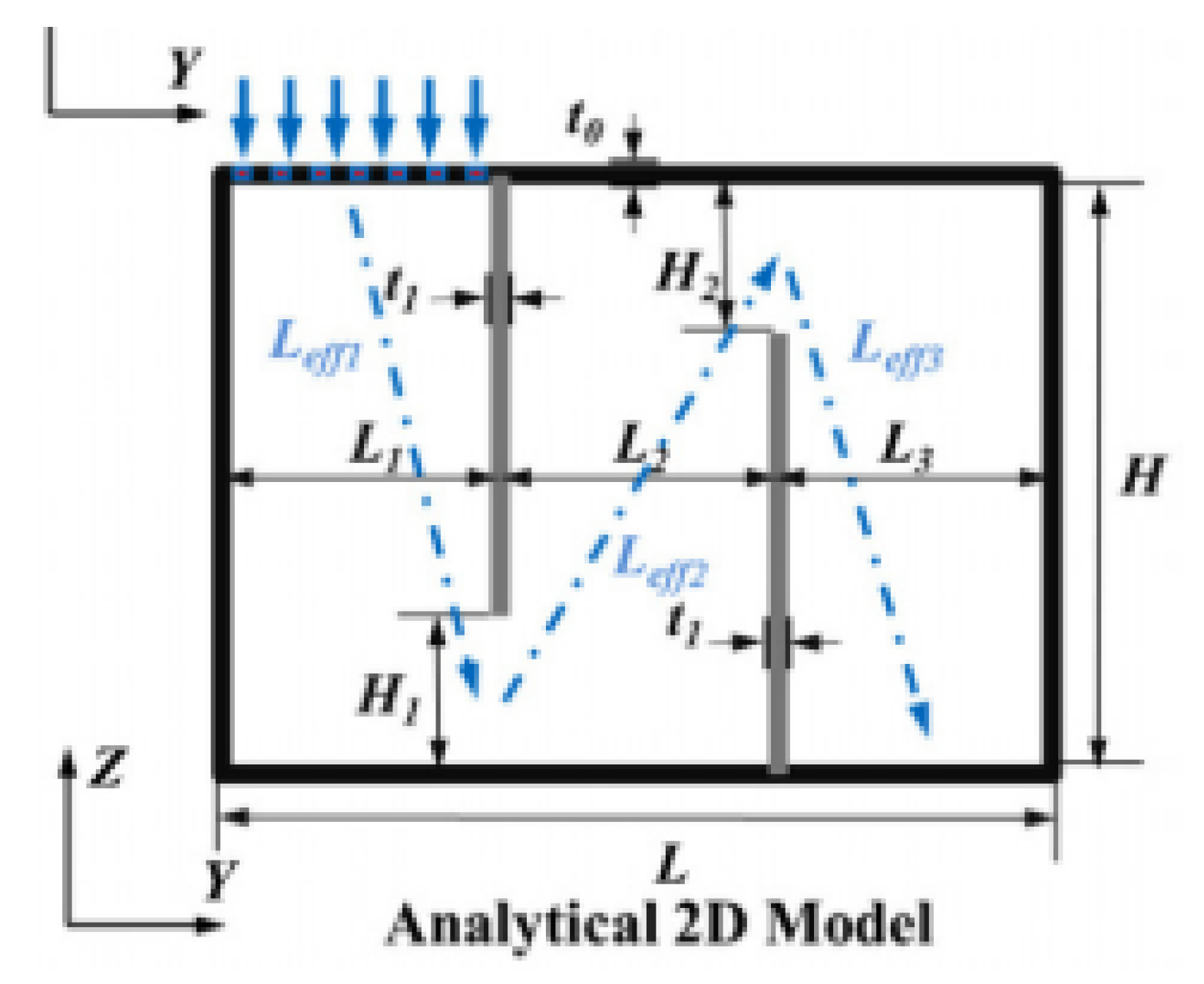
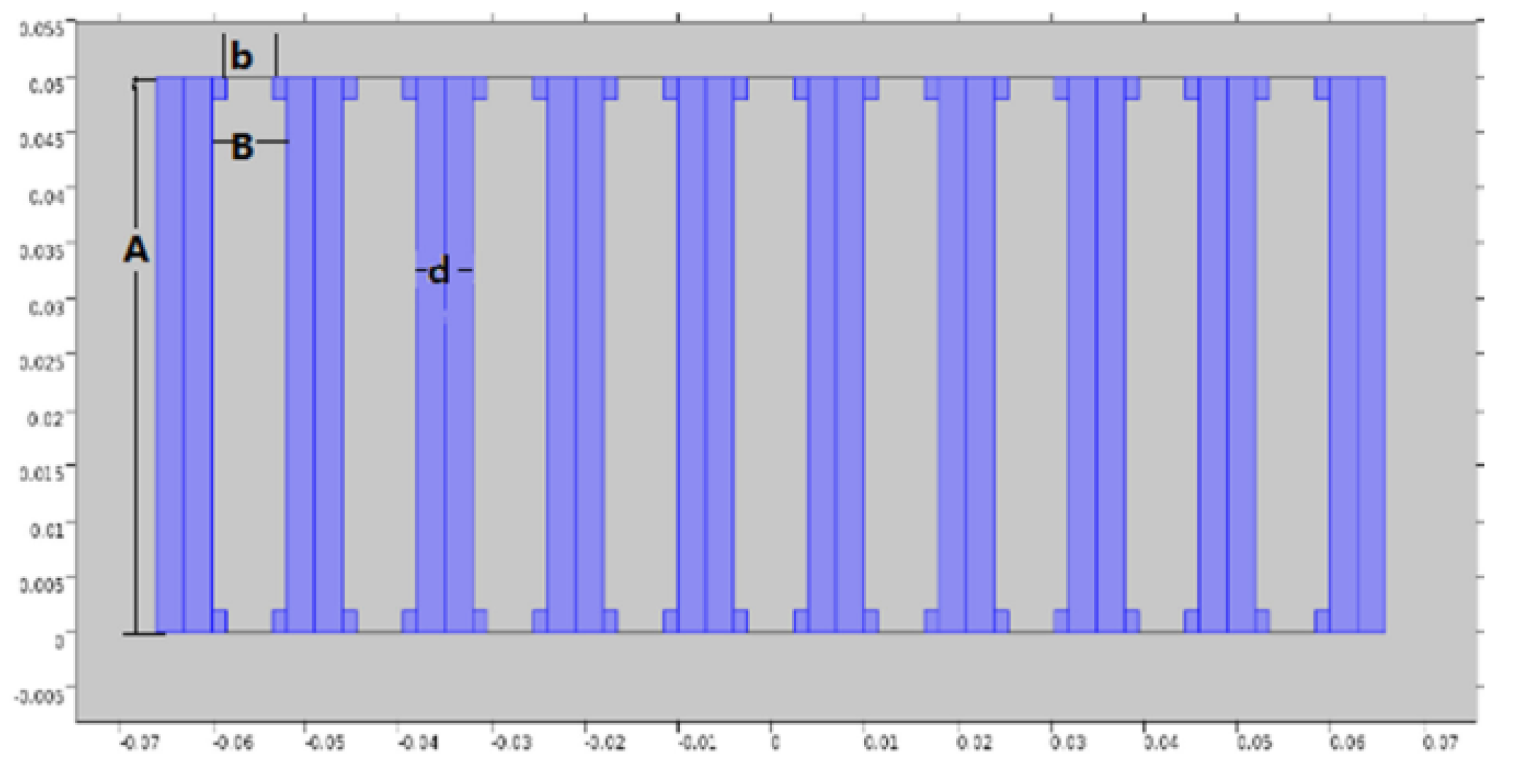
4.4. Space Coiling Structures
4.5. Other Structures
5. The Extraordinary Properties of Acoustic Metamaterials and Phononic Crystals
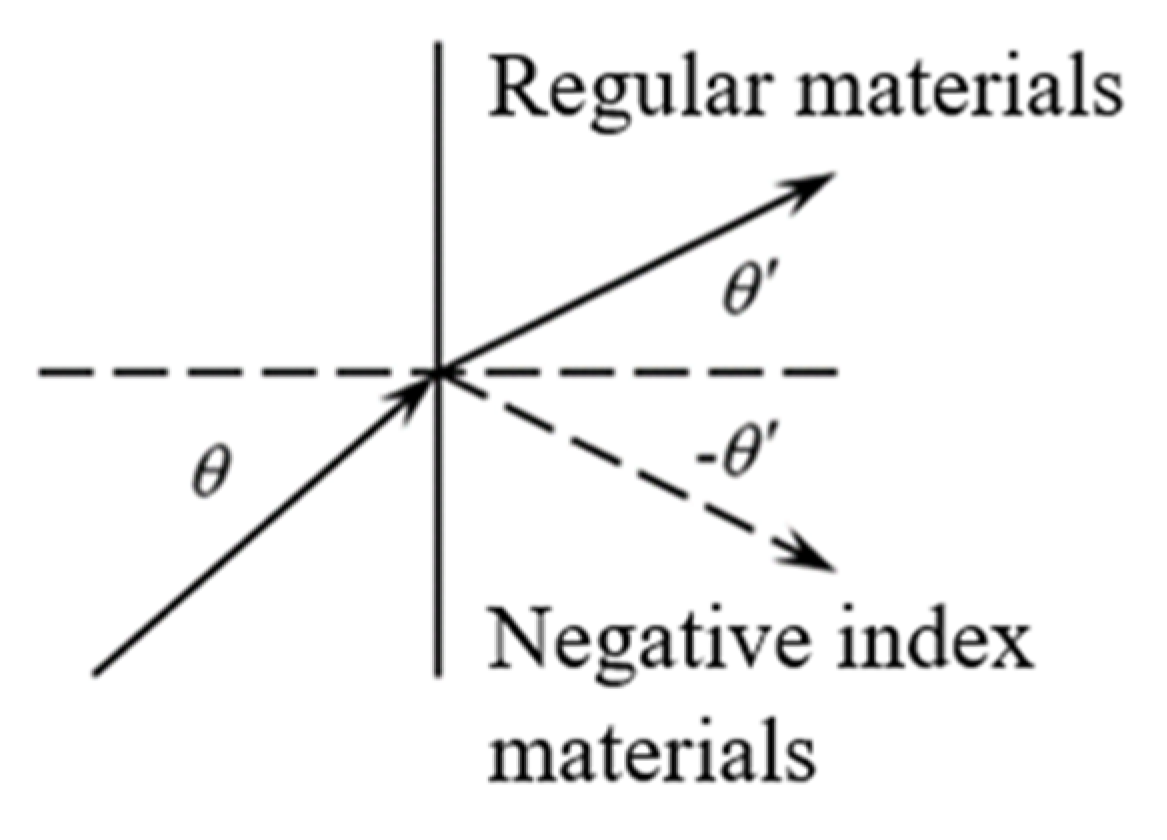
5.1. Negative Refraction Effect of Acoustic Waves [66]
5.2. Anomalous Doppler Effect
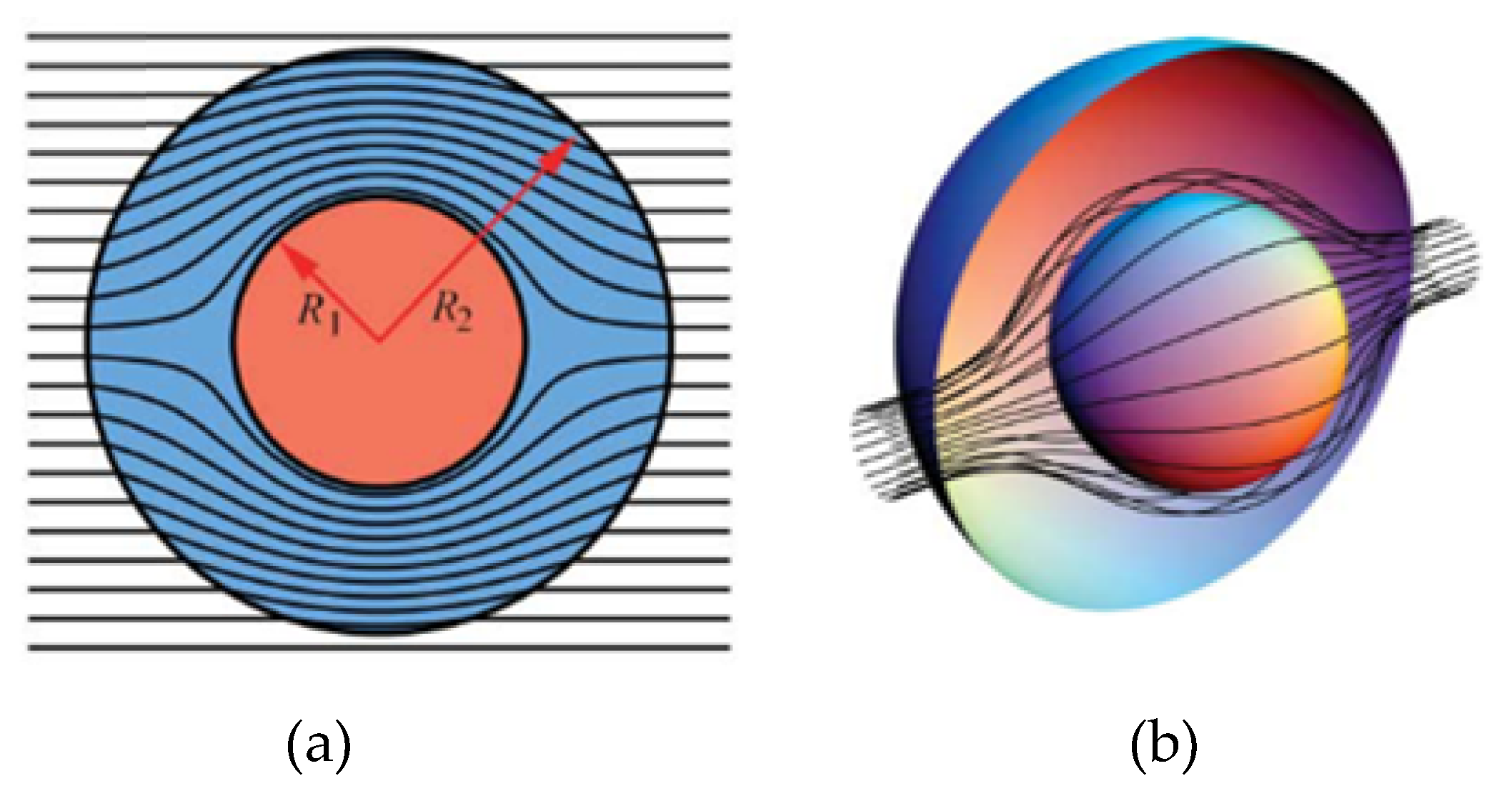
5.3. Enlargement of the Evanescent Wave
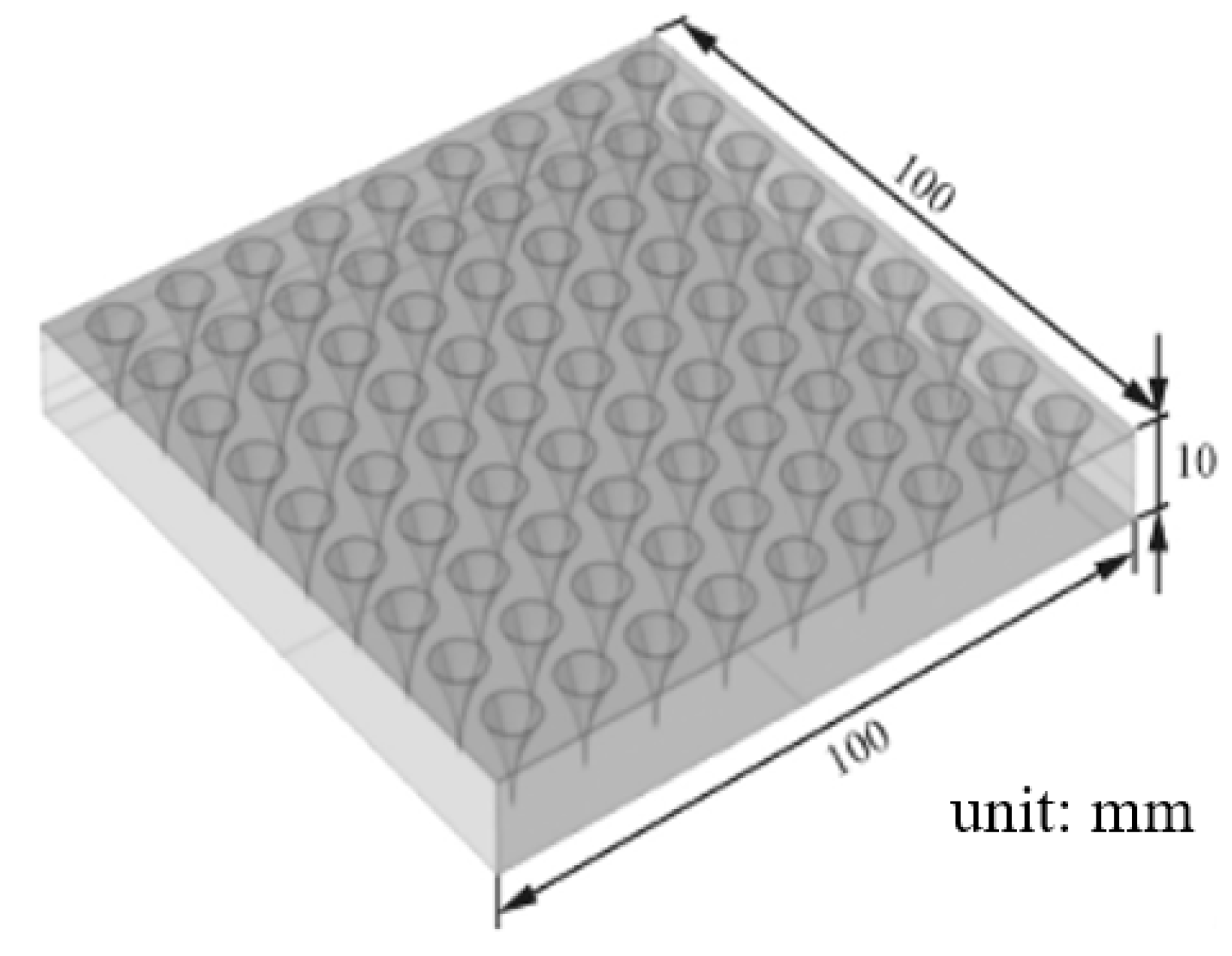
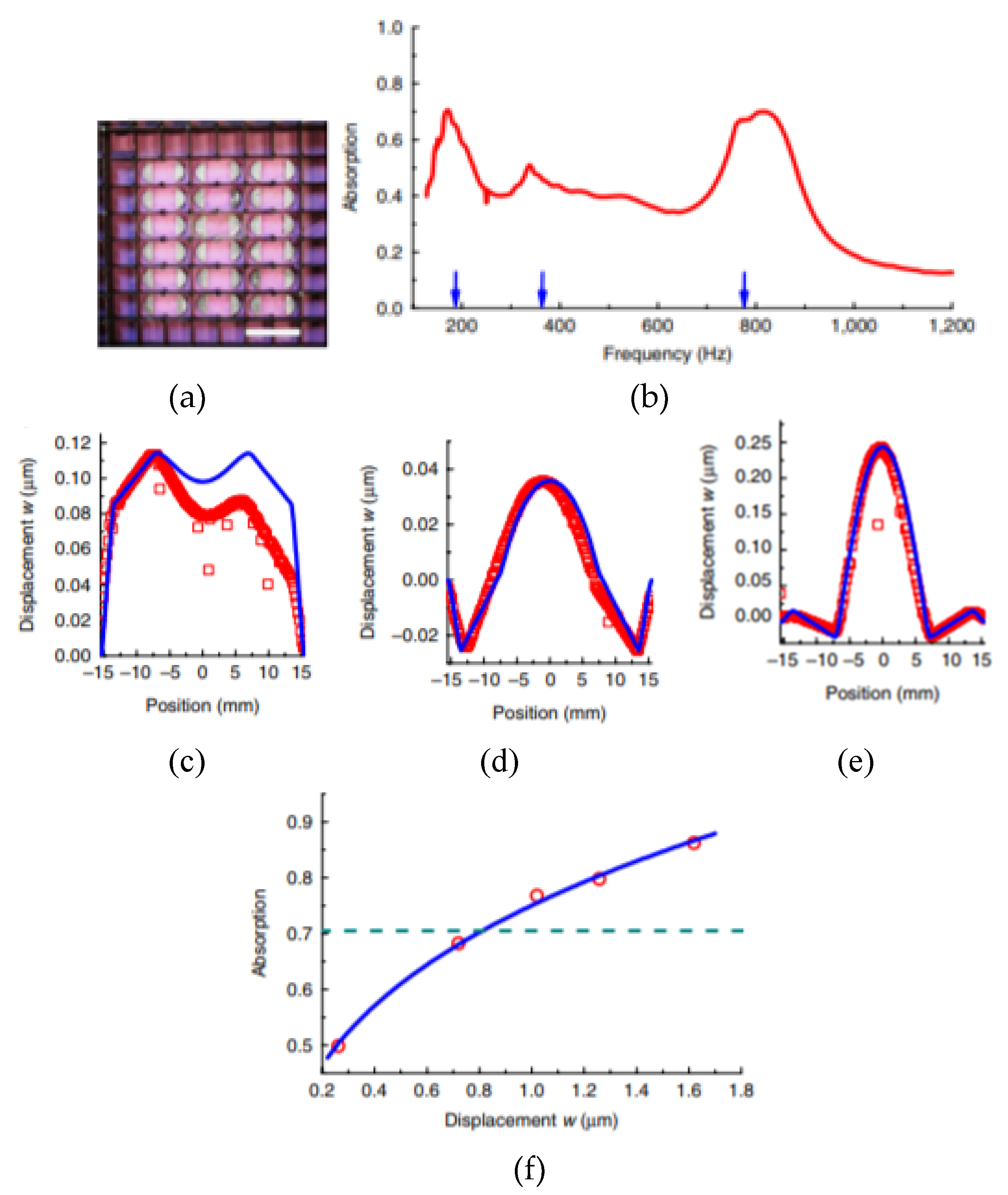
5.4. Perfect Sound Absorption Effects
6. Application of Acoustic Metamaterials and Phononic Crystals
6.1. Acoustic Stealth Cloaks
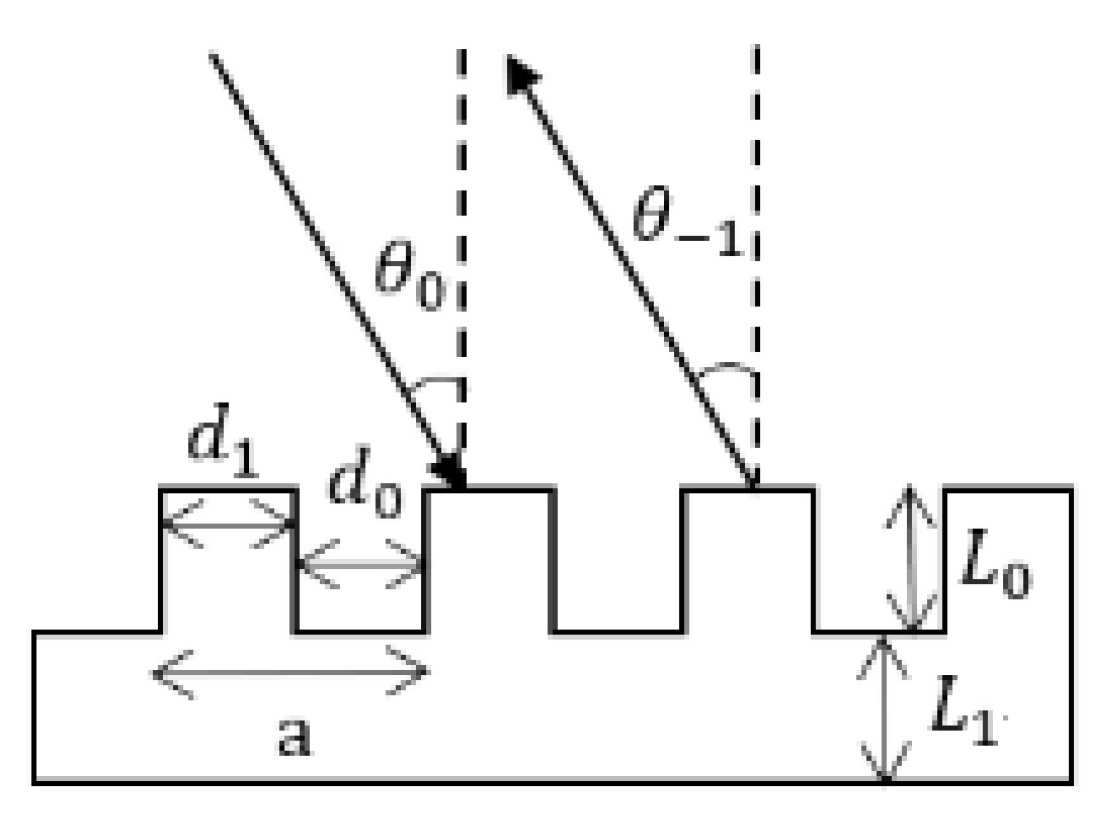
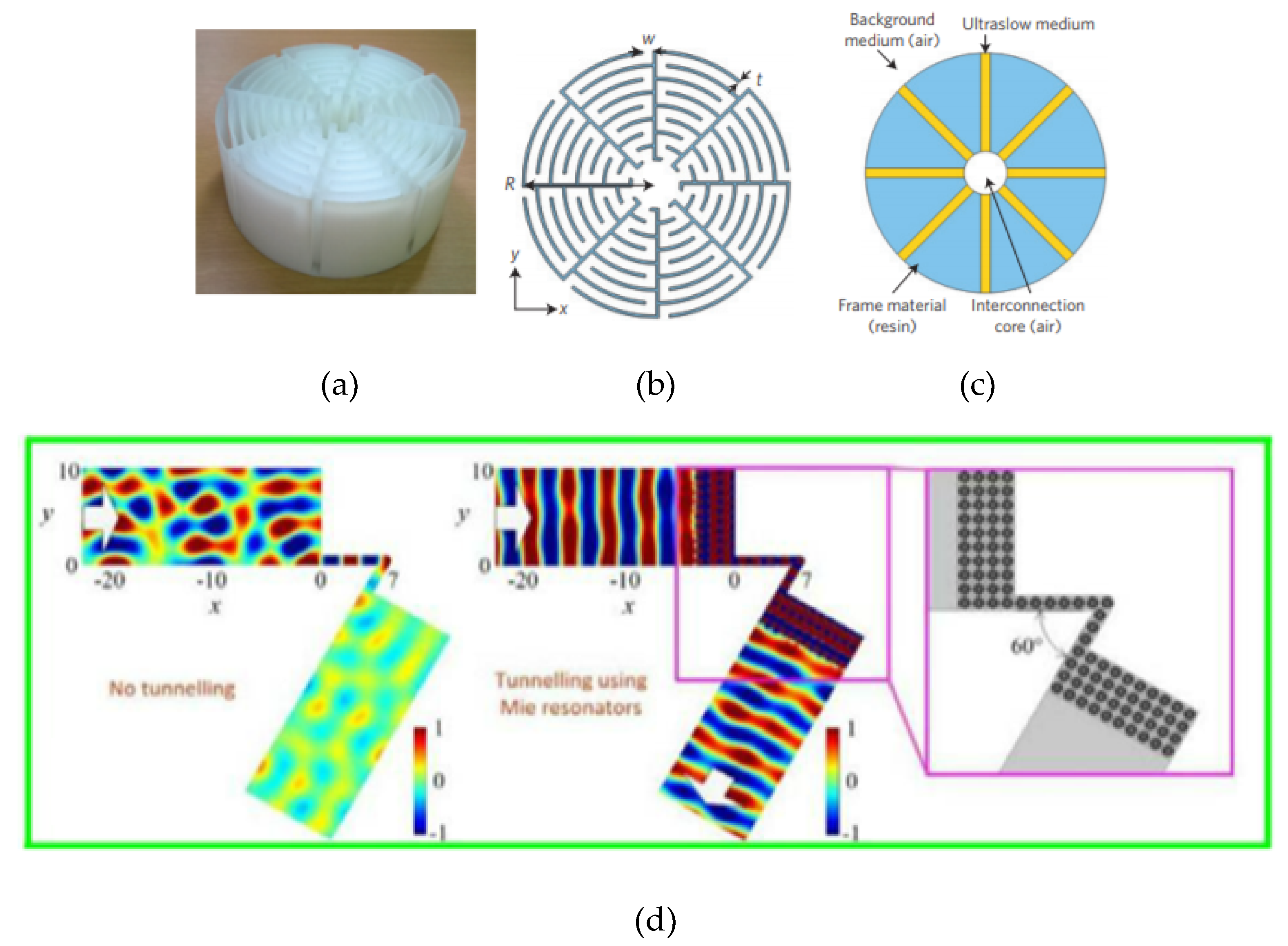
6.2. Extraordinary Acoustic Abnormal Transmission Effects
6.3. Underwater Sound Absorption
6.4. Other Applications
7. Concluding Remarks
- (1)
- Deepen the effect of lattice parameters, structural configurations, and material properties of phononic crystals and acoustic metamaterials on the band gap characteristics;
- (2)
- Based on existing research on phononic crystal forbidden bands, designing more phononic crystals with different materials, shapes and decreasing the lattice sizes to meet actual needs;
- (3)
- Continue to advance the research on the local resonance mechanism for acoustic metamaterials and strive to achieve the control of elastic waves in low frequency bands and broader width for forbidden bands;
- (4)
- Increase the experimental research of phononic crystals and acoustic metamateirals, and expand theoretical research to practical applications.
Author Contributions
Funding
Conflicts of Interest
References
- He, W.; Wang, Z.; Ling, H. Environmental noise pollution and inspection and control measures (In Chinese). Guangdong Chem. Ind. 2016, 43, 123. [Google Scholar]
- Ibrahim, R.A. Recent advances in nonlinear passive vibration isolators. J. Sound Vib. 2008, 314, 371–452. [Google Scholar] [CrossRef]
- Gripp, J.A.B.; Rade, D.A. Vibration and noise control using shunted piezoelectric transducers: A review. Mech. Syst. Signal Pr. 2018, 112, 359–383. [Google Scholar] [CrossRef]
- Aditya, L.; Mahlia, T.M.I.; Rismanchi, B.; Ng, H.M.; Hasan, M.H.; Metselaar, H.S.C.; Muraza, O.; Aditiya, H.B. A review on insulation materials for energy conservation in buildings. Renew. Sust. Eenrg. Rev. 2017, 73, 1352–1365. [Google Scholar] [CrossRef]
- Wu, J. Application of acoustic metamaterials in low-frequency vibration and noise reduction (In Chinese). J. Mech. Eng. 2016, 52, 68–78. [Google Scholar] [CrossRef]
- Veselago, V.G. The electrodynamics of substances with simultaneously negative values of e and μ. Sov. Phys. Usp. 1968, 10, 509–514. [Google Scholar] [CrossRef]
- Peng, H.; Pai, P. Acoustic metamaterial plates for elastic wave absorption and structural vibration suppression. Int. J. Mech. Sci. 2014, 89, 350–361. [Google Scholar] [CrossRef]
- Wen, J.; Han, X.; Wang, G.; Zhao, H.; Liu, Y. Review of phononic crystals (In Chinese). J. Func. Mater. 2003, 34, 364–367. [Google Scholar]
- Wu, Z.; Xu, S. Prospects for application of acoustic metamaterials and structure engineering (In Chinese). Audio Eng. 2017, 41, 16–27. [Google Scholar]
- John, S. Strong localization of photons in certain disordered dielectric superlattices. Phys. Rev. Lett. 1987, 58, 2486–2489. [Google Scholar] [CrossRef]
- Yablonovitch, E. Inhibited spontaneous emission in solid-state physics and electronics. Phys. Rev. Lett. 1987, 58, 2059–2062. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Chen, T.; Wang, X.; Ma, T.; Jiang, P. Acoustic confinement and waveguiding in two-dimensional phononic crystals with material defect states. J. Appl. Phys. 2014, 116, 024904. [Google Scholar] [CrossRef]
- Sigalas, M.M.; Economou, E.N. Elastic and acoustic wave band structure. J. Sound Vib. 1992, 158, 377–382. [Google Scholar] [CrossRef]
- Kushwaha, M.S.; Halevi, P.; Dobrzynski, L.; Djafari Rouhani, B. Acoustic band structure of periodic elastic composites. Phys. Rev. Lett. 1993, 71, 2022–2025. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Sun, H.; Chen, T.; Wang, X. Enhanced acoustic localization in the two-dimensional phononic crystals with slit tube defect. Phys. Lett. A 2019, 383, 125918. [Google Scholar] [CrossRef]
- Lu, M.; Feng, L.; Chen, Y. Phononic crystals and acoustic metamaterials(In Chinese). Mater. Today 2009, 12, 25–32. [Google Scholar] [CrossRef]
- Munjal, M.L. Response of a multi-layered infinite plate to an oblique plane wave by means of transfer matrices. J. Sound Vib. 1993, 162, 333–343. [Google Scholar] [CrossRef]
- Sigalas, M.M.; Soukoulis, C.M. Elastic-wave propagation through disordered and/or absorptive layered systems. Phys. Rev. B 1995, 51, 2780–2789. [Google Scholar] [CrossRef]
- Kushwaha, M.; Halevi, P.; Martínez, G.; Dobrzynski, L.; Djafari-Rouhani, B. Theory of acoustic band structure of periodic elastic composites. Phys. Rev. B 1994, 49, 2313–2322. [Google Scholar] [CrossRef]
- Wu, F.; Liu, Z.; Liu, Y. Band structure of elastic waves in the two dimensional periodic composites (In Chinese). Acta Acus. 2001, 319–323. [Google Scholar]
- Qi, G.; Yang, S.; Bai, S.; Zhao, X. A study of the band structure in two-dimensional phononic crystals based on plane-wave algorithm (In Chinese). Acta Phys. Sin. 2003, 154–157. [Google Scholar]
- Wu, F.; Liu, Z.; Liu, Y. Acoustic band gaps in 2d liquid phononic crystals of rectangular structure. J. Phys. D Appl. Phys. 2001, 35, 162. [Google Scholar] [CrossRef]
- Nikifor, R.; Arshad, M.; Mufei, X. Deposition-and-substrate tunable photonic bandgap in optical responses of hydrogenated amorphous silicon carbide thin films. Mod. Phys. Lett. B 2003, 17, 387–392. [Google Scholar]
- Wu, F.; Hou, Z.; Liu, Z.; Liu, Y. Point defect states in two-dimensional phononic crystals. Phys. Lett. A 2001, 292, 198–202. [Google Scholar] [CrossRef]
- Kushwaha, M.S. Stop-bands for periodic metallic rods: Sculptures that can filter the noise. Appl. Phys. Lett. 1997, 70, 3218. [Google Scholar] [CrossRef]
- Zhao, H.; Han, X.; Wen, J.; Wang, G. Studies on phononic band gaps of periodic hollow cylinders in the air (In Chinese). J. Mat. Sci. Eng. 2004, 71–73. [Google Scholar]
- Sigalas, M.M. Defect states of acoustic waves in a two-dimensional lattice of solid cylinders. J. Appl. Phys. 1998, 84, 3026–3030. [Google Scholar] [CrossRef]
- Kushwaha, M. Ultra-wide-band filter for noise control. J. Acoust. Soc. Am. 2008, 124, 2488. [Google Scholar] [CrossRef]
- Wang, G.; Wen, J.; Han, X.; Zhao, H. Finite difference time domain method for the study of band gap in two-dimensional phononic crystals (In Chinese). Acta Phys. Sin. 2003, 52, 1943–1947. [Google Scholar]
- Sigalas, M.M.; Garcia, N. Theoretical study of three dimensional elastic band gaps with the finite-difference time-domain method. J. Appl. Phys. 2000, 87, 3120–3122. [Google Scholar] [CrossRef]
- Liu, Z.; Chan, C.T.; Sheng, P.; Goertzen, A.L.; Page, J.H. Elastic wave scattering by periodic structures of spherical objects: Theory and experiment. Phys. Rev. B 2000, 62, 2446–2457. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally resonant sonic materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; Ge, H.; Lu, M.H.; Chen, Y.F. Research advances in acoustic metamaterials (In Chinese). Acta Phys. Sin. 2019, 68, 12. [Google Scholar]
- Huang, H.H.; Sun, C.T. Theoretical investigation of the behavior of an acoustic metamaterial with extreme young’s modulus. J. Mech. Phys. Solids 2011, 59, 2070–2081. [Google Scholar] [CrossRef]
- Zhu, X.; Xiao, Y.; Wen, J.; Yu, D. Flexural wave band gaps and vibration reduction prop erties of a lo cally resonant stiffened plate (In Chinese). Acta Phys. Sin. 2016, 65, 316–330. [Google Scholar]
- Wu, J.; Bai, X.C.; Xiao, Y.; Geng, X.M.; Yu, D.L.; Wen, J.H. Low frequency band gaps and vibration reduction prop erties of a multi-frequency lo cally resonant phononic plate (In Chinese). Acta Phys. Sin. 2016, 65, 209–219. [Google Scholar]
- Ma, J.; Sheng, M.; Han, Y. Structure design and experimental verification of multi-bandgap locally resonant unit (In Chinese). J. Vib. Eng. 2019, 32, 943–949. [Google Scholar]
- Fang, N.; Xi, D.; Xu, J.; Ambati, M.; Srituravanich, W.; Sun, C.; Zhang, X. Ultrasonic metamaterials with negative modulus. Nat. Mater. 2006, 5, 452–456. [Google Scholar] [CrossRef]
- Jiang, J.; Yao, H.; Du, J.; Zhao, J.; Deng, T. Low frequency band gap characteristics of double-split helmholtz lo cally resonant periodic structures (In Chinese). Acta Phys. Sin. 2017, 66, 136–142. [Google Scholar]
- Yu, D.; Shen, H.; Liu, J.; Yin, J.; Zhang, Z.; Wen, J. Propagation of acoustic waves in a fluid-filled pipe with periodic elastic helmholtz resonators (In Chinese). Chin. Phys. B 2018, 27, 064301. [Google Scholar] [CrossRef]
- Smith, D.R.; Pendry, J.B.; Wiltshire, M.C.K. Metamaterials and negative refractive index. Science 2004, 305, 788–792. [Google Scholar] [CrossRef] [PubMed]
- Pendry, J.B.; Holden, A.J.; Robbins, D.J.; Stewart, W.J. Magnetism from conductors and enhanced nonlinear phenomena. IEEE T. Microw. Theory 1999, 47, 2075–2084. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhu, H.; Luo, J.; Ma, B. The investigation on low-frequency broadband acoustic absorption performance of membrane sound-absorbing metamaterial (In Chinese). J. Appl. Acoust. 2019, 38, 869–875. [Google Scholar]
- Hashimoto, N.; Katsura, M.; Yasuoka, M.; Fujii, H. Sound insulation of a rectangular thin membrane with additional weights. Appl. Acoust. 1991, 33, 21–43. [Google Scholar] [CrossRef]
- Yang, Z.; Mei, J.; Min, Y.; Chan, N.; Ping, S. Membrane-type acoustic metamaterial with negative dynamic mass. Phys. Rev. Lett. 2008, 101, 204301. [Google Scholar] [CrossRef]
- Yang, Z.; Dai, H.M.; Chan, N.H.; Ma, G.C.; Sheng, P. Acoustic metamaterial panels for sound attenuation in the 50–1000 hz regime. Appl. Phys. Lett. 2010, 96, 041906. [Google Scholar] [CrossRef]
- He, Z.; Zhao, J.; Yao, H.; Jiang, J.; Chen, X. Sound insulation performance of thin-film acoustic metamaterials based on piezoelectric materials (In Chinese). Acta Phys. Sin. 2019, 68, 179–190. [Google Scholar]
- Wang, T.; Sheng, M.; Guo, Z.; Qin, Q. Flexural wave suppression by an acoustic metamaterial plate. Appl. Acoust. 2016, 114, 118–124. [Google Scholar] [CrossRef]
- Wang, T.; Sheng, M.; Ding, X.; Yan, X. Wave propagation and power flow in an acoustic metamaterial plate with lateral local resonance attachment. J. Phys. D Appl. Phys. 2018, 51. [Google Scholar] [CrossRef]
- Zhou, G.; Wu, J.; Lu, K.; Tian, X.; Huang, W.; Zhu, K.D. Low-frequency sound insulation performance of membrane-type acoustic metamaterials with multi-state anti-resonance synergy(In Chinese). J. Xi’an JiaoTong Univ. 2020, 54, 64–74. [Google Scholar]
- Li, Y.; Liang, B.; Zou, X.-Y.; Cheng, J.-C. Extraordinary acoustic transmission through ultrathin acoustic metamaterials by coiling up space. Appl. Phys. Lett. 2013, 103, 1–4. [Google Scholar]
- Yong, L.; Liang, B.; Xu, T.; Zhu, X.F.; Zou, X.Y.; Cheng, J.C. Acoustic focusing by coiling up space. Appl. Phys. Lett. 2012, 101, 233508. [Google Scholar]
- Li, Y.; Chen, T.; Wang, X.; Yu, K.; Song, R. Band structures in two-dimensional phononic crystals with periodic jerusalem cross slot. Physica B 2014, 456, 261–266. [Google Scholar] [CrossRef]
- Wang, T.; Sheng, M.; Wang, H.; Qin, Q. Band structures in two-dimensional phononic crystals with periodic s-shaped slot. Acoust. Aust. 2015, 43, 1–6. [Google Scholar] [CrossRef]
- Xia, B.; Liu, T.; Zheng, S.; Yu, D. Coiling up space acoustic metamaterial with hilbert fractal in a subwavelength scale (In Chinese). Sci. Sin. Tech. 2017, 6, 79–85. [Google Scholar]
- Dong, H.; Zhao, S.; Wei, P.; Cheng, L.; Wang, Y.; Zhang, C. Systematic design and realization of double-negative acoustic metamaterials by topology optimization. Acta Mater. 2019, 172, 102–120. [Google Scholar] [CrossRef]
- Wu, F.; Xiao, Y.; Yu, D.; Zhao, H.; Wang, Y.; Wen, J. Low-frequency sound absorption of hybrid absorber based on micro-perforated panel and coiled-up channels. Appl. Phys. Lett. 2019, 114, 151901. [Google Scholar] [CrossRef]
- Ouyang, S.; Meng, Y.; JING, X. Investigation of a balloon-like soft resonator for negative-bulk-modulus acoustic metamaterials (In Chinese). J. Nanjing Univ. 2015, 51, 10–15. [Google Scholar]
- Leroy, V.; Strybulevych, A.; Lanoy, M.; Lemoult, F.; Tourin, A.; Page, J.H. Superabsorption of acoustic waves with bubble metascreens. Phys. Rev. B 2015, 91, 020301. [Google Scholar] [CrossRef]
- Wang, T.; Wang, H.; Sheng, M.; Qin, Q. Complete low-frequency bandgap in a two-dimensional phononic crystal with spindle-shaped inclusions. Chin. Phys. B 2016, 25, 288–295. [Google Scholar] [CrossRef]
- Fang, H.; Zhou, K.; Song, Y. Introduction to acoustic black hole (In Chinese). Coll. Phys. 2013, 32, 30–41. [Google Scholar]
- Krylov, V.V. Acoustic black holes: Recent developments in the theory and applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2014, 61, 1296–1306. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Zhang, H.; Wang, K.; Wu, J. Acoustic black hole lightweight superstructure with low frequency broadband high efficiency sound insulation mechanism and experimental study (In Chinese). J. Xi’an JiaoTong Univ. 2019, 53, 128–134. [Google Scholar]
- Ding, C.; Dong, Y.; Zhao, X. Research advances in acoustic metamaterials and metasurface (In Chinese). Acta Phys. Sin. 2018, 67, 10–23. [Google Scholar]
- Ni, X.; Zhang, X.; Lu, M.; Chen, Y. Phononic crystals and acoustic metamaterials (In Chinese). Physics 2009, 41, 655–662. [Google Scholar]
- Ge, H.; Yang, M.; Ma, C.; Lu, M.; Chen, Y.; Fang, N.; Sheng, P. Breaking the barriers: Advances in acoustic functional materials. Natl. Sci. Rev. 2018, 5, 159–182. [Google Scholar] [CrossRef]
- Yang, S.; Page, J.H.; Liu, Z.; Cowan, M.L.; Chan, C.T.; Sheng, P. Focusing of sound in a 3d phononic crystal. Phys. Rev. Lett. 2004, 93, 024301. [Google Scholar] [CrossRef]
- Mokhtari, A.A.; Lu, Y.; Srivastava, A. On the emergence of negative effective density and modulus in 2-phase phononic crystals. J. Mech. Phys. Solids 2019, 126, 256–271. [Google Scholar] [CrossRef]
- Nemat Nasser, S. Inherent negative refraction on acoustic branch of two dimensional phononic crystals. Mech. Mater. 2019, 132, 1–8. [Google Scholar] [CrossRef]
- Lee, S.H.; Park, C.M.; Yong, M.S.; Kim, C.K. Reversed doppler effect in double negative metamaterials. Phys. Rev. B 2010, 81, 145–173. [Google Scholar] [CrossRef]
- Zhai, S.L.; Zhao, X.P.; Liu, S.; Shen, F.L.; Li, L.L.; Luo, C.R. Inverse doppler effects in broadband acoustic metamaterials. Sci. Rep. 2016, 6, 32388. [Google Scholar] [CrossRef]
- Liu, S.; Luo, C.; Zhai, S.; Chen, H.; Zhao, X. Inverse doppler effect of acoustic metamaterial with negative mass density (In Chinese). Acta Phys. Sin. 2017, 66, 204–208. [Google Scholar]
- Zhai, S.; Zhao, J.; Shen, F.; Li, L.; Zhao, X. Inverse doppler effects in pipe instruments. Sci. Rep. 2018, 8, 17833. [Google Scholar] [CrossRef] [PubMed]
- Pendry, J.B. Negative refraction makes a perfect lens. Phys. Rev. Lett. 2000, 85, 3966–3969. [Google Scholar] [CrossRef] [PubMed]
- Bavencoffe, M.; Morvan, B.; Hladky Hennion, A.C.; Izbicki, J.-L. Experimental and numerical study of evanescent waves in the mini stopband of a 1d phononic crystal. Ultrasonics 2013, 53, 313–319. [Google Scholar] [CrossRef] [PubMed]
- Ambati, M.; Fang, N.; Sun, C.; Zhang, X. Surface resonant states and superlensing in acoustic metamaterials. Phys. Rev. B 2007, 75, 195447. [Google Scholar] [CrossRef]
- Park, C.M.; Park, J.J.; Lee, S.H.; Yong, M.S.; Kim, C.K.; Lee, S.H. Amplification of acoustic evanescent waves using metamaterial slabs. Phys. Rev. Lett. 2011, 107, 194301. [Google Scholar] [CrossRef]
- Zhang, F.; Liu, F. Acoustic interface waves in double-negative metamaterials (In Chinese). J. Syn. Crystals 2019, 48, 365–368. [Google Scholar]
- Pai, P.F. Metamaterial-based broadband elastic wave absorber. J. Intel. Mat. Syst. Str. 2010, 21, 517–528. [Google Scholar] [CrossRef]
- Mei, J.; Ma, G.; Yang, M.; Yang, Z.; Wen, W.; Sheng, P. Dark acoustic metamaterials as super absorbers for low-frequency sound. Nat. Commun. 2012, 3, 756. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, Y.; Wen, J.; Lam, Y.W.; Umnova, O. A slim subwavelength absorber based on coupled microslits. Appl. Acoust. 2018, 142, 11–17. [Google Scholar] [CrossRef]
- Wu, P.; Mu, Q.; Wu, X.; Wang, L.; Li, X.; Zhou, Y.; Wang, S.; Huang, Y.; Wen, W. Acoustic absorbers at low frequency based on split-tube metamaterials. Phys. Lett. A 2019, 383, 2361–2366. [Google Scholar] [CrossRef]
- Ji, G.; Fang, Y.; Zhou, J. Porous acoustic metamaterials in an inverted wedge shape. Extreme Mech. Lett. 2020, 36, 100648. [Google Scholar] [CrossRef]
- Leonhardt, U. Optical conformal mapping. Science 2006, 312, 1777–1780. [Google Scholar] [CrossRef] [PubMed]
- Pendry, J.B.; Schurig, D.; Smith, D.R. Controlling electromagnetic fields. Science 2006, 312, 1780–1782. [Google Scholar] [CrossRef]
- Cummer, S.A.; Schurig, D. One path to acoustic cloaking. New J. Phys. 2007, 9, 45. [Google Scholar] [CrossRef]
- Chen, H.; Chan, C.T. Acoustic cloaking in three dimensions using acoustic metamaterials. Appl. Phys. Lett. 2007, 91, 183518. [Google Scholar] [CrossRef]
- Cummer, S.A.; Popa, B.I.; Schurig, D.; Smith, D.R.; Pendry, J.; Rahm, M.; Starr, A. Scattering theory derivation of a 3d acoustic cloaking shell. Phys. Rev. Lett. 2008, 100, 024301. [Google Scholar] [CrossRef]
- Cheng, Y.; Yang, F.; Xu, J.Y.; Liu, X.J. A multilayer structured acoustic cloak with homogeneous isotropic materials. Appl. Phys. Lett. 2008, 92, 151913. [Google Scholar] [CrossRef]
- Torrent, D.; Sánchez Dehesa, J. Acoustic cloaking in two dimensions: A feasible approach. New J. Phys. 2008, 10, 063015. [Google Scholar] [CrossRef]
- Chen, Y.; Zheng, M.; Liu, X.; Bi, Y.; Sun, Z.; Xiang, P.; Yang, J.; Hu, G. Broadband solid cloak for underwater acoustics. Phys. Rev. B 2017, 95, 180104. [Google Scholar] [CrossRef]
- Bi, Y.; Jia, H.; Lu, W.; Ji, P.; Yang, J. Design and demonstration of an underwater acoustic carpet cloak. Sci. Rep. 2017, 7, 705. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Jiang, X.; Ta, D. The ultrasound cloaking based on acoustic metamaterials (In Chinese). In Proceedings of the National Acoustic Conference in 2019, Shenzhen, China, 1–2 July 2019; Technical Acoustics: Shenzhen, China, 2019; p. 2. [Google Scholar]
- Ebbesen, T.W.; Lezec, H.; Ghaemi, H.F.; Thio, T.; Wolff, P.A. Extraordinary optical transmission through sub-wavelength hole arrays. Nature 1998, 391, 667–669. [Google Scholar] [CrossRef]
- Lu, M.; Liu, X.; Feng, L.; Li, J.; Huang, C.; Chen, Y.; Zhu, Y.; Zhu, S.; Ming, N. Extraordinary acoustic transmission through a 1d grating with very narrow apertures. Phys. Rev. Lett. 2007, 99, 174301. [Google Scholar] [CrossRef]
- He, Z.; Jia, H.; Qiu, C.; Peng, S.; Mei, X.; Cai, F.; Peng, P.; Ke, M.; Liu, Z. Acoustic transmission enhancement through a periodically structured stiff plate without any opening. Phys. Rev. Lett. 2010, 105, 074301. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhou, C.; Yuan, B.G.; Wu, D.J.; Wei, Q.; Liu, X.J. Ultra-sparse metasurface for high reflection of low-frequency sound based on artificial mie resonances. Nat. Mater. 2015, 14, 1013–1019. [Google Scholar] [CrossRef]
- Dong, Y.; Wang, P.; Yu, G. Far field super-resolution imaging based on an acoustic superlens (In Chinese). In Proceedings of the 2018 Acoustic Technology Academic Exchange Meeting of Four Provinces of Shandong, Zhejiang, Jiangsu and Heilongjiang, Qingdao, China, 20–22 September 2018; Technical Acoustics: Qingdao, China, 2018; p. 4. [Google Scholar]
- Dong, H.; Zhao, S.; Wang, Y.; Cheng, L.; Zhang, C. Robust 2d/3d multi-polar acoustic metamaterials with broadband double negativity. J. Mech. Phys. Solids 2020, 137, 103889. [Google Scholar] [CrossRef]
- Zhong, J.; Zhao, H.; Yang, H.; Wang, Y.; Yin, J.; Wen, J. Theoretical requirements and inverse design for broadband perfect absorption of low-frequency waterborne sound by ultrathin metasurface. Sci. Rep. 2019, 9, 1181. [Google Scholar] [CrossRef]
- Shi, K.; Jin, G.; Liu, R.; Ye, T.; Xue, Y. Underwater sound absorption performance of acoustic metamaterials with multilayered locally resonant scatterers. Results Phys. 2019, 12, 132–142. [Google Scholar] [CrossRef]
- Zhong, H.; Gu, Y.; Bao, B.; Wang, Q.; Wu, J. 2d underwater acoustic metamaterials incorporating a combination of particle-filled polyurethane and spiral-based local resonance mechanisms. Compos. Struct. 2019, 220, 1–10. [Google Scholar] [CrossRef]
- Christensen, J.; Fernandez-Dominguez, A.I.; de Leon-Perez, F.; Martin-Moreno, L.; Garcia-Vidal, F.J. Collimation of sound assisted by acoustic surface waves. Nat. Phys. 2007, 3, 851–852. [Google Scholar] [CrossRef]
- Cox, T.J. Acoustic iridescence. J. Acoust. Soc. Am. 2011, 129, 1165–1172. [Google Scholar] [CrossRef] [PubMed]
- Liang, B.; Yuan, B.; Cheng, J. Acoustic diode: Rectification of acoustic energy flux in one-dimensional systems. Phys. Rev. Lett. 2009, 103, 104301. [Google Scholar] [CrossRef] [PubMed]
- Liang, B.; Guo, X.S.; Tu, J.; Zhang, D.; Cheng, J.C. An acoustic rectifier. Nat. Mater. 2010, 9, 989–992. [Google Scholar] [CrossRef] [PubMed]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Guo, H.; Wang, T. A Review of Acoustic Metamaterials and Phononic Crystals. Crystals 2020, 10, 305. https://doi.org/10.3390/cryst10040305
Liu J, Guo H, Wang T. A Review of Acoustic Metamaterials and Phononic Crystals. Crystals. 2020; 10(4):305. https://doi.org/10.3390/cryst10040305
Chicago/Turabian StyleLiu, Junyi, Hanbei Guo, and Ting Wang. 2020. "A Review of Acoustic Metamaterials and Phononic Crystals" Crystals 10, no. 4: 305. https://doi.org/10.3390/cryst10040305
APA StyleLiu, J., Guo, H., & Wang, T. (2020). A Review of Acoustic Metamaterials and Phononic Crystals. Crystals, 10(4), 305. https://doi.org/10.3390/cryst10040305




