Abstract
In this paper, we propose a reflective polarizer in terahertz regime, which utilizes the Bulk-Dirac-Semimetal (BDS) metasurface can be dynamically tuned in broadband. The proposed polarizer is capable of converting the linear polarized wave into the circular polarized or the cross polarized waves by adjusting the Fermi energy (EF) of the BDS. In the frequency range of 0.51 THz and 1.06 THz, the incident linear polarized wave is converted into a circular polarized wave with an axial ratio (AR) less than 3 dB when EF = 30 meV. When EF = 45 meV, the cross-polarization conversion is achieved with the polarization conversion ratio (PCR) greater than 90% in the band of 0.57−1.12 THz. Meanwhile, the conversion efficiencies for both polarization conversions are in excess of 90%. Finally, the physical mechanism is revealed by the decomposition of two orthogonal components and the verification is presented by the interference theory.
1. Introduction
In recent years, terahertz (THz) technology has developed rapidly in many fields, such as sensing [1], imaging [2] and radar [3] because terahertz waves have very low photon energy, strong penetrability, and obvious characteristic absorption peaks, making terahertz technology show significant research value and great prospects in material detection, security inspection, military, and wireless communications. The increasing demand of unoccupied and unregulated bandwidth for wireless communication systems inevitably leads to the extension of operation frequency toward the lower THz frequency range. THz communication, with a higher carrier frequency, allows for fast transmission of huge amounts of data as needed for new emerging applications [4]. However, the practical application of THz technology has great limitations due to the lack of THz devices such as absorber, sensor, and polarizer. As a basic THz device, polarizer, controlling and manipulating the polarization of THz waves can convert the linear polarization waves into circular polarization waves or cross polarization waves [5]. Conventionally, the THz polarizer is designed by using the techniques of birefringent material [6], photonic crystals [7] or the grating [8]; nevertheless, these techniques suffer from demerits such as bulky configurations and low efficiency.
Metamaterials, with the feature being easy to integrate, have enabled the realization of many phenomena and functionalities unavailable through use of naturally occurring materials. Many basic metamaterial structures, such as metal split-ring resonators [9], exhibit a birefringence suitable for polarization conversion [10], have been mostly investigated in both microwave range and THz range. In recent years, exhibiting extraordinary responses in various desired frequency regime, metamaterials have been widely applied as an effective means to manipulate polarization of the electromagnetic waves [11,12]. The manipulation of metasurface is highly dependent on the geometric structures of the cells [13]. Therefore, metasurface-based polarizers have been widely studied because they are capable of flexibly and effectively regulating the polarization state of the THz wave. Grady et al. demonstrated ultrathin, broadband, and highly efficient metamaterial-based THz polarizer that can reflect a linear polarization wave and convert it into a cross polarization one [5]. Liu et al. proposed a broadband THz cross-polarizer operating in transmission mode using a single-layer metasurface [14]. Moreover, an ultra-wideband high-efficiency reflective linear-to-circular (LTC) polarizer based on metasurface at THz frequencies was proposed by Jiang et al [15]. However, the above metasurface-based polarizers, designed by using gold, are restricted in some practical applications due to a lack of reconfigurability.
With the increasing demand for reconfigurable devices, two-dimensional (2D) materials such as graphene and black phosphorus (BP), with the adjustable conductivity, have attracted tremendous attention in the light of the reconfigurable metasurfaces [16,17]. Graphene, with its unique electronic and optical properties, has been widely applied in reconfigurable polarizer. Utilizing the tunability of graphene, an ultra-broadband LTC polarizer and a cross-polarizer are, respectively, present in [18] and [19], and the operating bands can be easily switched to other frequencies. BP, due to its puckered hexagonal honeycomb structure with ridges caused by sp3 hybridization, offers attractive alternatives to narrow-gap semiconductors for optoelectronics across mid-infrared and THz frequencies [20]. For example, [21] proposed a broadband reflective LTC polarizer in a mid-infrared regime based on monolayer BP (phosphorene) metamaterial. Generally, 2D matearials have been attracting increasing attention as a candidate in the design of THz polarizer. However, their moderate carrier mobility (e.g., 2 × 105 cm2V−1s−1 at 5 K for graphene [22] and 5 × 105 cm2V−1s−1 at 30 K for BP [23]) are still a limitation in their application.
Because of the ultrahigh mobility of 9 × 106 cm2V−1s−1 at 5 K [24,25], recently, Bulk Dirac semimetals (BDSs) showed promise in the design potential of a THz polarizer. For instance, Dai et al. investigated a broadband tunable THz cross-polarizer based on BDSs [26]. With increasing EF, the cross-conversion bandwidth is widened and exhibits a blue-shift. Furthermore, they proposed a dynamically tunable broadband LTC polarizer based on metasurface [27], where the proposed metasurface consists of a center-cut cross-shaped metallic patterned structure with a sandwiched BDS ribbon. Both of the above-mentioned designs in [26] and [27] achieve the adjustable performance in terms of frequency, but the absence of polarization reconfigurability is still a limitation to their application.
In this paper, we present a BDS-based broadband reconfigurable polarizer operating in the THz region. By controlling the Fermi energy of the BDS, the proposed polarizer can dynamically switch the conversion mode between cross polarization and LTC polarization without reoptimizing the structures. The LTC polarization conversion with AR < 3 dB and cross-polarization conversion with PCR > 80% opera at an identical frequency band with a relative bandwidth (RBW) of 64%. Then, the physical mechanism and the verification were investigated by the decomposition of two orthogonal components and the interference theory, respectively.
2. Materials and Methods
The schematic of the proposed metasurface-based polarizer is shown in Figure 1. The polarizer consists of a double-arc BDS structure with a thickness of 0.17 μm, a dielectric layer with permittivity εr = 3.0 and a loss tangent tanθ = 0.001, and a fully reflective gold mirror. The circular-polarized (CP) wave or x-polarized (XP) wave can be reflected when the y-polarized (YP) wave is incident on the polarizer. The geometric parameters of the polarizer include unit length L = 94.0 μm, dielectric thickness h = 50.0 μm, the distance from the center of the arc to the edge of the cell a = 22.0 μm, outer radius Ro = 70.7 μm, inner radius Ri = 57.7 μm, and half of the angle corresponding to the outer arc α = 31.5° and inner arc β = 25.2°.
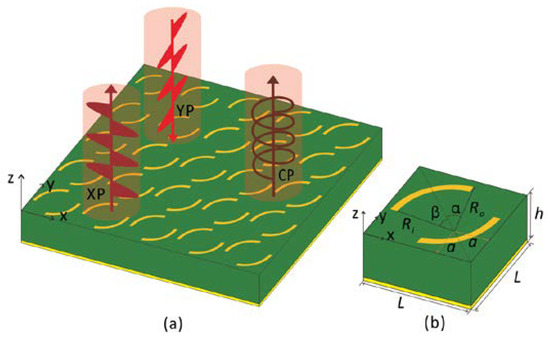
Figure 1.
Design of the polarizer, (a) 5 × 5 unit structure diagram, (b) A unit cell diagram.
At the long wavelength limit (the local response approximation), the longitudinal dynamic conductivity of the Dirac 3D electron gas in BDSs can be calculated by the Kubo formalism [28]:
where σintra and σinter represent the intraband and interband contributions, respectively. ħ and g are respectively the reduced Planck constant and the degeneracy factor, EF, vF, and kF are respectively the Fermi level, Fermi speed, and Fermi Momentum, moreover kF is calculated by EF/ħvF. G(E) = n(−E) − n(E), and n(E) is the Fermi distribution function. In the case of electron-hole (e−h) symmetry of the Dirac spectrum for the nonzero temperature T, the real and imaginary parts of the longitudinal dynamic conductivity of the Dirac semimetal can be expressed as
In more detail, with a low-temperature limit, such as T ≪ EF, in the electron-hole (e−h) symmetry of the Dirac spectrum, the complex conductivity is expressed as [28]
where Ω = ħω/EF + jvF/(EFkFμ) is the normalized frequency, and the relative permittivity of the BDSs can be expressed as ε = εb + iσ/ωε0, where εb = 1 is the effective background dielectric constant and ε0 is the permittivity of vacuum.
Table 1 shows some representative BDSs with various εb and g. In this study, AlCuFe was selected as the BDS material and its dynamic conductivity is shown in Figure 2, where g = 40, Ec = 3, vF = 106 m/s, and μ = 3 × 104 cm2V−1s−1. The hatched regions indicate the normalized frequency range for the THz gap, ħω/EF ≈ 1.30, 0.87, and 0.65 corresponding to EF = 30 meV, 45 meV, and 65 meV when f = 10 THz. It is clear that in the low frequency of THz gap, the real component can be neglected because it is far lower than the imaginary component.

Table 1.
Representative Bulk Dirac semimetals (BDSs) with different εb and g.
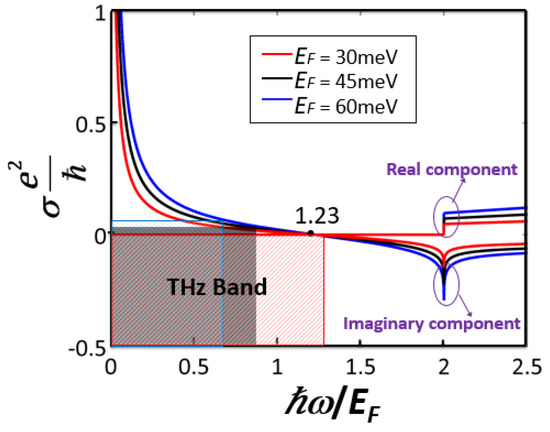
Figure 2.
Normalized frequency-dependent conductivity of BDS.
This periodic structure is emulated by CST Microwave Studio, in which the infinite periodic array is simulated by the utilization of the periodic boundary conditions in x and y directions. Because of the anisotropy of the proposed metasurface, the x and y polarized components are simultaneously produced, with a YPincident wave, in the reflective wave. Therefore, the conversion principle can be clearly demonstrated by the reflective wave expression of Er = rxyexp(jφxy)Eyiex + ryyexp(jφyy)Eyiey, where rxy and ryy are, respectively, the magnitudes of the reflection coefficient for y-to-x and y-to-y polarization conversion, φxy and φyy are the corresponding phases. Then, phase difference is defined by Δφ = φyy − φxy. When rxy = ryy = √2/2 and Δφ = 2n ± π/2 (n is an integer), the perfect LTC polarization conversion is brought; with “−” and “+”, the reflected waves are, respectively, the right-hand circular polarization (RHCP) wave and the left-hand circular polarization (LHCP) wave. On contrast, the total cross polarization conversion is brought with rxy = 1 and Δφ = 2n ± π [29]. In order to achieve a high efficiency of polarization conversion, the reflection coefficient amplitudes should be controlled as highly as possible within the demanded Δφ.
3. Results and Discussions
With EF = 30 meV of BDS (AlCuFe), the reflection coefficient magnitudes and the phase difference are shown in Figure 3a. One can observe that rxy ≈ ryy ≈ √2/2 and Δφ ≈ −90° or 270° in the frequency range of 0.51–1.06 THz. Similarly, Δφ ≈ 90° in the range of 0.41–0.46 THz with rxy ≈ ryy ≈ √2/2. The results indicate that the incident linear polarized wave is converted into a RHCP wave within a broadband and a LHCP wave within a narrow band. When the EF is adjusted to 45 meV, ryy < 0.3 and rxy > 0.9 in the frequency range of 0.57–1.12 THz, as shown in Figure 3b, which means that the YPincident waves are converted into the cross-polarized reflected waves by the polarizer.
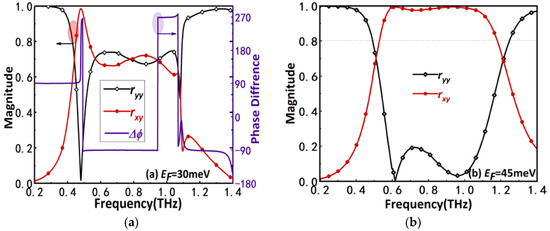
Figure 3.
Reflective coefficients ryy and rxy with the Fermi energy of (a) 30 meV and (b) 45 meV.
For the LTC polarization conversion, the remarkable characteristic can also be measured by the efficiency ηLTC = rxy2 + ryy2 and the axial ratio, AR = 10 lg(tanβ) with β = arcsin(V/I)/2 [13], obtained from the stokes parameter in Equation (3) [30]. In contrast, for cross-polarization conversion, the cross polarization conversion efficiency is estimated as ηcross = rxy2 and PCR = rxy2/(rxy2 + ryy2) is defined to further investigate the performance [31].
For different EF, the calculated PCR and AR are presented in Figure 4a. One can observe that the relative bandwidth (RBW) with PCR > 0.8 reaches 71% and the RBW of RHCP and LHCP with AR < 3 dB are, respectively, 71% and 11%. More significantly, a RBW of 64% is obtained in the identical frequency band; moreover, both ηLTC and ηcross are greater than 90%, as shown in Figure 4b, which indicates the high performance of the proposed polarizer.
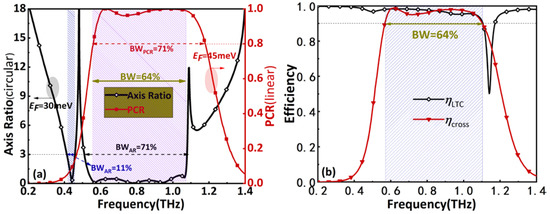
Figure 4.
(a) AR and PCR and (b) efficiencies.
In addition, the AR and PCR of the proposed design as the function of incident angle (θ) and frequency are simulated, as shown in Figure 5a,b. It is clear that in the θ range of 0° and 50°, the BWs of AR < 3 dB and PCR > 0.8 are almost invariant. One can obtain the robustness of the proposed polarizer in case of oblique incidence.
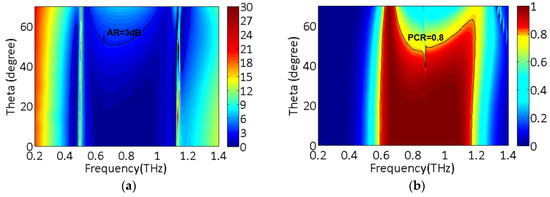
Figure 5.
Frequency and Theta-dependent (a) AR and (b) PCR.
With various EF, the conductivity of the BDS (AlCuFe) is adjustable, which causes the reconfigurability of the proposed BDS-based polarizer. Therefore, it is reasonable to study the effects of various EF on the conversion performance. The AR for EF = 25, 30, and 35 meV are shown in Figure 6a. It can be seen that an optimal LTC polarization conversion performance can be obtained when EF = 30 meV. Figure 6b shows the PCR gradually improves with increasing EF from 25 to 45 meV, and the operating frequency band exhibits a blue shift. Furthermore, the bandwidth of PCR becomes narrower gradually with increasing EF, which will lead to the degradation of the conversion performance. From Figure 6, one can conclude that the design polarizer achieves the optimized performances of cross polarization conversion with EF = 45 meV and the LTC polarization conversion with EF = 30 meV.
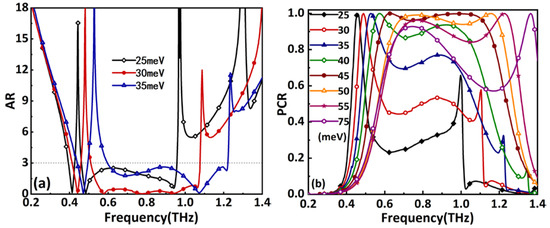
Figure 6.
(a) AR and (b) PCR related to EF.
4. Mechanism and Verification
In order to analyze the physical mechanism of polarization conversion, the incident YP wave is decomposed into two orthogonal components presenting in Figure 7a, wherein the u-v coordinate system is obtained by rotating the x−y coordinate system counterclockwise for 45° [29]. The incident wave is set to be a YP wave propagating in the -z direction and can be decomposed into
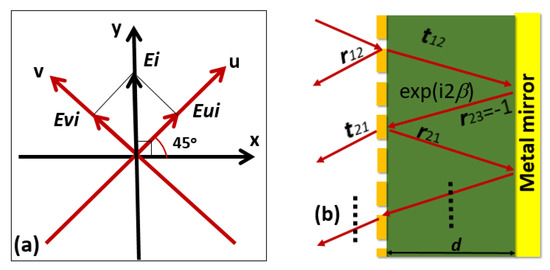
Figure 7.
(a) u-v coordinate system, (b) Multiple reflection interference.
In the above formula, ruu, rvu, rvv, and ruv represent the reflection coefficient amplitudes for the polarization conversion of u−u, u−v, v−v, and v−u respectively, φuu, φvu, φvv and φuv represent the corresponding phases. When rvu = ruv = 0, ruu = rvv = r and Δφ = φvv − φuu = 2n ± π/2, the reflected wave is expressed as
It can be seen from Equation (6) that the reflected wave is a CP wave. Moreover, when rvu = ruv = 0, ruu = rvv = r and Δφ = φvv – φuu = 2n ± π the reflected wave is a cross-polarized wave and can be expressed as
When the u and v components excite simultaneously and EF = 30 meV, as shown in Figure 8a, ruu = rvv ≈ 1, rvu = ruv ≈ 0 and Δφ = φvv − φuu closing to −90°/270° are obtained in the frequency range of 0.5 and 1.08 THz, incidentally Δφ being approximately 90° is obtained in the band of 0.41–0.46 THz, i.e., the reflected waves are respectively RHCP wave and LHCP wave in these two bands. In contrast, when EF = 45 meV, ruu = rvv ≈ 1, rvu = ruv ≈ 0 and Δφ ≈ −180°/180° is obtained, as shown in Figure 8b, the cross-polarization conversion is realized. It is observed that the polarization conversions are consistent with that in Figure 3.
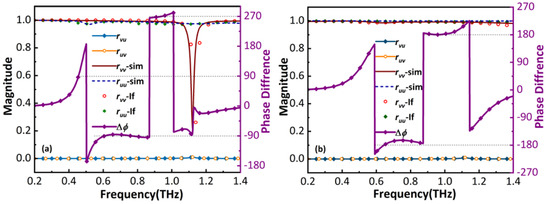
Figure 8.
The calculated and simulated reflection coefficients of u- and v-polarized reflected waves. (a) LTC polarization conversion, (b) Cross-polarization conversion.
The verification can be further elaborated by the interference theory in the u−v coordinate system. As present in Figure 7b, at the double-arc array interface, the incident wave is partially reflected with a reflection coefficient of r12 = r12exp(iφ12) and transmitted into the substrate with a transmission coefficient of t12 = t12exp(iθ12). The transmitted wave continues to propagate with a propagation phase β = √εkd until it reaches the metal mirror, where ε and d are, respectively, the permittivity and the thickness of the substrate, and k is the propagation constant in the substrate. After the reflection at the metal mirror and the addition of another β, partial reflection and transmission occur again at the double-arc interface with coefficients r21 = r21exp(iφ21) and t21 = t21exp(iθ21). Similarly to the wave propagation in a stratified media, the total reflection is the superposition of the multiple reflections [32]:
The results calculated by the interference theory are shown in Figure 8. The reflection coefficients of the LTC polarization conversion and the cross-polarization conversion are consistent with the simulation results, which verities the simulated results of the proposed polarizer.
5. Conclusions
In conclusion, a reconfigurable polarizer based on BDS metasurface is investigated in this paper, and the conversion performance and physical mechanism are analyzed and presented. Our results show that the proposed polarizer achieves a highly efficient linear-to-circular polarization conversion or cross polarization conversion in broadband with different EF. This design is of great significance in the wide application of metamaterials and the rapid development of THz technology.
Author Contributions
Conceptualization, Y.J.; writing—original draft preparation, J.Z.; validation, J.W.; writing—review and editing, Y.J., J.Z. and J.W.; All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number (61661012), Natural Science Foundation of Guangxi, grant number (2019GXNSFFA245002, 2018GXNSFAA281190, 2017GXNSFBA198121), Dean Project of Guangxi Key Laboratory of Wireless Wideband Communication and Signal Processing, grant number (GXKL06170104, GXKL06180108, 11GXKL06190118), and Innovation Project of GUET Graduate Education, rant number(2019YCXS036).
Acknowledgments
The authors acknowledge support from the School of Information and Communication, Guilin University of Electronic Technology.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dean, P.; Lim, Y.L. Terahertz sensing through self-mixing in a quantum cascade laser. Opt. Lett. 2011, 36, 2587–2589. [Google Scholar] [CrossRef] [PubMed]
- Chan, W.L.; Deibel, J.; Mittleman, D.M. Imaging with terahertz radiation. Rep. Prog. Phys. 2007, 70, 1325–1379. [Google Scholar] [CrossRef]
- Koenig, S.; Lopez-Diaz, D.; Antes, J. Wireless sub-THz communication system with high data rate. Nat. Photonics 2013, 7, 977–981. [Google Scholar] [CrossRef]
- Kleine-Ostmann, T.; Nagatsuma, T. A Review on Terahertz Communications Research. J. Infrared Millim. Terahertz Waves 2011, 32, 143–171. [Google Scholar] [CrossRef]
- Grady, N.K.; Heyes, J.E.; Chowdhury, D.R. Terahertz Metamaterials for Linear Polarization Conversion and Anomalous Refraction. Science 2013, 340, 1304–1307. [Google Scholar] [CrossRef]
- Sinchuk, K.; Dudley, R.; Graham, J.D. Tunable negative group index in metamaterial structures with large form birefringence. Opt. Express 2010, 18, 463–472. [Google Scholar] [CrossRef]
- Noda, S.; Yokoyama, M.; Imada, M. Polarization mode control of two-dimensional photonic crystal laser by unit cell structure design. Science 2001, 293, 1123–1125. [Google Scholar] [CrossRef]
- Kanda, N.; Konishi, K.; Kuwatagonokami, M. Terahertz wave polarization rotation with double layered metal grating of complimentary chiral patterns. Opt. Express 2007, 15, 11117–11125. [Google Scholar] [CrossRef]
- Pendry, J.B.; Holden, A.J.; Robbins, D.J. Magnetism from conductors and enhanced nonlinear phenomena. IEEE Transactions on Microwave Theory Techniques. IEEE Trans. Microw. Theory 1997, 47, 2075–2084. [Google Scholar] [CrossRef]
- Hao, J.; Yuan, Y.R.; Li, X. Manipulating Electromagnetic Wave Polarizations by Anisotropic Metamaterials. Phys. Rev. Lett. 2007, 99, 063908. [Google Scholar] [CrossRef]
- Yu, N.; Capasso, F. Flat optics with designer metasurfaces. Nat. Mater. 2014, 13, 139–150. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Alù, A. Manipulating light polarization with ultrathin plasmonic metasurfaces. Phys. Rev. B 2011, 84, 205428. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, W.; Liu, A.Q. Tunable Polarization Conversion and Rotation based on a Reconfigurable Metasurface. Sci. Rep. 2017, 7, 12068. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Chen, S.; Li, Z. Realization of broadband cross-polarization conversion in transmission mode in the terahertz region using a single-layer metasurface. Opt. Lett. 2015, 40, 3185–3188. [Google Scholar] [CrossRef]
- Jiang, Y.N.; Wang, L.; Wang, J. Ultra-wideband high-efficiency reflective linear-to-circular polarization converter based on metasurface at terahertz frequencies. Opt. Express 2017, 25, 27616–27623. [Google Scholar] [CrossRef]
- Katsnelson, M.I.; Novoselov, K.S.; Geim, A.K. Chiral tunnelling and the Klein paradox in graphene. Nat. Phys. 2006, 2, 620–625. [Google Scholar] [CrossRef]
- Low, T.; Rodin, A.S.; Carvalho, A.; Jiang, Y.; Wang, H. Tunable optical properties of multilayer black phosphorus thin films. Phys. Rev. B 2014, 90, 075434. [Google Scholar] [CrossRef]
- Zeng, L.; Huang, T.; Liu, G.B. A tunable ultra-broadband linear-to-circular polarization converter containing the graphene. Opt. Commun. 2019, 436, 7–13. [Google Scholar] [CrossRef]
- Luo, S.; Li, B.; Yu, A. Broadband tunable terahertz polarization converter based on graphene metamaterial. Opt. Commun. 2018, 413, 184–189. [Google Scholar] [CrossRef]
- Koenig, S.P.; Doganov, R.A.; Schmidt, H. Electric field effect in ultrathin black phosphorus. Appl. Phys. Lett. 2014, 104, 103106. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhao, H.; Wang, L.; Wang, J. Broadband linear-to-circular polarization converter based on phosphorene metamaterial. Opt. Mater. Express 2019, 5, 2088–2097. [Google Scholar] [CrossRef]
- Bolotin, K.I.; Sikes, K.J.; Jiang, Z. Ultrahigh electron mobility in suspended graphene. Solid State Commun. 2008, 146, 351–355. [Google Scholar] [CrossRef]
- Xia, F.; Wang, H.; Xiao, D. Two-dimensional material nanophotonics. Nat. Photonics 2015, 8, 899–907. [Google Scholar] [CrossRef]
- Liang, T.; Gibson, Q.; Ali, M.N. Ultrahigh mobility and giant magnetoresistance in the Dirac semimetal Cd3As2. Nat. Mater. 2014, 14, 280–284. [Google Scholar] [CrossRef]
- Jiang, Y.; Wan, X.; Wang, J. Tunable terahertz absorber based on bulk-Dirac-semimetal metasurface. IEEE Photonics J. 2018, 10, 4600607. [Google Scholar] [CrossRef]
- Dai, L.; Zhang, Y.; Zhang, H. Broadband tunable terahertz cross-polarization converter based on Dirac semimetals. Appl. Phys. Express 2019, 12, 075003. [Google Scholar] [CrossRef]
- Dai, L.; Zhang, Y.; Guo, X. Dynamically tunable broadband linear-to-circular polarization converter based on Dirac semimetals. Opt. Mater. Express 2018, 10, 3238–3249. [Google Scholar] [CrossRef]
- Kotov, O.V.; Lozovik, Y.E. Dielectric response and novel electromagnetic modes in three-dimensional Dirac semimetal films. Phys. Rev. B 2016, 93, 235417. [Google Scholar] [CrossRef]
- Zahn, M. Electromagnetic Field Theory: A Problem Solving Approach; Krieger Publishing Company: Malabar, FL, USA, 2003; pp. 135–139. [Google Scholar]
- Li, Y.; Zhang, J.; Qu, S. Achieving wide-band linear-to-circular polarization conversion using ultra-thin bi-layered metasurfaces. J. Appl. Phys. 2015, 117, 044501. [Google Scholar] [CrossRef]
- Winkler, S.A.; Wei, H.; Bozzi, M. Polarization Rotating Frequency Selective Surface Based on Substrate Integrated Waveguide Technology. IEEE Trans. Antennas Propag. 2010, 58, 1202–1213. [Google Scholar] [CrossRef]
- Chen, H.T. Interference theory of metamaterial perfect absorbers. Opt. Express 2012, 20, 7165–7172. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).