Numerical Study of Three-Dimensional Melt Flows during the TSSG Process of SiC Crystal for the Influence of Input Parameters of RF-Coils and an External Rotating Magnetic Field
Abstract
1. Introduction
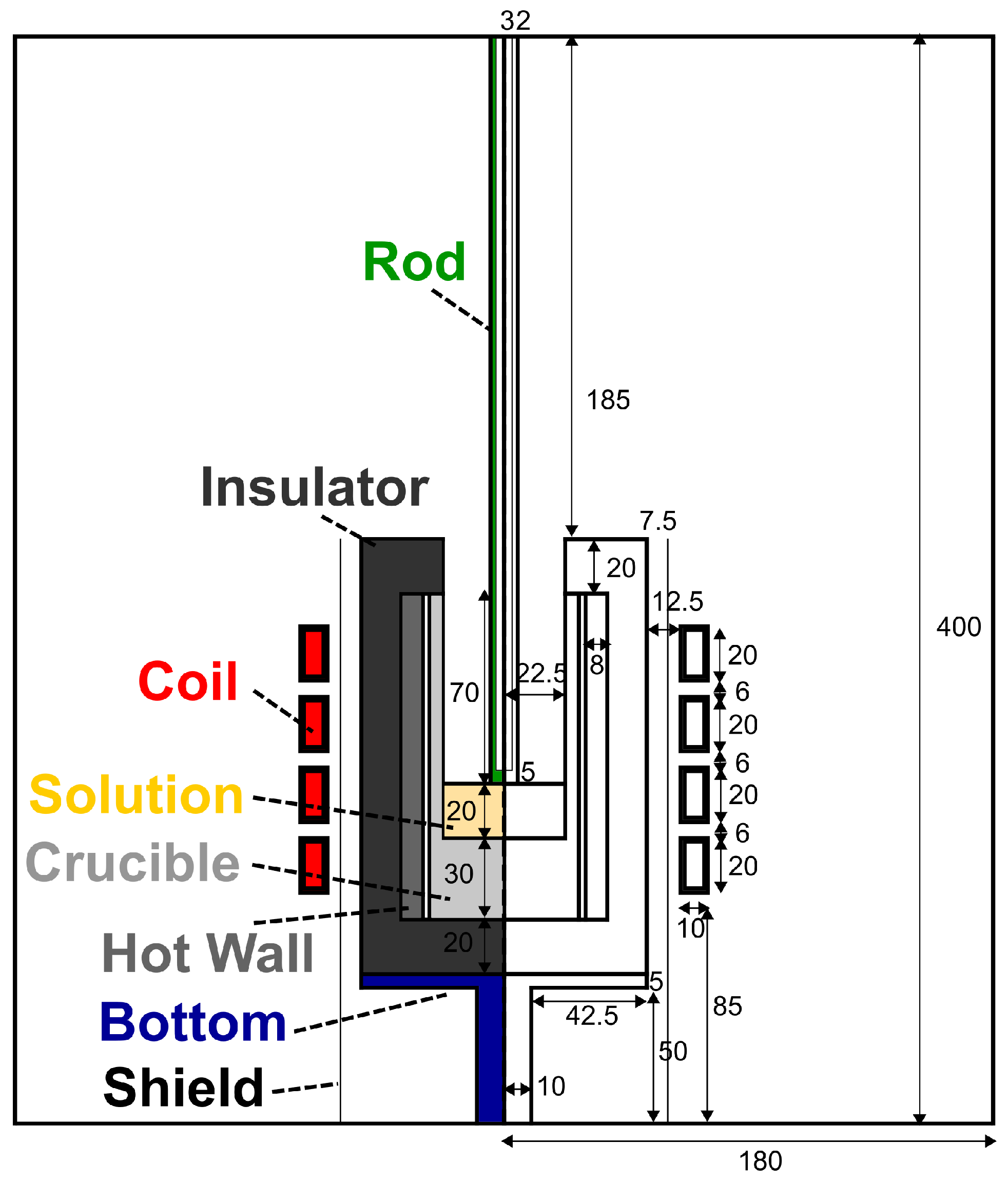
2. Numerical Model
2.1. Governing Equations
2.2. Rotating Magnetic Field
3. Results and Discussion
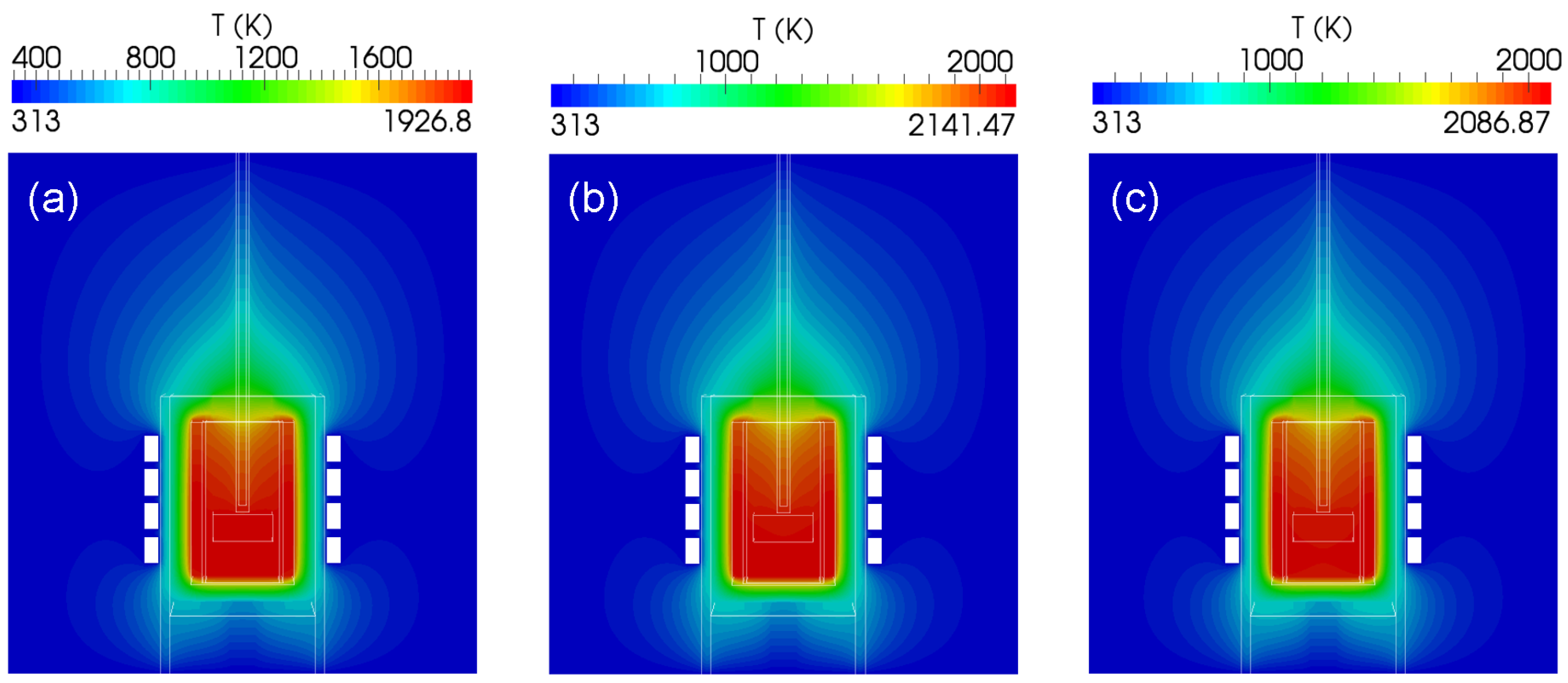
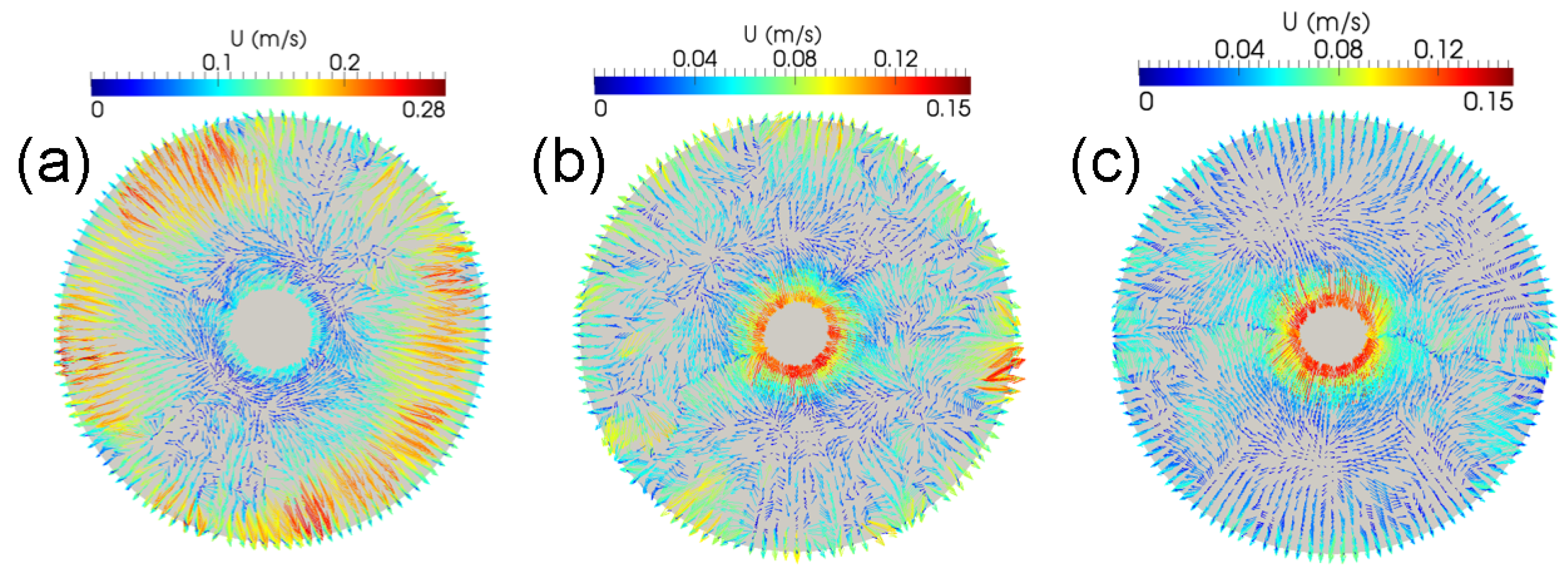
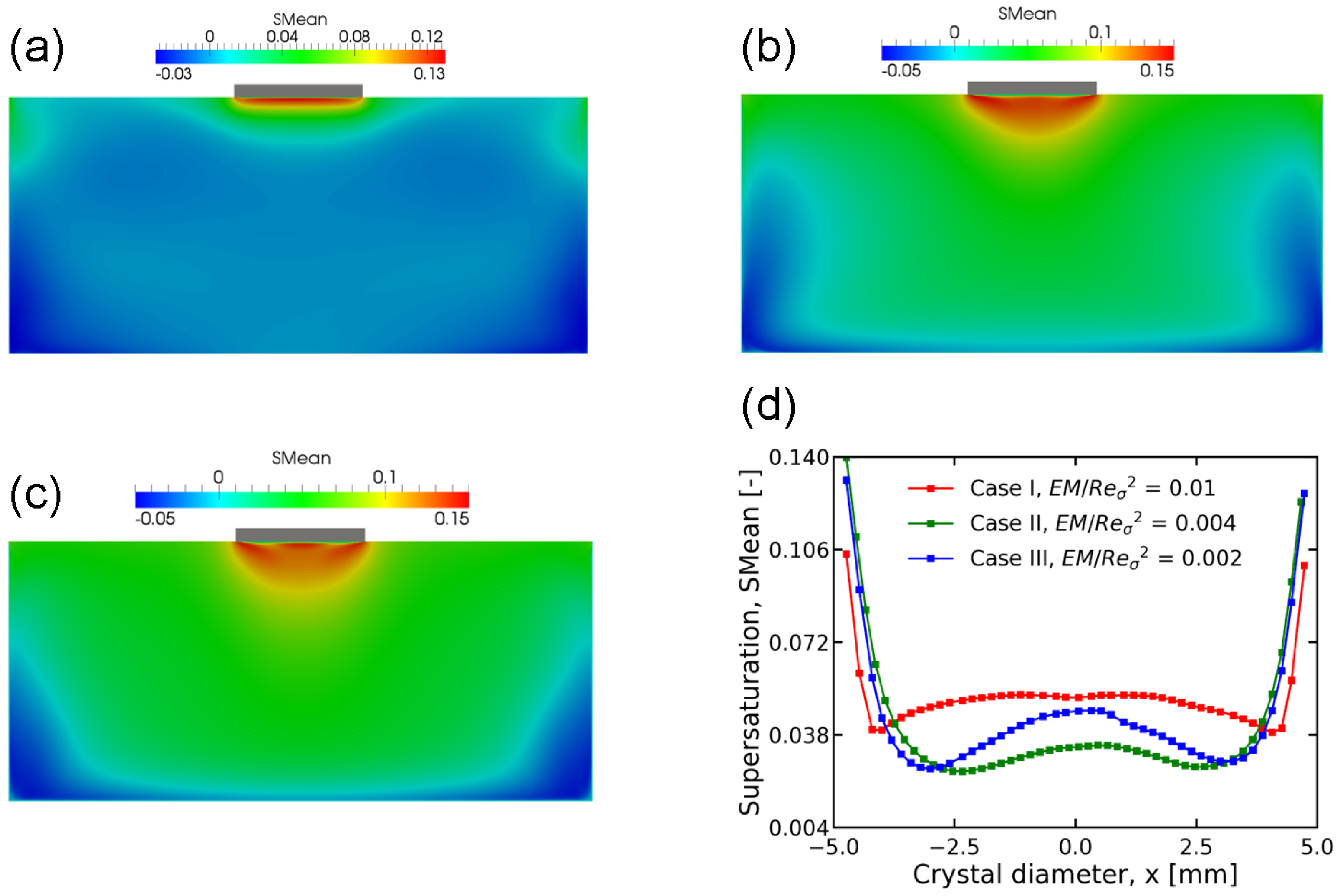
3.1. Effect of Input Parameters on the Melt Flow
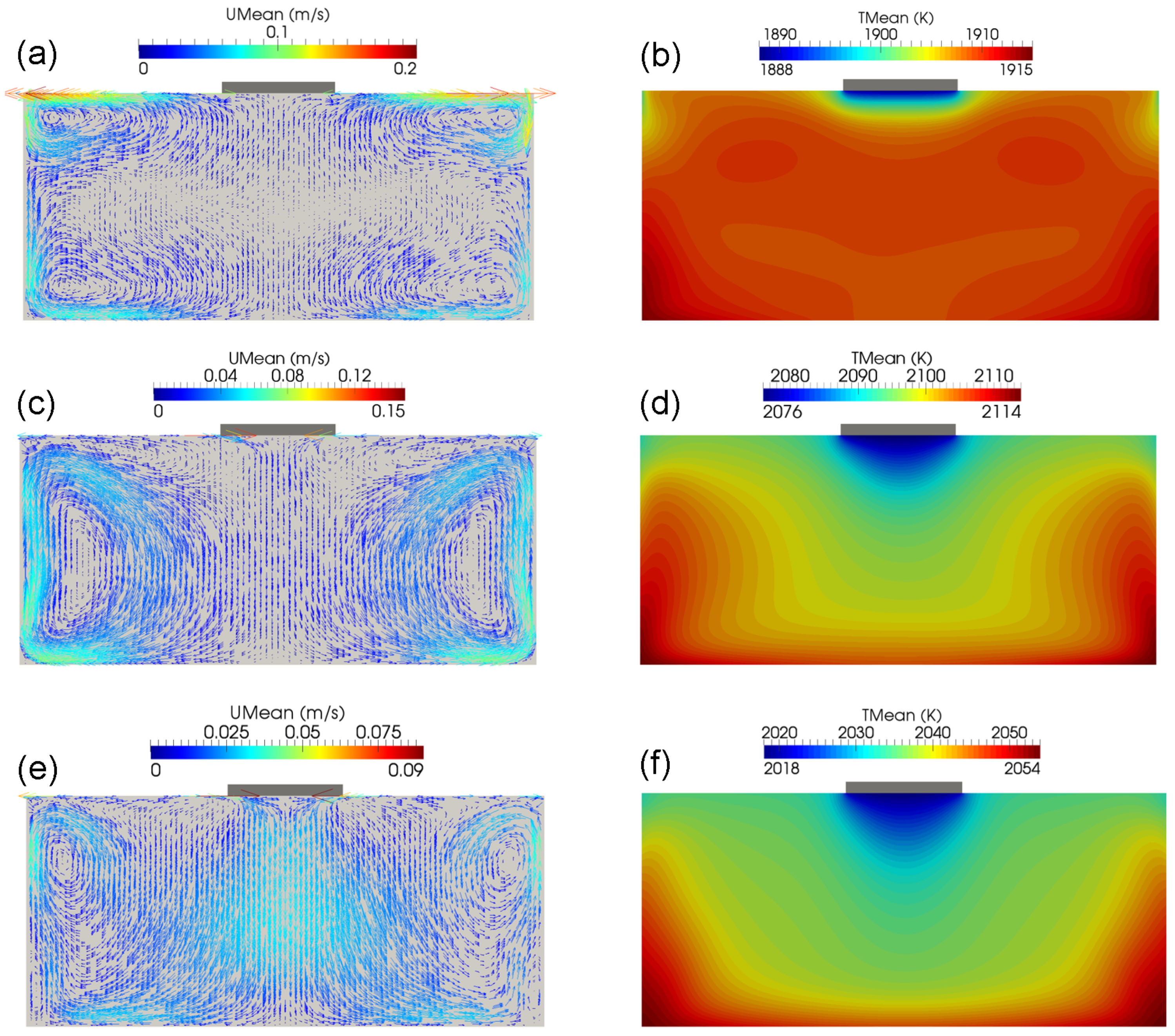
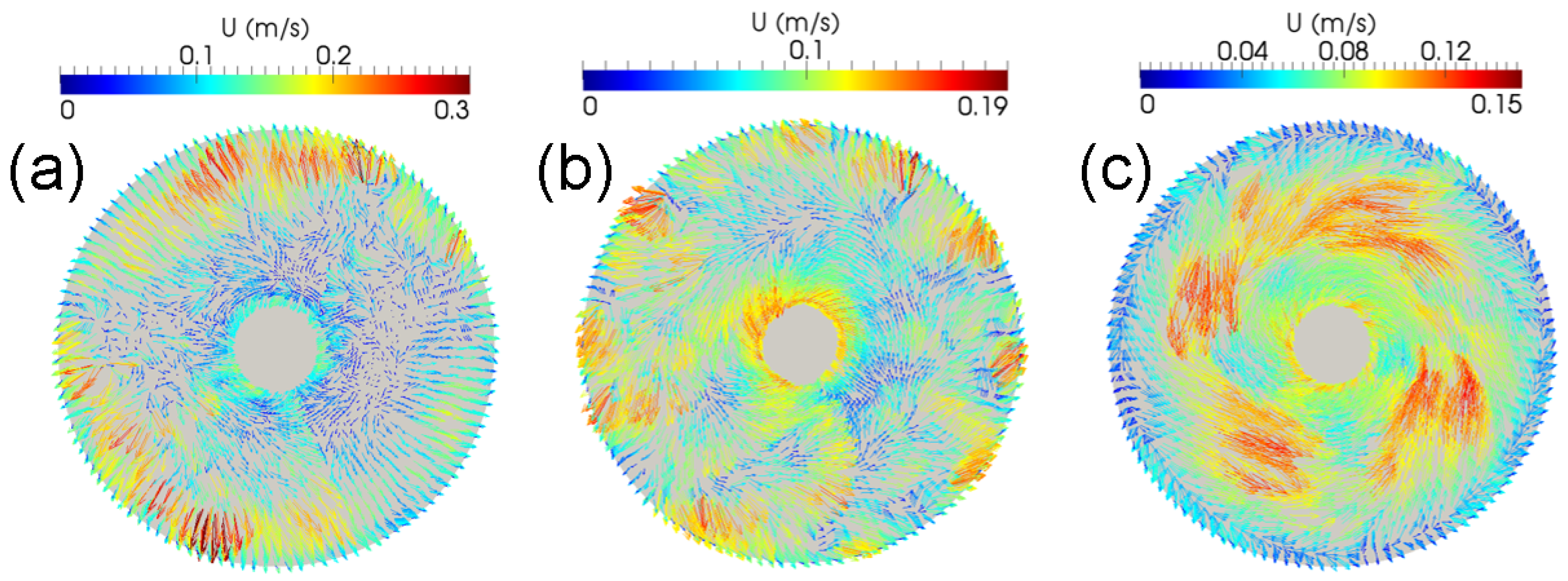
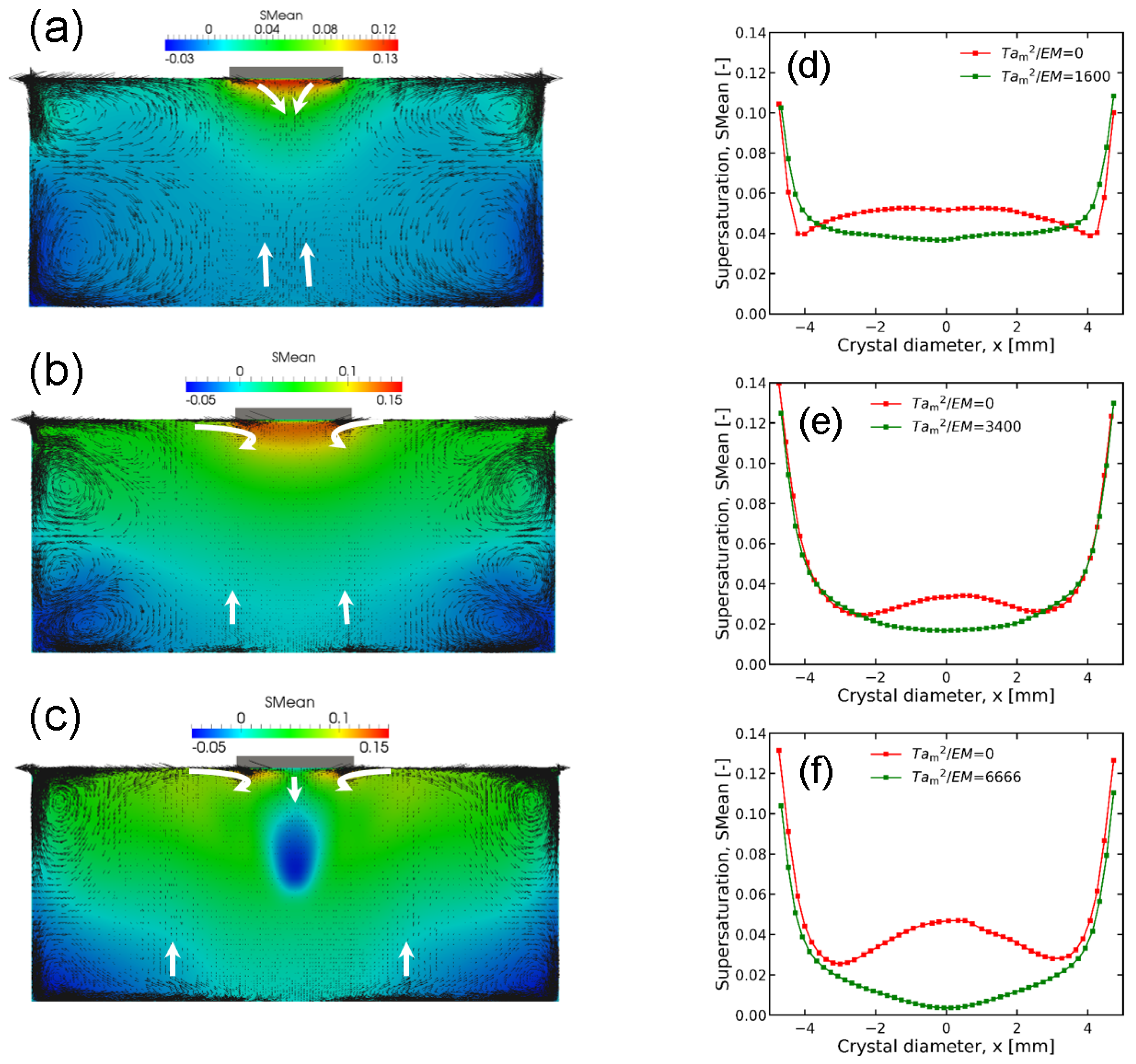
3.2. Effect of External RMF on the Melt Flow
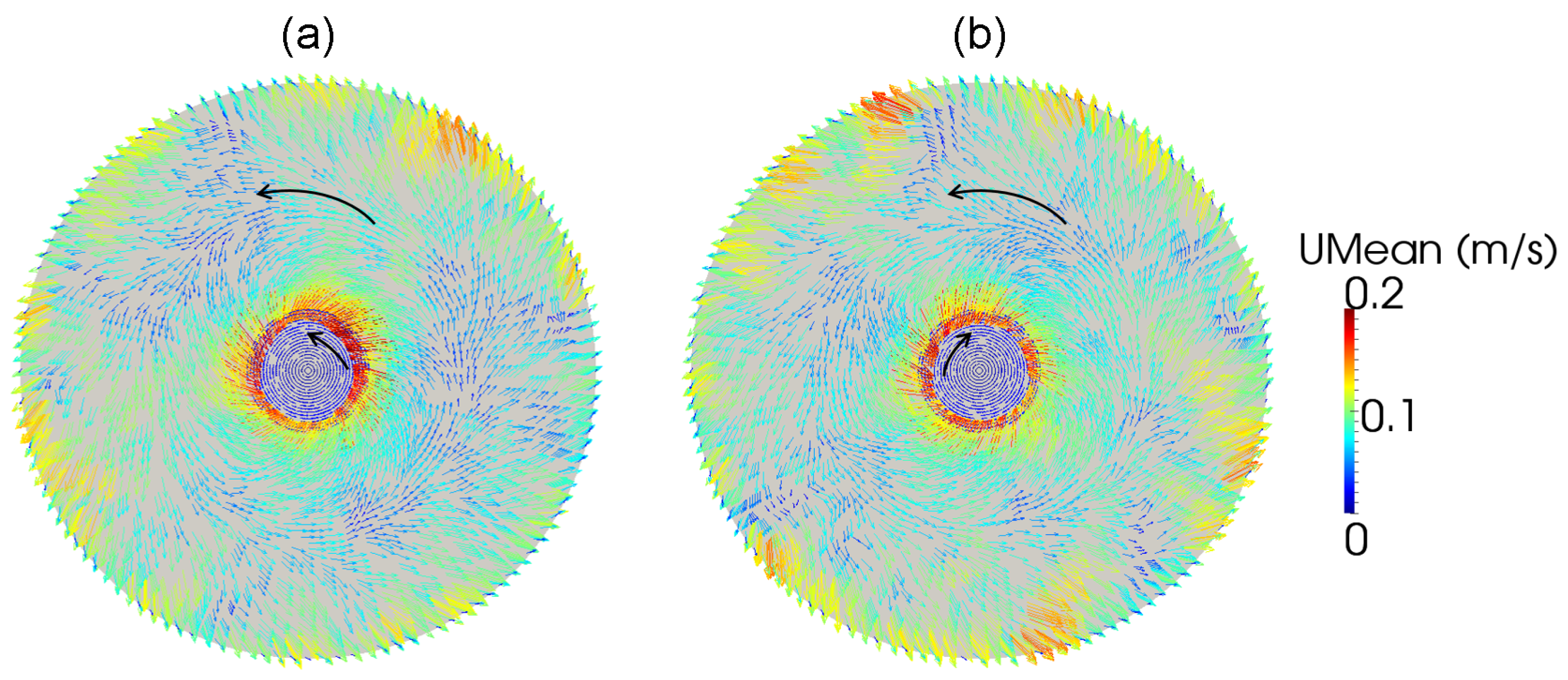
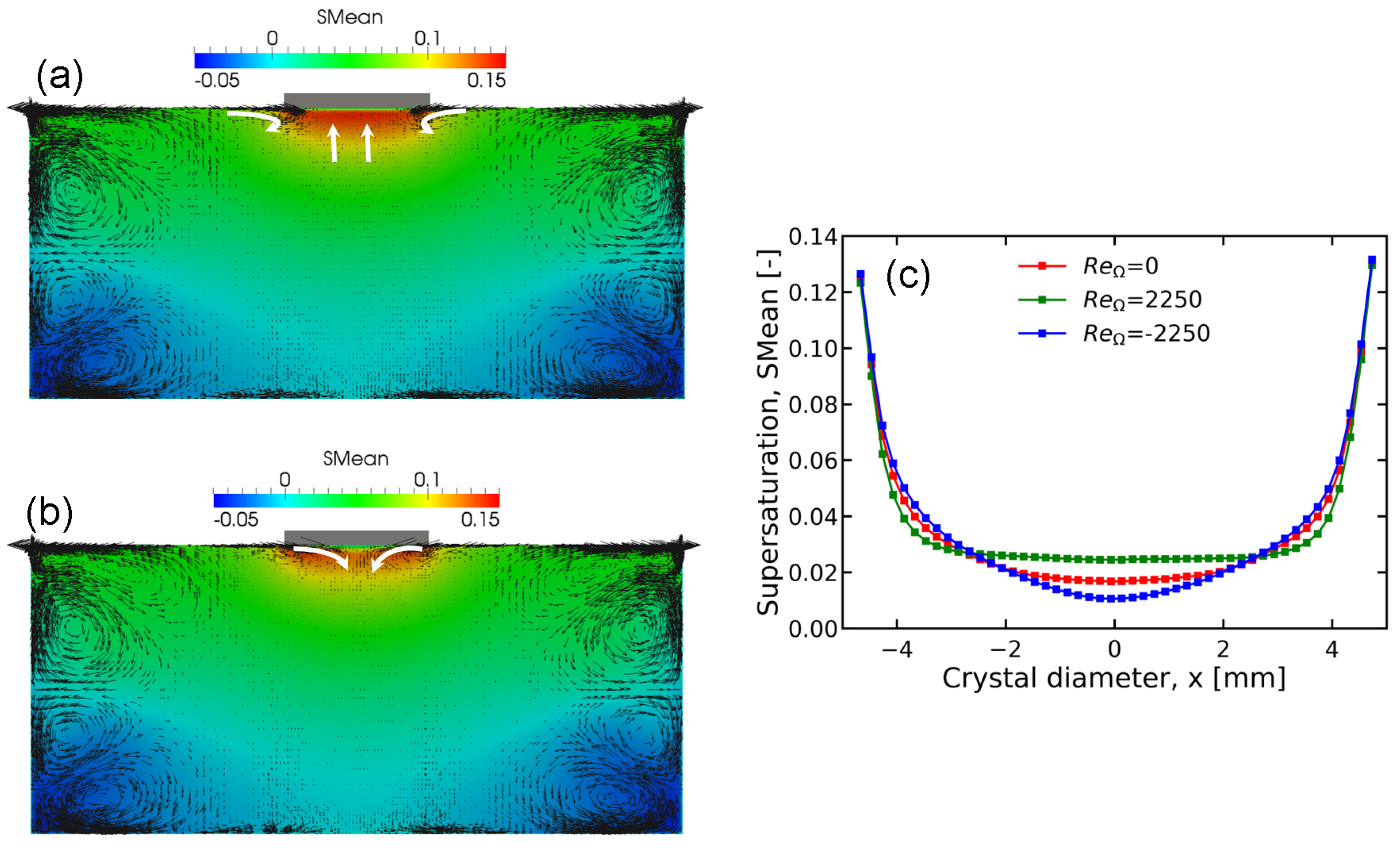
3.3. Combined Effect of Seed Rotation and RMF
4. Conclusions
- Fluid flow in the melt of the TSSG system is mainly the combination of an electromagnetic flow induced by the Lorentz force in the melt body, and Marangoni convection along the melt free surface driven by surface tension gradient.
- Higher coil frequency can reduce the Lorentz force density and enhance the heating temperature.
- Electromagnetic flow can suppress Marangoni convection near the seed. At the higher coil frequency, the downward flow below the seed due to Marangoni convection becomes more pronounced.
- Marangoni convection leads to a non-uniform supersaturation distribution in the melt along the seed surface. The supersaturation profile exhibits a high-low-high pattern from the seed center to its edge.
- An applied RMF can reduce supersaturation below the seed center, and the effect of RMF becomes more significant as the electromagnetic field weakens. When 3400, / is 3.6 or slightly smaller than 3.6 a uniform supersaturation distribution can be achieved; however, when 3400, / should be reduced significantly in order to obtain the desired uniformity.
- When RMF and the seed rotate in the same direction, supersaturation below the seed increases.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, L.; Horiuchi, T.; Sekimoto, A.; Okano, Y.; Ujihara, T.; Dost, S. Three-dimensional numerical analysis of Marangoni convection occurring during the growth process of SiC by the RF-TSSG method. J. Cryst. Growth 2019, 520, 72–81. [Google Scholar] [CrossRef]
- Wang, L.; Horiuchi, T.; Sekimoto, A.; Okano, Y.; Ujihara, T.; Dost, S. Numerical investigation of the effect of static magnetic field on the TSSG growth of SiC. J. Cryst. Growth 2018, 498, 140–147. [Google Scholar] [CrossRef]
- Takehara, Y.; Sekimoto, A.; Okano, Y.; Ujihara, T.; Dost, S. Bayesian optimization for a high- and uniform-crystal growth rate in the top-seeded solution growth process of silicon carbide under applied magnetic field and seed rotation. J. Cryst. Growth 2020, 532, 125437. [Google Scholar] [CrossRef]
- Yamamoto, T.; Adkar, N.; Okano, Y.; Ujihara, T.; Dost, S. Numerical investigation of the transport phenomena occurring in the growth of SiC by the induction heating TSSG method. J. Cryst. Growth 2017, 474, 50–54. [Google Scholar] [CrossRef]
- Brückner, F.U.; Schwerdtfeger, K. Single crystal growth with the Czochralski method involving rotational electromagnetic stirring of the melt. J. Cryst. Growth 1994, 139, 351–356. [Google Scholar] [CrossRef]
- Ghaddar, C.; Lee, C.; Motakef, S.; Gillies, D. Numerical simulation of THM growth of CdTe in the presence of rotating magnetic fields (RMF). J. Cryst. Growth 1999, 205, 97–111. [Google Scholar] [CrossRef]
- Dold, P.; Cröll, A.; Lichtensteiger, M.; Kaiser, T.; Benz, K.W. Floating zone growth of silicon in magnetic fields:: IV. Rotating magnetic fields. J. Cryst. Growth 2001, 231, 95–106. [Google Scholar] [CrossRef]
- Kakimoto, K. Effects of rotating magnetic fields on temperature and oxygen distributions in silicon melt. J. Cryst. Growth 2002, 237-239, 1785–1790. [Google Scholar] [CrossRef]
- Liu, Y.; Ai, F.; Pan, X.H.; Zhang, Y.; Zhou, Y.F.; Feng, C.D. Effects of rotating magnetic field on Bi12SiO20 crystal growth by vertical zone-melting technique. J. Cryst. Growth 2010, 312, 1622–1626. [Google Scholar] [CrossRef]
- Hoshikawa, K.; Kohda, H.; Hirata, H.; Nakanishi, H. Low oxygen content Czochralski silicon crystal growth. Jpn. J. Appl. Phys. 1980, 19, 1–7. [Google Scholar] [CrossRef]
- Zhou, X.; Huang, H. Numerical simulation of Cz crystal growth in rotating magnetic field with crystal and crucible rotations. J. Cryst. Growth 2012, 340, 166–170. [Google Scholar] [CrossRef]
- Mercier, F.; Nishizawa, S. Comparative numerical study of the effects of rotating and traveling magnetic fields on the carbon transport in the solution growth of SiC crystals. J. Cryst. Growth 2013, 362, 99–102. [Google Scholar] [CrossRef]
- Yamamoto, T.; Okano, Y.; Ujihara, T.; Dost, S. Global simulation of the induction heating TSSG process of SiC for the effects of Marangoni convection, free surface deformation and seed rotation. J. Cryst. Growth 2017, 470, 75–88. [Google Scholar] [CrossRef]
- Mercier, F.; Dedulle, J.M.; Chaussende, D.; Pons, M. Coupled heat transfer and fluid dynamics modeling of high-temperature SiC solution growth. J. Cryst. Growth 2010, 312, 155–163. [Google Scholar] [CrossRef]
- Du, D.X.; Munakata, T. Temperature distribution in an inductively heated CZ crucible. J. Cryst. Growth 2005, 283, 563–575. [Google Scholar] [CrossRef]
- Springer, G.Ś.; Wingeier, E.W. Thermal conductivity of neon, argon, and xenon at high temperatures. J. Chem. Phys. 1973, 59, 2747. [Google Scholar] [CrossRef]
- Yao, L.; Zeng, Z.; Li, X.; Chen, J.; Zhang, Y.; Mizuseki, H.; Kawazoe, Y. Effects of rotating magnetic fields on thermocapillary flow in a floating half-zone. J. Cryst. Growth 2011, 316, 177–184. [Google Scholar] [CrossRef]

| Materials | Property (Symbol) | Value | Unit |
|---|---|---|---|
| Si melt | Density () | 2550 | kg m |
| Viscosity () | 8.0 | Pa s | |
| Electrical conductivity () | 1.2 | S m | |
| Thermal conductivity (k) | 65 | W m K | |
| Specific heat () | 1.0 | J kg K | |
| Surface tension coefficient of temperature () | −2.5 | N m K | |
| Thermal expansion coefficient () | 1.4 | K | |
| Emissivity () | 0.3 | - | |
| Graphite | Electrical conductivity () | 7.54 | S m |
| Thermal conductivity (k) | 108 − 0.0864T + 2.304 | W m K | |
| Emissivity () | 0.66 | - | |
| Insulator | Electrical conductivity () | 0 | S m |
| Thermal conductivity (k) | 0.3 | W m K | |
| Emissivity () | 0.5 | - | |
| Helium | Electrical conductivity () | 0 | S m |
| Thermal conductivity (k) | 6.35 + 3.1 −2.44 | W m K | |
| Quartz | Thermal conductivity (k) | 1 + 1.25 | W m K |
| Emissivity () | 0.4 | - | |
| Chamber | Emissivity () | 0.1 | - |
| Coil | Emissivity () | 0.005 | - |
| Case | RF Frequency (kHz) | RF Current (A/m) | RMF Intensity (mT) | RMF Frequency (Hz) | Seed Rotation (rpm) |
|---|---|---|---|---|---|
| 1 | 10 | 8.57 | - | - | - |
| 2 | 25 | 6.285 | - | - | - |
| 3 | 40 | 5.285 | - | - | - |
| 4 | 10 | 8.57 | 3 | 50 | - |
| 5 | 25 | 6.285 | 3 | 50 | - |
| 6 | 40 | 5.285 | 3 | 50 | - |
| 7 | 25 | 6.285 | 3 | 50 | 60 |
| 8 | 25 | 6.285 | 3 | 50 | −60 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Takehara, Y.; Sekimoto, A.; Okano, Y.; Ujihara, T.; Dost, S. Numerical Study of Three-Dimensional Melt Flows during the TSSG Process of SiC Crystal for the Influence of Input Parameters of RF-Coils and an External Rotating Magnetic Field. Crystals 2020, 10, 111. https://doi.org/10.3390/cryst10020111
Wang L, Takehara Y, Sekimoto A, Okano Y, Ujihara T, Dost S. Numerical Study of Three-Dimensional Melt Flows during the TSSG Process of SiC Crystal for the Influence of Input Parameters of RF-Coils and an External Rotating Magnetic Field. Crystals. 2020; 10(2):111. https://doi.org/10.3390/cryst10020111
Chicago/Turabian StyleWang, Lei, Yuto Takehara, Atsushi Sekimoto, Yasunori Okano, Toru Ujihara, and Sadik Dost. 2020. "Numerical Study of Three-Dimensional Melt Flows during the TSSG Process of SiC Crystal for the Influence of Input Parameters of RF-Coils and an External Rotating Magnetic Field" Crystals 10, no. 2: 111. https://doi.org/10.3390/cryst10020111
APA StyleWang, L., Takehara, Y., Sekimoto, A., Okano, Y., Ujihara, T., & Dost, S. (2020). Numerical Study of Three-Dimensional Melt Flows during the TSSG Process of SiC Crystal for the Influence of Input Parameters of RF-Coils and an External Rotating Magnetic Field. Crystals, 10(2), 111. https://doi.org/10.3390/cryst10020111





