Identification of Local Structure in 2-D and 3-D Atomic Systems through Crystallographic Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Characteristic Crystallographic Element Norm
2.2. Molecular Simulations
3. Results
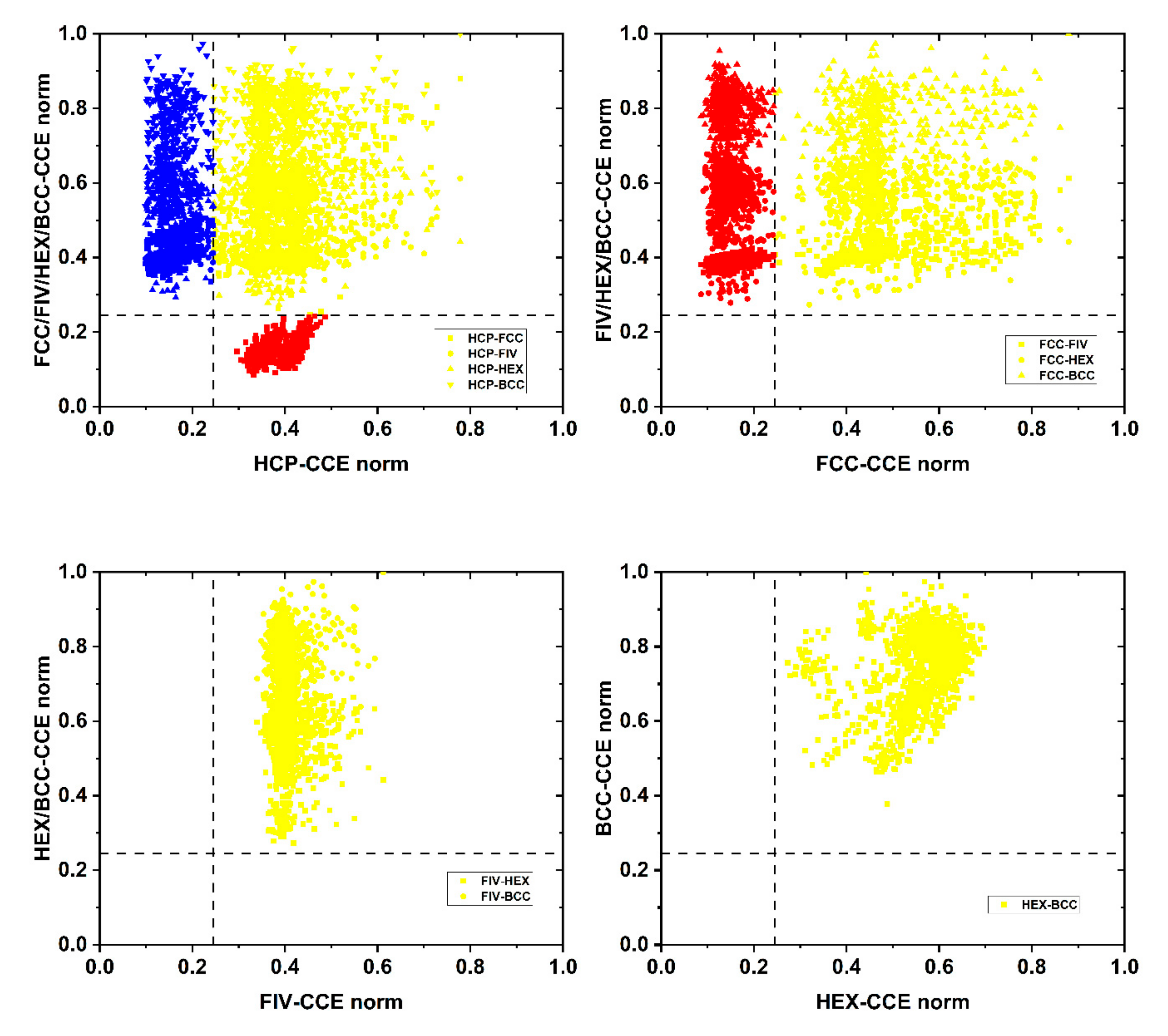
3.1. CCE Norm Application to Perfect Crystals
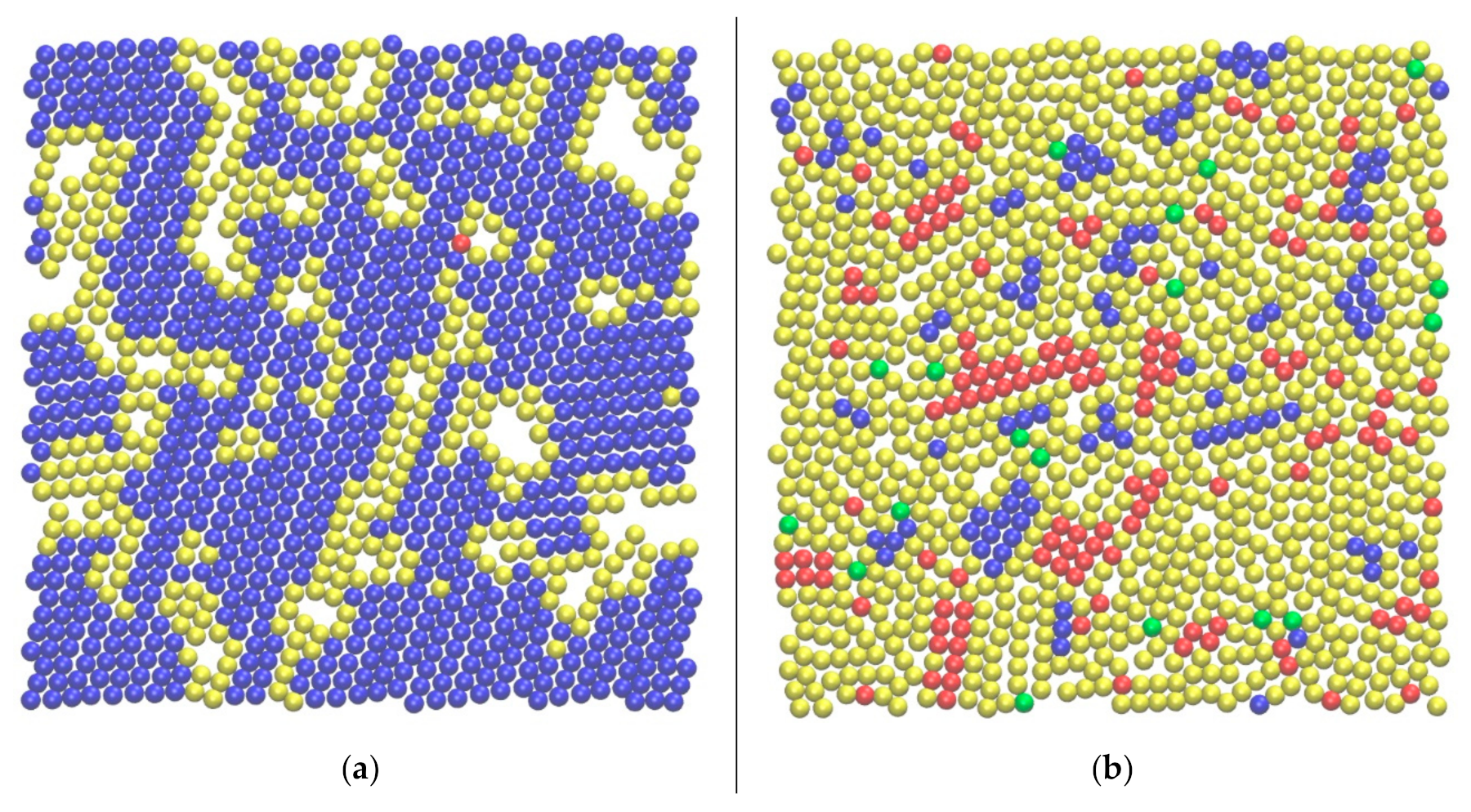
3.2. CCE Norm Application to Computer-Generated, 3-D Bulk Systems
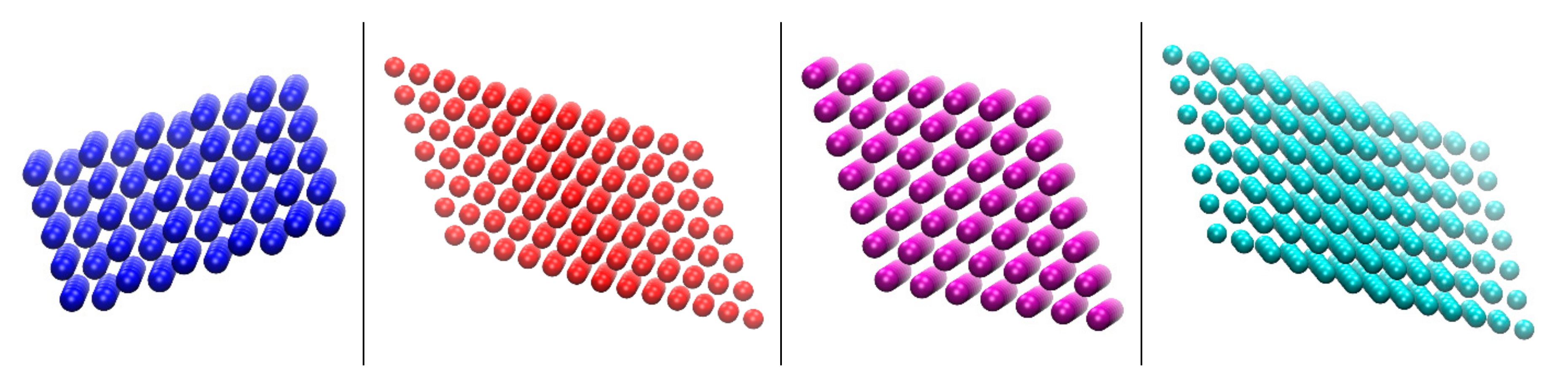
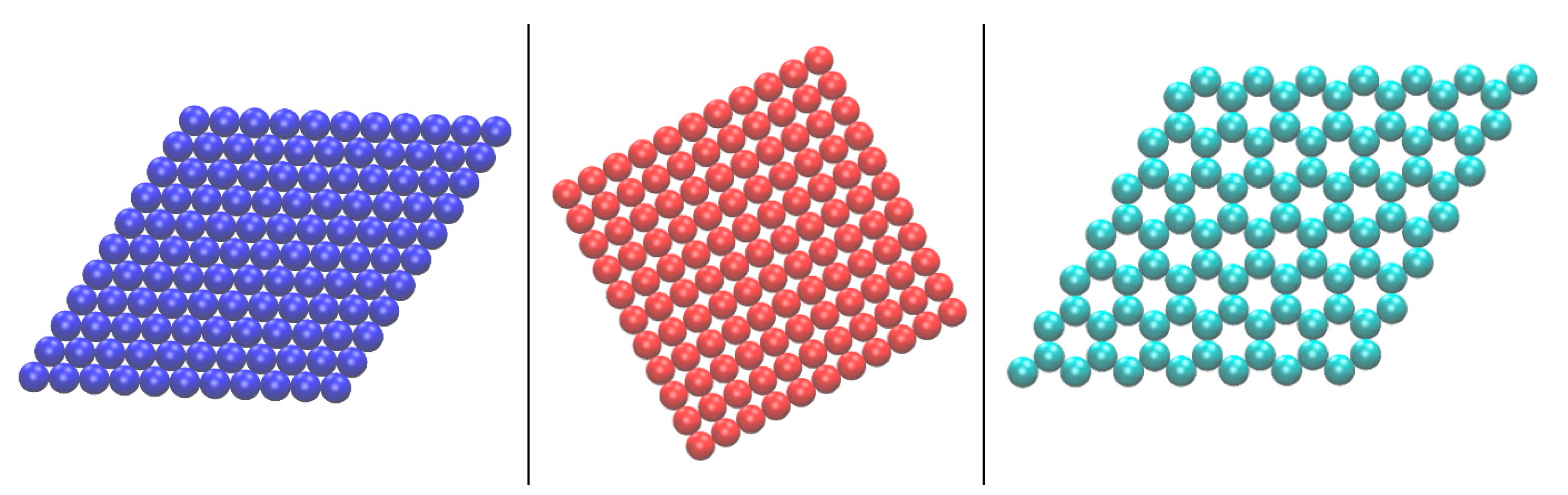
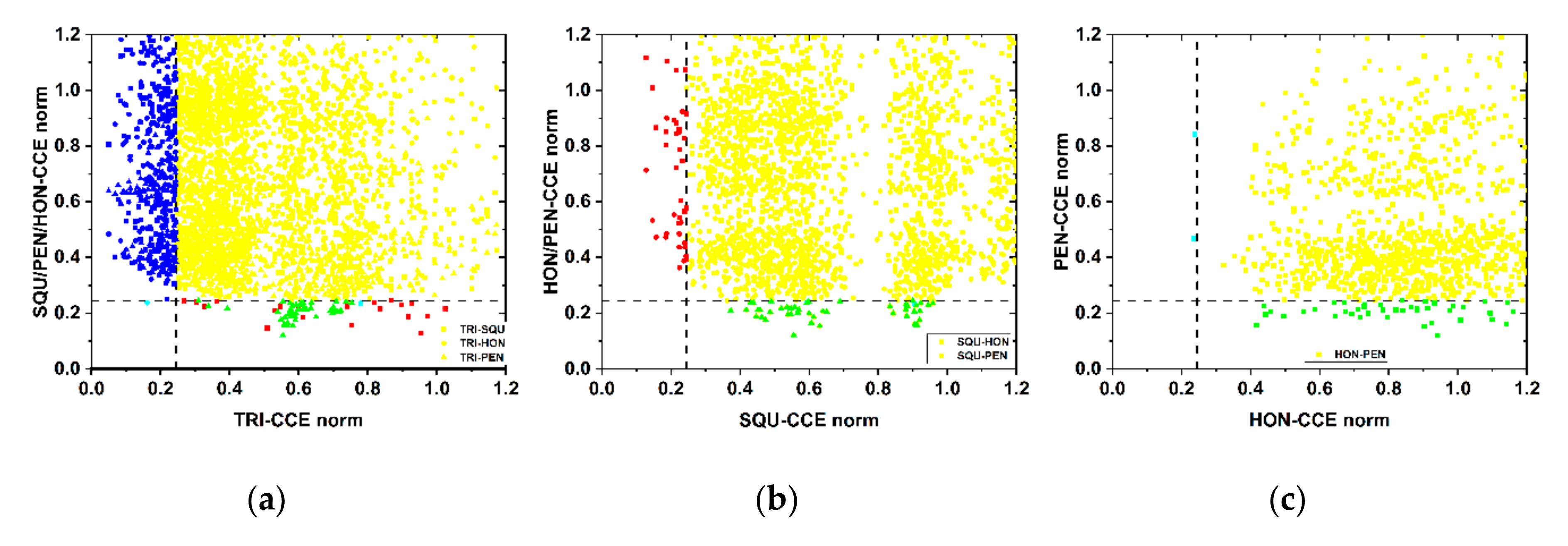
3.3. CCE Application to Computer-Generated, 2-D Thin-Film Systems
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BCC | Body Centered Cubic |
| CCE | Characteristic Crystallographic Element (norm) |
| CAN | Common Neighbor Analysis |
| FCC | Face Centered Cubic |
| FIV | Fivefold |
| HCP | Hexagonal Close Packed |
| HEX | Hexagonal |
| HON | Honeycomb |
| HS | Hard Sphere |
| MC | Monte Carlo |
| RCP | Random Close Packing |
| PEN | Pentagonal |
| RHCP | Random Hexagonal Close Packed |
| SQU | Square |
| SSP | Short-Range Order Symmetry Parameter |
| SW | Square Well |
| TRI | Triangular |
Appendix A


References
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids, 2nd ed.; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms to Applications, 2nd ed.; Academic Press: San Diego, CA, USA, 2002. [Google Scholar]
- Ma, E. Tuning order in disorder. Nat. Mater. 2015, 14, 547–552. [Google Scholar] [CrossRef] [PubMed]
- Tong, H.; Tanaka, H. Structural order as a genuine control parameter of dynamics in simple glass formers. Nat. Commun. 2019, 10. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. Vmd: Visual molecular dynamics. J. Mol. Graph. Model. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Ahrens, J.; Geveci, B.; Law, C. Paraview: An End-User Tool for Large Data Visualization; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Pettersen, E.F.; Goddard, T.D.; Huang, C.C.; Couch, G.S.; Greenblatt, D.M.; Meng, E.C.; Ferrin, T.E. Ucsf chimera—A visualization system for exploratory research and analysis. J. Comput. Chem. 2004, 25, 1605–1612. [Google Scholar] [CrossRef] [PubMed]
- Stukowski, A. Visualization and analysis of atomistic simulation data with ovito-the open visualization tool. Modell. Simul. Mater. Sci. Eng. 2010, 18. [Google Scholar] [CrossRef]
- Bumstead, M.; Liang, K.Y.; Hanta, G.; Hui, L.S.; Turak, A. Dislocate: Tools to rapidly quantify local intermolecular structure to assess two-dimensional order in self-assembled systems. Sci. Rep. 2018, 8. [Google Scholar] [CrossRef]
- McQuarrie, D.A. Statistical Mechanics; Viva Books: Kolkata, India, 2011. [Google Scholar]
- Honeycutt, J.D.; Andersen, H.C. Molecular-dynamics study of melting and freezing of small lennard-jones clusters. J. Phys. Chem. 1987, 91, 4950–4963. [Google Scholar] [CrossRef]
- Ganesh, P.; Widom, M. Signature of nearly icosahedral structures in liquid and supercooled liquid copper. Phys. Rev. B 2006, 74. [Google Scholar] [CrossRef]
- Faken, D.; Jónsson, H. Systematic analysis of local atomic structure combined with 3d computer graphics. Comput. Mater. Sci. 1994, 2, 279–286. [Google Scholar] [CrossRef]
- Martin, A.V.; Kozlov, A.; Berntsen, P.; Roque, F.G.; Flueckiger, L.; Saha, S.; Greaves, T.L.; Conn, C.E.; Hawley, A.M.; Ryan, T.M.; et al. Fluctuation x-ray diffraction reveals three-dimensional nanostructure and disorder in self-assembled lipid phases. Commun. Mater. 2020, 1, 1–8. [Google Scholar] [CrossRef]
- Steinhardt, P.J.; Nelson, D.R.; Ronchetti, M. Bond-orientational order in liquids and glasses. Phys. Rev. B 1983, 28, 784–805. [Google Scholar] [CrossRef]
- Larsen, P.M.; Schmidt, S.; Schiotz, J. Robust structural identification via polyhedral template matching. Modell. Simul. Mater. Sci. Eng. 2016, 24. [Google Scholar] [CrossRef]
- Torquato, S. Cell and random-field models. In Random Heterogeneous Materials. Interdisciplinary Applied Mathematics; Springer: New York, NY, USA, 2002; Volume 16. [Google Scholar] [CrossRef]
- Voronoi, G. New applications of continuous parameters to the theory of quadratic forms.—First memoir—Some properties of perfect positive quadratic forms. Journal Fur Die Reine Und Angewandte Mathematik 1908, 133, 97–178. [Google Scholar] [CrossRef]
- Finney, J.L. Random packings and structure of simple liquids.1. Geometry of random close packing. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1970, 319, 479–493. [Google Scholar] [CrossRef]
- Tanemura, M.; Hiwatari, Y.; Matsuda, H.; Ogawa, T.; Ogita, N.; Ueda, A. Geometrical analysis of crystallization of soft-core model. Prog. Theor. Phys. 1977, 58, 1079–1095. [Google Scholar] [CrossRef]
- Anikeenko, A.V.; Medvedev, N.N.; Aste, T. Structural and entropic insights into the nature of the random-close-packing limit. Phys. Rev. E 2008, 77. [Google Scholar] [CrossRef] [PubMed]
- Ackland, G.J.; Jones, A.P. Applications of local crystal structure measures in experiment and simulation. Phys. Rev. B 2006, 73. [Google Scholar] [CrossRef]
- Cohen, M.H.; Grest, G.S. Liquid-glass transition, a free-volume approach. Phys. Rev. B 1979, 20, 1077–1098. [Google Scholar] [CrossRef]
- Egami, T.; Maeda, K.; Vitek, V. Structural defects in amorphous solids—A computer-simulation study. Philos. Mag. A Phys. Condens. Matter Struct. Defects Mech. Prop. 1980, 41, 883–901. [Google Scholar] [CrossRef]
- Ding, J.; Cheng, Y.Q.; Sheng, H.; Asta, M.; Ritchie, R.O.; Ma, E. Universal structural parameter to quantitatively predict metallic glass properties. Nat. Commun. 2016, 7. [Google Scholar] [CrossRef]
- Malins, A.; Williams, S.R.; Eggers, J.; Royall, C.P. Identification of structure in condensed matter with the topological cluster classification. J. Chem. Phys. 2013, 139. [Google Scholar] [CrossRef] [PubMed]
- Stukowski, A. Structure identification methods for atomistic simulations of crystalline materials. Modell. Simul. Mater. Sci. Eng. 2012, 20. [Google Scholar] [CrossRef]
- Paret, J.; Jack, R.L.; Coslovich, D. Assessing the structural heterogeneity of supercooled liquids through community inference. J. Chem. Phys. 2020, 152. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. The characteristic crystallographic element norm: A descriptor of local structure in atomistic and particulate systems. J. Chem. Phys. 2009, 130. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. Entropy-driven crystallization in dense systems of athermal chain molecules. Phys. Rev. Lett. 2009, 103. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Foteinopoulou, K.; Abrams, C.F.; Laso, M. Modeling of crystal nucleation and growth in athermal polymers: Self-assembly of layered nano-morphologies. Soft Matter 2010, 6, 2160–2173. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. Spontaneous crystallization in athermal polymer packings. Int. J. Mol. Sci. 2013, 14, 332–358. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. Jamming and crystallization in athermal polymer packings. Philos. Mag. 2013, 93, 4108–4131. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. The role of bond tangency and bond gap in hard sphere crystallization of chains. Soft Matter 2015, 11, 1688–1700. [Google Scholar] [CrossRef] [PubMed]
- Karayiannis, N.C.; Malshe, R.; de Pablo, J.J.; Laso, M. Fivefold symmetry as an inhibitor to hard-sphere crystallization. Phys. Rev. E 2011, 83. [Google Scholar] [CrossRef] [PubMed]
- Karayiannis, N.C.; Malshe, R.; Kroger, M.; de Pablo, J.J.; Laso, M. Evolution of fivefold local symmetry during crystal nucleation and growth in dense hard-sphere packings. Soft Matter 2012, 8, 844–858. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. Twinning of polymer crystals suppressed by entropy. Symmetry 2014, 6, 758–780. [Google Scholar] [CrossRef]
- Hoy, R.S.; Karayiannis, N.C. Simple model for chain packing and crystallization of soft colloidal polymers. Phys. Rev. E 2013, 88. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Smith, T.B.; Hoy, R.S.; Karayiannis, N.C. Effect of chain stiffness on the competition between crystallization and glass-formation in model unentangled polymers. J. Chem. Phys. 2015, 143. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Karayiannis, N.C.; Laso, M.; Qu, D.D.; Luo, Q.; Shen, J. A metric to gauge local distortion in metallic glasses and supercooled liquids. Acta Mater. 2014, 72, 229–238. [Google Scholar] [CrossRef]
- Herranz, M.; Santiago, M.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Crystal, fivefold and glass formation in clusters of polymers interacting with the square well potential. Polymers 2020, 12, 1111. [Google Scholar] [CrossRef]
- Malgrange, C.; Ricolleau, C.; Schlenker, M. Symmetry and Physical Properties of Crystals; Springer: Dordrecht, The Netherlands, 2014. [Google Scholar] [CrossRef]
- Nye, J.F. Physical Properties of Crystals: Their Representation by Tensors and Matrices; Oxford Science Publications: Oxford, UK, 2010. [Google Scholar]
- Laso, M.; Jimeno, N. Representation Surfaces for Physical Properties of Materials: A Visual Approach to Understanding Anisotropic Materials; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Giacovazzo, C.; Monaco, H.L.; Artioli, G.; Viterbo, D.; Ferraris, G.; Gilli, G.; Zanotti, G.; Gatti, M. Fundamentals of Crystallography; Oxford Science: Oxford, UK, 2005. [Google Scholar]
- Rycroft, C.H. Voro plus plus: A three-dimensional voronoi cell library in c plus. Chaos 2009, 19. [Google Scholar] [CrossRef]
- Barber, C.B.; Dobkin, D.P.; Huhdanpaa, H. The quickhull algorithm for convex hulls. Acm Trans. Math. Softw. 1996, 22, 469–483. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Laso, M. Monte carlo scheme for generation and relaxation of dense and nearly jammed random structures of freely jointed hard-sphere chains. Macromolecules 2008, 41, 1537–1551. [Google Scholar] [CrossRef]
- Ramos, P.M.; Karayiannis, N.C.; Laso, M. Off-lattice simulation algorithms for athermal chain molecules under extreme confinement. J. Comput. Phys. 2018, 375, 918–934. [Google Scholar] [CrossRef]
- Laso, M.; Karayiannis, N.C.; Foteinopoulou, K.; Mansfield, M.L.; Kroger, M. Random packing of model polymers: Local structure, topological hindrance and universal scaling. Soft Matter 2009, 5, 1762–1770. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. The structure of random packings of freely jointed chains of tangent hard spheres. J. Chem. Phys. 2009, 130. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. Contact network in nearly jammed disordered packings of hard-sphere chains. Phys. Rev. E 2009, 80. [Google Scholar] [CrossRef] [PubMed]
- Karayiannis, N.C.; Laso, M. Dense and nearly jammed random packings of freely jointed chains of tangent hard spheres. Phys. Rev. Lett. 2008, 100. [Google Scholar] [CrossRef]
- Lucarini, V. Three-dimensional random voronoi tessellations: From cubic crystal lattices to poisson point processes. J. Stat. Phys. 2009, 134, 185–206. [Google Scholar] [CrossRef]
- Schoenholz, S.S.; Cubuk, E.D.; Kaxiras, E.; Liu, A.J. Relationship between local structure and relaxation in out-of-equilibrium glassy systems. Proc. Natl. Acad. Sci. USA 2017, 114, 263–267. [Google Scholar] [CrossRef]
- Cubuk, E.D.; Ivancic, R.J.S.; Schoenholz, S.S.; Strickland, D.J.; Basu, A.; Davidson, Z.S.; Fontaine, J.; Hor, J.L.; Huang, Y.R.; Jiang, Y.; et al. Structure-property relationships from universal signatures of plasticity in disordered solids. Science 2017, 358, 1033–1037. [Google Scholar] [CrossRef]
- Parreno, O.; Ramos, P.M.; Karayiannis, N.C.; Laso, M. Self-avoiding random walks as a model to study athermal linear polymers under extreme plate confinement. Polymers 2020, 12, 799. [Google Scholar] [CrossRef]
- Benito, J.; Karayiannis, N.C.; Laso, M. Confined polymers as self-avoiding random walks on restricted lattices. Polymers 2018, 10, 1394. [Google Scholar] [CrossRef]
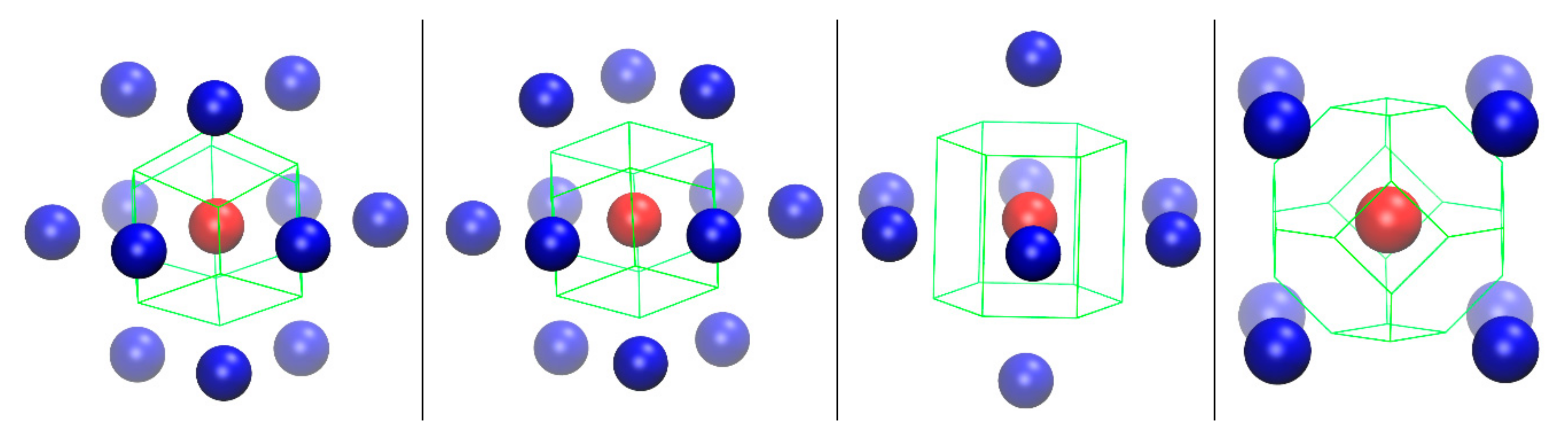

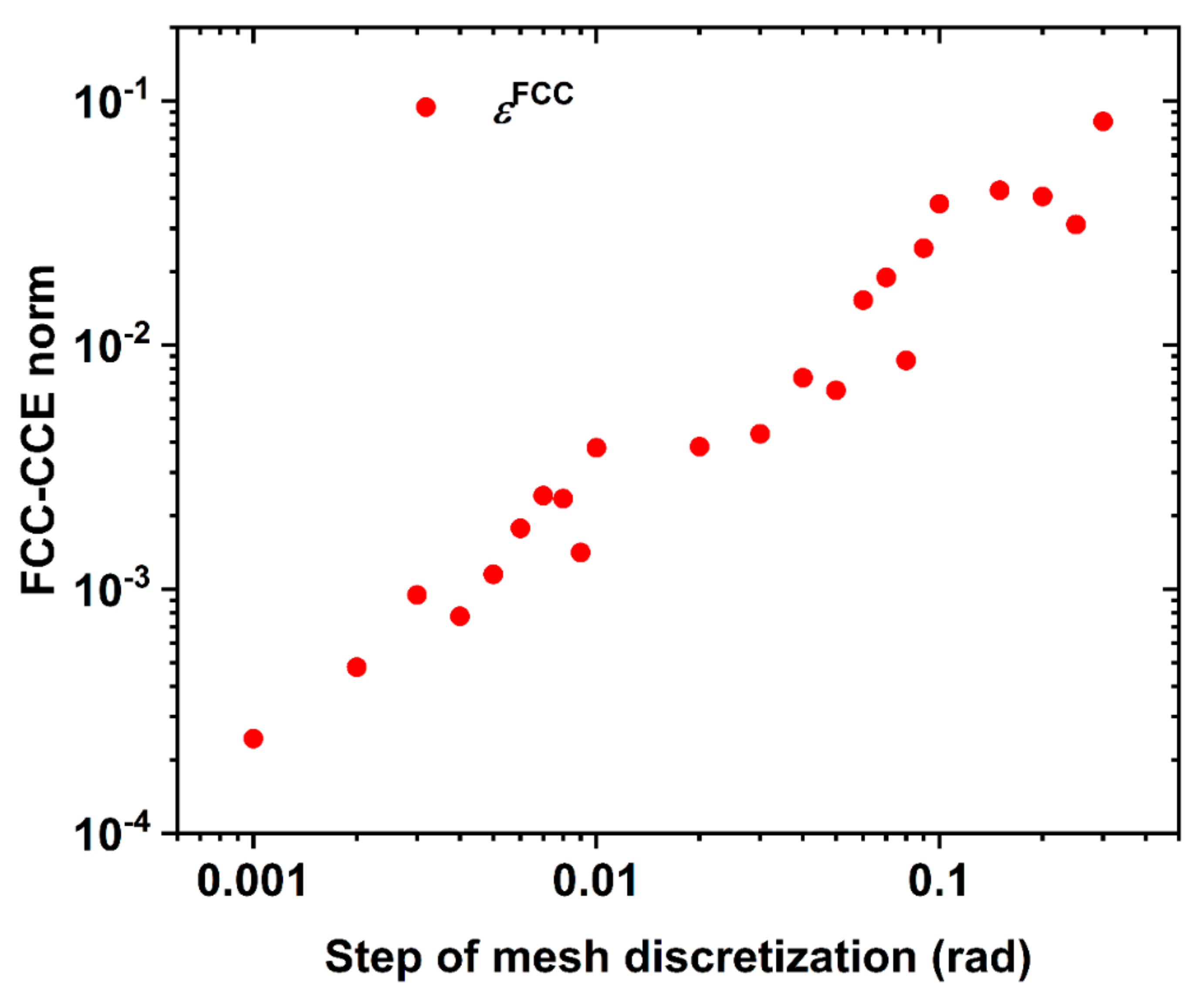
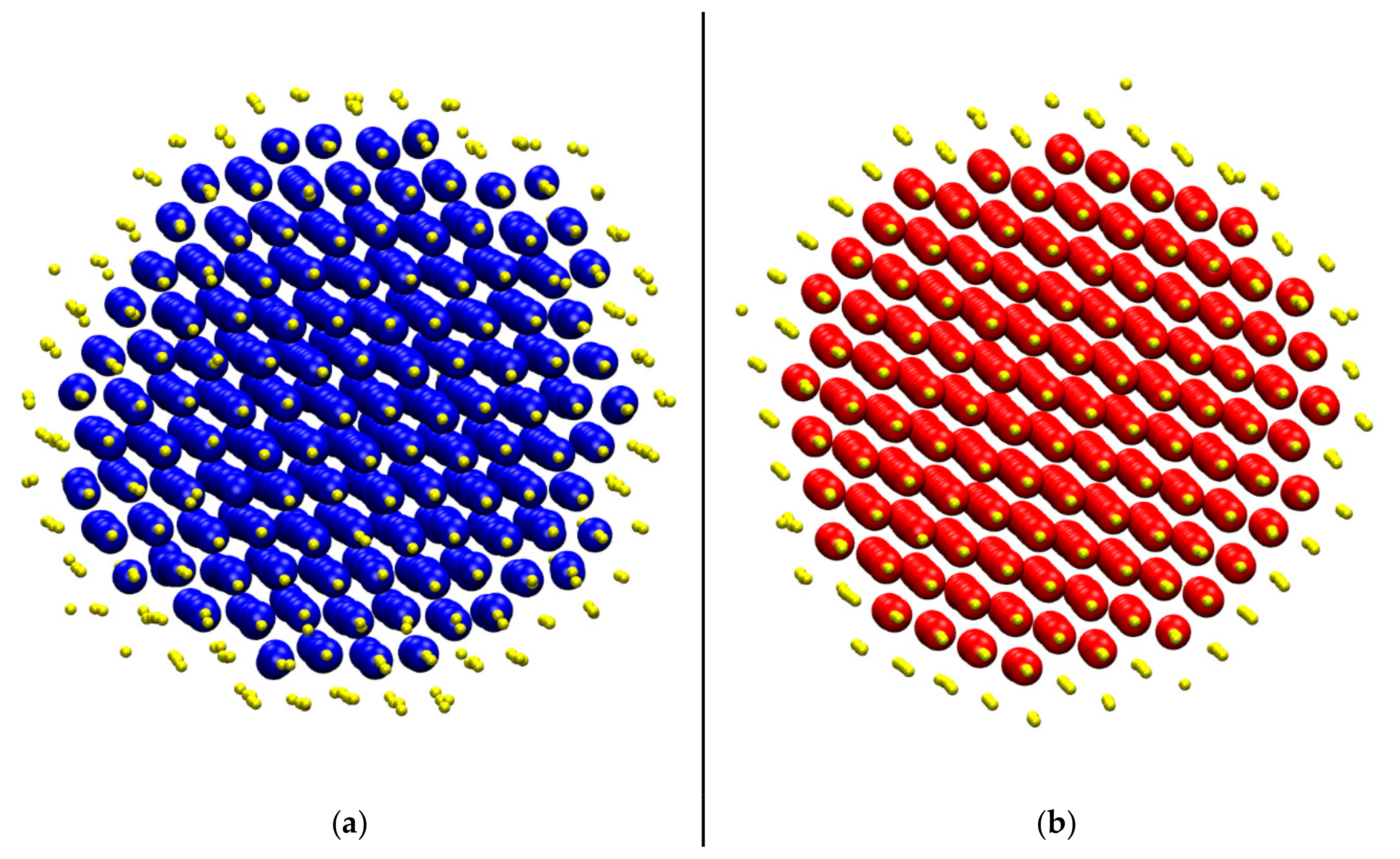
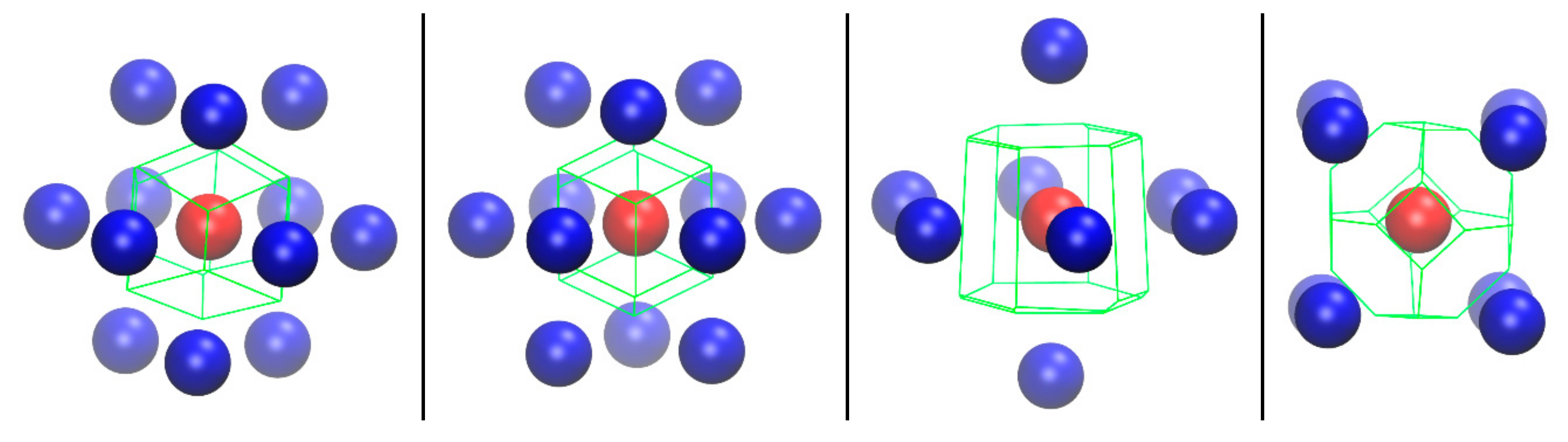


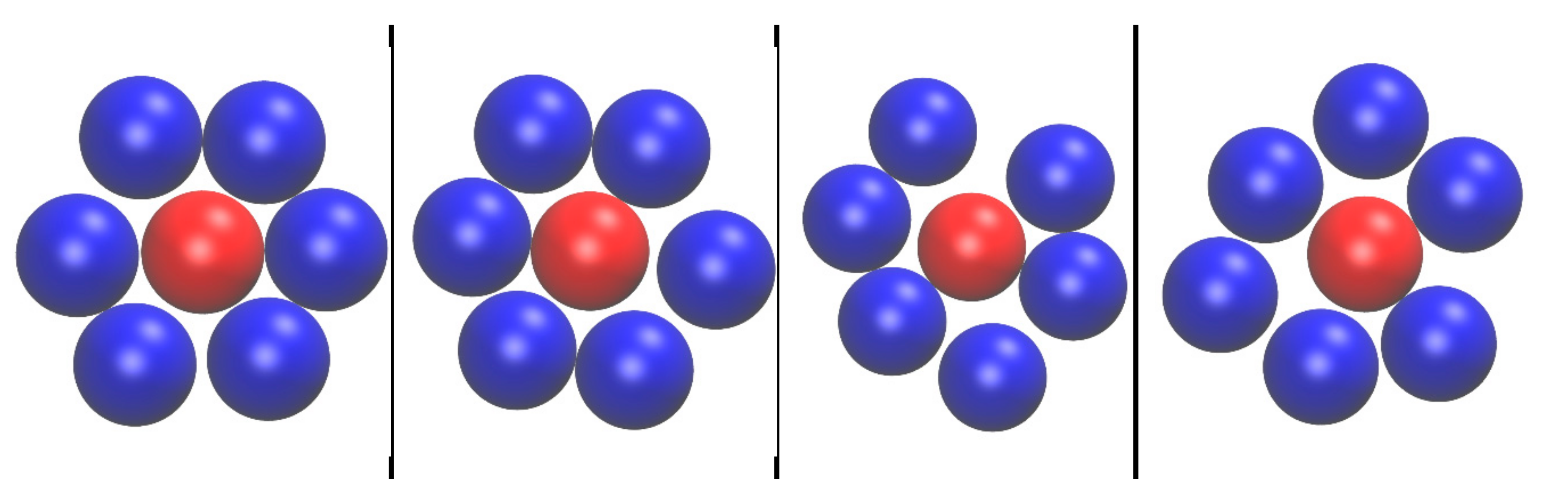
| Reference Structure → Fingerprint ↓ | HCP | FCC | HEX | BCC | FIV |
|---|---|---|---|---|---|
| Ncoord(X) | 12 | 12 | 8 | 8 | 12 |
| Nel(X) | 1 | 5 | 2 | 5 | 2 |
| Geometric Symmetry Element k | (k = 1) Roto-inversion Axis | (k = 1,…,4) Roto-inversion Axes (k = 5) Inversion Center | (k = 1) Rotation Axis (k = 2) Inversion Center | (k = 1,…,4) Roto-inversion Axes (k = 5) Inversion Center | (k = 1) Rotation Axis (k = 2) Inversion Center |
| Nact(k,X) | (k = 1) 5 | (k = 1,…,4) 5 (k = 5) 1 | (k = 1) 5 (k = 2) 1 | (k =1,…,4) 5 (k = 5) 1 | (k = 1) 4 (k = 2) 1 |
| Symmetry Actions of Geometric Element k | (k = 1) , , , , | (k = 1,…,4) , , , , (k = 5) | (k = 1) , , , , (k = 2) | (k = 1,…,4) , , , , (k = 5) | (k = 1) , , , , (k = 2) |
| Reference Structure → Fingerprint ↓ | TRI | SQU | HON | PEN |
|---|---|---|---|---|
| Ncoord(X) | 6 | 4 | 3 | 5 |
| Nel(X) | 2 | 2 | 1 | 1 |
| Geometric Symmetry Element k | (k = 1) Rotation Axis (k = 2) Inversion Center | (k = 1) Rotation Axis (k = 2) Inversion Center | (k = 1) Rotation Axis | (k = 1) Rotation Axis |
| Nact(k,X) | (k = 1) 5 (k = 2) 1 | (k = 1) 3 (k = 2) 1 | (k = 1) 2 | (k = 1) 4 |
| Symmetry Actions of Geometric Element k | (k = 1) , , , , (k = 2) | (k = 1) , , (k = 2) | (k = 1) , , | (k = 1) , , , |
| εX → Reference Lattice ↓ | HCP | FCC | HEX | BCC | FIV |
|---|---|---|---|---|---|
| HCP | 0 | 0.257 | 0.290 | 0.412 | 0.228 |
| FCC | 0.246 | 0.000244 | 0.377 | 0.518 | 0.229 |
| HEX | 0.280 | 0.239 | 0 | 0.239 | 0.185 |
| BCC | 0.284 | 0.165 | 0.246 | 0.000190 | 0.276 |
| εX → Reference Lattice ↓ | TRI | SQU | HON | PEN |
|---|---|---|---|---|
| TRI | 0 | 0.275 | 0.699 | 0.397 |
| SQU | 0.301 | 0 | 0.613 | 0.318 |
| HON | 0.649 | 0.465 | 0 | 0.420 |
| X | Ncoord(X) | F(X) | V(X) | E(X) | VVP(X) | AVP(X) | ρn(X) | φ(X) | Q(X) |
|---|---|---|---|---|---|---|---|---|---|
| HCP | 12 | 12 | 14 | 14 | 0.7071 | 4.243 | 1.414 | 0.7404 | 0.7405 |
| FCC | 12 | 12 | 14 | 24 | 0.7071 | 4.243 | 1.414 | 0.7404 | 0.7405 |
| HEX | 8 | 8 | 12 | 18 | 0.8660 | 5.196 | 1.155 | 0.6046 | 0.6045 |
| BCC | 8 | 14 | 24 | 36 | 0.7698 | 4.464 | 1.299 | 0.6800 | 0.7534 |
| X-like | Ncoord(X) | F(X) | V(X) | E(X) | VVP(X) | AVP(X) | ρn(X) | φ(X) | Q(X) |
|---|---|---|---|---|---|---|---|---|---|
| HCP | 12 | 13 | 22 | 33 | 0.7534 | 4.426 | 1.327 | 0.6950 | 0.7404 |
| FCC | 12 | 13 | 22 | 33 | 0.7311 | 4.339 | 1.368 | 0.7162 | 0.7400 |
| HEX | 8 | 15 | 26 | 39 | 1.038 | 5.806 | 0.9634 | 0.5044 | 0.6226 |
| BCC | 8 | 14 | 24 | 36 | 0.9214 | 5.045 | 1.085 | 0.5683 | 0.7478 |
| X | % VVP(X) | % AVP(X) | % Q(X) | X-CCE norm |
|---|---|---|---|---|
| HCP | 6.55 | 4.31 | 0.0135 | 0.0340 |
| FCC | 3.39 | 2.26 | 0.0675 | 0.0223 |
| HEX | 19.9 | 10.5 | 2.99 | 0.0466 |
| BCC | 19.7 | 13.0 | 0.743 | 0.0536 |
| X | Ncoord(X) | V(X) | E(X) | AVP(X) | PVP(X) | q(X) | ||
|---|---|---|---|---|---|---|---|---|
| TRI | 6 | 6 | 6 | 0.8660 | 3.464 | 1.155 | 0.907 | 0.907 |
| SQU | 4 | 4 | 4 | 1.000 | 4.000 | 1.000 | 0.785 | 0.785 |
| HON | 3 | 3 | 3 | 1.299 | 5.196 | 0.7698 | 0.604 | 0.604 |
| εTRI | Ncoord(TRI) | V(TRI) | E(TRI) | AVP(TRI) | PVP(TRI) | q(TRI) | ||
|---|---|---|---|---|---|---|---|---|
| 0.00 | 6 | 6 | 6 | 0.8660 | 3.464 | 1.155 | 0.907 | 0.907 |
| 0.05 | 6 | 6 | 6 | 0.9160 | 3.564 | 1.093 | 0.858 | 0.905 |
| 0.10 | 6 | 6 | 6 | 0.9420 | 3.620 | 1.062 | 0.834 | 0.903 |
| 0.20 | 6 | 6 | 6 | 1.006 | 3.766 | 0.9940 | 0.781 | 0.891 |
| 0.30 | 6 | 6 | 6 | 1.000 | 3.776 | 1.000 | 0.786 | 0.881 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramos, P.M.; Herranz, M.; Foteinopoulou, K.; Karayiannis, N.C.; Laso, M. Identification of Local Structure in 2-D and 3-D Atomic Systems through Crystallographic Analysis. Crystals 2020, 10, 1008. https://doi.org/10.3390/cryst10111008
Ramos PM, Herranz M, Foteinopoulou K, Karayiannis NC, Laso M. Identification of Local Structure in 2-D and 3-D Atomic Systems through Crystallographic Analysis. Crystals. 2020; 10(11):1008. https://doi.org/10.3390/cryst10111008
Chicago/Turabian StyleRamos, Pablo Miguel, Miguel Herranz, Katerina Foteinopoulou, Nikos Ch. Karayiannis, and Manuel Laso. 2020. "Identification of Local Structure in 2-D and 3-D Atomic Systems through Crystallographic Analysis" Crystals 10, no. 11: 1008. https://doi.org/10.3390/cryst10111008
APA StyleRamos, P. M., Herranz, M., Foteinopoulou, K., Karayiannis, N. C., & Laso, M. (2020). Identification of Local Structure in 2-D and 3-D Atomic Systems through Crystallographic Analysis. Crystals, 10(11), 1008. https://doi.org/10.3390/cryst10111008