Effect of 3D Representative Volume Element (RVE) Thickness on Stress and Strain Partitioning in Crystal Plasticity Simulations of Multi-Phase Materials
Abstract
:1. Introduction
2. Numerical Simulation Model Development
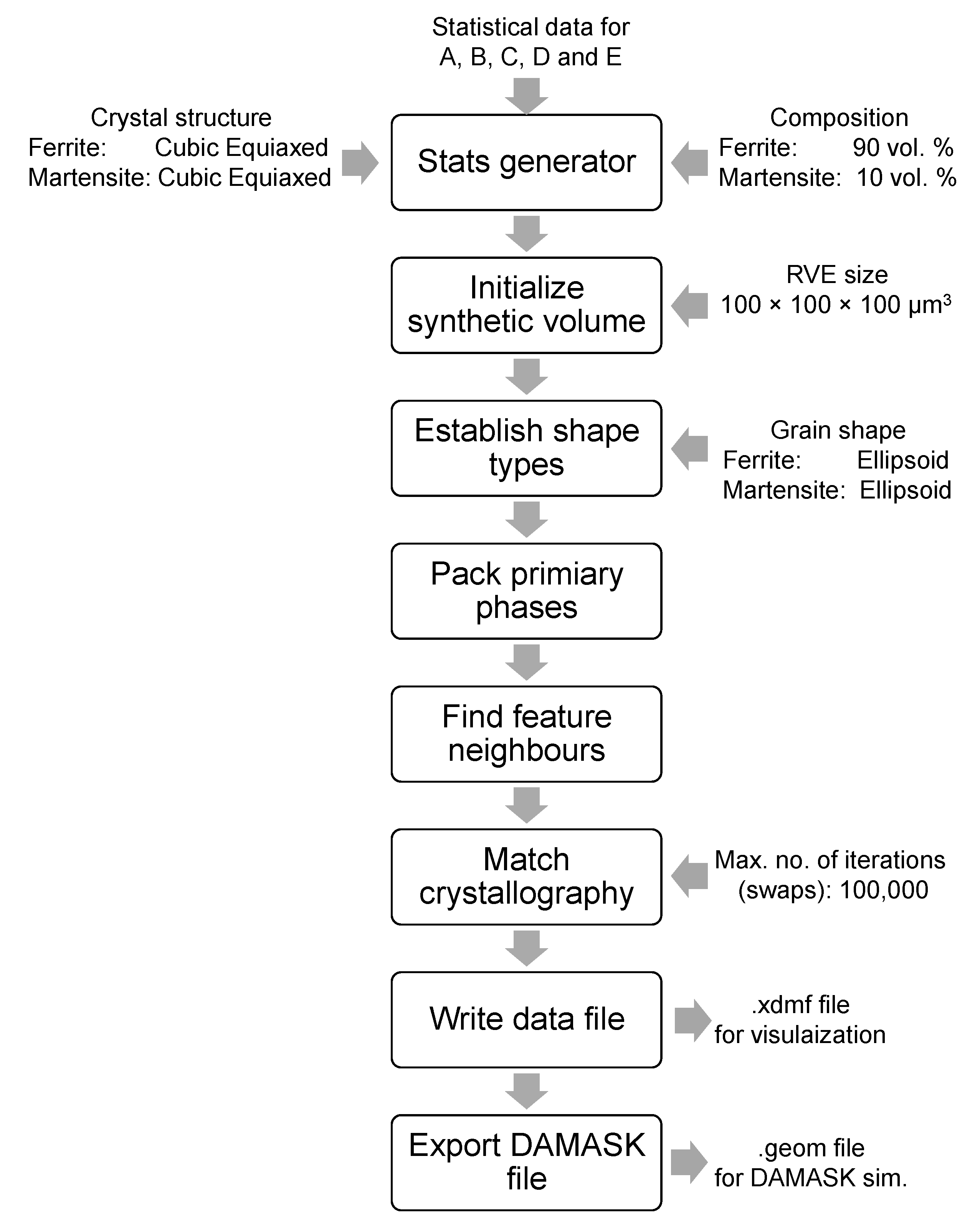
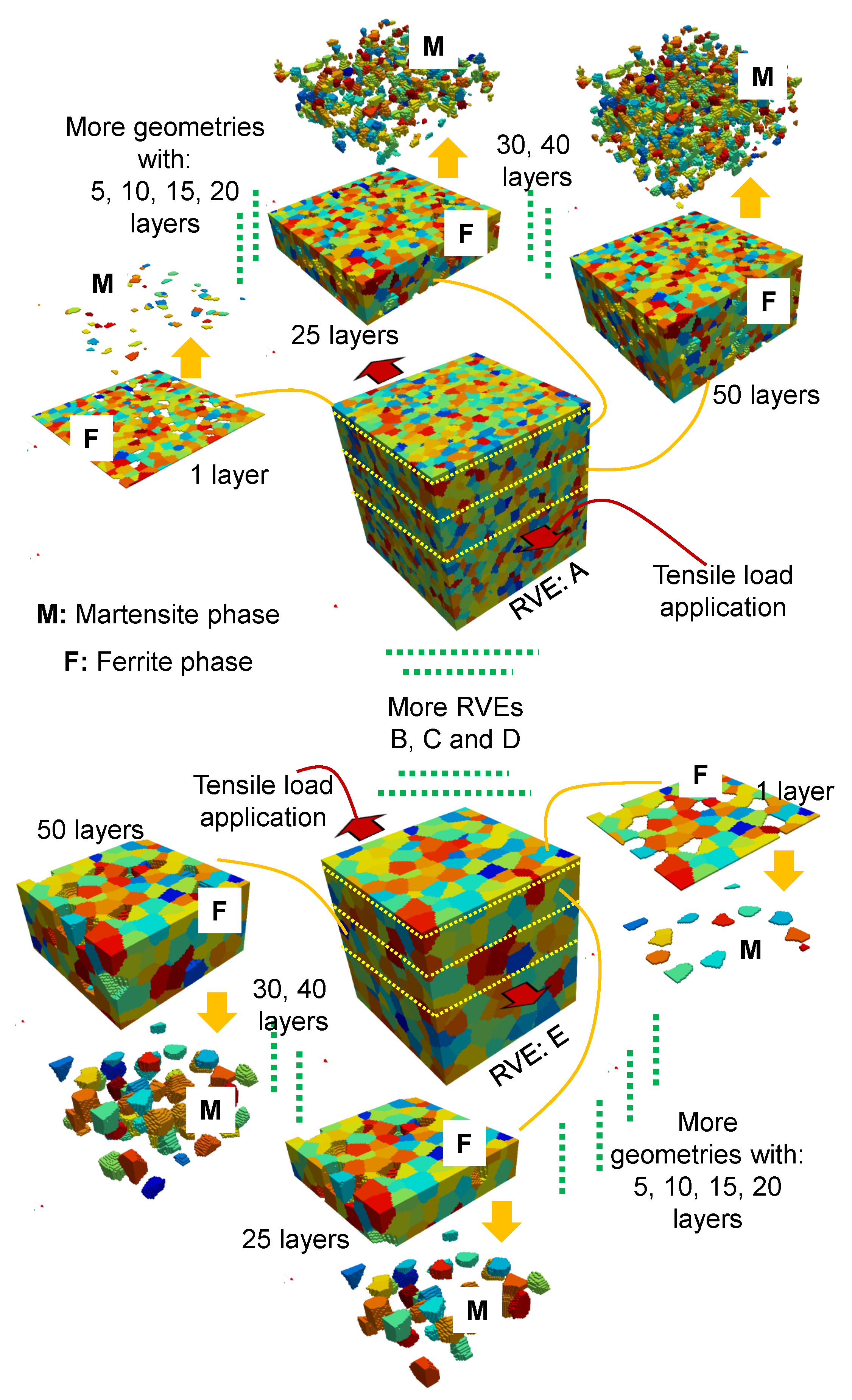
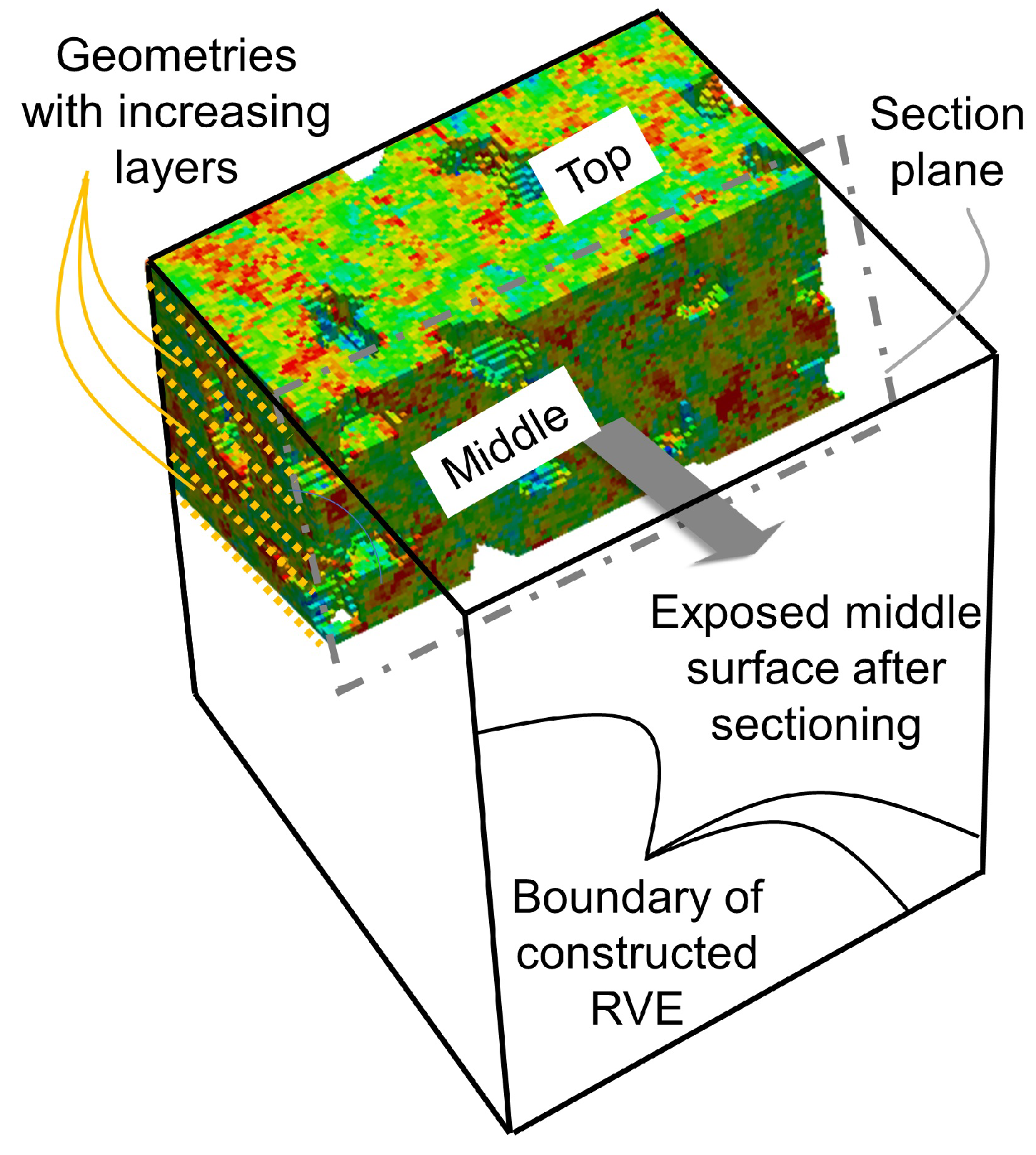
2.1. RVE Construction and Geometry Files Production
2.2. Material Properties and Loading Conditions
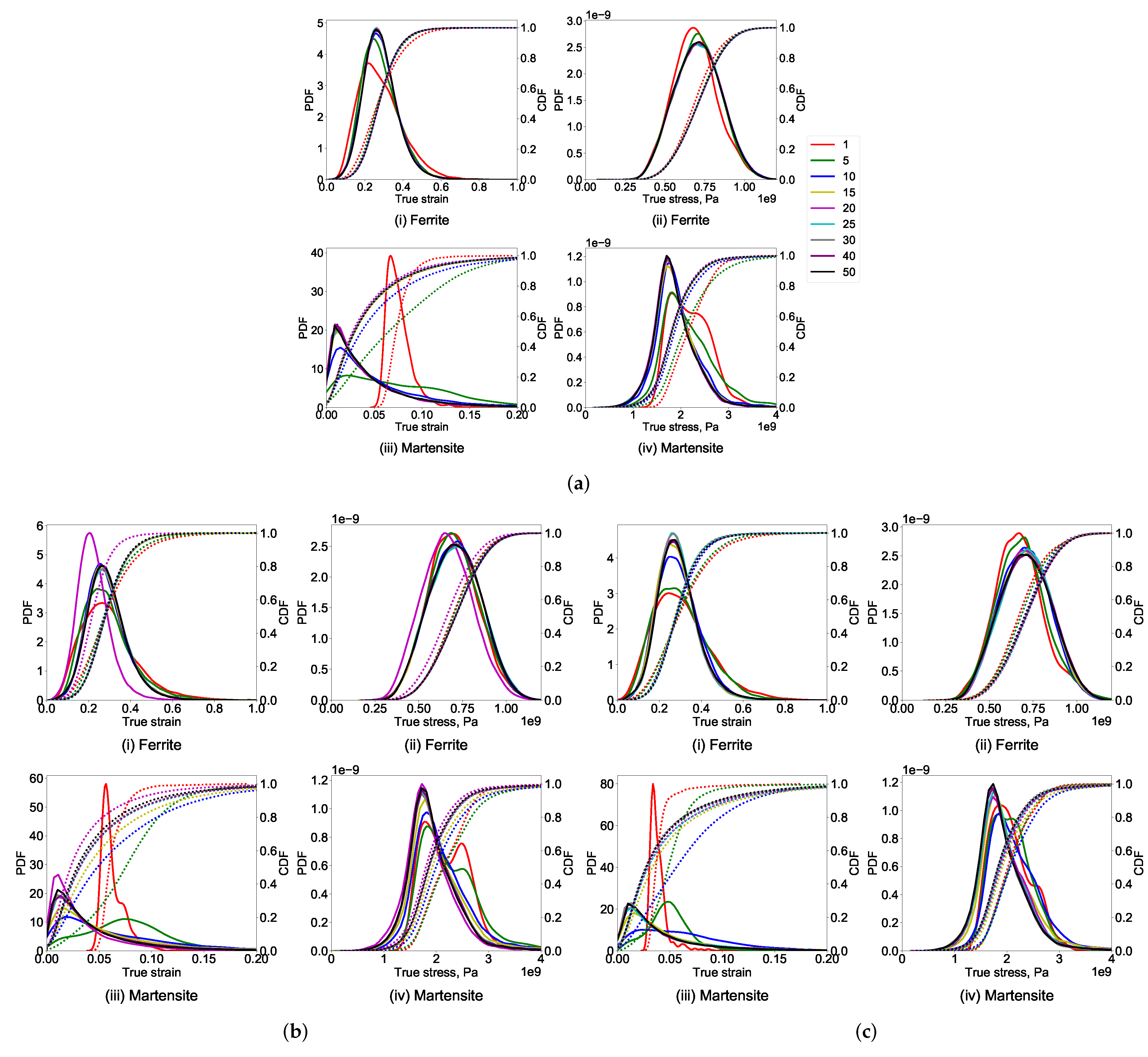
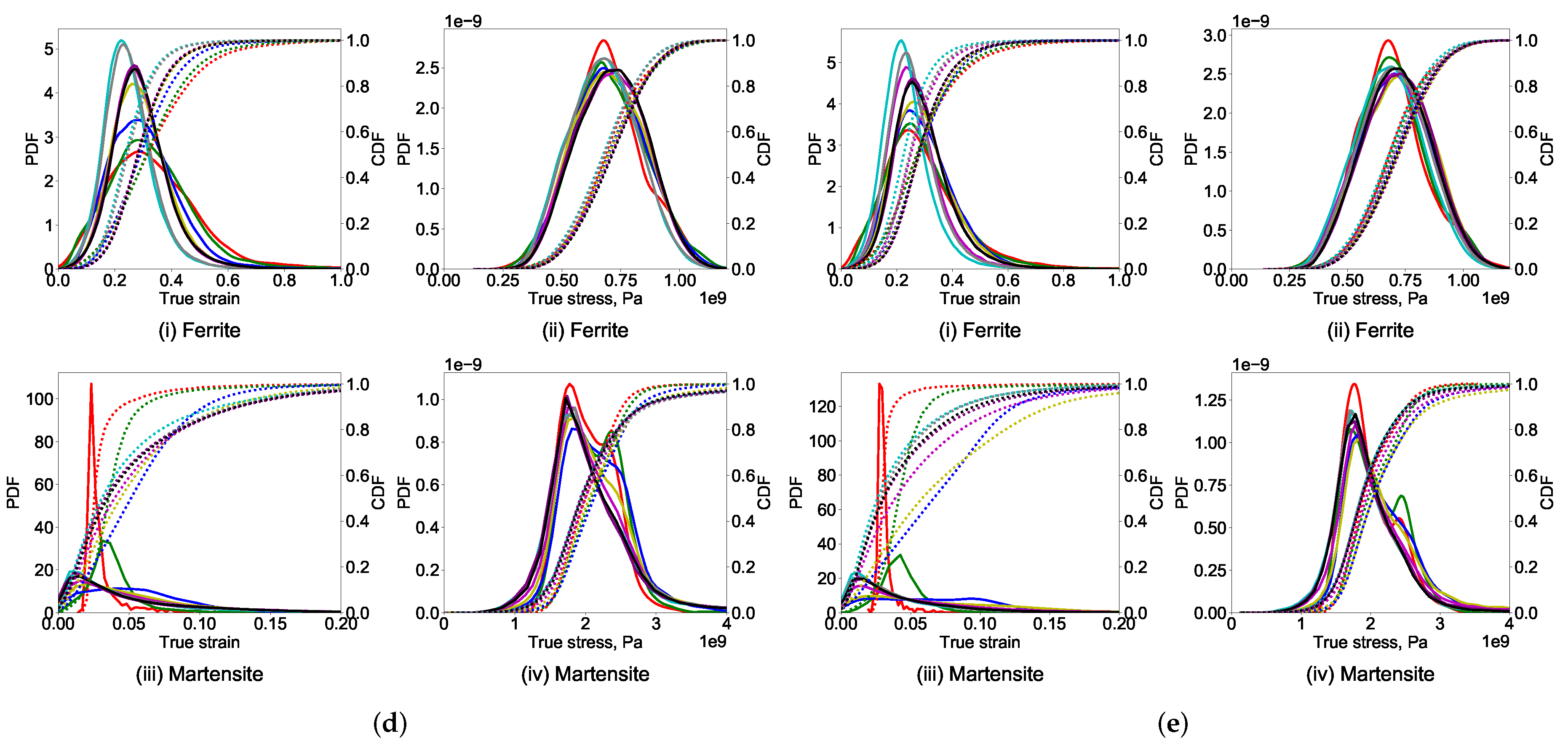
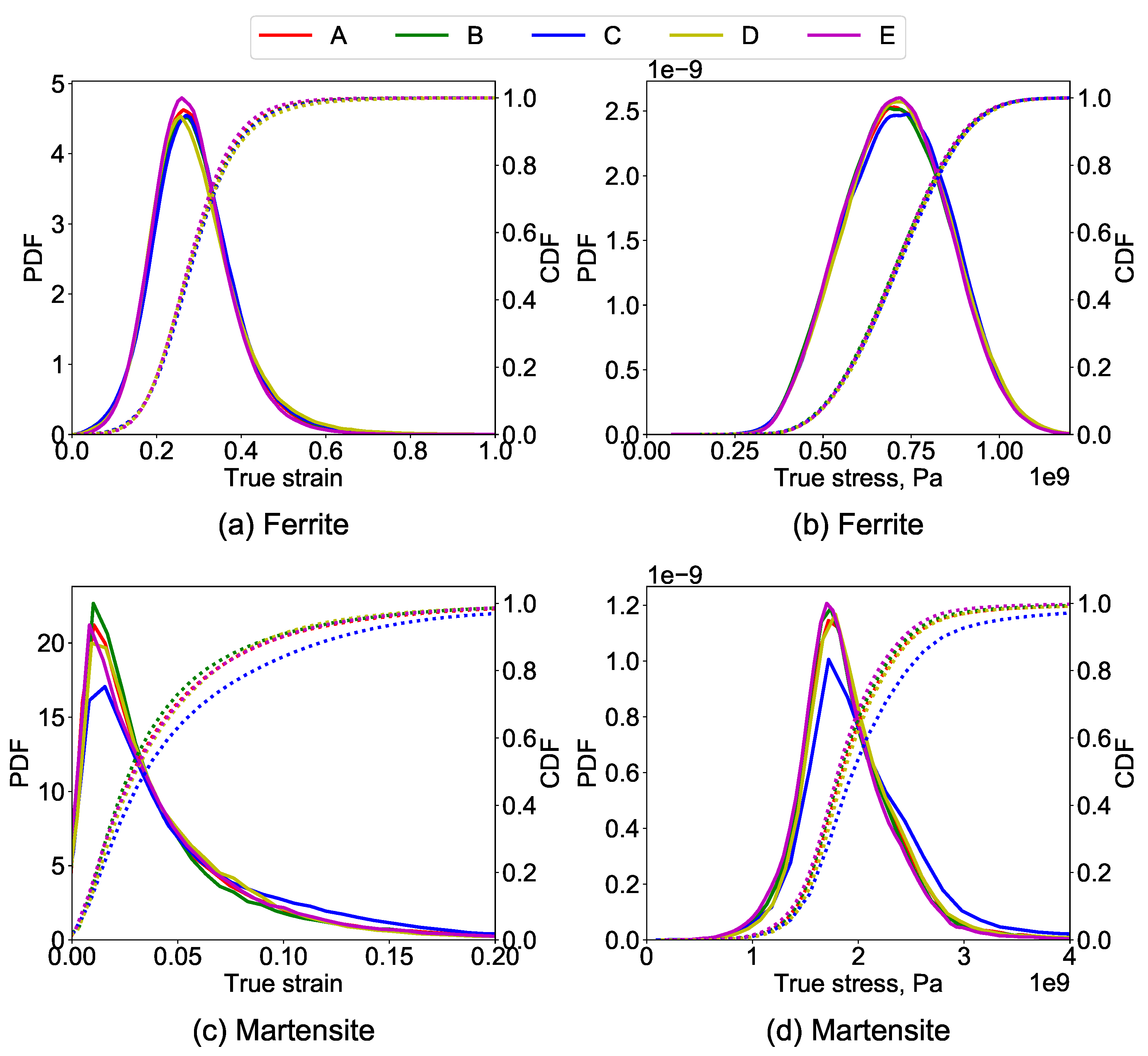
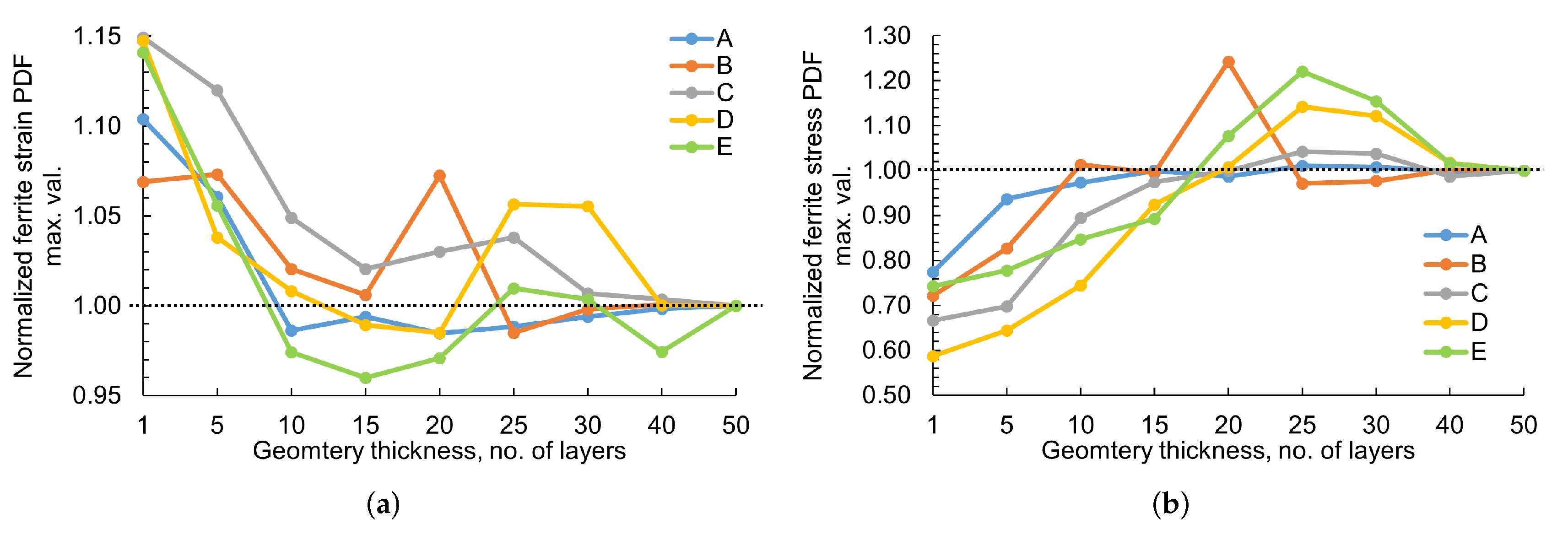
3. Results
4. Discussion
5. Conclusions
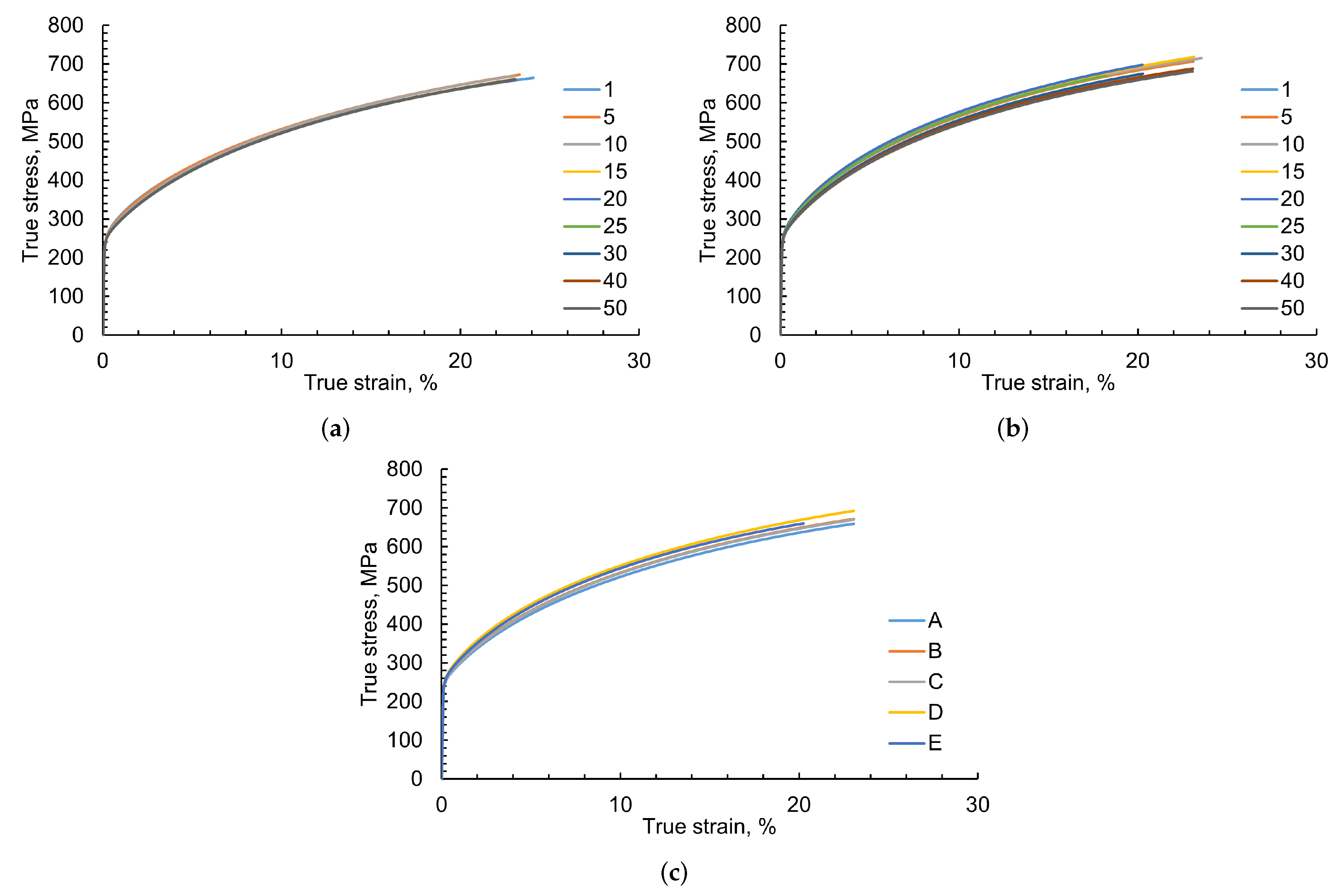
- As long as the orientation distribution and composition of the material is the same—even with changing mean feature size, the total number of grains and geometry thickness—the global deformation and stress–strain behavior of the material does not change drastically (<5% divergence)
- Although the global stress–strain behavior of different RVEs is similar, a large variation in the local stress—strain of RVEs with varying thickness and the feature size is observed during the visual and statistical comparison.
- Stress and strain probability distribution in 2D RVEs is drastically different from 3D RVEs. In 2D RVEs, the strain prediction in the soft phase is higher, in the hard phase is lower, whereas the stress prediction in the soft phase is lower and the hard phase is higher.
- It is necessary to consider 3D RVEs, which are at least five times larger than the average grain size for stabilized and more accurate local deformation behavior determination. This estimation helps in optimizing the computation time for accurate mesoscale simulations.
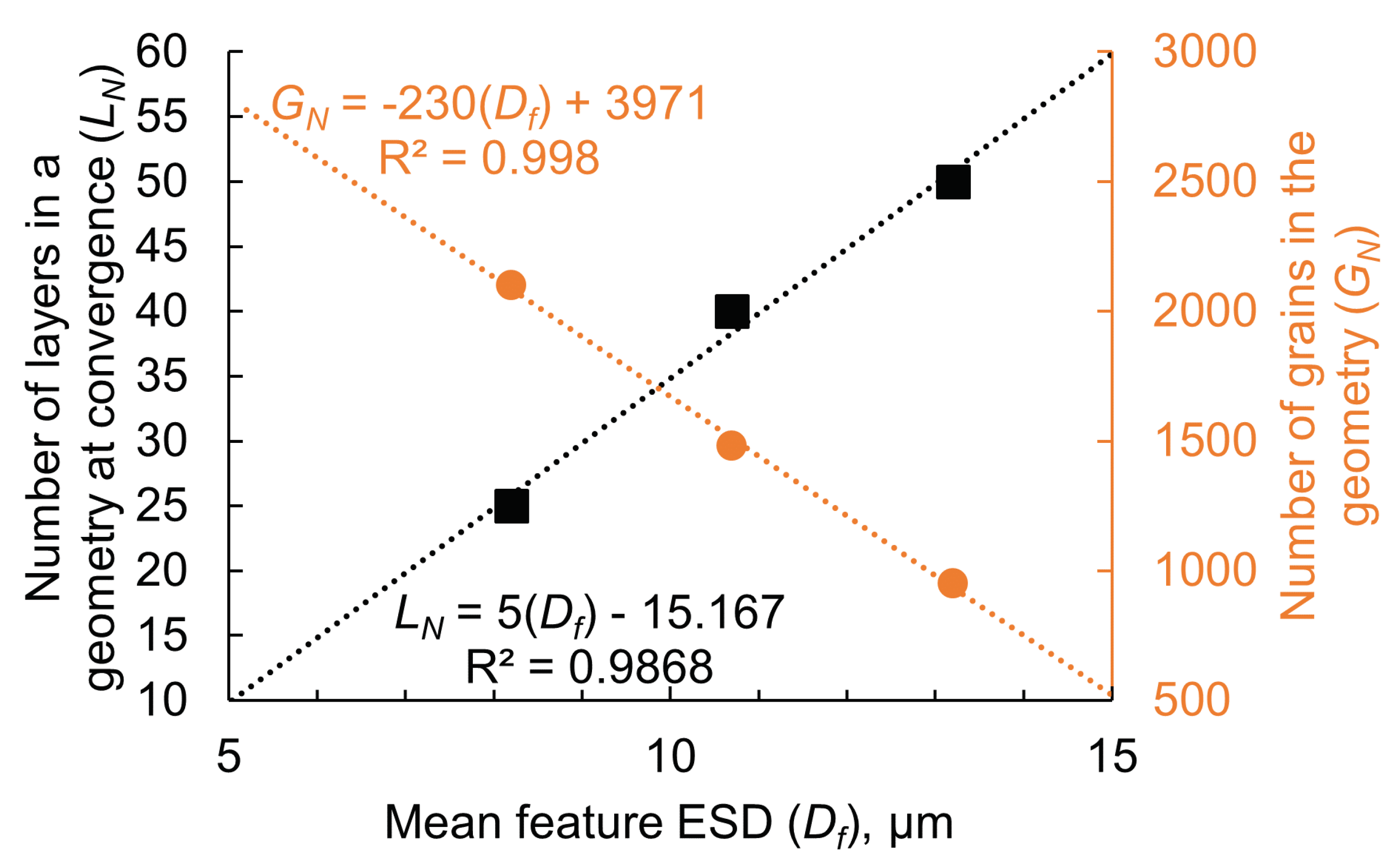
- Figure 10 and Equations (4) & (5) provide a criterion for choosing the mean feature ESD and effective RVE thickness. This criterion should be fulfilled for full phase simulations carried out using DAMASK in the future for obtaining converged simulation results for multi-phase materials i.e., DP steel.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Acronyms | ||
| Symbol | Description | Unit |
| RVE | Representative Volume Element | – |
| EBSD | Electron Back Scatter Diffraction | – |
| CP | Crystal Plasticity | – |
| TRIP | Transformation Induced Plasticity | – |
| Greek Symbols | ||
| Symbol | Description | Unit |
| ESD | Estimated Sphere Diameter | m |
| Mg-PSZ | Magnesium Partially Stabilized Zirconia | – |
| Probability Distribution Function | – | |
| CDF | Cummulative Distribution Function | – |
| Number of considered grains | – | |
| Number of considered layers | – | |
| Mean feature estimated sphere diameter | m | |
| RVE thickness | m | |
Appendix A. Phenomenological Crystal Plasticity Model
References
- Clyne, T.; Withers, P. An Introduction to Metal Matrix Composites; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Ullah, M.; Wu, C.S.; Qayyum, F. Prediction of crack tip plasticity induced due to variation in solidification rate of weld pool and its effect on fatigue crack propagation rate (FCPR). J. Mech. Sci. Technol. 2018, 32, 3625–3635. [Google Scholar] [CrossRef]
- Mukhtar, F.; Qayyum, F.; Anjum, Z.; Shah, M. Effect of chrome plating and varying hardness on the fretting fatigue life of AISI D2 components. Wear 2019, 418, 215–225. [Google Scholar] [CrossRef]
- Berisha, B.; Hirsiger, S.; Hippke, H.; Hora, P.; Mariaux, A.; Leyvraz, D.; Bezençon, C. Modeling of anisotropic hardening and grain size effects based on advanced numerical methods and crystal plasticity. Arch. Mech. 2019, 71, 489–505. [Google Scholar]
- Hazanov, S. Hill condition and overall properties of composites. Arch. Appl. Mech. 1998, 68, 385–394. [Google Scholar] [CrossRef]
- Ullah, M.; Pasha, R.A.; Chohan, G.Y.; Qayyum, F. Numerical simulation and experimental verification of CMOD in CT specimens of TIG welded AA2219-T87. Arab. J. Sci. Eng. 2015, 40, 935–944. [Google Scholar] [CrossRef]
- Hussain, N.; Qayyum, F.; Pasha, R.A.; Shah, M. Development of multi-physics numerical simulation model to investigate thermo-mechanical fatigue crack propagation in an autofrettaged gun barrel. Def. Technol. 2020, in press. [Google Scholar] [CrossRef]
- Mukhtar, F.; Qayyum, F.; Elahi, H.; Shah, M. Studying the Effect of Thermal Fatigue on Multiple Cracks Propagating in an SS316L Thin Flange on a Shaft Specimen Using a Multi-Physics Numerical Simulation Model. Strojniški Vestnik J. Mech. Eng. 2019, 65, 565–573. [Google Scholar] [CrossRef]
- Zaoui, A. Changement d’échelle: Motivation et méthodologie. In Homogénéisation en Mécanique des Matériaux, Tome 1: Matériaux Aléatoires Élastiques et Milieux Périodiques; Hermes Science: Paris, France, 2001; pp. 19–39. [Google Scholar]
- Besson, J.; Cailletaud, G.; Chaboche, J.L.; Forest, S. Mécanique Non Linéaire des Matériaux; Hermès Science Publications: Paris, France, 2001. [Google Scholar]
- Lebensohn, R.A.; Kanjarla, A.K.; Eisenlohr, P. An elasto-viscoplastic formulation based on fast Fourier transforms for the prediction of micromechanical fields in polycrystalline materials. Int. J. Plast. 2012, 32, 59–69. [Google Scholar] [CrossRef]
- Qayyum, F.; Guk, S.; Kawalla, R.; Prahl, U. Experimental investigations and multiscale modeling to study the effect of sulfur content on formability of 16MnCr5 alloy steel. Steel Res. Int. 2019, 90, 1800369. [Google Scholar] [CrossRef]
- Anbarlooie, B.; Hosseini-Toudeshky, H.; Hosseini, M.; Kadkhodapour, J. Experimental and 3D Micromechanical Analysis of Stress–Strain Behavior and Damage Initiation in Dual-Phase Steels. J. Mater. Eng. Perform. 2019, 28, 2903–2918. [Google Scholar] [CrossRef]
- Kim, D.K.; Kim, E.Y.; Han, J.; Woo, W.; Choi, S.H. Effect of microstructural factors on void formation by ferrite/martensite interface decohesion in DP980 steel under uniaxial tension. Int. J. Plast. 2017, 94, 3–23. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, W.; Lévy, B.; Sun, F.; Yan, D.M.; Lu, L.; Yang, C. On centroidal voronoi tessellation—energy smoothness and fast computation. ACM Trans. Graph. (ToG) 2009, 28, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Kok, P.; Spanjer, W.; Vegter, H. A microstructure based model for the mechanical behavior of multiphase steels. Key Eng. Mater. 2015, 651, 975–980. [Google Scholar] [CrossRef]
- Diehl, M.; Groeber, M.; Haase, C.; Molodov, D.A.; Roters, F.; Raabe, D. Identifying Structure–Property Relationships Through DREAM.3D Representative Volume Elements and DAMASK Crystal Plasticity Simulations: An Integrated Computational Materials Engineering Approach. J. Miner. 2017, 69, 848–855. [Google Scholar] [CrossRef] [Green Version]
- Qayyum, F.; Guk, S.; Prüger, S.; Schmidtchen, M.; Saenko, I.; Kiefer, B.; Kawalla, R.; Prahl, U. Investigating the local deformation and transformation behavior of sintered X3CrMnNi16-7-6 TRIP steel using a calibrated crystal plasticity-based numerical simulation model. Int. J. Mat. Res. (Zeitschrift für Metallkunde) 2020, 111, 392–404. [Google Scholar] [CrossRef]
- Diehl, M.; An, D.; Shanthraj, P.; Zaefferer, S.; Roters, F.; Raabe, D. Crystal plasticity study on stress and strain partitioning in a measured 3D dual phase steel microstructure. Phys. Mesomech. 2017, 20, 311–323. [Google Scholar] [CrossRef]
- Liu, C.; Shanthraj, P.; Diehl, M.; Roters, F.; Dong, S.; Dong, J.; Ding, W.; Raabe, D. An integrated crystal plasticity–phase field model for spatially resolved twin nucleation, propagation, and growth in hexagonal materials. Int. J. Plast. 2018, 106, 203–227. [Google Scholar] [CrossRef]
- Diehla, M.; Naunheim, Y.; Yan, D.; Morsdorf, L.; An, D.; Tasan, C.C.; Zaefferer, S.; Roters, F.; Raabe, D. Coupled Experimental-Numerical Analysis of Strain Partitioning in Metallic Microstructures: The Importance of Considering the 3D Morphology. In Proceedings of the BSSM 12th International Conference on Advances in Experimental Mechanics, Sheffield, UK, 29–31 August 2017; pp. 1–2. [Google Scholar]
- Tasan, C.C.; Hoefnagels, J.P.M.; Diehl, M.; Yan, D.; Roters, F.; Raabe, D. Strain localization and damage in dual phase steels investigated by coupled in-situ deformation experiments and crystal plasticity simulations. Int. J. Plast. 2014, 63, 198–210. [Google Scholar] [CrossRef] [Green Version]
- Ramazani, A.; Mukherjee, K.; Quade, H.; Prahl, U.; Bleck, W. Correlation between 2D and 3D flow curve modelling of DP steels using a microstructure-based RVE approach. Mater. Sci. Eng. A 2013, 560, 129–139. [Google Scholar] [CrossRef]
- Knezevic, M.; Savage, D.J. A high-performance computational framework for fast crystal plasticity simulations. Comput. Mater. Sci. 2014, 83, 101–106. [Google Scholar] [CrossRef]
- He, Q.C. Effects of size and boundary conditions on the yield strength of heterogeneous materials. J. Mech. Phys. Solids 2001, 49, 2557–2575. [Google Scholar] [CrossRef]
- Gitman, I.; Askes, H.; Sluys, L. Representative volume: Existence and size determination. Eng. Fract. Mech. 2007, 74, 2518–2534. [Google Scholar] [CrossRef]
- Jiang, M.; Jasiuk, I.; Ostoja-Starzewski, M. Apparent elastic and elastoplastic behavior of periodic composites. Int. J. Solids Struct. 2002, 39, 199–212. [Google Scholar] [CrossRef]
- Jiang, M.; Ostoja-Starzewski, M.; Jasiuk, I. Scale-dependent bounds on effective elastoplastic response of random composites. J. Mech. Phys. Solids 2001, 49, 655–673. [Google Scholar] [CrossRef]
- Groeber, M.A.; Jackson, M.A. DREAM. 3D: A digital representation environment for the analysis of microstructure in 3D. Integr. Mater. Manuf. Innov. 2014, 3, 5. [Google Scholar] [CrossRef] [Green Version]
- Barrett, T.J.; Savage, D.J.; Ardeljan, M.; Knezevic, M. An automated procedure for geometry creation and finite element mesh generation: Application to explicit grain structure models and machining distortion. Comput. Mater. Sci. 2018, 141, 269–281. [Google Scholar] [CrossRef]
- Qayyum, F.; Guk, S.; Schmidtchen, M.; Kawalla, R.; Prahl, U. Modeling the Local Deformation and Transformation Behavior of Cast X8CrMnNi16-6-6 TRIP Steel and 10% Mg-PSZ Composite Using a Continuum Mechanics-Based Crystal Plasticity Model. Crystals 2020, 10, 221. [Google Scholar] [CrossRef] [Green Version]
- Diehl, M.; Shanthraj, P.; Eisenlohr, P.; Roters, F. Neighborhood influences on stress and strain partitioning in dual-phase microstructures. Meccanica 2016, 51, 429–441. [Google Scholar] [CrossRef]
- Hitti, K.; Laure, P.; Coupez, T.; Silva, L.; Bernacki, M. Precise generation of complex statistical Representative Volume Elements (RVEs) in a finite element context. Comput. Mater. Sci. 2012, 61, 224–238. [Google Scholar] [CrossRef]
- Bargmann, S.; Klusemann, B.; Markmann, J.; Schnabel, J.E.; Schneider, K.; Soyarslan, C.; Wilmers, J. Generation of 3D representative volume elements for heterogeneous materials: A review. Prog. Mater. Sci. 2018, 96, 322–384. [Google Scholar] [CrossRef]
- Lee, S.B.; Lebensohn, R.; Rollett, A.D. Modeling the viscoplastic micromechanical response of two-phase materials using Fast Fourier Transforms. Int. J. Plast. 2011, 27, 707–727. [Google Scholar] [CrossRef]
- Zhang, C.; Li, H.; Eisenlohr, P.; Liu, W.; Boehlert, C.; Crimp, M.; Bieler, T. Effect of realistic 3D microstructure in crystal plasticity finite element analysis of polycrystalline Ti-5Al-2.5 Sn. Int. J. Plast. 2015, 69, 21–35. [Google Scholar] [CrossRef] [Green Version]
- Prüger, S.; Seupel, A.; Kuna, M. A thermomechanically coupled material model for TRIP-steel. Int. J. Plast. 2014, 55, 182–197. [Google Scholar] [CrossRef]
- Madivala, M.; Schwedt, A.; Wong, S.L.; Roters, F.; Prahl, U.; Bleck, W. Temperature dependent strain hardening and fracture behavior of TWIP steel. Int. J. Plast. 2018, 104, 80–103. [Google Scholar] [CrossRef]
- Roters, F.; Diehl, M.; Shanthraj, P.; Eisenlohr, P.; Reuber, C.; Wong, S.L.; Maiti, T.; Ebrahimi, A.; Hochrainer, T.; Fabritius, H.O.; et al. DAMASK–The Düsseldorf Advanced Material Simulation Kit for modeling multi-physics crystal plasticity, thermal, and damage phenomena from the single crystal up to the component scale. Comput. Mater. Sci. 2019, 158, 420–478. [Google Scholar] [CrossRef]
- Shanthraj, P.; Eisenlohr, P.; Diehl, M.; Roters, F. Numerically robust spectral methods for crystal plasticity simulations of heterogeneous materials. Int. J. Plast. 2015, 66, 31–45. [Google Scholar] [CrossRef]
- Zeghadi, A.; N’guyen, F.; Forest, S.; Gourgues, A.F.; Bouaziz, O. Ensemble averaging stress–strain fields in polycrystalline aggregates with a constrained surface microstructure–Part 1: Anisotropic elastic behaviour. Philos. Mag. 2007, 87, 1401–1424. [Google Scholar] [CrossRef]
- Zeghadi, A.; Forest, S.; Gourgues, A.F.; Bouaziz, O. Ensemble averaging stress–strain fields in polycrystalline aggregates with a constrained surface microstructure–Part 2: Crystal plasticity. Philos. Mag. 2007, 87, 1425–1446. [Google Scholar] [CrossRef]
- Harris, W.M.; Chiu, W.K. Determining the representative volume element size for three-dimensional microstructural material characterization. Part 1: Predictive models. J. Power Sources 2015, 282, 552–561. [Google Scholar] [CrossRef] [Green Version]
- Harris, W.M.; Chiu, W.K. Determining the representative volume element size for three-dimensional microstructural material characterization. Part 2: Application to experimental data. J. Power Sources 2015, 282, 622–629. [Google Scholar] [CrossRef] [Green Version]
- Tjahjanto, D.; Turteltaub, S.; Suiker, A. Crystallographically based model for transformation-induced plasticity in multiphase carbon steels. Contin. Mech. Thermodyn. 2008, 9, 399–422. [Google Scholar] [CrossRef]
- Jiang, Z.; Guan, Z.; Lian, J. Effects of microstructural variables on the deformation behaviour of dual-phase steel. Mater. Sci. Eng. A 1995, 190, 55–64. [Google Scholar] [CrossRef]
- Eisenlohr, P.; Diehl, M.; Lebensohn, R.A.; Roters, F. A spectral method solution to crystal elasto-viscoplasticity at finite strains. Int. J. Plast. 2013, 46, 37–53. [Google Scholar] [CrossRef]
- Michel, J.; Moulinec, H.; Suquet, P. A computational scheme for linear and non-linear composites with arbitrary phase contrast. Int. J. Numer. Methods Eng. 2001, 52, 139–160. [Google Scholar] [CrossRef]
- Ahrens, J.; Geveci, B.; Law, C. Paraview: An end-user tool for large data visualization. In The Visualization Handbook; Academic Press: New York, NY, USA, 2005; Volume 717. [Google Scholar]
- Maiti, T.; Eisenlohr, P. Fourier-based spectral method solution to finite strain crystal plasticity with free surfaces. Scr. Mater. 2018, 145, 37–40. [Google Scholar] [CrossRef]
- Peirce, D.; Asaro, R.; Needleman, A. An analysis of nonuniform and localized deformation in ductile single crystals. Acta Metall. 1982, 30, 1087–1119. [Google Scholar] [CrossRef]


| Nomenclature | Ferrite Grains | Martensite Grains | Total Grains | ||||
|---|---|---|---|---|---|---|---|
| Min. | Max | Avg. | Min. | Max | Avg. | ||
| A | 5.1 | 7.6 | 6.35 | 3.5 | 5.7 | 4.6 | 8400 |
| B | 6.6 | 9.9 | 8.25 | 5.2 | 8.4 | 6.8 | 3700 |
| C | 8.5 | 12.7 | 10.6 | 5.4 | 8.8 | 7.1 | 1900 |
| D | 9.7 | 14.5 | 12.1 | 8.2 | 13.2 | 10.7 | 1200 |
| E | 11.2 | 16.8 | 14.0 | 9.8 | 15.8 | 12.8 | 770 |
| Parameter Definition | Symbol | Attributes for Ferrite | Attributes for Martensite | Unit |
|---|---|---|---|---|
| First elastic stiffness constant with normal strain | 233.3 | 417.4 | GPa | |
| Second elastic stiffness constant with normal strain | 135.5 | 242.4 | GPa | |
| First elastic stiffness constant with shear strain | 128.0 | 211.1 | GPa | |
| Shear strain rate | 1 | 1 | 10/s | |
| Initial Shear resistance on | 95 | 406 | MPa | |
| Saturation shear resistance on | 222 | 873 | MPa | |
| Initial Shear resistance on | 96 | 457 | MPa | |
| Saturation shear resistance on | 412 | 971 | MPa | |
| Slip hardening parameter | 1.0 | 563 | GPa | |
| Interaction hardening parameter | 1.0 | 1.0 | - | |
| Stress exponent | n | 20 | 20 | - |
| Curve fitting parameter | w | 2.0 | 2.0 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qayyum, F.; Chaudhry, A.A.; Guk, S.; Schmidtchen, M.; Kawalla, R.; Prahl, U. Effect of 3D Representative Volume Element (RVE) Thickness on Stress and Strain Partitioning in Crystal Plasticity Simulations of Multi-Phase Materials. Crystals 2020, 10, 944. https://doi.org/10.3390/cryst10100944
Qayyum F, Chaudhry AA, Guk S, Schmidtchen M, Kawalla R, Prahl U. Effect of 3D Representative Volume Element (RVE) Thickness on Stress and Strain Partitioning in Crystal Plasticity Simulations of Multi-Phase Materials. Crystals. 2020; 10(10):944. https://doi.org/10.3390/cryst10100944
Chicago/Turabian StyleQayyum, Faisal, Aqeel Afzal Chaudhry, Sergey Guk, Matthias Schmidtchen, Rudolf Kawalla, and Ulrich Prahl. 2020. "Effect of 3D Representative Volume Element (RVE) Thickness on Stress and Strain Partitioning in Crystal Plasticity Simulations of Multi-Phase Materials" Crystals 10, no. 10: 944. https://doi.org/10.3390/cryst10100944
APA StyleQayyum, F., Chaudhry, A. A., Guk, S., Schmidtchen, M., Kawalla, R., & Prahl, U. (2020). Effect of 3D Representative Volume Element (RVE) Thickness on Stress and Strain Partitioning in Crystal Plasticity Simulations of Multi-Phase Materials. Crystals, 10(10), 944. https://doi.org/10.3390/cryst10100944











