Control of Thermophysical Properties of Langasite-Type La3Ta0.5Ga5.5O14 Crystals for Pressure Sensors
Abstract
1. Introduction
2. Materials and Methods
2.1. Thermal Stress Calculation
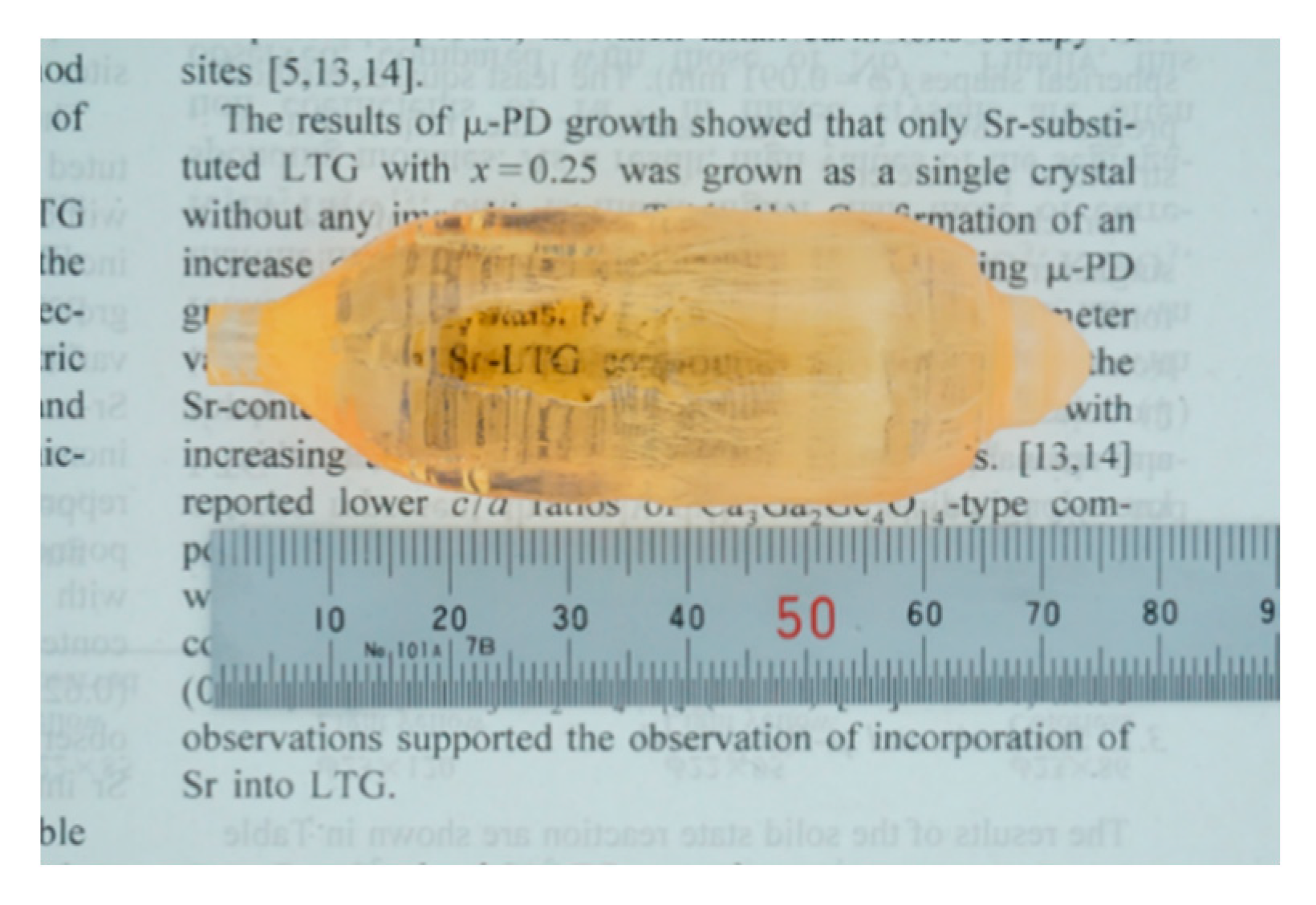
2.2. Crystal Growth and Characterization
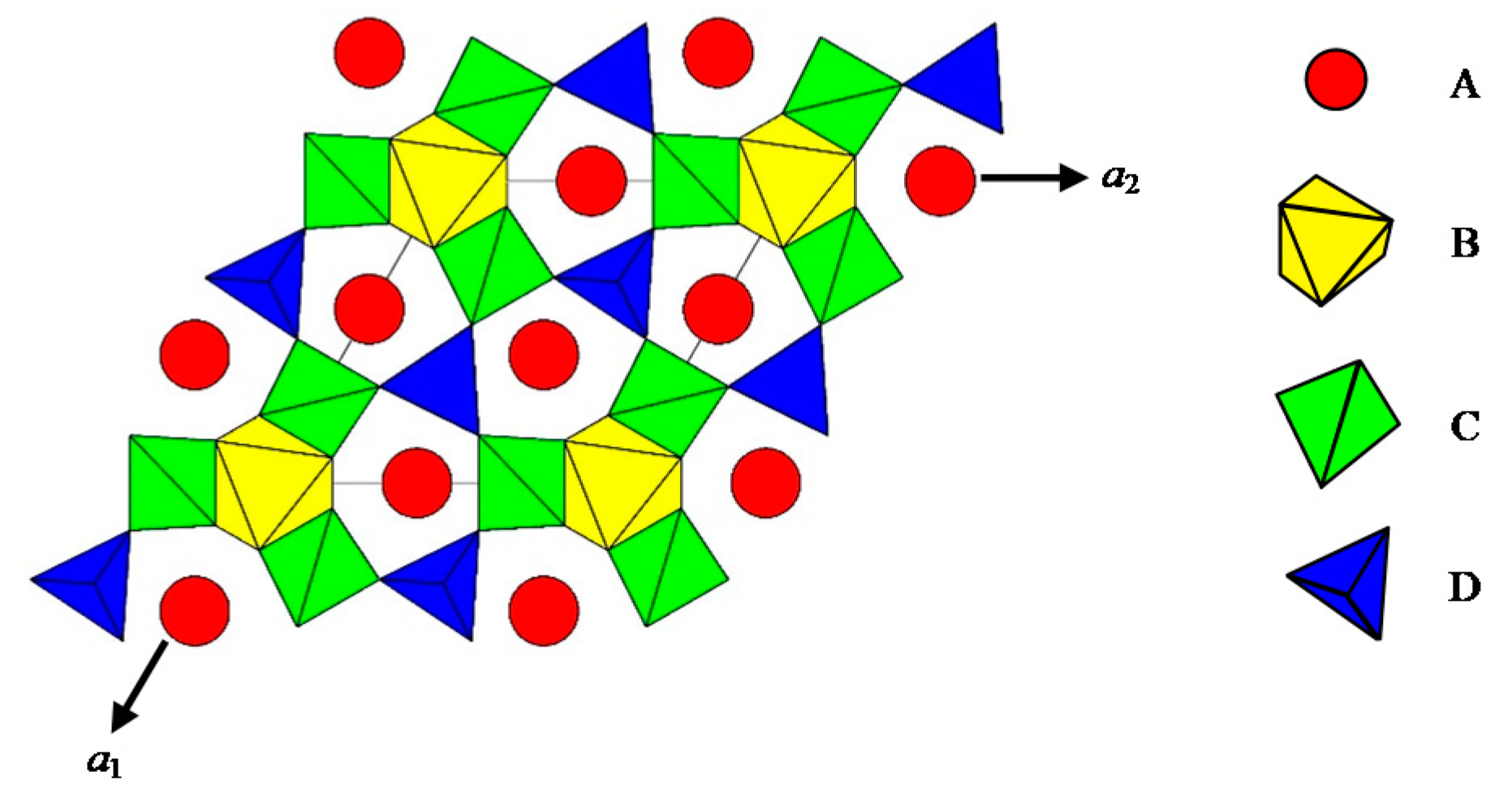
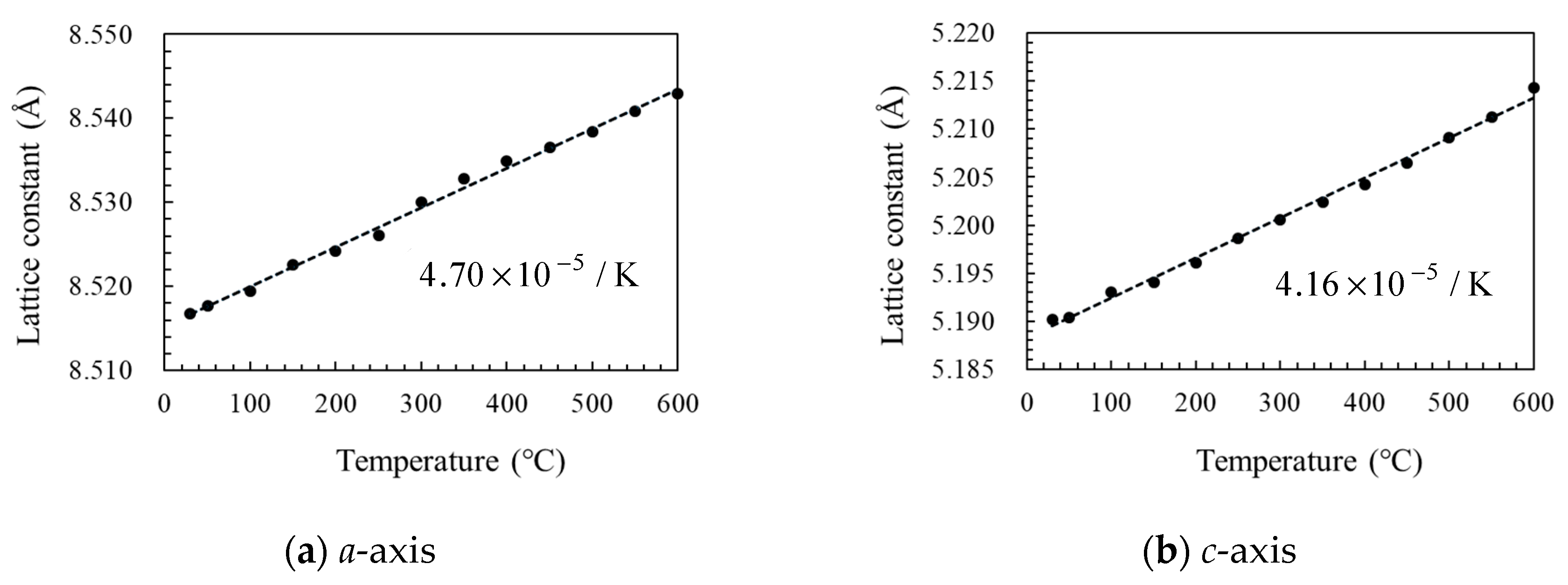
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rogers, D.R. Engine Combustion: Pressure Measurement and Analysis; SAE International: Warrendale, PA, USA, 2010. [Google Scholar]
- Tsukada, K.; Takeuchi, M.; Tokumitsu, S.; Ohmura, Y.; Kawaguchi, K. Combustion pressure sensor. R&D Rev. Toyota CRDL 1993, 28, 49–57. (In Japanese) [Google Scholar]
- Shimamura, K.; Takeda, H.; Kohno, T.; Fukuda, T. Growth and characterization of lanthanum gallium silicate La3Ga5SiO14 single crystals for piezoelectric application. J. Cryst. Growth 1996, 163, 388–392. [Google Scholar] [CrossRef]
- Takeda, H.; Shimamura, K.; Kohno, T.; Fukuda, T. Growth and Characterization of La3Nb0.5Ga5.5O14 Single Crystals. J. Cryst. Growth 1996, 169, 503–508. [Google Scholar] [CrossRef]
- Bohm, J.; Heimann, R.B.; Hengst, M.; Roewer, R.; Schindler, J. Czochralski growth and characterization of piezoelectric single crystals with langasite structure: La3Ga5SiO14 (LGS), La3Ga5.5Nb0.5O14 (LGN), and La3Ga5.5Ta0.5O14 (LGT). Part I. J. Cryst. Growth 1999, 204, 128–136. [Google Scholar] [CrossRef]
- Takeda, H.; Fukuda, T.; Kawanaka, H.; Onozato, N. Effect of starting melt composition on growth of La3Ta0.5Ga5.5O14 crystal. J. Mater. Sci. Mater. Electron. 2001, 12, 199–202. [Google Scholar] [CrossRef]
- Uda, S.; Wang, S.Q.; Konishi, N.; Inaba, H.; Harada, J. Growth habits of 3 and 4-inch langasite single crystals. J. Cryst. Growth 2002, 237, 707–713. [Google Scholar] [CrossRef]
- Boutahraoui, B.; Nehari, A.; Boy, J.J.; Vacheret, X.; Allani, M.; Cabane, H.; Dumortier, M.; Derbal, M.; Lebbou, K. LGT (La3Ga5.5Ta0.5O14) langatate bulk crystal grown from the melt by Czochralski technique and characterization. Opt. Mater. 2017, 65, 103–105. [Google Scholar] [CrossRef]
- Allani, M.; Batis, N.; Laroche, T.; Nehari, A.; Cabane, H.; Lebbou, K.; Vacheret, X.; Boy, J.J. Effects of the Langatate crystal quality on the resonance frequency stability of bulk acoustic wave resonators. Adv. Appl. Ceram. 2018, 117, 279–284. [Google Scholar] [CrossRef]
- Krempl, P.; Schleinzer, G.; Wallnöfer, W. Gallium phosphate, GaPO4: A new piezoelectric crystal material for high-temperature sensorics. Sens. Actuators A Phys. 1997, 61, 361–363. [Google Scholar] [CrossRef]
- Yu, F.; Zhang, S.; Zhao, X.; Yuan, D.; Qin, L.; Wang, Q.-M.; Shrout, T.R. Dielectric and electromechanical properties of rare earth calcium oxyborate piezoelectric crystals at high temperatures. IEEE Trans. Ultra. Ferro. Freq. Contr. 2011, 58, 868–873. [Google Scholar]
- Balitsky, D.V.; Philippot, E.; Papet, P.; Balitsky, V.S.; Pey, F. Comparative crystal growth of GaPO4 crystals in the retrograde and direct solubility range by hydrothermal methods of temperature gradient. J. Cryst. Growth 2005, 275, e887–e894. [Google Scholar] [CrossRef]
- Takeda, H.; Sako, H.; Shimizu, H.; Kodama, K.; Nishida, M.; Nakao, H.; Nishida, T.; Okamura, S.; Shikida, T.; Shiosaki, T. Growth and characterization of lanthanum Calcium Oxoborate LaCa4O(BO3)3 single crystals. Jpn. J. Appl. Phys. 2003, 42, 6081–6085. [Google Scholar] [CrossRef]
- Takeda, H.; Hagiwara, M.; Noguchi, H.; Hoshina, T.; Takahashi, T.; Kodama, N.; Tsurumi, T. Calcium aluminate silicate Ca2Al2SiO7 single crystal applicable to piezoelectric sensors at high temperature. Appl. Phys. Lett. 2013, 102, 242907. [Google Scholar] [CrossRef]
- Shen, C.; Zhang, S.; Cao, W.; Cong, H.; Yu, H.; Wang, J.; Zhang, H. Thermal and electromechanical properties of melilite-type piezoelectric single crystals. J. Appl. Phys. 2015, 117, 064106. [Google Scholar] [CrossRef]
- Yaokawa, R.; Kimura, H.; Aota, K.; Uda, S. Precipitation phenomena in and electrical resistivity of high-temperature treated langatate (La3Ta0.5Ga5.5O14). IEEE Trans. Ultra. Ferro. Freq. Contr. 2011, 58, 1131–1139. [Google Scholar] [CrossRef] [PubMed]
- Spassky, D.A.; Kozlova, N.S.; Kozlova, A.P.; Zabelina, E.V.; Buzanov, O.A.; Buryi, M.; Laguta, V.; Lebbou, K.; Nehari, A.; Cabane, H.; et al. Study of the defects in La3Ta0. 5Ga5.5O14 single crystals. J. Lumin. 2016, 180, 95–102. [Google Scholar] [CrossRef]
- Takahashi, I. (CITIZEN FINEDEVICE CO., LTD, Fujikawaguchiko-Machi, Yamanashi, Japan). Personal communication, 2019.
- Kasano, H.; Hara, T.; Minakuchi, Y. Thermal stress (Netsuouryoku). In Fundamental of Mechanics of Materials (Kisozairyorikigaku), 1st ed.; Koizumi, T., Ed.; Yokendo: Tokyo, Japan, 2014; pp. 30–33. (In Japanese) [Google Scholar]
- Wang, Z.; Cheng, X.; Yuan, D.; Pan, L.; Guo, S.; Xu, D.; Lv, M. Crystal growth and properties of Ca3NbGa3Si2O14 single crystals. J. Cryst. Growth 2003, 249, 240–244. [Google Scholar] [CrossRef]
- Takeda, H.; Sato, J.; Kato, T.; Kawasaki, K.; Morikoshi, H.; Shimamura, K.; Fukuda, T. Synthesis and characterization of Sr3TaGa3Si2O14 single crystals. Mater. Res. Bull. 2000, 35, 245–252. [Google Scholar] [CrossRef]
- Shi, X.; Yuan, D.; Yin, X.; Wei, A.; Guo, S.; Yu, F. Crystal growth and dielectric, piezoelectric and elastic properties of Ca3TaGa3Si2O14 single crystal. Solid State Commun. 2007, 142, 173–176. [Google Scholar] [CrossRef]
- Usui, H.; Kusakabe, H.; Tokuda, M.; Sugiyama, K.; Hoshina, T.; Tsurumi, T.; Takeda, H. Structure and electrical properties of Ba3TaGa3Si2O14 single crystals grown by Czochralski method. J. Ceram. Soc. Jpn. 2020, 128, 441–446. [Google Scholar] [CrossRef]
- Karaki, T.; Sato, R.; Adachi, M.; Kushibiki, J.; Arakawa, M. Piezoelectric properties of Ca3NbGa3Si2O14 single crystal. Jpn. J. Appl. Phys. 2004, 43, 6721–6724. [Google Scholar] [CrossRef]
- Fu, X.; Víllora, E.G.; Matsushita, Y.; Kitanaka, Y.; Noguchi, Y.; Miyayama, M.; Shimamura, K.; Ohashi, N. Piezoelectric Ca3TaAl3Si2O14 (CTAS): High quality 2-in. single-crystal growth and electro-elastic properties from room to high (650 °C) temperature. J. Cryst. Growth 2018, 501, 38–42. [Google Scholar] [CrossRef]
- Takeda, H.; Kato, T.; Chani, V.I.; Morikoshi, H.; Shimamura, K.; Fukuda, T. Effect of (Sr, Ba) substitution in La3Ga5SiO14 and La3M0.5Ga5.5O14 (M = Nb5+, Ta5+) crystals on their synthesis, structure and piezoelectricity. J. Alloys Compd. 1999, 290, 79–84. [Google Scholar] [CrossRef]
- ANSI/IEEE Std 176. IEEE Standard on Piezoelectricity; IEEE: New York, NY, USA, 1987. [Google Scholar]
- Ikeda, T. Fundamentals of Piezoelectricity; Oxford University Press: New York, NY, USA, 1990. [Google Scholar]
- Chilla, E.; Flannery, C.M.; Frohlich, H.-J.; Straube, U. Elastic properties of langasite-type crystals determined by bulk and surface acoustic waves. J. Appl. Phys. 2001, 90, 6084–6091. [Google Scholar] [CrossRef]
- Beaucage, T.R.; Beenfeldt, E.P.; Speakman, S.A.; Porter, W.D.; Payzant, E.A.; Pereira Da Cunha, M. Comparison of high temperature crystal lattice and bulk thermal expansion measurements of LGT single crystal. In Proceedings of the 2006 IEEE International Frequency Control Symposium and Exposition, Miami, FL, USA, 4–7 June 2006; pp. 658–663. [Google Scholar]
- Shannon, R.D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. A 1976, 32, 751–766. [Google Scholar] [CrossRef]
- Bohm, J.; Chilla, E.; Flannery, C.; Frohlich, H.-J.; Hauke, T.; Heimann, R.B.; Hengst, M.; Straube, U. Czochralski growth and characterization of piezoelectric single crystals with langasite structure: La3Ga5SiO14 (LGS), La3Ga5.5Nb0.5O14 (LGN) and La3Ga5.5Ta0.5O14 (LGT) II. Piezoelectric and elastic properties. J. Cryst. Growth 2000, 216, 293–298. [Google Scholar] [CrossRef]
- Trolier-McKinstry, S.; Cross, L.E.; Yamashita, Y. (Eds.) Piezoelectric Single Crystals and Their Applications; Pennsylvania State University: University Park, PA, USA, 2004. [Google Scholar]

| Crystal | ESC (GPa) | TEC (10−6 K−1) | ||
|---|---|---|---|---|
| cy | cz | αy | αz | |
| CTGS | 123.2 | 178.1 | 8.30 | 7.13 |
| BTGS | 211.0 | 423.0 | 5.52 | 8.02 |
| CNGS | 155.0 | 226.0 | 8.02 | 7.70 |
| CTAS | 184.4 | 477.4 | 8.08 | 8.12 |
| LTG | 189.8 | 263.5 | 7.99 | 5.97 |
| Crystal | ESC (GPa) | LTEC (10−6 K−1) | Thermal Stress (MPa) | Ratio | |||
|---|---|---|---|---|---|---|---|
| cy | cz | αy | αz | σy | σz | σy/σz | |
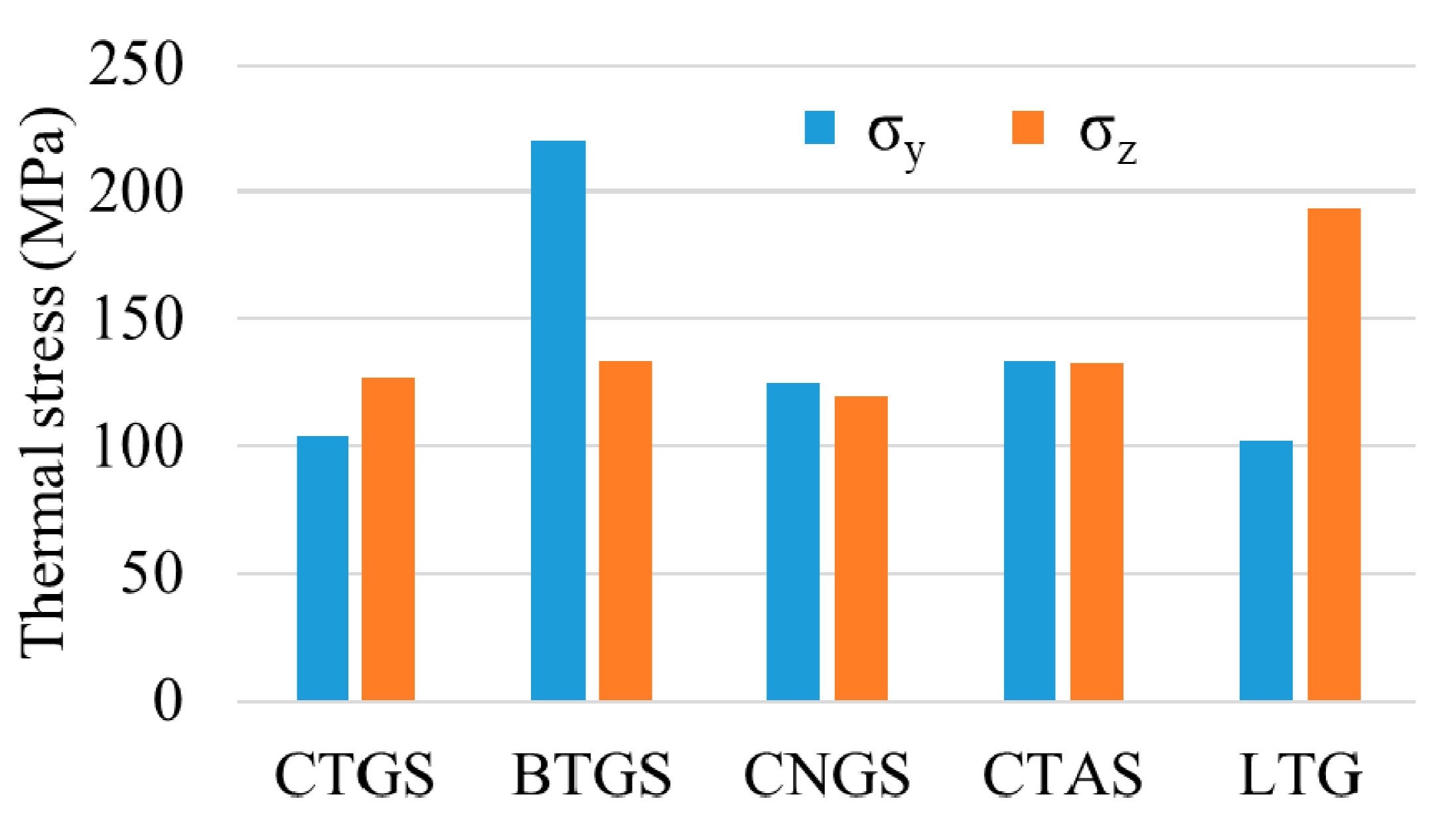
| LTG [29,30] | 189.8 | 263.5 | 7.99 | 5.97 | 101.9 | 193.9 | 0.53 |
| Sr-LTG | 206 | 214 | 7.80 | 6.43 | 112.2 | 162.5 | 0.69 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Usui, H.; Tokuda, M.; Sugiyama, K.; Hoshina, T.; Tsurumi, T.; Lebbou, K.; Yanase, I.; Takeda, H. Control of Thermophysical Properties of Langasite-Type La3Ta0.5Ga5.5O14 Crystals for Pressure Sensors. Crystals 2020, 10, 936. https://doi.org/10.3390/cryst10100936
Usui H, Tokuda M, Sugiyama K, Hoshina T, Tsurumi T, Lebbou K, Yanase I, Takeda H. Control of Thermophysical Properties of Langasite-Type La3Ta0.5Ga5.5O14 Crystals for Pressure Sensors. Crystals. 2020; 10(10):936. https://doi.org/10.3390/cryst10100936
Chicago/Turabian StyleUsui, Haruki, Makoto Tokuda, Kazumasa Sugiyama, Takuya Hoshina, Takaaki Tsurumi, Kheirreddine Lebbou, Ikuo Yanase, and Hiroaki Takeda. 2020. "Control of Thermophysical Properties of Langasite-Type La3Ta0.5Ga5.5O14 Crystals for Pressure Sensors" Crystals 10, no. 10: 936. https://doi.org/10.3390/cryst10100936
APA StyleUsui, H., Tokuda, M., Sugiyama, K., Hoshina, T., Tsurumi, T., Lebbou, K., Yanase, I., & Takeda, H. (2020). Control of Thermophysical Properties of Langasite-Type La3Ta0.5Ga5.5O14 Crystals for Pressure Sensors. Crystals, 10(10), 936. https://doi.org/10.3390/cryst10100936






