Fatigue Crack Initiation of Metals Fabricated by Additive Manufacturing—A Crystal Plasticity Energy-Based Approach to IN718 Life Prediction
Abstract
1. Introduction
2. Materials and Methods
2.1. Fatigue Crack Initiation Model
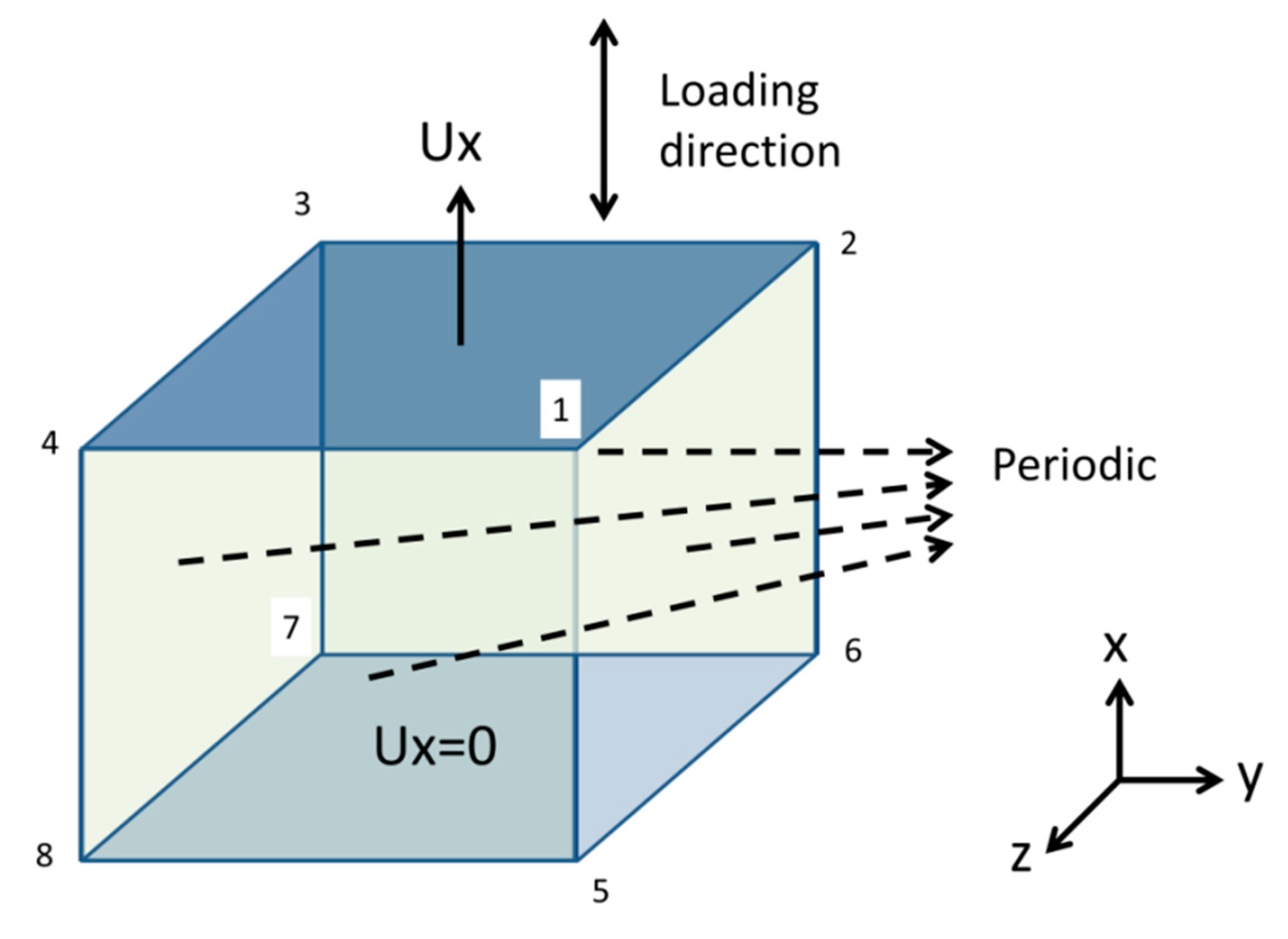
2.2. Crystal Plasticity Finite Element Model
2.3. Experiments
3. Results
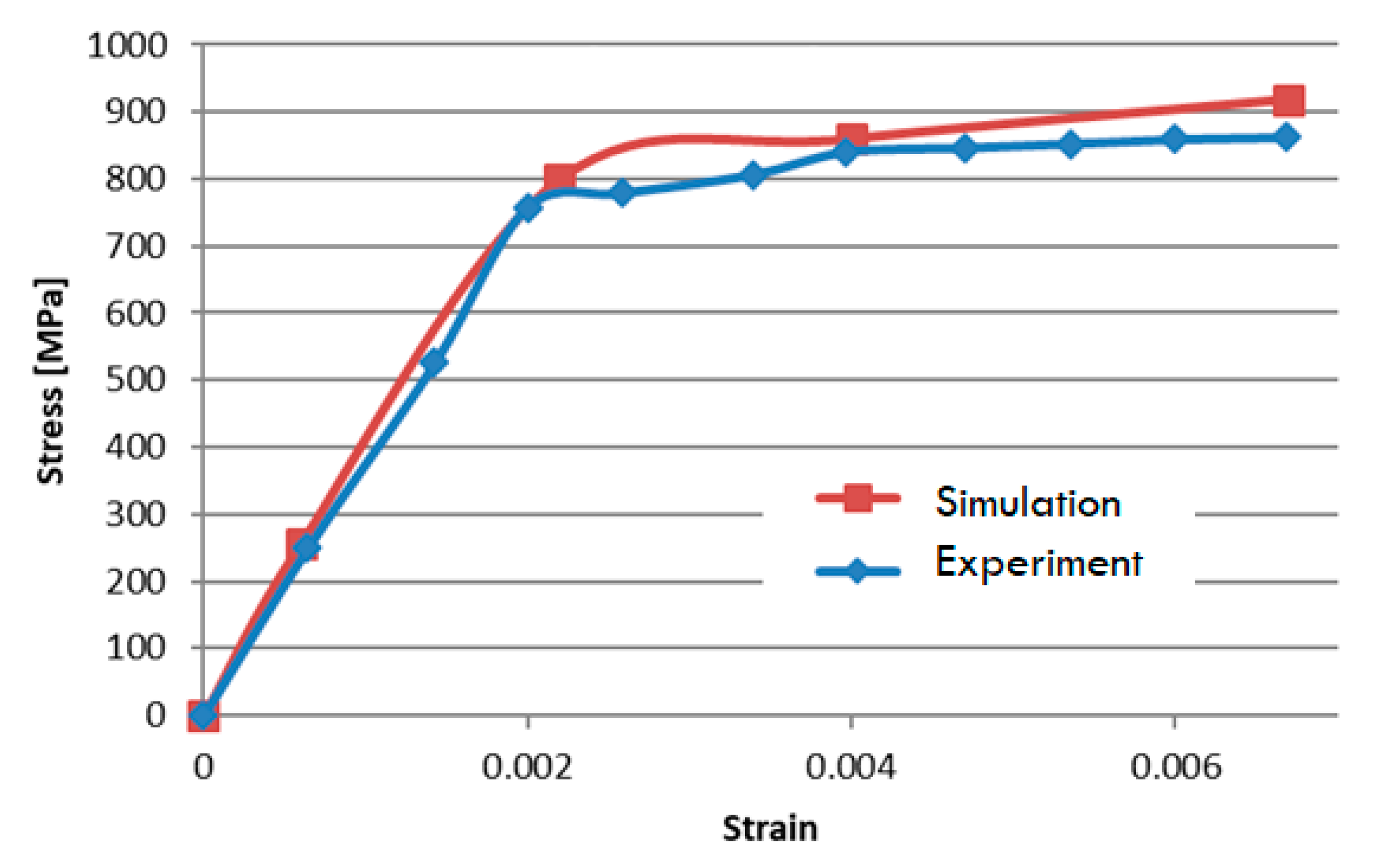
3.1. Fatigue Parameter Estimation
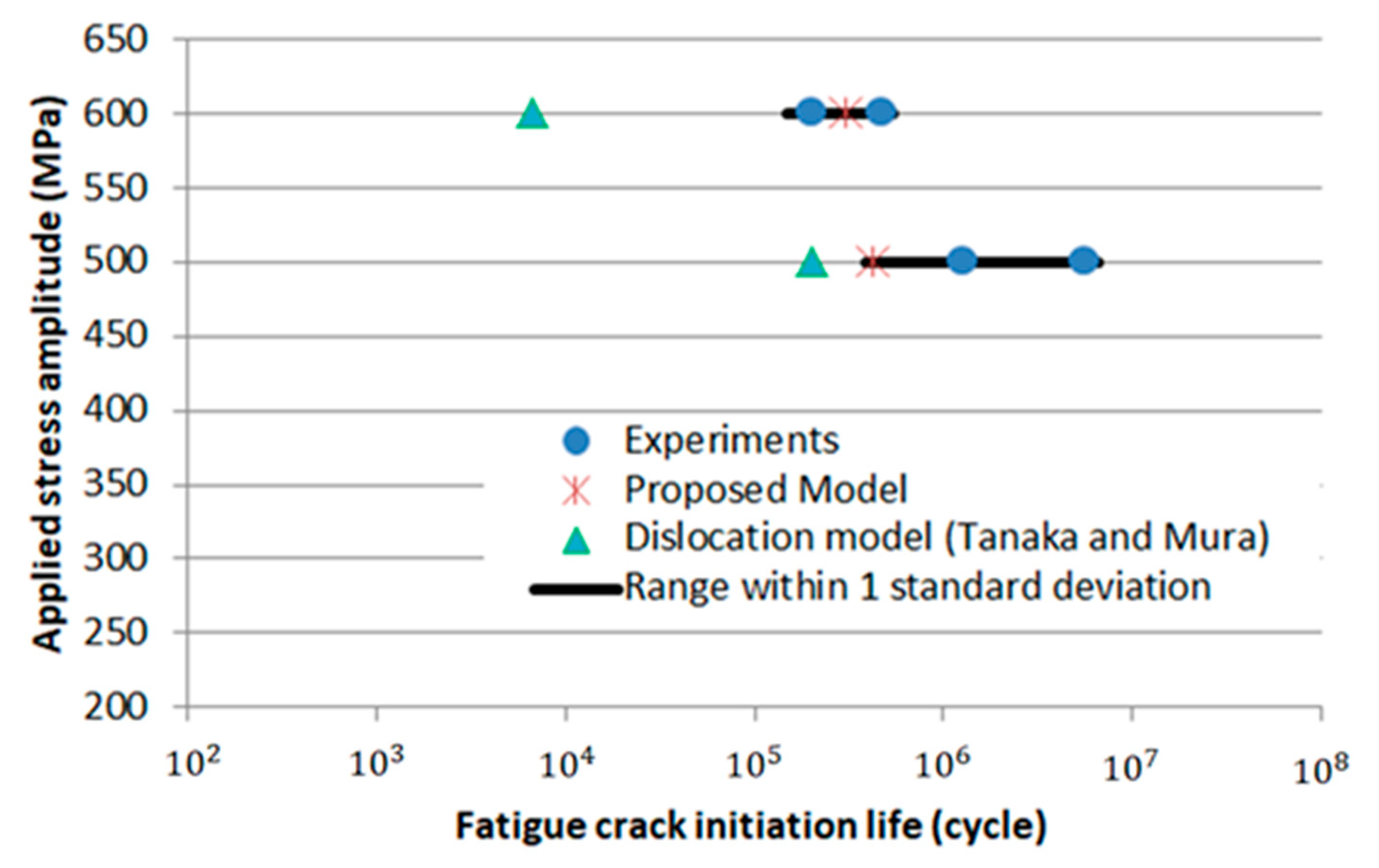
3.2. Fatigue Crack Initiation Life Estimation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Seifi, M.; Salem, A.A.; Beuth, J.; Harrysson, O.; Lewandowski, J.J. Overview of Materials Qualification Needs for Metal Additive Manufacturing. JOM 2016, 68, 747–764. [Google Scholar] [CrossRef]
- Draper, S.; Locci, I.; Lerch, B.; Ellis, D.; Senick, P.; Meyer, M.; Free, J.; Cooper, K.; Jones, Z. Materials Characterization of Additively Manufactured Components for Rocket Propulsion. In Proceedings of the 66th International Astronautical Congress, Jerusalem, Israel, 12–16 October 2015; pp. 1–9. [Google Scholar]
- Wohler’s Report, Additive Manufacturing and 3D Printing State of the Industry Annual Worldwide Progress Report. 2017. Available online: https://wohlersassociates.com/press72.html (accessed on 3 April 2017).
- Li, P.; Warner, D.; Fatemi, A.; Phan, N. Critical assessment of the fatigue performance of additively manufactured Ti–6Al–4V and perspective for future research. Int. J. Fatigue 2016, 85, 130–143. [Google Scholar] [CrossRef]
- Edwards, P.; Ramulu, M. Fatigue performance evaluation of selective laser melted Ti–6Al–4V. Mater. Sci. Eng. A 2014, 598, 327–337. [Google Scholar] [CrossRef]
- Kobryn, P.A.; Semiatin, S.L. Mechanical properties of laser-deposited Ti–6Al–4V. In Proceedings of the Solid Freeform Fabrication Proceedings, Austin, TX, USA, 6–8 August 2001. [Google Scholar]
- Walker, K.; Liu, Q.; Brandt, M. Evaluation of fatigue crack propagation behaviour in Ti-6Al-4V manufactured by selective laser melting. Int. J. Fatigue 2017, 104, 302–308. [Google Scholar] [CrossRef]
- Zhai, Y.; Galarraga, H.; Lados, D.A. Microstructure, static properties, and fatigue crack growth mechanisms in Ti-6Al-4V fabricated by additive manufacturing: LENS and EBM. Eng. Fail. Anal. 2016, 69, 3–14. [Google Scholar] [CrossRef]
- Gordon, J.; Haden, C.; Nied, H.; Vinci, R.P.; Harlow, D. Fatigue crack growth anisotropy, texture and residual stress in austenitic steel made by wire and arc additive manufacturing. Mater. Sci. Eng. A 2018, 724, 431–438. [Google Scholar] [CrossRef]
- Yadollahi, A.; Shamsaei, N. Additive manufacturing of fatigue resistant materials: Challenges and opportunities. Int. J. Fatigue 2017, 98, 14–31. [Google Scholar] [CrossRef]
- Choi, Y.; Liu, C.R. Rolling contact fatigue life of finish hard machined surfaces. Wear 2006, 261, 485–491. [Google Scholar] [CrossRef]
- Mughrabi, H. Microstructural mechanisms of cyclic deformation, fatigue crack initiation and early crack growth. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2015, 373, 20140132. [Google Scholar] [CrossRef]
- Kazymyrovych, V.; Bergström, J.; Burman, C. The Significance of Crack Initiation Stage in Very High Cycle Fatigue of Steels. Steel Res. Int. 2010, 81, 308–314. [Google Scholar] [CrossRef]
- Yang, K.; Huang, Q.; Wang, Q.; Chen, Q. Competing crack initiation behaviors of a laser additively manufactured nickel-based superalloy in high and very high cycle fatigue regimes. Int. J. Fatigue 2020, 136, 105580. [Google Scholar] [CrossRef]
- Fine, M.E.; Bhat, S.P. A model of fatigue crack nucleation in single crystal iron and copper. Mater. Sci. Eng. A 2007, 468, 64–69. [Google Scholar] [CrossRef]
- Ou, C.-Y.; Liu, C.R. The Effects of Grain Size and Strain Amplitude on Persistent Slip Band Formation and Fatigue Crack Initiation. Met. Mater. Trans. A 2019, 50, 5056–5065. [Google Scholar] [CrossRef]
- Kruth, J.; Mercelis, P.; Van Vaerenbergh, J.; Froyen, L.; Rombouts, M. Binding mechanisms in selective laser sintering and selective laser melting. Rapid Prototyp. J. 2005, 11, 26–36. [Google Scholar] [CrossRef]
- Gu, D.; Shen, Y. Balling phenomena in direct laser sintering of stainless steel powder: Metallurgical mechanisms and control methods. Mater. Des. 2009, 30, 2903–2910. [Google Scholar] [CrossRef]
- Fine, M. Phase transformation theory applied to elevated temperature fatigue. Scr. Mater. 2000, 42, 1007–1012. [Google Scholar] [CrossRef]
- Bhat, S.P.; Fine, M.E. Fatigue crack nucleation in iron and a high strength low alloy steel. Mater. Sci. Eng. A 2001, 314, 90–96. [Google Scholar] [CrossRef]
- Tanaka, K.; Mura, T. A Dislocation Model for Fatigue Crack Initiation. J. Appl. Mech. 1981, 48, 97–103. [Google Scholar] [CrossRef]
- Voothaluru, R.; Liu, C.R. Determination of lattice level energy efficiency for fatigue crack initiation. Fatigue Fract. Eng. Mater. Struct. 2013, 36, 670–678. [Google Scholar] [CrossRef]
- Ou, C.-Y.; Voothaluru, R.; Liu, C.R. A Methodology for Incorporating the Effect of Grain Size on the Energy Efficiency Coefficient for Fatigue Crack Initiation Estimation in Polycrystalline Metal. Metals 2020, 10, 355. [Google Scholar] [CrossRef]
- Voothaluru, R.; Liu, C.R. A crystal plasticity based methodology for fatigue crack initiation life prediction in polycrystalline copper. Fatigue Fract. Eng. Mater. Struct. 2014, 37, 671–681. [Google Scholar] [CrossRef]
- Rohit, V. A Crystal Plasticity Based Methodology for Modeling Fatigue Crack Initiation and Estimating Material Coefficients to Predict Fatigue Crack Initiation Life at Micro, Nano and Macro Scales. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 2014. [Google Scholar]
- Taylor, G.I. Plastic Strain in Metals. Inst. Met. 1938, 62, 307. [Google Scholar]
- Asaro, R.J. Crystal Plasticity. J. Appl. Mech. 1983, 50, 921–934. [Google Scholar] [CrossRef]
- Hutchinson, J.W. Bounds and self-consistent estimates for creep of polycrystalline materials. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1976, 348, 101–127. [Google Scholar] [CrossRef]
- Brown, S.; Kim, K.; Anand, L. An internal variable constitutive model for hot working of metals. Int. J. Plast. 1989, 5, 95–130. [Google Scholar] [CrossRef]
- Huang, Y. A User-Material Subroutine Incorporating Single Crystal Plasticity in the ABAQUS Finite Element Program; Harvard University Research Report; Harvard University: Cambridge, MA, USA, 1991. [Google Scholar]
- Liu, B.; Raabe, D.; Roters, F.; Eisenlohr, P.; Lebensohn, R.A. Comparison of Finite Element and Fast Fourier Transform Crystal Plasticity Solvers for Texture Prediction Model. Simul. Mater. Sci. Eng. 2010, 18, 085005. [Google Scholar] [CrossRef]
- Bedekar, V.; Voothaluru, R.; Yu, D.; Wong, A.; Galindo-Nava, E.; Gorti, S.B.; An, K.; Hyde, R.S. Effect of nickel on the kinematic stability of retained austenite in carburized bearing steels—In-situ neutron diffraction and crystal plasticity modeling of uniaxial tension tests in AISI 8620, 4320 and 3310 steels. Int. J. Plast. 2020, 131, 102748. [Google Scholar] [CrossRef]
- Smit, R.; Brekelmans, W.; Meijer, H. Prediction of the mechanical behavior of nonlinear heterogeneous systems by multi-level finite element modeling. Comput. Methods Appl. Mech. Eng. 1998, 155, 181–192. [Google Scholar] [CrossRef]
- Kumar, R.S.; Wang, A.-J.; McDowell, D.L. Effects of Microstructure Variability on Intrinsic Fatigue Resistance of Nickel-base Superalloys—A Computational Micromechanics Approach. Int. J. Fract. 2006, 137, 173–210. [Google Scholar] [CrossRef]
- Zhang, J.; Prasannavenkatesan, R.; Shenoy, M.M.; McDowell, D.L. Modeling fatigue crack nucleation at primary inclusions in carburized and shot-peened martensitic steel. Eng. Fract. Mech. 2009, 76, 315–334. [Google Scholar] [CrossRef]
- Verma, R.K.; Biswas, P. Crystal plasticity-based modelling of grain size effects in dual phase steel. Mater. Sci. Technol. 2016, 32, 1553–1558. [Google Scholar] [CrossRef]
| 230 GPa | 170 GPa | 100 GPa | 0.42 GPa | 6.4 GPa |
| 500 MPa | 412.4 MPa | MPa |
| 600 MPa | 491.7 MPa | MPa |
| 700 MPa | 578.6 MPa | MPa |
| Experiments | Simulations | ||||
|---|---|---|---|---|---|
| Standard Deviation (SD) | Upper Bound | Lower Bound | |||
| 500 MPa | |||||
| 600 MPa | |||||
| 700 MPa | – | – | – | Benchmark | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ou, C.-Y.; Voothaluru, R.; Liu, C.R. Fatigue Crack Initiation of Metals Fabricated by Additive Manufacturing—A Crystal Plasticity Energy-Based Approach to IN718 Life Prediction. Crystals 2020, 10, 905. https://doi.org/10.3390/cryst10100905
Ou C-Y, Voothaluru R, Liu CR. Fatigue Crack Initiation of Metals Fabricated by Additive Manufacturing—A Crystal Plasticity Energy-Based Approach to IN718 Life Prediction. Crystals. 2020; 10(10):905. https://doi.org/10.3390/cryst10100905
Chicago/Turabian StyleOu, Chun-Yu, Rohit Voothaluru, and C. Richard Liu. 2020. "Fatigue Crack Initiation of Metals Fabricated by Additive Manufacturing—A Crystal Plasticity Energy-Based Approach to IN718 Life Prediction" Crystals 10, no. 10: 905. https://doi.org/10.3390/cryst10100905
APA StyleOu, C.-Y., Voothaluru, R., & Liu, C. R. (2020). Fatigue Crack Initiation of Metals Fabricated by Additive Manufacturing—A Crystal Plasticity Energy-Based Approach to IN718 Life Prediction. Crystals, 10(10), 905. https://doi.org/10.3390/cryst10100905





