Mode Transition of Filaments in Packed-Bed Dielectric Barrier Discharges
Abstract
1. Introduction
2. Results and Discussion
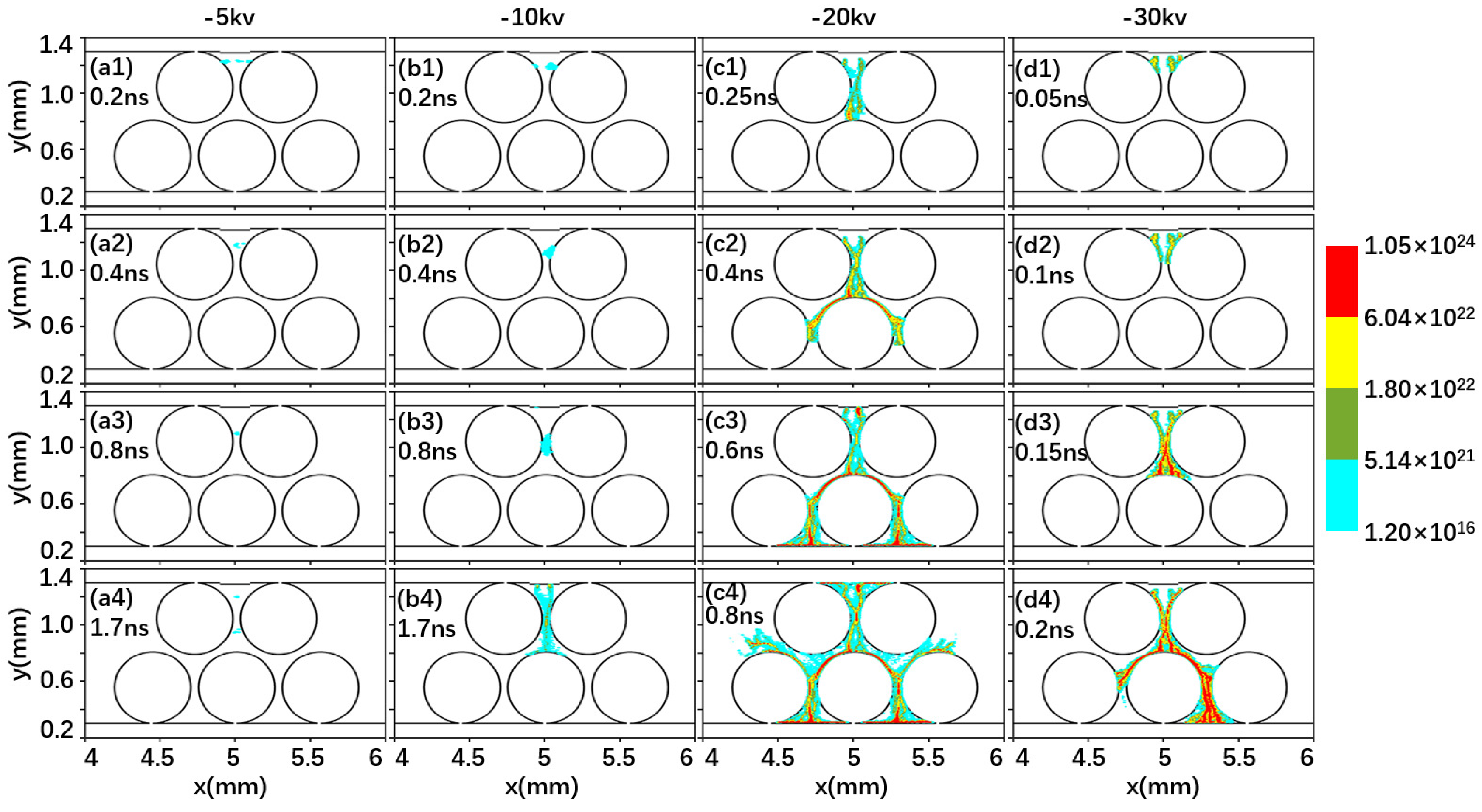
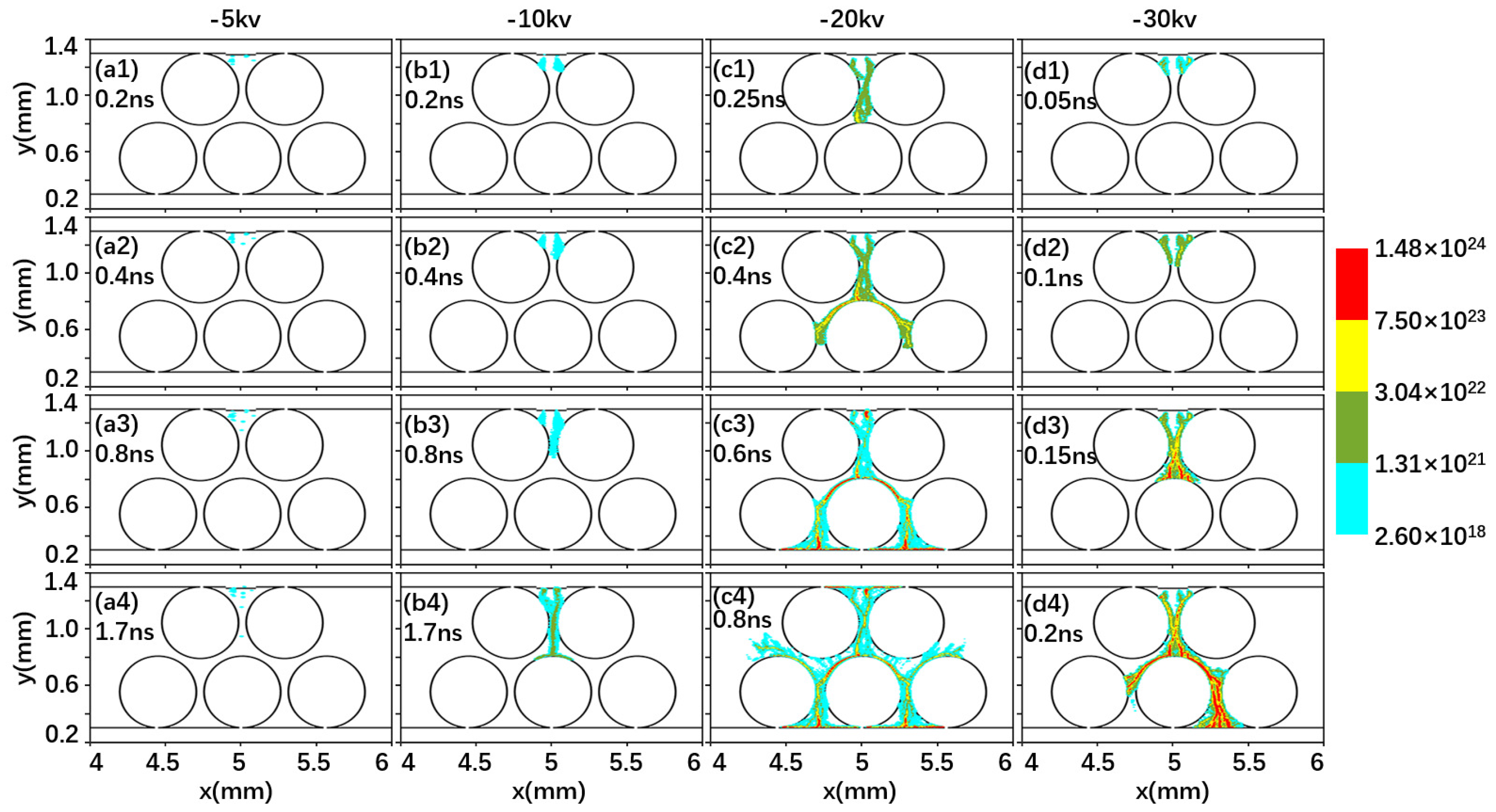
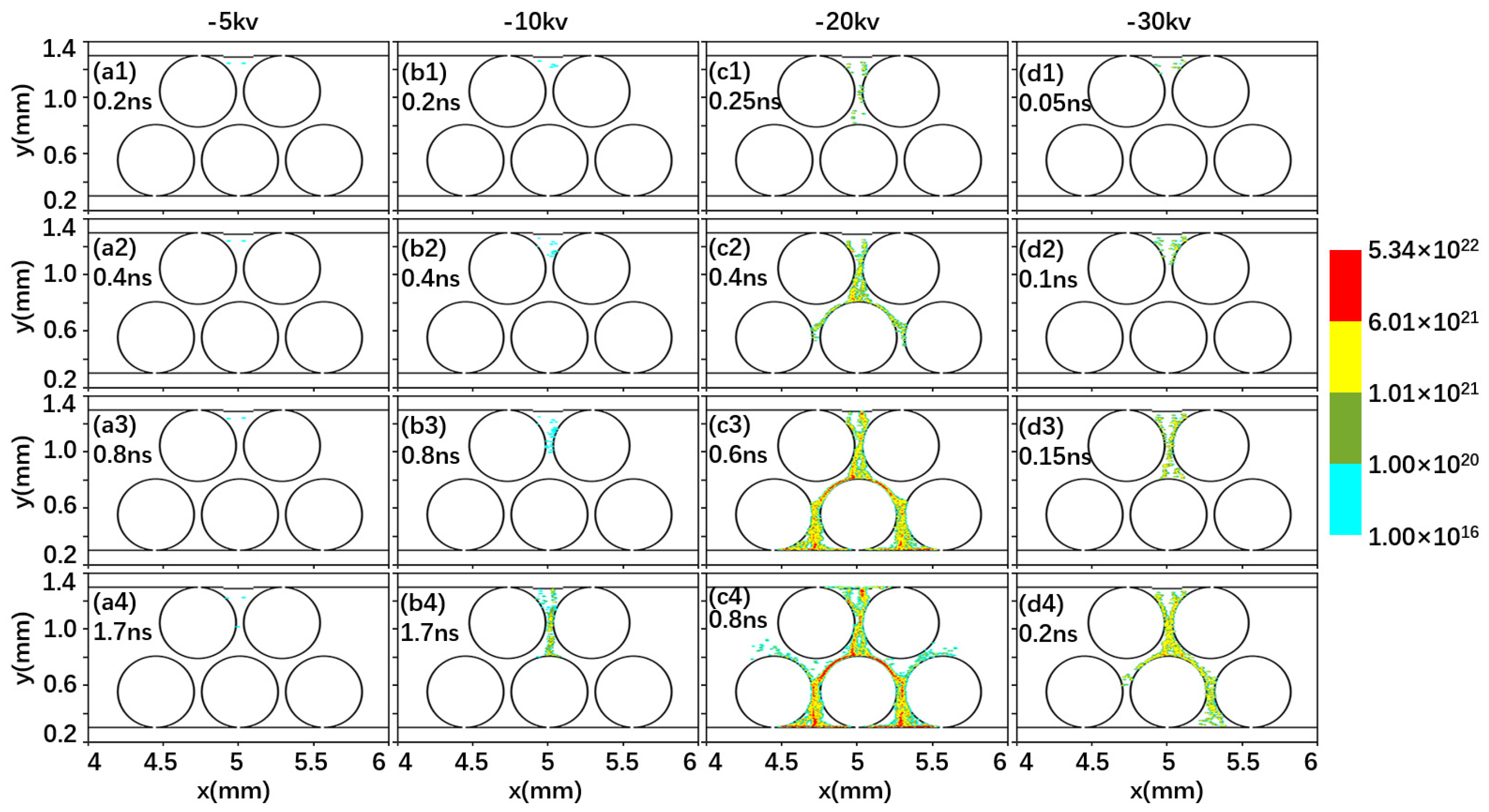
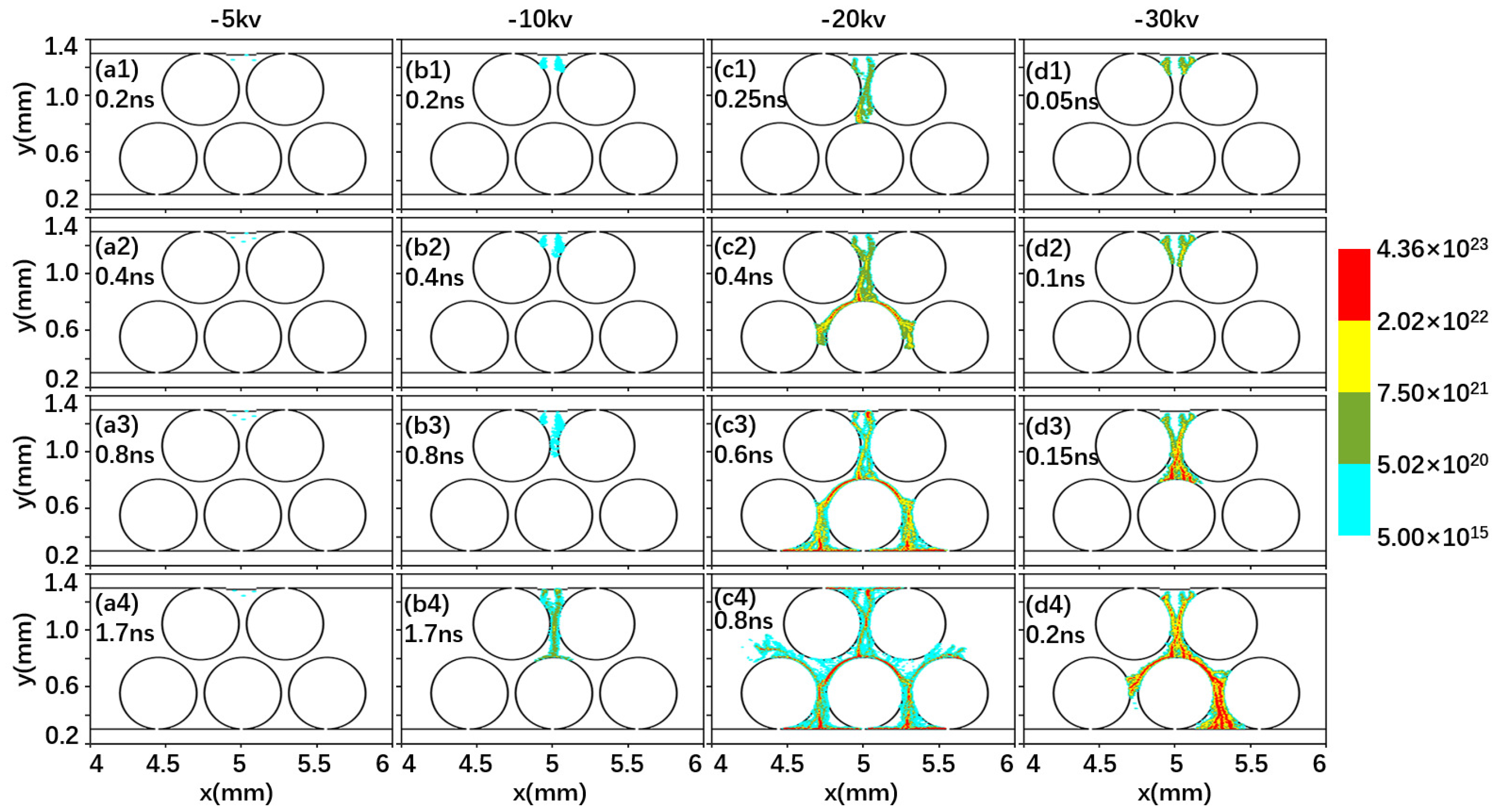
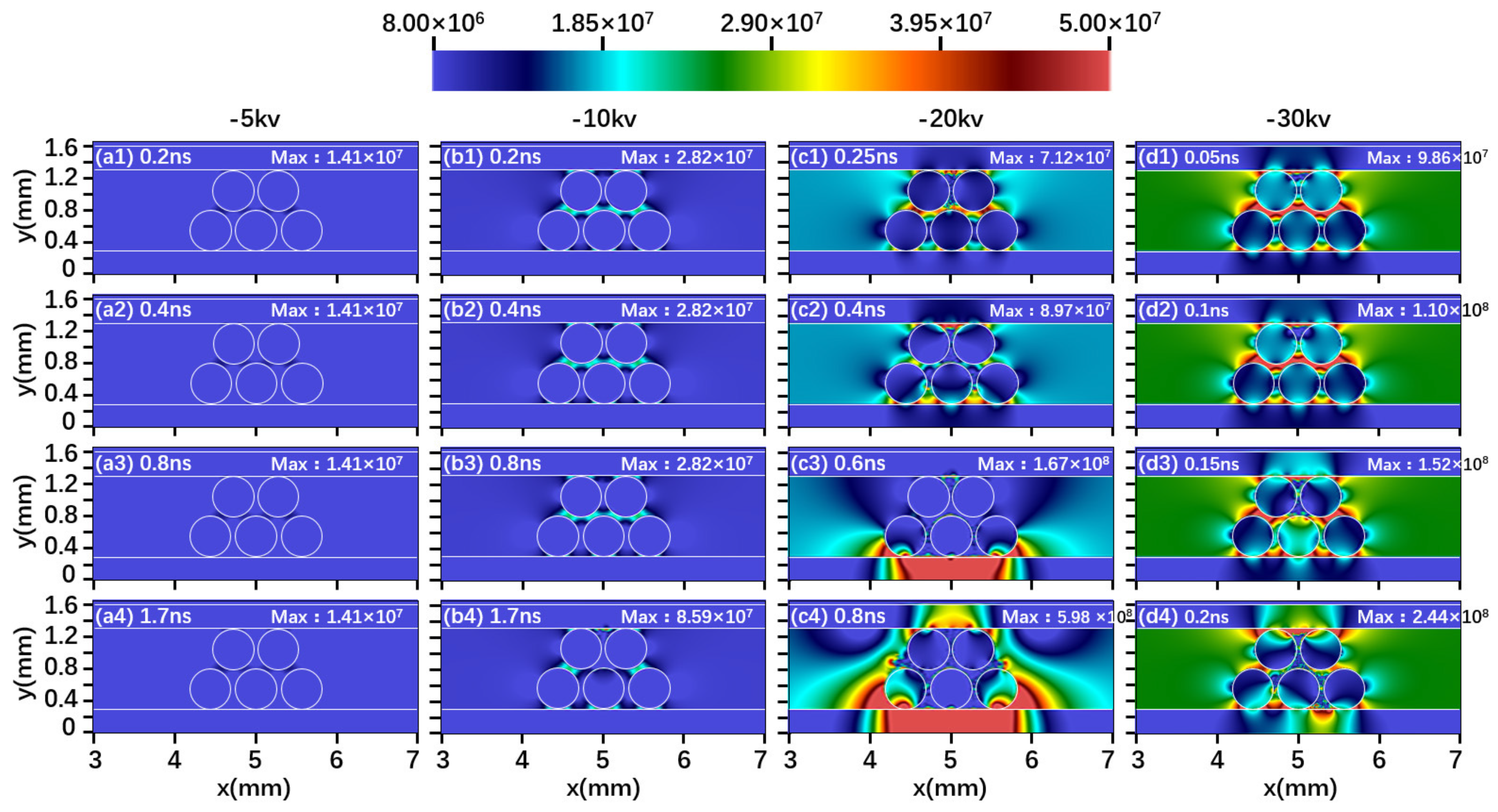
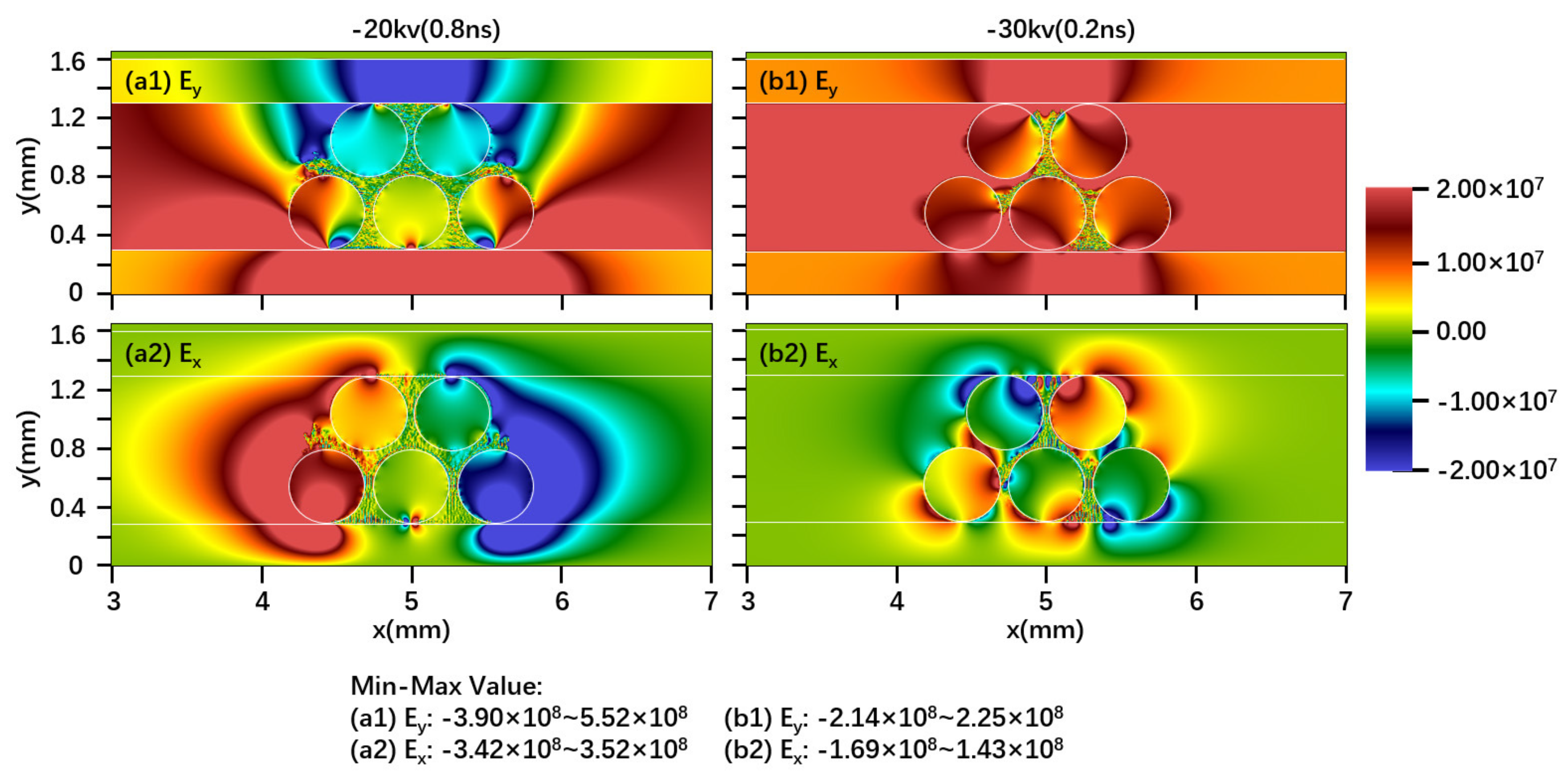
2.1. Effect of Driving Voltage
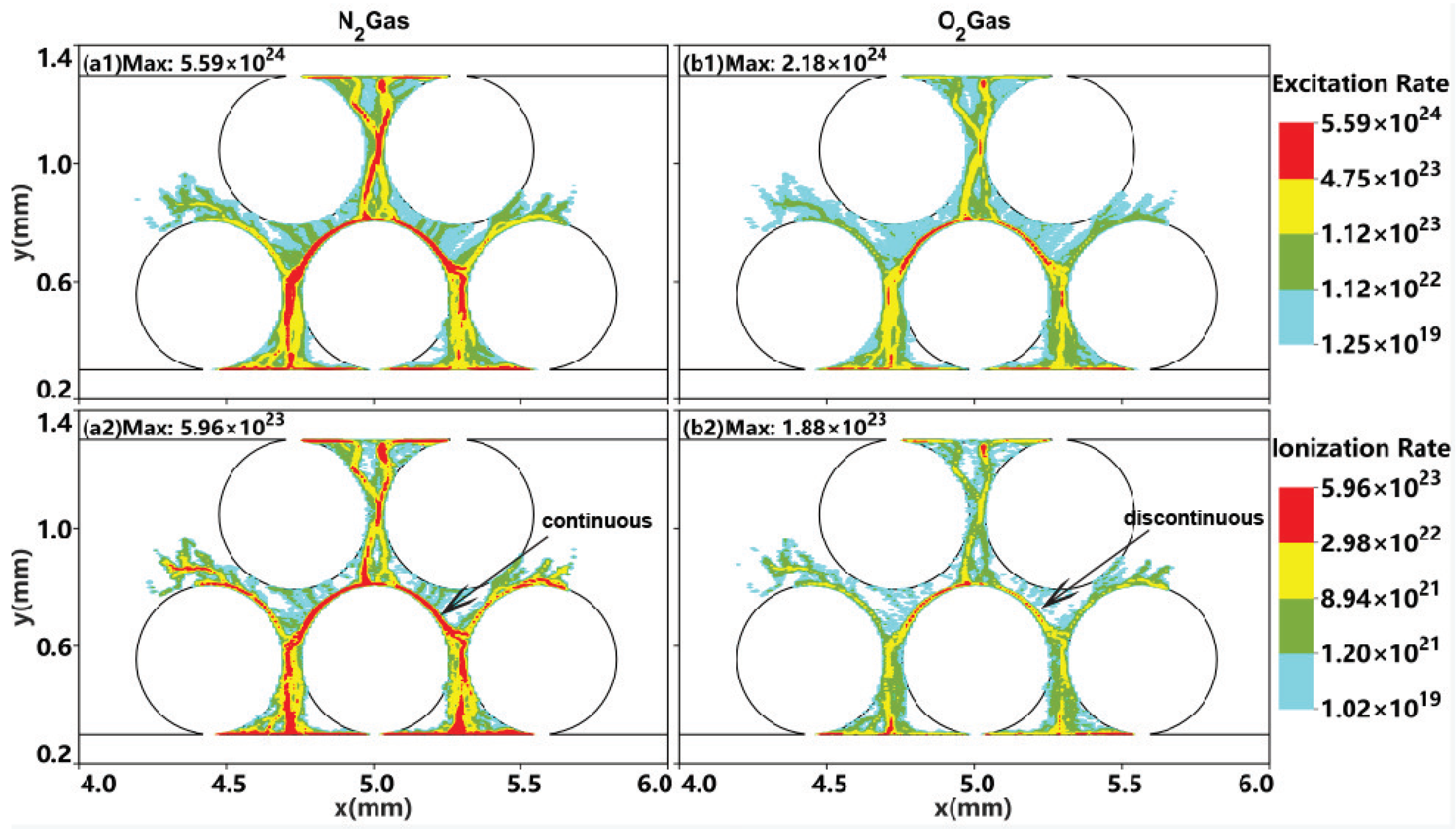
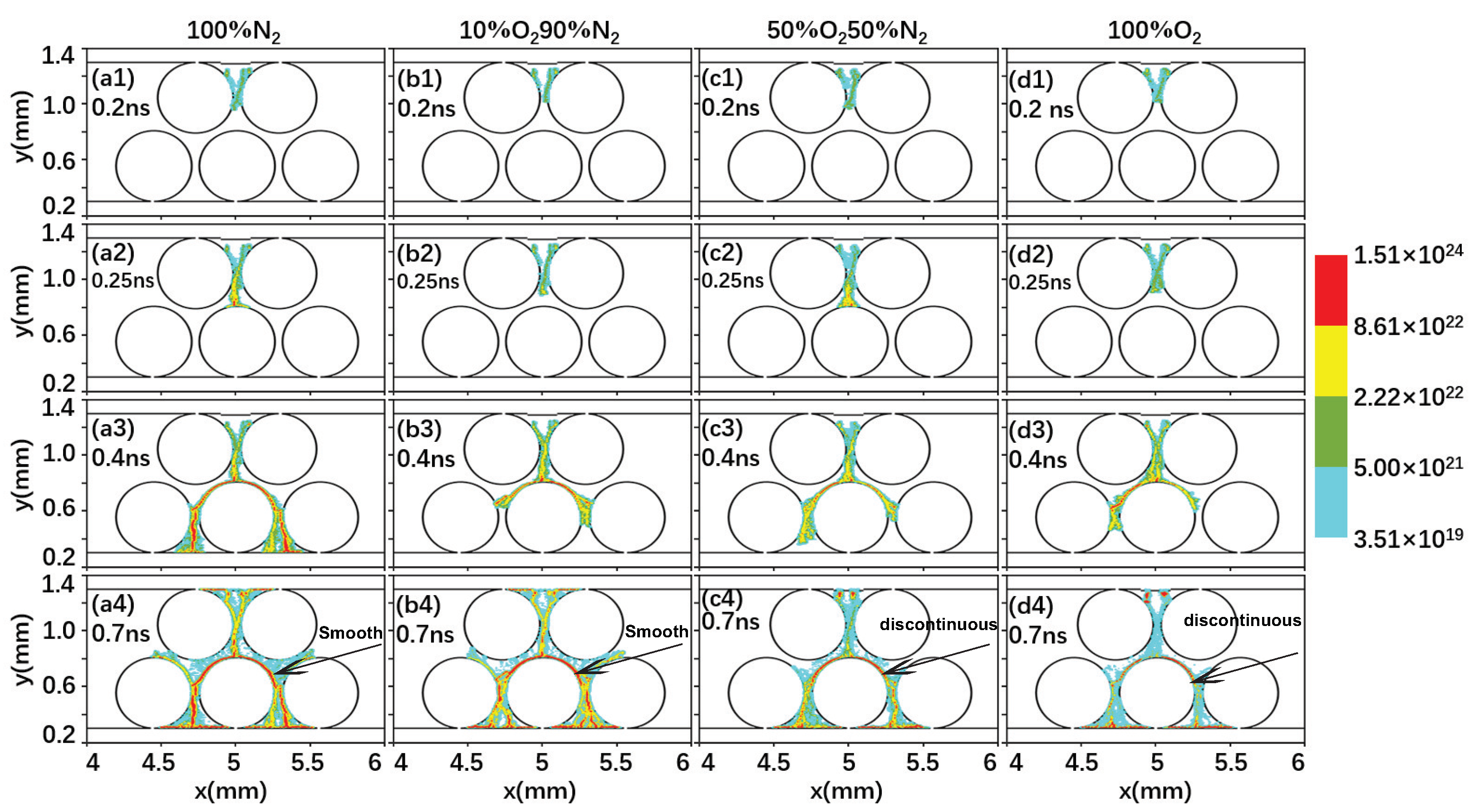
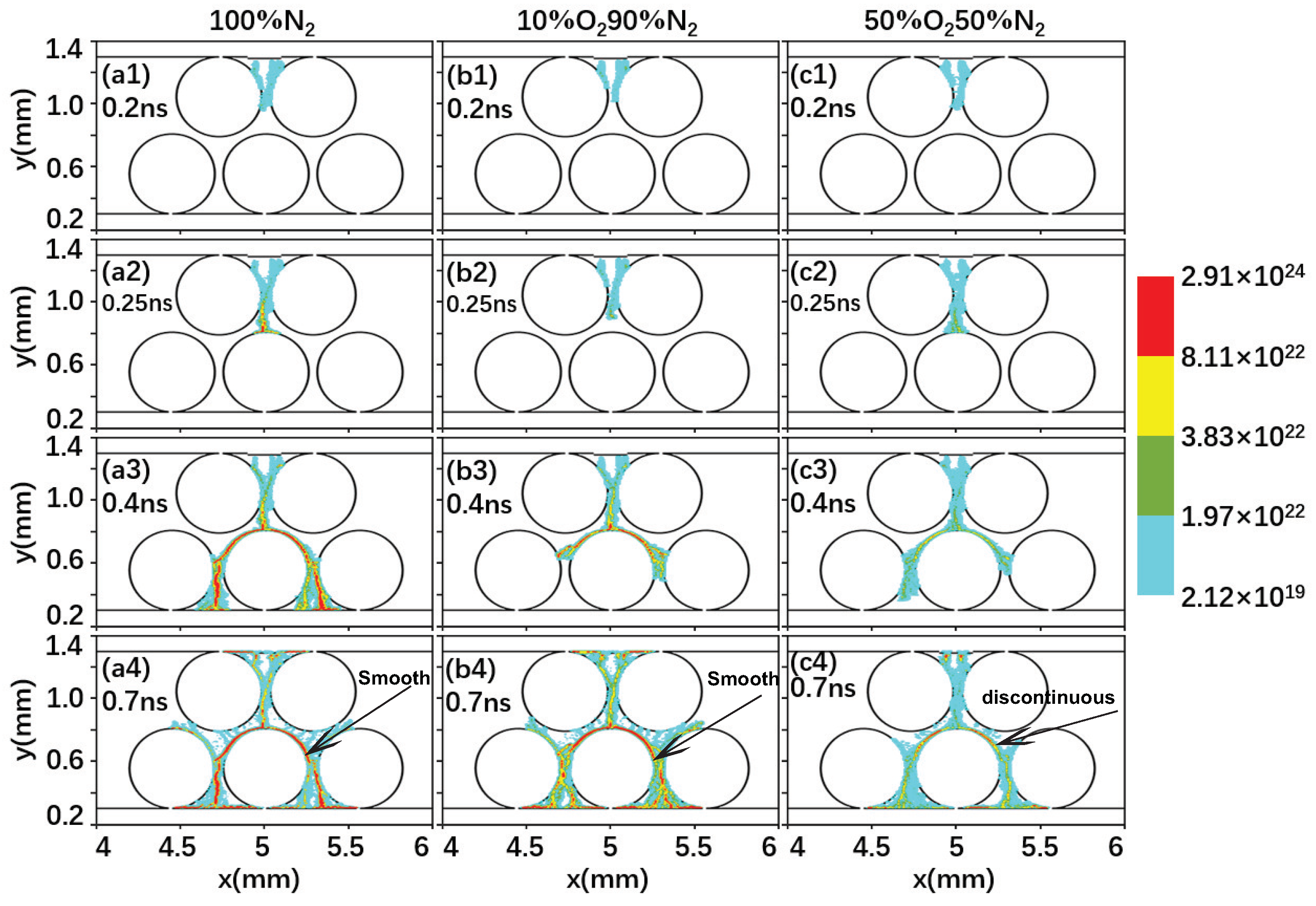
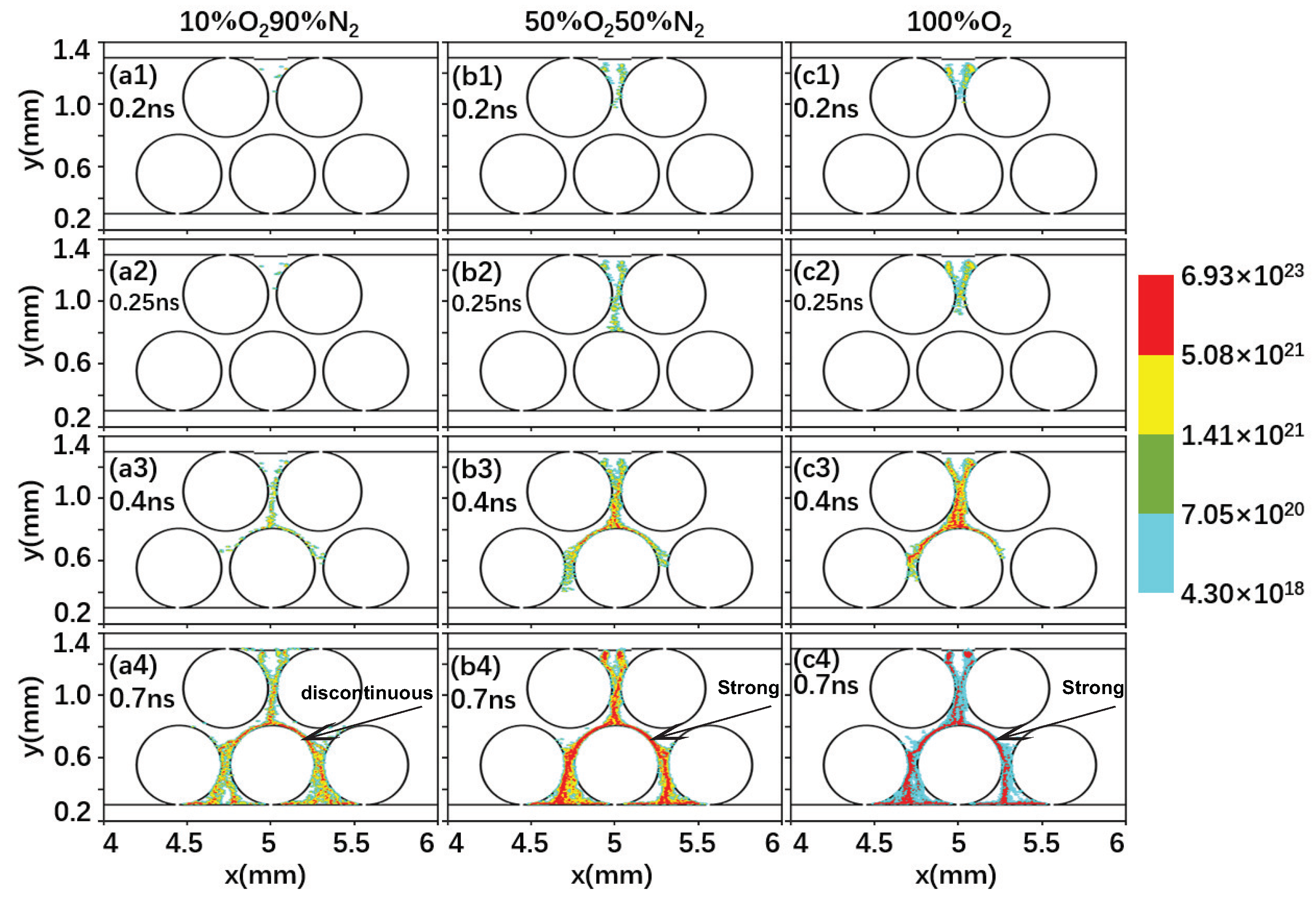
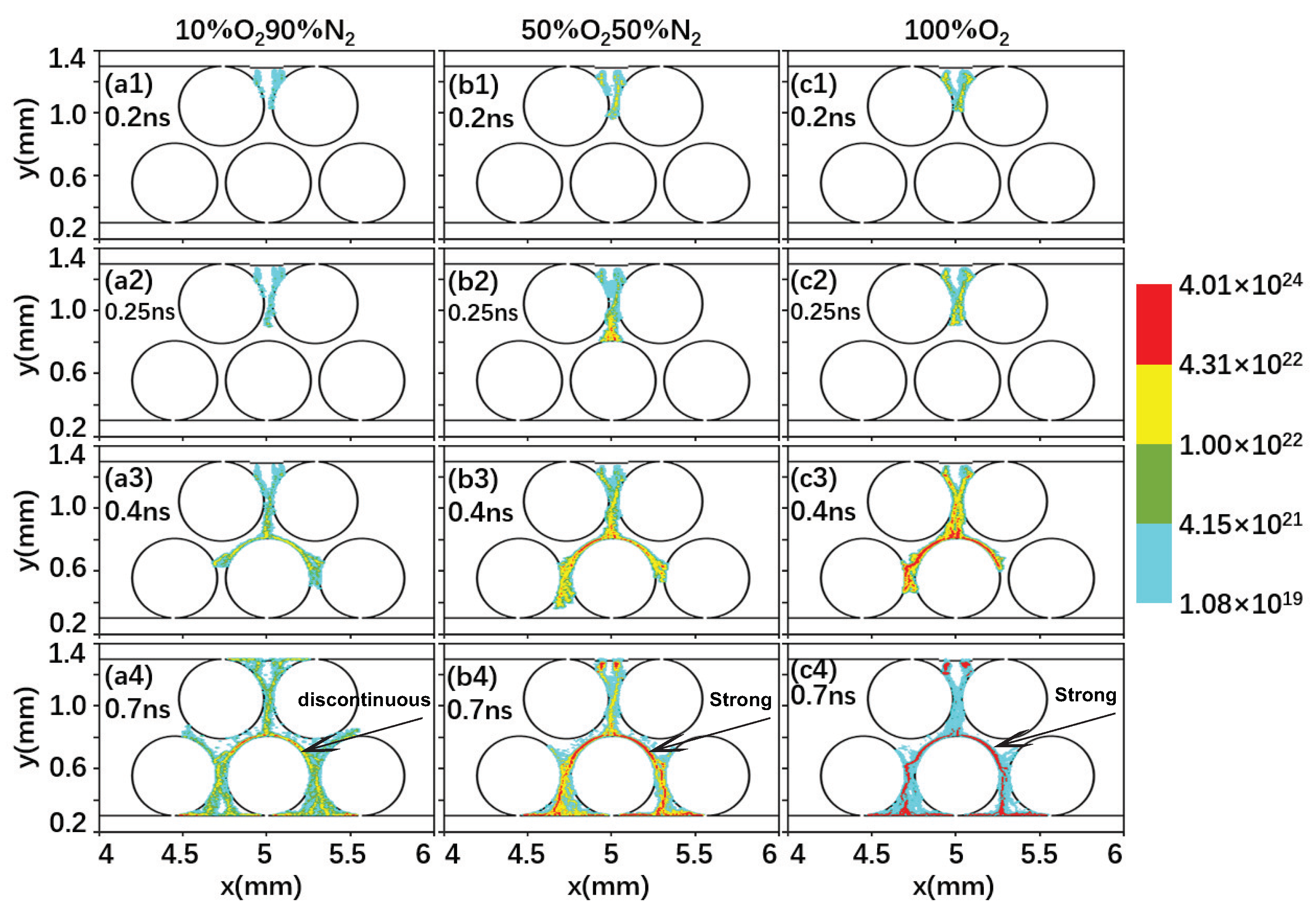
2.2. Effect of the Gas Composition
3. Description of the Model
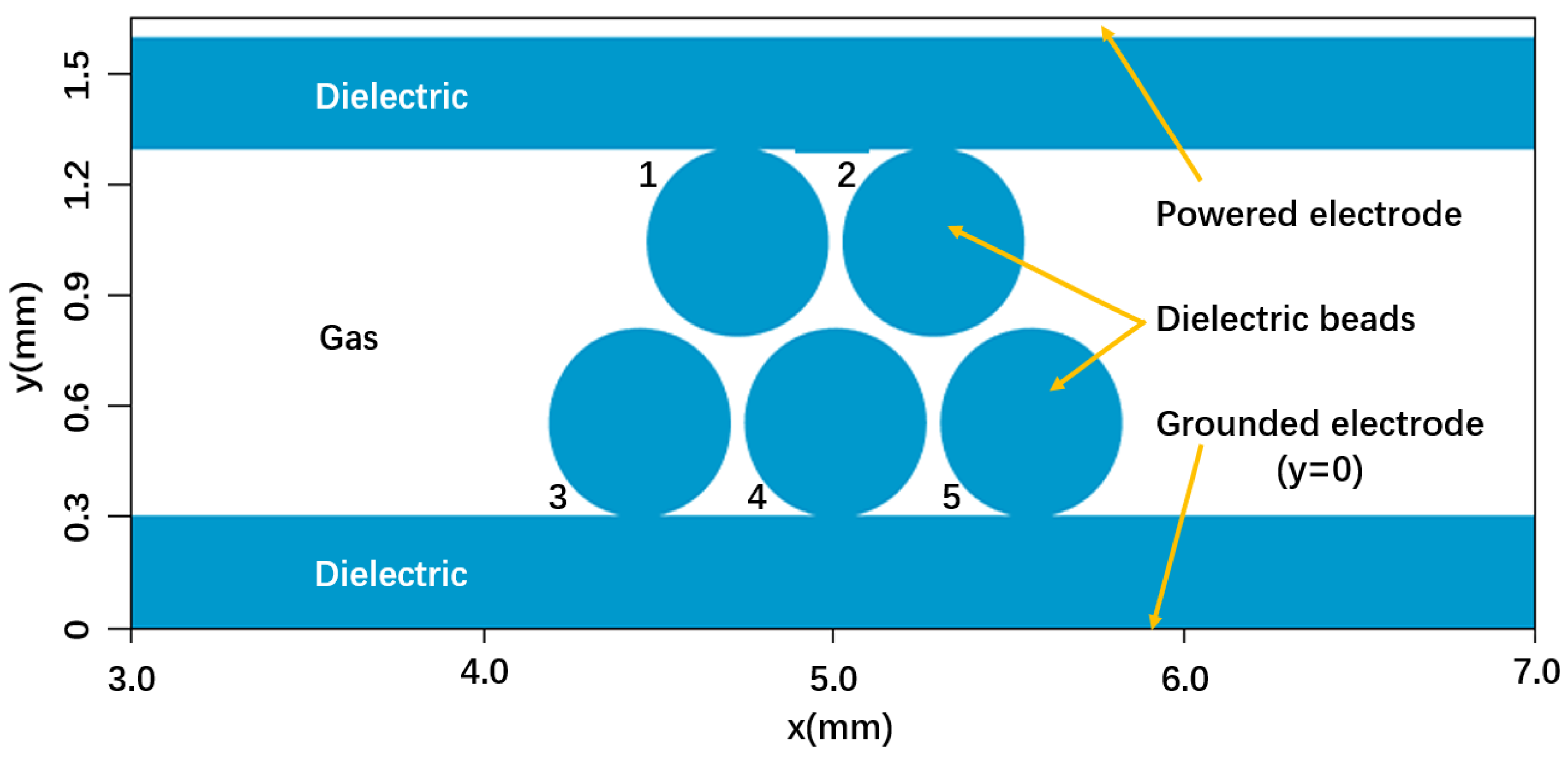
3.1. Model Assumptions
3.2. Simulation Method
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Neyts, E.C.; Ostrikov, K.; Sunkara, M.K.; Bogaerts, A. Plasma Catalysis: Synergistic Effects at the Nanoscale. Chem. Rev. 2015, 115, 13408–13446. [Google Scholar] [CrossRef] [PubMed]
- Yi, H.; Du, H.; Hu, Y.; Yan, H.; Jiang, H.L.; Lu, J. Precisely Controlled Porous Alumina Overcoating on Pd Catalyst by Atomic Layer Deposition: Enhanced Selectivity and Durability in Hydrogenation of 1,3-Butadiene. ACS Catal. 2015, 5, 2735–2739. [Google Scholar] [CrossRef]
- O’Neill, B.J.; Jackson, D.H.; Lee, J.; Canlas, C.; Stair, P.C.; Marshall, C.L.; Elam, J.W.; Kuech, T.F.; Dumesic, J.A.; Huber, G.W. Catalyst design with atomic layer deposition. ACS Catal. 2015, 5, 1804–1825. [Google Scholar] [CrossRef]
- Chen, H.L.; Lee, H.M.; Chen, S.H.; Chao, Y.; Chang, M.B. Review of plasma catalysis on hydrocarbon reforming for hydrogen production—Interaction, integration, and prospects. Appl. Catal. B Environ. 2008, 85, 1–9. [Google Scholar] [CrossRef]
- Van Durme, J.; Dewulf, J.; Leys, C.; Van Langenhove, H. Combining non-thermal plasma with heterogeneous catalysis in waste gas treatment: A review. Appl. Catal. B Environ. 2008, 78, 324–333. [Google Scholar] [CrossRef]
- Chen, H.L.; Lee, H.M.; Chen, S.H.; Chang, M.B.; Yu, S.J.; Li, S.N. Removal of volatile organic compounds by single-stage and two-stage plasma catalysis systems: A review of the performance enhancement mechanisms, current status, and suitable applications. Environ. Sci. Technol. 2009, 43, 2216–2227. [Google Scholar] [CrossRef] [PubMed]
- Whitehead, J.C. Plasma catalysis: A solution for environmental problems. Pure Appl. Chem. 2010, 82, 1329–1336. [Google Scholar] [CrossRef]
- Neyts, E.; Bogaerts, A. Understanding plasma catalysis through modelling and simulation—A review. J. Phys. D Appl. Phys. 2014, 47, 224010. [Google Scholar] [CrossRef]
- Takashima, K.; Kaneko, T. Ozone and dinitrogen monoxide production in atmospheric pressure air dielectric barrier discharge plasma effluent generated by nanosecond pulse superimposed alternating current voltage. Plasma Sources Sci. Technol. 2017, 26, 065018. [Google Scholar] [CrossRef]
- Dong, L.; Xiao, H.; Fan, W.; Yin, Z.; Zhao, H. Temporal symmetry of individual filaments in different spatial symmetry filaments pattern in a dielectric barrier discharge. Phys. Plasmas 2010, 17, 102314. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, H.y.; Jiang, W.; Bogaerts, A. Two-dimensional particle-in cell/Monte Carlo simulations of a packed-bed dielectric barrier discharge in air at atmospheric pressure. New J. Phys. 2015, 17, 083056. [Google Scholar] [CrossRef]
- Babaeva, N.Y.; Kushner, M.J. Self-organization of single filaments and diffusive plasmas during a single pulse in dielectric-barrier discharges. Plasma Sources Sci. Technol. 2014, 23, 065047. [Google Scholar] [CrossRef]
- Babaeva, N.Y.; Naidis, G.V.; Kushner, M.J. Interaction of positive streamers in air with bubbles floating on liquid surfaces: Conductive and dielectric bubbles. Plasma Sources Sci. Technol. 2018, 27. [Google Scholar] [CrossRef]
- Fan, W.; Sheng, Z.; Liu, F.; Zhong, X.; Dong, L. Mechanisms of fine structure formation in dielectric barrier discharges. Phys. Plasmas 2018, 25, 023502. [Google Scholar] [CrossRef]
- Chanrion, O.; Neubert, T. A PIC-MCC code for simulation of streamer propagation in air. J. Comput. Phys. 2008, 227, 7222–7245. [Google Scholar] [CrossRef]
- Papageorghiou, L.; Panousis, E.; Loiseau, J.; Spyrou, N.; Held, B. Two-dimensional modelling of a nitrogen dielectric barrier discharge (DBD) at atmospheric pressure: Filament dynamics with the dielectric barrier on the cathode. J. Phys. D Appl. Phys. 2009, 42, 105201. [Google Scholar] [CrossRef]
- Babaeva, N.Y.; Kushner, M.J. Ion energy and angular distributions onto polymer surfaces delivered by dielectric barrier discharge filaments in air: I. Flat surfaces. Plasma Sources Sci. Technol. 2011, 20, 035017. [Google Scholar] [CrossRef]
- Akishev, Y.; Aponin, G.; Balakirev, A.; Grushin, M.; Karalnik, V.; Petryakov, A.; Trushkin, N. DBD surface streamer expansion described using nonlinear diffusion of the electric potential over the barrier. J. Phys. D Appl. Phys. 2013, 46, 464014. [Google Scholar] [CrossRef]
- Inada, Y.; Aono, K.; Ono, R.; Kumada, A.; Hidaka, K.; Maeyama, M. Two-dimensional electron density measurement of pulsed positive primary streamer discharge in atmospheric-pressure air. J. Phys. D Appl. Phys. 2017, 50, 174005. [Google Scholar] [CrossRef]
- Kogelschatz, U. Dielectric-barrier discharges: Their history, discharge physics, and industrial applications. Plasma Chem. Plasma Process. 2003, 23, 1–46. [Google Scholar] [CrossRef]
- Vasilyak, L.M.; Kostyuchenko, S.; Kudryavtsev, N.N.; Filyugin, I. Fast ionisation waves under electrical breakdown conditions. Physics-Uspekhi 1994, 37, 247–268. [Google Scholar] [CrossRef]
- Petrishchev, V.; Leonov, S.; Adamovich, I.V. Studies of nanosecond pulse surface ionization wave discharges over solid and liquid dielectric surfaces. Plasma Sources Sci. Technol. 2014, 23, 065022. [Google Scholar] [CrossRef]
- Goldberg, B.M.; Böhm, P.S.; Czarnetzki, U.; Adamovich, I.V.; Lempert, W.R. Electric field vector measurements in a surface ionization wave discharge. Plasma Sources Sci. Technol. 2015, 24, 055017. [Google Scholar] [CrossRef]
- Kushner, M.J. Modeling of microdischarge devices: Pyramidal structures. J. Appl. Phys. 2004, 95, 846–859. [Google Scholar] [CrossRef]
- Bruggeman, P.; Brandenburg, R. Atmospheric pressure discharge filaments and microplasmas: Physics, chemistry and diagnostics. J. Phys. D Appl. Phys. 2013, 46, 464001. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, W.; Zhang, Q.; Bogaerts, A. Computational study of plasma sustainability in radio frequency micro-discharges. J. Appl. Phys. 2014, 115, 193301. [Google Scholar] [CrossRef]
- Šimek, M. Optical diagnostics of streamer discharges in atmospheric gases. J. Phys. D Appl. Phys. 2014, 47, 463001. [Google Scholar] [CrossRef]
- Tu, X.; Gallon, H.J.; Whitehead, J.C. Transition behavior of packed-bed dielectric barrier discharge in argon. IEEE Trans. Plasma Sci. 2011, 39, 2172–2173. [Google Scholar] [CrossRef]
- Kruszelnicki, J.; Engeling, K.W.; Foster, J.E.; Xiong, Z.; Kushner, M.J. Propagation of negative electrical discharges through 2-dimensional packed bed reactors. J. Phys. D Appl. Phys. 2017, 50, 025203. [Google Scholar] [CrossRef]
- Russ, H.; Neiger, M.; Lang, J.E. Simulation of micro discharges for the optimization of energy requirements for removal of NO x from exhaust gases. IEEE Trans. Plasma Sci. 1999, 27, 38–39. [Google Scholar] [CrossRef]
- Kang, W.S.; Park, J.M.; Kim, Y.; Hong, S.H. Numerical study on influences of barrier arrangements on dielectric barrier discharge characteristics. IEEE Trans. Plasma Sci. 2003, 31, 504–510. [Google Scholar] [CrossRef]
- Takaki, K.; Chang, J.S.; Kostov, K.G. Atmospheric pressure of nitrogen plasmas in a ferroelectric packed bed barrier discharge reactor. Part I. Modeling. IEEE Trans. Dielectr. Electr. Insul. 2004, 11, 481–490. [Google Scholar] [CrossRef]
- Van Laer, K.; Bogaerts, A. Fluid modelling of a packed bed dielectric barrier discharge plasma reactor. Plasma Sources Sci. Technol. 2016, 25, 015002. [Google Scholar] [CrossRef]
- Van Laer, K.; Bogaerts, A. Influence of gap size and dielectric constant of the packing material on the plasma behaviour in a packed bed DBD reactor: A fluid modelling study. Plasma Process. Polym. 2017, 14. [Google Scholar] [CrossRef]
- Van Laer, K.; Bogaerts, A. How bead size and dielectric constant affect the plasma behaviour in a packed bed plasma reactor: A modelling study. Plasma Sources Sci. Technol. 2017, 26, 085007. [Google Scholar] [CrossRef]
- Wang, W.; Kim, H.H.; Van Laer, K.; Bogaerts, A. Streamer propagation in a packed bed plasma reactor for plasma catalysis applications. Chem. Eng. J. 2018, 334, 2467–2479. [Google Scholar] [CrossRef]
- Kang, W.S.; Kim, H.H.; Teramoto, Y.; Ogata, A.; Lee, J.Y.; Kim, D.W.; Hur, M.; Song, Y.H. Surface streamer propagations on an alumina bead: Experimental observation and numerical modeling. Plasma Sources Sci. Technol. 2018, 27, 015018. [Google Scholar] [CrossRef]
- Hensel, K.; Martišovitš, V.; Machala, Z.; Janda, M.; Leštinskỳ, M.; Tardiveau, P.; Mizuno, A. Electrical and optical properties of AC microdischarges in porous ceramics. Plasma Process. Polym. 2007, 4, 682–693. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, H.Y.; Zhang, Y.R.; Bogaerts, A. Formation of microdischarges inside a mesoporous catalyst in dielectric barrier discharge plasmas. Plasma Sources Sci. Technol. 2017, 26, 054002. [Google Scholar] [CrossRef]
- Zhang, Y.R.; Van Laer, K.; Neyts, E.C.; Bogaerts, A. Can plasma be formed in catalyst pores? A modeling investigation. Appl. Catal. B Environ. 2016, 185, 56–67. [Google Scholar] [CrossRef]
- Lieberman, M.A.; Lichtenberg, A.J. Principles of Plasma Discharges and Materials Processing; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Furman, M.; Pivi, M. Probabilistic model for the simulation of secondary electron emission. Phys. Rev. Spec. Top. 2002, 5, 124404. [Google Scholar] [CrossRef]
- Phelps, A.; Petrovic, Z.L. Cold-cathode discharges and breakdown in argon: Surface and gas phase production of secondary electrons. Plasma Sources Sci. Technol. 1999, 8, R21. [Google Scholar] [CrossRef]
- Pancheshnyi, S.; Biagi, S.; Bordage, M.; Hagelaar, G.; Morgan, W.; Phelps, A.; Pitchford, L. The LXCat project: Electron scattering cross sections and swarm parameters for low temperature plasma modeling. Chem. Phys. 2012, 398, 148–153. [Google Scholar] [CrossRef]
- LXCat Website. Biagi-v8.9 Database. Available online: www.lxcat.net (accessed on 11 June 2015).
- Kim, H.H.; Prieto, G.; Takashima, K.; Katsura, S.; Mizuno, A. Performance evaluation of discharge plasma process for gaseous pollutant removal. J. Electrost. 2002, 55, 25–41. [Google Scholar] [CrossRef]
- Song, H.K.; Choi, J.W.; Yue, S.H.; Lee, H.; Na, B.K. Synthesis gas production via dielectric barrier discharge over Ni/γ-Al2O3 catalyst. Catal. Today 2004, 89, 27–33. [Google Scholar] [CrossRef]
- Van Durme, J.; Dewulf, J.; Sysmans, W.; Leys, C.; Van Langenhove, H. Efficient toluene abatement in indoor air by a plasma catalytic hybrid system. Appl. Catal. B Environ. 2007, 74, 161–169. [Google Scholar] [CrossRef]
- Kim, H.H.; Teramoto, Y.; Sano, T.; Negishi, N.; Ogata, A. Effects of Si/Al ratio on the interaction of nonthermal plasma and Ag/HY catalysts. Appl. Catal. B Environ. 2015, 166, 9–17. [Google Scholar] [CrossRef]
- Tskhakaya, D.; Matyash, K.; Schneider, R.; Taccogna, F. The Particle-In-Cell Method. Contrib. Plasma Phys. 2007, 47, 563–594. [Google Scholar] [CrossRef]
- Nieter, C.; Cary, J.R. VORPAL: A versatile plasma simulation code. J. Comput. Phys. 2004, 196, 448–473. [Google Scholar] [CrossRef]
- Birdsall, C.K. Particle-in-cell charged-particle simulations, plus Monte Carlo collisions with neutral atoms, PIC-MCC. IEEE Trans. Plasma Sci. 1991, 19, 65–85. [Google Scholar] [CrossRef]
- Nanbu, K.; Mitsui, K.; Kondo, S. Self-consistent particle modelling of dc magnetron discharges of an O2 /Ar mixture. J. Phys. D Appl. Phys. 2000, 33, 2274. [Google Scholar] [CrossRef]
| Reactions | Threshold Energy (eV) |
|---|---|
| Electron-impact ionization | |
| 12.06 | |
| 15.58 | |
| Attachment | |
| Electron-impact excitation | |
| 0.98 | |
| 1.63 | |
| 6.0 | |
| 8.4 | |
| 10.00 | |
| 6.169 | |
| 7.353 | |
| 7.362 | |
| 8.165 | |
| 8.399 | |
| 8.549 | |
| 8.89 | |
| 9.7537 | |
| 11.032 | |
| 12.771 | |
| 13.37 | |
| 13.382 | |
| 14.0 | |
| Elastic collision | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, M.; Zhang, Y.; Wang, H.; Guo, B.; Zhang, Q.; Bogaerts, A. Mode Transition of Filaments in Packed-Bed Dielectric Barrier Discharges. Catalysts 2018, 8, 248. https://doi.org/10.3390/catal8060248
Gao M, Zhang Y, Wang H, Guo B, Zhang Q, Bogaerts A. Mode Transition of Filaments in Packed-Bed Dielectric Barrier Discharges. Catalysts. 2018; 8(6):248. https://doi.org/10.3390/catal8060248
Chicago/Turabian StyleGao, Mingxiang, Ya Zhang, Hongyu Wang, Bin Guo, Quanzhi Zhang, and Annemie Bogaerts. 2018. "Mode Transition of Filaments in Packed-Bed Dielectric Barrier Discharges" Catalysts 8, no. 6: 248. https://doi.org/10.3390/catal8060248
APA StyleGao, M., Zhang, Y., Wang, H., Guo, B., Zhang, Q., & Bogaerts, A. (2018). Mode Transition of Filaments in Packed-Bed Dielectric Barrier Discharges. Catalysts, 8(6), 248. https://doi.org/10.3390/catal8060248






