A SET Approach to the Interplay of Catalysts and Reactants
Abstract
1. Introduction
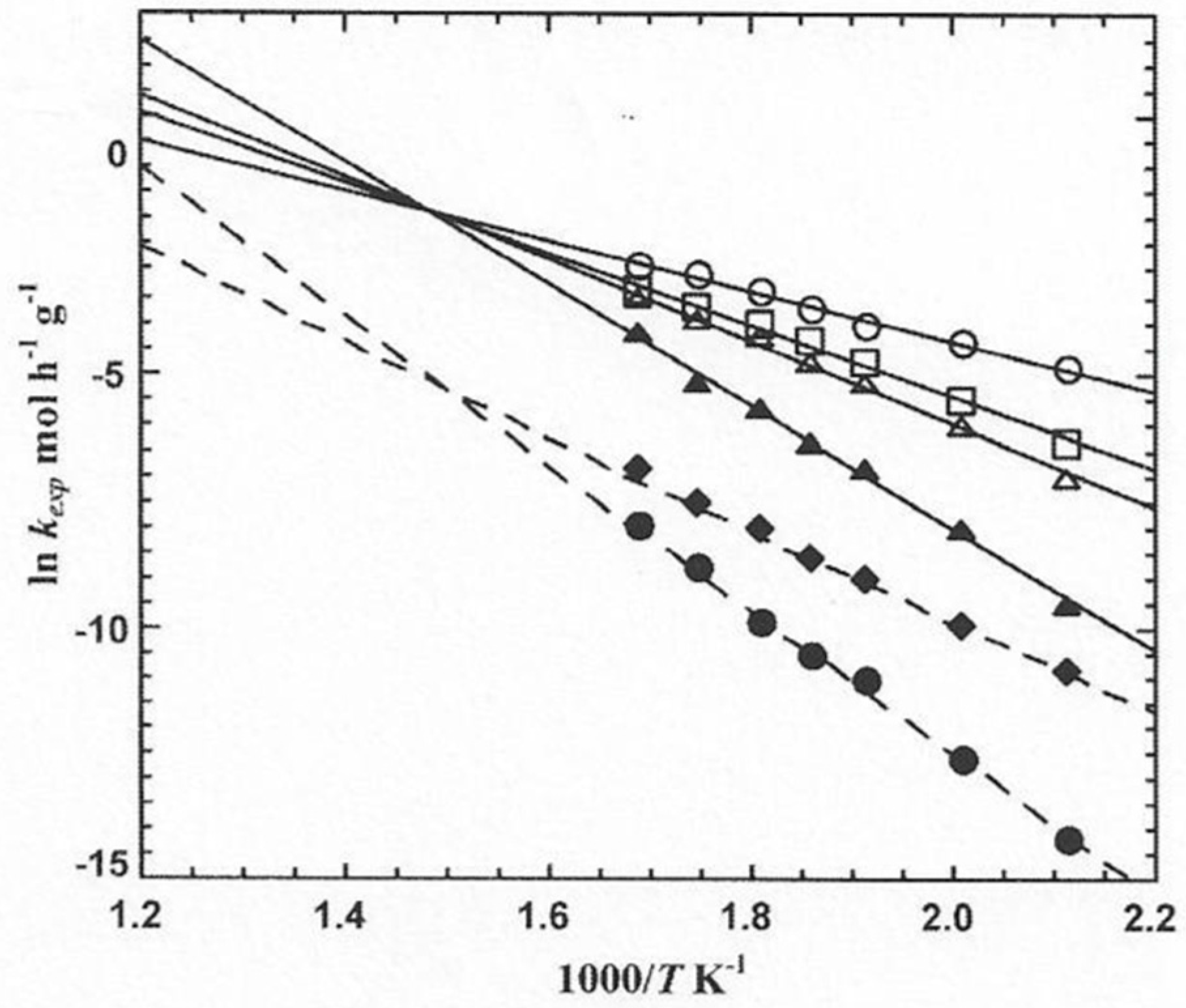
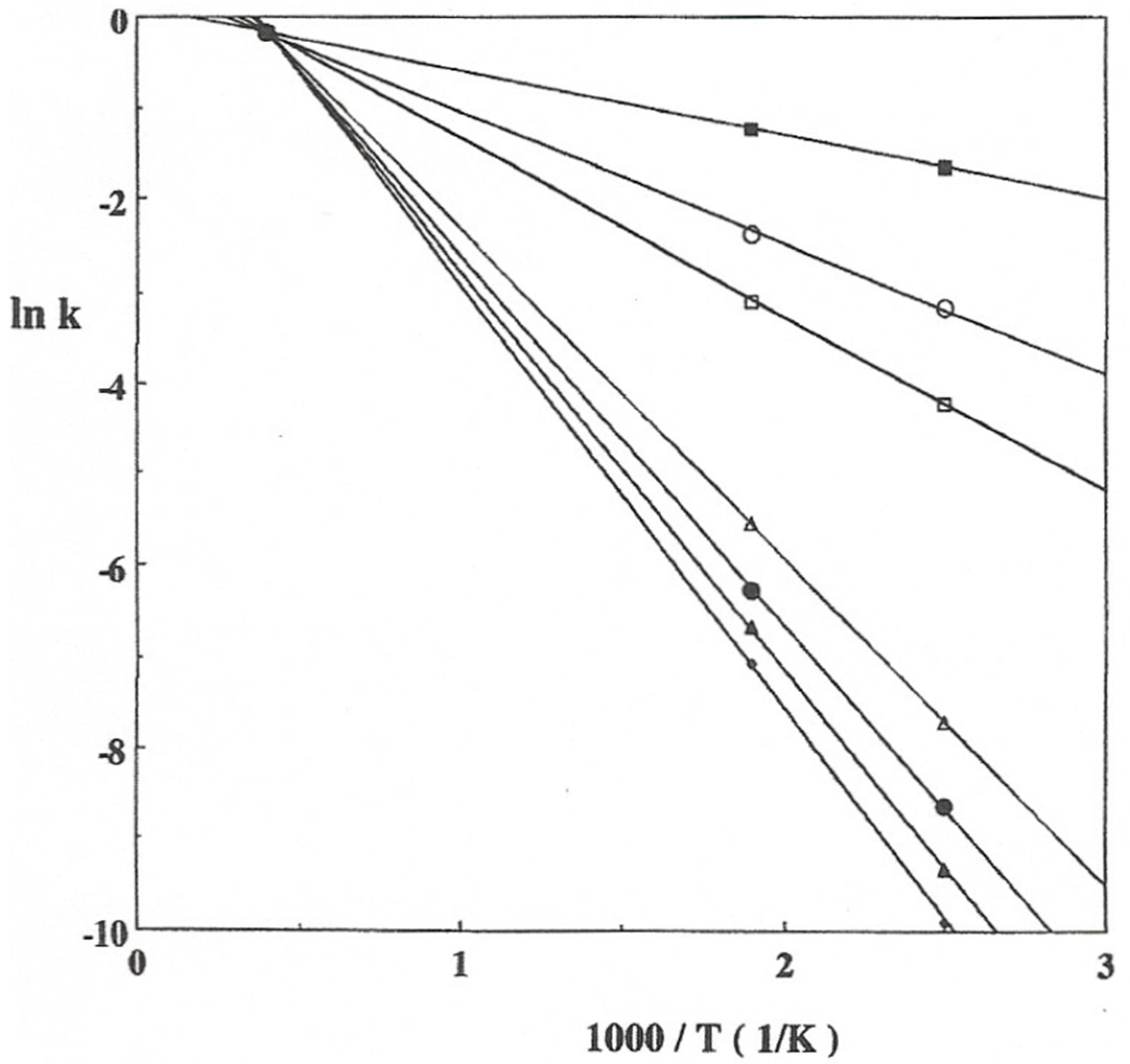
2. Isokinetic Effects on Solid State Catalysts
3. Gas Phase Interactions
3.1. Experimental Data and Indications of a Reaction Route
3.2. Suggested Mechanisms
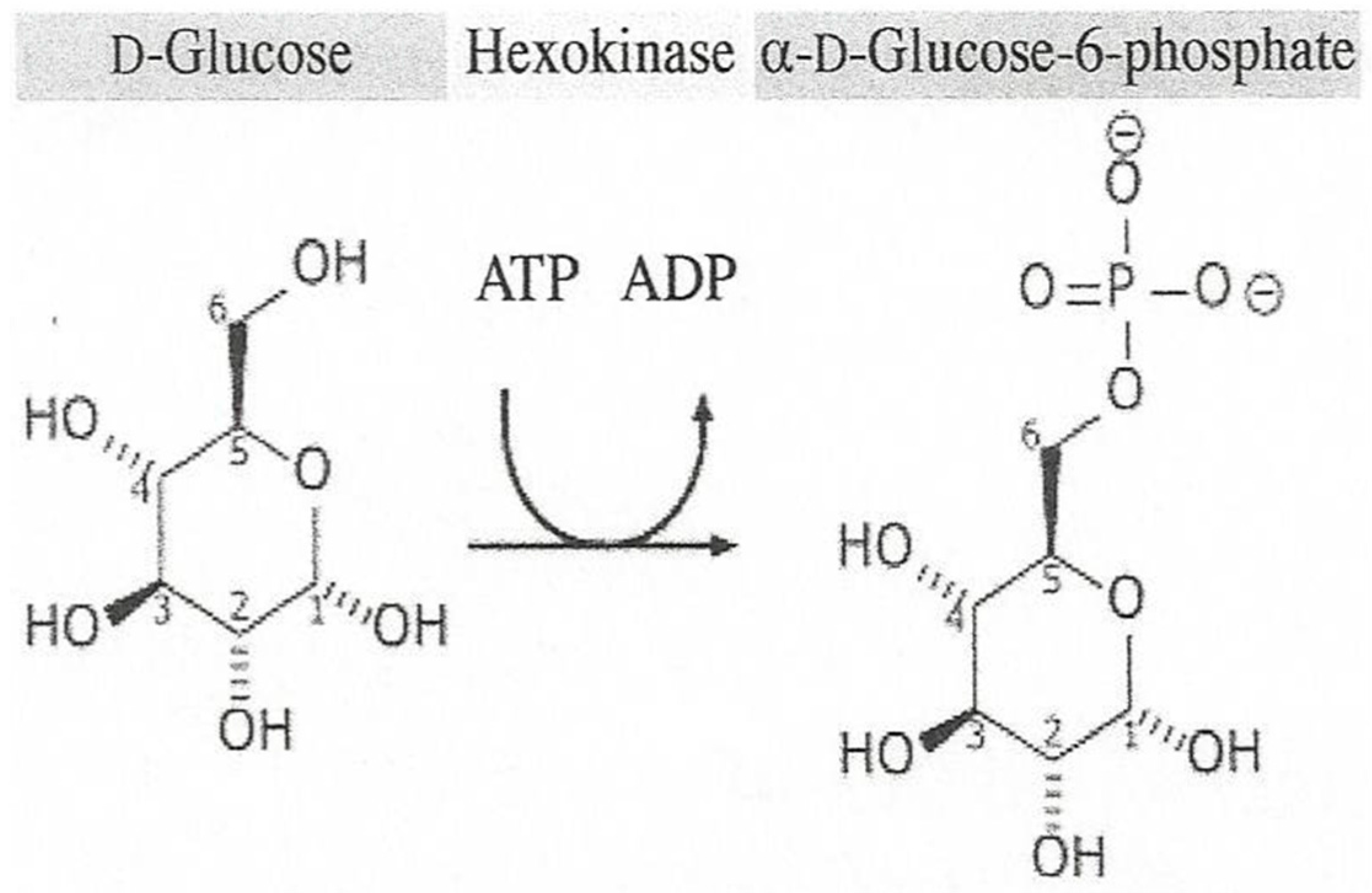
4. Enzymes
5. Discussion and Conclusions
Acknowledgments
Conflicts of Interest
References
- Kittel, C.; Knight, W.D.; Ruderman, M.A. Mechanics, Berkeley Physics Course, Volume 1; McGraw-Hill: New York, NY, USA, 1966; Chapter 7. [Google Scholar]
- Larsson, R. A Model of Selective Energy Transfer at the Active Site of the Catalyst. J. Mol. Catal. 1989, 55, 70–83. [Google Scholar] [CrossRef]
- Larsson, R. Concluding remarks on the theory of selective energy transfer and exemplification on a zeolite kinetics study. Monatshefte Chem. 2013, 144, 21–24. [Google Scholar] [CrossRef]
- Bond, G.C.; Keane, M.A.; Kral, H.; Lercher, J.A. Compensation Phenomena in Heterogeneous Catalysis: General Principles and a Possible Explanation. Catal. Rev. 2000, 42, 323–383. [Google Scholar] [CrossRef]
- Larsson, R. Catalysis as a Resonance Effect. I. The Hydrogenation of Olefines. Chem. Scr. 1977, 12, 78–86. [Google Scholar]
- Larsson, R. A Comparison between the Hydrogenation of Ethene and Propene from a Hypothesis on Vibrational Resonance in Catalytic Reactions. J. Catal. 1984, 88, 509–512. [Google Scholar] [CrossRef]
- Jonson, B.; Larsson, R.; Rebenstorf, B. Toluene Oxidation over Metal Oxides in Relation to Oxide Vibrations. J. Catal. 1986, 102, 29–36. [Google Scholar] [CrossRef]
- Larsson, R. Zeolite Catalysis and Molecular Vibrations. Catal. Today 1988, 3, 387–394. [Google Scholar] [CrossRef]
- Larsson, R. On the Catalytic Decomposition of Nitrous Oxide over Metal Oxides. Catal. Today 1989, 4, 235–251. [Google Scholar] [CrossRef]
- Larsson, R.; Mascetti, J. On the Isokinetic Effect for Reactions of Carbon Dioxide with Metal Surfaces. Catal. Lett. 1997, 48, 185–189. [Google Scholar] [CrossRef]
- Larsson, R. The Compensation Effect for some Hydrodesulfurization Catalysts and a Simple Model for Catalysis. J. Catal. 1987, 107, 568–570. [Google Scholar] [CrossRef]
- Larsson, R.; Jamroz, M.H.; Borowiak, M.A. On the Catalytic Decomposition of Formic Acid. I. The Activation Energies for Oxide Catalysts. J. Mol. Catal. A Chem. 1998, 129, 41–51. [Google Scholar] [CrossRef]
- Larsson, R.; Lieske, H. On the isokinetic effect in the Rochow reaction. ACH-Models Chem. 2000, 137, 691–700. [Google Scholar]
- Bratlie, K.M.; Li, Y.; Larsson, R.; Somorjai, G.A. Compensation Effect of Benzene Hydrogenation on Pt(111) and Pt(100) Analyzed by the Selective Energy Transfer Model. Catal. Lett. 2008, 121, 173–178. [Google Scholar] [CrossRef]
- Keane, M.A.; Larsson, R. Application of the Selective Energy Transfer Model to Account for an Isokinetic Response in the Gas Phase Reductive Cleavage of Hydroxyl, Carbonyl and Carboxyl Groups from Benzene over Nickel/Silica. Catal. Lett. 2012, 129, 93–103. [Google Scholar] [CrossRef]
- Keane, M.A.; Larsson, R. Isokinetic behavior in the gas phase hydrogenation of nitroarenes over Au/TiO2: Application of the selective energy transfer model. React. Kinet. Mech. Catal. 2012, 106, 267–288. [Google Scholar] [CrossRef]
- Larsson, R. Propane Dehydrogenation Catalyzed by ZSM-5 Zeolites. A Mechanistic Study Based on the Selective EnergyTransfer (SET) Theory. Molecules 2015, 20, 2529–2535. [Google Scholar] [CrossRef] [PubMed]
- Keane, M.A.; Larsson, R. Isokinetic Behaviour in Gas Phase Catalytic Hydrodechlorination of Chlorobenzene over supported Nickel. J. Mol. Catal. A Chem. 2007, 268, 87–94. [Google Scholar] [CrossRef]
- Keane, M.A.; Larsson, R. Isokinetic Behaviour in Gas Phase Catalytic Haloarene Hydrodehalogenation Reactions: Mechanistic Considerations. J. Mol. Catal. A Chem. 2006, 249, 158–165. [Google Scholar] [CrossRef]
- Varsanyi, G. Assignments for Vibrational Spectra of Seven Hundred Benzene Derivatives; Adam Hilger: London, UK, 1974. [Google Scholar]
- Campbell, M.L. Temperature dependent rate constants for the reactions of gas phase lanthanides with CO2. Phys. Chem. Chem. Phys. 1999, 1, 3731–3735. [Google Scholar] [CrossRef]
- Andrews, L.; Zhou, M.; Liang, B.; Li, J.; Bursten, E. Reactions of Laser-Ablated U and Th with CO2: Neon Matrix Infrared Spectra and Density Functional Calculations of OUCO, OThCO, and Other Products. J. Am. Chem. Soc. 2000, 122, 11440–11449. [Google Scholar] [CrossRef]
- Chen, M.; Wang, X.; Zhang, L.; Qin, Q. IR Spectroscopic and DFT Studies on the Reactions of Laser-Ablated Nb Atoms with Carbon Dioxide. J. Phys. Chem. A 2000, 104, 7010–7015. [Google Scholar] [CrossRef]
- Larsson, R.; Mascetti, J. The Gas Phase Reaction between CO2 and Lanthanide Atoms. A Test of a Model, for the Isokinetic Effect. React. Kinet. Catal. Lett. 2005, 85, 107–113. [Google Scholar] [CrossRef]
- Adel, A.; Dennison, D.M. The Infrared Spectrum of Carbon Dioxide. Part I. Phys. Rev. 1933, 41, 717–723. [Google Scholar] [CrossRef]
- Herzberg, G. Vibrational Infrared and Raman Spectra. 3. Individual Molecules. In Infrared and Raman Spectra of Polyatomic Molecules; D. Van Nostrand Company: New York, NY, USA, 1945; Chapter III; pp. 271–369. [Google Scholar]
- Glucose 6-Phosphate. Available online: https://en.wikipedia.org/wiki/Glucose_6-phosphate (accessed on 8 February 2018).
- Frost, R.L.; Xi, Y.; Scholz, R.; Lopez, A.; Belatti, F.M. Vibrational spectroscopic characterization of the phosphate mineral hureaulite—(Mn, Fe)5(PO4)2(HPO4)2·4(H2O). Vib. Spectrosc. 2013, 66, 69–75. [Google Scholar] [CrossRef]
- Kovacs, A.; Ivanov, A.Y. Vibrational Analysis of d-Glucose Trapped in Ar Matrix. J. Phys. Chem. B 2009, 113, 2151–2159. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, M.; Alaam, M.; El-Haes, H.; Jalbout, A.F.; de Leon, A. Analysis of the structure and vibrational spectra of glucose and fructose. ECLETICA 2006, 31, 15–21. [Google Scholar] [CrossRef]
- Vasko, P.D.; Blackwell, J.; Koenig, J.L. Infrared and Raman Spectroscopy of Carbohydratees. Part II: Normal Coordinate Analysis of d-Glucose. Carbohydr. Res. 1972, 23, 407–416. [Google Scholar] [CrossRef]
- Meejoo, S.; Maneeprakorn, W.; Winotai, P. Phase and thermal stability of nanocrystalline hydroxyapatite prepared via microwave heating. Thermochim. Acta 2006, 447, 115–120. [Google Scholar] [CrossRef]
| Denotation | Calc. | Observed | Reference |
|---|---|---|---|
| V1 V2 V3 | |||
| 0 3 0 | 1933.2 | 1933.5 | [25] |
| 0 3 0 | 1931.0 | 1943.5 | [26] |
| 0 1 0 | 667.5 | [26] |
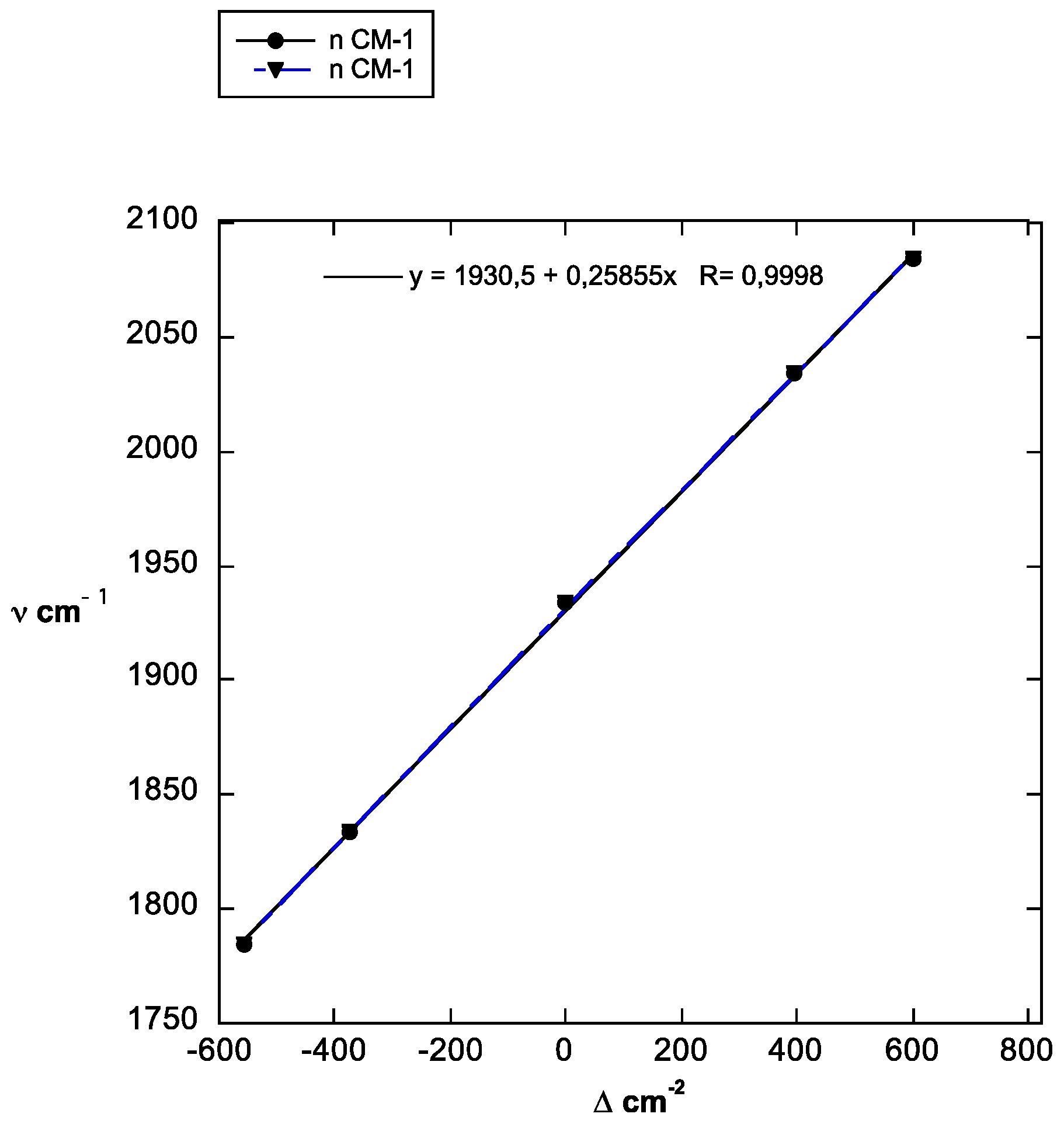
| ν cm−1 | 1784 | 1834 | 1934 | 2034 | 2084 |
| Δ cm−2 | −557 | −376 | 0 | 397 | 603 |
| Assignment | Glucose | Phosphate | References |
|---|---|---|---|
| PO43−/HPO42− asym str. | 1044 | [28] | |
| C-O-H | 1047 | [29] | |
| νCO + νCC | 1050 | [30] | |
| CO(79%) + CC(19%) PED | 1047 | [31] | |
| PO43− asym str. | 1046 | [32] |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Larsson, R. A SET Approach to the Interplay of Catalysts and Reactants. Catalysts 2018, 8, 97. https://doi.org/10.3390/catal8030097
Larsson R. A SET Approach to the Interplay of Catalysts and Reactants. Catalysts. 2018; 8(3):97. https://doi.org/10.3390/catal8030097
Chicago/Turabian StyleLarsson, Ragnar. 2018. "A SET Approach to the Interplay of Catalysts and Reactants" Catalysts 8, no. 3: 97. https://doi.org/10.3390/catal8030097
APA StyleLarsson, R. (2018). A SET Approach to the Interplay of Catalysts and Reactants. Catalysts, 8(3), 97. https://doi.org/10.3390/catal8030097




