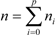1. Introduction
Atoms, atomic quantum clusters (AQCls), nanoparticles (NP) and bulk matter are the actual sequence of matter classification in terms of their size-dependent physical properties. Small atomic quantum clusters are formed by two up to five hundred atoms, with stable compositions that fill in the gap between the atomic range and the nanoscale. Their size, comparable to fundamental quantities, such as the Fermi wavelength, places them in the scale range where quantum confinement effects govern the material properties.
Catalysis in clusters is the result of an intricate combination among a set of non-independent parameters: the clusters’ size and shape, interaction with the supporting material, oxidation state and quantum size effects [
1].
The catalytic behavior of subnanometric clusters has been rarely studied, due to the scarcity of well-controlled synthetic routes and limitations in the characterization techniques; although, recent advancements in these two fields are making it possible to study the catalytic activity and the factors affecting it. In the last few years, the developments in the synthesis of nanomaterials have been taken advantage of by means of microemulsion procedures to extend it for the preparation of metallic quantum clusters. In addition, in recent years, clusters have been reported as surprisingly good and selective catalysts in different reactions.
In this review, we will report different examples of catalytic activity (heterogeneous catalysis, photocatalysis and electrocatalysis) by subnanometric clusters in terms of their small size, geometric structure, bandgap value and relative position of the HOMO-LUMO bands.
2. Noble Metal Clusters, Quantum Properties and Band Gaps
One of the main characteristics of metallic systems that makes them leaders in technological applications is their mobile electron cloud, which easily couples to electromagnetic excitations and gives rise to, among other phenomena, their good electronic conductivity performance, in the bulk scale, or to a strong resonant effect, known as the Mie surface plasmon resonance, in metallic nanoparticles.
Moreover, from the theoretical point of view, metallic systems are an interesting subject of study due to the fact that their description, in terms of a quasi-free valence electron gas, holds valid along many length scales and allows using them as a generic test laboratory for finite fermionic systems [
2].
In this regard, metal clusters, with their technologically interesting molecular-like optical properties and their paradigmatic insulator-to-metal transition, are placed in a leading theoretical and technological position of the clusters’ field.
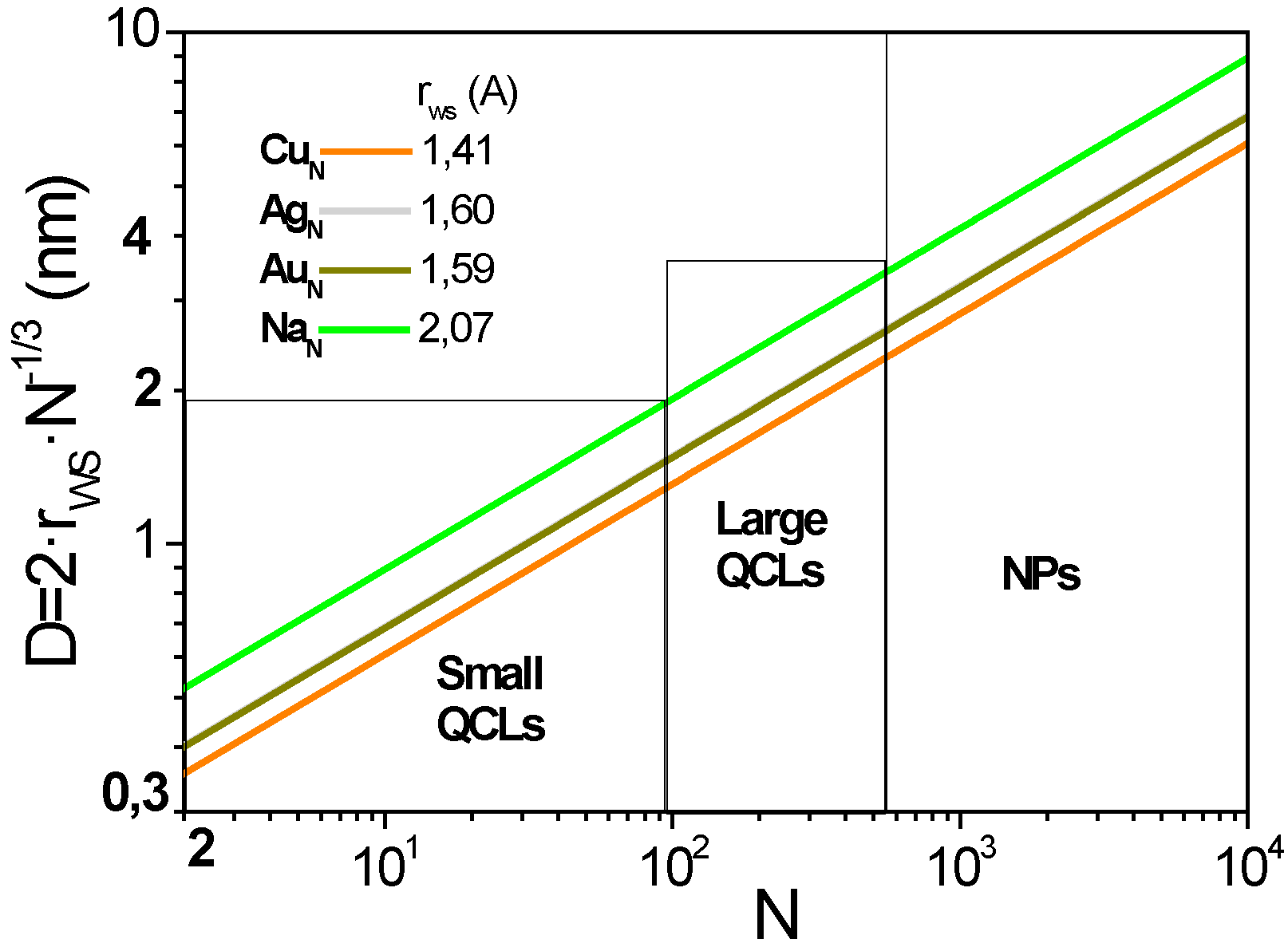
Atomic clusters are generally defined as those particles composed of two up to approximately 500 atoms, with sizes that range between 0.3 and 4 nm. The size is usually estimated in terms of the number of atoms in the cluster, by the Wigner–Seitz approach [
3],
, where
rWS stands as the Wigner–Seitz radius of each element. Based on this, a classification into small and large QCLs, as sketched in
Figure 1, is done attending to the physical consequences of size reduction.
The effects of reducing the size from 100 to 4 (nm) are already well known in nanoparticles, where many of their properties show a scaling law behavior that arises from the large fraction surface atoms that dominate their physical response (in nanoparticles with a diameter around 10 nm, 30% of atoms belong to the surface [
4]).
NPs maintain some of the bulk physical properties: an almost continuous density of states around the Fermi level with a negligible energy gap that preserves metallicity; the same crystalline structure as the bulk matter; and the added unique new properties that scale with size, like the dominance of the surface anisotropy with size reduction [
5], the appearance of the superparamagnetic behavior below the single domain size or the surface plasmon resonance [
6].
Figure 1.
Classification scheme based on the size/number of atoms. QCL, quantum cluster.
Figure 1.
Classification scheme based on the size/number of atoms. QCL, quantum cluster.
Further reducing the size, below 4 (nm), produces quantum confinement effects in the AQCLs, whose main signature is the discretization of energy levels and, consequently, a dramatic change in their physical properties. For small metallic AQCLs, with sizes below 1–2 nm, comparable to the Fermi wavelength, λF < 1 nm, quantum confinement is severe and shows its most paradigmatic effect: the loss of metallicity.
For large AQCLs, with sizes 2–4 nm, size confinement is less stringent, and the energy gap between the different states tends to reduce, up to a critical size, where the transition to zero energy gaps happens and metal clusters recover bulk matter properties, such as metallicity or surface plasmon resonance [
7].
2.1. Shells and Jellium Spherical Symmetric Potentials
The early development of the clusters’ field dates back to the 1980s, when Knight
et al. [
8] first observed, in the mass spectra pattern of Na clusters, intense peaks corresponding to clusters of enhanced stability, which contained a specific number of atoms,
N = {2,8,20,40,58,92}, the so-called “magic numbers”. Initially, and after measuring similar mass spectra of other alkali metals, the stability enhancement of the “magic numbers” clusters was attributed to some electronic and geometrical effects.
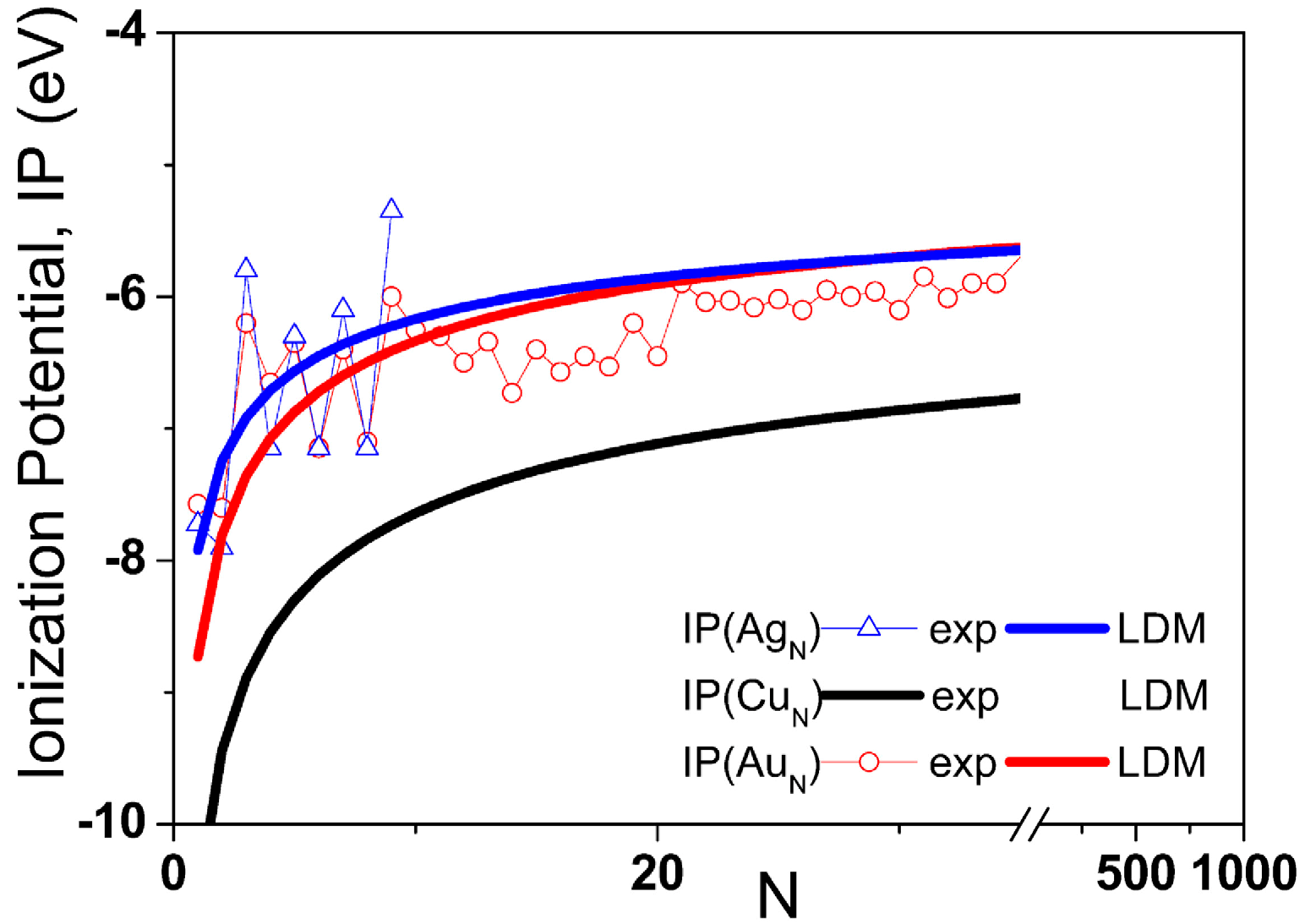
Figure 2.
Compilation of Experimental values of the ionization potential of Cu
N [
9], Ag
N and Au
N [
10] atomic quantum clusters (AQCLs) and the fitting to the liquid drop model (LDM).
Figure 2.
Compilation of Experimental values of the ionization potential of Cu
N [
9], Ag
N and Au
N [
10] atomic quantum clusters (AQCLs) and the fitting to the liquid drop model (LDM).
However, later on, complementary measurements on electronic affinity or ionization potential (IP) (see
Figure 2) revealed the same magic number pattern and allowed confirmation that only the electronic configuration was responsible for the clusters’ properties.
Therefore, inspired by the magic numbers of atomic nuclei shell models [
11], Eckardt [
12,
13] and Knight
et al. [
8,
14] proposed a physical model, known as the jellium model, to describe the electronic shell structure of free AQCLs. This low level approach describes the valence electrons of the AQCLs as a free gas with
–we charge, moving in a weakly attractive mean field created by the spherically symmetric potential of the N ionic cores that are positively charged,
+we.
The simplest approach, known as the jellium model, is valid to describe clusters from 20 to about a thousand atoms [
15] and assumes that each electron is almost delocalized and weakly perturbed by an attractive 3D harmonic potential created by the core ions:
This low level approach, although being less accurate, has the advantage of being analytically solvable. The solution to this spherically symmetric problem is a set of discrete and degenerate electronic states with eigenvalues:
where
nr is the radial quantum number,
l the angular momentum and
ℏω
0 the fundamental oscillation. Applying the virial theorem, a size-dependent relationship for the fundamental oscillation is obtained,
[
16], which allows quantifying the energy levels as:
By filling up states of increasing energy (Aufbau rule), this model allows obtaining the main shell structure observed in AQCLs as a function of size and predicts a set of magic numbers that show a good concordance to those observed experimentally. In
Table 1, the degenerate single-electron states and the magic numbers obtained for the 3D harmonic oscillator are shown.
Table 1.
Magic numbers, N, obtained following the rule of increasing energy (Aufbau rule), correspond to the shell closures and the ordering of degenerate states obtained with the 3D harmonic potential for metal clusters.
Table 1.
Magic numbers, N, obtained following the rule of increasing energy (Aufbau rule), correspond to the shell closures and the ordering of degenerate states obtained with the 3D harmonic potential for metal clusters.
| Degenerate states | 1S2 | 1P6 | 1D10 2S2 | 1F14 2P6 | 1G18 2D10 3S2 |
|---|
| Occupation number np | 2 | 6 | 12 | 20 | 30 |
Magic numbers ![Catalysts 04 00356 i001]() | 2 | 8 | 20 | 40 | 70 |
Since noble metal atoms, with their delocalized valence electron (
n)
s1, are good candidates to be described in terms of the jellium model [
15], we have chosen Cu
N AQCLs to illustrate the performance of this approach, by quantifying the HOMO (highest occupied molecular orbital) and LUMO (lowest unoccupied molecular orbital) levels, applying Equation (3), where
EF(Cu) = 7 (eV). For comparison purposes, the numerical data of HOMO and LUMO are plotted in
Figure 3, together with the experimental data of ionization potential (IP) and electron affinity (EA) [
17,
18], since both sets of magnitudes differ only in a relaxation energy produced by the respective removal or addition of an electron in the cluster.
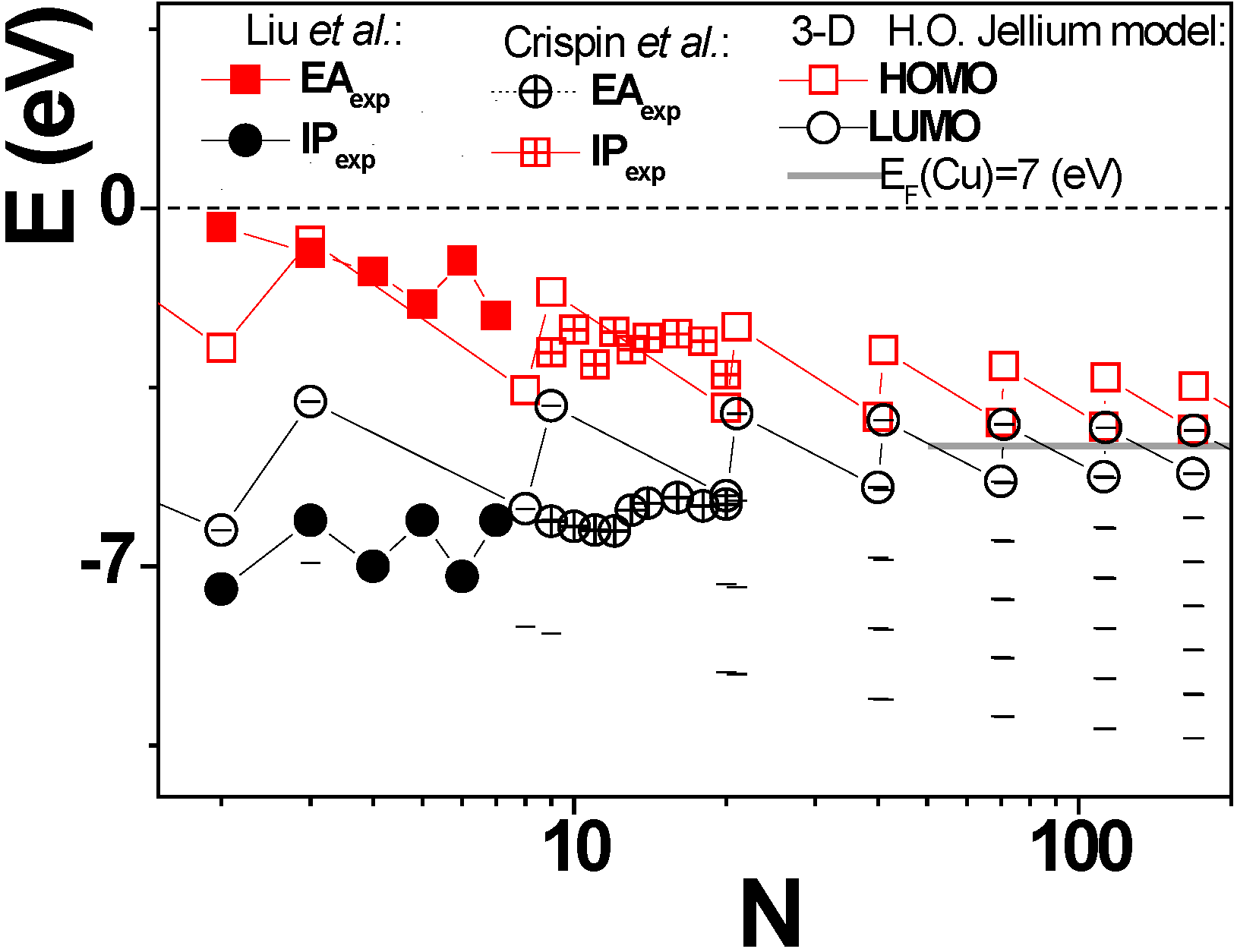
Figure 3.
Shell structure obtained for Cu
N AQCLs under the approach of the 3D harmonic oscillator potential. The HOMO and LUMO show enhanced stability for certain N, which corresponds to magic numbers (shell closures). Experimental data of ionization potential (IP) and electron affinity (EA)EA are from Crispin
et al. [
17] and Liu
et al. [
18].
Figure 3.
Shell structure obtained for Cu
N AQCLs under the approach of the 3D harmonic oscillator potential. The HOMO and LUMO show enhanced stability for certain N, which corresponds to magic numbers (shell closures). Experimental data of ionization potential (IP) and electron affinity (EA)EA are from Crispin
et al. [
17] and Liu
et al. [
18].
Besides some odd-even effects produced by spin-spin interaction, which the jellium model does not account for, the concordance between the theoretical and experimental data sets is acceptable, even though the size of the analyzed clusters is below the range of validity of jellium approaches (
N = 20). Moreover, the expected shell structure reproduces the magic numbers found experimentally for noble metal clusters
N = (2, 8, 20, 34, 40, 58, 92) [
19] and corresponds, as can be seen, to shell closures where energy attains a minimum and clusters show enhanced stability.
Further refinements of jellium approaches have been developed [
15] that take into account the non-spherical features of the attractive potential, like the ellipsoidal or Nilsson’s modified oscillator jellium models that split up the spherical symmetry degeneracy and produce sets of magic numbers closer to the experimental results; although, the simple spherical jellium approach remains a predictive model of the main features on metal AQCLs.
2.2. Extensions to Ligand Protected Clusters
Together with the development of the jellium model for free noble metal clusters, an intense effort is being devoted to obtain a predictive model for ligand protected clusters.
Walter
et al. [
20] have given a unified view of the principles that stabilize a set of structurally well-characterized gold compounds (Au
102(SR)
44; (Au
39(PR
3)
14X
6)
−; Au
11(PR
3)
7X
3; Au
13(PR
3)
10X
23+) (ligands: thiolate (SR), phosphine and halide (PR
3,
X)) under DFT calculations. The action of the ligands is to withdraw electrons from the metal core (localize them into covalent bonds), X, or get weakly attached to the surface (by dative bonds) L; therefore, in order to obtain a stable ligand-protected cluster (Ls∙A
NX
M)
z, the total charge account has to provide a magic number of shell closing n
−:
where
N stands as the number of core metal atoms (A),
vA the atomic valence,
M the electron withdrawing of ligand X (considering one electron per ligand X) and,
z, the overall charge of the compound. Experimental and computed HOMO-LUMO gaps compiled from this study [
20] are shown in
Table 2 compared to the values predicted by the jellium model, showing a good agreement, suggesting that shell closures play a major role in the properties of ligand protected clusters.
Table 2.
Compilation of data from [
20] combining experimental data for gas-phase Au AQCL anions obtained by photoelectron spectroscopy and DFT computations for a set of ligand protected Au AQCLs, compared to the jellium model predictions (for AuN AQCLs with
N > 25, an anharmonicity correction of −0.4 (eV) is applied).
Table 2.
Compilation of data from [20] combining experimental data for gas-phase Au AQCL anions obtained by photoelectron spectroscopy and DFT computations for a set of ligand protected Au AQCLs, compared to the jellium model predictions (for AuN AQCLs with N > 25, an anharmonicity correction of −0.4 (eV) is applied).
| Shell closing n− | Experimental | DFT computations | Jellium model |
|---|
| Cluster | Gap (eV) | Cluster compound | Gap (eV) | Eg = 5.32/N1/3 (eV) |
|---|
| 8 (1S21P6) | | | Au11(PH3)7(SMe)3 | 1.5 | 2.4 |
| 8 | | | Au11(PH3)7Cl3 | 2.1 | 2.4 |
| 8 | | | Au13(PH3)10Cl23+ | 1.8 | 2.3 |
| 8 | | | Au25 (SMe)18− | 1.2 | 1.3a |
| 34 (8 + 1D102S21F14) | Au34− | 10 | Au39 Cl6 (PH3)14− | 0.8 | 1.0a |
| 58 (34 + 2P61G18 ) | Au58− | 0.6 | Au102(p-MBA)44 | 0.5 | 0.6a |
| 58 | | | Au102(SMe)44 | 0.5 | 0.6a |
2.4. Structure: Two-Dimensional and Three-Dimensional Clusters
In noble metal clusters, the energy minimizes with respect to the global geometric structure to obtain the most desirable electronic structure, producing, therefore, a complex interplay between electronic and geometric structure [
27]. The resulting ground states for noble metal clusters present a variability of shapes comprising planar, cage-like and tube-like structures; a compilation of geometries reported in [
28] is presented in
Table 3.
Table 3.
Compilation of theoretical results [
28] obtained for isomer geometries in free Au AQCLs.
Table 3.
Compilation of theoretical results [28] obtained for isomer geometries in free Au AQCLs.
| | Geometric structure |
|---|
| Cationic AuN AQCLs | N < 7 2D fragments of closed-packed hexagonal | 8 ≤ N ≤ 13 2D and 3D relaxed fcc fragments | N > 13 3D fragments of fcc |
| Anionic AuN AQCLs | N < 12 2D: triangles and closed-packed flakes | N = 12 2D to 3D cross-over transition flakes | 13 ≤ N ≤ 24 3D tetrahedral cages and tube-like structures |
3. Microemulsions: Controlled Synthetic Routes for Clusters
Microemulsions are thermodynamically stable colloidal dispersions of two immiscible liquids (typically water and oil) that coexist in one phase due to the presence of a monolayer of surfactant molecules with balanced hydrophilic-lipophilic properties [
29]. These colloidal systems are optically isotropic, with a very small characteristic size (2–50 nm).
Microemulsion is a widely used technique for preparing metallic nanoparticles, because it allows one to precisely control the droplet size, and as a consequence, this droplet can act as a nanoreactor for preparing metallic nanoparticles [
30,
31]. For this purpose, the two more interesting systems are water-in-oil microemulsions (water-swollen inverse micelles dispersed in oil) and oil-in-water microemulsions (oil-swollen direct micelles dispersed in water). There are several reviews in the literature describing the preparation of nanomaterials and, in particular, metallic nanoparticles in water-in-oil microemulsions [
32,
33], water-in-supercritical fluid microemulsions [
33] and oil-in-water microemulsions [
34]; however, it is very difficult to find publications about the synthesis of metallic clusters in microemulsions, due to the difficulties related to their appropriate characterization.
The droplets are kinetically unstable, and a process of dynamic exchange of material between the polar cores is known to occur in water-in-oil microemulsions [
35]. Therefore, taking advantage of this exchange of reactants between droplets, the most common way to prepare metallic nanoparticles is by mixing two different microemulsions, one with the metallic salt and another with the reducing agent [
30].
The size of the droplet is a key parameter for limiting the size and shape of the formed metallic nanoparticles. In this way, narrow size distributions can be achieved. For the case of water-in-oil microemulsion (the most widely used for preparing metallic nanoparticles), the main factor that affects the droplet size is the water-surfactant molar ratio (
w = [H
2O]/[surfactant]). The smaller the parameter
w is, the smaller the droplet size is, and as a consequence, smaller nanoparticles can be prepared. This trend was deeply studied for copper nanoparticles synthesized in microemulsions with isooctane or cyclohexane as the oil phase and a mixture of sodium bis(2-ethylhexyl) sulfosuccinateand (AOT) and copper AOT as surfactants [
36,
37,
38].
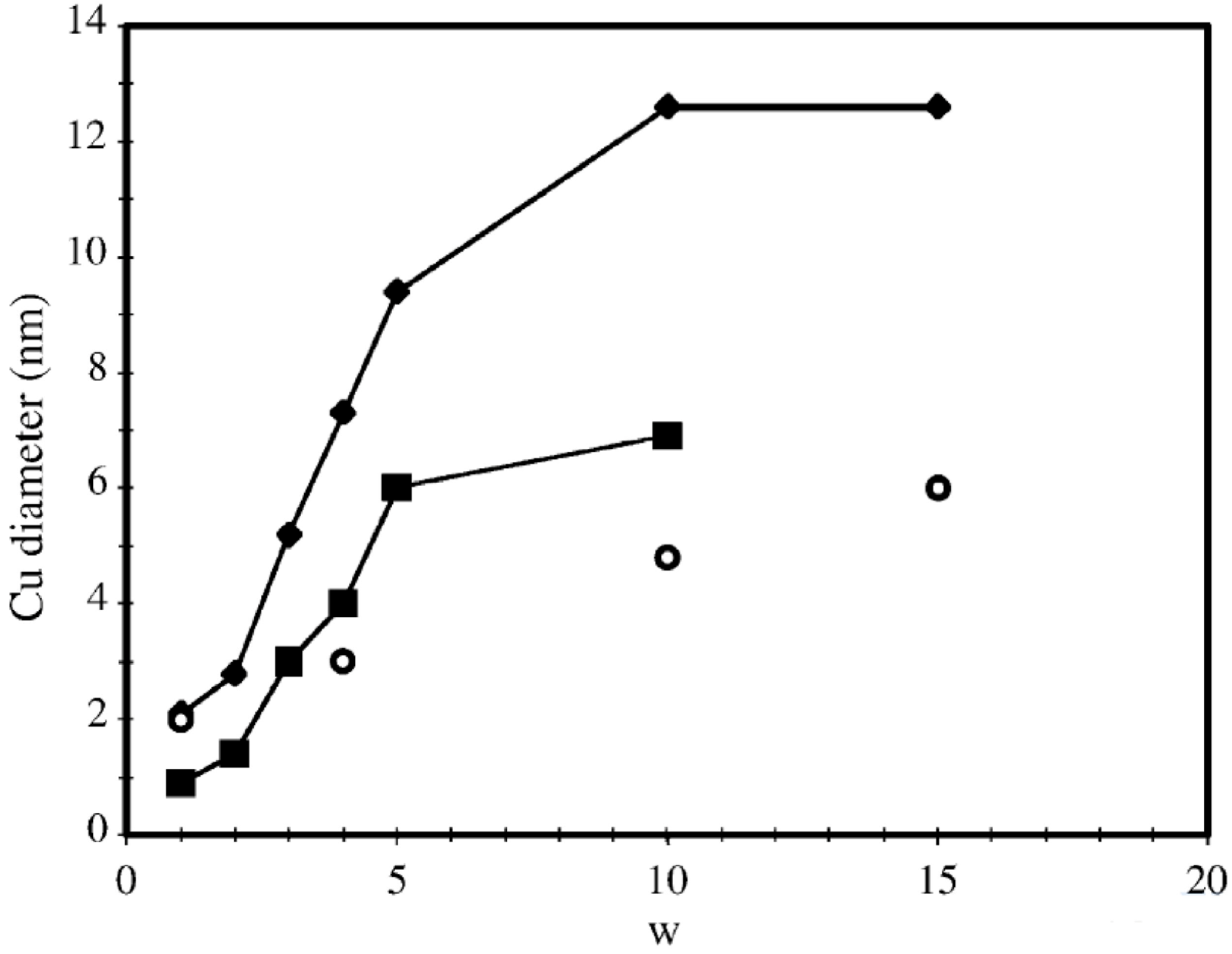
Figure 7 shows how the mean size diameter obtained by TEM decreases as the water-to-surfactant ratio (
w) decreases, going down to diameters in the range 1–2 nm.
However, for a fixed w value, the particle size is also affected by other parameters (keeping all others constant) [
38]:
- (1)
The concentration of metallic cations in the aqueous solution;
- (2)
The volume fraction of the dispersed polar phase, Φ (i.e., aqueous solution and surfactant vs. oil phase); and
- (3)
The concentration ratio between the reducing agent and metal cations, R.
The salt concentration is a parameter that largely affects the droplet size and the reverse micelle stability. In particular, by increasing the salt additions, the droplet size decreases until a critical concentration is reached. This critical concentration is start of the system destabilization [
39].
Figure 7.
Variation of the mean diameter of copper nanocrystals synthesized in mixed AOT reverse micelles at various water contents w. The solvents are isooctane (♦) and cyclohexane (■). This variation can be compared with the diameter of AOT reserve micelles (○) with the w value (from reference [
38]).
Figure 7.
Variation of the mean diameter of copper nanocrystals synthesized in mixed AOT reverse micelles at various water contents w. The solvents are isooctane (♦) and cyclohexane (■). This variation can be compared with the diameter of AOT reserve micelles (○) with the w value (from reference [
38]).
Properly selecting the previous parameters (for example, by using very small metallic cation concentrations or using a reactant in large excess), it is possible to obtain metallic clusters of sizes below ~2 nm. These metallic clusters show different properties than the larger metallic nanoparticles (sizes larger than ~2–3 nm). One of these differences is the absence of a plasmonic band. Using an extended version of Mie’s theory for taking into account the surface contribution of small size particles, it is possible to describe the absorption spectra of the colloidal copper nanoparticles. For copper nanoparticles with a diameter below 4 nm, a strong broadening of the plasmonic resonance band (λ
max = 560–570 nm) was observed [
36].
The absence of a plasmonic band has also been observed for Ag clusters prepared in AOT microemulsions by the addition of a mild reducing agent (sodium hypophosphite) [
40,
41]. The reaction was studied at room temperature through a period of six weeks. After a few days, the color of the microemulsion changed, and new bands were observed in the absorption spectra, at 250–270 (nm) and 400–450 (nm), associated with the formation of small Ag clusters (with
n < 10) with planar geometries, whose presence was confirmed by STM [
41]. After approximately four weeks, the sample became colorless, and a new band appeared at 287 (nm) associated with the formation of tridimensional geometries.
In order to obtain small metallic nanoparticles, the most common procedure is to add the reducing agent in large stoichiometric excess with respect to the metallic salt; however, if the reducing agent is added in very small excess or with the stoichiometric amount, metallic clusters can be obtained. This was observed for the case of Pt clusters prepared in water/Brij30/
n-heptane water-in-oil microemulsions [
42]. In this case, the platinum salt (H
2PtCl
6) was reduced with hydrazine using just 25% excess. The formation of platinum clusters with planar geometry was confirmed by STM. After dropping 1 μL of microemulsion onto a Au(111) surface and copiously washing with acetone and water, Pt deposits were observed of around 4–6 (nm) in diameter (in good agreement with TEM results), but just with 1–2 atoms in height.
Another interesting approach for preparing metallic clusters of different sizes is to control the reduction of the metallic salt by adding small aliquots of the reducing agent. The parameter α is defined as the moles of reducing agent added up to attain the stoichiometric reduction of Cu(II) cations. This approach was followed during the synthesis of small copper nanoparticles in a water/SDS/isopentanol/cyclohexane water-in-oil microemulsion using sodium borohydride as the reducing agent [
43]. In this case, additional absorption bands were observed at low α values in the ultraviolet and visible regions related to the formation of different copper clusters (
Figure 8). By adding small aliquots of the reducing agent, we can follow the formation of different types of copper clusters and their transformation into larger ones (as can be concluded by the appearance or disappearance of absorption bands). This evidence of the formation of particularly stable clusters, which further grow into larger clusters during the formation of particles, questions the limits of application of the well-accepted nucleation and growth theory [
7,
44].
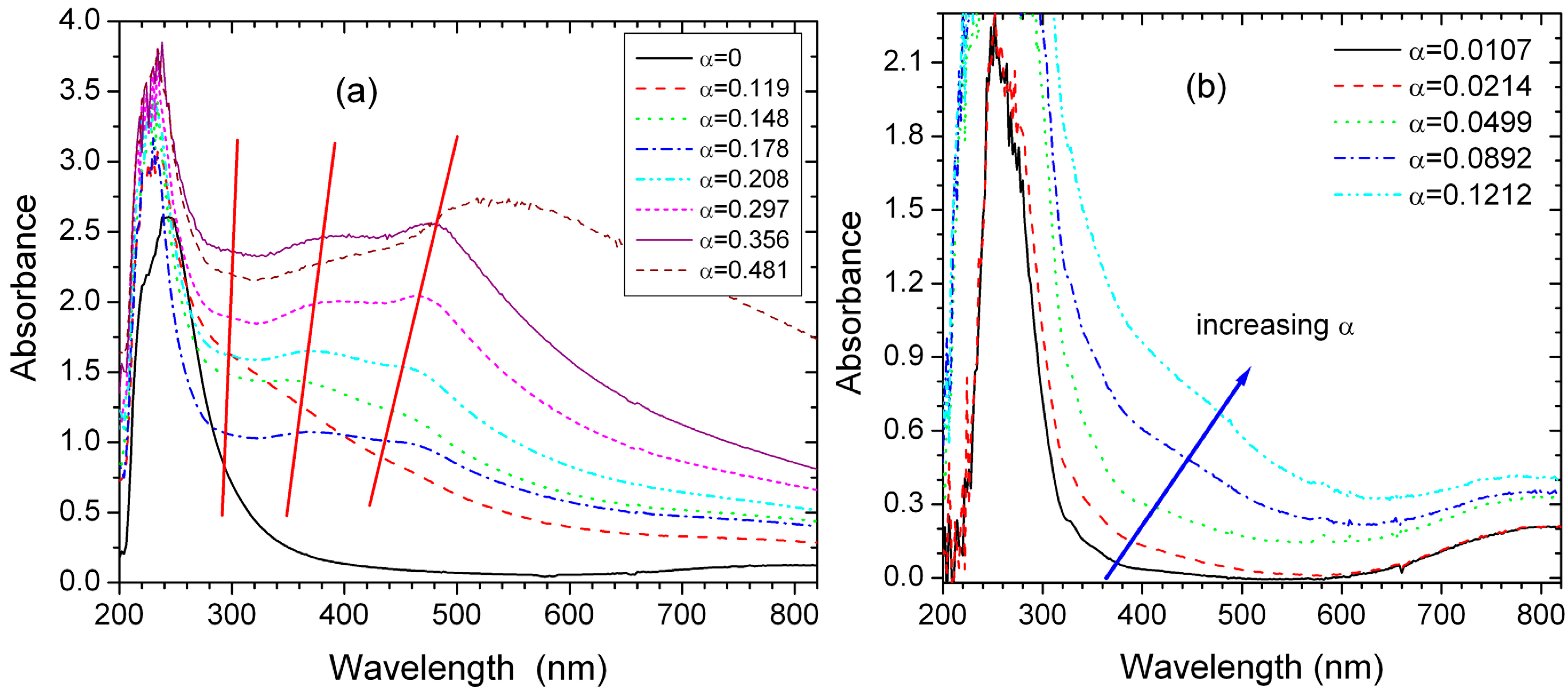
Figure 8.
(
a) UV-visible absorption spectra of the stoichiometric reduction of Cu(II) cations as a function of the relative amount, α, of reducing agent. The vertical lines show the evolution of the bands with the addition of the reducing agent. (
b) UV-visible absorption spectra at small α values, with α ≤ 0.20. (from reference [
43]).
Figure 8.
(
a) UV-visible absorption spectra of the stoichiometric reduction of Cu(II) cations as a function of the relative amount, α, of reducing agent. The vertical lines show the evolution of the bands with the addition of the reducing agent. (
b) UV-visible absorption spectra at small α values, with α ≤ 0.20. (from reference [
43]).
Gold clusters have also been prepared in a polyelectrolyte-modified reverse microemulsion, using poly(ethyleneimine) (PEI) as a cationic polyelectrolyte [
45]. PEI incorporated into a ternary water-in-oil microemulsion consisting of water, heptanol and a zwitterionic surfactant (3-(
N,
N-dimethyl-dodecylammonio)-propanesulfonate) acts as both a reducing and stabilizing agent and shows an additional template effect, favoring the formation of small gold clusters. The nanoparticle synthesis is performed by a simple mixing of two microemulsions, one containing the PEI and the other one containing the gold chloride precursor. They obtained polymer-coated Au nanoparticles with diameters larger than 5 (nm), but also an important fraction of smaller gold clusters (diameter < 2 (nm)) that show a UV absorption at 360 (nm) and a fluorescence peak at 450 (nm) (not present in classical gold nanoparticle dispersions).
4. Catalytic Applications of Clusters: Not Only Conventional Catalysis, Also Bioelectrocatalysis and Electrocatalysis
Although the catalytic behavior of subnanometric clusters has been rarely studied, probably due to the lack of adequate synthetic routes and limitations in the characterization techniques, there have been many different results reported that place them as being surprisingly good and selective catalysts in different reactions.
Different examples of catalytic activity by subnanometric clusters by means of their small size, geometric structure, bandgap value and relative position of the HOMO-LUMO bands will be shown.
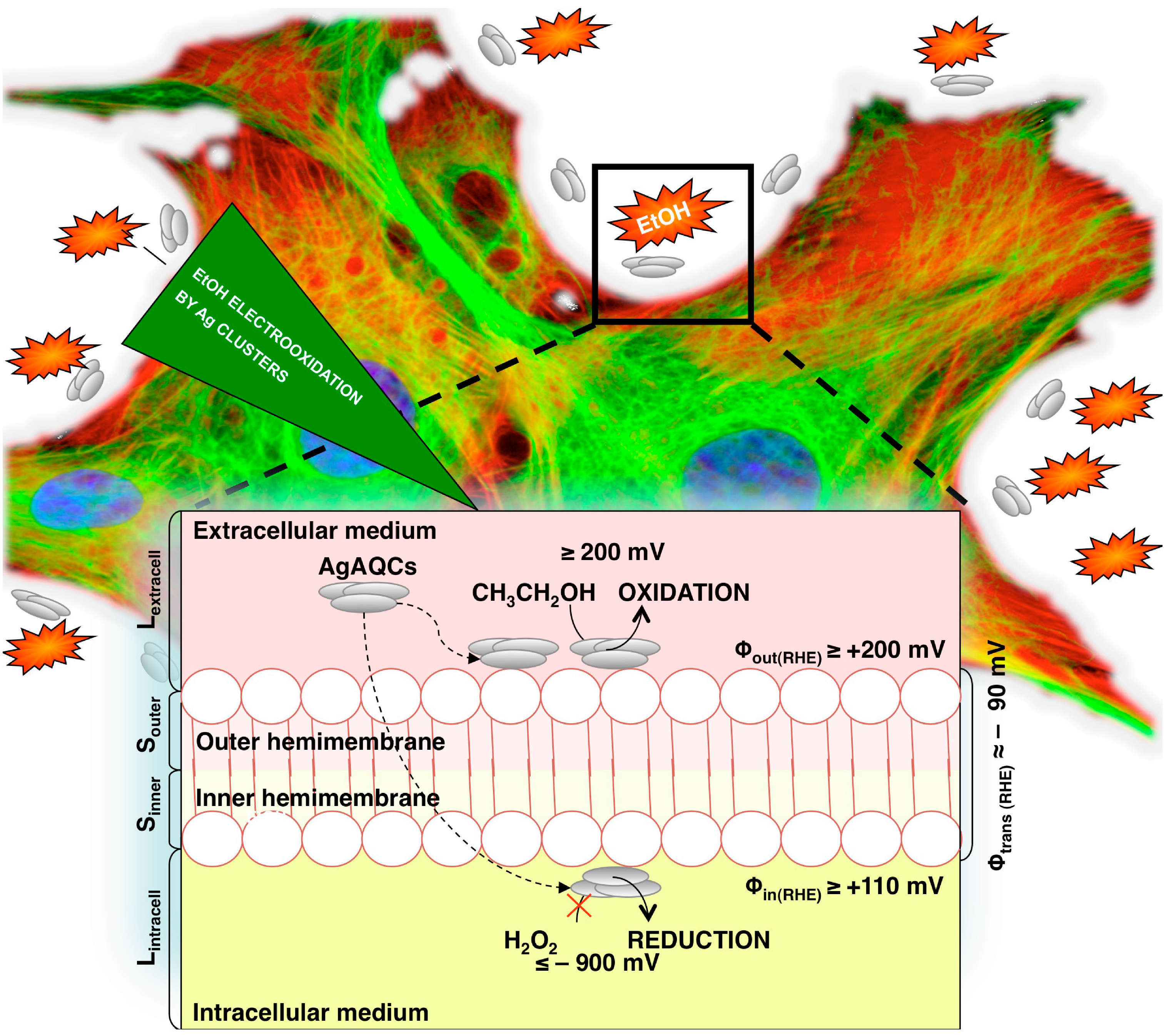
Figure 9.
The scheme of the cytoprotective action of AgACQ against Ethanol in mammalian cells. The image was obtained from [
25].
Figure 9.
The scheme of the cytoprotective action of AgACQ against Ethanol in mammalian cells. The image was obtained from [
25].
The first example, schematically represented in
Figure 9, consists of the prevention of alcohol toxicity for mammalian cells by the presence of AgAQC (Ag atomic quantum clusters) [
25]. This cytoprotection is possible by the combination of two important properties of AgAQC, absent in its bigger counterparts. On one side, these clusters are active for the electro-oxidation of alcohols at very low potentials (close to 0 V) at physiological pH, opposite of nanoparticles and bulk Ag. On the other hand, the very small size and the tendency of the clusters to go to the interfaces [
40] forces them to interact preferentially with the cellular membrane. The membrane potential is enough for these clusters to electro-oxidize the ethanol, methanol and butanol, allowing them to protect the cells against these toxic agents. This suggests that cells can be used as real power sources for diverse bioelectrocatalytical reactions and opens up new possibilities for the exploitation of subnanometric clusters as cytoprotective agents to prevent different pathologies.
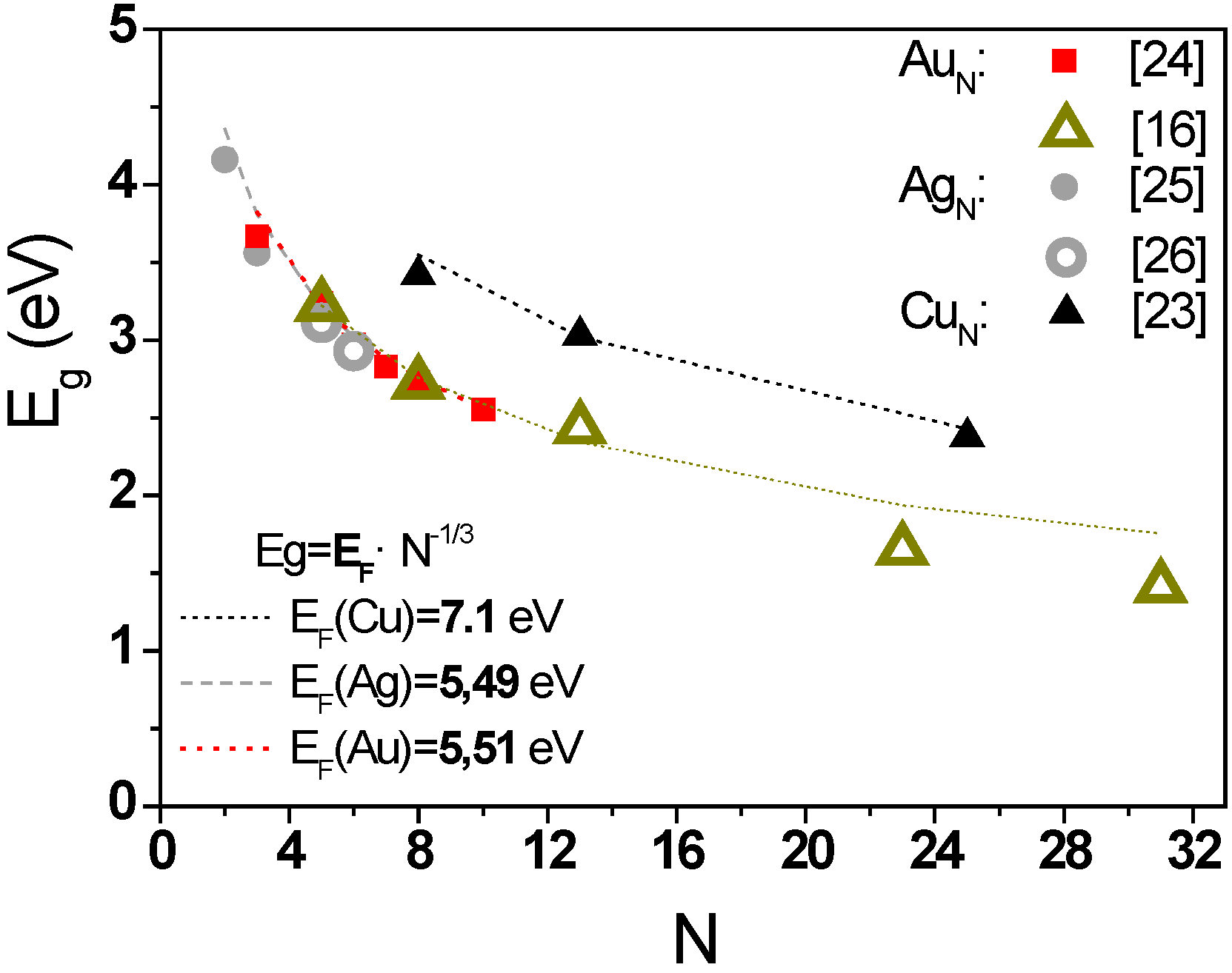
Although the small size of the clusters is an important parameter for application purposes, probably the most interesting and important characteristic for catalytically applications is the HOMO-LUMO gap. The size and position of this gap was shown to be crucial for the appearance of new and attractive catalytic activities, establishing a framework that could be a new paradigm in the understanding of catalysis.
The exceptional oxidation activity for the oxidation of thiophenol by small gold clusters (between five and 10 atoms) has been reported recently [
24]. This extraordinary activity compares to that of sulfhydryl oxidase enzymes and is not found either for gold nanoparticles (or bulk) or for single gold atoms or clusters with less than five atoms.
The origin of this activity can be explained by the HOMO-LUMO gap of the clusters and its position relative to an absolute energy scale.
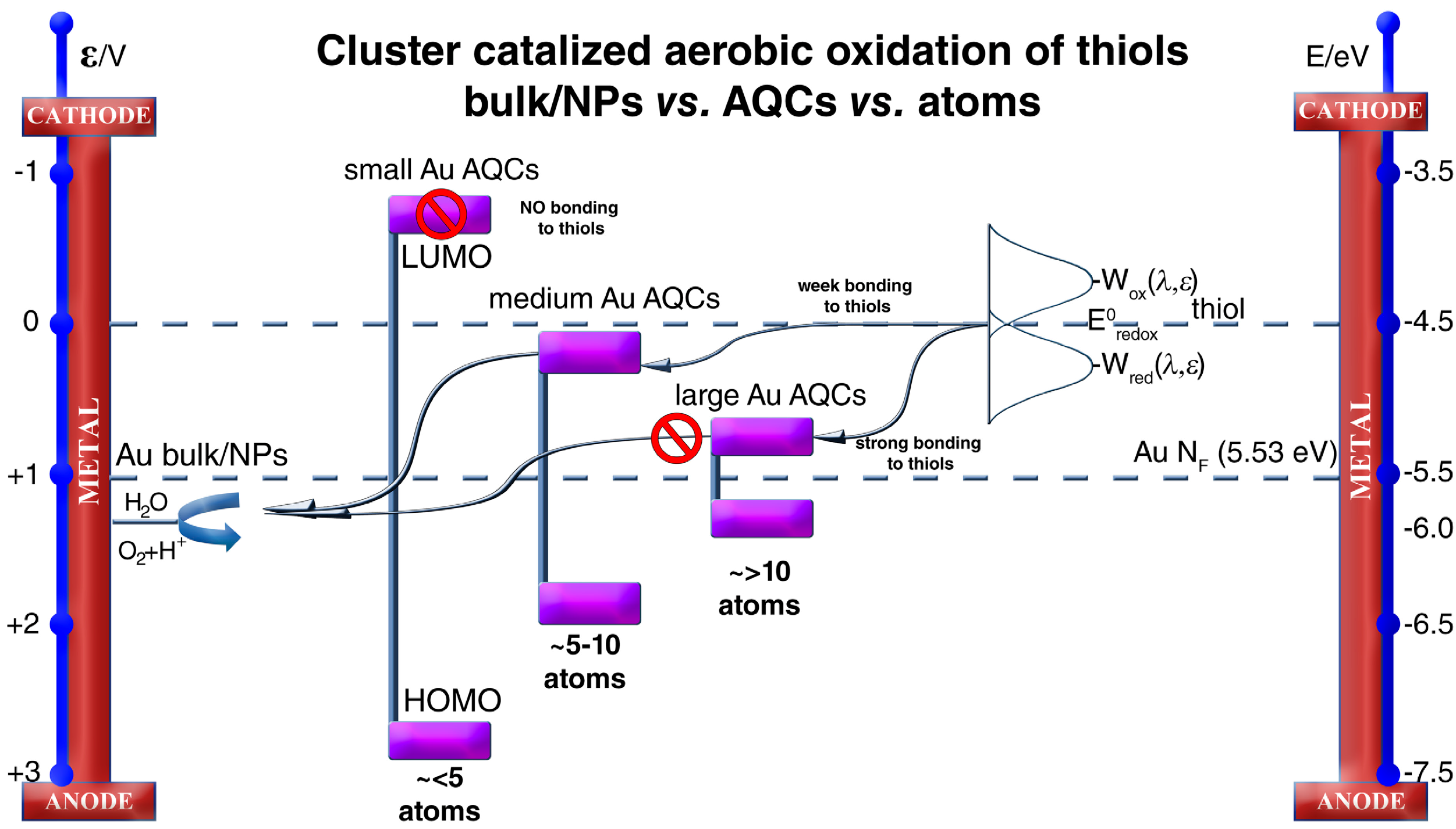
Figure 10 shows a schematic representation of the aerobic oxidation of thiols by bulk matter, nanoparticles and different cluster sizes.
Figure 10.
Schematic representation of possible aerobic oxidation routes of thiols by bulk, NPs and gold clusters. The electronic band structure of Au clusters of different sizes on an absolute scale is represented (right) and the potential scale relative to a standard hydrogen electrode (SHE). Wox (λ,ε) and Wred (λ,ε) stand for the oxidized and reduced states of thiols in solution, which can be represented by Gaussian distributions with a standard deviation of 2 λkBT, with their maxima located at E0redox ± λ, λ being the reorganization energy (≥0.3 eV) and E0redox the standard energy of the thiol redox couple.
Figure 10.
Schematic representation of possible aerobic oxidation routes of thiols by bulk, NPs and gold clusters. The electronic band structure of Au clusters of different sizes on an absolute scale is represented (right) and the potential scale relative to a standard hydrogen electrode (SHE). Wox (λ,ε) and Wred (λ,ε) stand for the oxidized and reduced states of thiols in solution, which can be represented by Gaussian distributions with a standard deviation of 2 λkBT, with their maxima located at E0redox ± λ, λ being the reorganization energy (≥0.3 eV) and E0redox the standard energy of the thiol redox couple.
For this catalysis to take place, a smooth bonding of a thiol to the gold is necessary, in such a way that further interaction with oxygen could be possible. As can be seen in
Figure 10, the interaction energy between bulk gold or nanoparticles to thiols is great, resulting in a strong bond that prevents further interaction with oxygen and inhibits the catalytic process. The same happens to large Au QCLs, which also bond strongly to the thiol, and no catalysis is observed.
On the other hand, very small clusters (less than five atoms) and single gold atoms present a LUMO with a higher energy than the thiol for which electronic bonding is not possible, and no activity will be found either for the smaller sizes.
Nevertheless, medium-sized clusters (between five and 10 atoms) bond to thiols, but weakly enough to allow the interaction with oxygen and the oxidation catalysis to take place. The equilibrium between this week interaction with thiols and the strong interaction with oxygen causes this clusters to be highly active for this oxidation, as was shown, reaching enzymatic levels.
Within the electrocatalysis, we can find another example of the importance of the HOMO-LUMO position. The HOR (Hydrogen oxidation reaction) by Au clusters between 10 and 40 atoms with high activity has been reported recently [
46]. As in the previous case, there is an upper and lower limit between which this reaction can take place, explained in terms of the HOMO-LUMO position.
It is well known that gold, both bulk and nanoparticles, does not catalyze the electro-oxidation of hydrogen, due to the nobleness of this metal, which makes the adsorption and dissociation of the hydrogen molecule impossible [
47]. As we can see in
Figure 10, the Au Fermi level is located above the H 1s–Au d antibonding resonance, thus filling H
2 antibonding states and so causing repulsion between H
2 and Au. Whenever the size of the particle is reduced under the nanometric level, the bandgap increases, lowering the HOMO level of the cluster. Therefore, Au clusters with HOMO below the antibonding resonance would absorb H
2, allowing the HOR to take place. This defines an upper size limit of around 40 atoms. On the other hand, if the cluster’s bandgap is very big, the LUMO energy will be higher than the H
2 redox potential, the electron transfer being unattainable. This sets as the lower limit around 10 atoms for the HOR to take place over gold.
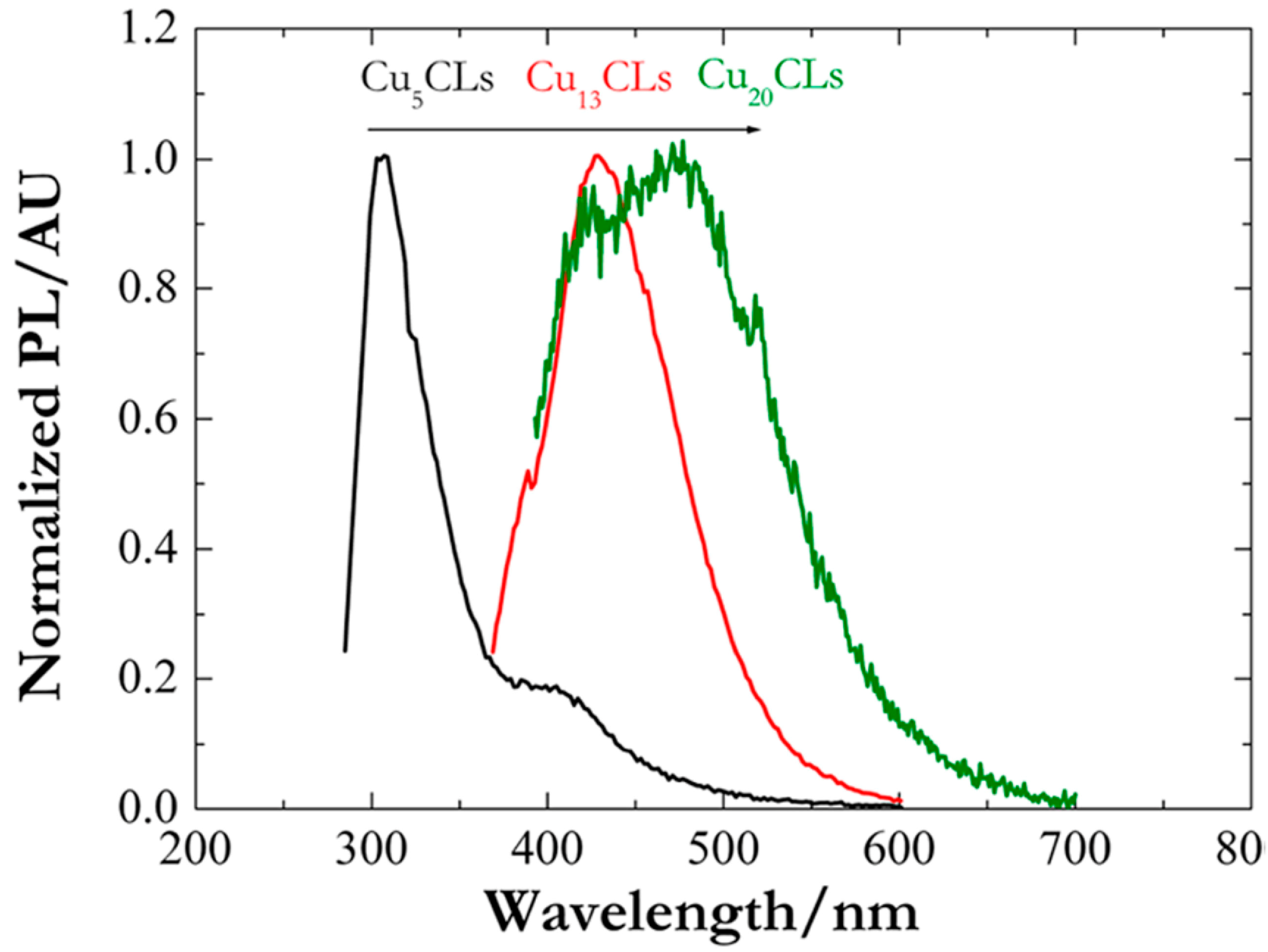
The last example that highlights the influence of the HOMO-LUMO energy level location is about the catalytic reduction of methylene blue (MB) by hydrazine in the presence of copper clusters [
23]. In this work, it is reported that only clusters with sizes smaller than 10–13 atoms are able to enhance the reduction rate of MB. The explanation relays the location of HOMO-LUMO bands, which in the present case, reveals the catalysis to be of critical importance: only those clusters (
N < 10–13 atoms) with their LUMO placed between hydrazine and MB redox potentials were able to facilitate the electron transfer. Bigger size clusters (
N > 13 atoms) with their LUMO position below the MB redox potential were not catalytically active.
Based on the above examples, it is clear that the position of the HOMO-LUMO gap is a determining factor in the catalytic properties of metal clusters.
4.2. Photocatalysis: Green Chemistry and Hydrogen Photoproduction
Given the importance of the size, geometric structure and relative position of the HOMO-LUMO bands, it becomes imperative to analyze the relevance of the absolute value of the bandgap.
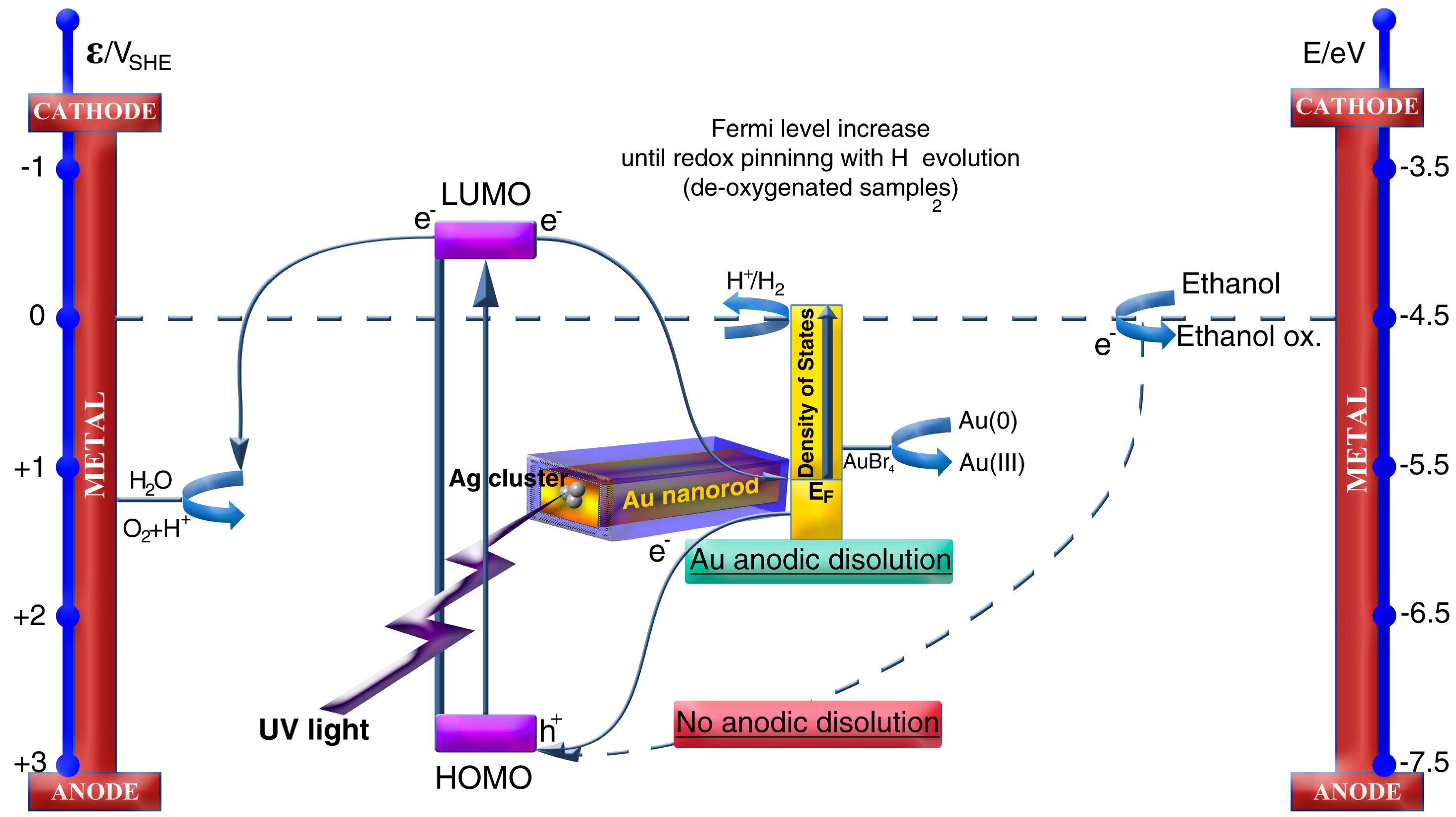
Following the previous example, when adsorbed on a metal surface, a metal cluster retains its semiconductor properties [
51]. In the same publication, it is reported that, when irradiated with UV light, Ag
3 clusters adsorbed on the tips of Au nanorods are able to oxidize them in the presence of atmospheric oxygen. A scheme of the mechanism can be seen in
Figure 12. The bandgap of Ag
3 clusters is around 3.5 eV [
25], and therefore, their maximum absorption stands in the UV region. When irradiated with UV light, an electron is excited in the cluster up to the LUMO level, and oxygen, as an electron scavenger, will trap this electron. The Au nanorod will then be oxidized by the highly oxidizing photogenerated holes in the Ag clusters. With the incorporation of a hole scavenger, like ethanol, in the system, this photodissolution is inhibited, since the hole scavenger oxidizes faster than the Au nanorod.
Figure 12.
Schematic representation of the Au photodissolution and H
2 photoproduction by Ag clusters. The figure is form [
51].
Figure 12.
Schematic representation of the Au photodissolution and H
2 photoproduction by Ag clusters. The figure is form [
51].
The authors found that when the electron scavenger (oxygen) is eliminated from the solution, irradiation in the presence of the hole scavenger produces hydrogen with high efficiencies up to 10% without any further optimization of the process. The mechanism of this hydrogen photoproduction is also explained in
Figure 12. When Ag clusters are irradiated in the presence of a hole scavenger without any further electron scavenger, Au nanorods act as an electron sink. Accumulation of electrons causes the Fermi level of such nanorods to increase. When this Fermi level is pinned by the H
2/H
+ redox potential, hydrogen is produced in solution. Since the absolute value of the bandgap is the key point in this reasoning, this allows one to think of the possibility that bigger clusters, with smaller bandgaps, will absorb less energetic radiations, thus being able to present similar activities with visible light.
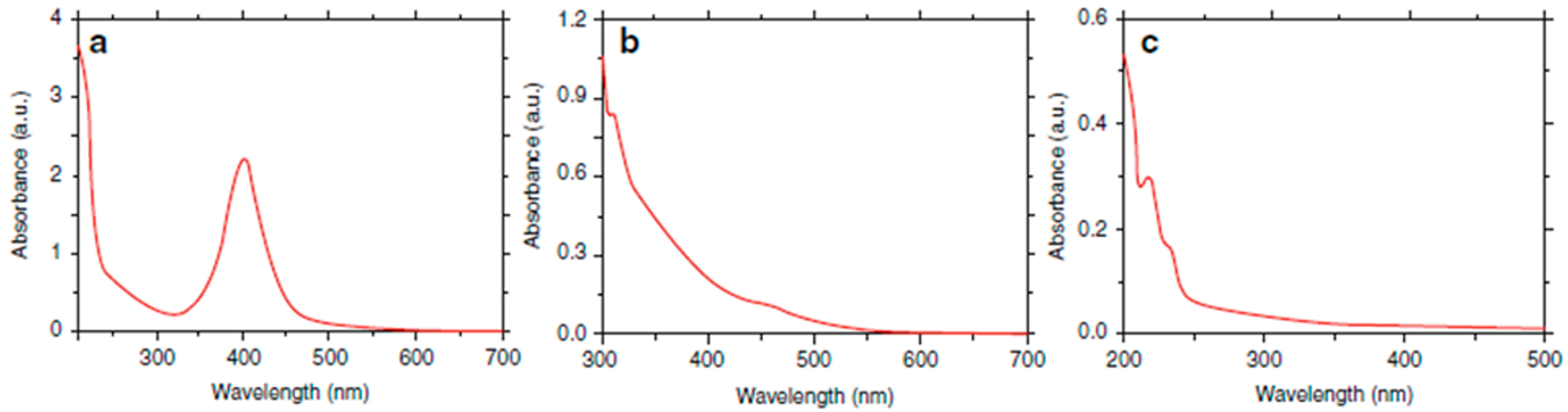
A demonstration of this last assumption has been given in a recently reported work [
52] in which the visible photooxidation activity of MB by Cu atomic clusters was obtained with a very high efficiency. The authors show that Cu clusters between 18 and 34 atoms are able to photooxidate methylene blue in both solution and when deposited when irradiated with visible light. The mechanism is analogous to the one explained before: the photogenerated holes in the cluster are extremely oxidative, and as a consequence, they oxidize the MB in contact with them. Since the clusters are atom level semiconductors, several problems associated with the recombination of electrons and holes (such as bulk and surface impurities and interface mismatching [
53,
54]), which lessen the photocatalytic efficiencies in common semiconductors, could be avoidable.
These examples clarify the importance that the absolute value of the bandgap has on the catalytic activity of the subnanometric clusters.
All of these results open up a whole new catalytic source of materials not explored until recent times, where one can “tailor” catalyst a la carte. By selecting the metal and the size of the cluster, one can tune the position of the HUMO-LUMO bands and the value of the bandgap, and therefore, one can select the most efficient catalyst to solve problems in many important reactions that, from the subnanometric world, would not be possible.