A Recurring Misconception Regarding the Fitting and Plotting of Enzyme Kinetics Data Leads to the Loss of Significant Reaction Parameters and Rate Constants
Abstract
1. Introduction
2. Results and Discussion
2.1. Explanatory Examples
2.2. Validation of the Explanatory Examples
3. Methods and Tools
3.1. Summary
3.2. Useful Remarks
- kcat/Km = (k1 × k2)/(k−1 + k2) refers to the reaction of the free enzyme with the free substrate, towards the formation of the product(s) and the release of the enzyme, in order to be ready for the next catalytic cycle, in cases where Equation (2) holds. Consequently, the profiles of kcat/Km vs. either the pH value or absolute temperature or other factors reveal changes in the free enzyme and free substrate molecules.
- kcat = k2 refers to the irreversible step of the three-step enzymatic reaction model (Scheme 1a), according to Equation (3), and therefore the profiles of kcat vs. the abovementioned factors reveal changes in the enzyme–substrate complex (ES).
- Km = (k−1 + k2)/k1 generally represents the substrate concentration that drives the enzymatic reaction to half its maximum value and could be characterized as the dissociation constant of the ES complex only under specific conditions (Scheme 1a). Km profiles vs. the aforementioned factors reveal changes in enzyme–substrate complexes (ES, ES′, etc.); however, such profiles are beyond the aims of this work and will not be discussed further.
3.3. Subject Matter
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sharma, V.; Tsai, M.-L.; Nargotra, P.; Chen, C.-W.; Kuo, C.-H.; Sun, P.-P.; Dong, C.-D. Agro-Industrial Food Waste as a Low-Cost Substrate for Sustainable Production of Industrial Enzymes: A Critical Review. Catalysts 2022, 12, 1373. [Google Scholar] [CrossRef]
- Chia, X.K.; Hadibarata, T.; Kristanti, R.A.; Jusoh, M.N.H.; Tan, I.S.; Foo, H.C.Y. The function of microbial enzymes in breaking down soil contaminated with pesticides: A review. Bioproc. Biosyst. Eng. 2024, 47, 597–620. [Google Scholar] [CrossRef] [PubMed]
- Rolle, R.S. Review: Enzyme applications for agro-processing in developing countries: An inventory of current and potential applications. World J. Microb. Biot. 1998, 14, 611–619. [Google Scholar] [CrossRef]
- Chapman, J.; Ismail, A.E.; Dinu, C.Z. Industrial Applications of Enzymes: Recent Advances, Techniques, and Outlooks. Catalysts 2018, 8, 238. [Google Scholar] [CrossRef]
- Arya, P.S.; Yagnik, S.M.; Rajput, K.N.; Panchal, R.R.; Raval, V.H. Valorization of agro-food wastes: Ease of concomitant-enzymes production with application in food and biofuel industries. Bioresour. Technol. 2022, 361, 127738. [Google Scholar] [CrossRef] [PubMed]
- Fersht, A. Structure and Mechanism in Protein Science. In A Guide to Enzyme Catalysis and Protein Folding, 1st ed.; W. H. Freeman & Co.: New York, NY, USA, 1999; pp. 103–111 and 169–190. [Google Scholar]
- Theodorou, L.G.; Bieth, J.G.; Papamichael, E.M. The catalytic mode of cysteine proteinases of papain (C1) family. Bioresour. Technol. 2007, 98, 1931–1939. [Google Scholar] [CrossRef] [PubMed]
- Stergiou, P.-Y.; Foukis, A.; Gkini, O.A.; Barouni, B.; Georgoulia, P.S.; Kanellaki, M.; Koutinas, A.A.; Papagianni, M.; Papamichael, E.M. Novel FRET-substrates of Rhizomucor pusillus rennin: Activity and mechanistic studies. Food Chem. 2018, 245, 926–933. [Google Scholar] [CrossRef] [PubMed]
- Papamichael, E.M.; Stamatis, H.; Stergiou, P.-Y.; Foukis, A.; Gkini, O.A. Enzyme Kinetics and Modeling, of Enzymatic Systems, in Biomass, Biofuels, Biochemicals. In Advances in Enzyme Technology, 1st ed.; Singh, R.S., Singhania, R.R., Pandey, A., Larroche, C., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 71–104. [Google Scholar]
- Herschlag, D.; Natarajan, A. Fundamental challenges in mechanistic enzymology: Progress toward understanding the rate enhancements of enzymes. Biochemistry 2013, 52, 2050–2067. [Google Scholar] [CrossRef] [PubMed]
- Sárkány, Z.; Polgár, L. The unusual catalytic triad of poliovirus protease 3C. Biochemistry 2003, 42, 516–522. [Google Scholar] [CrossRef] [PubMed]
- Foukis, A.; Stergiou, P.-Y.; Theodorou, L.G.; Papagianni, M.; Papamichael, E.M. Purification, kinetic characterization and properties of a novel thermo-tolerant extracellular protease from Kluyveromyces marxianus IFO 0288 with potential biotechnological interest. Bioresour. Technol. 2012, 123, 214–220. [Google Scholar] [CrossRef] [PubMed]
- Papamichael, E.M.; Stergiou, P.-Y. (Enzyme Biotechnology and Genetic Engineering Group, Department of Chemistry, University of Ioannina, P.C 45110 Ioannina, Greece). Personal communication, 2023. manuscript in preparation; to be submitted.
- Vindigni, A.; Di Cera, E. Release of Fibrinopeptides by the Slow and Fast Forms of Thrombin. Biochemistry 1996, 35, 4417–4426. [Google Scholar]
- Sárkány, Z.; Polgár, L. Thiolate-Imidazolium Ion Pair Is Not an Obligatory Catalytic Entity of Cysteine Peptidases: The Active Site of Picornain 3C. Biochemistry 2001, 40, 10601–10606. [Google Scholar] [CrossRef] [PubMed]
- Lente, G.; Fábián, I.; Poë, A.J. A common misconception about the Eyring equation. New J. Chem. 2005, 29, 759–760. [Google Scholar] [CrossRef]
- Laidler, K.J.; Meiser, J.H. Physical Chemistry, 1st ed.; The Benjamin/Cummigs Publishing Company, Inc.: Amsterdam, The Netherlands, 1982; pp. 114–119 and 378–383. [Google Scholar]
- Stergiou, P.-Y.; Athanasios Foukis, A.; Gkini, O.A.; Bieth, J.G.; Papamichael, E.M. Kinetic and computational analysis of the reversible inhibition of porcine pancreatic elastase: A structural and mechanistic approach. J. Enzyme Inhib. Med. Chem. 2016, 31, 131–139. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Topham, C.M.; Salih, E.; Frazao, C.; Kowlessur, D.; Overington, J.P.; Thomas, M.; Brocklehurst, S.M.; Patel, M.; Thomas, E.W.; Brocklehurst, K. Structure-function relationships in the cysteine proteinases actinidin, papain and papaya proteinase W: Three-dimensional structure of papaya proteinase W deduced by knowledge-based modelling and active-centre characteristics determined by two-hydronic-state reactivity probe kinetics and kinetics of catalysis. Biochem. J. 1991, 280, 79–92. [Google Scholar] [PubMed]
- Thomas, M.P.; Topham, C.M.; Kowlessur, D.; Mellor, G.W.; Thomas, E.W.; Whitford, D.; Brocklehurst, K. Structure of chymopapain M the late-eluted chymopapain deduced by comparative modelling techniques and active-centre characteristics determined by pH-dependent kinetics of catalysis and reactions with time-dependent inhibitors: The Cys-25/His-159 ion-pair is insufficient for catalytic competence in both chymopapain M and papain. Biochem. J. 1994, 300, 805–820. [Google Scholar]

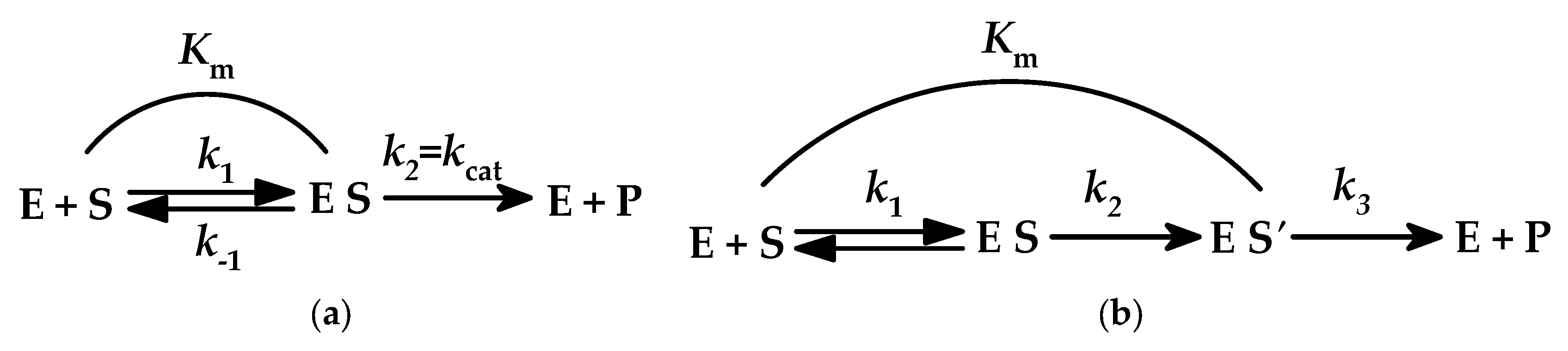
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papamichael, E.M.; Stergiou, P.-Y. A Recurring Misconception Regarding the Fitting and Plotting of Enzyme Kinetics Data Leads to the Loss of Significant Reaction Parameters and Rate Constants. Catalysts 2025, 15, 582. https://doi.org/10.3390/catal15060582
Papamichael EM, Stergiou P-Y. A Recurring Misconception Regarding the Fitting and Plotting of Enzyme Kinetics Data Leads to the Loss of Significant Reaction Parameters and Rate Constants. Catalysts. 2025; 15(6):582. https://doi.org/10.3390/catal15060582
Chicago/Turabian StylePapamichael, Emmanuel M., and Panagiota-Yiolanda Stergiou. 2025. "A Recurring Misconception Regarding the Fitting and Plotting of Enzyme Kinetics Data Leads to the Loss of Significant Reaction Parameters and Rate Constants" Catalysts 15, no. 6: 582. https://doi.org/10.3390/catal15060582
APA StylePapamichael, E. M., & Stergiou, P.-Y. (2025). A Recurring Misconception Regarding the Fitting and Plotting of Enzyme Kinetics Data Leads to the Loss of Significant Reaction Parameters and Rate Constants. Catalysts, 15(6), 582. https://doi.org/10.3390/catal15060582






