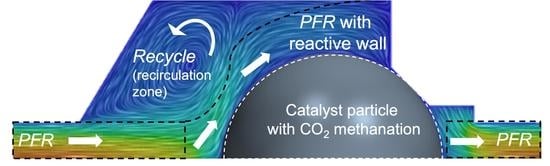
Non-Idealities in Lab-Scale Kinetic Testing: A Theoretical Study of a Modular Temkin Reactor
Abstract
:1. Introduction
2. Materials and Methods
2.1. Computational Fluid Dynamics
2.1.1. Governing Equations
2.1.2. Modeling Surface Reactions
2.1.3. CFD Setup
2.2. Simplification of Fluid Dynamics
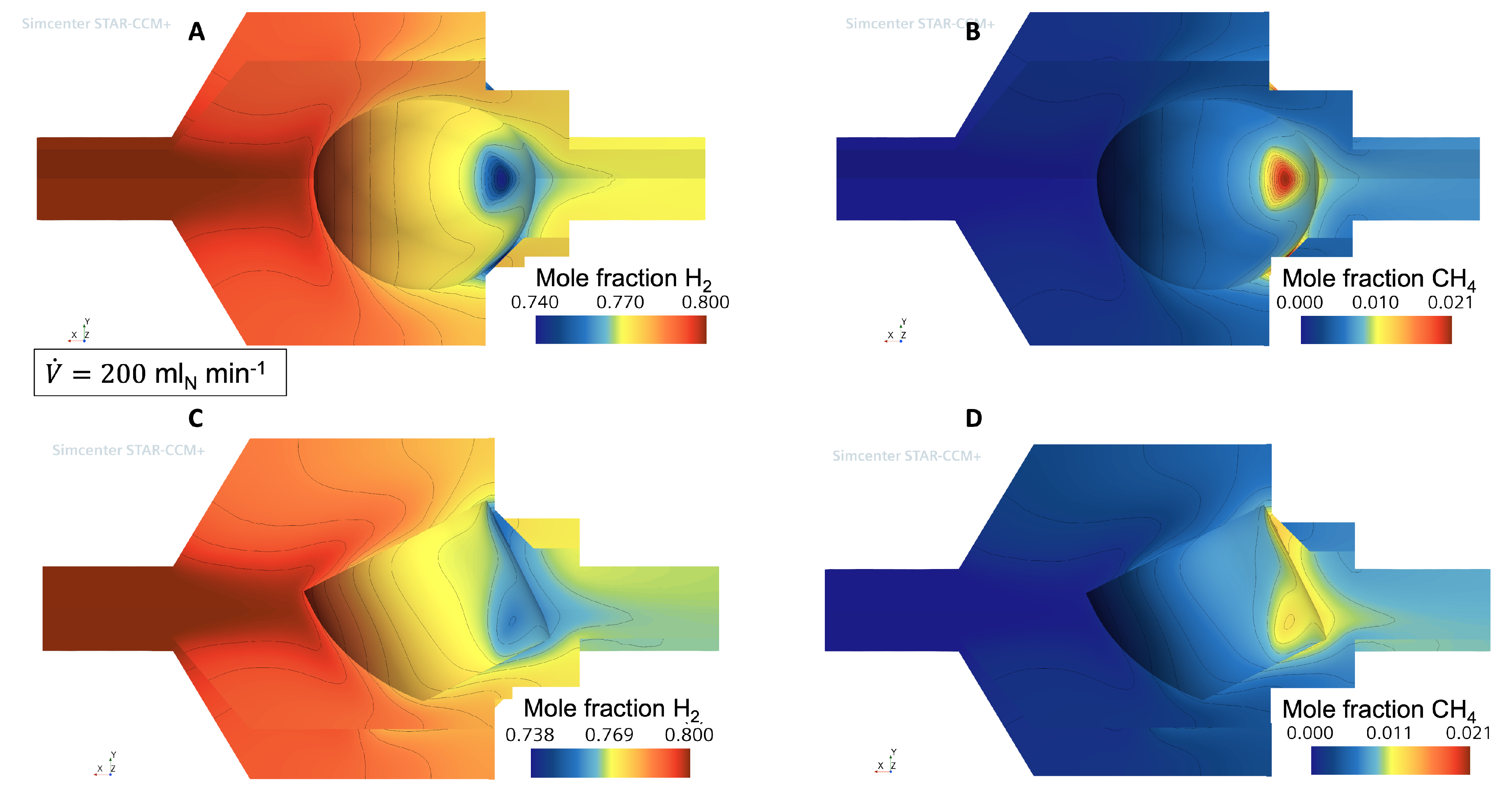
2.3. Carbon Dioxide Methanation
3. Results and Discussion
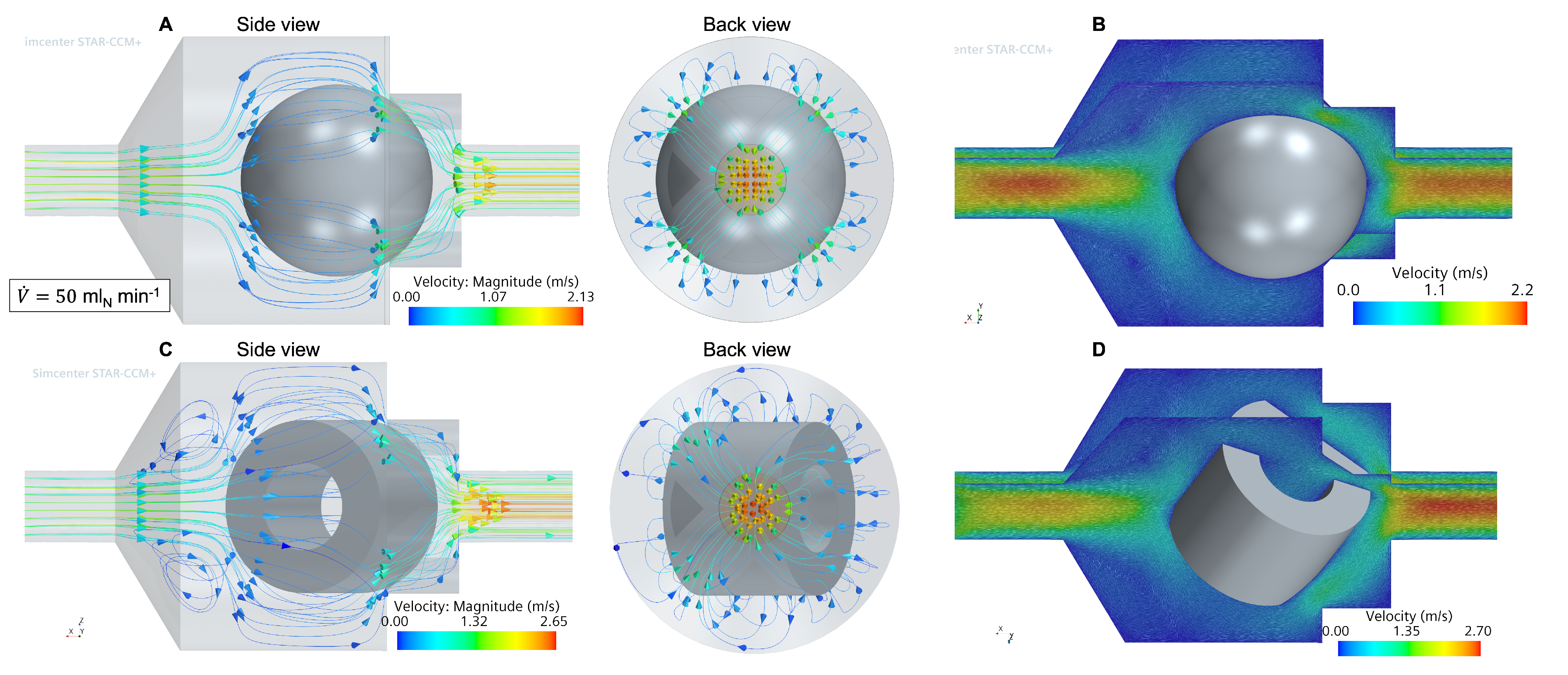
3.1. Flow and Species Fields from CFD Simulations
3.2. External Mass Transport Evaluation
3.3. Comparison between CFD and Simplified Models
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| CRN | Chemical reactor network |
| CSTR | Continuously stirred tank reactor |
| iri | inert–active–inert |
| PFR | Plug flow reactor |
| RTD | Residence time distribution |
References
- Kapteijn, F.; Moulijn, J.A. Chapter 9: Laboratory Testing of Solid Catalysts. In Handbook of Heterogeneous Catalysis, 2nd ed.; Ertl, G., Knözinger, H., Schüth, F., Weitkamp, J., Eds.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2008; pp. 2019–2045. [Google Scholar]
- Berty, J.M. 20 Years of recycle reactors in reaction engineering. Plant/Oper. Prog. 1984, 3, 163–168. [Google Scholar] [CrossRef]
- Borman, P.C.; Bos, A.N.R.; Westerterp, K.R. A novel reactor for determination of kinetics for solid catalyzed gas reactions. AIChE J. 1994, 40, 862–869. [Google Scholar] [CrossRef] [Green Version]
- Komiyama, M. Design and Preparation of Impregnated Catalysts. Catal. Rev. 1985, 27, 341–372. [Google Scholar] [CrossRef]
- Takehira, K.; Kawabata, T.; Shishido, T.; Murakami, K.; Ohi, T.; Shoro, D.; Honda, M.; Takaki, K. Mechanism of reconstitution of hydrotalcite leading to eggshell-type Ni loading on MgAl mixed oxide. J. Catal. 2005, 231, 92–104. [Google Scholar] [CrossRef]
- Badano, J.; Betti, C.; Rintoul, I.; Vich-Berlanga, J.; Cagnola, E.; Torres, G.; Vera, C.; Yori, J.; Quiroga, M. New composite materials as support for selective hydrogenation; egg-shell catalysts. Appl. Catal. A Gen. 2010, 390, 166–174. [Google Scholar] [CrossRef]
- Fratalocchi, L.; Visconti, C.G.; Lietti, L.; Tronconi, E.; Cornaro, U.; Rossini, S. A novel preparation method for “small” eggshell Co/γ-Al2O3 catalysts: A promising catalytic system for compact Fischer–Tropsch reactors. Catal. Today 2015, 246, 125–132. [Google Scholar] [CrossRef]
- Zimmermann, R.T.; Bremer, J.; Sundmacher, K. Optimal catalyst particle design for flexible fixed-bed CO2 methanation reactors. Chem. Eng. J. 2020, 387, 123704. [Google Scholar] [CrossRef]
- Temkin, M.I.; Kulkova, N.V. Laboratory reactor with ideal displacement. Kinet. Catal. 1969, 10, 461–463. [Google Scholar]
- Scott, D.; Lee, W.; Papa, J. The measurement of transport coefficients in gas-solid heterogeneous reactions. Chem. Eng. Sci. 1974, 29, 2155–2167. [Google Scholar] [CrossRef]
- Hipolito, A.I.; Rolland, M.; Boyer, C.; de Bellefon, C. Single Pellet String Reactor for Intensification of Catalyst Testing in Gas/Liquid/Solid Configuration. Oil Gas Sci. Technol. Rev. Ifp Energies Nouv. 2010, 65, 689–701. [Google Scholar] [CrossRef] [Green Version]
- Klyushina, A.; Pacultová, K.; Obalová, L. Advantage of the single pellet string reactor for testing real-size industrial pellets of potassium-doped CoMnAl catalyst for the decomposition of N2O. React. Kinet. Mech. Catal. 2015, 115, 651–662. [Google Scholar] [CrossRef]
- Moonen, R.; Alles, J.; Ras, E.J.; Harvey, C.; Moulijn, J.A. Performance Testing of Hydrodesulfurization Catalysts Using a Single-Pellet-String Reactor. Chem. Eng. Technol. 2017, 40, 2025–2034. [Google Scholar] [CrossRef] [Green Version]
- Behnam, M.; Dixon, A.; Wright, P.; Nijemeisland, M.; Stitt, E. Comparison of CFD simulations to experiment under methane steam reforming reacting conditions. Chem. Eng. J. 2012, 207–208, 690–700. [Google Scholar] [CrossRef]
- Fernengel, J.; Bolton, L.; Hinrichsen, O. Characterisation and design of single pellet string reactors using numerical simulation. Chem. Eng. J. 2019, 373, 1397–1408. [Google Scholar] [CrossRef]
- Wehinger, G.D.; Kreitz, B.; Nagy, A.; Turek, T. Characterization of a modular Temkin reactor with experiments and computational fluid dynamics simulations. Chem. Eng. J. 2020, 389, 124342. [Google Scholar] [CrossRef]
- Mestl, G. High throughput development of selective oxidation catalysts at Süd-Chemie. Comb. Chem. High Throughput Screen. 2012, 15, 114–122. [Google Scholar] [CrossRef]
- Kuhn, M.; Lucas, M.; Claus, P. Advanced-TEMKIN Reaktor: Testung von industriellen Schalenkatalysatoren im Labormaßstab. Chem. Ing. Technol. 2014, 86, 1925–1932. [Google Scholar] [CrossRef]
- Kuhn, M.; Lucas, M.; Claus, P. Precise recognition of catalyst deactivation during acetylene hydrogenation studied with the advanced TEMKIN reactor. Catal. Commun. 2015, 72, 170–173. [Google Scholar] [CrossRef]
- Götz, D.; Kuhn, M.; Claus, P. Numerical modelling and performance studies of the original and advanced TEMKIN reactor in laboratory scale testing of industrial egg shell catalysts for the selective hydrogenation of acetylene. Chem. Eng. Res. Des. 2015, 94, 594–604. [Google Scholar] [CrossRef]
- Deutschmann, O. Modeling of the Interactions Between Catalytic Surfaces and Gas-Phase. Catal. Lett. 2015, 145, 272–289. [Google Scholar] [CrossRef]
- Hettel, M.; Diehm, C.; Bonart, H.; Deutschmann, O. Numerical simulation of a structured catalytic methane reformer by DUO: The new computational interface for OpenFOAM® and DETCHEM™. Catal. Today 2015, 258, 230–240. [Google Scholar] [CrossRef]
- Wehinger, G.D.; Heitmann, H.; Kraume, M. An artificial structure modeler for 3D CFD simulations of catalytic foams. Chem. Eng. J. 2016, 284, 543–556. [Google Scholar] [CrossRef]
- Jurtz, N.; Kraume, M.; Wehinger, G.D. Advances in fixed-bed reactor modeling using particle-resolved computational fluid dynamics (CFD). Rev. Chem. Eng. 2019, 35, 139. [Google Scholar] [CrossRef] [Green Version]
- Wehinger, G.D.; Flaischlen, S. Computational Fluid Dynamics Modeling of Radiation in a Steam Methane Reforming Fixed-Bed Reactor. Ind. Eng. Chem. Res. 2019, 58, 14410–14423. [Google Scholar] [CrossRef]
- Wehinger, G.D.; Fütterer, C.; Kraume, M. Contact Modifications for CFD Simulations of Fixed-Bed Reactors: Cylindrical Particles. Ind. Eng. Chem. Res. 2017, 56, 87–99. [Google Scholar] [CrossRef]
- Kutscherauer, M.; Böcklein, S.; Mestl, G.; Turek, T.; Wehinger, G.D. An improved contact modification routine for a computationally efficient CFD simulation of packed beds. Chem. Eng. J. Adv. 2022, 9, 100197. [Google Scholar] [CrossRef]
- Gossler, H.; Maier, L.; Angeli, S.; Tischer, S.; Deutschmann, O. CaRMeN: A tool for analysing and deriving kinetics in the real world. Phys. Chem. Chem. Phys. 2018, 20, 10857–10876. [Google Scholar] [CrossRef]
- Hettel, M.; Wörner, M.; Deutschmann, O. Computational Fluid Dynamics of Catalytic Reactors. In Handbook of Materials Modeling; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; p. 1. [Google Scholar] [CrossRef]
- Poling, B.; Prausnitz, J.; O’Connell, J. The Properties of Gases and Liquids, 5th ed.; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Shih, T.H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new k-ϵ eddy viscosity model for high reynolds number turbulent flows. Comput. Fluids 1995, 24, 227. [Google Scholar] [CrossRef]
- Kee, R.J.; Colin, M.E.; Glarborg, P. Chemically Reacting Flow, Theory and Pratice; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Deutschmann, O. Computational Fluid Dynamics Simulation of Catalytic Reactors. In Ullmann’s Encyclopedia of Industrial Chemistry; Chapter 6.6; Handbook of Heterogeneous Catalysis; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2008; pp. 1811–1828. [Google Scholar] [CrossRef] [Green Version]
- Siemens Digital Industries Software. Simcenter STAR-CCM+ 16.06. 2021. Available online: https://www.plm.automation.siemens.com/global/de/products/simcenter/STAR-CCM.html48 (accessed on 28 January 2022).
- Daymo, E.A.; Hettel, M.; Deutschmann, O.; Wehinger, G.D. Accelerating particle-resolved CFD simulations of catalytic fixed-bed reactors with DUO. Chem. Eng. Sci. 2022, 250, 117408. [Google Scholar] [CrossRef]
- Novosselov, I.V.; Malte, P.C.; Yuan, S.; Srinivasan, R.; Lee, J.C.Y. Chemical Reactor Network Application to Emissions Prediction for Industial DLE Gas Turbine. In Proceedings of the ASME Turbo Expo: Power for Land, Sea, and Air, Barcelona, Spain, 8–11 May 2006; ASME: New York, NY, USA, 2006; Volume 1, pp. 221–235. [Google Scholar] [CrossRef]
- Pedersen, L.S.; Breithauptb, P.; DAM-Johansen, K.; Weber, R. Residence Time Distributions in Confined Swirling Flames. Combust. Sci. Technol. 1997, 127, 251–273. [Google Scholar] [CrossRef]
- Pedersen, L.; Glarborg, P.; Dam-Johansen, K.; Hepburn, P.W.; Hesselmann, G. A Chemical Engineering Model for Predicting NO Emissions and Burnout from Pulverised Coal Flames. Combust. Sci. Technol. 1998, 132, 251–314. [Google Scholar] [CrossRef]
- Falcitelli, M.; Tognotti, L.; Pasini, S. An algorithm for extracting chemical reactor network models from CFD simulation of industrial combustion systems. Combust. Sci. Technol. 2002, 174, 27–42. [Google Scholar] [CrossRef]
- Park, J.; Nguyen, T.H.; Joung, D.; Huh, K.Y.; Lee, M.C. Prediction of NOx and CO Emissions from an Industrial Lean-Premixed Gas Turbine Combustor Using a Chemical Reactor Network Model. Energy Fuels 2013, 27, 1643–1651. [Google Scholar] [CrossRef]
- Fichet, V.; Kanniche, M.; Plion, P.; Gicquel, O. A reactor network model for predicting NOx emissions in gas turbines. Fuel 2010, 89, 2202–2210. [Google Scholar] [CrossRef]
- Levenspiel, O. Chemical Reaction Engineering, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1999. [Google Scholar]
- Vrábel, P.; Van der Lans, R.; Cui, Y.; Luyben, K. Compartment Model Approach: Mixing in Large Scale Aerated Reactors with Multiple Impellers. Chem. Eng. Res. Des. 1999, 77, 291–302. [Google Scholar] [CrossRef]
- Pigou, M.; Morchain, J. Investigating the interactions between physical and biological heterogeneities in bioreactors using compartment, population balance and metabolic models. Chem. Eng. Sci. 2015, 126, 267–282. [Google Scholar] [CrossRef] [Green Version]
- Tajsoleiman, T.; Spann, R.; Bach, C.; Gernaey, K.V.; Huusom, J.K.; Krühne, U. A CFD based automatic method for compartment model development. Comput. Chem. Eng. 2019, 123, 236–245. [Google Scholar] [CrossRef]
- Vanderveen, J.W.; Luss, D.; Amundson, N.R. Stability of adiabatic packed bed reactors. Effect of flow variations and coupling between the particles. AIChE J. 1968, 14, 636–643. [Google Scholar] [CrossRef]
- Iordanidis, A.A. Mathematical Modeling of Catalytic Fixed Bed Reactors. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 2002. [Google Scholar]
- Goodwin, D.G.; Speth, R.L.; Moffat, H.K.; Weber, B.W. Cantera: An Object-Oriented Software Toolkit for Chemical Kinetics, Thermodynamics, and Transport Processes. Version 2.5.1. 2021. Available online: https://www.cantera.org (accessed on 28 January 2022). [CrossRef]
- Kreitz, B.; Wehinger, G.D.; Turek, T. Dynamic simulation of the CO2 methanation in a micro-structured fixed-bed reactor. Chem. Eng. Sci. 2019, 195, 541–552. [Google Scholar] [CrossRef]
- Gao, C.W.; Allen, J.W.; Green, W.H.; West, R.H. Reaction Mechanism Generator: Automatic construction of chemical kinetic mechanisms. Comput. Phys. Commun. 2016, 203, 212–225. [Google Scholar] [CrossRef] [Green Version]
- Goldsmith, C.F.; West, R.H. Automatic Generation of Microkinetic Mechanisms for Heterogeneous Catalysis. J. Phys. Chem. C 2017, 121, 9970–9981. [Google Scholar] [CrossRef]
- Liu, M.; Grinberg Dana, A.; Johnson, M.S.; Goldman, M.J.; Jocher, A.; Payne, A.M.; Grambow, C.A.; Han, K.; Yee, N.W.; Mazeau, E.J.; et al. Reaction Mechanism Generator v3.0: Advances in Automatic Mechanism Generation. J. Chem. Inf. Model. 2021, 61, 2686–2696. [Google Scholar] [CrossRef] [PubMed]
- Kreitz, B.; Sargsyan, K.; Blöndal, K.; Mazeau, E.J.; West, R.H.; Wehinger, G.D.; Turek, T.; Goldsmith, C.F. Quantifying the Impact of Parametric Uncertainty on Automatic Mechanism Generation for CO2 Hydrogenation on Ni(111). JACS Au 2021, 1, 1656–1673. [Google Scholar] [CrossRef] [PubMed]
- van Santen, R.A.; Neurock, M.; Shetty, S.G. Reactivity theory of transition-metal surfaces: A Brønsted-Evans-Polanyi linear activation energy-free-energy analysis. Chem. Rev. 2010, 110, 2005–2048. [Google Scholar] [CrossRef] [PubMed]
- Abild-Pedersen, F.; Greeley, J.; Studt, F.; Rossmeisl, J.; Munter, T.R.; Moses, P.G.; Skúlason, E.; Bligaard, T.; Nørskov, J.K. Scaling properties of adsorption energies for hydrogen-containing molecules on transition-metal surfaces. Phys. Rev. Lett. 2007, 99, 016105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mazeau, E.J.; Satpute, P.; Blöndal, K.; Goldsmith, C.F.; West, R.H. Automated Mechanism Generation Using Linear Scaling Relationships and Sensitivity Analyses Applied to Catalytic Partial Oxidation of Methane. ACS Catal. 2021, 73, 7114–7125. [Google Scholar] [CrossRef]
- Blondal, K.; Jelic, J.; Mazeau, E.; Studt, F.; West, R.H.; Goldsmith, C.F. Computer-Generated Kinetics for Coupled Heterogeneous/Homogeneous Systems: A Case Study in Catalytic Combustion of Methane on Platinum. Ind. Eng. Chem. Res. 2019, 58, 17682–17691. [Google Scholar] [CrossRef]
- Kreitz, B.; Martínez Arias, A.; Martin, J.; Weber, A.P.; Turek, T. Spray-Dried Ni Catalysts with Tailored Properties for CO2 Methanation. Catalysts 2020, 10, 1410. [Google Scholar] [CrossRef]
- Kreitz, B.; Wehinger, G.D.; Goldsmith, C.F.; Turek, T. Microkinetic Modeling of the CO2 Desorption from Supported Multifaceted Ni Catalysts. J. Phys. Chem. C 2021, 125, 2984–3000. [Google Scholar] [CrossRef]







| Reaction | A in (cm min s) or | in (kJ mol) | |
|---|---|---|---|
| 1 | 0.8 | 0.0 | |
| 2 | 4.20 · 1019 | 74.5 | |
| 3 | 0.1 | 0.0 | |
| 4 | 7.00 · 10−3 | 0 | |
| 5 | 0.1 | 0.0 | |
| 6 | 0.1 | 17.8 | |
| 7 | 3.20 · 1021 | 22.2 | |
| 8 | 6.40 · 1021 | 97.1 | |
| 9 | 6.40 · 1021 | 0.0 | |
| 10 | 9.60 · 1021 | 67.0 | |
| 11 | 1.28 · 1022 | 102.4 | |
| 12 | 3.20 · 1021 | 77.5 | |
| 13 | 3.20 · 1021 | 74.0 | |
| 14 | 3.20 · 1021 | 21.5 | |
| 15 | 3.20 · 1021 | 0.0 | |
| 16 | 3.20 · 1021 | 43.7 | |
| 17 | 3.20 · 1021 | 61.5 | |
| 18 | 3.20 · 1021 | 28.8 | |
| 19 | 3.20 · 1021 | 57.0 | |
| 20 | 3.20 · 1021 | 0.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wehinger, G.D.; Kreitz, B.; Goldsmith, C.F. Non-Idealities in Lab-Scale Kinetic Testing: A Theoretical Study of a Modular Temkin Reactor. Catalysts 2022, 12, 349. https://doi.org/10.3390/catal12030349
Wehinger GD, Kreitz B, Goldsmith CF. Non-Idealities in Lab-Scale Kinetic Testing: A Theoretical Study of a Modular Temkin Reactor. Catalysts. 2022; 12(3):349. https://doi.org/10.3390/catal12030349
Chicago/Turabian StyleWehinger, Gregor D., Bjarne Kreitz, and C. Franklin Goldsmith. 2022. "Non-Idealities in Lab-Scale Kinetic Testing: A Theoretical Study of a Modular Temkin Reactor" Catalysts 12, no. 3: 349. https://doi.org/10.3390/catal12030349
APA StyleWehinger, G. D., Kreitz, B., & Goldsmith, C. F. (2022). Non-Idealities in Lab-Scale Kinetic Testing: A Theoretical Study of a Modular Temkin Reactor. Catalysts, 12(3), 349. https://doi.org/10.3390/catal12030349