Octahedral Growth of PtPd Nanocrystals
Abstract
1. Introduction
2. Results and Discussion
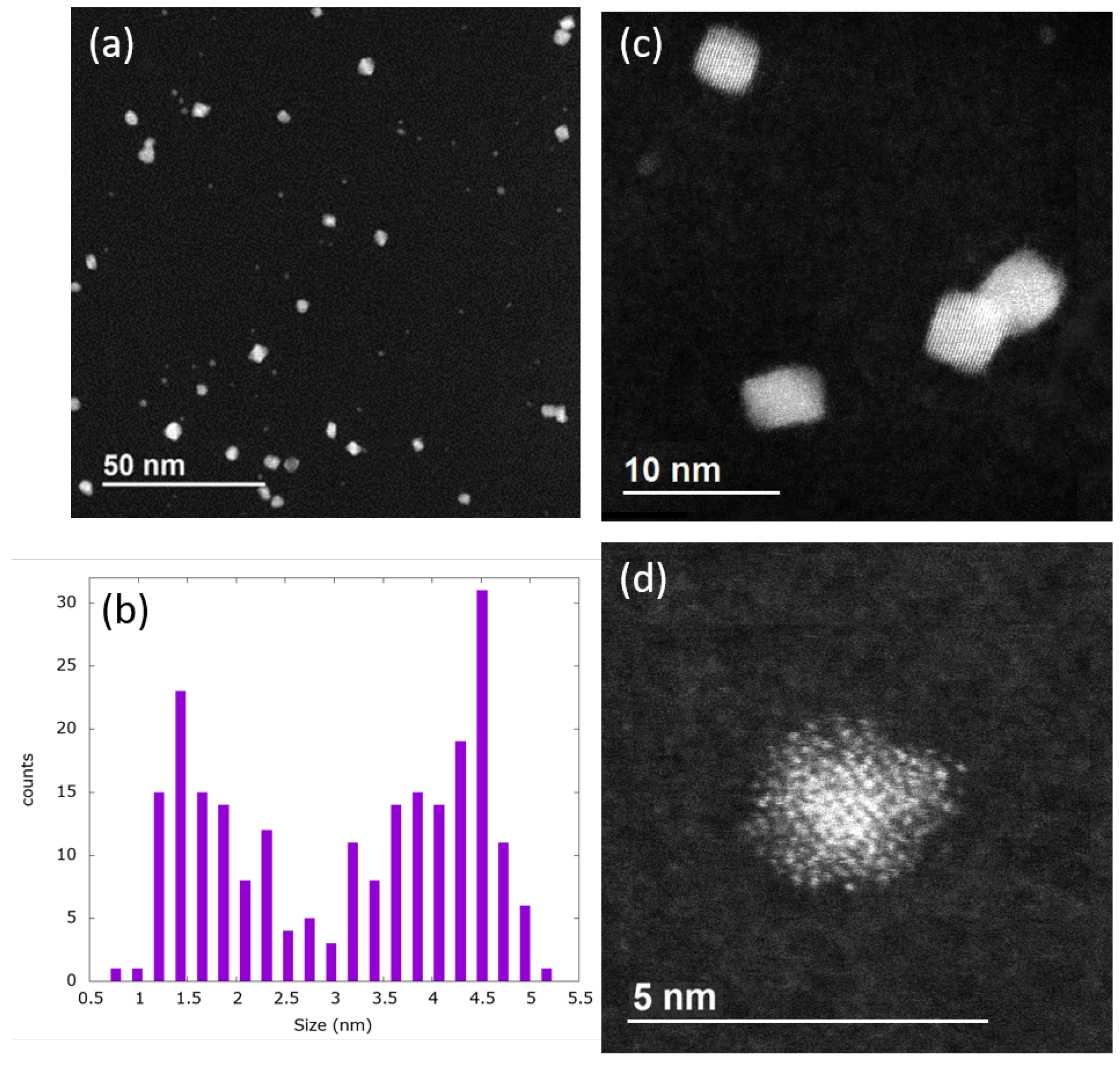
2.1. Bimodal Distribution
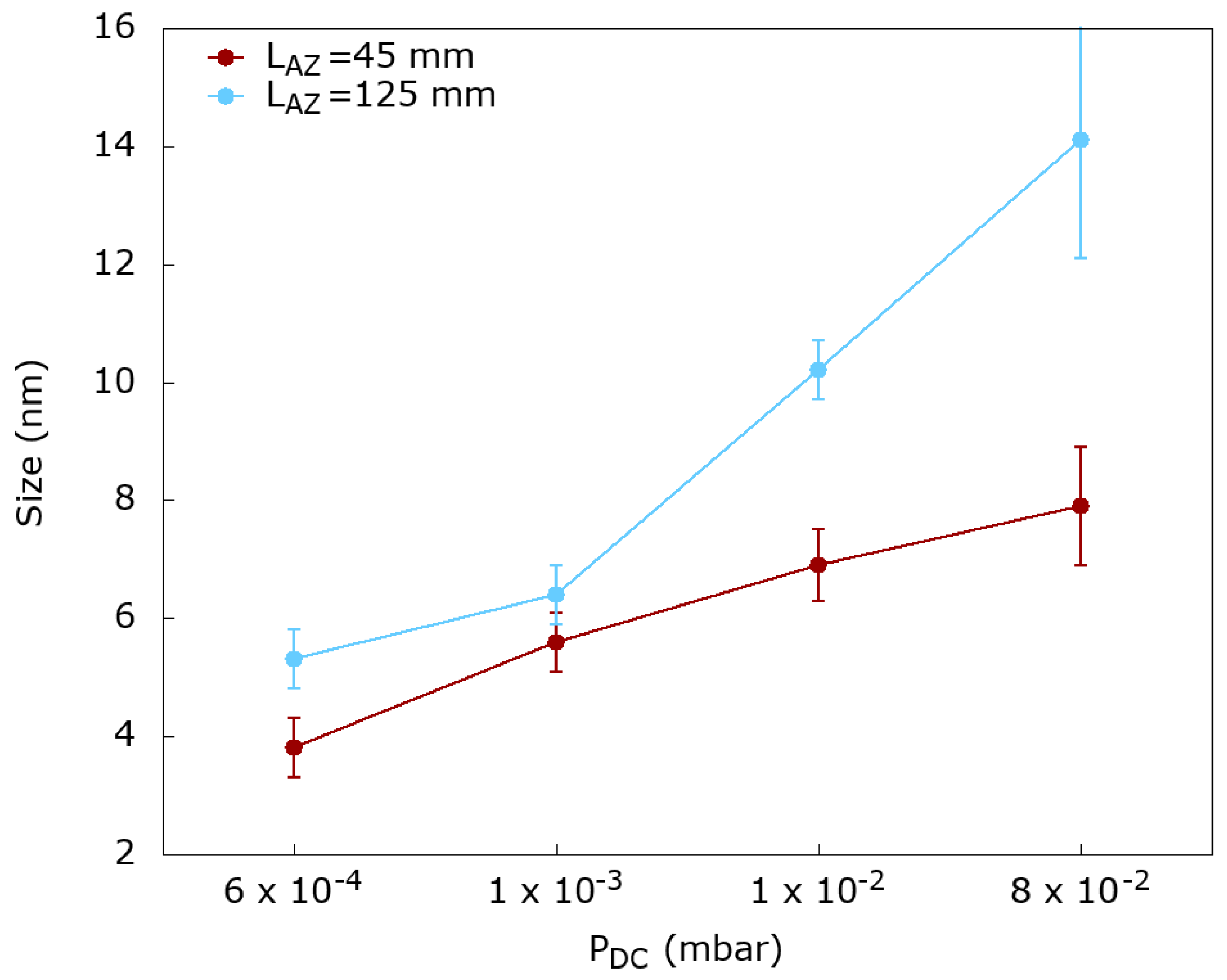
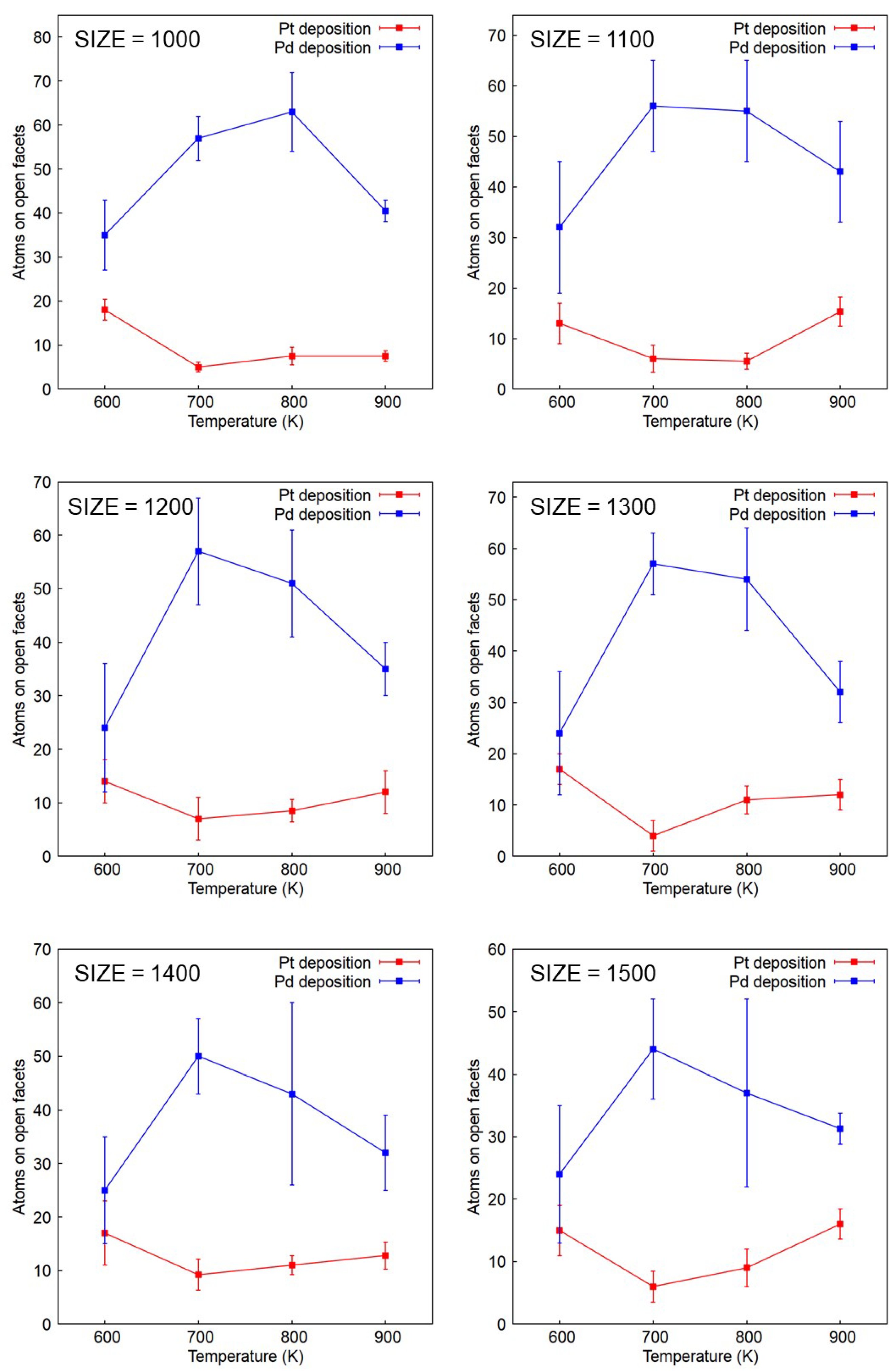
2.2. Controlling the Size Distribution of Ptpd Nps
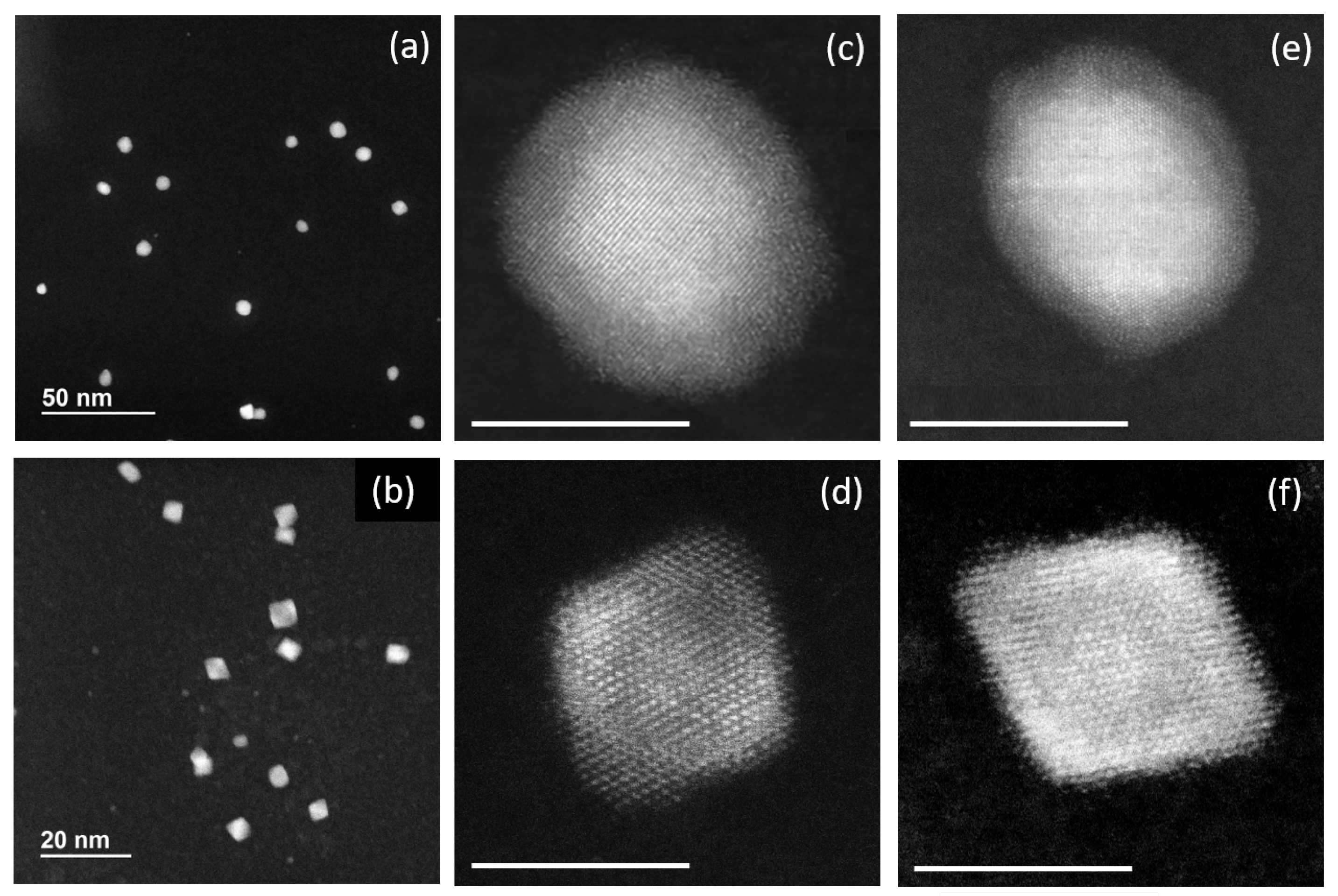
2.3. Composition vs. Facets
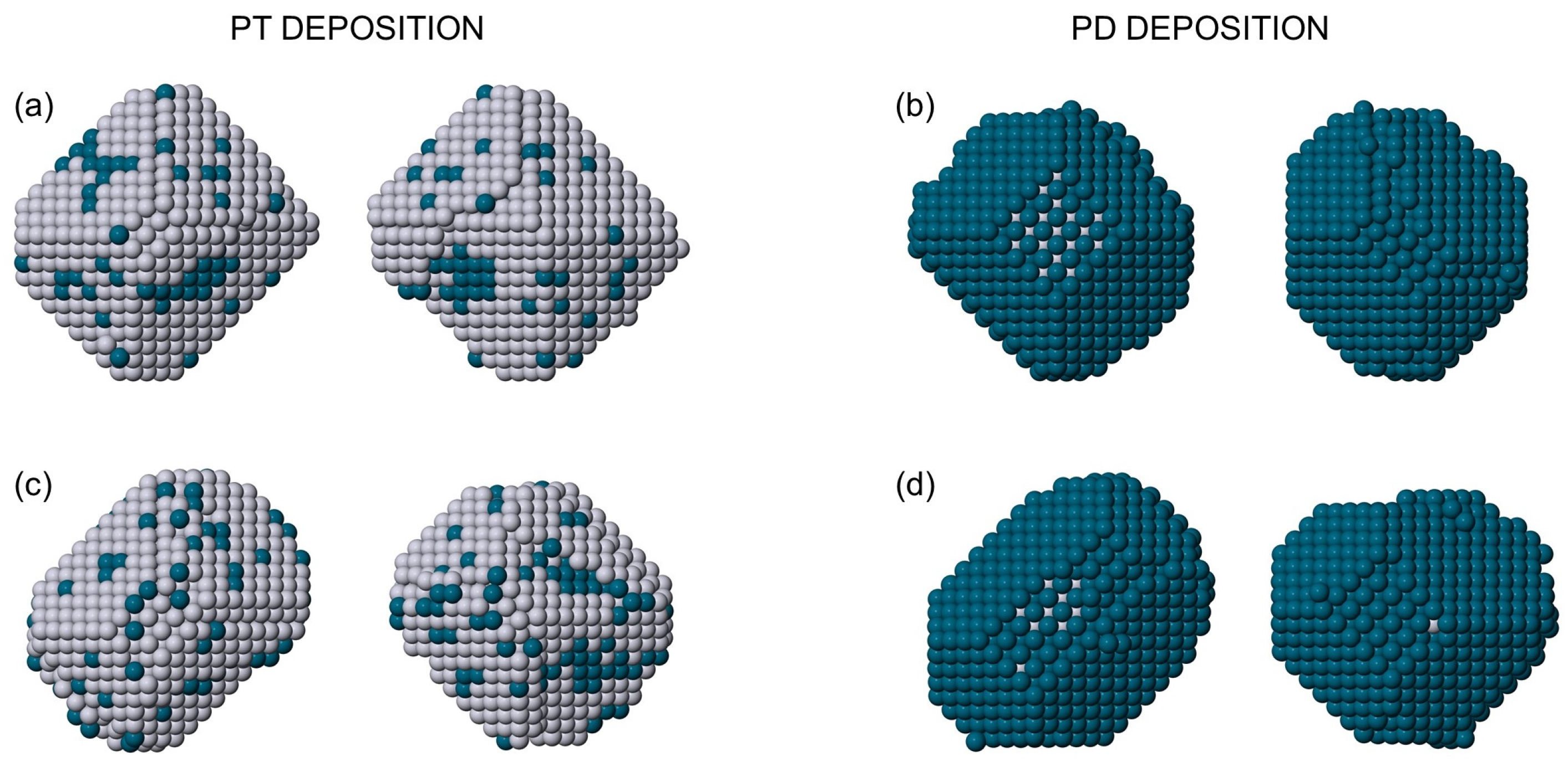
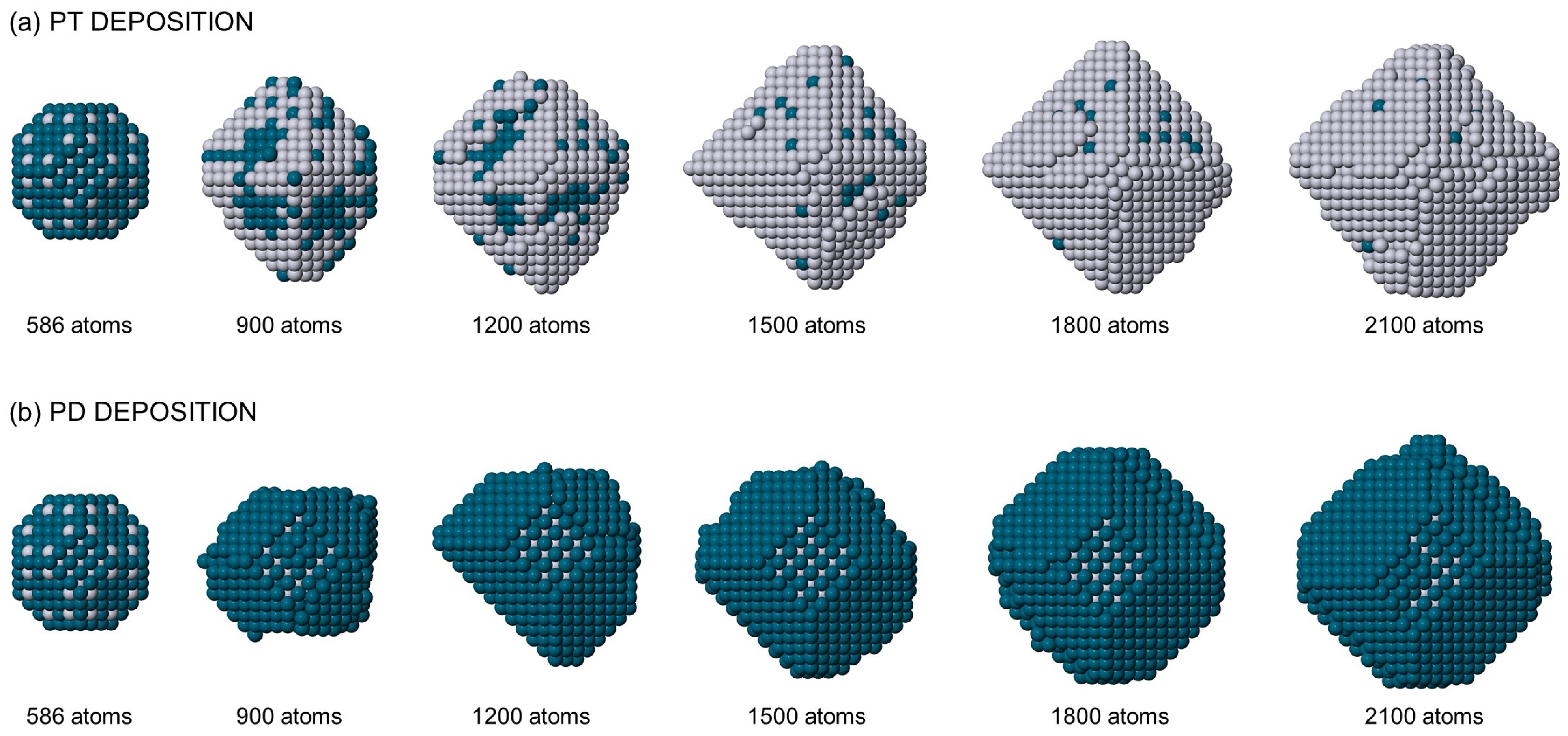
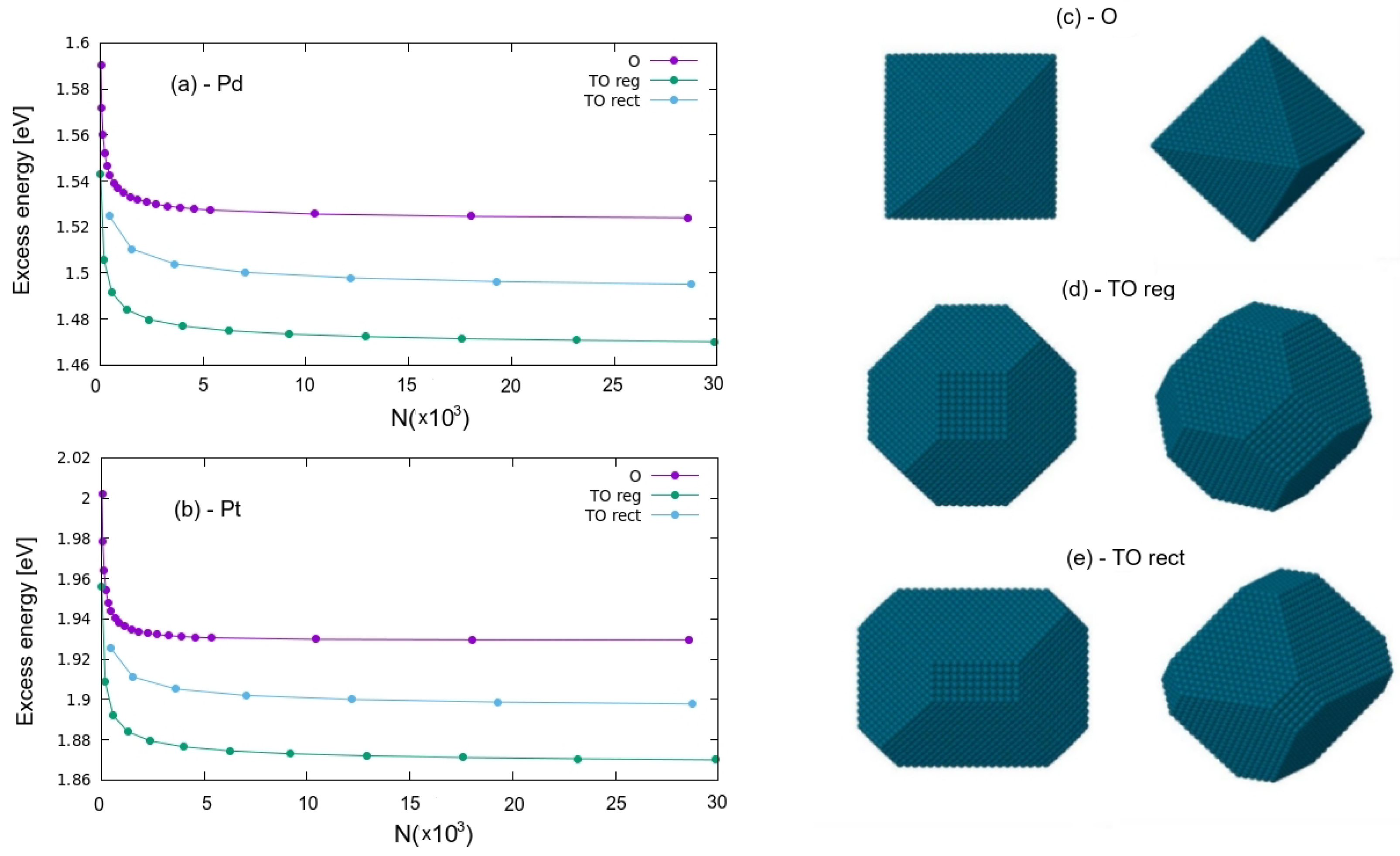
2.4. Simulation Results
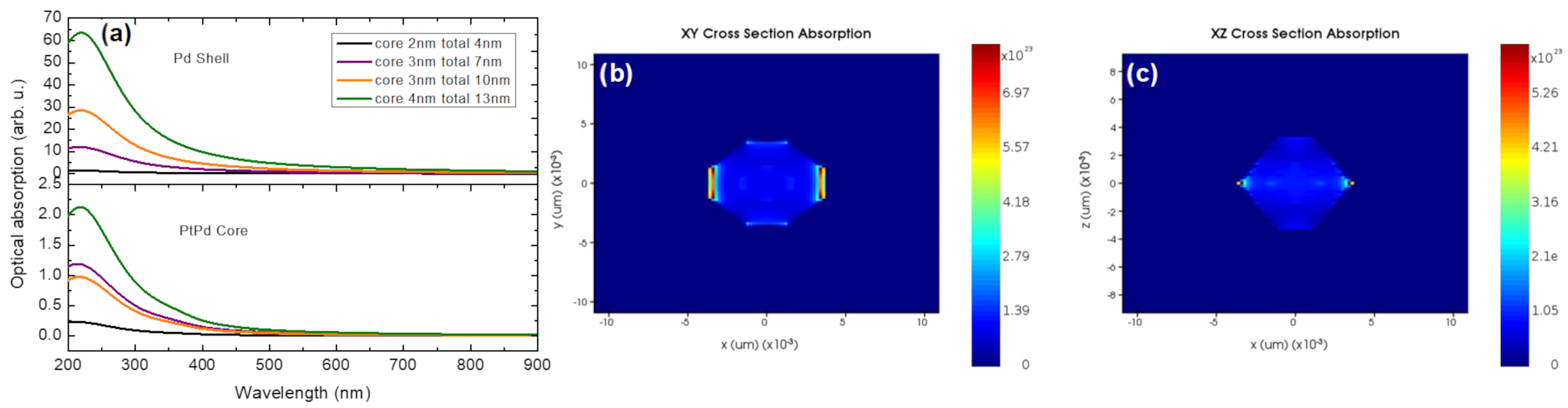
3. Optical Simulations of (Ptpd)@Pd Nanocrystals
4. Materials and Methods
4.1. Experimental Methods
4.2. Model and Simulation Methods
4.3. Optical Simulation Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ferrando, R.; Jellinek, J.; Johnston, R.L. Nanoalloys: From Theory to Applications of Alloy Clusters and Nanoparticles. Chem. Rev. 2008, 108, 845–910. [Google Scholar] [CrossRef] [PubMed]
- Ghosh Chaudhuri, R.; Paria, S. Core/Shell Nanoparticles: Classes, Properties, Synthesis Mechanisms, Characterization, and Applications. Chem. Rev. 2012, 112, 2373–2433. [Google Scholar] [CrossRef] [PubMed]
- Calvo, F. (Ed.) Nanoalloys from Fundamentals to Emergent Applications; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Ferrando, R. Structure and Properties of Nanoalloys; Frontiers of Nanoscience; Elsevier: Amsterdam, The Netherlands, 2016; Volume 10. [Google Scholar]
- Gilroy, K.D.; Ruditskiy, A.; Peng, H.C.; Qin, D.; Xia, Y. Bimetallic Nanocrystals: Syntheses, Properties, and Applications. Chem. Rev. 2016, 116, 10414–10472. [Google Scholar] [CrossRef] [PubMed]
- McNamara, K.; Tofail, S.A.M. Nanoparticles in biomedical applications. Adv. Phys. X 2017, 2, 54–88. [Google Scholar] [CrossRef]
- Huttel, Y.; Martinez, L.; Mayoral, A.; Fernández, I. Gas-phase synthesis of nanoparticles: Present status and perspectives. MRS Commun. 2018, 8, 947–954. [Google Scholar] [CrossRef]
- Nelli, D.; Krishnadas, A.; Ferrando, R.; Minnai, C. One-Step Growth of Core–Shell (PtPd)@Pt and (PtPd)@Pd Nanoparticles in the Gas Phase. J. Phys. Chem. C 2020, 124, 14338–14349. [Google Scholar] [CrossRef]
- Nelli, D.; Cerbelaud, M.; Ferrando, R.; Minnai, C. Tuning the coalescence degree in the growth of Pt–Pd nanoalloys. Nanoscale Adv. 2021, 3, 836–846. [Google Scholar] [CrossRef]
- Zhao, J.; Baibuz, E.; Vernieres, J.; Grammatikopoulos, P.; Jansson, V.; Nagel, M.; Steinhauer, S.; Sowwan, M.; Kuronen, A.; Nordlund, K.; et al. Formation Mechanism of Fe Nanocubes by Magnetron Sputtering Inert Gas Condensation. ACS Nano 2016, 10, 4684–4694. [Google Scholar] [CrossRef]
- Vernieres, J.; Steinhauer, S.; Zhao, J.; Grammatikopoulos, P.; Ferrando, R.; Nordlund, K.; Djurabekova, F.; Sowwan, M. Site-Specific Wetting of Iron Nanocubes by Gold Atoms in Gas-Phase Synthesis. Adv. Sci. 2019, 6, 1900447. [Google Scholar] [CrossRef]
- Wells, D.M.; Rossi, G.; Ferrando, R.; Palmer, R.E. Metastability of the atomic structures of size-selected gold nanoparticles. Nanoscale 2015, 7, 6498–6504. [Google Scholar] [CrossRef]
- Grammatikopoulos, P.; Kioseoglou, J.; Galea, A.; Vernieres, J.; Benelmekki, M.; Diaz, R.E.; Sowwan, M. Kinetic trapping through coalescence and the formation of patterned Ag-Cu nanoparticles. Nanoscale 2016, 8, 9780–9790. [Google Scholar] [CrossRef] [PubMed]
- Liao, T.W.; Yadav, A.; Hu, K.J.; van der Tol, J.; Cosentino, S.; D’Acapito, F.; Palmer, R.E.; Lenardi, C.; Ferrando, R.; Grandjean, D.; et al. Unravelling the nucleation mechanism of bimetallic nanoparticles with composition-tunable core-shell arrangement. Nanoscale 2018, 10, 6684–6694. [Google Scholar] [CrossRef] [PubMed]
- Pirart, J.; Front, A.; Rapetti, D.; Andreazza-Vignolle, C.; Andreazza, P.; Mottet, C.; Ferrando, R. Reversed size-dependent stabilization of ordered nanophases. Nat. Commun. 2019, 10, 1982. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, N.; Bon, M.; Passerone, D.; Erni, R. Template-Assisted in Situ Synthesis of Ag@Au Bimetallic Nanostructures Employing Liquid-Phase Transmission Electron Microscopy. ACS Nano 2019, 13, 13333–13342. [Google Scholar] [CrossRef] [PubMed]
- Nelli, D.; Rossi, G.; Wang, Z.; Palmer, R.E.; Ferrando, R. Structure and orientation effects in the coalescence of Au clusters. Nanoscale 2020, 12, 7688–7699. [Google Scholar] [CrossRef] [PubMed]
- Nelli, D.; Ferrando, R. Core-shell vs. multi-shell formation in nanoalloy evolution from disordered configurations. Nanoscale 2019, 11, 13040–13050. [Google Scholar] [CrossRef]
- Foster, D.M.; Ferrando, R.; Palmer, R.E. Experimental determination of the energy difference between competing isomers of deposited, size-selected gold nanoclusters. Nat. Commun. 2018, 9, 1323. [Google Scholar] [CrossRef]
- Andreazza, P.; Lemoine, A.; Coati, A.; Nelli, D.; Ferrando, R.; Garreau, Y.; Creuze, J.; Andreazza-Vignolle, C. From metastability to equilibrium during the sequential growth of Co–Ag supported clusters: A real-time investigation. Nanoscale 2021, 13, 6096–6104. [Google Scholar] [CrossRef]
- Llamosa, D.; Ruano, M.; Martinez, L.; Mayoral, A.; Roman, E.; Garcia-Hernández, M.; Huttel, Y. The ultimate step towards a tailored engineering of core@ shell and core@ shell@ shell nanoparticles. Nanoscale 2014, 6, 13483–13486. [Google Scholar] [CrossRef]
- Minnai, C.; Cremonesi, L.; Milani, P.; Potenza, M.A. A very simple scheme for spectrally resolved imaging by means of curved polymeric gratings. Mater. Res. Express 2019, 6, 065044. [Google Scholar] [CrossRef]
- Minnai, C.; Di Vece, M.; Milani, P. Mechanical-optical-electro modulation by stretching a polymer-metal nanocomposite. Nanotechnology 2017, 28, 355702. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Li, Y.; Li, Y.; Zhou, H.; Duan, X.; Huang, Y. Synthesis of PtPd bimetal nanocrystals with controllable shape, composition, and their tunable catalytic properties. Nano Lett. 2012, 12, 4265–4270. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Jin, M.; Xia, Y. Enhancing the catalytic and electrocatalytic properties of Pt-based catalysts by forming bimetallic nanocrystals with Pd. Chem. Soc. Rev. 2012, 41, 8035–8049. [Google Scholar] [CrossRef] [PubMed]
- Lim, B.; Jiang, M.; Camargo, P.H.C.; Cho, E.C.; Tao, J.; Lu, X.; Zhu, Y.; Xia, Y. Pd-Pt Bimetallic Nanodendrites with High Activity for Oxygen Reduction. Science 2009, 324, 1302–1305. [Google Scholar] [CrossRef] [PubMed]
- Peng, Z.; Yang, H. Synthesis and Oxygen Reduction Electrocatalytic Property of Pt-on-Pd Bimetallic Heteronanostructures. J. Am. Chem. Soc. 2009, 131, 7542–7543. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Nemoto, Y.; Yamauchi, Y. Direct Synthesis of Spatially-Controlled Pt-on-Pd Bimetallic Nanodendrites with Superior Electrocatalytic Activity. J. Am. Chem. Soc. 2011, 133, 9674–9677. [Google Scholar] [CrossRef] [PubMed]
- Yin, A.X.; Min, X.Q.; Zhang, Y.W.; Yan, C.H. Shape-Selective Synthesis and Facet-Dependent Enhanced Electrocatalytic Activity and Durability of Monodisperse Sub-10 nm Pt−Pd Tetrahedrons and Cubes. J. Am. Chem. Soc. 2011, 133, 3816–3819. [Google Scholar] [CrossRef]
- Khanal, S.; Casillas, G.; Velazquez-Salazar, J.J.; Ponce, A.; Jose-Yacaman, M. Atomic resolution imaging of polyhedral PtPd core–shell nanoparticles by Cs-corrected STEM. J. Phys. Chem. C 2012, 116, 23596–23602. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Zhang, D.; Zhao, W.; Cui, M.; Liang, R.; Ou, Q.; Zhang, S. Plasma-synthesized octahedral PtPd alloy/reduced graphene oxide nanocomposites with boosted electrocatalytic activity for methanol oxidation. J. Alloy. Compd. 2020, 835, 155334. [Google Scholar] [CrossRef]
- Faraone, G.; Modi, R.; Marom, S.; Podestà, A.; Di Vece, M. Increasing the optical absorption in a-Si thin films by embedding gold nanoparticles. Opt. Mater. 2018, 75, 204–210. [Google Scholar] [CrossRef]
- Popok, V.N.; Gurevich, L. Charge states of size-selected silver nanoparticles produced by magnetron sputtering. J. Nanoparticle Res. 2019, 21, 171. [Google Scholar] [CrossRef]
- Huang, D.B.; Yuan, Q.; Wang, H.H.; Zhou, Z.Y. Facile synthesis of PdPt nanoalloys with sub-2.0 nm islands as robust electrocatalysts for methanol oxidation. Chem. Commun. 2014, 50, 13551–13554. [Google Scholar] [CrossRef] [PubMed]
- Huttel, Y. Gas-Phase Synthesis of Nanoparticles; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Pratontep, S.; Carroll, S.J.; Xirouchaki, C.; Streun, M.; Palmer, R.E. Size-selected cluster beam source based on radio frequency magnetron plasma sputtering and gas condensation. Rev. Sci. Instrum. 2005, 76, 045103. [Google Scholar] [CrossRef]
- Baletto, F.; Ferrando, R. Structural properties of nanoclusters: Energetic, thermodynamic, and kinetic effects. Rev. Mod. Phys. 2005, 77, 371–423. [Google Scholar] [CrossRef]
- Baletto, F.; Ferrando, R.; Fortunelli, A.; Montalenti, F.; Mottet, C. Crossover among structural motifs in transition and noble-metal clusters. J. Chem. Phys. 2002, 116, 3856. [Google Scholar] [CrossRef]
- Baletto, F.; Mottet, C.; Ferrando, R. Molecular dynamics simulations of surface diffusion and growth on silver and gold clusters. Surf. Sci. 2000, 446, 31–45. [Google Scholar] [CrossRef]
- Bigall, N.C.; Hartling, T.; Klose, M.; Simon, P.; Eng, L.M.; Eychmuller, A. Monodisperse platinum nanospheres with adjustable diameters from 10 to 100 nm: Synthesis and distinct optical properties. Nano Lett. 2008, 8, 4588–4592. [Google Scholar] [CrossRef]
- Tao, A.R.; Habas, S.; Yang, P. Shape control of colloidal metal nanocrystals. Small 2008, 4, 310–325. [Google Scholar] [CrossRef]
- Ozbay, E. Plasmonics: Merging photonics and electronics at nanoscale dimensions. science 2006, 311, 189–193. [Google Scholar] [CrossRef]
- Johnson, G.E.; Colby, R.; Laskin, J. Soft landing of bare nanoparticles with controlled size, composition, and morphology. Nanoscale 2015, 7, 3491–3503. [Google Scholar] [CrossRef]
- Mayoral, A.; Mejia-Rosales, S.; Mariscal, M.M.; Perez-Tijerina, E.; Jose-Yacaman, M. The Co-Au interface in bimetallic nanoparticles: A high resolution STEM study. Nanoscale 2010, 2, 2647–2651. [Google Scholar] [CrossRef] [PubMed]
- Cyrot-Lackmann, F.; Ducastelle, F. Binding Energies of Transition-Metal Atoms Adsorbed on a Transition Metal. Phys. Rev. B 1971, 4, 2406–2412. [Google Scholar] [CrossRef]
- Rosato, V.; Guillopé, M.; Legrand, B. Thermodynamical and structural properties of f.c.c. transition metals using a simple tight-binding model. Phil. Mag. A 1989, 59, 321. [Google Scholar] [CrossRef]
- Rossi, G.; Ferrando, R.; Rapallo, A.; Fortunelli, A.; Curley, B.C.; Lloyd, L.D.; Johnston, R.L. Global optimization of bimetallic cluster structures. I. Size-matched Ag-Pd, Ag-Au, and Pd-Pt systems. J. Chem. Phys. 2005, 122, 194309. [Google Scholar] [CrossRef] [PubMed]
- Paz-Borbón, L.O.; Johnston, R.L.; Barcaro, G.; Fortunelli, A. A Mixed Structural Motif in 34-Atom Pd-Pt Clusters. Phys. Chem. Chem. Phys. 2007, 111, 2936–2941. [Google Scholar] [CrossRef]
- Palik, E.D. Handbook of Optical Constants of Solids; Academic Press: Cambridge, MA, USA, 1998; Volume 3. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nelli, D.; Roncaglia, C.; Ahearn, S.; Di Vece, M.; Ferrando, R.; Minnai, C. Octahedral Growth of PtPd Nanocrystals. Catalysts 2021, 11, 718. https://doi.org/10.3390/catal11060718
Nelli D, Roncaglia C, Ahearn S, Di Vece M, Ferrando R, Minnai C. Octahedral Growth of PtPd Nanocrystals. Catalysts. 2021; 11(6):718. https://doi.org/10.3390/catal11060718
Chicago/Turabian StyleNelli, Diana, Cesare Roncaglia, Samuel Ahearn, Marcel Di Vece, Riccardo Ferrando, and Chloé Minnai. 2021. "Octahedral Growth of PtPd Nanocrystals" Catalysts 11, no. 6: 718. https://doi.org/10.3390/catal11060718
APA StyleNelli, D., Roncaglia, C., Ahearn, S., Di Vece, M., Ferrando, R., & Minnai, C. (2021). Octahedral Growth of PtPd Nanocrystals. Catalysts, 11(6), 718. https://doi.org/10.3390/catal11060718






