Prediction of a Stable Organic Metal-Free Porous Material as a Catalyst for Water-Splitting
Abstract
1. Introduction
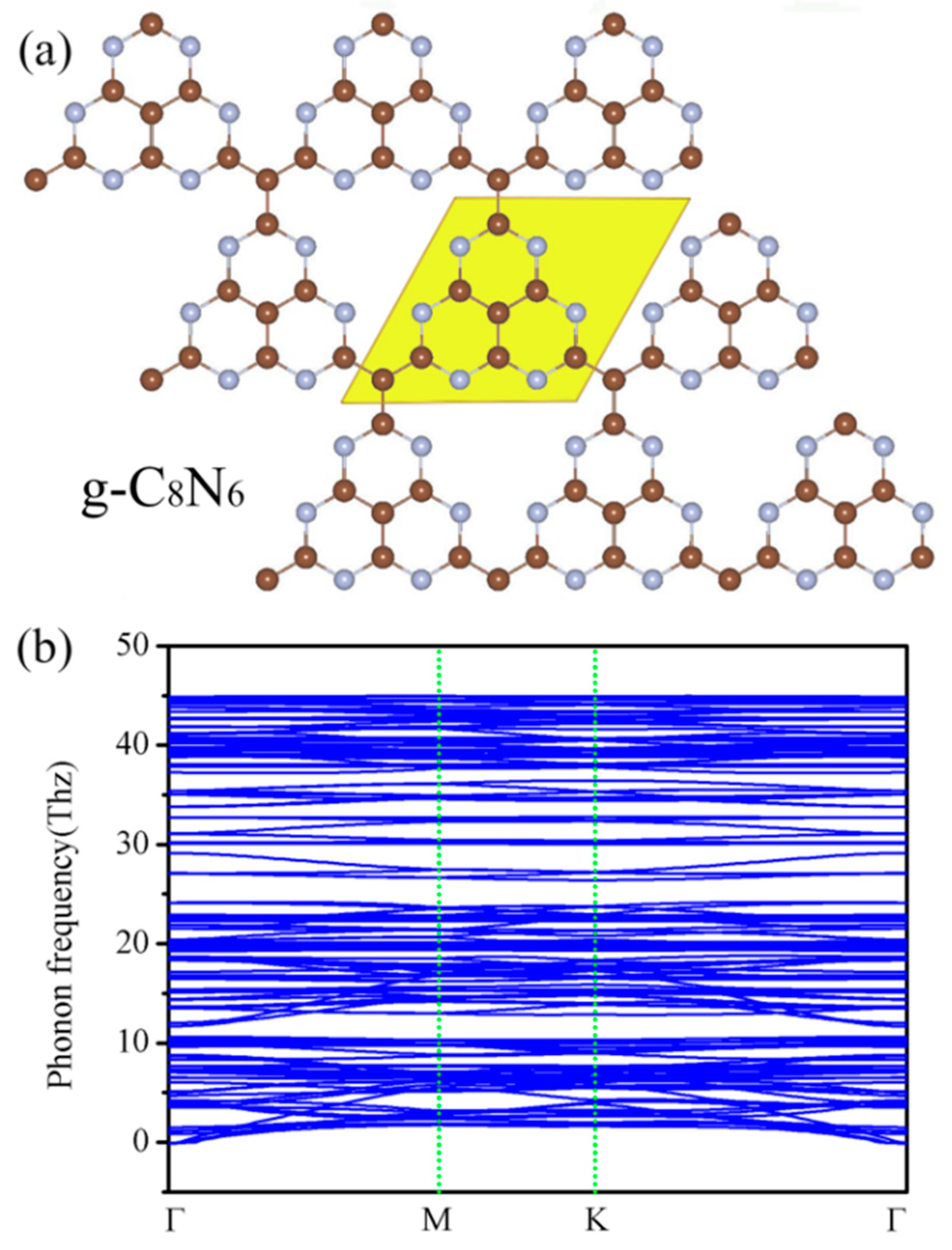
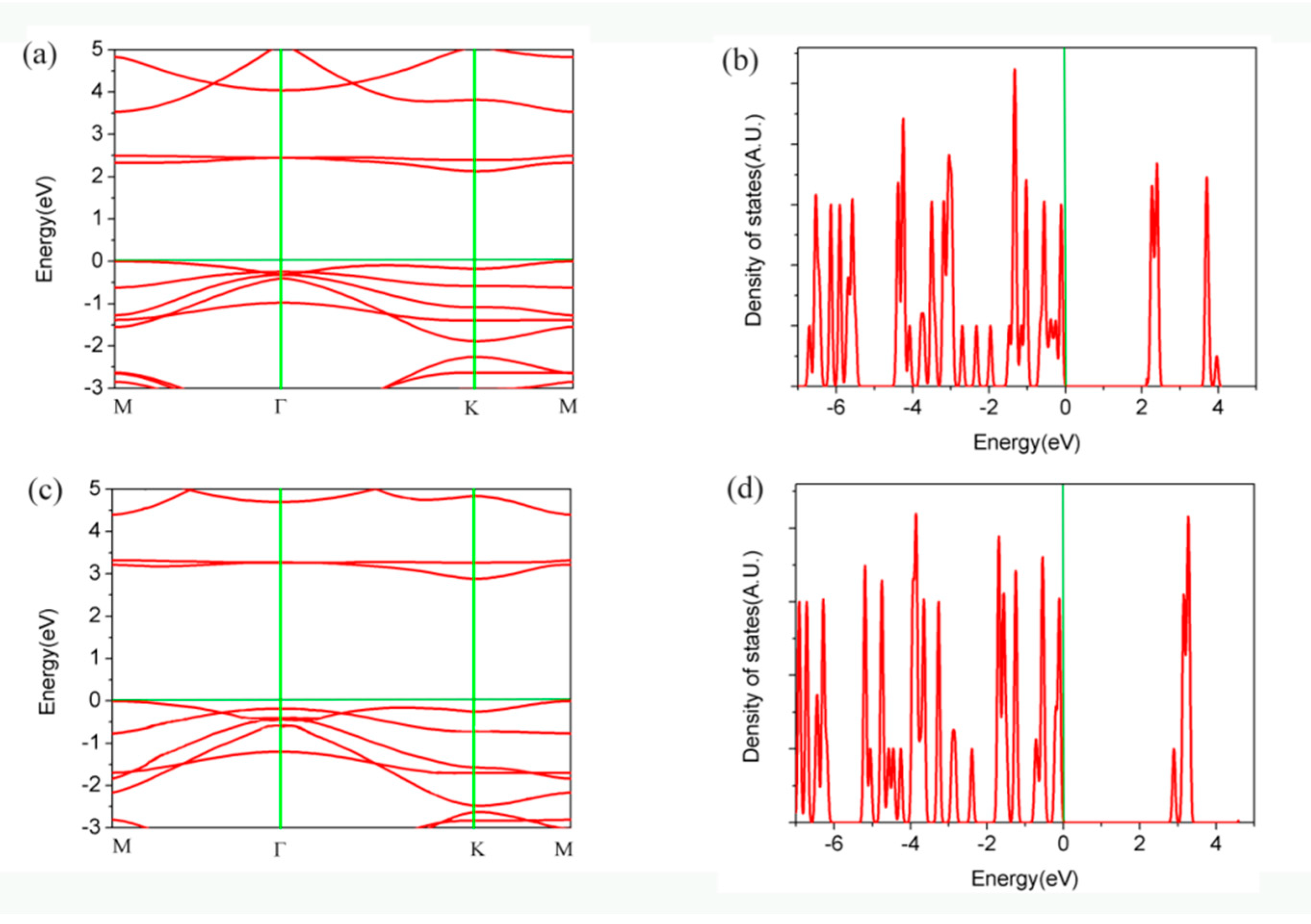
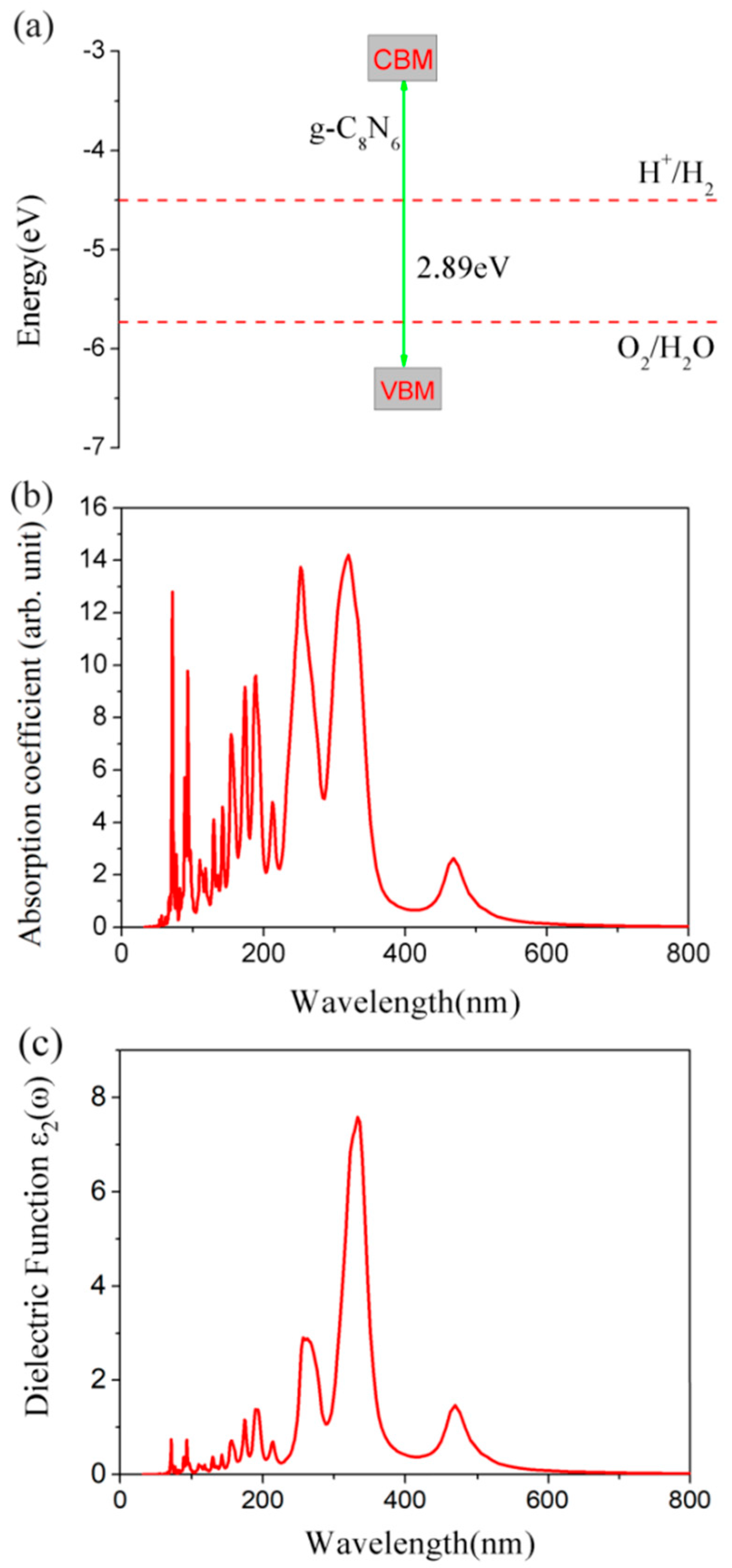
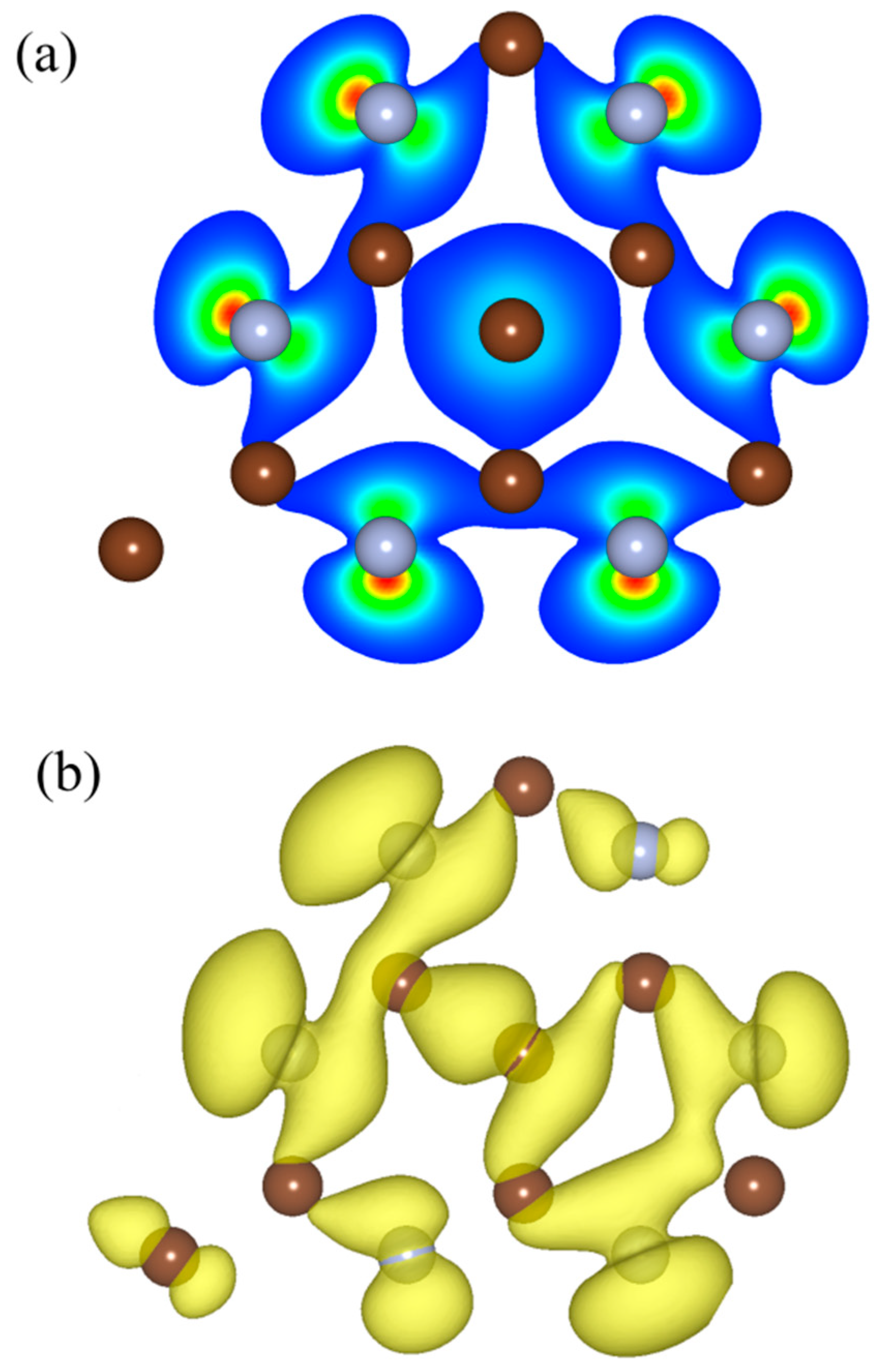
2. Results and Discussion
3. Method and Computational Details
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kroke, E.; Schwarz, M. Novel group 14 nitrides. Coord. Chem. Rev. 2004, 248, 493–532. [Google Scholar] [CrossRef]
- Chen, X.; Shen, S.; Guo, L.; Mao, S.S. Semiconductor-based photocatalytic hydrogen generation. Chem. Rev. 2010, 110, 6503–6570. [Google Scholar] [CrossRef] [PubMed]
- Fujishima, A.; Honda, K. Electrochemical photolysis of water at a semiconductor electrode. Nature 1972, 238, 37–38. [Google Scholar] [CrossRef] [PubMed]
- Kumaravel, V.; Kang, M. Photocatalytic Hydrogen Evolution. Catalysts 2020, 10, 492. [Google Scholar] [CrossRef]
- Ming, H.; Ming, J.; Oh, S.-M.; Lee, E.-J.; Huang, H.; Zhou, Q.; Zheng, J.; Sun, Y.-K. High dispersion of TiO2 nanocrystals within porous carbon improves lithium storage capacity and can be applied batteries to LiNi0.5Mn1.5O4. J. Mater. Chem. A 2014, 2, 18938–18945. [Google Scholar] [CrossRef]
- Xu, L.; Cui, Q.; Zhang, H.; Jiao, A.; Tian, Y.; Li, S.; Li, H.; Chen, M.; Chen, F. Ultra-clean PtPd nanoflowers loaded on GO supports with enhanced low-temperature electrocatalytic activity for fuel cells in harsh environment. Appl. Surf. Sci. 2020, 511, 145603. [Google Scholar] [CrossRef]
- Park, J.H.; Kim, S.; Bard, A.J. Novel carbon-doped TiO2 nanotube arrays with high aspect ratios for efficient solar water splitting. Nano Lett. 2006, 6, 24–28. [Google Scholar] [CrossRef]
- Hua, J.; Liu, Y.L.; Li, H.S.; Zhao, M.W.; Liu, X.D. Effect of the alloying element titanium on the stability and trapping of hydrogen in pure vanadium: A first-principles study. Int. J. Mod. Phys. B 2014, 28, 1450207. [Google Scholar] [CrossRef]
- Ksibi, M.; Rossignol, S.; Tatibouët, J.-M.; Trapalis, C. Synthesis and solid characterization of nitrogen and sulfur-doped TiO2 photocatalysts active under near visible light. Mater. Lett. 2008, 62, 4204–4206. [Google Scholar] [CrossRef]
- Cheng, Y.W.; Chan, R.C.; Wong, P. Disinfection of Legionella pneumophila by photocatalytic oxidation. Water Res. 2007, 41, 842–852. [Google Scholar] [CrossRef]
- Yu, J.; Xiang, Q.; Zhou, M. Preparation, characterization and visible-light-driven photocatalytic activity of Fe-doped titania nanorods and first-principles study for electronic structures. Appl. Catal. B: Environ. 2009, 90, 595–602. [Google Scholar] [CrossRef]
- Liu, S.; Yu, J.; Jaroniec, M. Tunable photocatalytic selectivity of hollow TiO2 microspheres composed of anatase polyhedra with exposed {001} facets. J. Am. Chem. Soc. 2010, 132, 11914–11916. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Xie, X.; Wang, H.; Zhang, J.; Pan, B.; Xie, Y. Enhanced photoresponsive ultrathin graphitic-phase C3N4 nanosheets for bioimaging. J. Am. Chem. Soc. 2013, 135, 18–21. [Google Scholar] [CrossRef] [PubMed]
- Su, D.S.; Zhang, J.; Frank, B.; Thomas, A.; Wang, X.; Paraknowitsch, J.; Schlögl, R. Metal-free heterogeneous catalysis for sustainable chemistry. Chemsuschem: Chem. Sustain. Energy Mater. 2010, 3, 169–180. [Google Scholar] [CrossRef]
- Hua, J.; Liu, Y.L.; Li, H.S.; Zhao, M.W.; Liu, X.D. Energetics of carbon and nitrogen impurities and their interactions with vacancy in vanadium. Chin. Phys. B 2016, 25, 036104. [Google Scholar] [CrossRef]
- Xiao, W.; Jin, X.; Chen, G.Z. Up-scalable and controllable electrolytic production of photo-responsive nanostructured silicon. J. Mater. Chem. A 2013, 1, 10243–10250. [Google Scholar] [CrossRef]
- Ng, C.H.; Winther-Jensen, O.; Ohlin, C.A.; Winther-Jensen, B. Exploration and optimisation of poly (2, 2′-bithiophene) as a stable photo-electrocatalyst for hydrogen production. J. Mater. Chem. A 2015, 3, 11358–11366. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef]
- Bunch, J.S.; Van Der Zande, A.M.; Verbridge, S.S.; Frank, I.W.; Tanenbaum, D.M.; Parpia, J.M.; Craighead, H.G.; McEuen, P.L. Electromechanical resonators from graphene sheets. Science 2007, 315, 490–493. [Google Scholar] [CrossRef]
- Lee, C.; Wei, X.W.; Kysar, J.W.; Hone, J. Measurement of the elastic properties and intrinsic strength of monolayer grapheme. Science 2008, 321, 385–388. [Google Scholar] [CrossRef]
- Meyer, J.C.; Geim, A.K.; Katsnelson, M.I.; Novoselov, K.S.; Booth, T.J.; Roth, S. The structure of suspended graphene sheets. Nature 2007, 446, 60. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef] [PubMed]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183. [Google Scholar] [CrossRef]
- Li, H.; Hu, H.; Bao, C.; Zhang, X.; Wang, A.; Zhou, H.; Zhao, M. The strability and electronic structure of Fe atoms embedded in zigzag graphene nanoribbons. Phys. B: Condens. Matter 2014, 441, 28–32. [Google Scholar] [CrossRef]
- Xu, M.; Liang, T.; Shi, M.; Chen, H. Graphene-like two-dimensional materials. Chem. Rev. 2013, 113, 3766–3798. [Google Scholar] [CrossRef]
- Zhang, H.; Cui, Q.; Xu, L.; Jiao, A.; Tian, Y.; Liu, X.; Li, S.; Li, H.; Chen, M.; Chen, F. Blue laser-induced photochemical synthesis of CuAg nanoalloys on h-BN supports with enhanced SERS activity for trace-detection of residual pesticides on tomatoes. J. Alloy. Compd. 2020, 825, 153996. [Google Scholar] [CrossRef]
- Saleem, Z.; Pervaiz, E.; Yousaf, M.U.; Niazi, M.B.K. Two-dimensional materials and composites as potential water splitting photocatalysts: A review. Catalysts 2020, 10, 464. [Google Scholar] [CrossRef]
- Li, H.; Hu, H.; Bai, C.; Bao, C.; Feng, Z.; Guo, F. The metal-free magnetism and ferromagnetic narrow gap semiconductor properties in graphene-like carbon nitride. Phys. B: Condens. Matter 2019, 555, 91–95. [Google Scholar] [CrossRef]
- Wang, X.; Maeda, K.; Thomas, A.; Takanabe, K.; Xin, G.; Carlsson, J.M.; Domen, K.; Antonietti, M. A metal-free polymeric photocatalyst for hydrogen production from water under visible light. Nat. Mater. 2009, 8, 76–80. [Google Scholar] [CrossRef]
- Liu, G.; Niu, P.; Sun, C.; Smith, S.C.; Chen, Z.; Lu, G.Q.; Cheng, H.-M. Unique electronic structure induced high photoreactivity of sulfur-doped graphitic C3N4. J. Am. Chem. Soc. 2010, 132, 11642–11648. [Google Scholar] [CrossRef]
- Zhang, J.; Sun, J.; Maeda, K.; Domen, K.; Liu, P.; Antonietti, M.; Fu, X.; Wang, X. Sulfur-mediated synthesis of carbon nitride: Band-gap engineering and improved functions for photocatalysis. Energy Environ. Sci. 2011, 4, 675–678. [Google Scholar] [CrossRef]
- Wu, F.; Liu, Y.; Yu, G.; Shen, D.; Wang, Y.; Kan, E. Visible-light-absorption in graphitic C3N4 bilayer: Enhanced by interlayer coupling. J. Phys. Chem. Lett. 2012, 3, 3330–3334. [Google Scholar] [CrossRef]
- Maeda, K.; Wang, X.; Nishihara, Y.; Lu, D.; Antonietti, M.; Domen, K. Photocatalytic activities of graphitic carbon nitride powder for water reduction and oxidation under visible light. J. Phys. Chem. C 2009, 113, 4940–4947. [Google Scholar] [CrossRef]
- Zhu, Y.-P.; Li, M.; Liu, Y.-L.; Ren, T.-Z.; Yuan, Z.-Y. Carbon-doped ZnO hybridized homogeneously with graphitic carbon nitride nanocomposites for photocatalysis. J. Phys. Chem. C 2014, 118, 10963–10971. [Google Scholar] [CrossRef]
- Du, A.; Sanvito, S.; Li, Z.; Wang, D.; Jiao, Y.; Liao, T.; Sun, Q.; Ng, Y.H.; Zhu, Z.; Amal, R. Hybrid graphene and graphitic carbon nitride nanocomposite: Gap opening, electron–hole puddle, interfacial charge transfer, and enhanced visible light response. J. Am. Chem. Soc. 2012, 134, 4393–4397. [Google Scholar] [CrossRef]
- Takanabe, K.; Kamata, K.; Wang, X.; Antonietti, M.; Kubota, J.; Domen, K. Photocatalytic hydrogen evolution on dye-sensitized mesoporous carbon nitride photocatalyst with magnesium phthalocyanine. Phys. Chem. Chem. Phys. 2010, 12, 13020–13025. [Google Scholar] [CrossRef]
- Suter, T.M.; Brazdova, V.; Mccoll, K.; Miller, T.S.; Nagashima, H.; Salvadori, E.; Sella, A.; Howard, C.H.; Kay, C.W.M.; Cora, F.; et al. Synthesis, structure and electronic properties of graphitic carbon nitride films. J. Phys. Chem. C 2018, 122, 25183–25194. [Google Scholar] [CrossRef]
- Li, H.; Hu, H.; Bao, C.; Hua, J.; Zhou, H.; Liu, X.; Liu, X.; Zhao, M. Tensile strain induced half-metallicity in graphene-like carbon nitride. Phys. Chem. Chem. Phys. 2015, 17, 6028–6035. [Google Scholar] [CrossRef]
- Mahmood, J.; Lee, E.K.; Jung, M.; Shin, D.; Jeon, I.-Y.; Jung, S.-M.; Choi, H.-J.; Seo, J.-M.; Bae, S.-Y.; Sohn, S.-D. Nitrogenated holey two-dimensional structures. Nat. Commun. 2015, 6, 6486. [Google Scholar] [CrossRef]
- Li, H.; Hu, H.; Bao, C.; Feng, Z.; Guo, F.; Tian, G.; Liu, Y. Potential application of a porous graphitic carbon nitride as an organic metal-free photocatalyst for water splitting. Diam. Relat. Mater. 2018, 87, 50–55. [Google Scholar] [CrossRef]
- Li, H.; Hu, H.; Bao, C.; Guo, F.; Zhang, X.; Liu, X.; Hua, J.; Tan, J.; Wang, A.; Zhou, H. Forming heterojunction: An effective strategy to enhance the photocatalytic efficiency of a new metal-free organic photocatalyst for water splitting. Sci. Rep. 2016, 6, 29327. [Google Scholar] [CrossRef] [PubMed]
- Guan, S.; Cheng, Y.; Liu, C.; Han, J.; Lu, Y.; Yang, S.A.; Yao, Y. Effects of strain on electronic and optic properties of holey two-dimensional C2N crystals. Appl. Phys. Lett. 2015, 107, 231904. [Google Scholar] [CrossRef]
- Li, H.; Hu, H.; Bai, C.; Bao, C.; Guo, F.; Feng, Z.; Liu, Y. The charge regulation of electronic structure and optical properties of graphitic carbon nitride under strain. Rsc. Adv. 2019, 9, 7464–7468. [Google Scholar] [CrossRef]
- Yang, G.; Li, L.; Lee, W.B.; Ng, M.C. Structure of graphene and its disorders: A review. Sci. Technol. Adv. Mater. 2018, 19, 613–648. [Google Scholar] [CrossRef]
- Van, T.B.; Torrent, M.; Gonze, X. Interatomic force constants including the DFT-D dispersion contribution. Phys. Rev. B 2016, 93, 144304. [Google Scholar]
- Pike, N.; Dewandre, A.; Van Troeye, B.; Gonze, X.; Verstraete, M. Vibrational and dielectric properties of the bulk transition metal dichalcogenides. Phys. Rev. Mater. 2018, 2, 063608. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.E. Efficient hybrid density functional calculations in solids: Assessment of the Heyd–Scuseria–Ernzerhof screened Coulomb hybrid functional. J. Chem. Phys. 2004, 121, 1187–1192. [Google Scholar] [CrossRef] [PubMed]
- Gajdoš, M.; Hummer, K.; Kresse, G.; Furthmüller, J.; Bechstedt, F. Linear optical properties in the projector-augmented wave methodology. Phys. Rev. B 2006, 73, 045112. [Google Scholar]
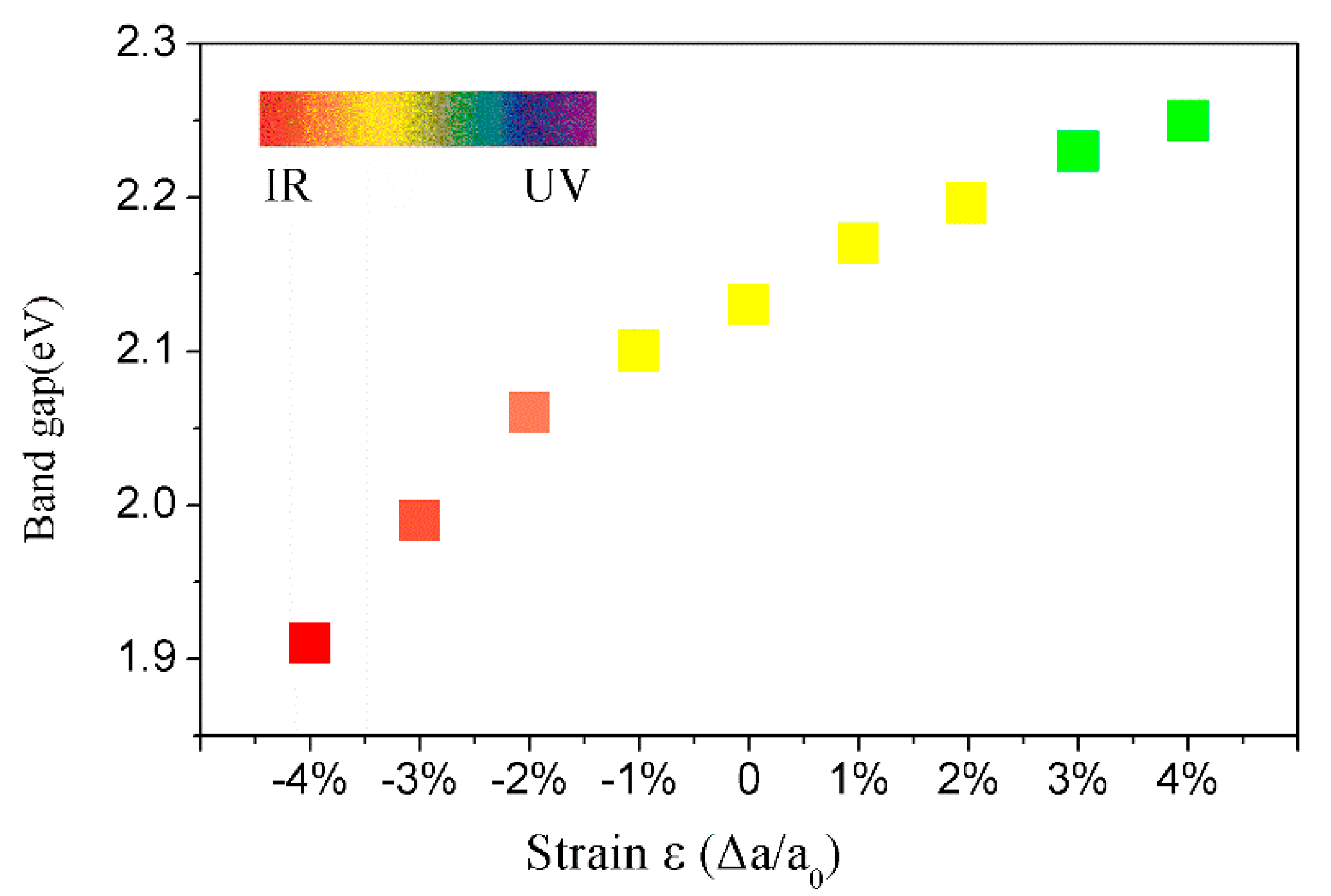
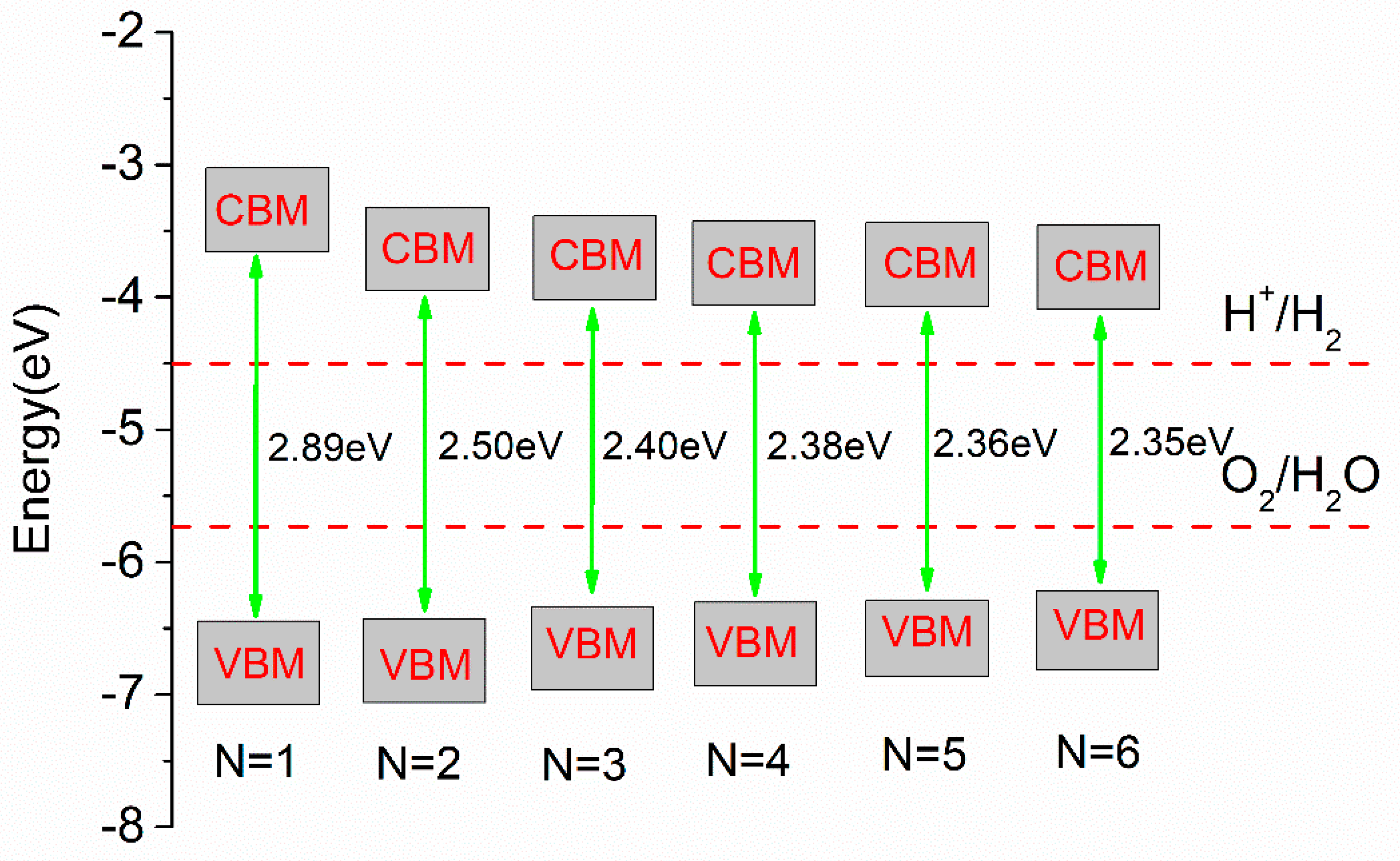
| N | 1 | 2 | 3 | 4 | 5 | 6 | N |
|---|---|---|---|---|---|---|---|
| WF (eV) | 5.30 | 5.28 | 5.30 | 5.26 | 5.29 | 5.30 | 5.30 |
| Eg (eV) | 2.89 | 2.50 | 2.40 | 2.38 | 2.36 | 2.35 | 2.35 |
| ΔEg (eV) | 0.00 | 0.39 | 0.49 | 0.51 | 0.53 | 0.54 | 0.54 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Hu, H.; Bai, C.; Bao, C.; Liu, C.; Wang, Q.; Guo, F.; Feng, Z.; Yu, H.; Chen, M.; et al. Prediction of a Stable Organic Metal-Free Porous Material as a Catalyst for Water-Splitting. Catalysts 2020, 10, 836. https://doi.org/10.3390/catal10080836
Li H, Hu H, Bai C, Bao C, Liu C, Wang Q, Guo F, Feng Z, Yu H, Chen M, et al. Prediction of a Stable Organic Metal-Free Porous Material as a Catalyst for Water-Splitting. Catalysts. 2020; 10(8):836. https://doi.org/10.3390/catal10080836
Chicago/Turabian StyleLi, Hengshuai, Haiquan Hu, Chenglin Bai, Chunjiang Bao, Cailong Liu, Qinglin Wang, Feng Guo, Zhenbao Feng, Hanwen Yu, Ming Chen, and et al. 2020. "Prediction of a Stable Organic Metal-Free Porous Material as a Catalyst for Water-Splitting" Catalysts 10, no. 8: 836. https://doi.org/10.3390/catal10080836
APA StyleLi, H., Hu, H., Bai, C., Bao, C., Liu, C., Wang, Q., Guo, F., Feng, Z., Yu, H., Chen, M., & Qu, K. (2020). Prediction of a Stable Organic Metal-Free Porous Material as a Catalyst for Water-Splitting. Catalysts, 10(8), 836. https://doi.org/10.3390/catal10080836





