Prescriptive Norms and Social Comparisons
Abstract
:1. Introduction
2. Model
3. Equilibrium Contributions Under Each Social Comparison Method
3.1. Bottom-Contributor Comparison
3.2. Top-Contributor Comparison
3.3. Median-Contributor Comparison
4. Comparing the Social-Comparison Methods
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Proofs
Appendix A.1. Proof of Proposition 1
Appendix A.2. Proof of Proposition 2
Appendix A.3. Proof of Proposition 3
Appendix A.4. Proof of Proposition 4
Appendix A.4.1. Proof of the proposition
References
- Cialdini, R.B.; Kallgren, C.A.; Reno, R.R. A focus theory of normative conduct: A theoretical refinement and reevaluation of the role of norms in human behavior. In Advances in Experimental Social Psychology; Academic Press: Cambridge, MA, USA, 1991; Volume 24, pp. 201–234. [Google Scholar]
- Schelling, T.C. The Strategy of Conflict; Harvard University Press: Cambridge, MA, USA, 1960. [Google Scholar]
- Lewis, D.K. Convention: A Philosophical Study; Harvard University Press: Cambridge, MA, USA, 1969. [Google Scholar]
- Granovetter, M. Threshold Models of Collective Behavior. Am. J. Sociol. 1978, 83, 1420–1443. [Google Scholar] [CrossRef]
- Young, H.P. The Evolution of Conventions. Econometrica 1993, 61, 57–84. [Google Scholar] [CrossRef]
- Michaeli, M.; Spiro, D. From Peer Pressure to Biased Norms. Am. Econ. J. Microecon. 2017, 9, 152–216. [Google Scholar] [CrossRef]
- Carvalho, J.P. Coordination and culture. Econ. Theory 2017, 64, 449–475. [Google Scholar] [CrossRef]
- Krupka, E.L.; Weber, R.A. Identifying social norms using coordination games: Why does dictator game sharing vary? J. Eur. Econ. Assoc. 2013, 11, 495–524. [Google Scholar] [CrossRef]
- Cialdini, R.B. Crafting normative messages to protect the environment. Curr. Directi. Psychol. Sci. 2003, 12, 105–109. [Google Scholar] [CrossRef]
- Blumenthal, M.; Christian, C.; Slemrod, J.; Smith, M.G. Do normative appeals affect tax compliance? Evidence from a controlled experiment in Minnesota. Natl. Tax J. 2001, 54, 125–138. [Google Scholar] [CrossRef]
- Booij, A.S.; Leuven, E.; Oosterbeek, H. Ability peer effects in university: Evidence from a randomized experiment. Rev. Econ. Stud. 2017, 84, 547–578. [Google Scholar] [CrossRef]
- Young, H.P. Social norms and economic welfare1. Eur. Econ. Rev. 1998, 42, 821–830. [Google Scholar] [CrossRef]
- Jackson, M.O.; Zenou, Y. Games on networks. In Handbook of Game Theory with Economic Applications; Elsevier: Amsterdam, The Netherlands; New York, NY, USA, 2015; Volume 4, pp. 95–163. [Google Scholar]
- Nyborg, K. Social Norms and the Environment. Annu. Rev. Resour. Econ. 2018, 10, 405–423. [Google Scholar] [CrossRef]
- Bénabou, R.; Tirole, J. Incentives and Prosocial Behavior. Am. Econ. Rev. 2006, 96, 1652–1678. [Google Scholar] [CrossRef] [Green Version]
- Bénabou, R.; Tirole, J. Laws and Norms; Discussion Paper Series 6290; Institute for the Study of Labor (IZA): Bonn, Germany, 2012. [Google Scholar]
- Andreoni, J. Impure Altruism and Donations to Public Goods: A Theory of Warm-Glow Giving. Econ. J. 1990, 100, 464–477. [Google Scholar] [CrossRef]
- Harbaugh, W.T. What do donations buy?: A model of philanthropy based on prestige and warm glow. J. Public Econ. 1998, 67, 269–284. [Google Scholar] [CrossRef]
- Ledyard, J.O. Is there a problem with public goods provision. In The Handbook of Experimental Economics; Princeton University Press: Princeton, NJ, USA, 1995; pp. 111–194. [Google Scholar]
- Kandel, E.; Lazear, E.P. Peer pressure and partnerships. J. Polit. Econ. 1992, 100, 801–817. [Google Scholar] [CrossRef]
- Clark, A.E.; Oswald, A.J. Comparison-concave utility and following behaviour in social and economic settings. J. Public Econ. 1998, 70, 133–155. [Google Scholar] [CrossRef] [Green Version]
- Shang, J.; Croson, R. A field experiment in charitable contribution: The impact of social information on the voluntary provision of public goods. Econ. J. 2009, 119, 1422–1439. [Google Scholar] [CrossRef]
- Chen, Y.; Harper, F.M.; Konstan, J.; Li, S.X. Social comparisons and contributions to online communities: A field experiment on movielens. Am. Econ. Rev. 2010, 100, 1358–1398. [Google Scholar] [CrossRef]
- Rege, M.; Telle, K. The impact of social approval and framing on cooperation in public good situations. J. Public Econ. 2004, 88, 1625–1644. [Google Scholar] [CrossRef]
- Allcott, H. Social norms and energy conservation. J. Public Econ. 2011, 95, 1082–1095. [Google Scholar] [CrossRef] [Green Version]
- Frey, B.S.; Meier, S. Social comparisons and pro-social behavior: Testing “conditional cooperation” in a field experiment. Am. Econ. Rev. 2004, 94, 1717–1722. [Google Scholar] [CrossRef]
- Festinger, L. A theory of social comparison processes. Hum. Relat. 1954, 7, 117–140. [Google Scholar] [CrossRef]
- Sugden, R. Reciprocity: The supply of public goods through voluntary contributions. Econ. J. 1984, 94, 772–787. [Google Scholar] [CrossRef]
- Brekke, K.A.; Kverndokk, S.; Nyborg, K. An Economic Model of Moral Motivation. J. Public Econ. 2003, 87, 1967–1983. [Google Scholar] [CrossRef]
- Fehr, E.; Gächter, S. Cooperation and Punishment in Public Goods Experiments. Am. Econ. Rev. 2000, 90, 980–994. [Google Scholar] [CrossRef] [Green Version]
- Herrmann, B.; Thöni, C.; Gächter, S. Antisocial punishment across societies. Science 2008, 319, 1362–1367. [Google Scholar] [CrossRef] [PubMed]
- Kahneman, D.; Tversky, A. Prospect Theory: An Analysis of Decision under Risk. Econometrica 1979, 47, 263–292. [Google Scholar] [CrossRef]
| 1. | Theoretically, descriptive norms are typically modeled using coordination games (e.g., Schelling [2], Lewis [3], Granovetter [4], Young [5]). If an agent deviates from the actions of others then she will perceive a social pressure (or equivalently, losses of miscoordination). Examples of such settings would be choosing what side of the road to drive or, for situations where agents disagree about the preferred convention, when to have public holidays. The strength of and adherence to descriptive social norms has been studied by Michaeli and Spiro [6] and Carvalho [7]. |
| 2. | |
| 3. | We thus relax the strict requirement used by Young [12] who makes the very existence of the social reward contingent on others contributing something too. This requirement is also implicit in most of the network literature that analyzes public-good games with social rewards, see e.g., p. 26 in the survey by Jackson and Zenou [13]. See Nyborg [14] for a further discussion. |
| 4. | We thus depart from models, such as Bénabou and Tirole [15,16], where the social incentive of one player is independent of the actions of the others. We also depart from models with warm-glow utility from contributing to the public good (see Andreoni [17], Harbaugh [18], Ledyard [19]). Typically, warm glow preferences have the feature that the good feeling of contributing is independent of what others do. Our setting is essentially one where there is warm glow (we call it social esteem) but where the strength of this feeling depends on an endogenous reference point. Furthermore, since a player in our setting experiences a negative esteem when contributing less than the reference, we also allow for what can be interpreted as “bad conscience”. |
| 5. | We thus depart from models, such as those by Kandel and Lazear [20] and Clark and Oswald [21], where the average contribution sets the reference point. We also depart from network models since there it is typically assumed that an agent gives an exogenous weight to the comparison with each other agent independently of what the other agent does (see the survey by Jackson and Zenou [13]). In our model, this weight changes depending on what the other agent does, for instance, depending on whether she is the bottom contributor or not. |
| 6. | If instead f were convex, then the social esteem would have grown unboundedly and no finite equilibrium would have existed. |
| 7. | The functional form for f and how it is normalized based on are akin to the reference-point effect of Kahneman and Tversky [32]. This reference-point effect also differentiates our model from that of Clark and Oswald (1998), who assume the same curvature on both sides of the reference point. Thus, our model relates to theirs like Prospect Theory relates to vNM’s Expected Utility Theory. |
| 8. | Note that is the average slope of the function in the range , in which its slope decreases from to . Thus, the intersection of the two conditions and is non empty. For example, if is a concave power function (i.e., for some ), restriction (iii) translates to . |
| 9. | Hence, restriction (iii) is required for the existence of a pure NE. |
| 10. | If the game was extended to n players the nature of the result would be similar: the bottom contributor would contribute zero and the remaining n-1 players would contribute . |
| 11. | In the special case of there exists another pure-strategy NE in which for the bottom contributor while for the two others. In this equilibrium all players are indifferent between choosing and . |
| 12. | To see this graphically, imagine moving the reference point rightward in Figure 1 and how this changes the negative esteem of contributing zero. |
| 13. | If the game was extended to n players, the nature of the result would be similar: there would exist multiple equilibria which differ in the level of the reference point but where all players contribute the same. |
| 14. | Another potential deviation is that the median could surpass the top contributor. This would make the current top contributor the “new median” implying that the most profitable deviation is to surpass the “new median” by . As is clear from the proof, the relative costs and benefits of this potential deviation are independent of the reference point and it is ruled out by the restrictions we have imposed on f to fulfill . If this condition does not hold there would exist no equilibrium in pure strategies. |
| 15. | If the game was extended to an odd number of n players the nature of the result would be similar. There would exist multiple equilibria differing in the reference point contribution, where in each equilibrium the bottom players would contribute the same as the median reference while the remaining players would contribute . |
| 16. | (by Lemma A2 in Appendix A) , implying that the welfare difference given by (4) is greater than . |
| 17. | Since in this comparison in all methods, also the welfare is higher under the bottom-contributor comparison method. |
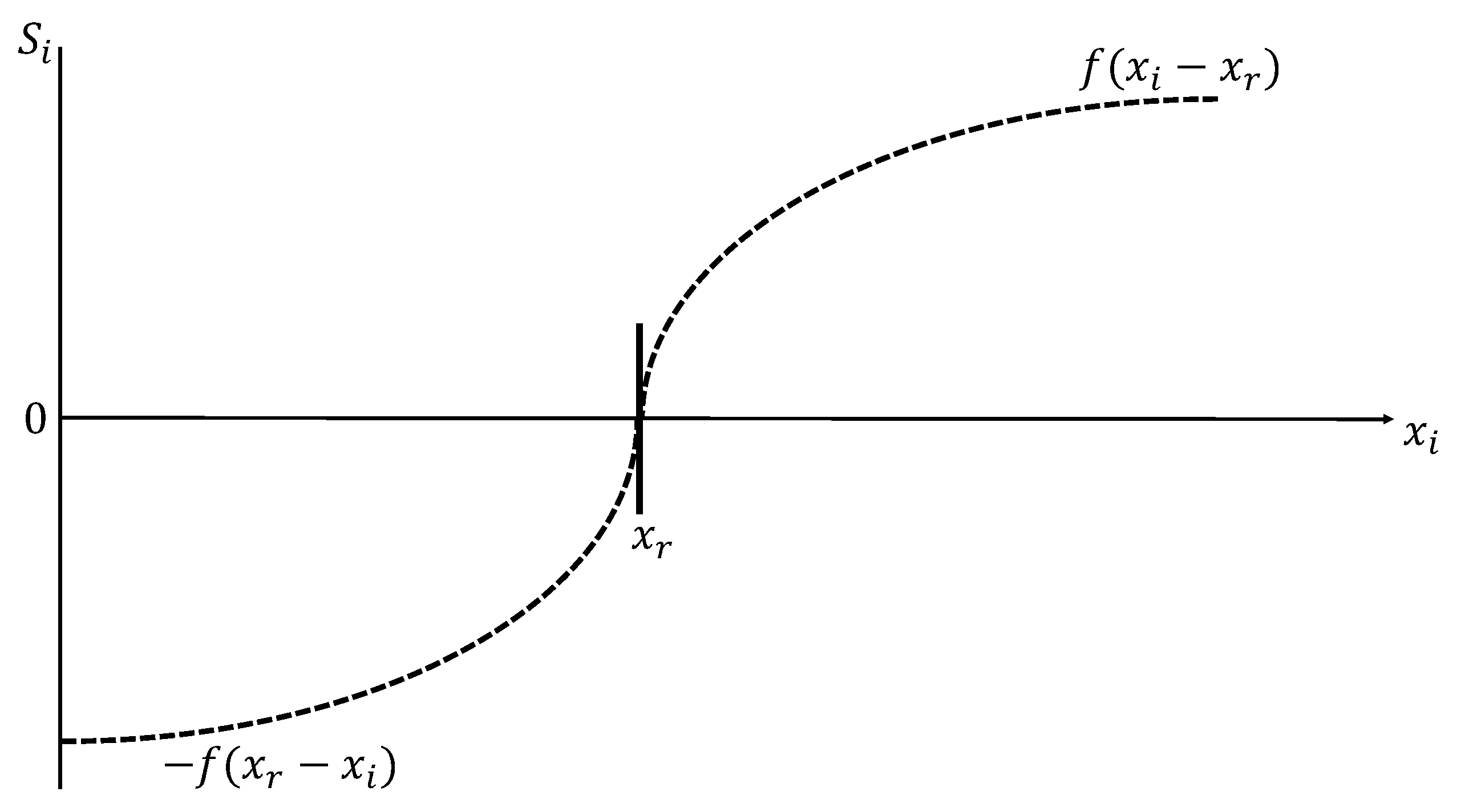
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Michaeli, M.; Spiro, D. Prescriptive Norms and Social Comparisons. Games 2018, 9, 97. https://doi.org/10.3390/g9040097
Michaeli M, Spiro D. Prescriptive Norms and Social Comparisons. Games. 2018; 9(4):97. https://doi.org/10.3390/g9040097
Chicago/Turabian StyleMichaeli, Moti, and Daniel Spiro. 2018. "Prescriptive Norms and Social Comparisons" Games 9, no. 4: 97. https://doi.org/10.3390/g9040097
APA StyleMichaeli, M., & Spiro, D. (2018). Prescriptive Norms and Social Comparisons. Games, 9(4), 97. https://doi.org/10.3390/g9040097




