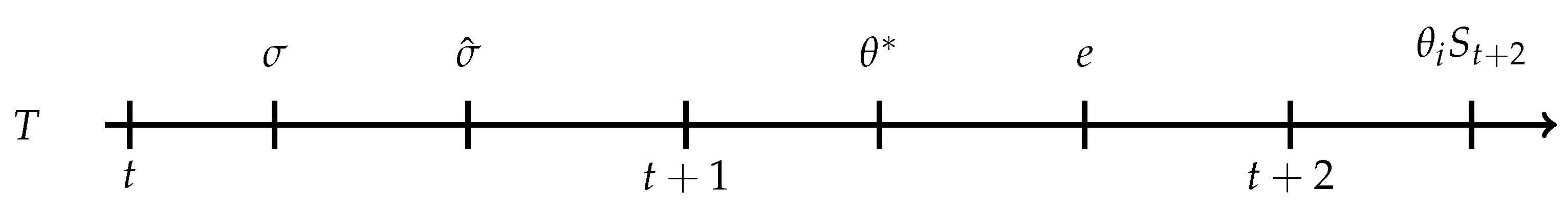This Is How We Do It: How Social Norms and Social Identity Shape Decision Making under Uncertainty

Abstract

The current study aims to investigate how the presence of social norms defines belief formation on future changes in social identity (i.e., diachronic identity), and how those beliefs affect individual decisions under uncertainty. The paper proposes a theoretical model in which individuals have preferences over their own attributes and over specific information structures. The individual preferences are motivated by the presence of social norms. The norms, while establishing the socially acceptable attributes of an individual identity, also drive individuals’ preferences for information acquisition or avoidance. The model incorporates social norms as empirical expectations and provides a prior dependent theory that allows for prior-dependent information attitudes. Firstly, the model implies that decisions are mitigated by socially grounded behavioral and cognitive biases; and secondly, that it can create an incentive to avoid information, even when the latter is useful, free, and independent of strategic considerations. These biases bring out individual trade-offs between the accuracy of decision making and self-image motivated by social conformity. The two behavioral motivations are represented through a game of an intra-personal model of choice under uncertainty in which self-deception and memory manipulation mechanisms are used to overcome the individuals’ internal trade-off.

1. Introduction

The standard assumption in economics is that decision makers (DMs) are endowed with perfect reflection. They are likely to embark on a process of conscious mental revision of their available alternatives in order to characterize each choice and evaluate their consequences. To sustain the perfect reflection assumption, the theory of decision making first postulates that individual preferences are exogenous, and secondly, that information is always (weakly) valuable even when it is bad news. Yet, the robustness of the assumption of perfect reflection depends on both the complexity of the decision problem and on the individual’s subjective beliefs about the value of information. Complex decision problems are those in which payoff-relevant variables are defined endogenously and are entangled as part of the choice. By the same account, standard economics assumes that the value of information is instrumental to make better decisions. However, a growing body of theoretical and experimental literature suggests that information also has an affective value that may directly enter the agent’s utility function—a phenomenon known as “belief-based utility”. This can create an incentive to avoid information, even when it is useful, free, and independent of strategic considerations. In such cases, the assumption of perfect reflection becomes difficult to justify. The difficulty stems from the relaxation of one or more conditions of exogeneity, rationality, and self-knowledge.

To cast light on the process of relaxing the assumption of perfect reflection, let us start with a simple scenario and complicate it little by little. In many situations, real life is complex because choices are accompanied by aspirations, motivations, emotions, dispositions, and beliefs that alter the characteristics of the alternatives as well as the nature of the decision problem. Imagine choosing between investing in education to get career A or B. In a simple framework, the DM chooses A over B only if the pleasure or the profit received from A is greater than that received from B. It follows that she will choose to invest in A when both the possibilities are available. In this scenario, she has a precise definition of the objects of her choice: career A over B. Suppose, now, that the availabilities of the alternatives are uncertain, as the outcomes (and the preferences over them) are endogenous—that is, explained through mental states such as motivations and beliefs. Specifically, we assume that the individual has incomplete information about the outcomes of the alternatives and decides to undertake a conscious mental revision about which is the best, also inferring which one is the most socially acceptable. The object of her choice is therefore changed. It is no longer presented to her eyes on the basis of only the intrinsic value of the alternatives, but also on the value that society attributes to the alternatives. The nature of the decision problem is now changed since the DM’s motivational structure is changed because it is informed by the heuristic “the most socially acceptable”. Heuristics represent a shortcut that the DM chooses in order to solve the uncertainty.

For the DM, her decision problem is no longer between the outcomes of each career path, but between career paths together with their degree of social acceptance. Specifically, the career path finds its value in the social recognition as an ideal career for a specific type of DM that belongs to a given community. The “socially acceptable” mental states (i.e., beliefs and motivations) are originated by the presence of norms, which ultimately define the mental representation that the DM has of herself and her identity. Consequently, the DM has to internalize the consequences of both actions and motivations. A DM with imperfect reflection will not anticipate that her conformist motivation might play a role, whereas a perfectly reflective DM will know how to handle the endogeneity. Hence, given the objections to the assumption of bounded rationality, it seems reasonable to ask ourselves the question: where do a DM’s mental states come from? Consider again the “heuristics” example. It has two features that are worthy of further analysis: the mental states and the sampling of the information.

According to Elster [1,2], mental states, as beliefs and motivations, define behavior. Beliefs and motivations1 help the DM to navigate in life, to justify the undertaken action and to experience emotions. If we want to order the states in a causal relation, motivations are causal determinants of the states and, then, of the belief formation. A complete analysis of the mental states should look at both costs and constraints of the motivated mental states. The costs of mental states are the false or inaccurate beliefs that even though they are pleasant they can induce suboptimal choices or emotional drawback. In turn, constraints2 are the information processing that can be biased and affected by overconfidence or optimism, or can be constrained by priors or social norms. While the earlier attempts of bounded rationality theory were based on the costs [4,5], recent theory has focused on the investigation of the constraints. When motivated mental states enter the framework, the traditional exogeneity assumption no longer holds, nor the other assumptions of accurate knowledge of the preferences and of fixed inter-temporal preferences. The “heuristic” example supports an analysis of both costs and constraints. The choice of career A over B could be explained by a motivated mental state that favors a conformist behavior. This motivated belief drives the DM to strategically sample only the information that is considered important for the conformist extent and to disregard the information that does not match it. That is, the DM organizes the information structure to favor the priors that career A is better. Hence the norms, while establishing the socially acceptable attributes of an individual identity, also drive individuals’ preferences for information acquisition or avoidance.

On the last account, the example can be taken to a higher level of sophistication that specifies a further particular mechanism. The social norms that suggest the DM’s choice of A over B, reinforce their grip on the DM by arousing feeling linked to the anticipation of the future identity, which could mean either savoring future success or dreading future failures. In this way, “being a professional A”3 will not only be good because it is socially accepted, but because A is highly considered, the anticipation of the future identity A has an impact on immediate well-being [6]. This particular way of framing the effect of beliefs about future events and identity over current feelings is called anticipatory utility [6,7] (henceforth AU). In the framework of AU, beliefs enter the utility function directly via emotional predisposition, highlighting the importance of information gathering and avoidance. This result is more interesting in light of Simon’s perspective4 on the role of information. In fact, in the general case of self-conflicting goals, or intra-personal conflict motives, as in Brocas and Carillo [9] or Bénabou and Tirole [10,11], an individual may choose to avoid information even when it is freely available. Moreover, even if being informed will improve the DM’s current decision, the information could be completely or partially shared with her future incarnations, affecting her future optimal choice and thus creating an intra-personal conflict. Ignorance would be a rational and strategic behavior.

With the elements of sampling information and AU, this paper models how social norms and identity are linked from an intertemporal perspective that is different from Akerlof and Kranton’s [12,13]. The work presents a dual-self model [14] within a monotonic decision problem [15]. The main structure posits the decision problem as a game between a short- and a long-run self. The two selves may incur inconsistent decisions in time. Because of this, they might want to manipulate the information structure they possess.

This work is closely related to and borrows from Kószegi [16] and Bénabou and Tirole [10,11]. As in the model, in Kószegi ignorance is costly in terms of inefficient actions and the DM is information-averse. Bénabou and Tirole face the two topics in different papers. In Bénabou and Tirole [10], imperfect recall is the tool through which the DM can keep a high self-esteem, however the scenario with a second stage of the action strategy is not considered and the cases of analysis consider only the situation in which a low signal is subjected to a recall strategy. In [11], the authors show that a DM with an anticipatory utility function and with preferences for the future outcome can be led to make inefficient decisions. The current paper merges the three works, obtaining the result that ignorance is costly in terms of inefficient actions whenever the DM is information-averse. However, the inefficiencies can be offset by the gains in the DM’s self-image (or self-esteem). The aversion for the information is analyzed in both cases of receiving good or bad signals, because both matter for the consequence of inefficient actions and self-esteem maintenance. Their existence is determined by the presence of social norms that inform the DM not only in terms of the socially accepted identity but also in how to respond to information conflicting with it. The existing literature on ignorance as a strategic action to maintain self-serving biases focuses mostly on the asymmetric recall of good signal [10,11,16,17,18,19,20,21]. Recalling a good signal is always appealing when the outcome of that signal dominates any other outcomes. For example, signaling a high IQ or scoring a high point in a student laboratory experiment is always better than signaling the opposite [18], because the identity of “being a good student” is the dominant in such environment, hence any feedback contrasting that ideal identity would be forgotten. Another example could be the one of showing a high moral stand in a society in which morality is an important feature [11]. A final example is served by [11], in which recalling a good signal could be used as a strategy to maintain personal motivation for people who lack self-control in seeing their plans through. In these and other contexts, the asymmetric recall of good signal is justified by the fact that being good is the most socially acceptable identity. Yet, there are social situations in which identity and social norms identify being both good and bad as socially acceptable. Let us consider, for example, the case of the student groups “nerds”, “jocks”, “leading crowd”, and “burnouts” in Akerlof and Kranton’s [13], and their effects on matching the image and the behavior of an ideal group member. In contrast to existing work, this study first emphasizes the important role of social norms as underlying reasons for motivated beliefs (i.e., the demand side of self-deception), and second the necessity to generalize the selective recall strategy (i.e., the supply side of self-deception). This model tries to generalize the asymmetric recall strategy by proposing a thicker strategic input to the second result of Kószegi [16] in which he introduces the possibility of partial information acquisition. Even with the generalization of the recall strategy, the model shows the existence of the trade-off [10,22] between affective benefits from the biased self-image based on social conformity to a specific social norm on the one hand, and the incentive for accuracy of decision making on the other hand.

The rest of this paper is organized as follow. In Section 2 a literature review accommodating all the above phenomena is presented. To follow, Section 3 and Section 4 introduce and solve the model, respectively. Section 5 provides comments and discussions. Finally, Section 6 offers conclusions. An Appendix section for complementary results and graphs follows.

2. Literature Review

This paper contributes to the literature in identity economics. Following Akerlof and Kranton [12,13], although we move slightly away from their core assumptions in three directions, we consider the social categories as variables that enter in the decision maker’s utility function.

2.1. On Diachronic Identity

The diachronic identity [23] refers to changes in the content and consequences of the identity over time, as opposed to the synchronic identity, which refers to the relative salience of different aspects of an individual at one point in time that depends on the presence of relevant cues. Let us consider an example of the synchronic identity in gender studies. The category of being a woman has different sub-categories, such as being a mother, a professional, a spouse, etc. At a specific point in time, being a mother and a professional can be in conflict and one of the sub-categories could be more salient than the other for that specific point in time where the DM finds herself.

Diachronic identity theory mostly focuses on how the DM tracks continuity of her identities over time and on how the aim of reaching this perceived continuity affects her choices and information set. For example, in gender issues, the ideal of being a good woman will be valued both when the DM is a student and for the following years. As a consequence, the decisions that she makes now will impact not only the single current dimension, but future ones, as well. Thus, understanding how people make judgments about the continuity of their identity can give us different reasons to comprehend why people do not act as often as they should and might suggest a new way to help people to act in accordance with their long-term interests. The way this mechanism is presented in the model occurs by using a particular functional form called an AU function [7,24,25,26], which takes into account utility over beliefs and outcomes with particular inter-temporal implications.

2.2. On Social Norms

The matching mechanism between behavior and ideal identity is retained from Akerlof’s analytical framework. Henceforth, the matching mechanism is not determined by fixed preferences5, but is the outcome of a deliberative process. In fact, the matching mechanism in this paper is not a generic endorsement of the prescriptions imposed by the ideal categories to which individuals decide to belong. Rather, it is a prescription originated by social norms. The origin lies in the existence of descriptive norms [31]. Descriptive norm regulates the mechanism of interaction between the constraints through the work that empirical expectations produce on the definition of “similar” and “attainable”. In the model, an individual draws her aspirations from the lives, achievements, or ideals of those who exist in her cognitive window. The definition of norms as empirical expectations helps us to understand the complex problem of social identity and educational investment, for three reasons.

First, the presence of descriptive norms that define a given identity as ideal reduces the incentive to experiment and search for information on the alternatives to the ideal identity. In other words, if the descriptive norm and the social context make specific traits of identity salient, then the preferences of individuals can be shaped by cues leading to an observation of inconsistent choice and behavior6, even in the absence of any explicit awareness of how such cues trigger and arrange the goal pursued. In this case, the individual will be trapped in self-fulfilling expectations situations.

Second, descriptive norms are helpful in playing the role of heuristics during a decision-making process, and they characterize it under uncertainty as a prior dependent process. Namely, people dealing with investment decision problems, as with any decision under uncertainty, appeal to empirical expectations to handle the imperfect information [32,33] typical of this kind of problem. When information about the future outcomes of an action is difficult to gather or is imperfect, the norms are the best and less-expensive way to extract that information. However, this information can be biased or untrue.

Third, another consequence of the presence of the norms on the information process is whether individuals treat information differently when it comes from a social context. That is to say, individuals might suffer from confirmation bias7, conservative bias8, or persuasion bias9. Namely, they are constrained in their ability to process information, making some cues more accessible than others in affecting their preferences. For example, let us again consider the phenomenon of “acting white”. This phenomenon allows the subject of a stereotype to notice stereotype-consistent information more likely that of other stereotypes. She would probably construct a sequence of information that gives validity to her beliefs, while discarding or forgetting those signals that do not. Accordingly, the observed choice may be consistent with several combinations of expectations and preferences. Once again, these combinations are the result of the social cognitive process10 to which everyone is subjected.

2.3. On Cognitive Dissonance

On the latter account, the appeal to the use of descriptive norms as a heuristic is motivated by the attempt to resolve what Festinger [41] calls cognitive dissonance. Dissonance arises when individuals are confronted with information that is inconsistent with their already-existing beliefs, ideas, or values. Hence, it produces the “unpleasant experience of being caught between two contradictory forces” (Iyengar [42], p. 97): information conflicting with beliefs. The resolution process of the conflict occurs in a self-deceiving way [43]. Self-deception is the temptation of people in believing something that they want to be true. That is to say, individuals have false beliefs not because of a lack of information. Rather, the self-deceiver is at some level aware of information that would lead her to form the correct belief, but some motivational bias leads her to hold the opposite. In this model, empirical expectations and the desire to respect them represent the motivational bias.

Traditionally, self-deception has been modeled on interpersonal deception, yet the current paper uses an intra-personal approach. However, the traditional model of self-deception raises two paradoxes. One concerns the self-deceiver’s state of mind, the so-called static paradox. How can a person simultaneously hold contradictory beliefs? The other concerns the process or dynamics of self-deception—the so-called dynamic or strategic paradox. How can a person intend to deceive herself without rendering her intentions ineffective [43]?

The answer to these questions and the strategies to solve the dissonance depend on the type of dissonance faced by the DM. According to [44], the dissonance is called nomothetic when it is generated by the presence of cultural and social customs, whereas it is called idiographic when it is related to individual-specific cognitions. The distinction matters when it comes to identifying the strategies that can be followed to minimize the discomfort caused by the dissonance. In principle, the choice is between three options: avoiding the dissonance by not performing the action leading to it; reducing the dissonance by changing the environment (i.e., by removing (some of) the circumstances that induce dissonance); or solving the dissonance by changing one’s own opinions about the circumstances that cause it (i.e., by changing one’s subjective evaluation of these circumstances—the sour grape evaluation).

When the DM faces idiographic dissonance, the latter two strategies are implemented. Several strategies have been largely found for sustaining a particular self-assessment belief: for example, selective recall of information [45]; dismissing the importance of skills not possessed and emphasizing the value of traits one does possess. In the economic literature, the approach to cognitive dissonance ([4,5,46]) studies the change of the DM’s beliefs ex-post to the actions taken. The DM tries to make a coherent mirroring between the result of the action (or the recollection of the result) and the initial beliefs.

In the case of nomothetic dissonance (i.e., the one discussed in this paper), the best strategy is the first. Because of the strategic paradox, the modification of one’s beliefs is not useful in solving the cognitive dissonance. Instead, it is necessary to intervene either in the information set—through misconception, refutation, or rejection—or through seeking support from the “relevant others” who share the same beliefs [47]. Then, the DM will strategically select the information received in order to reflect the initial beliefs. In the literature, these self-deception actions are modeled in three different ways. The first is to adjust the Bayesian model of belief formation [48]. The second is to solve an intra-personal signaling model, in which the DM is represented as a series of temporal incarnations which manipulate the beliefs from one period of time to another ([10,11,17,20,24,25,49]). The third approach uses a self-signaling model, adding psychological structure ([14,21,50,51]). The current work implements the third approach, enriched with a monotone information structure.

3. The Model

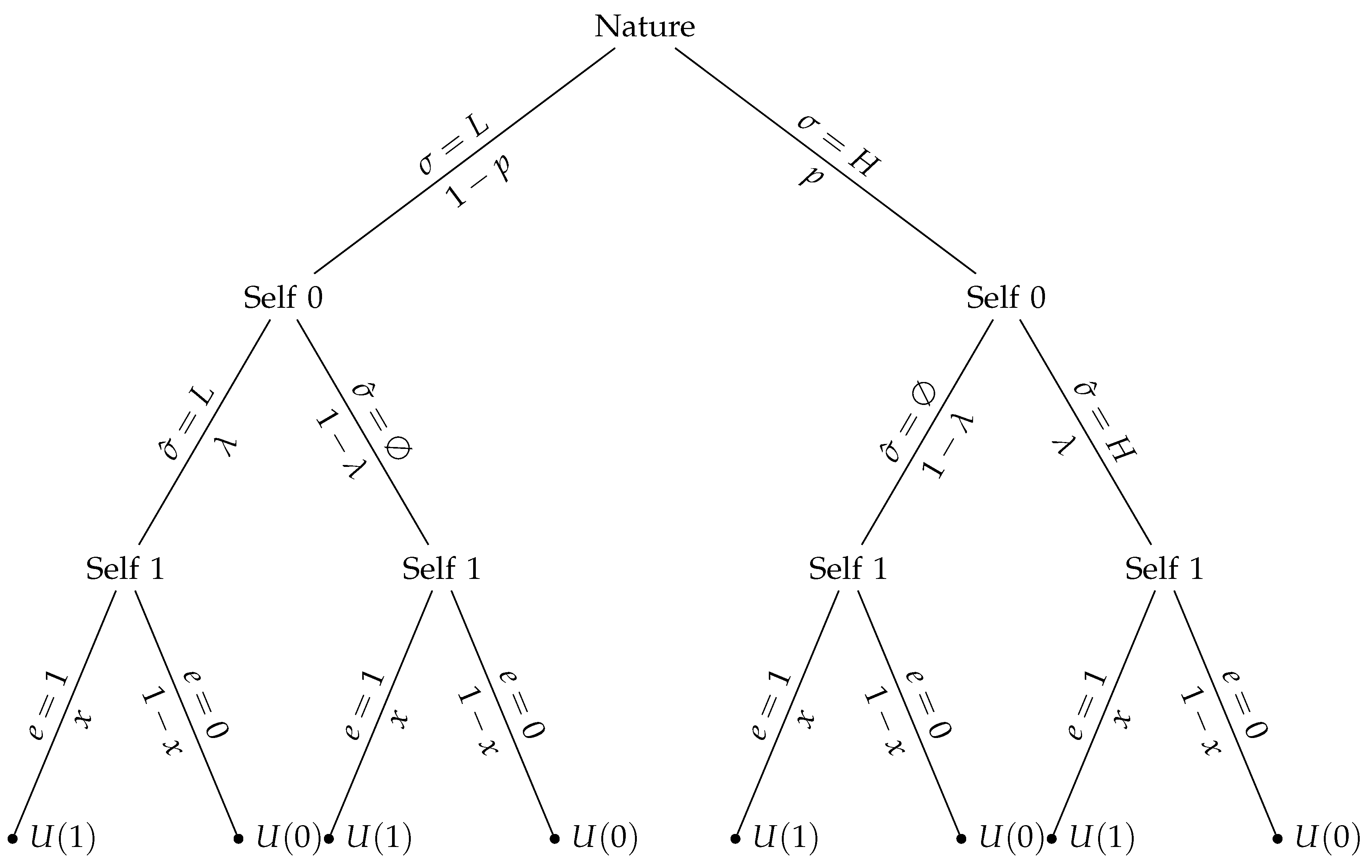
Consider a decision problem in which an intra-personal game is played by a sequence of temporal incarnations of the DM: a myopic short-run self and a long-run self. Both incarnations have preferences over their identity $\theta \in \mathsf{\Theta }$, where $\mathsf{\Theta }$ is a non-empty, compact subset of ℜ. The identity is validated according to the group’s expectations in terms of membership to one of the two social groups in which the society is divided in this current model. Each social group has its own distribution of type H or L. The DM’s utility is a function of economic outcomes and anticipatory emotions towards the outcomes, either positive or negative. The total utility is built over three periods of time, according to which at the beginning of period t the DM is endowed with an initial endowment, or amount of human capital, $S_t$. At this stage the DM receives a signal, ${\sigma }_t\in \mathsf{\Sigma }=\{H,L\}$, that is informative about her identity traits, $\theta$. The probability of observing an H signal is $p\in (0,1)$. The signal is informative in the sense that it can either broaden or restrict the set of opportunities available to the DM if it does not clash with the expectations of the group. The evaluation of available opportunities is grounded on the existence of two kinds of expectation that support the presence of social norms associated to the social group to which DM belongs or aspires to take part of.

Definition 1.

Empirical expectations state what the DM “expects the other in her position will do” in a particular situation. Normative expectations define what “they think other people believe ought to be done”(Bicchieri [31]).

The presence of the two kinds of expectation transform the DM’s decision into a monotone decision problem, whereby the posterior beliefs induced by the signal can be ordered so that specific actions are chosen in response to their corresponding signal realizations sustained by the norms. This is because:

Definition 2.

A social norm is a code of conduct shared by society and enforced through internal sanctions like guilt, shame, and loss of self-esteem.

The presence of strong norms dictating a certain type of behavior is a possible source of cognitive dissonance for the individual whenever the realization of the signal does not accord with that norm. Accordingly, the DM who has internalized the norm needs to solve the dissonance caused by the signal, $\sigma$. Since it is a nomothetic dissonance in our case, the best option is normally to avoid the source of the dissonance—that is, to choose the interpretation and recall strategy of the signal, $\widehat{\sigma }$, with probability ${\lambda }_{\sigma }\in [0,1]$. At $t+1$, the DM updates her beliefs about her identity, ${\theta }^{*}$, according to Bayes’ rule and chooses to invest in education, $e\in \{1,0\}$, and experiences emotional utility from the outcome of the investment choice, $\widehat{\theta }\left(e\right)$. In period $t+1$, the DM faces a choice regarding the investment that is individually deemed socially worthy: investing (or not) at time $t+1$ has an impact on the identity that the DM wants to signal at $t+2$ and produces at $t+1$ an emotional reaction related to signaling the new identity at $t+2$. The action is the main variable that allows the DM to pursue her plan over the future identity. The plan will have as return both the material outcome and the self-esteem outcome. The latter comes from the DM’s perception of enacting her plan. The plan can go in two directions: maintaining the status quo of her neighborhood, with probability $1-x_i$; or changing the status and undertaking a new path with probability $x_i$. The individual has the theoretical possibility of choosing to not replicate the identity trait of her reference group and to go for her own identity according to her aspiration level and autonomy. The outcome of the action has material payoff only on the last period, $t+2$, and it is the final amount of human capital gained after the investment choice, ${\theta }_i{S}_{t+2}$. The timing is pictured in Figure A1, in Appendix A.

An important assumption of the model is that it is a non-cooperative game between the long-run self and the short-run incarnation, namely, the individual cannot commit ex ante to her future decisions. Instead, the long-run self chooses a self-control action causing a current cost that influences the utility function of the myopic self, producing externalities on her future welfare. The magnitude of externality depends on the individual’s identity trait, whose value is subject to imperfect information.

Timet. The expected value of the identity is conditional on each possible realization of such signals, and it is given by:

$${\theta }_i=\left\{\begin{array}{cc}\hfill {\theta }_H& \mathrm{with}\mathrm{probability}p,\hfill \\ \hfill {\theta }_L& \mathrm{with}\mathrm{probability}(1-p),\hfill \end{array}\right.$$

(1)

with ${\theta }_H>{\theta }_L$ and $\overline{\theta }\equiv p{\theta }_H+(1-p){\theta }_L$.

Assupmtion 1.

The DM has a prior distribution $f\left(\theta \right)$ on Θ, and she observes a signal σ with likelihoods $l\left(\sigma \right|\theta )$. If $l\left(\sigma \right|\theta )$ satisfies the Monotone Likelihood Ratio Property (MLRP), then the posterior belief $f\left(\theta \right|\sigma )$ follows the MLRP. Hence, the high signal first-order stochastically dominates (FOSD) the low signal:

$$F\left({\theta }_i\right|{\sigma }_t=H)\le F\left({\theta }_i\right|{\sigma }_t=L)\mathit{for}\mathit{all}\theta \in \mathsf{\Theta }.$$

(2)

Thus, the stochastic order of the information structure tells us that for any values of the identity parameter (${\theta }_i$), higher values of the signal make the higher parameter value relatively more likely. In the absence of empirical expectations and social norms, better information allows for a more accurate match between beliefs and actions. If beliefs are formed through the group’s expectations, then their match with the actions could be driven by a further specification of the signal structure: there are going to be some signal realizations that are more preferred than others. For example, a group with a majority of L type (namely, with a biased prior that shows that L types are more frequent in that group) could tend to welcome more other L types rather than H types, and in terms of the stochastic orderings, the information structure considered more informative will be the one that on average will produce with higher probability an L signal than any other informative structure. Then, in cases where the signal realization does not respect the ordering, the DM decides how to recall the signal.

$$Pr\left({\theta }_i\right|{\sigma }_t={\sigma }_{t-1})\le Pr\left({\theta }_i\right|{\sigma }_t\ne {\sigma }_{t-1})\mathrm{for}\mathrm{all}\theta \in \mathsf{\Theta }$$

(3)

Accordingly and following Bénabou and Tirole [10,21] and Rabin [5], I admit that the individual can decide how to record the signal at time t. Whether to interpret it realistically $\widehat{\sigma }=\sigma$ or to rationalize it $\widehat{{\sigma }_t}\ne {\sigma }_t$ with $\widehat{{\sigma }_t}\in \widehat{\mathsf{\Omega }}=\{H,L,\varnothing \}$. Rationalization means that the long-run self at time t may either communicate the signal truthfully to the short-run self at stage $t+1$, or suppress it. The DM’s decision at time t is to make a recall strategy that is the probability, ${\lambda }_{\sigma }\in [0,1]$, of truthfully transmitting to self-$t+1$ the signal, $i\in \{H,L\}$:

$${\lambda }_{\sigma }=Pr[\widehat{{\sigma }_t}=i|{\sigma }_t=i].$$

(4)

The DM will observe the signal if the gain of making an informed decision will exceed the cost of memory manipulation. ${\lambda }_{\sigma }$ will be chosen according to how reliable or informative the signal is—namely, if it is pivotal in the decision.

The recall strategy has its own justification based on the DM’s preferences over $\theta$. If the signal confirms her prior on her initial identity trait ($\theta$), she will not discard the original signal (${\lambda }_{\sigma }=1$), and then she will make the investment choice correlated with her characteristics. The incentive is also justified by the fact that the DM will make another evaluation that will trigger her choice. She may envisage what the consequences of sending specific signals are, whether it comes from a recollection or an action, to her circle.

Examples. A girl in a social circle of non-educated women who decides to continue her education will signal a message diverging from the circle identity. The heir of a wealthy family that decides not to pursue the family profession may find some hurdle in gaining the acceptance of her peers. A woman facing a tradeoff between work and family, when all the people around her seem to have chosen one of the two spheres, will hinder her choice of labour supply.

Hence, at time t the long-run self chooses the strategy to recall the signal. Endogenizing the imperfect recall allows the DM to reduce the externalities from one self to another. Following Festinger [41], reducing dissonance is not costless, whether it is implemented via attitude change or via memory manipulation. It requires re-valuing past behavior or information and breaking cognitive habits. Because the DM has preferences over her identity, and because she may want to solve the cognitive dissonance, she has the incentive to manipulate her recollection (or ex-post denial11) by exerting an effort. Let us consider the example of the little girl. Let us imagine that the girl has received a signal H that goes against the empirical expectations displayed in her circle that want all the girls to be uneducated (i.e., all the girls signal to be L). Now, she has to decide how to recall the signal, considering the trade-off between following the old path of no investment in education or to continue her education, signaling a message diverging from the circle identity. It seems necessary to stress the fact that recall strategies in an awareness-management context do not lead the individual to fool herself. Yet, she is aware that what she may have forgotten are not random events but rather the result of an incentivized inference. The memory effort is associated to a cost12 function, $M_{\sigma }\left({\lambda }_{\sigma }\right)$, that will impose further restriction to the choice and the agency of the individual13.

Assupmtion 2.

The cost is strictly increasing, convex, twice-continuously differentiable, and if ${\lambda }_{\sigma }=0$, then $M_{\sigma }\left(0\right)=0$ and $M_{\sigma }^{{}^{\prime }}\left(0\right)>0$.

Timet+ 1. The short-run self updates her beliefs and chooses the action e (i.e., investing in education) from a finite set A, given the signal recalled. The DM is rational and then before updating she evaluates the precision of the signal received by her previous incarnation. She considers the possibility that the long-run self at time t may have manipulated the true signal. Accordingly, she needs to estimate the probability that the signal is accurate. If ${\lambda }_{\sigma }$ expresses the probability that Self-t has truly transmitted the signal, ${\lambda }_{\sigma }^{*}$ represents Self-t + 1’s belief concerning Self-t’s communication strategy. Yet, the accuracy of the signal is given by:

$$\begin{array}{cc}\hfill r^{*}\left(\lambda \right)& \equiv Pr[\sigma =H|\widehat{\sigma }=\varnothing ;{\lambda }_{\sigma }]\hfill \\ & =\frac{p(1-{\lambda }_H)}{p(1-{\lambda }_H)+(1-p)(1-{\lambda }_L)}\in [p,1],\hfill \end{array}$$

(5)

implying that if Self-t + 1 receives $\widehat{\sigma }=\varnothing$, by using Bayes’ rule, she will assign the probability $(1-p)(1-{\lambda }_L)$ that $\sigma =L$ was observed and the probability $p(1-{\lambda }_H)$ that $\sigma =H$ occurred. The incentive constraints for Self-t + 1 do not change at this stage. However, the degree of self-assessment needs to take the accuracy of the recall into account. Hence, the DM’s revised beliefs are:

$$\theta {{}_i}^{*}=\theta \left(r^{*}\right)\equiv r^{*}{\theta }_H+(1-r^{*}){\theta }_L.$$

After the updating, the DM will choose the investment actions taking into account both the future material outcome (i.e., in the example of the girl, the future material outcome is an increase of her human capital level) and the anticipatory emotion of the outcome (i.e., feeling good/bad with that increase of human capital) realized that depends on the action taken (i.e., investing one more year in education).

The individual will implement the action strategy $e\left({\theta }_i\right):\mathsf{\Theta }\to A$, where A is a non-empty, compact, and convex set in ℜ. The investment in education will impact the DM’s human capital. Let us assume that each individual at time (t) is endowed with an initial level of human capital, $S_t>0$. $S_t>0$ is the initial endowment, and is interpreted in such way as to permit complementarities between the family’s human capital and the quality of community the family lives in. In this way, according to the initial level we give a representation of initial stratification that may determine the future one. In this scenario, the population is divided in two groups according to income and social status: H-types belong to the portion of the population characterized by high income, good social connections, and communities; while L-types represent the complement portion of the population. Human capital accumulates according to the following equation:

$$S_{t+1}=S_t+e_{t}r,$$

where $S_t$ is the DM’s human capital at time t, $e_t$ is the educational investment faced at time t, and $r>0$ is the interest rate of that investment. The educational investment will determine the future group affiliation of the DM. The sense of affiliation is the motivation for the action. The DM’s probability to invest is of the form:

$$x_i\left(p\right)=Pr\left(e=1|{\theta }_i\right),$$

and it represents the conditional probability law of the action e for each possible value of $\theta$. Since the decision of investment takes the persistence of identity into account, we need to express how the future identity enters the DM’s decision problem. The anticipatory emotion at time t aroused by the thought of the future identity is derived rationally by calculating the posterior identity the DM gains by means of the investment choice. The posterior identity evaluated to the investment decision is $\widehat{\theta }=\widehat{\theta }\left(e\right)\in \left[{\theta }_H;{\theta }_L\right]$, where:

$$\widehat{\theta }=\left\{\begin{array}{cc}\hfill \theta \left(0\right)=\widehat{q}{\theta }_H+(1-\widehat{q}){\theta }_L& \mathrm{if}e=0,\hfill \\ \hfill \theta \left(1\right)=\widehat{p}{\theta }_H+(1-\widehat{p}){\theta }_L& \mathrm{if}e=1.\hfill \end{array}\right.$$

(6)

After the action, the DM experiences a shift in beliefs by assuming that she is sophisticated, in foreseeing this shift, by applying the Bayesian calculation:

$$\widehat{p}=Pr\left({\theta }_H\right|e=1)=\frac{Pr\left(e=1\right|{\theta }_H^{*})Pr\left({\theta }_H^{*}\right)}{Pr(e=1)}$$

(7)

and

$$\widehat{q}=Pr\left({\theta }_H\right|e=0)=\frac{Pr\left(e=0\right|{\theta }_H^{*})Pr\left({\theta }_H^{*}\right)}{Pr(e=1)},$$

(8)

where the prior beliefs at time $t+1$ are represented by $Pr\left({\theta }_H^{*}\right)=r^{*}$, the probability of being H-type given the recall. Moreover, recalling the probability of investing given the type, $x_i\left(p\right)=Pr(e=1|{\theta }_i)$, then $Pr(e=1,0)$ is defined as

$$Pr(e=1)=Pr(e=1|{\theta }_H^{*})Pr\left({\theta }_H^{*}\right)+Pr(e=1|{\theta }_L^{*})Pr\left({\theta }_L^{*}\right)$$

and

$$Pr(e=0)=Pr(e=0|{\theta }_H^{*})Pr\left({\theta }_H^{*}\right)+Pr(e=0|{\theta }_L^{*})Pr\left({\theta }_L^{*}\right).$$

Then, the posterior probabilities in the two scenarios will be:

$$\widehat{p}=\frac{r^{*}{x}_H}{r^{*}{x}_H+(1-r^{*})x_L}$$

(9)

and

$$\widehat{q}=\frac{r^{*}(1-x_H)}{r^{*}(1-x_H)+(1-r^{*})(1-x_L)}.$$

(10)

Table A1. Posterior beliefs.

$\mathit{\sigma }=\mathit{i}$	prob($\mathit{\sigma }$)	prob($\widehat{\mathit{\sigma }}=\mathit{i}|\mathit{\sigma }=\mathit{i}$)	prob($\mathit{\sigma }=\mathit{H}|\widehat{\mathit{\sigma }}=\varnothing$)	prob(${\mathit{\theta }}_{\mathit{i}}|\mathit{e}=1$)
H	p	$\lambda$	$r^{*}$	$\widehat{p}$
L	$1-p$	$\lambda$	$1-r^{*}$	$\widehat{p}$

in Appendix A shows the probabilities of the two signals and the posterior beliefs.

Preferences. The model extends for three periods, from t to $t+2$.

In the last period, the DM will receive the outcomes of the action taken at time $t+1$.

$$U_{t+2}^i={\theta }_i{S}_{t+2}$$

The DM’s preferences at time $t+1$ are represented by the anticipatory utility function: namely, at time $t+1$ the DM gets an instantaneous utility of her current identity and a utility from the anticipation of time $t+2$ identity outcomes. Consistent with Carrillo et al. [3], the instantaneous utility is represented by the cost function related to the action that will produce externalities in the future stages. Hence, the instantaneous utilities at time t and $t+1$ are represented by the current effort the DM has to exercise in order to perform the action after, $c\left(e\right)$. The DM has perfect foresight, namely, she is sophisticated in the sense that she applies Bayesian operators to foresee her dynamic inconsistency.

The utility at time $t+1$ is represented by $U(\theta ,\widehat{\theta },S_t):A\times \mathsf{\Theta }\to \mathsf{\Re }$, and its expression is the following:

$$\begin{array}{cc}\hfill U_{t+1}^i(\theta ,\widehat{\theta },S_t)& =-c\left(e\right)+V(\theta ,\widehat{\theta },S_t|\sigma )\hfill \\ & =-c\left(e\right)+s{E}_{t+1}^i\left[U_{t+2}^i\right]+\delta E_{t+1}^i\left[U_{t+2}^i\right].\hfill \end{array}$$

(11)

The anticipation at time $t+1$ of the utility at time $t+2$ is expressed by $V(\theta ,\widehat{\theta },S_t|\sigma )$, the value function in which both the future outcome of the investment, $\delta \theta$, and the aspiration level, $\widehat{\theta }=\theta \left(e\right)$ (i.e., the DM’s expected identity given the investment decision), are represented:

$$V(\theta ,\widehat{\theta },S_t|\sigma )\equiv (s\widehat{\theta }+\delta \theta )S_{t+1}.$$

In the value function $\delta$ is a traditional time discount factor ($0<\delta <1$), and s is the anticipatory factor. Hence, $\left(\delta \theta \right)S_{t+1}$ is represented by the schooling return times the identity trait. The trait identity is represented in such a way that it takes into account the anticipatory utility at time $t_{t+1}$, $s\widehat{\theta }$ and the discounted utility from identity at time $t_{t+2}$, $\left(\delta \theta \right)S_{t+1}$.

The psychological insight of s is what Lowenstein [6] calls savoring of the agent’s belief about the contribution of $S_{t+1}$ to her future welfare and identity. s represents the feeling of pleasure, if $s>0$, or of fear, if $s<0$, derived by the anticipation of the contribution of the final identity. However, in this context, the feeling experienced is socially grounded in the sense that it depends upon the evaluation of the neighbors. In different but related words, this attitude can be explained by the individual’s compliance with the norm that her social background proposes to her. The agent indulges in pleasant beliefs (conversely, avoiding the disagreeable ones) about the signal she sends to her peers when considering whether to invest or not. This sentiment in the model is anticipated at time 0 and measured by s. The anticipation of future blame or praise related to the decision taken represents a further constraint to consider during the decision making. In period $t+2$, the agent obtains the return ${\theta }_i{S}_{t+2}$ from investing in $S_{t+1}$. At time $t+1$, she derives feelings (pleasure or pain) from anticipating the prospect future identity, $s\widehat{\theta }{S}_{t+1}$.

Assupmtion 3.

The value function is continuous and supermodular: it is strictly increasing and continuous in the aspiration level $\widehat{\theta }$, and continuous for every $\theta \in \mathsf{\Re }$, but it also has increasing differences for all pairs of aspiration level, and education choice ($V(·)$ satisfies Milgrom–Shannon’s single-crossing condition). Besides, the value function satisfies the following assumption: $V_{\widehat{\theta }}>0$, if $r>0$, $V_{\theta S_t+1}>0$ and $V_{\theta \widehat{\theta }}=0$.

The requirements enlighten three aspects: the first is a condition of good expected behavior with respect to the decision of investment; the second requirement points out the beneficial effect of the investment on the utility. Finally, the third requirement shows that the action has informational content feeding conformist behavior to a norm. On this account a clarification is due. According to Caplin and Leahy [7], anticipatory emotions affect the behavior when the total utility function is strictly concave. In this way, the DM is averse to variation to future anticipatory emotion. However, according to Bernheim and Thomadsen [53], the assumption of non-linearity can be relaxed in the case of imperfect recall.

One important property of this set-up is that, as [7] pointed out, anticipatory emotions can affect behavior when $U_t$ is non-linear, determining the DM’s preference for information. Whenever the utility function is concave, the DM is information-averse to variation in future anticipatory emotion—she suffers from anxiety. Consequently, the individual prefers to take an ignorant action rather than receiving information prior to making the decision unless this allows her to select an action that sufficiently improves her outcome. This is true when the information is perfectly recalled. However, as [53] showed, the non-linearity assumption can be relaxed when memory of the signal is imperfect and the anticipatory emotions still matter, because the imperfect recall breaks down the law of iterated expectations.

Moreover, considering the fact that aspiration level and education choice are complementary, and that $\theta (·)$ is a function of the unknown identity, $\theta$, and of the signal and its recall, if the value function respects specific conditions, according to [15] we can investigate the comparative statics of the educational investment with respect to the original signal.

Assupmtion 4.

If $V(·)$ is single-crossing in e and θ holds, then $V(·,\theta (1\left)\right)-V(·,\theta (0\left)\right)$ is non-decreasing in ${\theta }_i$ if $\theta \left(1\right)>\theta \left(0\right)$ and if $\frac{{\partial }^{2}V(·)}{\partial e\partial {\theta }_i}>0$. Additionally, since by Assumption 1 we know that $f({\theta }_i,{\sigma }_i)$ satisfies the monotone likelihood ratio property, then the expected value function is single crossing in e and σ and therefore the optimal choice, $e^{*}(·)$, is weakly increasing in σ.

Regarding the cost function at time $t+1$, the DM needs to decide whether to invest in the old path at no cost or in the new path at a cost $C_i$. Let us again consider the example of the girl. In the first case, the girl pursues the old track of being un-educated (i.e., $e=0$, the one her peers and family expect from her), while in the second case she faces the cost of deviation from the marked path by investing (i.e., $e=1$) one more year in school. The cost function of the investment in education (i.e., $c\left(e\right)$) is assumed to be smooth, increasing, convex, and known at time 0. The cost $c\left(e\right)$ is given by $c\left(e\right)=e{C}_i$, where $C_i\in \{C_H;C_L\}$.

I assume that investing in the new path supports both the participation constraint and the sorting condition, considering that $C_H<C_L$.

Finally, the total utility at time t takes into consideration the memory manipulation costs and the discounted values of the future utility. Here, the DM’s trade-off between accuracy of decision making and self-image takes place:

$$U_t^i(\theta ,\widehat{\theta },{\lambda }_{\sigma },S_t)=-M_{\sigma }\left({\lambda }_{\sigma }\right)+\delta E_t^i\left[U_{t+1}^i\right]+{\delta }^2{E}_t^i\left[U_{t+2}^i\right].$$

(12)

Figure A2 in Appendix A represents the decision tree of the entire model.

4. The DM’s Problem

The properties of the Perfect Bayesian Equilibria (PBE) can be studied in two parts by applying backward induction. First, we compute the optimal Investment of the short-run self at time $t+1$ taking the recall strategy as given. Second, we obtain the Memory Manipulation decision of the long-run self at time t, taking the optimal investment strategy into account. The existence of a PBE is established in the online appendix.

Choice of e. By the end of $t+1$, the DM updates her beliefs and chooses the action given the recall of the signal. She does this by maximizing anticipatory utility given the beliefs set she owns at that time. The optimal action is

$$e^{*}=\underset{e\in \{0,1\}}{arg\; max}{E}_x\left[U_{t+1}(\theta ,\widehat{\theta },{\lambda }_{\sigma },S_{t+1})\right]=E_x\left\{E_{r^{*}\left({\lambda }_{\sigma }\right)}\left[U_{t+1}(\theta ,\widehat{\theta },{\lambda }_{\sigma },S_{t+1})\right]-c\left(e\right)\right\}.$$

(13)

Choice of${\lambda }_{\sigma }$. At the end of period t, the DM chooses how to recall the signal received at the beginning of the stage. This occurs whenever the benefits of memory manipulation both in terms of self-esteem and efficient future actions overcome the cost of the manipulation.

$${\lambda }_{\sigma }^{*}\in {arg\; max}_{{\lambda }_{\sigma }}\left\{{\lambda }_{\sigma }{E}_{r^{*}\left({\lambda }_{\sigma }\right)}\left[U_t(\theta ,\theta \left(\widehat{\sigma }\right),{\lambda }_{\sigma },S_t)|\widehat{\sigma }=\sigma \right]+(1-{\lambda }_{\sigma })E_{r^{*}\left({\lambda }_{\sigma }\right)}\left[U_t(\theta ,\theta \left(\widehat{\sigma }\right),{\lambda }_{\sigma },S_t)|\widehat{\sigma }=\varnothing \right]-M_{\sigma }\left({\lambda }_{\sigma }\right)\right\}$$

(14)

Then, the decision made by the agent with endogenous imperfect recall is modeled as the PBE of the multi-self game. It is constituted of a strategy profile that comprises an interpretation strategy (${\widehat{\sigma }}^{*}$) and an action strategy ($e^{*}$), and of a posterior belief.

Definition 3.

A PBE of the game is the set of strategy profiles $({\widehat{\sigma }}^{*},e^{*})$, where ${\widehat{\sigma }}^{*}$ is given by the pair $({\lambda }_{\sigma }^{*};r^{*})\in [0,1]\times [p,1]$ and $e^{*}\in \{0;1\}$, and the posterior beliefs $F(\theta |\widehat{\sigma })$ such that

1.

${\lambda }_{\sigma }^{*}\in {arg\; max}_{{\lambda }_{\sigma }}\left\{{\lambda }_{\sigma }{E}_{r^{*}({\lambda }_{\sigma })}\left[U(\theta ,\theta (\widehat{\sigma }),{\lambda }_{\sigma },S_t)|\widehat{\sigma }=\sigma \right]+(1-{\lambda }_{\sigma })E_{r^{*}({\lambda }_{\sigma })}\left[U(\theta ,\theta (\widehat{\sigma }),{\lambda }_{\sigma },S_t)|\widehat{\sigma }=\varnothing \right]-M_{\sigma }({\lambda }_{\sigma })\right\}$;

2.

$e^{*}\in {arg\; max}_e{E}_x\left\{{\mathit{E}}_{r^{*}({\lambda }_{\sigma })}\left[U(\theta ,\theta (e),{\lambda }_{\sigma },S_t)|\widehat{\sigma }\right]\right\}$;

3.

$F(\theta |\widehat{\sigma })$ is obtained by the Bayes’ rule if $Pr(\widehat{\sigma }|{\lambda }_{\sigma }^{*})>0$, $\forall \widehat{\sigma }\in \{L,H,\varnothing \}$.

Condition 1 states that Self-t chooses the amount of memory manipulation that maximizes the agent’s expected payoff conditional on each outcome $\sigma \in \{H,L\}$. Condition 2 states that the short-run Self-$t+1$ takes an ex-post action e with positive probability if and only if this action maximizes her utility given the beliefs she holds about the manipulation employed by Self-t. She might consider the fact that she might have forgotten about previous status. At this point, the imperfect recall is not strategic. Hence, the short-run self does not have to take in consideration the possibility that her previous self might have suppressed the signal. Condition 3 is a consistency condition, requiring that the beliefs of Self-$t+1$ satisfy Bayes’ rule given the strategy of Self-t. This condition is stronger than Bayesian consistency because it requires beliefs to be consistent even for certain events that may not occur on the equilibrium path (namely, events associated with ex-ante actions that are not played in equilibrium). This condition ensures that the PBE satisfies subgame perfection, which would not be the case if one only restricted beliefs on the equilibrium path to be consistent with Bayes’ rule.

4.1. Self-t + 1 Investment Game

Given ${\lambda }_{\sigma }$, at $t+1$ the individual will choose the action that maximizes her future plan14. For the DM, the incentive criterion (IC) to invest at time $t+1$ in the new path, $e=1$, requires that the gains of investment, measured in terms of utility differentials, are greater than the cost of facing the investment

$$\begin{array}{cc}\hfill I{C}_i(1)& =V\left(\theta ,\theta (1),S_{t+2}\right)-V\left(\theta ,\theta (0),S_{t+1}\right)-C_i\ge 0\hfill \\ & =\delta {\theta }^{*}r+s[\theta (1)(S_{t+1}+r)-\theta (0)S_{t+1}]\ge C_i.\hfill \end{array}$$

(15)

The criterion to invest at time $t+1$ in the old path, $e=0$:

$$\begin{array}{cc}\hfill I{C}_i(0)& =V\left(\theta ,\theta (1),S_{t+2}\right)-V\left(\theta ,\theta (0),S_{t+1}\right)-C_i\le 0\hfill \\ & =\delta {\theta }^{*}r+s[\theta (1)(S_{t+1}+r)-\theta (0)S_{t+1}]\le C_i.\hfill \end{array}$$

(16)

That is to say, whenever the utility differentials are not so large for the DM to confront the cost of investing in a new path, then it is more efficient to remain in her status quo.

Given the parameters, the individual will maximize her total plan under the set of strategies and beliefs expressed above. If at any stage of the game the strategies are sequentially rational, namely, optimal given the beliefs, and the belief system is consistent given the equilibrium strategies, and considering that $\mathsf{\Theta }$ and A and $U(·)$ respect the requirements for the existence of a fixed point according to Kakutani’s theorem, then:

Proposition 1.

There exists a unique monotonic undominated equilibrium, characterized by thresholds $\tilde{p}$ and $\overline{p}$ with $0<\tilde{p}\le \overline{p}\le 1$ and investment probabilities $x_H(p)$ and $x_L(p)$ such that:

$$x_H(p)=\left\{\begin{array}{cc}\hfill 0& \mathit{if}p>\overline{p},\hfill \\ \hfill 1& \mathit{if}p<\overline{p},\hfill \end{array}\right.$$

(17)

$$x_L(p)=\left\{\begin{array}{cc}\hfill 0& \mathit{if}p\in [\overline{p};1],\hfill \\ \hfill 1& \mathit{if}p\in [\tilde{p};\overline{p}],\hfill \\ \hfill nondecreasing& \mathit{if}p\in [0;\tilde{p}].\hfill \end{array}\right.$$

(18)

Proof. 

See Appendix B. ☐

Because of Assumptions 3 and 4, $x_i^{*}$ is weakly increasing in $\theta$, and then respectively in p, imposing that a higher type cannot choose a lower investment choice.

$$x_L(1-x_H)=0,$$

(19)

hence, whenever $x_L>0$ then $x_H=1$.

Moreover, monotone comparative statics imply that $r^{*}$ is a cutpoint decision rule. There is a parameter value $r^{*}$, and respectively p such that the DM chooses the separating equilibria for some value moving from $r^{*}$, and she can instead have multiple equilibria at the cutpoint.

The equilibrium is evaluated for $0<\overline{p}<1$, for decreasing values of $C_i$. Moreover, the results above show that the probability of receiving a specific signal has a monotonic hump-shaped effect on the overall probability investment whose trend will increase in p on the interval $[0;\tilde{p})$15, then it will equal to 1 on $[\tilde{p};\overline{p})$, and after that it will fall to 0.

Characterization of Equilibria. Let us discuss the incentive criteria (15) and (16) in order to characterize the equilibria.

• Pooling toward null investment.
  Both agents will choose the strategy of non-investment in the new path. From the assumption on $V(·)$ and the incentive criteria specific for each type, the H types are those who might have some strategic interest in not investing in a different path, since for them the decision to invest could be less costly than for the L type. Assume that it means that

  $$\delta {\theta }^{*}+s[{\theta }_H{S}_{t+2}-\overline{\theta }{S}_{t+1}]<C_H.$$

  (20)
  In this equilibrium, we consider only the incentive constraint of an H-type, since for L-type it will be always costly to invest. We obtain the incentive constraint by knowing that if p is high enough (i.e., the self-image is behind the threshold $\overline{p}$), H-type can afford not to invest. Then, $x_H=x_L=0$ and the posterior beliefs are $\theta (0)=\overline{\theta }$ and $\theta (1)={\theta }_H$ since $\widehat{q}=\frac{1}{2}$ and $\widehat{p}=\epsilon \in [0;1]$. Then, type H can afford not to invest if $p>\overline{p}$, but when the latter relation does not hold, then H will take some action to distinguish herself from L. In this equilibrium, H-type will not invest in education for several other motivations. The fact that in this scenario $p>\overline{p}$ means that the agent is surrounded by people following the old path and it would be too costly for her to take action to prove being the eccentric one. If she deviates from the norm, this deviation will be self-justified, as the malleability of the beliefs will increase. In turn,
• Separating for ${\theta }_H$:

  $$\delta {\theta }^{*}+s[{\theta }_H{S}_{t+2}-{\theta }_L{S}_{t+1}]>C_H;$$

  (21)
• Separating for ${\theta }_L$:

  $$\delta {\theta }^{*}+s[{\theta }_H{S}_{t+2}-{\theta }_L{S}_{t+1}]<C_L.$$

  (22)
  In this equilibrium, we consider both the incentive constraints of an H-type and an L-type. We get the incentive constraint by knowing that if there is the possibility of separating the types, then $x_H=1$ and $x_L=0$ and the posterior beliefs are $\theta (0)={\theta }_L$ and $\theta (1)={\theta }_H$ since $\widehat{q}=0$ and $\widehat{p}=p$. Then, $\theta (1)>\theta (0)$ type H will invest and L will not since $0<p<\tilde{p}$ and the ${C_L}_0$ is so high that it is not worthwhile for L to invest. In this scenario, incentive constraints bind for the two types with $I{C}_L\le 0$ and $I{C}_H\ge 0$.
• Semi-separating (hybrid) by randomising for ${\theta }_L$:

  $$\delta {\theta }^{*}+s[\theta (1)S_{t+2}-{\theta }_L{S}_{t+1}]=C_L.$$

  (23)
  This scenario occurs when the cost of investment for L-type is small enough to imitate the H-type. However, the imitation is always constrained by the prior, and the credibility of signaling to be H-type depends on p and $x_L$: the lower the former, the more credible the strategy. Then, we have $x_H=1$ and $0<x_L<1$, and the posterior probabilities are $\widehat{p}=\overline{p}$ while $0<\widehat{q}<\widehat{p}(1)$, with the posterior beliefs represented by $\theta (0)={\theta }_L$ and $\overline{\theta }<\theta (1)<{\theta }_H$. Accordingly, type H will not invest and L will only depend on how credible the posterior probabilities are, $I{C}_L=0$.
• Pooling towards total investment:

  $$\delta {\theta }^{*}+s[\overline{\theta }{S}_{t+2}-{\theta }_L{S}_{t+1}]>C_L.$$

  (24)
  In the case of both types investing in further education, the incentive constraint that we need to consider is the one of the L-type, since by definition H-type will always have incentive to invest. In this scenario, we have that the probability to invest is $x_H=x_L=1$ and then, recalling (8), the posterior beliefs are $\theta (0)={\theta }_L$ and $\theta (1)=\overline{\theta }$ since $\widehat{q}=\epsilon \in [0;1]$ and $\widehat{p}=\frac{1}{2}$. Then, $\theta (1)>\theta (0)$ type H will invest and L will only if her $I{C}_L\ge 0$ binds and in that case $\tilde{p}\le p\le \overline{p}$. The incentive holds since it is worthy to pursue for costs facing even a small gain in self-image: as the cost increases, so does the threshold $\tilde{p}$.

Comparative Analysis. The probability to invest (x) is determined by both the internal (p, ${\lambda }_{\sigma }$, s) and external ($S_t$, r, $C_i$) constraints. Moreover, both individuals invest more when $x_H$ and $x_L$ (weakly) increase. In all cases, type H will go either for a separating, a full investment, or hybrid equilibrium, while type L will invest only in hybrid or full situation. Then, to show for what values of the main parameters the probability to invest increases, we need to study how the incentive constraint varies with respect to a variation of parameters. From

$$I{C}_i=\delta {\theta }^{*}r+s[\theta (1)(S_{t+1}+er)-\theta (0)S_t]-C_i,$$

if individuals invest in education, then $e=1$. We have:

$$\frac{\partial I{C}_i}{\partial S_{t+1}}=s(\theta (1)-\theta (0))>0.$$

$S_{t+1}$ is a measure of initial affiliation. Its level and quality are higher for the H type, driving her to show more incentive in eliciting identity-affirming investment. The positive impact of the stock on the willingness to invest is a consequence of the so-called escalating commitment, expressed by the requirement on $V_{\theta S_t+1}$: individuals have a higher demand for optimistic beliefs when they have more at stake (in this case, when they have higher identity-specific capital $S_t$ already invested). From here it is worth making another consideration:

$$\frac{{\partial }^{2}I{C}_i}{\partial S_{t+1}\partial s}=(\theta (1)-\theta (0)).$$

The higher the initial investment, the more positive the emotion attached to future identity and the higher the incentive to invest.

$$\frac{\partial I{C}_i}{\partial r}=\delta {\theta }^{*}+s\theta (1)>0$$

An increase in the evaluation of the interest rate means an enlargement of the perception and awareness of the opportunity available. The interest rate of education is important information for the decision mechanism, and its lack depends on how connected the society is vertically and horizontally. Whenever the society is highly stratified, this piece of information is lost.

$$\frac{\partial I{C}_i}{\partial s}=\left[(\theta (1)S_{t+1}-\theta (0)S_t)\right]>0$$

The more pleasant the sentiment related to the future identity conveyed by the investment possibility, the higher the incentive to invest. The positive feelings depend on how much the DM feels her current self connected with her future self, so that she can engage in forward-looking choices.

Finally, the impact of the cost on the probability of investment is inversely related regarding the type: for H-type, a decrease of the initial cost increases $\overline{p}$ (it gets closer to 1), decreasing her willingness to invest. For $L_{}$ type, a decrease of cost means a decrease of $\tilde{p}$ (it gets closer to 0) reducing the mixing region, then it increases her willingness to invest ($x_L$).

4.2. Self-t Memory Manipulation Game

Once the signal has been received, how will the DM interpret the new information in order to safeguard her beliefs? Here, the Self-t implements the recall strategy by using memory manipulation (or ex-post denial) to safeguard her beliefs. She has incentives to process the H and L signals asymmetrically. In order to do so, let us define what the expected utilities are given the signals and recollections16.

When the signal is recall and interpreted realistically, the expected utilities given either the signal and the recollection are the same, then:

$$U_i(\theta ;\theta (\widehat{{\sigma }_i}),{\sigma }_i)=E\left[U(\theta ;\theta (\widehat{{\sigma }_i});S_t;{\sigma }_i)|\widehat{\sigma }\right].$$

(25)

If the DM instead decides to rationalize the signal (i.e., if she recollects $\widehat{\sigma }=\varnothing$), the expected utilities will be:

$$\begin{array}{ccc}\hfill U_{\varnothing }(\theta ;\theta (\varnothing ),{\sigma }_i)& =& E_{r^{*}}\left[U(\theta ;\theta (\widehat{\varnothing });S_t;{\sigma }_i)|\widehat{\sigma }\right]\hfill \\ & =& r({\lambda }_{\sigma }^{*})\times U_H(\theta (\varnothing ))+[1-r({\lambda }_{\sigma }^{*})]\times U_L(\theta (\varnothing )),\hfill \end{array}$$

(26)

as illustrated in Figure A217. The rationalization of the signal represents an incentive for the DM, who has preferences over her identity. Since the manipulation of her beliefs is defined according to Bayes’ rule, the DM will eventually make correct inferences and learn her identity. However, the updating process is slower than what would normally be implied by Bayes’ rule. This situation is described as conservatism bias, according to which all new information is insufficiently weighted in the updating process.

Memory Manipulation. Individuals maximize utility not only through behavior but by adopting a view of reality that is consistent with their well-being. These views have direct effects on behavior. The adoption passes by the imperfect recall of information and manipulation of the beliefs. The main consequence is that the long-run self will recall the information received in such a way as to manipulate the information set18 that the short-run self will inherit. Hence, after observing a signal $\sigma =\{H;L\}$, the long-run self chooses ${\lambda }_{\sigma }$ to maximize the following function:

$${\lambda }_{\sigma }{U}_i(\theta ;\theta (\widehat{{\sigma }_i}),{\sigma }_i)+(1-{\lambda }_{\sigma })U_{\varnothing }(\theta ;\theta (\varnothing ),{\sigma }_i)-M_{\sigma }({\lambda }_{\sigma }).$$

By adding Equation (26), we get

$$\begin{array}{c}\hfill U_i(\theta ;\theta (\varnothing ),{\sigma }_i)+{\lambda }_{\sigma }[U_i(\theta ;\theta (\widehat{{\sigma }_i}),{\sigma }_i)-U_i(\theta ;\theta (\varnothing ),{\sigma }_i)]+\\ \hfill (1-{\lambda }_{\sigma })r({\lambda }_{\sigma }^{*})[U_j(\theta ;\theta (\varnothing ),{\sigma }_i)-U_i(\theta ;\theta (\varnothing ),{\sigma }_i)]-M_{\sigma }({\lambda }_{\sigma }).\end{array}$$

(27)

Definition 4.

$\Delta DM=U_i(\theta ;\theta (\widehat{{\sigma }_i}),{\sigma }_i)-U_i(\theta ;\theta (\varnothing ),{\sigma }_i)$ represents the decision-making factor.

Given the recall strategy, will the DM make a suboptimal decision?

Definition 5.

$\Delta U=U_j(\theta ;\theta (\varnothing ),{\sigma }_i)-U_i(\theta ;\theta (\varnothing ),{\sigma }_i)$ represents the self-image differential in utility, considering $j\ne i$.

Given the recall strategy, how much utility does the DM gain through a more favorable inference of her identity? Let us consider the two cases.

The expected utility of Self-t conditional on receiving a signal $\sigma =L$ is:

$$\begin{array}{c}\hfill U_L(\theta ;\theta (\varnothing ),L)+{\lambda }_{\sigma }[U_L(\theta ;\theta (L),L)-U_L(\theta ;\theta (\varnothing ),L]+\\ \hfill (1-{\lambda }_{\sigma })r({\lambda }_{\sigma }^{*})[U_H(\theta ;\theta (\varnothing ),L)-U_L(\theta ;\theta (\varnothing ),L)]-M_{\sigma }({\lambda }_{\sigma }).\end{array}$$

Because of the assumption on revealed preferences $U_L(\theta ;\theta (L),L)<U_L(\theta ;\theta (\varnothing ),L)$, hence the decision-making factor is negative for the L type. That is to say, forgetting L’s signal might lead to a suboptimal choice of the future action. However, the self-esteem will boost, because of the stochastic ordering of the signal, $U_H(\theta ;\theta (\varnothing ),L)>U_L(\theta ;\theta (\varnothing ),L)$.

Upon receiving a signal $\sigma =H$, and after a few manipulations, the expected utility will be:

$$\begin{array}{c}\hfill U_H(\theta ;\theta (\varnothing ),H)+(1-r({\lambda }_{\sigma }^{*}))U_L(\theta ;\theta (\varnothing ),H)+\\ \hfill {\lambda }_{\sigma }[U_H(\theta ;\theta (H),H)-U_i(\theta ;\theta (\varnothing ),H]+\\ \hfill ({\lambda }_{\sigma })r({\lambda }_{\sigma }^{*})[U_H(\theta ;\theta (\varnothing ),H)-U_L(\theta ;\theta (\varnothing ),H)]-M_{\sigma }({\lambda }_{\sigma }).\end{array}$$

In this case, forgetting the H signal has a negative effect on both decision-making and self-esteem. Because of both the revealed preferences and the stochastic ordering, receiving H signal is a situation in which memory manipulation should not be implemented.

Memory Manipulation in Hedonic Case. If we consider the decision of recalling the signal as in pure hedonic value19, then the DM will choose to consider only the self-image differential. The recall strategy will be dependent on it, on the cost function of memory, and on the content of the initial signal. In Appendix C it is possible to find the full characterization of the equilibria coming from the manipulation when both types of agent choose the amount of information to recall. Let us consider case-by-case. When ${\sigma }_t=L$ Self-t maximizes the following:

$$\begin{array}{c}{\lambda }_L{U}_L(\theta ;\theta (\widehat{{\sigma }_i}),{\sigma }_i)+(1-{\lambda }_L)U_{\varnothing }-M_L({\lambda }_L)\hfill \\ =U_L+r({\lambda }_L^{*})(1-{\lambda }_L)\Delta U-M_L({\lambda }_L),\hfill \end{array}$$

(28)

thus, Self-t will choose the amount of manipulation, then ${\lambda }_{\sigma }$, so as to maximize the previous formula. Then, for L-type we may observe that

$$\underset{{\lambda }_L}{max}{\lambda }_L{U}_L+r({\lambda }_L^{*})(1-{\lambda }_L)U_H+[1-r({\lambda }_L^{*})](1-{\lambda }_L)U_L-M_L({\lambda }_L),$$

(29)

then by Kuhn–Tucker Theorem,

$${\displaystyle \frac{\partial U_L}{\partial {\lambda }_L}}:-r({\lambda }_L^{*})\Delta U-M_L^{{}^{\prime }}({\lambda }_L)=0.$$

(30)

The recollection strategy would be different for H and L types.

Let us start by studying the L type. Her inference about the accuracy20 of the signal, with some manipulation, is

$$r({\lambda }_L^{*})=\frac{p}{p+(1-p)(1-{\lambda }_L^{*})},$$

whose values depend on whether ${\lambda }_L^{*}=0$, then $r^{*}=p$, or ${\lambda }_L^{*}=1$, then $r^{*}=1$. Hence, $r({\lambda }_L^{*})\in [p,1]$. By applying Kuhn–Tucker’s theorem, the FOC (30) becomes:

$$M_L^{{}^{\prime }}({\lambda }_L)=-\left[\frac{p}{p+(1-p)(1-{\lambda }_L^{*})}\Delta U\right].$$

(31)

By the implicit function theorem, ${\lambda }_L^{*}\in \mathsf{\Re }$ exists.

Proposition 2.

The PBEs for belief manipulation are defined by

$${\lambda }_L^{*}=\left\{\begin{array}{cc}\hfill 0& if \Delta U\le \frac{M_L^{\prime }(0)}{p},\hfill \\ \hfill 1& if \Delta U\ge M_L^{\prime }(1).\hfill \end{array}\right.$$

(32)

The amount of belief manipulation will be:

• Increasing in $\Delta U$;
• Decreasing in $M(\lambda )$;
• Increasing in p.

Proof. 

See Appendix B. ☐

Analogously, the expected utility of Self-t after observing an H signal is:

$$\begin{array}{c}{\lambda }_H{U}_H(\theta ;\theta (\widehat{{\sigma }_i}),{\sigma }_i)+(1-{\lambda }_H)U_{\varnothing }-M_H({\lambda }_H)\hfill \\ ={\lambda }_H{U}_H+r({\lambda }_H^{*})(1-{\lambda }_H)U_H+(1-r({\lambda }_H^{*}))(1-{\lambda }_H)U_L-M_H({\lambda }_H)\hfill \end{array}$$

(33)

$$\underset{{\lambda }_H}{max}{\lambda }_H{U}_H+r({\lambda }_H^{*})(1-\lambda )U_H+[1-r({\lambda }_H^{*})](1-{\lambda }_H)U_L-M_H({\lambda }_H)$$

(34)

and

$${\displaystyle \frac{\partial U_H}{\partial {\lambda }_H}}:[1-r({\lambda }_H^{*})]\Delta U-M_H^{{}^{\prime }}({\lambda }_H)=0.$$

(35)

Type H’s inference about the accuracy21 of the signal, with some manipulation is

$$r({\lambda }_H^{*})=\frac{p(1-{\lambda }_H^{*})}{p(1-{\lambda }_L^{*})+(1-p)},$$

whose values depend on whether ${\lambda }_H^{*}=0$, then $r^{*}=p$, or ${\lambda }_H^{*}=1$, then $r^{*}=0$. Hence, $r({\lambda }_H^{*})\in [0,p]$. By applying Kuhn–Tucker’s theorem, the FOC (35) becomes:

$$\left[1-\frac{p(1-{\lambda }_H^{*})}{p(1-{\lambda }_L^{*})+(1-p)}\right]\Delta U=M_H^{{}^{\prime }}(\lambda ).$$

(36)

By the implicit function theorem ${\lambda }_H^{*}\in \mathsf{\Re }$ exists.

Proposition 3.

The PBEs for belief manipulation follow:

$${\lambda }_H^{*}=\left\{\begin{array}{cc}\hfill 0& \mathit{if}\Delta U\le \frac{M_H^{\prime }(0)}{(1-p)},\hfill \\ \hfill 1& \mathit{if}\Delta U\ge M_H^{\prime }(1).\hfill \end{array}\right.$$

(37)

The amount of belief manipulation will be:

• Increasing in $\Delta U$;
• Decreasing in $M(\lambda )$;
• Increasing in $(1-p)$.

In both cases, for any increase of ${\lambda }_{\sigma }$ both sides of (31) and (36) are increasing in the belief strategy, then there may be multiple interior equilibria.

5. Discussion

Like in the investment decision, the possibility of different equilibria depends on the probability of investing that, in turn, rely on the decision of how to recollect the signal, ${\lambda }_{\sigma }$, in accordance with the prevailing empirical expectations on the identity types $l(\sigma |\theta )$. Moreover, the incentives to engage in manipulation are higher as the self-image payoff gain, $\Delta U$, increases. The assumption of the manipulation cost function allows us to have equilibria with both manipulation and no manipulation according to the magnitude of $\Delta U$. In a pure strategy with accurate recall, the initial division of the population will be reflected in the following periods, then no undermining of the self-esteem in terms of peer recognition.

In a pure strategy with suppression of the signal, the updated beliefs at time $t+1$ converge to the average level of $\overline{\theta }$, showing that DM has either overconfident or underconfident beliefs in absolute terms. Moreover, if we consider the initial proportion of H-type and L-type individuals in the population, then the sense of overconfidence or underconfidence will be held in relative terms: for example, in a population where $p<\frac{1}{2}=(\overline{p})$, the median identity will be the one of ${\theta }_L$. The norm is to be L-type. Accordingly, if we assume that the entire population is motivated to endorse the socially accepted type, then we may have L-type DM exercising ${\lambda }_{\sigma }=1$, and H-type choosing ${\lambda }_{\sigma }=0$, reinforcing the identity with trait L. Let us see how it works. As already stated at the beginning of the model, in the population a proportion $1-p$ of DMs are identified by ${\theta }_L$ having received the signal ${\sigma }_t=L$. The proportion of ${\theta }_H$ having received ${\sigma }_t=H$ is p. The average identity is given by $\overline{\theta }=p{\theta }_H+(1-p){\theta }_L$, which can be written as a function of the proportion of H-type individuals: $\theta (p)$. Now let us assume that the the median identity is given by ${\theta }_L$. What would be the distribution of the self-evaluation? Let us assume that ${\sigma }_t=L$ is a signal reducing the self-image of the DM and that everyone will use the choose the same probability of recalling the signal, ${\lambda }_{\sigma }^{*}\in (0,1)$, and accordingly they will impute the reliability of the memory by $r^{*}$. Now, the self-assessment considering the accuracy of the recall will be $\theta (r^{*})$, no longer $\overline{\theta }$. Then, the fraction of agents who will manipulate the recall is represented by $(1-p)(1-{\lambda }_{\sigma }^{*})$ and they are those who overestimate their identity by $\theta ({\lambda }_{\sigma }^{*})-{\theta }_L=r^{*}({\theta }_H-{\theta }_L)$. To those individuals, we have to add the fraction of people who did receive a good signal, and they are p: the latter and the former will enlarge the proportion of people considering beyond the average, $(1-{\lambda }_{\sigma }^{*})(1-p)$. While the fraction of those underestimating their ability by ${\theta }_L-\theta ({\lambda }_{\sigma }^{*})=(1-r^{*})({\theta }_H-{\theta }_L)$ is represented by the minority p, who will see confirmed their self-assessment as an agent below-average. Moreover, the less the manipulation cost, the higher the number of H-types repressing the good signal. Another perspective from which to look at the problem can be expressed in terms of the homogeneity of the social context in which the DM lives. Whenever $p=\frac{1}{2}$, the social system enforces the highest level of entropy and diversity and then the individual should not incur any dissonance problem. That is, in a society in which you have an equal chance of moving in one direction or another, then the self-esteem problem related to the quest of belonging can be downsized. Instead, whenever the context is highly homogeneous, then the choices of either the action and of the signal rationalization are driven by the sense of belonging to a precise social group.

Yet, the manipulation costs can be very high leaving individuals in self-trap situations caused by their beliefs. Then, as already proved, the initial proportion of identity has an effect on both recalling and action strategy. One question that arises is the following: if every strategy can be brought back primitively to p, would the DM be able to identify a signal as informative for her identity and aspirations and then make a decision accordingly? Additionally, why is this question so important? It is important because the initial beliefs work as a mental insurance tool affecting the propensity towards a new piece of information. Indeed, the cognitive neighborhood, or the the information about p through the experience of a “similar” other, matters. It also matters what fraction of information on p the DM draws from whom.

5.1. Characterizing Beliefs Updating Heuristics

The work on how the DM’s information processing can be restrained is very extensive. In the studies of belief updating (Tversky and Kahneman [54]; Cameron [55]; Eil and Rao [56]; Mobius et al. [57]), agents are provided with signals about the same quantity over which belief revisions are being analyzed. For example, in Eil and Rao [56], Mobius et al. [57], and Grossman and Owens [58], respondents revise their beliefs about either their own intelligence or beauty, and receive feedback about the same underlying entity for which beliefs are being reported. In Nguyen [59] and Zafar [37,38], information on future earnings has been provided to students in other contexts, and it has been shown to have an impact on actual schooling choices but not without a certain delay in updating. Recalling a good signal is appealing every time the outcome of that signal dominates any other outcomes. For example, signaling a high IQ or scoring a high point in a student laboratory experiment is always better than signaling the opposite [18,19], because the identity of “being a good student” is the dominant in such environment, hence any feedback contrasting that ideal identity would be forgotten.

In these and other contexts, the asymmetric recall of good signal is justified by the fact that being good is the most socially acceptable identity. Yet, there are social situations in which identity and social norms establish that being both good and bad are socially acceptable, in which the history of what is socially accepted matters in the way the DM will choose how to recollect information and on how fast she will update her beliefs. So far, the “bad norm” and the “persistence in time” of the norm have not been investigated throughly in the empirical literature of motivated beliefs. This model tries to approach the time variable showing how the presence of social norms can impose preferences over information structures that, in turn, make the DM execute a rational decision process in imperfectly recalling the signal received, regardless of its good or bad sign. Yet, empirical analysis is required.

Moreover, this literature classifies agents’ updating according to the heuristic used, which ranges from conservative to representative, taking distance from a Bayesian updating depending on the weight assigned to the recent information or on the adjustment mechanism.

The conservative heuristic is the one that better applies to the context of the model. Individuals are subjected to conservatism bias if they fail to sufficiently adjust their beliefs in light of new information. In other words, they update in the right direction but less than a Bayesian updater. In this regard, people suffering from conservatism bias are those sensitive to new information, and they prefer to infer their identity from their recollection rather than from the actual signal. If we consider ${\widehat{\theta }}_{\widehat{\sigma }}$ as the expected value of $\theta$ given the information structure based on the recalled signal $\widehat{\sigma }$, while ${\theta }_{\sigma }$ is the expected value of the identity parameter given the information structure produced by the observed signal $\sigma$ (i.e., the Bayesian estimate of $\theta$ given the original signal), then ${\widehat{\theta }}_{\widehat{\sigma }}$ dominates ${\theta }_{\sigma }$ in the sense of second-order stochastic dominance.

Let us consider $G({\theta }_{\sigma })$ as the cumulative distribution of the expected value of $\theta$ conditional on the actual signal $\sigma$.

Proposition 4.

Whenever the DM is uncertainty-averse and her decision-making is justified by the presence of social norms, and whenever she is exposed to two information structures (one of which is in conflict with the information released by the norm), she will order the two structures according to the Second order Stochastic Dominance (SOSD). Namely, she will choose the information structure that is less-variable with respect to the social norm. In our model, ${\widehat{\theta }}_{\widehat{\sigma }}$ is less variable than ${\theta }_{\sigma }$. Additionally, the updating process of the information produced by σ, used by the DM, is conservative in the sense that it is less than what Bayes’ rule implies.

Proof. 

See Appendix B. ☐

5.2. Welfare Analysis of Awareness

In order to further assess the analysis, the perspective to consider is an ex ante one that will try to answer the following question: if the DM could choose whether to engage in a manipulation strategy before receiving the initial signal, what would she do? Ex ante it would be optimal to commit not to engage in a rationalization strategy because the expected cost related to the strategy would outweigh the expected gain. Moreover, the DM would be willing to observe the signal if the expected costs of making an uninformative decision are greater than the premium of engagement. Otherwise, she would prefer to gain a lower expected payoff but also avoid the self-deception costs. If this did not happen, then the DM would follow one of the four methods22 that in psychology are used as resolution of the dissonance: the selective exposure to information (i.e., the tendency people have to avoid information that would create cognitive dissonance because it is incompatible with their current beliefs).

6. Conclusions

This paper proposes a diachronic approach to the study of identity. It identifies empirical expectations and monotone information structure to be the tools through which people form the conception of their identity. The social norms are the determinant of the genesis of the identity conception. The model shows that because of the presence of the norms people decide to conform or react against them by manipulating the information structure in a self-serving way. In doing so, it addresses both the demand and supply sides of motivated cognition. The manipulation is also justified to reach inter-temporal goals. That is to say, this work shows how people make choices between identity-relevant options and how they deliberately shape and manage not only their current identity but also their future one coherently with a specific informational structure.

The findings highlight that the relation between norms and identity is not as simple as commonly used in the literature of bounded rationality and synchronic identity theory. The presence of norms not only defines the action strategies that it are expected to be taken, but it also shapes the mental structure that people use to read the reality. The latter findings are important in light of the debate about the micro-level consequences that social norms such as gender or group norms have on macro-level inefficiencies such as decreasing female labour participation and the persistence of gender and social and economic inequalities. Interventions aiming to reduce the material cost of the action (e.g., reducing economic barriers, quota interventions, scholarships, etc.) might not be as effective as expected if also the individual cognitive costs are not also addressed. However, no internal costs nor distorted beliefs will be reduced if social norms are not considered and studied extensively.