Effects of Relatedness on the Evolution of Cooperation in Nonlinear Public Goods Games
Abstract
1. Introduction
2. Model Description
2.1. Demographical Dynamics
2.2. Evolutionary Dynamics
3. Results
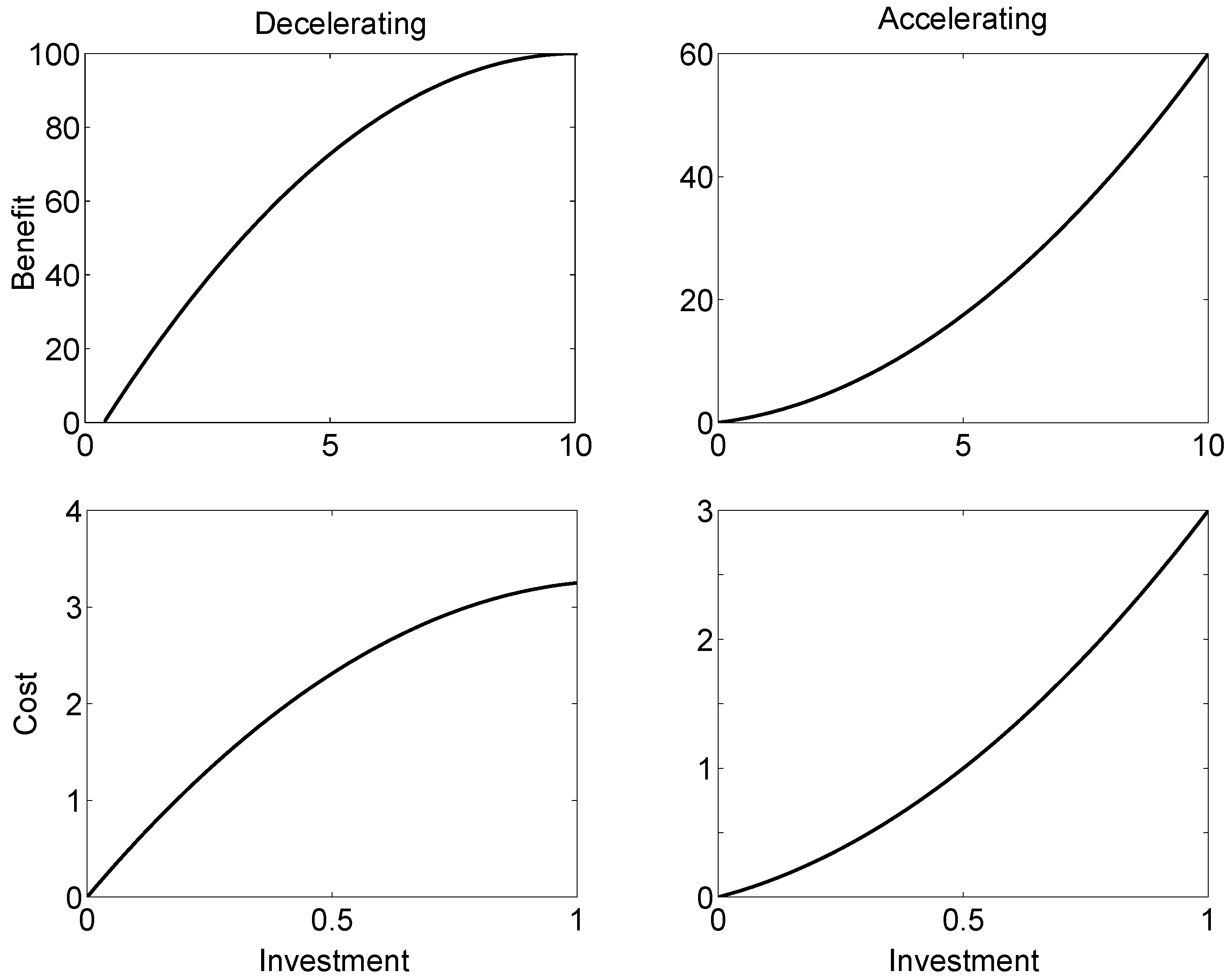
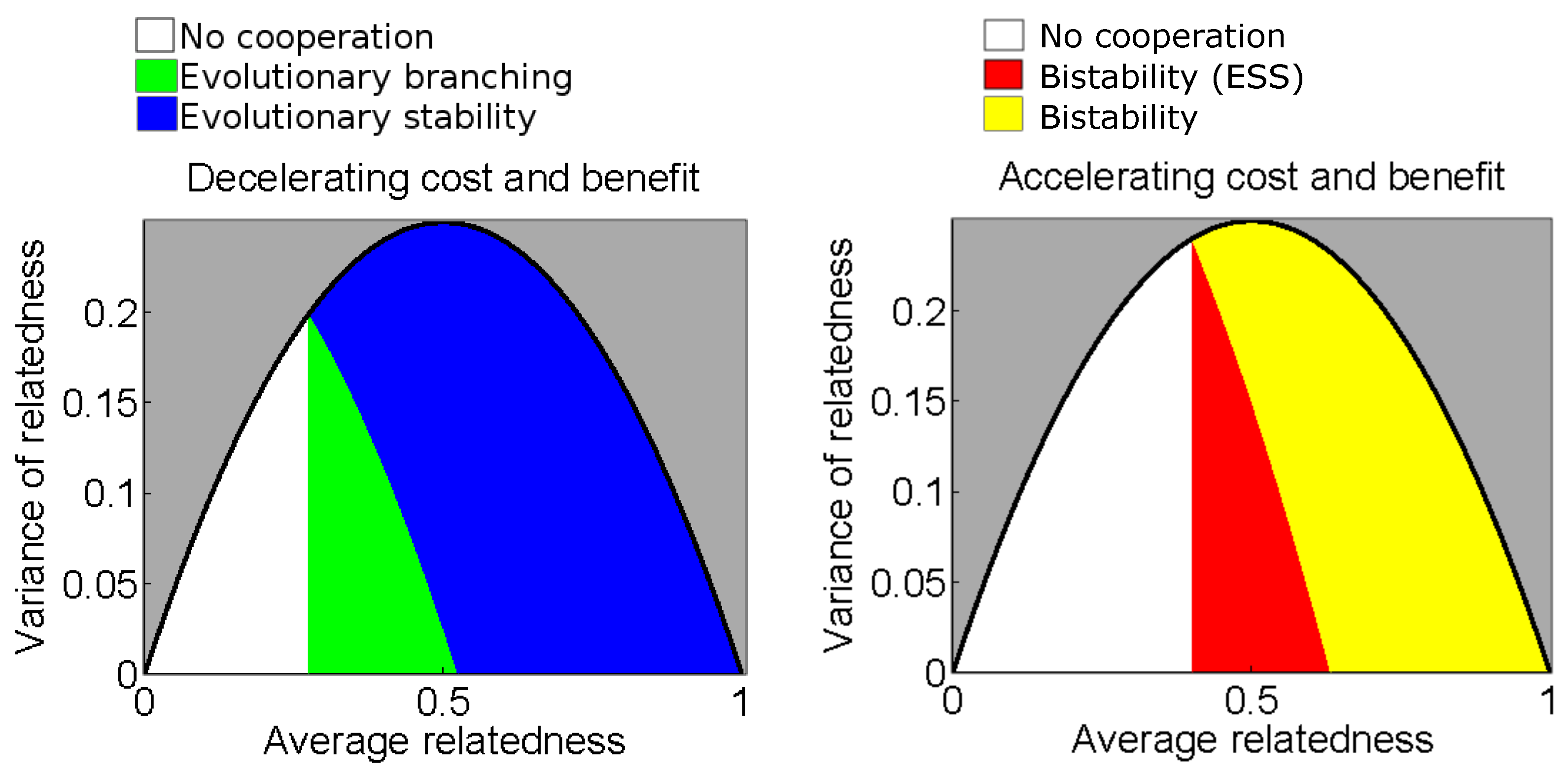
3.1. Quadratic Benefit and Cost Functions
- Assume B is accelerating and that , as is the case if C is decelerating. For , we have and selection is thus towards no cooperation. For , is decreasing and the evolutionary dynamics is bistable. For , we have and selection is thus towards full cooperation.
- Assume B is accelerating and that . For , we have and selection is thus towards no cooperation. For , we have is increasing and convergence stable, i.e., an evolutionary attractor. For , we have and selection is thus towards full cooperation.
- Assume B is decelerating and , as is the case if C is accelerating. For , we have and selection is thus towards no cooperation. For , is increasing and convergence stable, i.e., an evolutionary attractor.
- Assume B is decelerating and . For , is increasing and convergence stable, i.e., an evolutionary attractor. For , we have and selection is thus towards full cooperation.
3.2. General Cost and Benefit Functions
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Analytical Investigations
Appendix A.1. Condition for Evolutionary Stability
Appendix A.2. Impossible Region in the μ − σ2-Plane
Appendix A.3. Implicit Differentiation
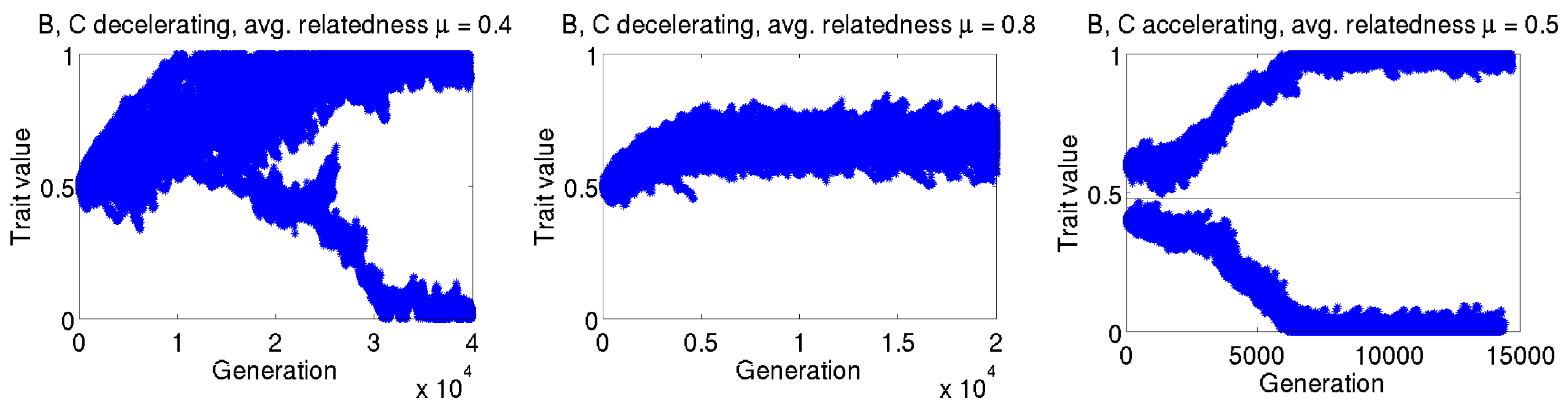
Appendix B. Individual-Based Simulations
References
- Dugatkin, L.A. Cooperation in animals: An evolutionary overview. Biol. Philos. 2002, 17, 459–476. [Google Scholar] [CrossRef]
- Hölldobler, B.; Wilson, E.O. The Ants. 1990. Available online: http://www.hup.harvard.edu/catalog.php?isbn=9780674040755 (accessed on 31 October 2018).
- Hamilton, W.D. Altruism and related phenomena, mainly in social insects. Ann. Rev. Ecol. Syst. 1972, 3, 193–232. [Google Scholar] [CrossRef]
- Cornforth, D.M.; Sumpter, D.J.T.; Brown, S.P.; Brännström, Å. Synergy and group size in microbial cooperation. Am. Nat. 2012, 180, 296–305. [Google Scholar] [CrossRef] [PubMed]
- Sachs, J.L.; Mueller, U.G.; Wilcox, T.P.; Bull, J.J. The evolution of cooperation. Q. Rev. Biol. 2004, 79, 135–160. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.A. Five rules for the evolution of cooperation. Science 2006, 314, 1560–1563. [Google Scholar] [CrossRef] [PubMed]
- Hamilton, W.D. The evolution of altruistic behaviour. Am. Nat. 1963, 97, 354–356. [Google Scholar] [CrossRef]
- Hofbauer, J.; Sigmund, K. Evolutionary Games Population Dynamics. 1998. Available online: https://www.cambridge.org/core/books/evolutionary-games-and-population-dynamics/A8D94EBE6A16837E7CB3CED24E1948F8 (accessed on 31 October 2018).
- Hofbauer, J.; Sigmund, K. Evolutionary game dynamics. Bull. Am. Math. Soc. 2003, 40, 479–519. [Google Scholar] [CrossRef]
- Grafen, A. The hawk-dove game played between relatives. Anim. Behav. 1979, 27, 905–907. [Google Scholar] [CrossRef]
- Eshel, I.; Cavalli-Sforza, L.L. Assortment of encounters and evolution of cooperativeness. Proc. Natl. Acad. Sci. USA 1982, 79, 1331–1335. [Google Scholar] [CrossRef] [PubMed]
- Tao, Y.; Lessard, S. Frequency-dependent selection in sexual family-structured populations. J. Theor. Biol. 2002, 217, 525–534. [Google Scholar] [CrossRef] [PubMed]
- Bergstrom, T.C. The algebra of assortative encounters and the evolution of cooperation. Int. Game Theor. Rev. 2003, 5, 211–228. [Google Scholar] [CrossRef]
- Taylor, C.; Nowak, M.A. Evolutionary game dynamics with non-uniform interaction rates. Theor. Popul. Biol. 2006, 69, 243–252. [Google Scholar] [CrossRef] [PubMed]
- Allen, B.; Nowak, M.A. Games among relatives revisited. J. Theor. Biol. 2015, 378, 103–116. [Google Scholar] [CrossRef] [PubMed]
- Cooney, D.; Allen, B.; Veller, C. Assortment and the evolution of cooperation in a Moran process with exponential fitness. J. Theor. Biol. 2016, 409, 38–46. [Google Scholar] [CrossRef] [PubMed]
- Brush, E.; Brännström, Å.; Dieckmann, U. Indirect reciprocity with negative assortment and limited information can promote cooperation. J. Theor. Biol. 2018, 443, 56–65. [Google Scholar] [CrossRef] [PubMed]
- Doebeli, M.; Hauert, C.; Killingback, T. Evolutionary origin of cooperators and defectors. Science 2004, 306, 859–862. [Google Scholar] [CrossRef] [PubMed]
- Deng, K.; Chu, T. Adaptive evolution of cooperation through Darwinian dynamics in public goods games. PLoS ONE 2011, 6, e25496. [Google Scholar] [CrossRef] [PubMed]
- Brännström, Å.; Gross, T.; Blasius, B.; Dieckmann, U. Consequences of fluctuating group size for the evolution of cooperation. J. Math. Biol. 2011, 63, 263–281. [Google Scholar] [CrossRef] [PubMed]
- Ito, K.; Ohtsuki, H.; Yamauchi, A. Relationship between aggregation of rewards and the possibility of polymorphism in continuous snowdrift games. J. Theor. Biol. 2015, 372, 47–53. [Google Scholar] [CrossRef] [PubMed]
- Sasaki, T.; Okada, I. Cheating is evolutionarily assimilated with cooperation in the continuous snowdrift game. Biosystems 2015, 131, 51–59. [Google Scholar] [CrossRef] [PubMed]
- Molina, C.; Earn, D.J. Evolutionary stability in continuous nonlinear public goods games. J. Math. Biol. 2017, 74, 499–529. [Google Scholar] [CrossRef] [PubMed]
- Geritz, S.A.H.; Kisdi, É.; Meszéna, G.; Metz, J.A.J. Evolutionarily singular strategies and the adaptive growth and branching of the evolutionary tree. Evolut. Ecol. 1998, 12, 35–57. [Google Scholar] [CrossRef]
- Metz, J.A.J.; Geritz, S.A.H.; Meszéna, G.; Jacobs, F.J.A.; Van Heerwaarden, J.S. Adaptive dynamics: A geometrical study of the consequences of nearly faithful reproduction. In Stochastic and Spatial Structures of Dynamical Systems; van Strien, S.J., Verduyn, L.S.M., Eds.; Amsterdam: New York, NY, USA, 1995; pp. 183–231. [Google Scholar]
- Dercole, F.; Rinaldi, S. Analysis of Evolutionary Processes: The Adaptive Dynamics Approach and Its Applications. 2008. Available online: https://press.princeton.edu/titles/8703.html (accessed on 31 October 2018).
- Brännström, Å.; Johansson, J.; von Festenberg, N. The hitchhiker’s guide to adaptive dynamics. Games 2013, 4, 304–328. [Google Scholar] [CrossRef]
- Gilbert, O.M.; Foster, K.R.; Mehdiabadi, N.J.; Strassmann, J.E.; Queller, D.C. High relatedness maintains multicellular cooperation in a social amoeba by controlling cheater mutants. Proc. Natl. Acad. Sci. USA 2007, 104, 8913–8917. [Google Scholar] [CrossRef] [PubMed]
- West, S.A.; Pen, I.; Griffin, A.S. Conflict and cooperation—Cooperation and competition between relatives. Science 2002, 296, 72–75. [Google Scholar] [CrossRef] [PubMed]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coder Gylling, K.; Brännström, Å. Effects of Relatedness on the Evolution of Cooperation in Nonlinear Public Goods Games. Games 2018, 9, 87. https://doi.org/10.3390/g9040087
Coder Gylling K, Brännström Å. Effects of Relatedness on the Evolution of Cooperation in Nonlinear Public Goods Games. Games. 2018; 9(4):87. https://doi.org/10.3390/g9040087
Chicago/Turabian StyleCoder Gylling, Kira, and Åke Brännström. 2018. "Effects of Relatedness on the Evolution of Cooperation in Nonlinear Public Goods Games" Games 9, no. 4: 87. https://doi.org/10.3390/g9040087
APA StyleCoder Gylling, K., & Brännström, Å. (2018). Effects of Relatedness on the Evolution of Cooperation in Nonlinear Public Goods Games. Games, 9(4), 87. https://doi.org/10.3390/g9040087




