Mean-Field Type Games between Two Players Driven by Backward Stochastic Differential Equations
Abstract
:1. Introduction
1.1. Related Work
1.2. Potential Applications of MFTG with Mean-Field BSDE Dynamics
1.3. Paper Contribution and Outline
2. Problem Formulation
List of Symbols
- —the time horizon.
- —the underlying filtered probability space.
- —the distribution of a random variable X under .
- —the set of -valued -measurable random variables X such that .
- —the progressive -algebra.
- —a stochastic process .
- —the set of -valued, continuous -measurable processes such that .
- —the set of -valued -measurable processes such that .
- — the set of admissible controls for player i.
- —the set of probability measures on .
- —the set of probability measures on with finite second moment.
- —the t-marginal of the state-, law- and control-tuple of player i.
- —the trace (Frobenius) norm of the matrix Z.
- —derivative of the -valued function f.
- —derivative of the -valued function f, see Appendix A for details.
- The Mean-field Type Game (MFTG): find the Nash equilibrium controls of
- The Mean-field Type Control Problem (MFTC): find the optimal control pair of
3. Problem 1: MFTG
4. Problem 2: MFTC
5. Example: The Linear-Quadratic Case
5.1. MFTG
5.2. MFTC
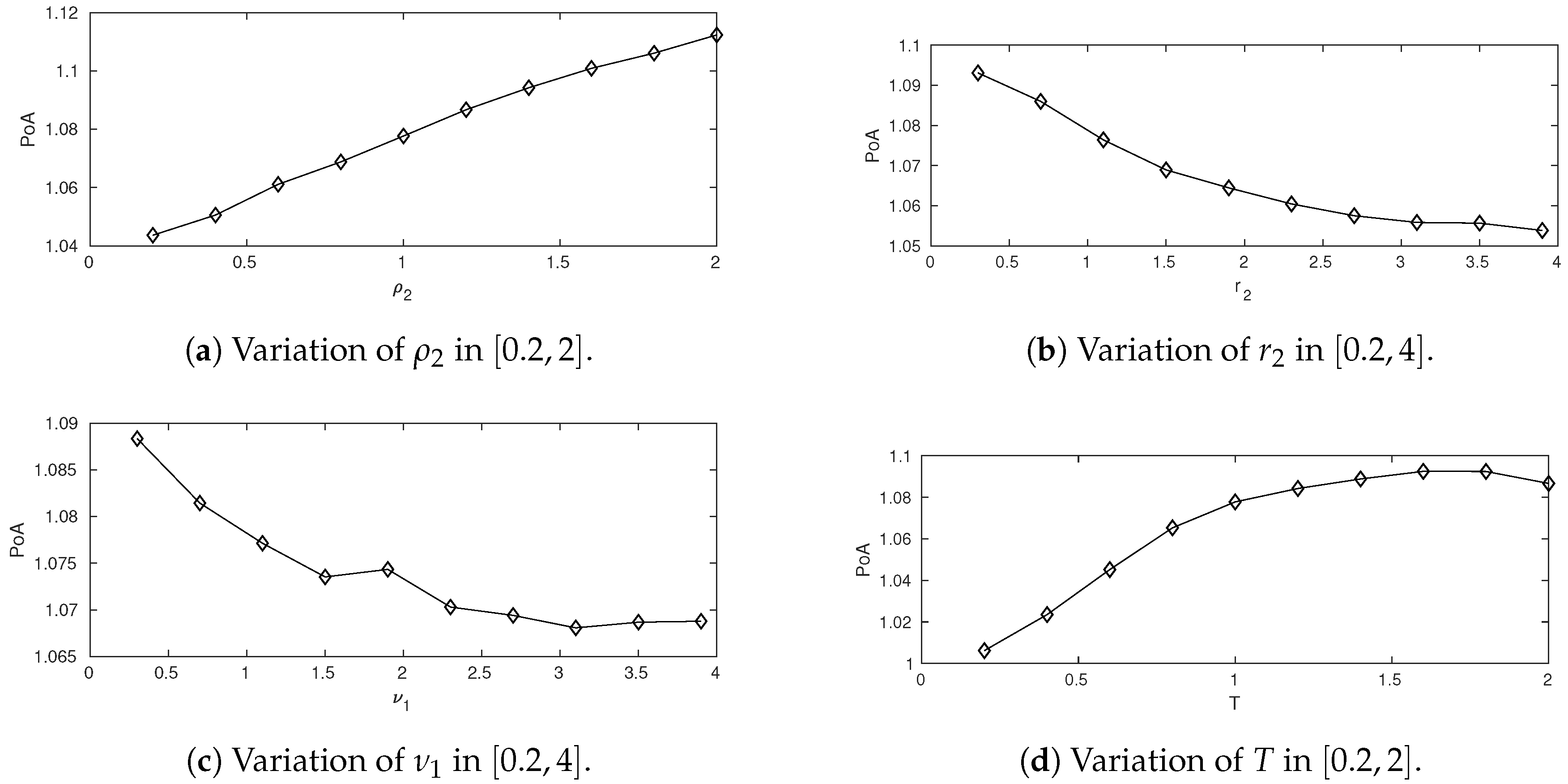
5.3. Simulation and the Price of Anarchy
6. Conclusions and Discussion
Acknowledgments
Conflicts of Interest
Abbreviations
| BSDE | Backward stochastic differential equation |
| FBSDE | Forward-backward stochastic differential equation |
| LQ | Linear-quadratic |
| MFTC | Mean-field type control problem |
| MFTG | Mean-field type game |
| ODE | Ordinary differential equation |
| PoA | Price of Anarchy |
| SDE | Stochastic differential equation |
Appendix A. Differentiation and Approximation of Measure-Valued Functions
Appendix B. Proofs
References
- Djehiche, B.; Tcheukam, A.; Tembine, H. Mean-Field-Type Games in Engineering. AIMS Electron. Electr. Eng. 2017, 1, 18–73. [Google Scholar] [CrossRef]
- Andersson, D.; Djehiche, B. A maximum principle for SDEs of mean-field type. Appl. Math. Optim. 2011, 63, 341–356. [Google Scholar] [CrossRef]
- Yong, J.; Zhou, X.Y. Stochastic Controls: Hamiltonian Systems and HJB Equations; Springer Science & Business Media: Berlin, Gremany, 1999; Volume 43. [Google Scholar]
- Kohlmann, M.; Zhou, X.Y. Relationship between backward stochastic differential equations and stochastic controls: A linear-quadratic approach. SIAM J. Control Optim. 2000, 38, 1392–1407. [Google Scholar] [CrossRef]
- Pardoux, É.; Peng, S. Adapted solution of a backward stochastic differential equation. Syst. Control Lett. 1990, 14, 55–61. [Google Scholar] [CrossRef]
- Peng, S. Probabilistic interpretation for systems of quasilinear parabolic partial differential equations. Stoch. Stoch. Rep. 1991, 37, 61–74. [Google Scholar] [CrossRef]
- Duffie, D.; Epstein, L.G. Stochastic differential utility. Econom. J. Econom. Soc. 1992, 60, 353–394. [Google Scholar] [CrossRef]
- El Karoui, N.; Peng, S.; Quenez, M.C. Backward stochastic differential equations in finance. Math. Financ. 1997, 7, 1–71. [Google Scholar] [CrossRef]
- Buckdahn, R.; Djehiche, B.; Li, J.; Peng, S. Mean-field backward stochastic differential equations: A limit approach. Ann. Probab. 2009, 37, 1524–1565. [Google Scholar] [CrossRef]
- Buckdahn, R.; Li, J.; Peng, S. Mean-field backward stochastic differential equations and related partial differential equations. Stoch. Process. Appl. 2009, 119, 3133–3154. [Google Scholar] [CrossRef]
- Moon, J.; Duncan, T.E.; Basar, T. Risk-Sensitive Zero-Sum Differential Games. IEEE Trans. Autom. Control 2018, in press. [Google Scholar] [CrossRef]
- Bensoussan, A.; Frehse, J.; Yam, P. Mean Field Games and Mean Field Type Control Theory; Springer: Berlin, Germany, 2013; Volume 101. [Google Scholar]
- Djehiche, B.; Tembine, H.; Tempone, R. A stochastic maximum principle for risk-sensitive mean-field type control. IEEE Trans. Autom. Control 2015, 60, 2640–2649. [Google Scholar] [CrossRef]
- Buckdahn, R.; Li, J.; Ma, J. A Stochastic Maximum Principle for General Mean-Field Systems. Appl. Math. Optim. 2016, 74, 507–534. [Google Scholar] [CrossRef]
- Carmona, R.; Delarue, F. Probabilistic Theory of Mean Field Games with Applications I–II; Springer: Berlin, Germany, 2018. [Google Scholar]
- Tembine, H. Mean-field-type games. AIMS Math. 2017, 2, 706–735. [Google Scholar] [CrossRef]
- Lacker, D. Limit Theory for Controlled McKean–Vlasov Dynamics. SIAM J. Control Optim. 2017, 55, 1641–1672. [Google Scholar] [CrossRef]
- Huang, M.; Malhamé, R.P.; Caines, P.E. Large population stochastic dynamic games: Closed-loop McKean-Vlasov systems and the Nash certainty equivalence principle. Commun. Inf. Syst. 2006, 6, 221–252. [Google Scholar]
- Lasry, J.M.; Lions, P.L. Mean field games. Jpn. J. Math. 2007, 2, 229–260. [Google Scholar] [CrossRef]
- Li, T.; Zhang, J.F. Asymptotically optimal decentralized control for large population stochastic multiagent systems. IEEE Trans. Autom. Control 2008, 53, 1643–1660. [Google Scholar] [CrossRef]
- Tembine, H.; Zhu, Q.; Başar, T. Risk-sensitive mean-field games. IEEE Trans. Autom. Control 2014, 59, 835–850. [Google Scholar] [CrossRef]
- Moon, J.; Basar, T. Linear Quadratic Risk-Sensitive and Robust Mean Field Games. IEEE Trans. Automat. Contr. 2017, 62, 1062–1077. [Google Scholar] [CrossRef]
- Peng, S. Backward stochastic differential equations and applications to optimal control. Appl. Math. Optim. 1993, 27, 125–144. [Google Scholar] [CrossRef]
- Dokuchaev, N.; Zhou, X.Y. Stochastic controls with terminal contingent conditions. J. Math. Anal. Appl. 1999, 238, 143–165. [Google Scholar] [CrossRef]
- Lim, A.E.; Zhou, X.Y. Linear-quadratic control of backward stochastic differential equations. SIAM J. Control Optim. 2001, 40, 450–474. [Google Scholar] [CrossRef]
- Wu, Z. A general maximum principle for optimal control of forward–backward stochastic systems. Automatica 2013, 49, 1473–1480. [Google Scholar] [CrossRef]
- Yong, J. Forward-backward stochastic differential equations with mixed initial-terminal conditions. Trans. Am. Math. Soc. 2010, 362, 1047–1096. [Google Scholar] [CrossRef]
- Li, X.; Sun, J.; Xiong, J. Linear Quadratic Optimal Control Problems for Mean-Field Backward Stochastic Differential Equations. Appl. Math. Optim. 2016, 1–28. [Google Scholar] [CrossRef]
- Tang, M.; Meng, Q. Linear-Quadratic Optimal Control Problems for Mean-Field Backward Stochastic Differential Equations with Jumps. arXiv, 2016; arXiv:1611.06434. [Google Scholar]
- Li, J.; Min, H. Controlled mean-field backward stochastic differential equations with jumps involving the value function. J. Syst. Sci. Complex. 2016, 29, 1238–1268. [Google Scholar] [CrossRef]
- Aurell, A.; Djehiche, B. Modeling tagged pedestrian motion: A mean-field type control approach. arXiv, 2018; arXiv:1801.08777. [Google Scholar]
- Aurell, A.; Djehiche, B. Mean-field type modeling of nonlocal crowd aversion in pedestrian crowd dynamics. SIAM J. Control Optim. 2018, 56, 434–455. [Google Scholar] [CrossRef]
- Chen, Z.; Epstein, L. Ambiguity, risk, and asset returns in continuous time. Econometrica 2002, 70, 1403–1443. [Google Scholar] [CrossRef]
- Koutsoupias, E.; Papadimitriou, C. Worst-case equilibria. In Annual Symposium on Theoretical Aspects of Computer Science; Springer: Berlin, Germany, 1999; pp. 404–413. [Google Scholar]
- Papadimitriou, C. Algorithms, games, and the internet. In Proceedings of the Thirty-Third Annual ACM Symposium on Theory of Computing, Crete, Greece, 6–8 July 2001; pp. 749–753. [Google Scholar]
- Pardoux, É. BSDEs, weak convergence and homogenization of semilinear PDEs. In Nonlinear Analysis, Differential Equations and Control; Springer: Berlin, Germany, 1999; pp. 503–549. [Google Scholar]
- Basar, T.; Olsder, G.J. Dynamic Noncooperative Game Theory; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1999; Volume 23. [Google Scholar]
- Zhang, J. Backward Stochastic Differential Equations: From Linear to Fully Nonlinear Theory; Springer: Berlin, Germany, 2017; Volume 86. [Google Scholar]
- Dubey, P. Inefficiency of Nash equilibria. Math. Oper. Res. 1986, 11, 1–8. [Google Scholar] [CrossRef]
- Koutsoupias, E.; Papadimitriou, C. Worst-case equilibria. Comput. Sci. Rev. 2009, 3, 65–69. [Google Scholar] [CrossRef]
- Başar, T.; Zhu, Q. Prices of anarchy, information, and cooperation in differential games. Dyn. Games Appl. 2011, 1, 50–73. [Google Scholar] [CrossRef]
- Duncan, T.E.; Tembine, H. Linear–Quadratic Mean-Field-Type Games: A Direct Method. Games 2018, 9, 7. [Google Scholar] [CrossRef]
- Carmona, R.; Graves, C.V.; Tan, Z. Price of anarchy for mean field games. arXiv, 2018; arXiv:1802.04644. [Google Scholar]
- Cardaliaguet, P.; Rainer, C. On the (in) efficiency of MFG equilibria. arXiv, 2018; arXiv:1802.06637. [Google Scholar]
- Ma, H.; Liu, B. Maximum principle for partially observed risk-sensitive optimal control problems of mean-field type. Eur. J. Control 2016, 32, 16–23. [Google Scholar] [CrossRef]
- Ma, H.; Liu, B. Linear-quadratic optimal control problem for partially observed forward-backward stochastic differential equations of mean-field type. Asian J. Control 2016, 18, 2146–2157. [Google Scholar] [CrossRef]
- Semasinghe, P.; Maghsudi, S.; Hossain, E. Game theoretic mechanisms for resource management in massive wireless IoT systems. IEEE Commun. Mag. 2017, 55, 121–127. [Google Scholar] [CrossRef]
- Tsiropoulou, E.E.; Vamvakas, P.; Papavassiliou, S. Joint customized price and power control for energy-efficient multi-service wireless networks via S-modular theory. IEEE Trans. Green Commun. Netw. 2017, 1, 17–28. [Google Scholar] [CrossRef]
- Katsinis, G.; Tsiropoulou, E.E.; Papavassiliou, S. Multicell Interference Management in Device to Device Underlay Cellular Networks. Future Internet 2017, 9, 44. [Google Scholar] [CrossRef]
- Cardaliaguet, P. Notes on Mean Field Games. Technical Report. 2010. Available online: https://www.researchgate.net/publication/228702832 (accessed on 3 September 2018).
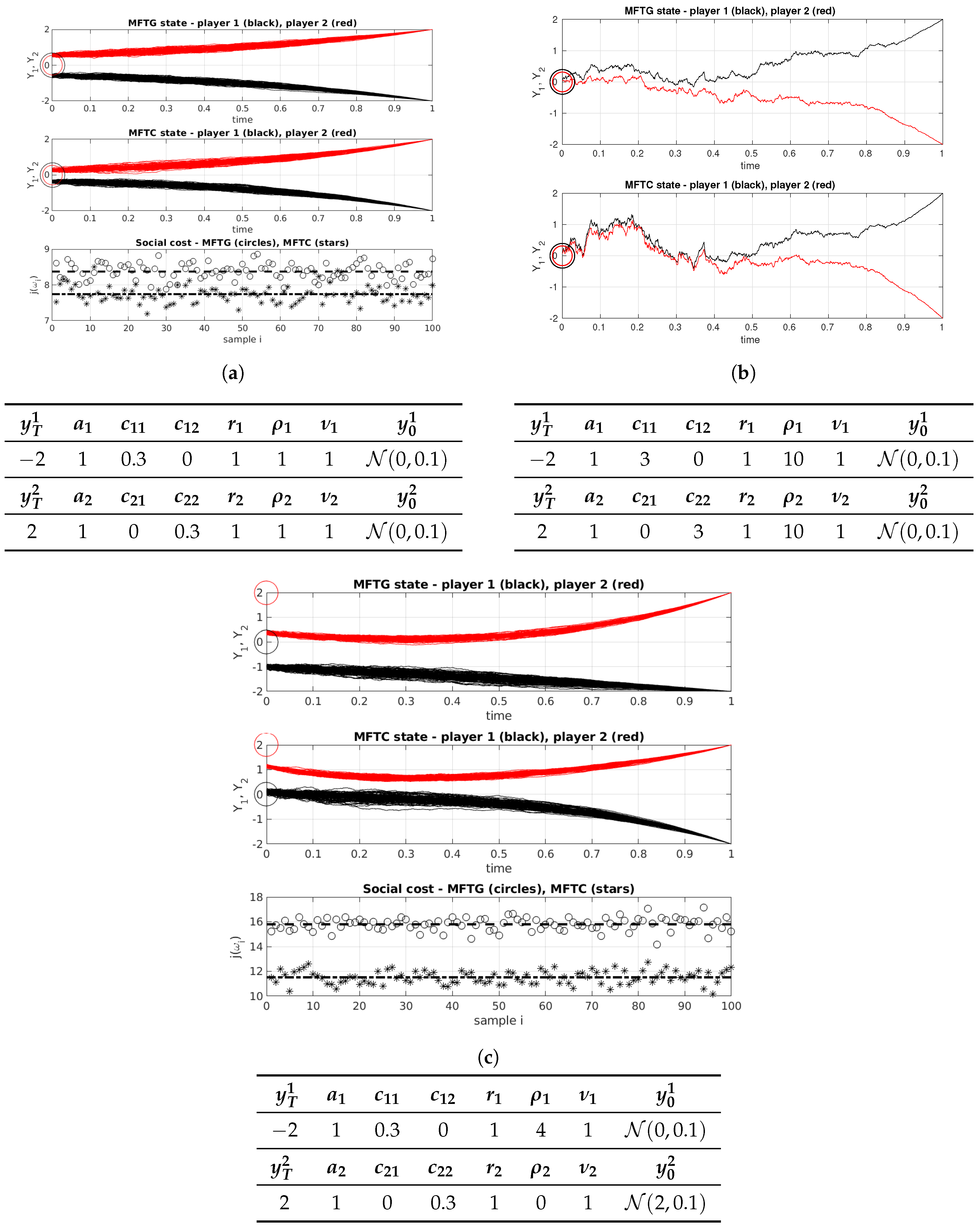
| −2 | 1 | 0.3 | 0 | 1 | 1 | 1 | |
| 2 | 1 | 0 | 0.3 | 1 | 1 | 1 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aurell, A. Mean-Field Type Games between Two Players Driven by Backward Stochastic Differential Equations. Games 2018, 9, 88. https://doi.org/10.3390/g9040088
Aurell A. Mean-Field Type Games between Two Players Driven by Backward Stochastic Differential Equations. Games. 2018; 9(4):88. https://doi.org/10.3390/g9040088
Chicago/Turabian StyleAurell, Alexander. 2018. "Mean-Field Type Games between Two Players Driven by Backward Stochastic Differential Equations" Games 9, no. 4: 88. https://doi.org/10.3390/g9040088
APA StyleAurell, A. (2018). Mean-Field Type Games between Two Players Driven by Backward Stochastic Differential Equations. Games, 9(4), 88. https://doi.org/10.3390/g9040088





