Game Theory of Tumor–Stroma Interactions in Multiple Myeloma: Effect of Nonlinear Benefits
Abstract
1. Introduction
1.1. From Intra-Tumor Cooperation to Tumor–Stroma Interactions
1.2. From Two-Player Games to Collective Interactions with Nonlinear Effects
1.3. Multiple Myeloma as a Modelling Case Study
2. Results
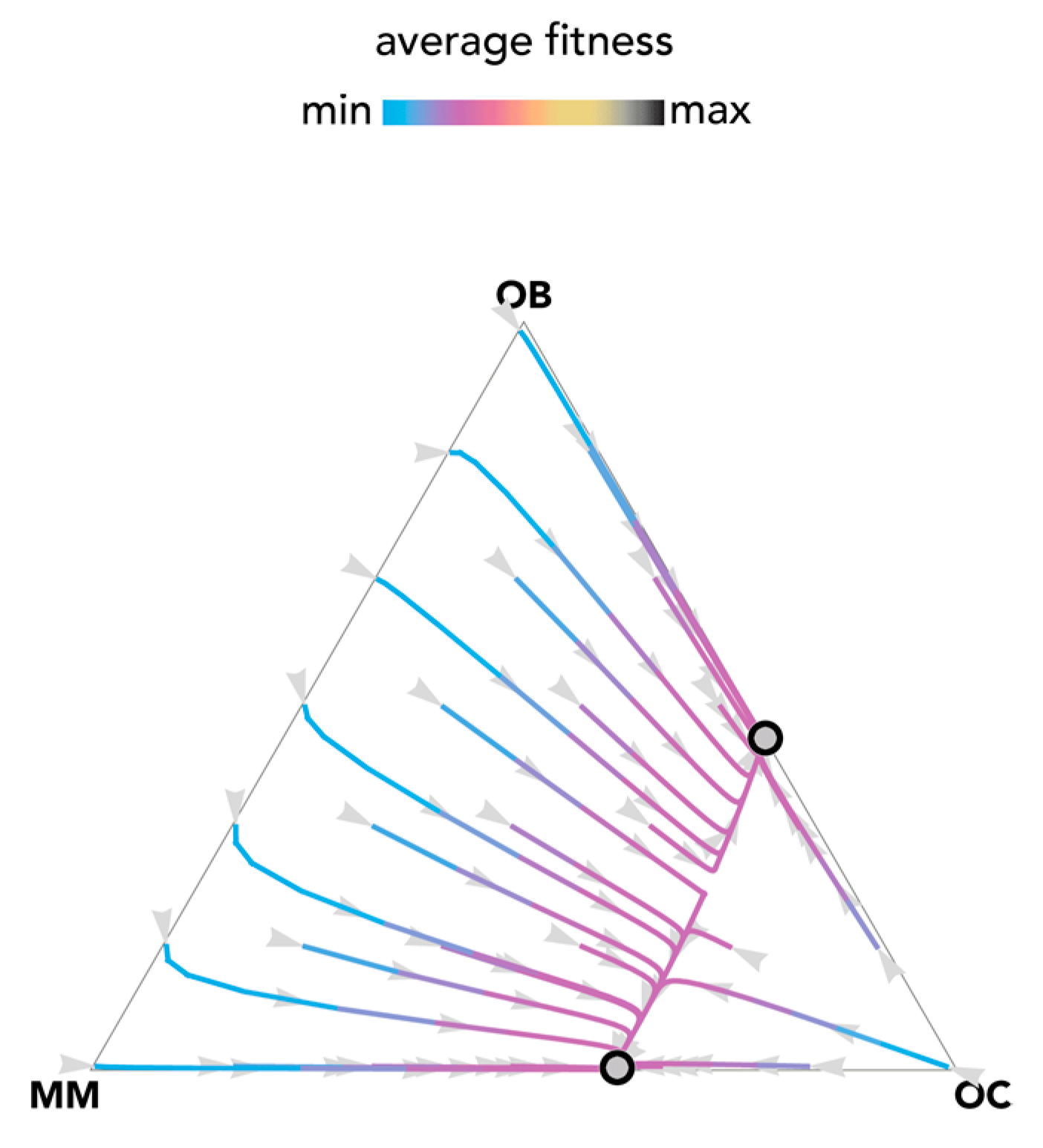
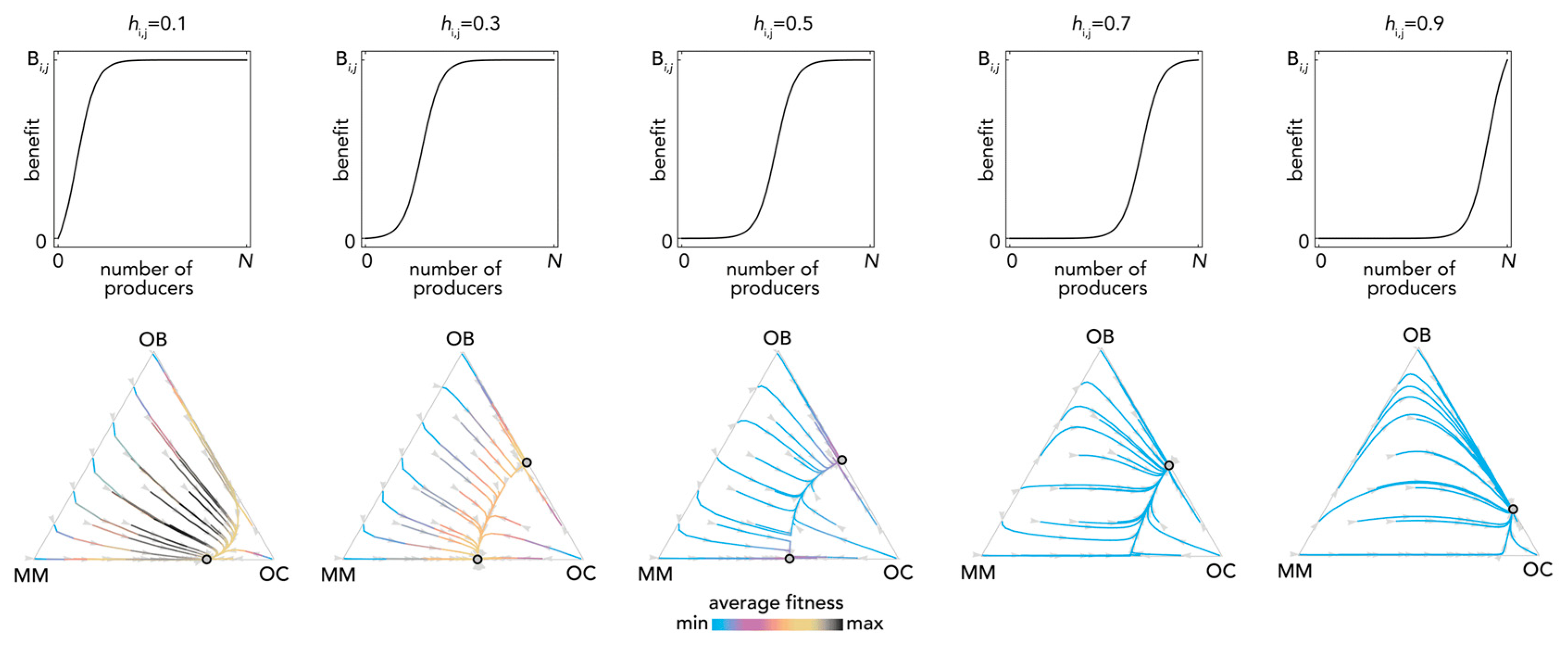
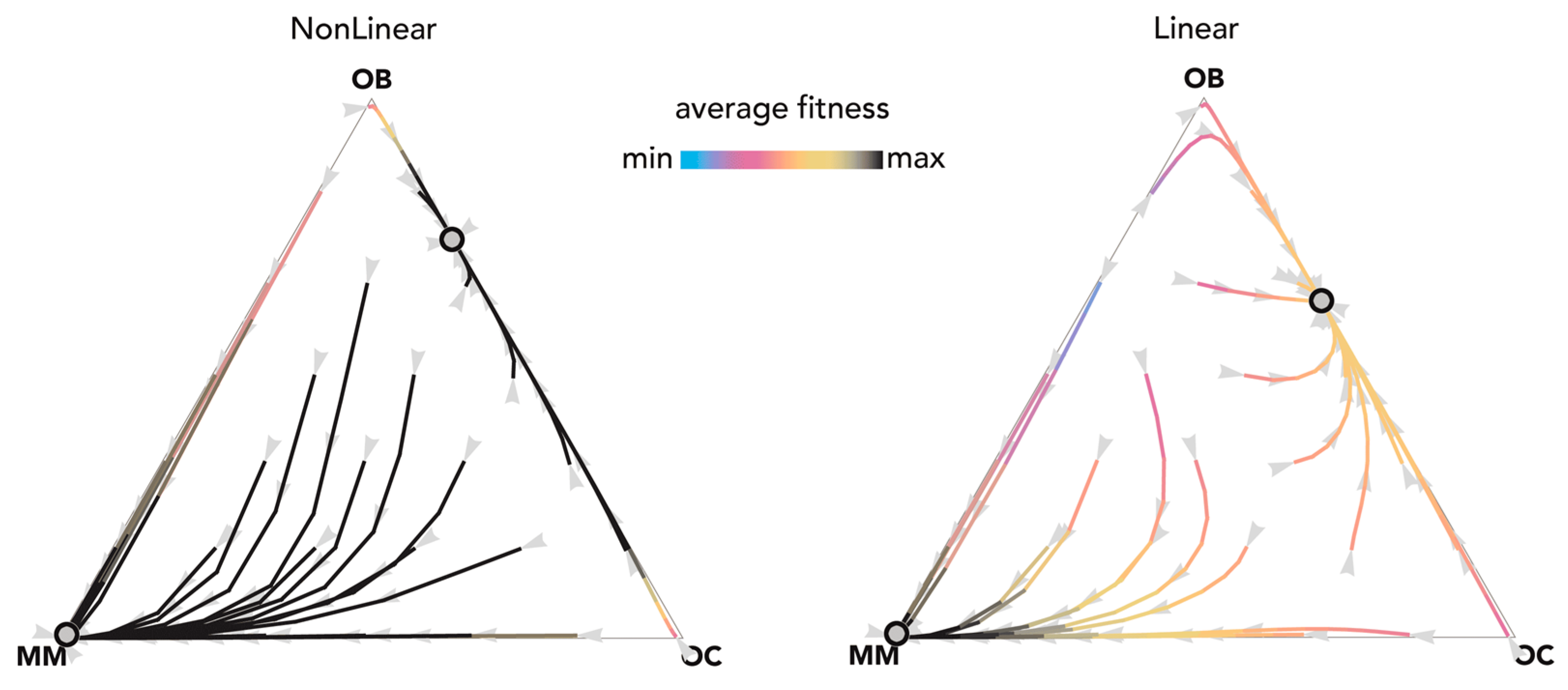
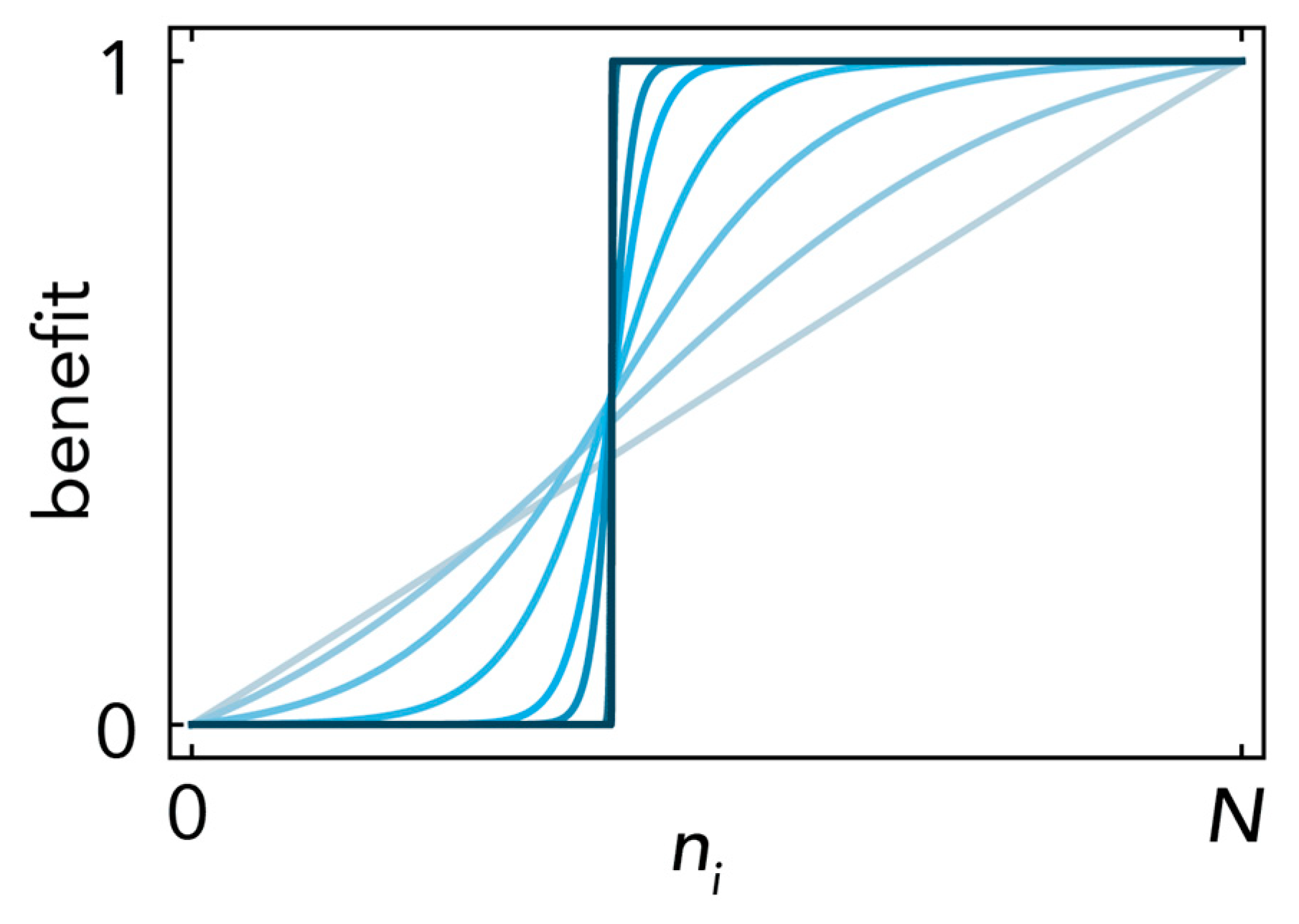
2.1. Stability (Bistability) Depends on the Shape of the Benefit Functions
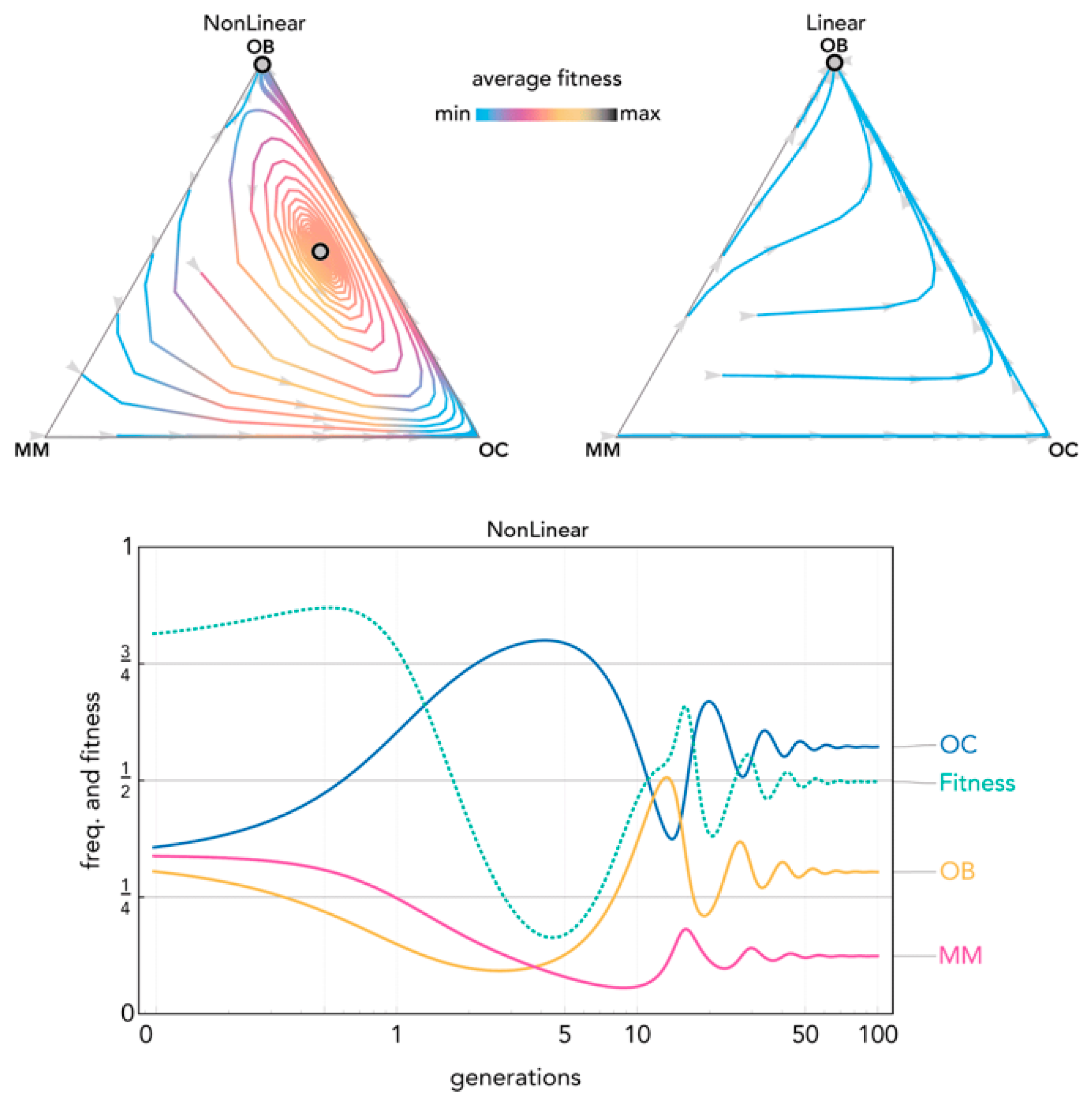
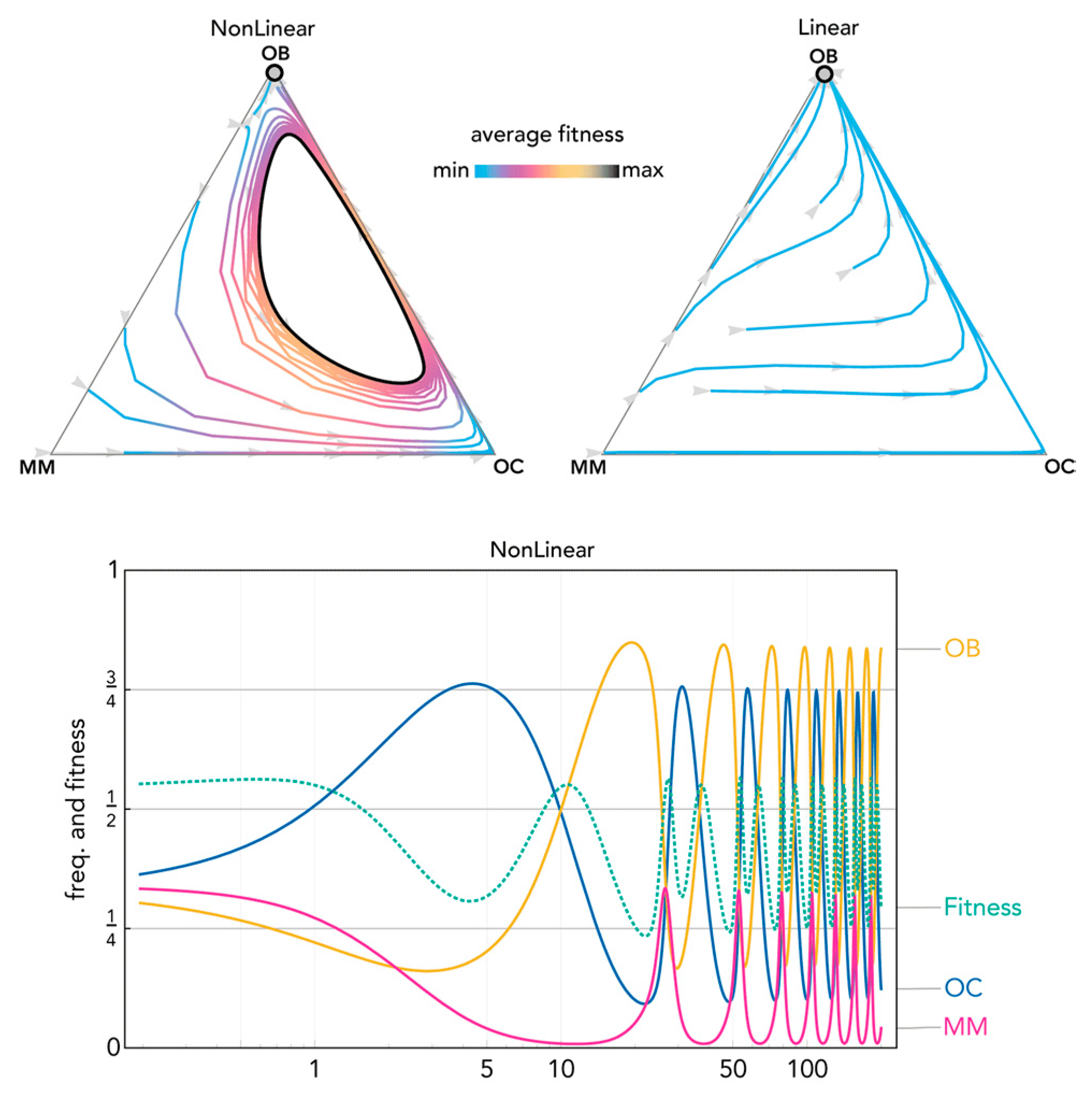
2.2. Nonlinear Benefits Can Lead to the Coexistence of Three Types and Cyclical Dynamics
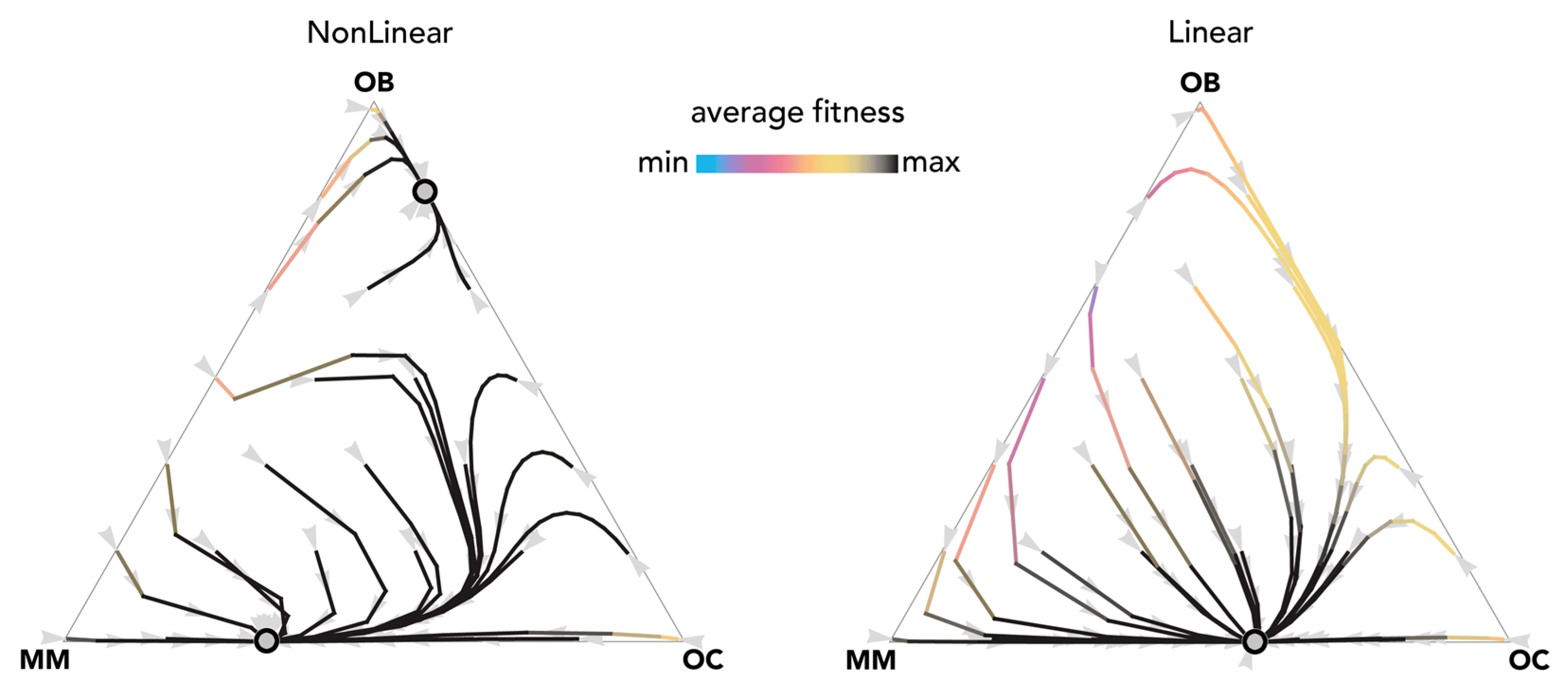
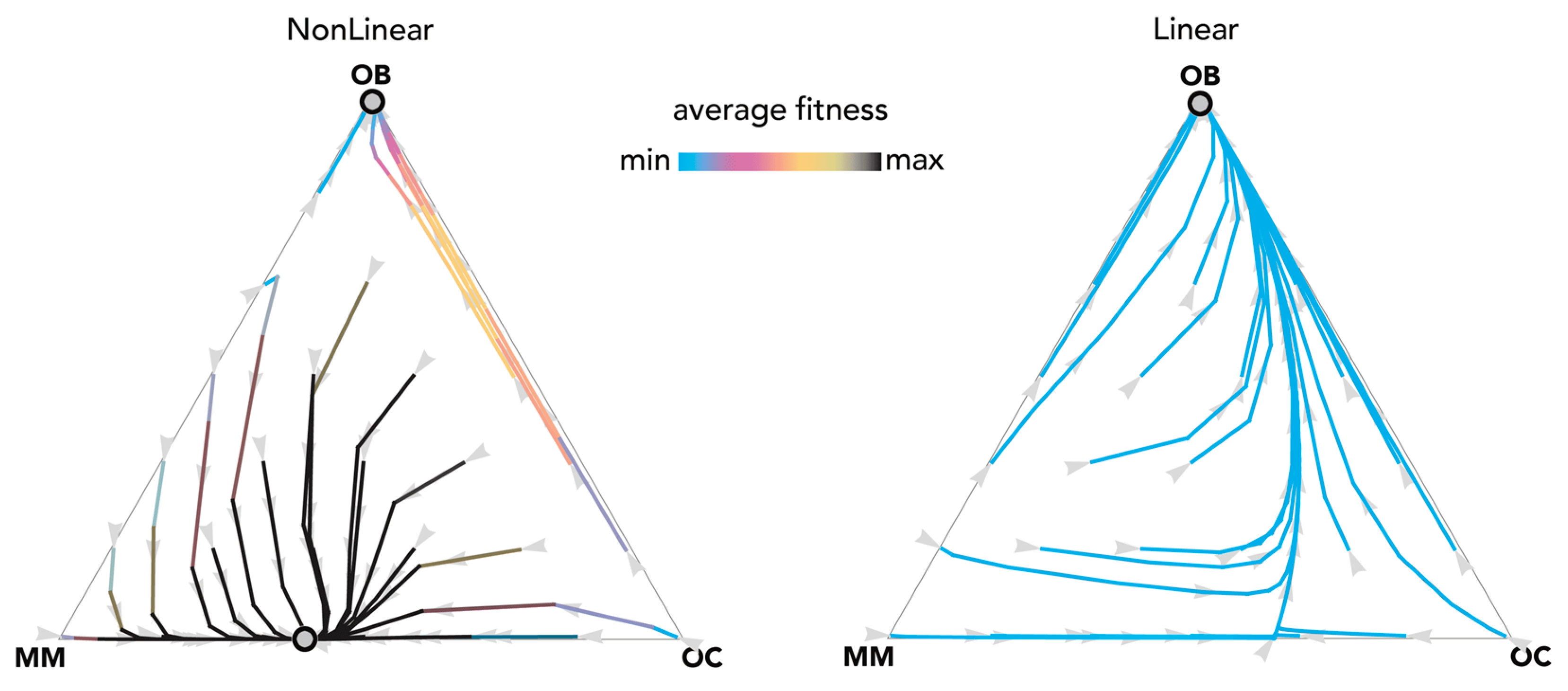
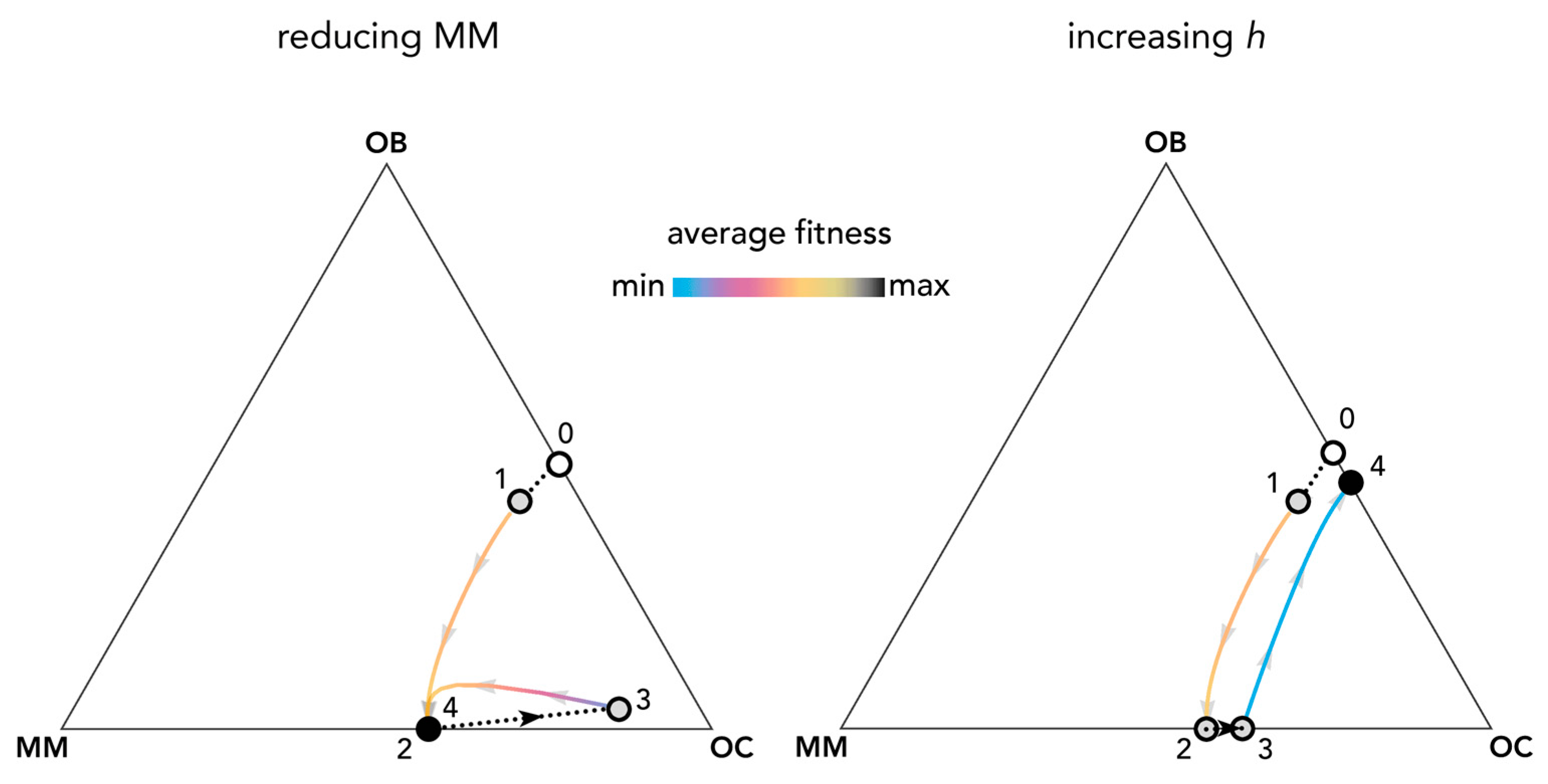
2.3. Therapies That Target Growth Factors May Be More Effective Than Chemotherapy
3. Discussion
4. Materials and Methods
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Axelrod, R.; Axelrod, D.E.; Pienta, K.J. Evolution of cooperation among tumor cells. Proc. Natl. Acad. Sci. USA 2006, 103, 13474–13479. [Google Scholar] [CrossRef] [PubMed]
- Archetti, M.; Ferraro, D.A.; Christofori, G. Heterogeneity for IGF-II production maintained by public goods dynamics in neuroendocrine pancreatic cancer. Proc. Natl. Acad. Sci. USA 2015, 112, 1833–1838. [Google Scholar] [CrossRef] [PubMed]
- Tomlinson, I.P. Game-theory models of interactions between tumour cells. Eur. J. Cancer 1997, 33, 1495–1500. [Google Scholar] [CrossRef]
- Tomlinson, I.P.; Bodmer, W.F. Modelling consequences of interactions between tumour cells. Br. J. Cancer 1997, 75, 157–160. [Google Scholar] [CrossRef] [PubMed]
- Dingli, D.; Chalub, F.; Santos, F.; Van Segbroeck, A.; Pacheco, J. Cancer phenotype as the outcome of an evolutionary game between normal and malignant cells. Br. J. Cancer 2009, 101, 1130–1136. [Google Scholar] [CrossRef] [PubMed]
- Basanta, D.; Simon, M.; Hatzikirou, H.; Deutsch, A. Evolutionary game theory elucidates the role of glycolysis in glioma progression and invasion. Cell Prolif. 2008, 41, 980–987. [Google Scholar] [CrossRef] [PubMed]
- Basanta, D.; Deutsch, A. A game theoretical perspective on the somatic evolution of cancer. In Selected Topics on Cancer Modelling: Genesis Evolution Immune Competition Therapy; Bellomo, N., Chaplain, M., De Angelis, E., Eds.; Birkhauser Boston: Cambridge, MA, USA, 2008. [Google Scholar]
- Basanta, D.; Scott, J.G.; Fishman, M.N.; Ayala, G.; Hayward, S.W.; Anderson, A.R. Investigating prostate cancer tumour-stroma interactions: Clinical and biological insights from an evolutionary game. Br. J. Cancer 2012, 106, 174–181. [Google Scholar] [CrossRef] [PubMed]
- Gerstung, M.; Nakhoul, H.; Beerenwinkel, N. Evolutionary games with affine fitness functions: Applications to cancer. Dyn. Games Appl. 2011, 1, 370–385. [Google Scholar] [CrossRef]
- Archetti, M. Evolutionary game theory of growth factor production: Implications for tumor heterogeneity and resistance to therapies. Br. J. Cancer 2013, 109, 1056–1062. [Google Scholar] [CrossRef] [PubMed]
- Archetti, M. Evolutionarily stable anti-cancer therapies by autologous cell defection. Evol. Med. Public Heatlh 2013, 1, 161–172. [Google Scholar] [CrossRef] [PubMed]
- Archetti, M. Dynamics of growth factor production in monolayers of cancer cells. Evol. Appl. 2013, 6, 1146–1159. [Google Scholar] [CrossRef] [PubMed]
- Archetti, M. Stable heterogeneity for the production of diffusible factors in cell populations. PLoS ONE 2014, 9, e108526. [Google Scholar] [CrossRef] [PubMed]
- Archetti, M. Cooperation among cancer cells as public goods games on Voronoi networks. J. Theor. Biol. 2016, 396, 191–203. [Google Scholar] [CrossRef] [PubMed]
- Basanta, D.; Hatzikirou, H.; Deutsch, A. Studying the emergence of invasiveness in tumours using game theory. Eur. Phys. J. 2008, 63, 393–397. [Google Scholar] [CrossRef]
- Basanta, D.; Scott, J.G.; Rockne, R.; Swanson, K.R.; Anderson, A.R. The role of IDH1 mutated tumour cells in secondary glioblastomas: An evolutionary game theoretical view. Phys. Biol. 2011, 8, 15016. [Google Scholar] [CrossRef] [PubMed]
- Archetti, M. Evolutionary dynamics of the Warburg effect: Glycolysis as a collective action problem among cancer cells. J. Theor. Biol. 2014, 341, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Archetti, M. Heterogeneity and proliferation of invasive cancer subclones in game theory models of the Warburg effect. Cell Prolif. 2015, 48, 259–269. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Fan, X.; Houghton, J. Tumor microenvironment: The role of the tumor stroma in cancer. J. Cell. Biochem. 2007, 101, 805–815. [Google Scholar] [CrossRef] [PubMed]
- Pietras, K.; Ostman, A. Hallmarks of cancer: Interactions with the tumor stroma. Exp. Cell Res. 2010, 316, 1324–1331. [Google Scholar] [CrossRef] [PubMed]
- Cirri, P.; Chiarugi, P. Cancer associated fibroblasts: The dark side of the coin. Am. J. Cancer Res. 2011, 1, 482–497. [Google Scholar] [PubMed]
- Hanahan, D.; Coussens, L.M. Accessories to the crime: Functions of cells recruited to the tumor microenvironment. Cancer Cell 2012, 21, 309–322. [Google Scholar] [CrossRef] [PubMed]
- Sartakhti, J.S.; Manshaei, M.H.; Bateni, S.; Archetti, M. Evolutionary Dynamics of Tumor-Stroma Interactions in Multiple Myeloma. PLoS ONE 2016, 11, e0168856. [Google Scholar] [CrossRef] [PubMed]
- Sartakhti, J.S.; Manshaei, M.H.; Sadeghi, M. MMP–TIMP interactions in cancer invasion: An evolutionary game- theoretical framework. J. Theor. Biol. 2017, 412, 17–26. [Google Scholar] [CrossRef] [PubMed]
- Archetti, M.; Scheuring, I. Review: Evolution of cooperation in one-shot social dilemmas without assortment. J. Theor. Biol. 2012, 299, 9–20. [Google Scholar] [CrossRef] [PubMed]
- Archetti, M. How to analyze models of nonlinear public goods. Games 2018, 9, 17. [Google Scholar] [CrossRef]
- Roodman, G. Pathogenesis of myeloma bone disease. Leukemia 2009, 23, 435–441. [Google Scholar] [CrossRef] [PubMed]
- Yaccoby, S. Advances in the understanding of myeloma bone disease and tumour growth. Br. J. Haematol. 2010, 149, 311–321. [Google Scholar] [CrossRef] [PubMed]
- Manier, S.; Sacco, A.; Leleu, X.; Ghobrial, I.M.; Roccaro, A.M. Bone marrow microenvironment in multiple myeloma progression. J. Biomed. Biotechnol. 2012, 2012, 157496. [Google Scholar] [CrossRef] [PubMed]
- Shalaby, M.R.; Waage, A.; Espevik, T. Cytokine regulation of interleukin-6 production by human endothelial cells. Cell. Immunol. 1989, 121, 372–382. [Google Scholar] [CrossRef]
- Bisping, G.; Leo, R.; Wenning, D.; Dankbar, B.; Padró, T.; Kropff, M.; Scheffold, C.; Kröger, M.; Mesters, R.M.; Berdel, W.E.; et al. Paracrine interactions of basic fibroblast growth factor and interleukin-6 in multiple myeloma. Blood 2003, 101, 2775–2783. [Google Scholar] [CrossRef] [PubMed]
- Dinarello, C.A. Interleukin-1 in the pathogenesis and treatment of inflammatory diseases. Blood 2011, 117, 3720–3732. [Google Scholar] [CrossRef] [PubMed]
- Carter, A.; Merchav, S.; Silvian-Draxler, I.; Tatarsky, I. The role of interleukin-1 and tumor necrosis factor-alpha in human multiple myeloma. Br. J. Haematol. 1990, 74, 424–431. [Google Scholar] [CrossRef] [PubMed]
- Urashima, M.; Ogata, A.; Chauhan, D.; Hatziyanni, M.; Vidriales, M.B.; Dedera, D.A.; Schlossman, R.L.; Anderson, K.C. Transforming growth factor-beta1: Differential effects on multiple myeloma versus normal B cells. Blood 1996, 87, 1928–1938. [Google Scholar] [PubMed]
- Dankbar, B.; Padró, T.; Leo, R.; Feldmann, B.; Kropff, M.; Mesters, R.M.; Serve, H.; Berdel, W.E.; Kienast, J. Vascular endothelial growth factor and interleukin-6 in paracrine tumor-stromal cell interactions in multiple myeloma. Blood 2000, 95, 2630–2636. [Google Scholar] [PubMed]
- Ehrlich, L.A.; Chung, H.Y.; Ghobrial, I.; Choi, S.J.; Morandi, F.; Colla, S.; Rizzoli, V.; Roodman, G.D.; Giuliani, N. IL-3 is a potential inhibitor of osteoblast differentiation in multiple myeloma. Blood 2005, 106, 1407–1414. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.W.; Chung, H.Y.; Ehrlich, L.A.; Jelinek, D.F.; Callander, N.S.; Roodman, G.D.; Choi, S.J. IL-3 expression by myeloma cells increases both osteoclast formation and growth of myeloma cells. Blood 2004, 103, 2308–2315. [Google Scholar] [CrossRef] [PubMed]
- Trikha, M.; Corringham, R.; Klein, B.; Rossi, J.F. Targeted anti-interleukin-6 monoclonal antibody therapy for cancer: A review of the rationale and clinical evidence. Clin. Cancer Res. 2003, 9, 4653–4665. [Google Scholar] [PubMed]
- Lonial, S.; Durie, B.; Palumbo, A.; San-Miguel, J. Monoclonal antibodies in the treatment of multiple myeloma: Current status and future perspectives. Leukemia 2016, 30, 526–535. [Google Scholar] [CrossRef] [PubMed]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sartakhti, J.S.; Manshaei, M.H.; Archetti, M. Game Theory of Tumor–Stroma Interactions in Multiple Myeloma: Effect of Nonlinear Benefits. Games 2018, 9, 32. https://doi.org/10.3390/g9020032
Sartakhti JS, Manshaei MH, Archetti M. Game Theory of Tumor–Stroma Interactions in Multiple Myeloma: Effect of Nonlinear Benefits. Games. 2018; 9(2):32. https://doi.org/10.3390/g9020032
Chicago/Turabian StyleSartakhti, Javad Salimi, Mohammad Hossein Manshaei, and Marco Archetti. 2018. "Game Theory of Tumor–Stroma Interactions in Multiple Myeloma: Effect of Nonlinear Benefits" Games 9, no. 2: 32. https://doi.org/10.3390/g9020032
APA StyleSartakhti, J. S., Manshaei, M. H., & Archetti, M. (2018). Game Theory of Tumor–Stroma Interactions in Multiple Myeloma: Effect of Nonlinear Benefits. Games, 9(2), 32. https://doi.org/10.3390/g9020032




