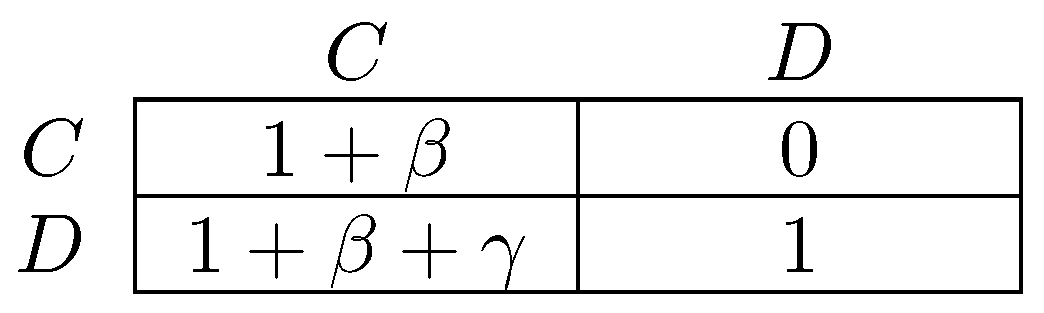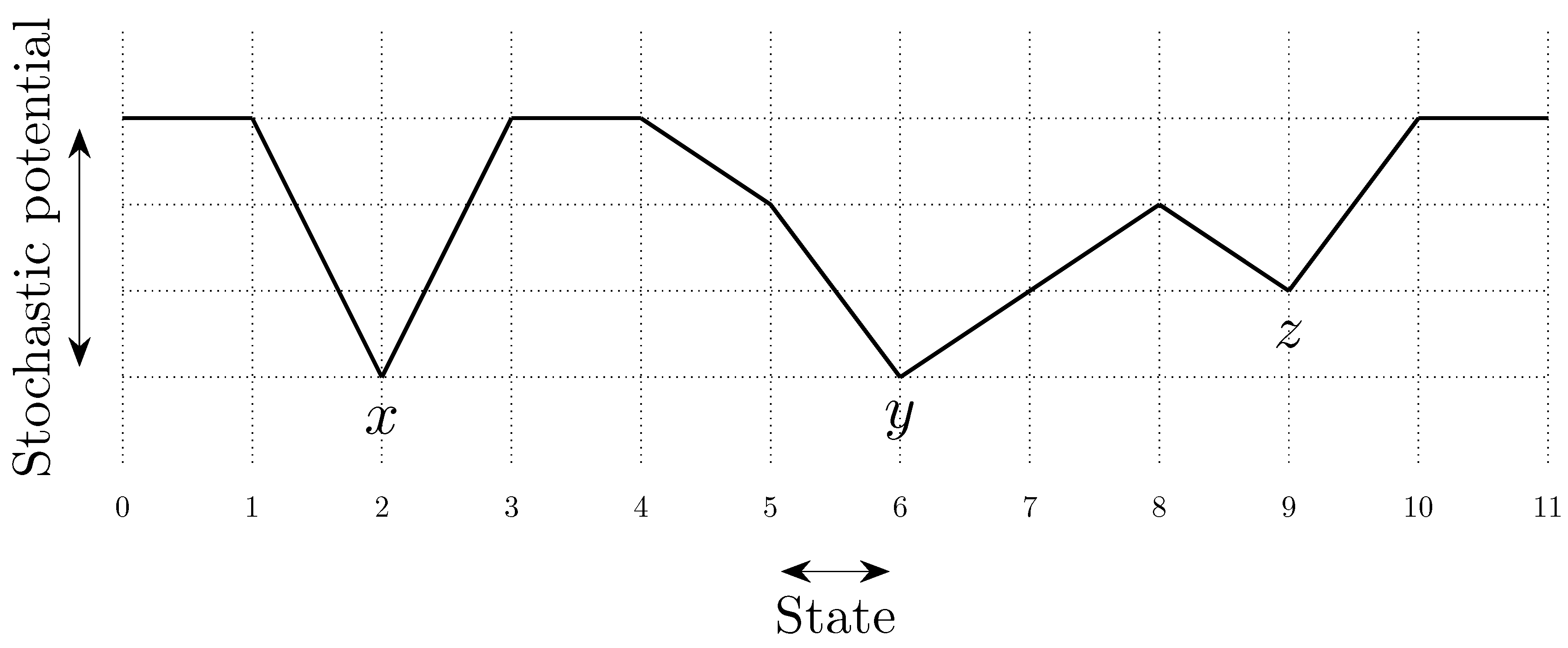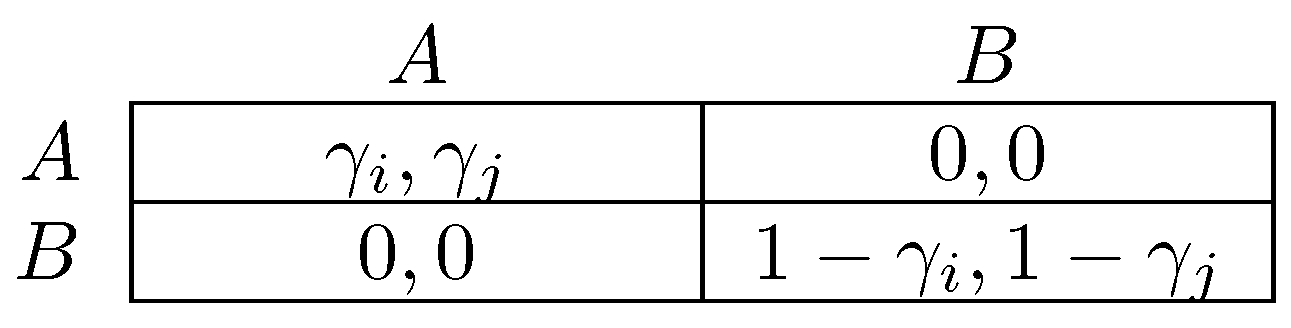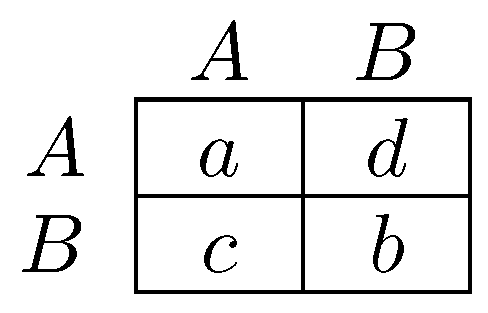Abstract
Economic agents are not always rational or farsighted and can make decisions according to simple behavioral rules that vary according to situation and can be studied using the tools of evolutionary game theory. Furthermore, such behavioral rules are themselves subject to evolutionary forces. Paying particular attention to the work of young researchers, this essay surveys the progress made over the last decade towards understanding these phenomena, and discusses open research topics of importance to economics and the broader social sciences.
JEL Classification:
C73
Table of contents
1 Introdiction P. 2
2 Agency—Who Makes Decisions? p. 3
Methodology · Implications · Evolution of Collective Agency · Links between Individual & Collective Agency
Assortativity & Preferences · Evolution of Assortativity · Generalized Matching · Conditional Dissociation · Network Formation
4 Evolution of Behavior p. 17
IntrodictionTraits · Conventions—Culture in Society · Culture in Individuals · Culture in Individuals & Society
5 Economic Applications p. 29
6 The Evolutionary Nash Program p. 30
Recontracting & Nash Demand Games · TU Matching · NTU Matching · Bargaining Solutions & Coordination Games
7 Behavioral Dynamics p. 36
Reinforcement Learning · Imitation · Best Experienced Payoff Dynamics · Best & Better Response · Continuous Strategy Sets · Completely Uncoupled
8 General Methodology p. 44
Perturbed Dynamics · Further Stability Results · Further Convergence Results · Distributed control · Software and Simulations
9 Empirics p. 50
10 Conclusions p. 54
References p. 54
1. Introduction
This essay surveys recent work in evolutionary game theory, primarily as it relates to the social sciences, with particular attention paid to the work of young researchers. The intended audience is current and potential researchers in evolutionary game theory, as well as a broader audience of interested readers whose specialisms lie in other fields. Evolutionary methods consider how a state variable changes over time. The state variable can be a biological or cultural trait or a profile of strategies in a game. The process by which it changes can be survival of the fittest, imitation or optimization arising from some deliberative rule. Thus, axioms on behavior and decision making are theoretically postulated and can be empirically tested. These axioms lead indirectly to predictions of medium and long run outcomes. This contrasts with fixed point solution concepts, such as Nash equilibrium or the Core, in which axioms on behavior are explicit restrictions on outcomes. In evolutionary game theory, behavioral rules and outcomes are distinct. The broad open spaces between behavior and outcomes are where evolutionary game theorists go to play.
1.1. The Shadow of Nash Equilibrium
To some, the period of intense activity in evolutionary game theory in the mid to late 1990s had two goals, firstly to justify Nash equilibrium and secondly to give some consistent and simple selection criterion for favoring some Nash equilibria over others. See Samuelson [303] for a brief description of this perspective. The author of the current survey sees such an approach as an exercise in begging the question. There are games for which no reasonable behavioral rule leads to Nash equilibrium (see Section 7.6). Moreover, even if we consider games for which constructing some behavioral rule that leads to Nash equilibrium is easy, there also exist alternative behavioral rules that do not lead to Nash equilibrium. Whether these rules are realistic is ultimately an empirical question, the answer to which can be determined independently of whether or not they lead to Nash equilibrium. Furthermore, different rules may lead to different outcomes and the rule that is applied may be sensitive to context. Again, this is an empirical question. Finally, a given Nash equilibrium might arise from many processes, even, as we shall see later in this survey, ones in which players are unaware of the existence of other players. Hence, in contrast to evolutionary models, the implications of an assumption of Nash equilibrium for out-of-equilibrium behavior are imprecise.
1.2. Renaissance and the Scope of This Survey
The author believes that the evolutionary approach is interesting simply because it is often the correct approach. The world comprises decision makers that are not always far sighted and make decisions according to basic heuristics that vary according to situation. Increasingly many interactions are with other parties who we have never met and know nothing about. Simple rules of decision making can lead to complex social phenomena, as institutions and social facts emerge, compete and disappear. The individual can be simple, but society will still be complex. High quality, book length treatments of such methods, varying in technical and conceptual breadth and depth, can be found in Bowles [68], Samuelson [301], Sandholm [306], Weibull [353], Young [363].
Inspired by such logic, away from the spotlight, a substantial body of researchers has continued to work on evolutionary game theory in the social sciences, taking it in interesting and sometimes unexpected directions. A disproportionate number of these researchers are relatively young, and this survey aims to draw attention to their work. The majority of work discussed at length in this survey was published over the last ten years by researchers awarded a doctoral degree in 2007 or later, though there are many exceptions to this rule.
It is intended that the topics covered here are treated with enough depth to leave the reader with a clear idea of the relevant concepts. Research is organized according to major themes and connections between studies both within and between these themes are remarked. Whilst the survey is predominantly neutral and descriptive, discussion of important growth areas (see Section 10) and open topics (see Open Topics throughout text) is necessarily subjective. The author values the reader’s disagreement in such matters. Naturally, the reader who wishes to go deeper should refer to the cited papers themselves, but the presentation here may assist in finding relevant and interesting topics. Furthermore, although we discuss a good deal of literature across many areas, no claim to completeness is made. In particular, once one has adopted an evolutionary perspective, almost any empirical data or hypothesis can be discussed with reference to evolutionary models. For concision, Section 9 restricts attention to a selection of empirical work explicitly related to such models.
1.3. Structure of the Survey
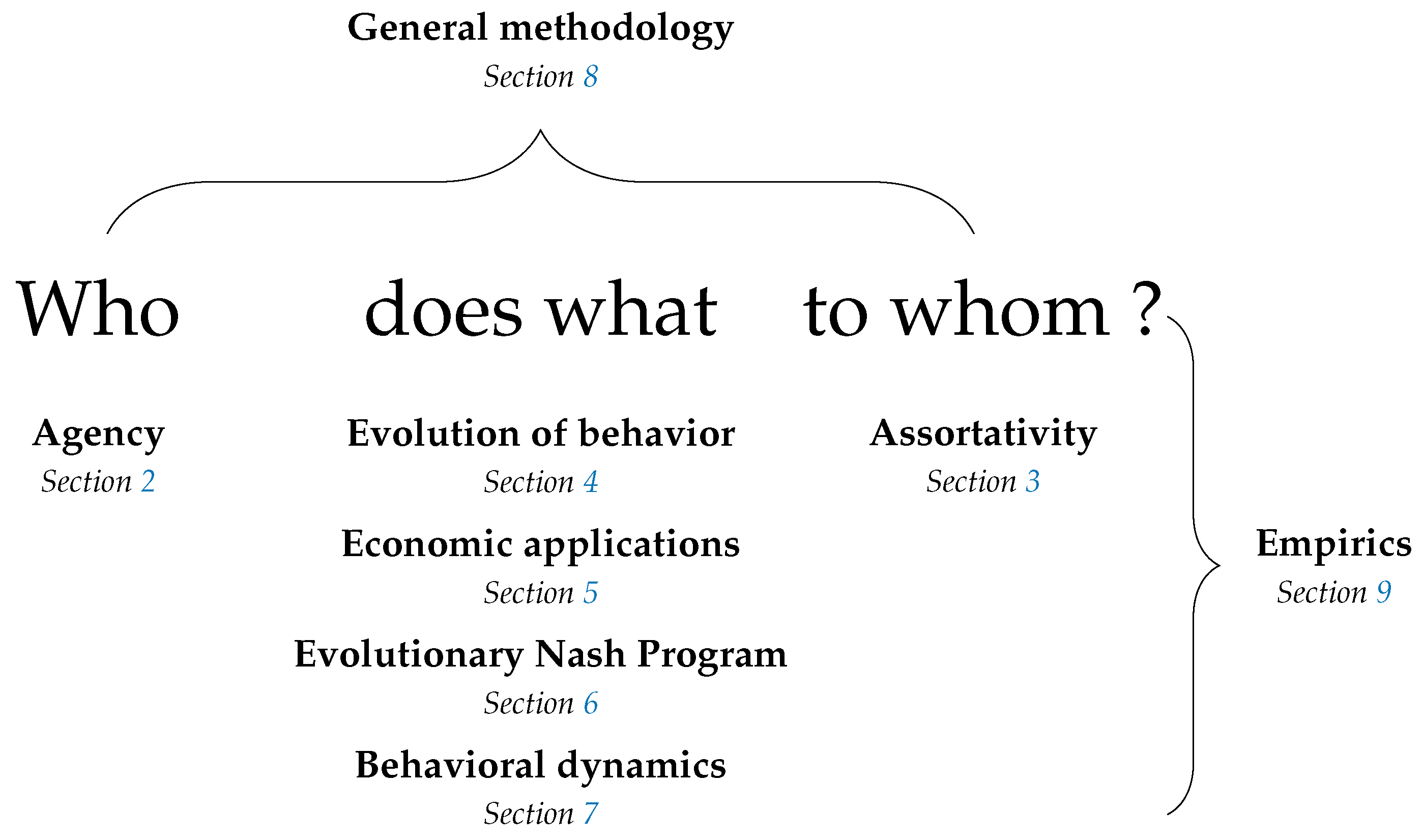
The structure of the survey is informed by the observation that a model of behavior must, either explicitly or implicitly, answer the question who does what to whom and in what circumstances? All topics discussed here can be thought of with reference to this question. A summary is provided in Figure 1.
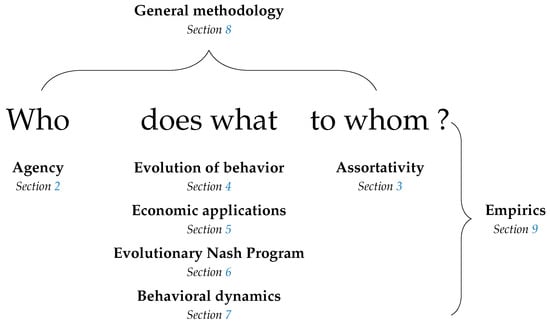
Figure 1.
Structure of this survey. A model of behavior answers the question who does what to whom and in what circumstances? Explicit rules of behavior address the circumstances of every state. Equilibrium models address the circumstances of equilibrium. The remaining parts of the question are addressed by the sections of this survey as given above.
Section 2 addresses who, considering the identity of agents, who may be individual humans, groups of friends, firms or even wind turbines. Methods for analyzing multiple levels of agency are considered, as are the implications of such agency, the question of what kind of agency might be expected to evolve, and links between individual and collective agency.
Section 3 addresses to whom, considering the identity of other agents with whom a given agent interacts. The implications of assortativity in interaction are considered, as are methods by which it might arise, such as agents choosing directly to interact with those similar to themselves, choosing institutions that determine their interactions, or deciding to forsake uncooperative partnerships.
Section 4, Section 5, Section 6 and Section 7 address what. Section 4 considers the evolution of traits that affect behavior and the evolution of culture, both embodied at the individual level and embodied at the collective level in conventions.
Section 5 considers economic applications in areas such as market selection, the learning of rational expectations equilibria, price dispersion, and fluctuations in aggregate inputs and productivity.
Section 6 considers the relationship between evolutionary game theory and cooperative game theory, addressing topics such as core convergence and selection, matching problems and the evolution of bargaining solutions.
Section 7 surveys work on a broad range of dynamics, including reinforcement learning, imitation, best experienced payoff dynamics, best and better response dynamics, dynamics for games with continuous strategy sets and completely uncoupled dynamics.
Section 8 considers methodology and technical results for perturbed dynamics, stochastic stability, evolutionary stability and systems of distributed control.
Section 9 discusses empirical work, divided into studies relevant to best and better response dynamics, imitation, completely uncoupled dynamics and the nature of errors in perturbed dynamics.
Sections of the survey can be read independently. However, to balance ease and clarity of reading, specialist terminology is precisely defined only once and referenced in the remainder of the text where it is appropriate to do so.
2. Agency—Who Makes Decisions?
An important consideration when modeling (human) action is the question of the identity of the agent that chooses an action or actions. We can think of many possible agents that might take actions. An agent could be an individual, a group of individuals, a module within a mind that contains many such modules, or even a piece of software. In particular, collaborative decision making is widespread amongst humans and something that humans are especially good at relative to other primates. In the words of Michael Tomasello:
“... humans are able to coordinate with others, in a way that other primates seemingly are not, to form a “we” that acts as a kind of plural agent to create everything from a collaborative hunting party to a cultural institution.”—Tomasello[342]
From an economic perspective, an agent could be a consumer, a family, or a firm. From a distributed control perspective, an agent might be a wind turbine or a group of wind turbines (Marden and Shamma [223]).
Evolutionary game theory studies adaptive rules that govern behavior. If realistic behavior involves decisions being made at multiple levels of agency, then this can be easily incorporated into such a rule. Consider a set of individuals N, such that individual adopts some strategy . Let S be the set of strategy profiles, such that . When strategy updating occurs, instead of an individual following an individualistic strategy updating rule of the form
we can have a coalition update by following a collective strategy updating rule of the form
For example, an individual better response dynamic mandates that chooses a strategy that is at least as good for himself as his current strategy, holding fixed the strategies of other players. That is, he chooses an individual better response from the set
For a coalitional better response dynamic this can be generalized so that chooses a strategy subprofile that weakly benefits all of its members. That is, coalition T chooses a coalitional better response from the set
Each of these rules can be made into a best response by the addition of a Pareto condition. Furthermore, such rules can be perturbed by errors in strategy choice, thus making applicable the methods and tools of perturbed adaptive dynamics and stochastic stability analysis Foster and Young [121], Freidlin and Wentzell [125], Kandori et al. [191], Young [361].
Strategy updating rules that incorporate collective agency have been used before (e.g., Feldman [117], Green [142]). Recently, however, substantial progress has been made in understanding how these rules can be used, the implications of such rules, and whether the ability of individuals to participate in such collective behavior is likely to evolve.
Open Topic 1.
The above discussion relates to multiple agency variants of best and better response dynamics. Multiple agency variants of other dynamics are still to be explored. For example, at some weddings, after the marrying couple has started dancing, other couples join the dancing. Some couples join the dancing early, while others wait until a large proportion of people are dancing, so we have something like a collective (pairwise) version of the threshold model of Granovetter [141]. Another example is a group of companies who collectively imitate successful contractual arrangements used by other groups of companies.
2.1. Advances in Methodology
2.1.1. Coalitional Stochastic Stability
It is clear that behavior under a dynamic with frequent coalitional strategy updating may differ from behavior under a purely individualistic dynamic. However, Newton [264] notes that even in contexts in which collective agency is infrequent, it may still be more frequent than the kind of errors in strategy choice that determine long run outcomes under perturbed adaptive dynamics. To give some background, the literature on perturbed adaptive dynamics and stochastic stability (see Section 4.2.1 for technical definitions) builds upon the fact that if individuals usually follow some behavioral rule, but occasionally make an error and deviate from this behavioral rule, then these small errors can have a large effect on long run outcomes. Similarly, the idea behind coalitional stochastic stability is that small probabilities of collective agency can have a large effect on long run outcomes.
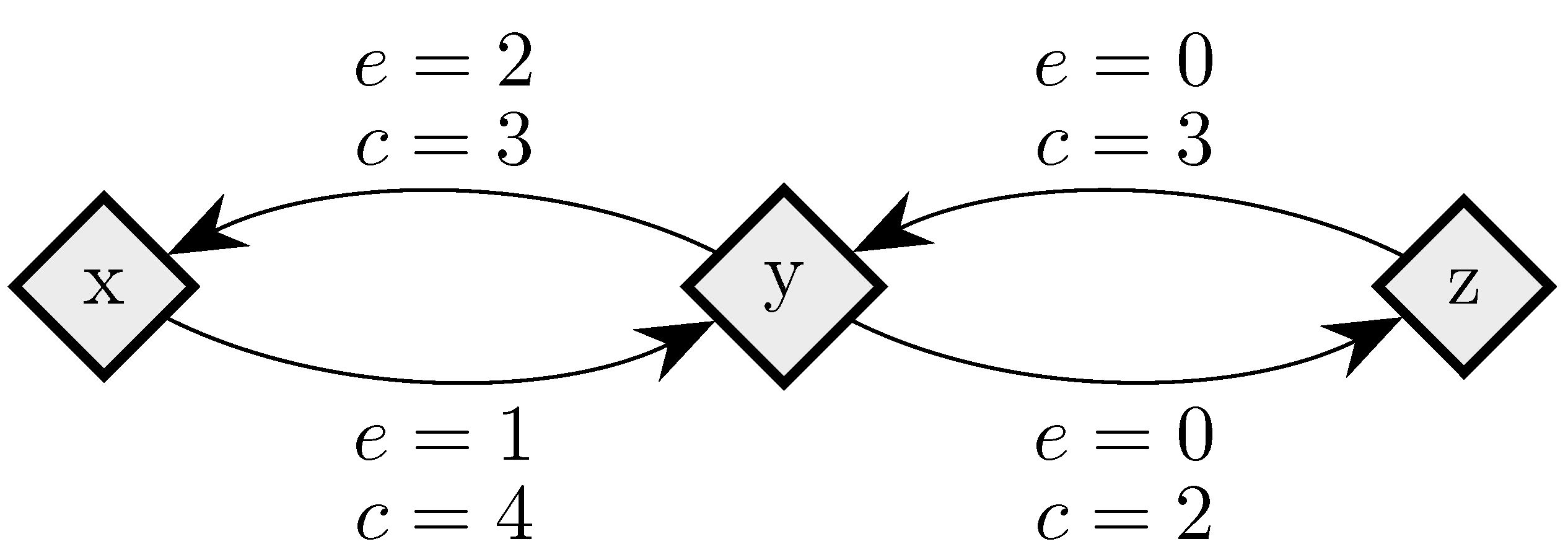
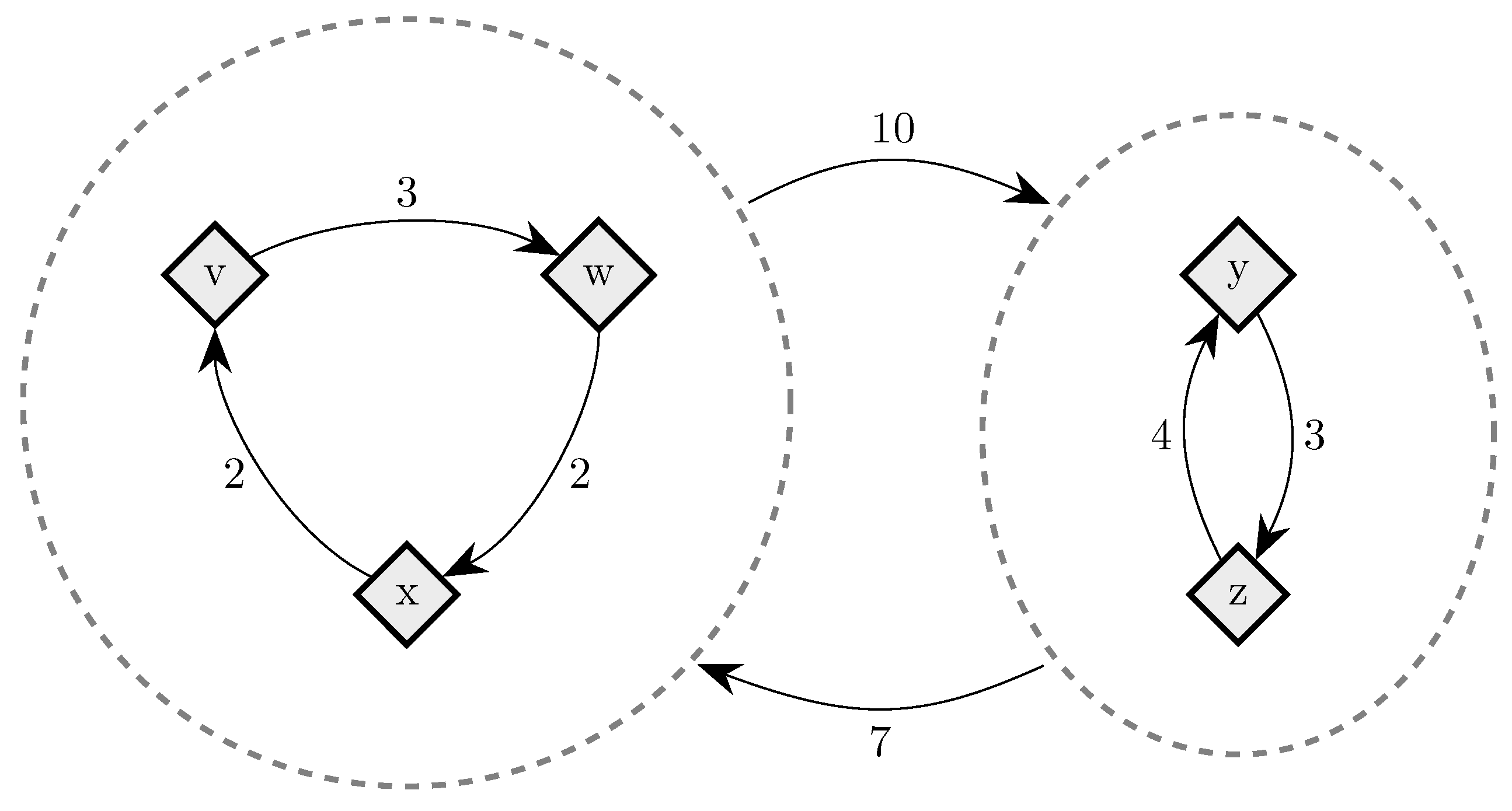
To fix ideas, consider a situation in which in any given period, with probability , , some player chooses an individual best response; with probability , some pair of players makes a coalitional best response; with probability , some trio of players makes a coalitional best response; and with probability , some player makes an error and chooses a strategy randomly. For small values of , it should be clear that coalitional best responses occur much more frequently than random errors. Moreover, implies that coalitional best responses by coalitions of size two occur much more frequently than coalitional best responses by coalitions of size three. If, in addition, we let , then identically to standard stochastic stability analysis, random errors can be used to select between recurrent classes of the process without random errors. Consider the example given in Figure 2, in which x, y and z are the rest points of an individualistic best response dynamic. In this example, one random error is required to move from x to , but two random errors are required to move in the opposite direction, so in the long run, the state will usually be in . However, unlike the standard model, once a recurrent class of the process without random errors is selected, further selection can be obtained. Coalitions of size three are required for transitions from z to y, whereas transitions from y to z only require coalitions of size two, which are much more likely. Therefore, in the long run, the process will spend most of the time at state z. Thus, a hierarchy of rare behaviors allows iterative ‘drilling down’ to select progressively smaller subsets of the strategy space. Note that changes to the ordering of rare behaviors, such as considering for example, do not present any additional technical difficulties.
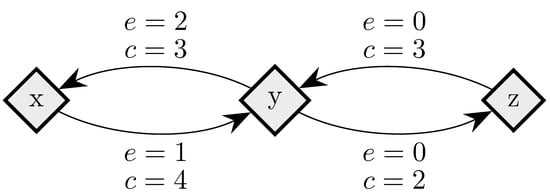
Figure 2.
Coalitional Stochastic Stability. There are three states, x, y and z, all assumed to be rest points of an individualistic best response dynamic. Arrows between states indicate, for the most probable transition path from one state to another, e, the number of random errors on this transition path, and c, the size of the largest coalition that makes a coalitional response on this path.
2.1.2. Coalitional Logit Choice
Sawa [312] describes a perturbed coalitional best response rule whereby at period t, some coalition is randomly chosen and has the opportunity to accept or reject a randomly chosen alternative strategy subprofile for itself. Let the current strategy profile be and the proposed alternative subprofile be . Let each independently accept the proposed new strategies with probability given by the logit choice rule
where . If every accepts the proposal, then the strategy profile becomes . If at least one does not accept, then the strategy profile remains .
With regards to perturbed adaptive dynamics, the salient feature of the individualistic logit choice rule is that the cost (the exponential decay rate of the probability as , see Section 4.2.1) of playing a given non-best response is equal to the expected payoff difference between playing a best response and playing the non-best response in question. Considering in (5), this corresponds to the cost of the transition from to being equal to
Now, when T is not a singleton, the probability that every accepts according to (5) is given by these probabilities being multiplied together. Note that each of the individual probabilities takes into account the proposed strategy change by all members of T. That is, this is not simply the probability of every member of T switching as per an individualistic logit rule. The exponential decay rate of this combined probability is then the sum of the exponential decay rates of the individual probabilities. That is, the cost of the transition is
This simple expression is easy to work with, although it should be noted that the clean characterization of stochastically stable states of potential games under individualistic logit choice (Blume [59]) does not transfer to coalitional settings (see Section 2.4 for a discussion of potential and agency).
2.1.3. Frequent or Infrequent Coalitional Behavior
One difference between the models of Newton [264] and Sawa [312] is that the former considers infrequent coalitional choice in dynamics, whereas the latter makes no assumption about frequency. An implication is that stable cyclic behavior will arise more frequently under the latter dynamic, precisely in situations in which there is some conflict between different levels of agency. The classic example of a game with conflict between different levels of agency is the prisoner’s dilemma, in which the tension between individual agency (defection as a dominant strategy) and collective agency (every pure strategy profile is efficient except for joint defection) defines the dilemma. Figure 3 gives a parameterized prisoner’s dilemma that will be occasionally referred to for the remainder of this survey. In prisoner’s dilemmas, the model of Newton [264] will select as coalitionally stochastically stable, whereas in the model of Sawa [312], cyclic behavior will be stable.
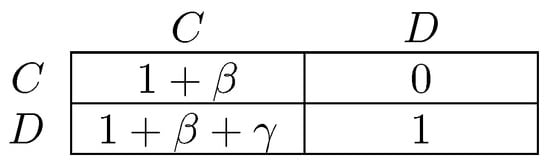
Figure 3.
Two player prisoner’s dilemma. Let . For each combination of C and D, entries give payoffs for the row player. is the payoff advantage of over . is the gain from defecting on a cooperator. The gain from defecting on a defector is normalized to 1.
In many situations, including many of the examples in Newton [264], there is no tension between different levels of agency and qualitative results do not differ according to whether coalitional behavior is rare or frequent. In particular, incentives at all levels of agency are perfectly aligned at a strong equilibrium (Aumann [26]), a strategy profile at which there is no profitable coalitional deviation available to any subset of players. Avrachenkov and Singh [27] show that, if every subset of players can coalitionally update its strategies and, when it does so, will choose a coalitional better response with probability , but with probability will choose from a full support distribution on all possible non-best responses, then any strong equilibrium is stochastically stable.
2.2. Implications of Collective Agency
The implications of collective agency for evolutionary models in economics have only recently begun to be explored. Nevertheless, some interesting results have emerged. Some of these results (Newton [265], Serrano and Volij [320]; results on matching) relate to the Evolutionary Nash Program, so discussion of these is deferred until Section 6.
2.2.1. Coordination Games on Networks.
Newton and Angus [259,260] consider players as vertices on a graph (a ‘network’) who each play a strategy A or B. A player’s payoff is the sum of his payoffs from playing his strategy against each of his neighbors in the game in Figure 4ii. They study the effect of coalitional behavior on the speed of dispersion of strategy A, the efficient strategy, starting from a state in which all players play B. It turns out that the introduction of coalitional behavior can have either of two effects, (a) a conservative effect (Figure 5i,ii), by which coalitional behavior greatly slows the adoption of the new strategy; or (b) a reforming effect (Figure 5i,iii), by which coalitional behavior greatly speeds the adoption of the new strategy.

Figure 4.
Two player coordination game. For each combination of A and B, entries give payoffs for the row player. Let so that is the risk dominant Nash equilibrium. Panel (i): general payoffs up to affine transformation; Panel (ii): zero payoff for miscoordination; Panel (iii): a stag hunt.
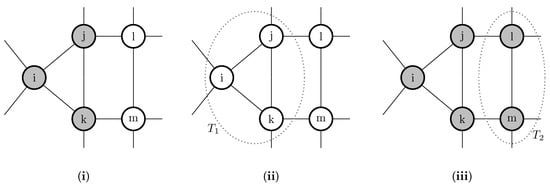
Figure 5.
Conservative and reforming effects of collective agency. Grey vertices are playing strategy A, white vertices are playing B, as are all vertices not shown. Payoffs are given by the game in Figure 4ii. Panel (i): an initial strategy profile. Without coalitional behavior, it is not a best response for any player to change strategy as long as . Panel (ii): Conservative effect. From the profile in Panel (i), if , then all of the members of coalition gain by switching to B. Panel (iii): Reforming effect. From the profile in Panel (i), if , then all of the members of coalition gain by switching to A.
Newton et al. [263] consider a similar setup, but with similar payoffs to the Stag hunt in Figure 4iii, and analyze how the size of teams in an organization (cliques on a network) affects long run behavior when small groups of players within a team meet to adjust their strategies. Large teams end up playing A as the risk-dominance effect of the classic individualistic model (Young [361]) outweighs the coordination effect of collaborative choice. Medium size teams end up playing B for the opposite reason. The behavior of small teams depends critically on their neighbors within the organization.
Note that in the individualistic model, as long as behavior only depends on payoff differences (either ordinal or cardinal) and not absolute payoff values, behavior in all of the games in Figure 4 is identical: is a redundant parameter. This is not the case in the presence of collective agency. The link between payoffs and agency is explored in depth in Newton and Sercombe [262], which is discussed further in Section 2.4.
2.2.2. Matching
If a coalition of size two decides to adjust its behavior to the mutual benefit of its members then it acts as a collective agent. Coalitions of size two are the objects considered by notions of pairwise stability in networks (see, e.g., Jackson [185]), a special case of which is pairwise stability in matching models. For example, in Roth and Vande Vate [293], a man and a woman meet randomly and match with one another if and only if they prefer one another to their current partners. Such a rematching is an instance of collective agency, as neither the man nor the woman can effect such a rematching on their own.
In recent years, there has been many studies on evolutionary dynamics in matching problems. Similarly to Roth and Vande Vate [293], the main results from these studies tend to concern the convergence of the dynamics to particular solutions from cooperative game theory. As such, they are part of the Evolutionary Nash Program and will be discussed at length in Section 6.
2.2.3. Social Choice Rules
Okada and Sawa [273] examine an evolutionary model in which the policy followed by a collective is determined by majority (or supermajority) voting by individuals. They consider policies that emerge under given voting rules. A voting rule is a way of choosing collectively. In fact, it can be regarded as a strong way of doing so because the wishes of individuals in a minority are disregarded. It follows that, in this sense, the weakest voting rule is the one that requires all individuals to agree: the unanimity voting rule. Under the unanimity rule, the only way a new policy x can defeat a status quo policy y is if every voting individual weakly prefers x to y. This is a coalitional better response rule based on pairwise comparison and can be compared to Expressions (2) and (4) at the beginning of Section 2. Okada and Sawa [273] find that when their voting dynamic is perturbed uniformly, Condorcet winning policies (policies that beat all others under simple majority rules) are stochastically stable. Furthermore, if the voting rule is the unanimity rule, then, under coalitional logit choice, Borda (points based rankings, de Borda [97]) winning policies are stochastically stable.
2.3. The Evolution of Collective Agency
It is possible to ask whether the ability of multiple individuals to act as a single collective agent is an ability that will be evolutionarily selected for. This may at first seem like a question with an easy answer. After all, we are considering the ability to participate in joint behavior that is mutually beneficial for all concerned. However, such a rush to conclusions proves to be ill founded for several reasons.
Firstly, as discussed above, the ability to participate in collective agency may slow the spread of efficient behavior on a network (Newton and Angus [259,260]). This means that populations in which such an ability is widespread may find that new technology is adopted more slowly than in populations in which such an ability is rare or absent. If this is the case, then under reasonable assumptions on migration and conflict, a group selection model, in which some selection occurs at the population (the ‘group’) level when high technology populations invade and replace low technology populations, can lead to selection against the ability to participate in collective agency (Angus and Newton [22]).
Secondly, in some situations, it may be beneficial to be a type of individual that cannot participate in collaborative behavior (Newton [267]). One case is when there exists the opportunity to free ride on the collaboration of others in such a way that free riders do better than those who collaborate. An example of this is when Alice and Bob collaborate to hunt an animal but Colm, lacking the ability to collaborate, can still eat the leftover meat without exposing himself to the risks of the hunt. Another case is when there is positive assortativity in types (see Section 3) and the externalities of collaboration are negative. An example of this is when Alice and Bob can collaborate to attack another individual, but due to positive assortativity, this individual is likely to also be a collaborative type. Consequently, those who cannot collaborate benefit from being less likely to be subject to such negative externalities.
Finally, it may be the case that people mistakenly think that they are collaborating with a partner when the partner does not in fact have the ability to collaborate. Rusch [297] examines this possibility in a model in which players play a variety of symmetric, two strategy, two player games, with the share of any given game given by a probability measure. He finds that as long as the prisoner’s dilemma (Figure 3) is not too likely under this measure, then the ability to collaborate will be selected for.
2.4. Links between Individual and Collective Agency
Nax and Perc [249] discuss payoff-based learning in public goods games. This process is completely uncoupled (see Section 7.6), relying neither on opponents’ payoffs nor their prior actions. They consider how simultaneous errors by multiple players can end up benefiting the error-making players. Although contribution to a public good may be suboptimal from an individualistic perspective, payoffs may increase when several players simultaneously start to contribute. Hence, profitable coalitional strategy changes are replicated by the errors of individuals. To replicate coalitional moves by larger numbers of players requires a larger number of mistakes and so such moves are relatively less likely. This is similar to the assumption made in Section 2.1.1, although there it is an assumption, whereas here it emerges endogenously. A Nash equilibrium is k-strong if there exists no profitable coalitional deviation for a coalition of any size up to and including k. The authors show that long run behaviour depends on the values of k for which the equilibria in their model are k-strong.
The evolution of preferences literature often follows the indirect evolutionary approach (Güth and Kliemt [143]) and assumes an outcome given the types of the players. This outcome is usually assumed to be a Nash equilibrium and, in the tradition of Harsanyi [148], types are usually taken to specify the payoffs of players. Examples of such models can be found in Dekel et al. [99], Heifetz et al. [154], Samuelson [302], Sethi and Somanathan [323]. In general, a change in the type of only one player can lead to a change in everyone’s behavior via the assumption of equilibrium. For example, in games of strategic substitutes (e.g., Cournot competition), if the type of one player changes so that he prefers to play higher actions than he did before, the equilibrium actions of the other players will decrease. However, Herold [165] gives a model in which sufficient numbers of rewarder or punisher types are required to induce a change in equilibrium behavior. When there are sufficient rewarders playing the game, the change in players’ behavior induced by the assumption of equilibrium benefits all players. Such a change may benefit rewarders less than non-rewarders in a similar way that collaborators may benefit less from collaboration than non-collaborators do in Newton [267], discussed in Section 2.3. However, in both these papers, the rewarder/collaborator type is more likely to find themselves in a group where there are a sufficient number of rewarder/collaborator types to induce the change in behavior. This observation lies behind both Proposition 1 of Herold [165] and Theorem 1 of Newton [267]. A major difference between the two approaches is that the equilibrium approach assumes that non-rewarder types change their behavior as a consequence of rewarders in the population, whereas non-collaborator types may, but are not required to, alter their behavior in response to collaboration.
A coordination game like that in Figure 4i played on a network admits an exact potential function (Monderer and Shapley [240]). A potential function retains information from individual payoff functions on the individual incentives of players, aggregating them into a single function. Young [368] calls a set of players autonomous if, fixing the strategies of all other players and regardless of what these strategies are, potential is maximized when all of the players in the set play A. Another way of thinking of this, as explored further in Section 4.2.2, is that it will be stochastically stable under logit choice for players in any such set to play A. Newton and Sercombe [262] link autonomy driven by a potential function, potential autonomy, to autonomy driven by collective agency, agency autonomy. A set of players is agency autonomous if, fixing the strategies of all other players and regardless of what these strategies are, players in the set would all gain from a simultaneous switch by every player in the set from B to A. It is shown that every potential autonomous set on every network is agency autonomous if and only if . Conversely, every agency autonomous set on every network is potential autonomous if and only if . That is, the payoffs of the game provide a connection between aggregation of agency and aggregation of incentives via a potential function.
Open Topic 2.
Consider the mind as software that applies an algorithm to solve problems. This software is modular, in that different sections of code achieve different tasks, but nevertheless communicate with one another towards some overall goal. In a similar manner, two people may collaborate and their two minds together be considered as one piece of software with two distinct modules that communicate. It would be interesting to see an evolutionary game theoretic model of choice based on this hierarchy (parts of a mind, whole mind, collective ‘mind’) in which the relationship between the lower and middle level of the hierarchy is qualitatively similar to the relationship between the middle and upper level.
3. Assortativity—With Whom Does Interaction Occur?
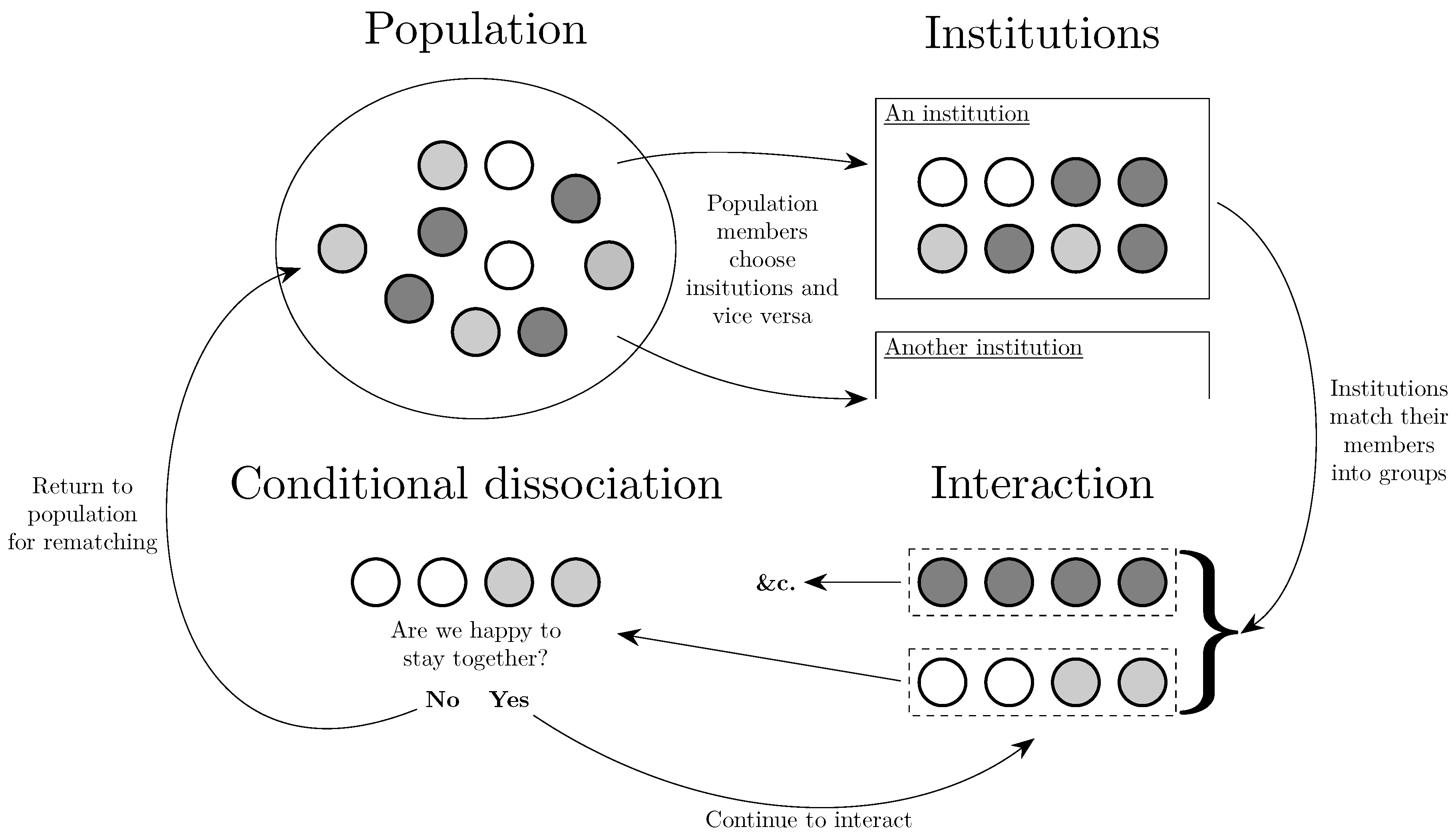
Assortativity is a tendency for agents to engage in a disproportionate share of their interactions with those who are either similar in a trait (positive assortativity) or dissimilar in a trait (negative assortativity). This can be as simple as spending more time with members of one’s family than one does with random strangers. Although assortativity and associated effects on behavior have been studied for a long time (see, e.g., Eshel and Cavalli-Sforza [112], Wilson and Dugatkin [355]), the relationship between the two has recently been attracting increased attention from economists. The general structure of the effects governing assortativity that are discussed in this section are given in Figure 6.
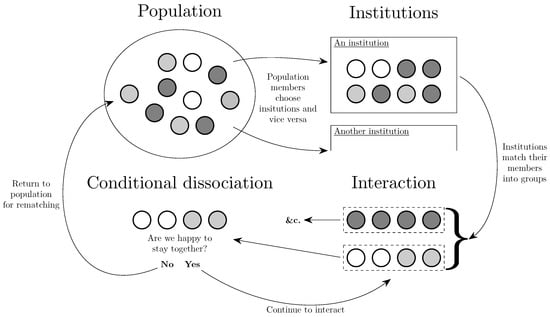
Figure 6.
Assortativity in matching. From a population, individuals are matched into groups to interact (Section 3.3). This matching may be affected by the traits of the individuals (Section 3.2.1) and also by institutions at a societal level (Section 3.2.2). Individuals may be able to choose to join institutions (Section 3.2.3) and the institutions may have their own preferences over their membership. Note that the institution in the Figure is highly positively assortative in that it matches individuals with other individuals of a similar type. Individuals may have the option to interact multiple times with those with whom they are matched, or to leave them and seek new partners (Section 3.4).
3.1. Assortativity and Preferences
There has long been interest in the relationship between assortativity and selection for altruistic preferences, often modeled as a predilection to play C in a prisoner’s dilemma (Figure 3) in which payoffs represent fitness. All evolutionary models of which the author is aware that work in favor of selection of such preferences rely on inducing positive assortativity in behavior. That is, for playing C to be profitable, it must be played a disproportionate amount of the time against C. Examples include repeated interaction (Trivers [344]), kin-selection (Fisher [119], Hamilton [145]) and group selection (Bowles [70], Choi and Bowles [89], Haldane [144]). For an extensive and detailed discussion of cooperation, the reader is referred to Bowles and Gintis [67], and for a specialized review of parochial altruism theory, to Rusch [296].
More recently, Alger and Weibull [6,7] have considered the relation of assortativity to a broader class of preferences. They study the evolution of preferences when players are matched to play a two player game. Payoffs in the game correspond to fitness. Types of players correspond to preferences over outcomes in the game. The matching protocol is exogenously given and exhibits a fixed amount of assortativity. Specifically, consider an incumbent type which comprises a share of the population and an invading type which comprises a share of the population. Let be the probability that a type is matched with a type. Let
where is independent of . That is, any invading mutant type that appears in small numbers will be such that any given mutant will be matched to another mutant with probability approximately equal to and matched to an incumbent with probability approximately equal to . This use of a coefficient of assortativity, , follows Bergstrom [42].
If , then any incumbent population that fails to achieve efficient payoffs will be vulnerable to invasions of mutants who play efficiently against one another. Conversely, if , then any incumbent population whose members do not behave in a way consistent with individual fitness maximization will be vulnerable to invasions of mutants who maximize individual fitness. This logic extends to intermediate values of , so it transpires that the most stable behavior accords with preferences that are a weighted average of fitness maximization and efficient symmetric choice:
where the weighting given to efficient behavior is increasing in assortativity . These arguments are expanded to m player symmetric games in Alger and Weibull [8]. See Section 3.3 for a discussion of assortativity of types in games with more than two players.
The preferences described in (9) were earlier derived in Bergstrom [41] for the special case of games between siblings and stability of preferences to small invasions of dominant mutant genes in a model of sexual reproduction. In this case, a mutant has a probability of one half of having a mutant sibling, equivalent to a level of assortativity in interaction of . The cited paper also gives results for the case of invasions of recessive mutant genes and compares these stable behaviors to preferences that correspond to Hamilton’s coefficient of relatedness (Hamilton [146,147]), which in siblings is equal to one half. Alger and Weibull [5] also make such a comparison for the specific case of altruism.
Hamilton’s rule (Hamilton [146]) states that a trait that reduces the fitness of each of its holders by c and gives a combined fitness benefit of b to others can spread in a population if and only if , where r is the coefficient of relatedness, the probability that any given recipient of the benefit also holds the trait. Van Veelen [345] shows that if fitness is given by the payoffs of a public goods game, the trait in question is contributing to the public good, and interaction takes place in groups drawn from the general population (see Section 3.3), then Hamilton’s rule only applies if the benefits and costs of contribution are independent of the number of other contributors in the group. Nowak et al. [272] draw on these insights as part of a general critique of the usefulness of the concept of inclusive fitness, a critique that has in turn been subject to intense criticism (e.g., Abbot et al. [1], Ferriere and Michod [118], Herre and Wcislo [166], Strassmann et al. [338]).
Bilancini et al. [46] consider the evolution of cooperation in a population comprised of individuals of two types. Each individual is matched to play a prisoner’s dilemma in which he can either cooperate or defect. Individuals of each type suffer a payoff loss from interacting with individuals of the other type. Such a desire to interact with those similar to oneself is known as homophily. Interaction is assumed to be positively assortative (per the specification of Cavalli-Sforza and Feldman [81]) according to strategies played but not according to types. If payoff losses from interacting with individuals of the other type are sufficiently large, it is then evolutionarily stable for one type to play C and the other type to play D, with individuals of each type choosing their strategy in order to minimize their chance of being matched with an individual of the other type. That is, they use positive assortativity according to strategy to induce positive assortativity according to type.
Note that the preferences described in (9) are defined for a fixed level of assortativity that applies to any invading type. The case of differing values of for alternative invading types will be considered next.
3.2. Evolution of Assortativity
3.2.1. Individual Types and Assortativity
Following work in the biology literature on the evolution of assortativity (e.g., Cara et al. [77], Dieckmann and Doebeli [102], Matessi et al. [234], Otto et al. [277], Pennings et al. [279], Servedio [321]), Newton [268] shows that under a specification of type-specific assortativity given by Cavalli-Sforza and Feldman [81] and applied to the model of Alger and Weibull [7] discussed in Section 3.1, stability is only possible when an incumbent population behaves efficiently and does not interact at all with invading types, thus ensuring that in (8). Perfectly assortative efficient behavior is not susceptible to invasion, but everything else is. The reasons for this are that (i) unless incumbent types only interact with one another, if they do not behave in a way consistent with individual fitness maximization, then they are vulnerable to invasion by a type that maximizes individual fitness and has no predilection for assorting with its own kind, and (ii) if incumbent types do not behave efficiently, then they are vulnerable to invasion by a type that behaves efficiently and only interacts with other types.
Even without assortativity in interaction, individuals can sometimes adjust their behavior so that it correlates with the types, and therefore the behavior, of those with whom they interact. Specific correlations are sometimes generated via the twin devices of equilibrium and preferences. For example, Herold and Kuzmics [164] show that an incumbent type that earns more than the minmax payoff when playing against itself can maintain stability by playing spitefully against invading mutants so as to minimize their fitness.
In practice, the maximum assortativity based on types that can be maintained may be bounded above, as mutants are not always easy to recognize. This has been considered in the evolution of preferences literature (e.g., Dekel et al. [99], Heifetz et al. [154]), in which non-observability of types reduces the possibility of assortativity in behavior according to type. That is, if Alice cannot observe that Bob is a mutant, she cannot condition her behavior towards him on whether or not he is a mutant. Nevertheless, high levels of assorting by phenotype (i.e., by observed behavior, not by types per se) can plausibly be maintained by shunning and ostracism of those who exhibit unusual behavior. Moreover, there may be gains to be had from considering different forms of recognition. Do two objects with different charges recognize each other as they attract each other? At what point in a conversation do two fluent English speakers recognize one another as such? Similar examples can be found in Newton [267]. Finally, note that the cause of differing behavior and assortativity need not be genetic and may be cultural. Types in the above models relate to individuals and hence to culture embodied at the individual level, models of which are discussed further in Section 4.3. Further discussion of assortativity in behavior can also be found in Section 4.1.4.
3.2.2. Institutions that Determine Assortativity
As well as varying according to individual traits, assortativity may also be embodied in institutions and determined at a societal level, similarly to other aspects of culture (see Section 4.2). Nax and Rigos [252] consider a model in which there are two types, each of which plays a given strategy in a two strategy, two player game drawn from a variety of social dilemmas. Assortativity in the matching protocol is determined by logit-style voting for higher or lower assortativity. So the probability of an individual voting for higher assortativity is increasing in his gain from an increased level of assortativity. This weighted majoritarian rule pushes assortativity in the direction favored by one of the types, who then grow as a share of the population and proceed to push assortativity even further in the same direction. Consequently, stability always involves either no assortativity or full positive assortativity (negative assortativity is not permitted by the model). Similar results were subsequently found in Wu [356], in a setting that considers unweighted majority voting and restricts itself to coordination games, while allowing negative or positive assortativity. This can lead to the stochastic stability, under a best response dynamic with uniform errors, of a Pareto efficient but non-risk dominant equilibrium in the coordination game, as individuals who play the strategy associated with the Pareto efficient equilibrium vote for high assortativity so as to segregate themselves from any players who play the strategy associated with the risk dominant equilibrium.
Wu [357] gives an institutional setup in which there are equal numbers of two positions, high and low, in a society. Individuals in high positions are matched to play a game against individuals in low positions. The high position in the game is associated with higher payoffs than the low position. There are two types of individual, , . Assortativity in interaction is then determined by the share of the high positions that are held by players of each type. For example, if players hold all of the high positions and players hold all of the low positions, then matching will be perfectly negatively assortative: individuals will never play against an individual of the same type. It is assumed that the share of each type in a high position is determined not by voting, but by a form of generalized Nash bargaining solution (Nash [246]) with the bargaining weights given by the population shares of each type.
Wu [358] considers a similar model to the above, with a continuum of types and payoffs that are continuous in types. The evolutionary stability of a population of a single type to invasions of slightly different types is considered. Under majoritarian voting for who holds high positions, homogeneous populations of any type are stable, as the incumbents, forming a majority, ensure that invaders occupy low positions. Under the Nash bargaining solution formulation, a type is only stable if, when matched against a slightly different type, it obtains a higher marginal benefit than the slightly different type from being in the high position rather than the low position.
3.2.3. Choosing an Institution
Another approach to the evolution of assortativity is found in Alós-Ferrer and Buckenmaier [11]. There are two types of trader, buyers and sellers. Each period, traders either choose an institution at which to trade or remain at the same institution as in the previous period. The role of the institution is to partition the traders at that institution into sets for the purpose of trade. For example, one type of institution, a bazaar, matches buyers and sellers into pairs and leaves the remaining traders unmatched. Another type of institution, a centralized institution, matches all of the buyers and sellers into a single set. In any case, buyers and sellers within the same set trade with each other at a price that is increasing in the ratio of the number of buyers in the set to the number of sellers in the set. Buyers prefer lower prices and sellers prefer higher prices. Over time, traders move between institutions and the environment evolves. Thus, it is the the matching algorithm itself, responsible for assortment, that is the unit of selection. The paper goes on to show that the centralized institution that matches all traders at that institution into one set, has strong attractive properties under updating rules that satisfy certain conditions. Thus the paper contributes to a set of papers that give results for classes of updating rule that satisfy criteria that are plausible in the given context (see also Klaus and Newton [199], discussed in Section 6). Note that the many to one matching of individuals to institutions is similar to the ‘college admissions’ matching problem, evolutionary models of which will be discussed in Section 6.3.
Open Topic 3.
In Section 3.2 we have seen how assortativity can arise from culture (or genes) embodied at an individual level (e.g., avoid people with tattoos) or at a collective level (e.g., systems of schooling and university attendance). Some collective cultures of assortativity will be subject to selection driven by individual choice as happens in Alós-Ferrer and Buckenmaier [11] and in Carvalho [79], discussed in Section 4.4. Study of such topics is extremely pertinent to societies with large cultural minorities and associated conflict.
3.3. Generalized Assortative Matching Protocols
Van Veelen [346] takes a general approach to exogenous assortativity. Individuals, whose types correspond to one of two strategies, are drawn from a population and matched into groups of m individuals to play a game. The share of each type of individual then evolves according to the replicator dynamic. Alger and Weibull [8] (see Section 3.1) consider a similar situation in which types correspond to a continuous space of preferences over fitness. Even more generally, Jensen and Rigos [186] consider matching protocols that group individuals from a population to play m player, n strategy symmetric games. Again, strategies correspond to types. Jensen and Rigos [186] refer to a population state and a matching protocol as an evolutionary optimum if they lead to the maximum average fitness amongst all pairs such that population state x is a stable state given matching rule f. It is shown that there exists a matching protocol h such that is also an evolutionary optimum and a Nash equilibrium of a game derived from the evolutionary setup: a Nash equilibrium under a matching rule. The result is obtained by constructing the matching rule h such that invading types that are not in the support of are matched into groups apart from other types. Finally, Newton [267] uses a similar setup, allowing asymmetric games and infinite strategy sets, but with only two types, which do not correspond to strategies but rather to the presence and absence of a behavioral trait, as discussed in Section 2.3.
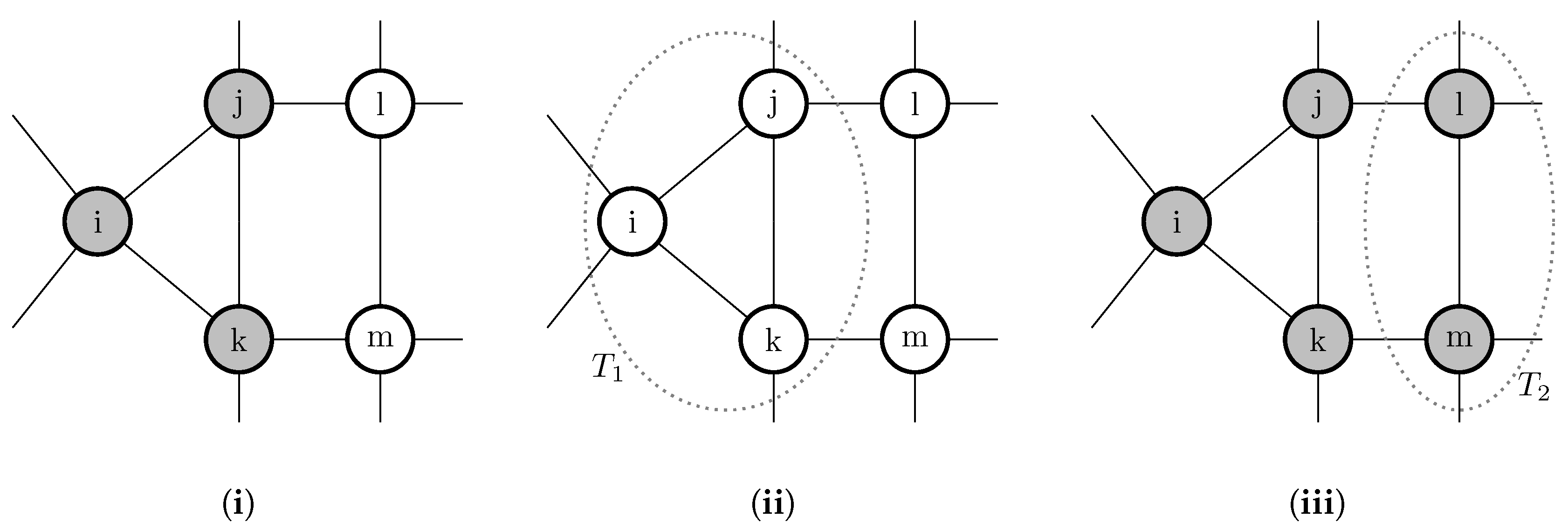
3.4. Conditional Dissociation
One way in which assortativity in interaction may be induced is by conditional dissociation, whereby individuals, who are partnered to play a game, can choose to either remain with the same partner for another period of play or to leave and randomly rematch with some other individual. Such an environment can be thought of as lying somewhere between random matching every period and a setting in which individuals play the same opponent for life.
Fujiwara-Greve and Okuno-Fujiwara [132] analyze a setting in which players are matched to play a repeated prisoner’s dilemma but have the opportunity to conditionally dissociate every period. Cooperation is assumed to be efficient as measured by sum of payoffs ( in Figure 3) for most of the analysis, though the alternative possibility is considered later in the paper. The strategy space is rich: strategies can be contingent on the entire history of play in a partnership, although cannot be conditioned on events prior to or outside of the current partnership. Mixed strategies are disallowed. They show the (neutral) stability of trust building strategies, in which players defect for a fixed number of periods against their partner before they start to cooperate, following which they continue to cooperate until one of them either dies or fails to cooperate. This initial period of defection reduces continuation payoffs after dissociation from a partner and thus discourages defection. Positive assortativity between types is induced as players only persist with their current partner when their strategies complement one another. Fujiwara-Greve et al. [133] analyze a variant of this model in which players can, each period, after observing play, furnish their opponent with a reference letter for a small cost. If the partnership terminates due, for example, to the death of one individual, then the other individual can take the reference letter with him. The trust building period between two individuals who hold reference letters can then be shortened.
Vesely and Yang [350] shows that consideration of mixed strategies can make some polymorphic neutrally stable states of the model of Fujiwara-Greve and Okuno-Fujiwara [132] no longer neutrally stable. The reason is that the polymorphism in the prior model causes some partnerships to terminate for reasons other than the death of one of the partners. This opens the door to the invasion of mutants who mimic, by playing a mixed strategy, the distribution of existing types in the population. The only difference in the behavior of the mutants is that they use a secret handshake (not terminating partnerships when they are expected to do so) to gain higher payoffs when playing against other mutants. Vesely and Yang [349] explore this in more detail, constructing neutrally stable states which are resistant to secret handshakes. This is done by avoiding voluntary dissociation (i.e., not caused by death) in equilibrium by punishing deviations within existing partnerships. Notably, such punishment is milder than traditional grim trigger punishments as the possibility of dissociation gives players an outside option, removing the ‘assortativity’ of remaining with the same partner forever.
Izquierdo et al. [181] obtain cooperation in a model which is similar to Fujiwara-Greve and Okuno-Fujiwara [132], but has a much simpler strategy space (see Sigmund [329] for discussion of similar models). Strategies are triplets that specify (i) Cooperate or defect when first matched with a partner; (ii) Cooperate, defect or dissociate when partner cooperated last period; (iii) Cooperate, defect or dissociate when partner defected last period. When individuals have short expected lives, defection dominates in stable equilibrium, but when individuals have long expected lives, the assortativity induced by strategies in which players start off cooperating and continue to do so as long as their partner also cooperates is enough to generate high levels of cooperation in stable equilibrium. High levels of cooperation can still be generated by tit-for-tat strategies (cooperate but defect if partner defects) in the model without the option to leave. However, without the option to leave, a tit-for-tat player will have to wait for any defecting partner to die, hence the model with the option to leave can generate even more cooperation. This advantage is one reason why in the model with the option to leave, players who cooperate but leave when their partner defects end up comprising a share of the population almost twelve times that of tit-for-tat players. Izquierdo et al. [182] analyze a similar model with a slightly reduced strategy space and give further analytic results for the dynamics and stable states. Rivas [286], also mentioned in Section 4.2.4, considers the case when pairs of cooperating players automatically remain together in the following period.
3.5. Network Formation
Returning briefly to the time honored topic of risk dominance versus Pareto efficiency in two strategy coordination games (see Figure 4iii), Staudigl and Weidenholzer [336] consider a setup in which any given player chooses both a strategy in the coordination game and a set of other players to play the game with (see Hellmann and Staudigl [162] for a discussion of previous work along these lines). The given player’s payoff is then given by the sum of his payoffs in the game played against each of these players, minus a fixed cost for each of the players with whom he plays the game (a linking cost). The number of other players with whom a player can play the game is bounded above by a constant k. Considering a perturbed best response dynamic, starting from a state in which all players play the strategy associated with the risk dominant equilibrium, it takes at most k players to make errors and switch to the strategy associated with the Pareto efficient equilibrium for any other player to benefit from switching to the strategy associated with the Pareto efficient equilibrium and choosing to interact with the k players who already play this strategy. This amounts to changing strategy and consciously engaging in positive assortment with those who play that strategy. In this manner, k errors suffice to move to a state in which all players play the strategy associated with the Pareto efficient equilibrium. For low values of k, this means that the Pareto efficient equilibrium can be stochastically stable. The reader will see the strong similarities between these arguments and the arguments of Wu [356] discussed in Section 3.2.2, although the papers come to the topic from differing perspectives.
Bilancini and Boncinelli [44] consider a model that differs from that of Staudigl and Weidenholzer [336] in that there are two types of player and players of each type suffer a cost from interacting with individuals of the other type. In choosing a best response, players know the types of their current neighbors, but are assumed not to know the types of those who are not their neighbors and instead only know the proportions of each type in the population that currently plays each strategy. When the cost of heterogeneous interaction is high, stochastically stable states involve players segregating by type. More surprisingly, one type plays one strategy and the other type plays the other strategy. The reason that such profiles are especially stable is that, starting from such a profile, following an error, the error making player can, with high probability, infer players’ types from the strategies that they are currently playing and use this information to rematch and recoordinate with those of the same type as himself.
Goyal et al. [140] consider a similar model of endogenous interaction to the above but for situations in which two players interact if and only if they both desire this. Payoffs for each interaction are similar to Figure 4ii, except that there is an additional payoff for coordinating with oneself; and, similarly to the language game of Neary [257] discussed in Section 4.2.2, the preferences of some players over and are reversed, so that these players obtain a payoff of 1 from and a payoff of from . Under a pairwise coalitional dynamic (see Section 2.2.2), conditions are given for the stochastic stability of the state at which every player interacts with every other player and plays the strategy corresponding to the preferred outcome of the majority of players.
Bilancini and Boncinelli [43] consider network formation in a situation akin to a multiplayer prisoner’s dilemma, in which cooperation by a player decreases his payoff relative to defection but creates a benefit to all of his neighbors in the network, with the maximum number of neighbors of each player bounded above. Each period, a player chooses whether to cooperate or defect, following which, players have the opportunity to sever any of a randomly chosen subset of their existing links then create new links before payoffs are realized. Players sever links with defectors, so if a player chooses to defect he faces the cost of other players severing links with him. The process converges to either full cooperation, full defection or a mixture of the two, depending on parameters.
Boncinelli and Pin [64] give a very simple model of the formation of networks in which players have a maximum degree of 1 (i.e., can be matched to at most one other player). Players get a payoff of 1 if they are matched and a payoff of 0 if they are not matched. A perturbed pairwise coalitional best response dynamic is considered under two models of perturbations. In the link-error model, a single perturbation, occuring with probability of order , suffices to create or destroy a link that would not otherwise be created or destroyed. In the agent-error model, errors that cause one player to lose payoff occur with probability of order , and errors that cause two players to lose payoff occur with probability of order . The substantive difference between the two models regards the creation of a link that benefits neither of the two players between whom the link is formed. Such an event occurs with probability of order under the link-error model and with probability of order under the agent error model. A maximal matching is a network to which no additional edge can be added without causing a player to have degree more than 1. A maximum matching is a maximal matching with the largest number of edges. It is shown that under the link-error model, the set of stochastically stable networks corresponds to the maximal matchings, whereas under the agent-error model, the set of stochastically stable networks corresponds to the maximum matchings.
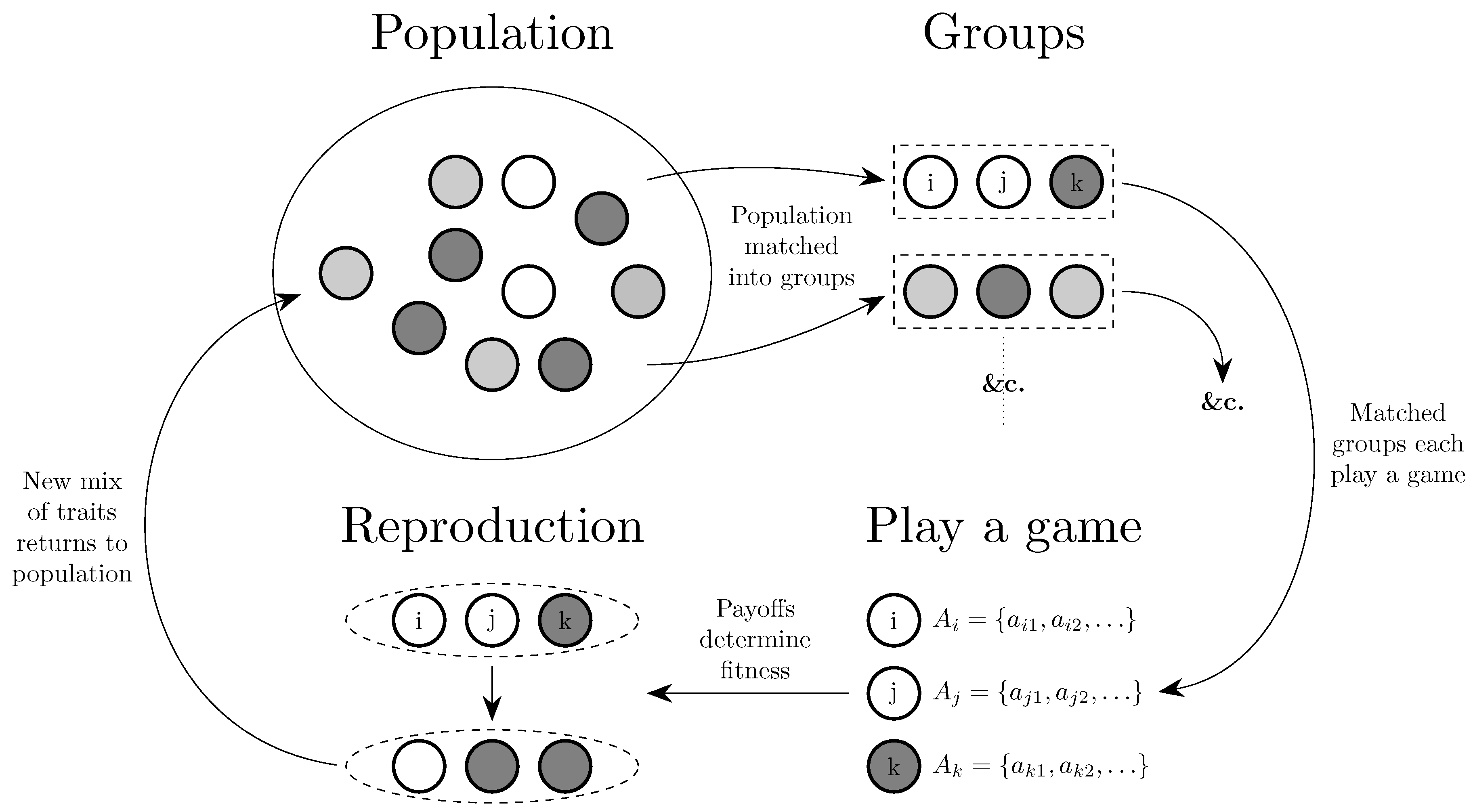
4. Evolution of Behavior
This section considers the evolution of behavior, broadly divided into the evolution of (i) traits that can be primarily thought of as genetic; (ii) conventions, the embodiment of culture at a societal level; and (iii) cultural values held by individuals. The general structure that tends to be followed by these models is given in Figure 7. Some work on the evolution of behavior in economic applications and as part of the Evolutionary Nash Program is deferred until Section 5 and Section 6 respectively, and general results for various behavioral dynamics are deferred until Section 7.
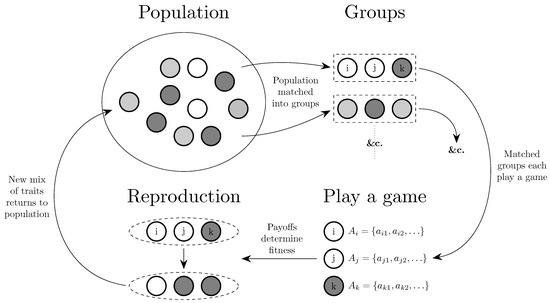
Figure 7.
The evolution of behavior. From a population, individuals are matched into groups to interact (Section 3). In some cases, the entire population will constitute a single group. Groups of matched players then play a game. How the game is played within a group may depend on the traits of individuals within the group, which may be genetic (Section 4.1) or cultural (Section 4.3). How the game is played may also depend on cultural conventions based on how the game has been played in the past (Section 4.2). Strategies are reproduced through intergenerational transmission or through individuals following some rule of strategic adjustment such as imitation or best response.
4.1. Evolution of Traits
Preferences in economics are a statistic derived from human choice behavior. However, preferences do not tell the whole story. Alice may believe that the world will end at midnight whereas Bob is a drug addict and doesn’t think much about the future. Both Alice’s choices and Bob’s choices will exhibit low discount factors but for quite different reasons. This is fine as long as preferences are descriptive, but in the evolution of preferences literature they are usually assumed to be prescriptive. That is, they are associated with payoffs and describe a goal function. When preferences are considered as a goal function instead of simply a reflection of revealed reality, it becomes necessary to consider other factors that can affect the pursuit of these goals. Much of the work discussed in this section considers attributes such as intelligence and farsightedness that can exist together with or even lead to such a preference ordering.
A few of the models here follow the indirect evolutionary approach (Güth and Kliemt [143]). This approach typically assumes that, given preferences that are some function of fitness, for example Expression (9) in Section 3.1, players play a Nash equilibrium of the game given by those preferences and have their fitness determined accordingly. Generalizing, the indirect method can be regarded as a ‘black box’ that gives an outcome given traits, with Nash equilibrium being only one possible setting for the black box. One case in which Nash equilibrium may be an inappropriate outcome is when collective agency is possible. However, the evolution of collaboration has been discussed in Section 2.3, so will not be discussed here.
Finally, note that the most well developed literature on the evolution of traits is the literature on the evolution of cooperation. This literature tends to consider how cooperation can be sustained in prisoner’s dilemmas, usually through some form of assortativity in interaction. See the beginning of Section 3.1 for a brief discussion and references to such work.
4.1.1. Self-Confirming Beliefs
Gamba [135] takes an indirect evolutionary approach to studying altruism in the centipede game, but considers self-confirming equilibria (Fudenberg and Levine [131]) instead of Nash equilibria. There are two types of player, selfish types and altruists. It is assumed that at every decision node, altruistic types take the opposite action to that specified by the subgame perfect equilibrium (SPE) of the centipede game. Selfish types assume that all players will always take the SPE action at every subsequent decision node, so they themselves always take the SPE action. Their beliefs are never disconfirmed, so we have a self confirming equilibrium. Altruists obtain lower payoffs than selfish types with whom they are matched, but they obtain very high payoffs when they are matched to other altruists. Hence, if there are enough altruists in the population, their population share grows under replicator dynamics and a monomorphic population of altruists is stable.
4.1.2. Level k Thinking
Kim and Hwang [195] also consider selfishness and altruism, but in a model of level k players (Stahl and Wilson [335]) playing a game with negative externalities and strategic substitutes. Level 0 types play a fixed strategy. Level 1 selfish types best respond to level 0 types, selfish level 2 types best respond to selfish level 1 types, and so on. Selfish level ∞ types play the Nash equilibrium strategy. Altruistic level types altruistically best respond, that is best respond according to an altruistic payoff function, to selfish level k types. Altruistic level ∞ types altruistically best respond to selfish level ∞ types. It is shown that, if we restrict the type space to level 0 types together with selfish and altruistic level k types for some k, then, under some conditions, a population of the selfish level k type is not evolutionarily stable, but a population of the altruistic level k type is evolutionarily stable.
Mohlin [239] considers two player, symmetric, normal form games and level k players. In this model, level 0 players uniformly randomize over the strategy space. A type-acyclic game is defined as a game such that for large enough k, level players play the same strategy as level k players, and consequently said strategy must be a Nash equilibrium. It is shown that if the highest k in the type space plays this Nash equilibrium strategy, then the set of states at which all types present in the population play this strategy is asymptotically stable. For example, a two strategy coordination game is type acyclic, as all players of level k, choose the same Nash equilibrium strategy, so the set of states in which every player has is asymptotically stable. Conversely, in type-cyclic games, games in which a cycle of best responses emerges as k increases, under some regularity conditions there exists a unique asymptotically stable set. Furthermore, if the highest k in the population is large enough, then states in this set will always include some players who do not play identically to the highest type player.
4.1.3. Foresight
Heller [160] considers a model of a finitely repeated prisoner’s dilemma, with sum of payoffs maximized at (i.e., in Figure 3), in which players have limited foresight in that they do not know which will be the final period of the game. Specifically, foresight is costly and any given player has a level of foresight as part of his strategy. Type only knows that the game is about to end when he reaches the final period. Type knows k periods ahead that the game will end. There is some probability that players observe the type of their opponent. This affects play. For example, an type who knows that he is playing against an type will know when the game is due to end two periods before his opponent does. He knows that his opponent, on realizing that it is the final period, will defect and that he will do likewise. Foreseeing this, he defects in the second last period as well. Similarly, if an type knows that he is playing against an type, he will defect in each of the final three periods. It is shown that combinations of and types that play tit-for-tat have good stability properties. In a population containing both of these types, types defect a period earlier and thus do better than types when playing against types, but types will sustain mutual cooperation against types for longer than types sustain cooperation against types.
4.1.4. Competing Cognition
Robalino and Robson [287] consider a finite extensive form game tree that is played repeatedly, with payoffs at each terminal node drawn randomly from a finite set of possible payoff vectors, to which new payoff vectors are occasionally added. There are two types of player, naive players, who cannot use information about other players’ payoffs in making their decisions, and theory of preferences players, who can learn information about other players’ payoffs and incorporate this information into their decision making. It is shown that theory of preferences players who optimize their payoffs come to dominate the population.
Heller and Mohlin [155] consider the evolution of preferences and cognition in an environment of symmetric two player normal form games. The cognition of a player is a natural number, with larger numbers representing higher levels of cognition. When two players, say Alice and Bob, with different cognitive levels play one another, if Alice has the higher level, then she may, with some probability, deceive Bob and choose Bob’s beliefs about her actions. It is shown that in a stable state, types matched with the same type must choose an efficient (with respect to fitness) strategy profile, as otherwise there is the possibility of invasion by mutants who obtain higher payoffs in such interactions. Furthermore, if multiple types are present at a stable state, then any two types must play efficiently against one another, otherwise homogeneous (same type) interactions would give higher fitness than heterogeneous interactions and the state would not be stable against a small increase in the share of either one of the types.
It is worth remarking that the secret handshake (Robson [288]) style arguments leading to efficiency amongst the same type in the model discussed above are a version of the assortativity arguments discussed in Section 3.1 and Section 3.2.1. The difference is that rather than a player having assortativity in interaction and interacting mainly with similar types, the player exhibits assortativity in behavior and behaves in one way when playing against one type and in another way when playing against another type. In fact, if we regard no interaction as a form of behavior, we can regard assortativity in interaction as a special case of assortativity in behavior.
4.1.5. Biases: Overconfidence and Endowment Effects
Heller [157] gives a simple theory of the evolution of overconfidence. Each generation, each individual in a population chooses between a status quo technology and an individual-specific technology. Each individual observes a public signal of the likelihood that they succeed when they use the status quo technology and a private signal of the likelihood that they succeed when they use their own technology. The success probabilities of individuals using the status quo technology are correlated. Individuals of different types may be over or underconfident regarding their own technologies, interpreting their signal as indicating an inaccurately high or low probability of success. Consequently, overconfident types will be more likely than a rational payoff maximizer to choose their own technology. The expected fitness of rational payoff maximizers will be higher than that of overconfident agents, but due to the correlation in success when using the status quo technology, average fitness of rational types will have a higher variance. Some level of overconfidence will thus lead overconfident types to have a higher expected logarithm of average fitness, which is the quantity that matters for long run population growth (Lewontin and Cohen [218], Robson [289]).
Frenkel et al. [126] consider barter trade and allow individuals to exhibit two biases, cursedness whereby a trader does not sufficiently adjust his beliefs about the quality of a trading partner’s good in response to the partner’s willingness to trade, and the endowment effect whereby a trader overvalues a good in his possession. These two biases can counteract one another so that in barter situations an individual with both biases can behave identically to, that is exhibit the same phenotype as, a rational decision maker. If, aside from barter situations, with small probability p other situations may be faced in which the biases cause their holders to lose payoff, then rational types can invade the population under the replicator dynamics. However, if we consider dynamics with imperfect replication (e.g., sexual reproduction) and two loci of selection (one for cursedness and one for the endowment effect), then offspring of rational types (e.g., from mating with a biased type) may be more likely to exhibit only one of the biases and thus achieve low fitness in barter situations. It transpires that populations of individuals that exhibit a rational phenotype in barter situations can only be invaded by type combinations that are close to them, so evolution can take a long time to eradicate the biases from the population. These results explicitly depend on p being low, so that biases do not harm payoffs greatly, and implicitly depend on assortativity amongst types being low, so that invading rational types do not mate too frequently with other rational types and produce rational offspring.
Open Topic 4.
The concept of Nash equilibrium depends on individual incentives yet requires social coordination. Evolutionary dynamics can sometimes justify this social coordination, but this is not always the case. Consequently, even assuming individualistic decision making, Nash equilibrium is not an obvious starting point for social analysis (e.g., for use in the indirect evolutionary method). Maximin strategies, strategies which maximize the lowest possible payoff that a player could obtain by playing them, are not socially determined and so may be a better starting point (see, e.g., Rusch [297]).
Open Topic 5.
Work on the evolution of traits is vulnerable to the criticism that it is merely telling ‘just so stories’ (Kipling [197]), inventing unverifiable creation myths that are not tested against alternative hypotheses. Studies often make no attempt to discuss testable implications that could potentially falsify their theories. Ideas could be borrowed from the evolutionary psychology literature, which has taken steps in this direction.
4.2. Conventions—Culture Embodied in Society
An example of culture embodied at a collective level is a system of justice. Even if Alice and Bob fail to tell their son Colm about trial by jury, Colm will still have the right to a trial by jury should he be accused of a serious crime. The right to a trial by jury is a social fact (Searle [317]) in that its continued existence as an institution relies upon the beliefs of those within a society, but it is a social fact that is robust to the ignorance of some members of society. Moreover, it is a convention (Lewis [217]) in that it exists as a social fact today because it has existed as a social fact in the past.
Conventions are a powerful tool for explaining stable behavior. Moreover, the properties of and relations between conventions can help to explain which conventions may be most stable in the long run. Examples of the effects discussed in this section are easily found in everyday life as well as in economic data, such as the survey data on conventional crop sharing contracts in Illinois considered in Young and Burke [360].
4.2.1. Perturbed Dynamics and Stochastic Stability
The approach of Lewis [217] to conventions was mathematically modeled by Young [361] using the methods of Foster and Young [121] and Freidlin and Wentzell [125]. Players update their strategies according to some adaptive dynamic, but occasionally make errors in strategy choice. The adaptive dynamic will often move society to a convention, but the errors generate the possibility of occasional transitions from one convention to another.
Consider a given family of perturbed adaptive dynamics (Markov processes) indexed by a parameter that measures the size of the perturbations. A convention is a state which is a rest point of the dynamic when . When , transitions of a society from one convention to another can be studied. The exponential decay rate of a transition probability as is typically referred to as the cost or resistance of the transition. The invariant measures of the processes, , give the share of time, , that a dynamic spends at any given state x in the long run. Conventions that have a non-vanishing probability of being visited as error probabilities approach zero, that is as , are referred to as stochastically stable (Foster and Young [121]).
The total cost of a path of consecutive transitions is the sum of the costs of the transitions on that path. Consider a weighted, directed graph on the set of conventions that, for any conventions x and y, includes an edge from x to y, the weight of which is the lowest total cost of any path of transitions from convention x to convention y. A spanning tree is a subgraph of this graph that contains no cycles and such that one convention, the root, has outdegree equal to zero, and every other convention has outdegree equal to one. Of all the possible spanning trees rooted at a convention x, consider one that minimizes the sum of edge weights. The stochastic potential of x equals this minimum value. Stochastically stable conventions can be shown to correspond to the conventions with the lowest stochastic potential (see, e.g., Kandori et al. [191], Young [361]).
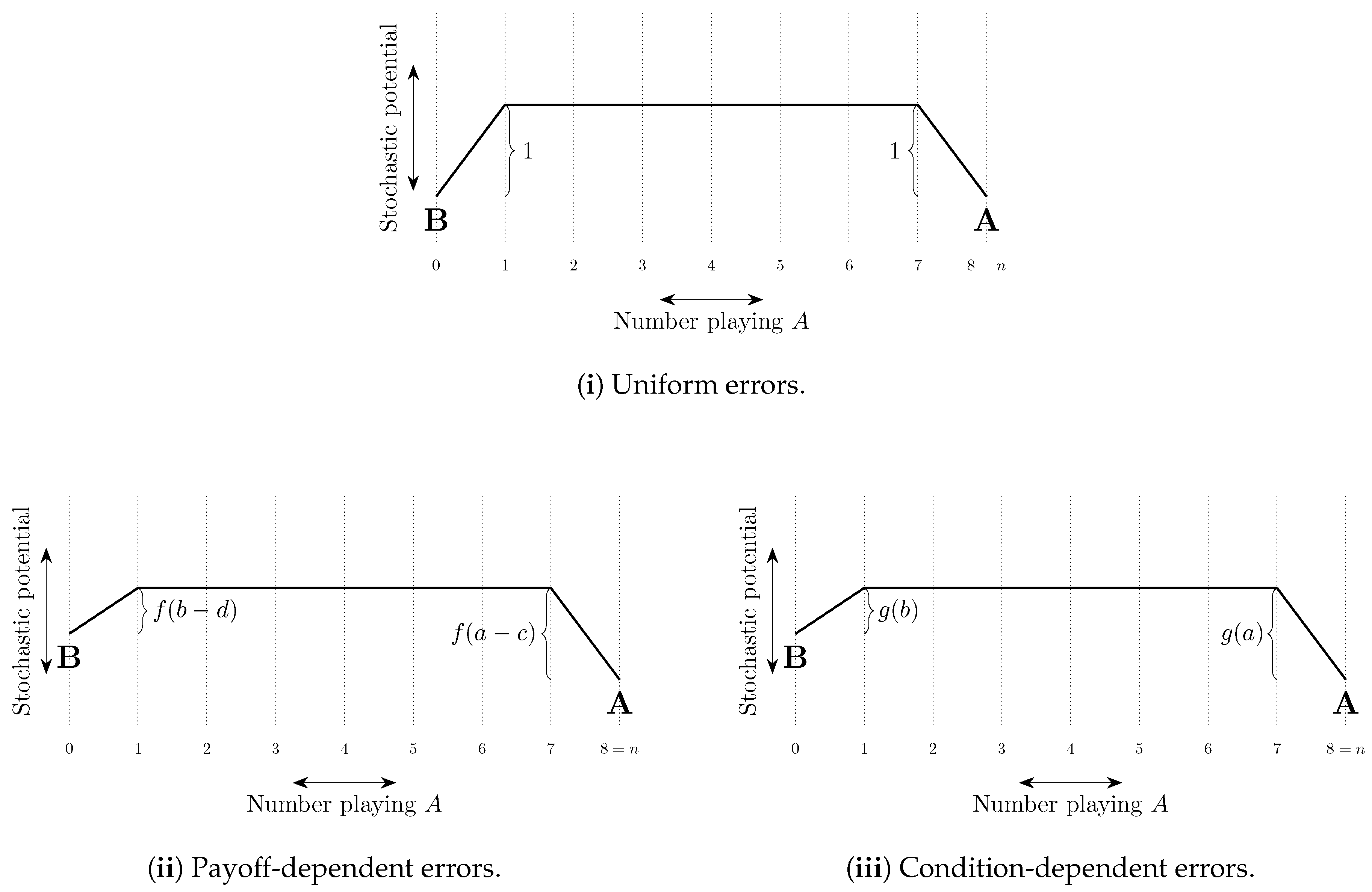
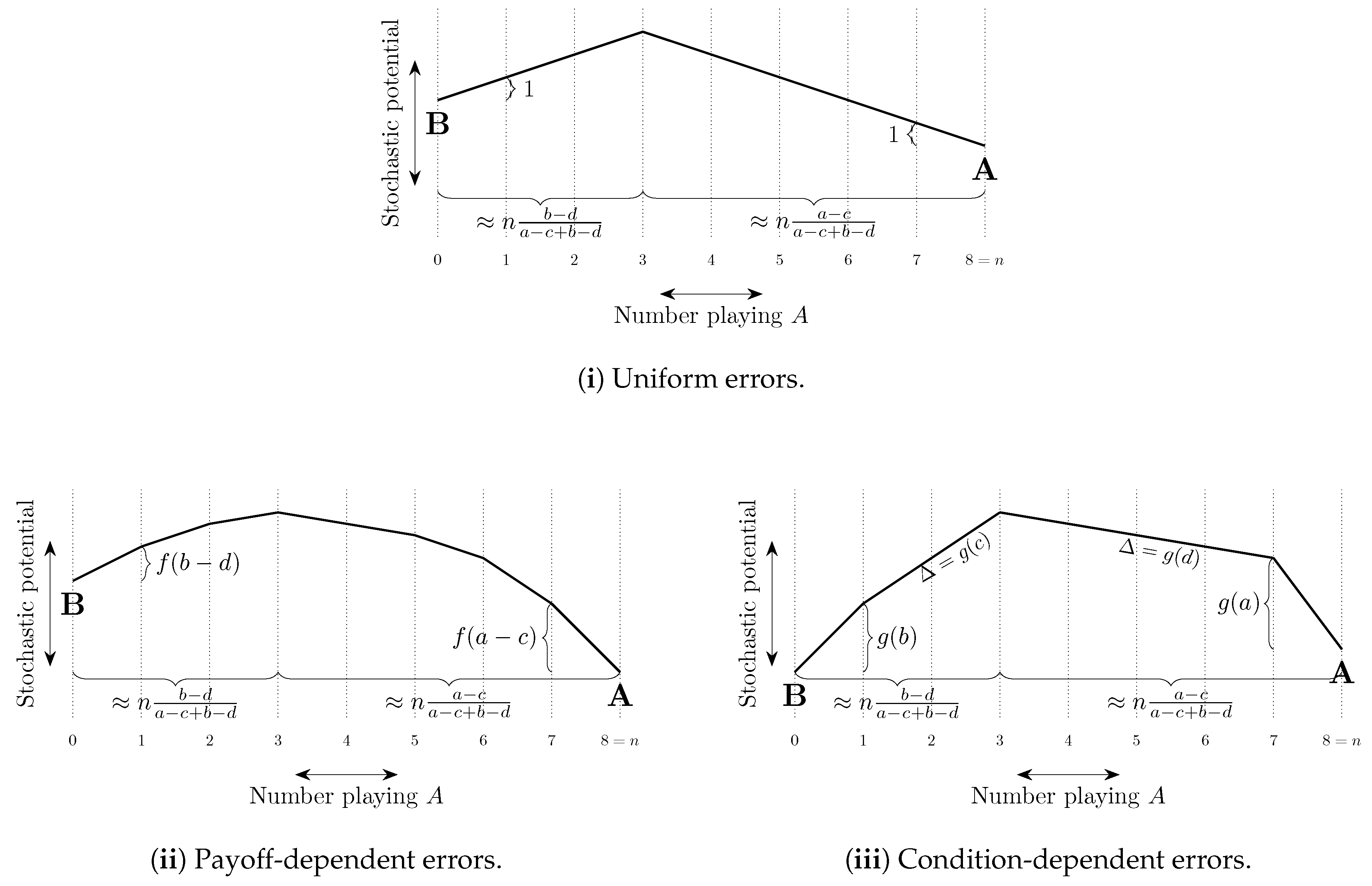
A typical perturbed adaptive dynamic involves strategy choice by players whose choice rule is composed of an unperturbed dynamic (e.g., best response) together with the possibility of errors (e.g., playing a non-best response).
Uniform errors are such that the cost of every error is the same, typically set equal to 1 with the probability of each error of order . Other errors are payoff-dependent and typically have a cost that increases in the payoff loss from making the error. For example, logit errors have a cost equal to the difference between the expected payoff of playing a best response and the expected payoff of playing the error in question. When choice is between two strategies, Probit errors have a cost equal to the square of this difference (see Sandholm [306]). Probit choice between three or more strategies is more complicated. For example, with three strategies, the cost of choosing the third best strategy can depend quadratically on the payoffs of all three strategies (Dokumaci and Sandholm [104]).
If there is some ordering on the strategies such that any given player only makes errors that correspond to strategies higher in the ordering than his best response strategy, then we say that errors are intentional (Naidu et al. [244]). For example, if there exist conventions corresponding to strategies and Alice attains higher payoffs at conventions corresponding to higher values of j, then when her best response is , it may be that the only strategies that she will play in error are , . Experimental evidence on errors is presented in Section 9.4.
The total cost of a path of transitions can be considered as a combination of two factors, (i) the length of the path—the number of errors on the path, and (ii) the steepness of the path—how unlikely the errors on the path are to occur. These ideas are illustrated in Figure 8. In some models, selection by stochastic stability arises from differences between the lengths of paths from one convention to another, whereas in other models it arises from differences in the steepness of such paths. We shall refer to such selection as length-based and steepness-based respectively.
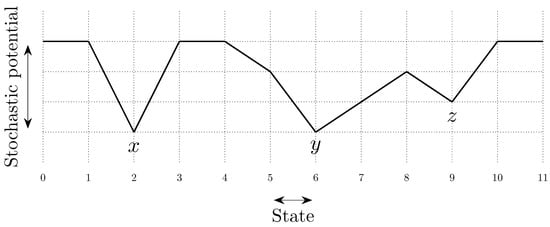
Figure 8.
Length, steepness and cost of transitions between conventions. The state space is the set of integers from 0 to 11. The only transitions that occur with positive probability are between adjacent states. The cost of a transition, the exponential decay rate of its probability, equals the change in height on the vertical axis if this quantity is positive. Otherwise, the cost is zero. For example, the cost of is two and the cost of is zero. The length of the path from x to y is one, as only a single transition on the path, , has strictly positive cost and is therefore an error. However, this transition is relatively steep, with a cost of three. In contrast, the path from y to z has length two as both and are errors, but is less steep as each error only has a cost of one, thus the total cost of the path is two. States x and y minimize stochastic potential and are thus stochastically stable.
4.2.2. Coordination Games
In two strategy, two player coordination games, length-based selection (see Section 4.2.1) works towards risk dominance, as, by definition, it is a best response to play a risk dominant strategy against a population of possible opponents that is divided equally between two possible strategies. Uniform errors do not give steepness-based selection as all errors that occur with positive probability are equally likely. Errors that decrease according to payoff loss relative to best response (such as logit or the class of weakly payoff-dependent mistakes of Klaus and Newton [199]) also work towards risk dominance via steepness-based selection.
Staudigl [337] considers asymmetric two strategy coordination games in a two population environment. For large population sizes, it is shown that the cost of transitions between conventions can be estimated by the solution to a continuous optimal control problem. This methodology is used to show that, if the two populations are the same size, then under uniform errors or logit choice, the convention corresponding to the risk dominant Nash equilibrium is uniquely stochastically stable. The same can be said for probit choice under a (non-generic) condition on the payoffs of the game.
Neary [257] discusses the language game, in which players in a finite population play a two strategy, two player coordination game against each of the other players (i.e., interaction is uniform). One type of player prefers one of the coordination outcomes and another type prefers the other (see also Goyal et al. [140], discussed in Section 3.5). There are three possible conventions, a homogeneous convention corresponding to each strategy and, if the minority type’s preferences are sufficiently strong, a heterogeneous convention in which each type plays their preferred strategy. The effect of a range of parameters on stochastic stability is studied.
Naidu et al. [245] consider a similar two population model in which asymmetry is interpreted as due to one of the strategies corresponding to egalitarian language and the other corresponding to inegalitarian language (e.g., ‘tu’ vs. ‘vous’ in French). One of the populations has high status and does better than the other, low status, population under the inegalitarian language. They show that under uniform intentional errors (see Section 4.2.1 for definition and Section 6.4 and Section 9.4 for further discussion), the inegalitarian convention may be stochastically stable if the low status population is large enough relative to the high status population. Belloc and Bowles [36] uses a similar model to explain the persistence of inferior cultural conventions, building on previous work that considers the role of conventions in sustaining poverty traps and inequality (Bowles [69,71]).
Neary and Newton [256] also consider two strategy, two player coordination games, and allow players on an arbitrary interaction network to have individual specific payoffs for each coordination outcome. When player i and j interact their payoffs are given by the game in Figure 9. The concept of autonomy governed by a potential function (Young [368], see Section 2.4 and Section 8.1.3) is used to make statements about long run behavior. In particular, a class of networks, corpulent graphs, is identified such that, for large enough networks in this class, random diversity in ordinal preferences will nearly always lead to heterogeneity in behavior at stochastically stable states, regardless of the cardinal strength of the preferences.

Figure 9.
Two player coordination game with heterogeneous preferences. Let . For each combination of A and B, entries give payoffs for the row player and column player respectively. Note that if or vice versa, this game is a Battle of the Sexes.
Sawa and Wu [310] analyze a dynamic in which players in a population make choices according to reference dependent utility, with losses relative to the reference point weighted more heavily than gains (Kahneman and Tversky [187]). When the dynamic is perturbed by uniform errors, it is shown that, for essentially any model of endogenously determined reference points, if a symmetric two strategy, two player coordination game has a super dominant strategy, defined as a strategy that is both maximin and payoff dominant (hence also risk dominant), then the state at which every player plays this strategy is uniquely stochastically stable. This is because, when we consider the payoffs of a two by two matrix under the reference dependent payoff transformation, a payoff dominant and maximin strategy is risk dominant after the transformation for any given reference point. That is, as long as half the population plays this strategy, it will be a best response to play this strategy, no matter which reference point is used. Sawa and Wu [309] consider a similar model, with similar intuition, that uses a weaker condition than super dominance, loss dominance (maximin and risk dominant), proving their result for a smaller class of preferences.
Bilancini and Boncinelli [45] compare stochastically stable conventions in two strategy, two player coordination games for (i) uniform errors; (ii) payoff-dependent errors (like logit and probit), in which the cost of an error is an increasing function of the loss in expected payoff to the player making the error; and (iii) condition-dependent errors, in which the cost of an error is an increasing function of the last realized payoff of the player making the error. The effects of condition-dependent errors on steepness-based selection vary. Initial errors are hardest from payoff dominant conventions, but subsequent errors will also depend on payoffs off the main diagonal, with a higher probability of errors by players who are not playing the maximin strategy. Now, consider a model of random matching with varying probabilities of match termination. When players rematch infrequently, it is always a best response to coordinate with one’s current partner, so rematching can lead to the spread, without the aid of errors, of any action that is present in the population. Consequently, transitions from one convention to another only require a single error. In such cases, selection is then steepness-based. For the coordination game in Figure 10, this is illustrated in Figure 11. At the opposite extreme, in the standard model of rematching every period, as discussed earlier in this section, length and steepness-based selection favour risk dominance under uniform and payoff-dependent errors. For condition-dependent errors, length and steepness can work in opposing directions. Figure 12 illustrates these effects.
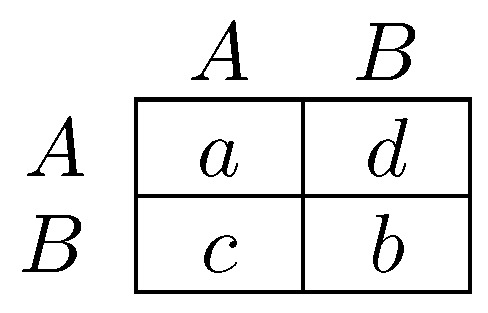
Figure 10.
Two player coordination game with payoff restrictions. For each combination of A and B, entries give payoffs for the row player. Let and so that is the risk dominant and payoff dominant Nash equilibrium, but B is the maximin strategy. This corresponds to setting in our general coordination game in Figure 4[i].
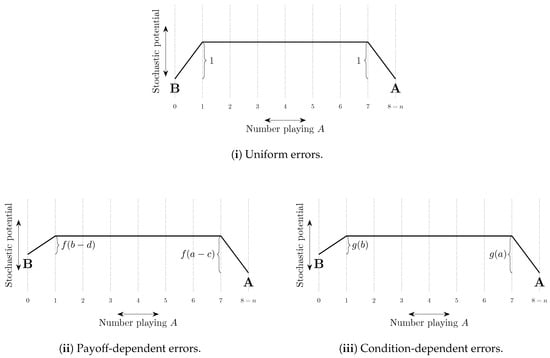
Figure 11.
Stochastic potential under perturbed best response for coordination games under infrequent rematching. The game in Figure 10 is played by a population of size . As rematching is infrequent, any updating individual chooses the same action as his current partner, so a path escaping the basin of attraction of any convention only requires a single error. In Panel (i), as all errors have equal steepness, this results in both conventions being stochastically stable. In Panel (ii), payoff losses and are compared, resulting in the risk dominant convention being stochastically stable. In Panel (iii), current conventional payoffs b and a are compared, resulting in the payoff dominant convention being stochastically stable.
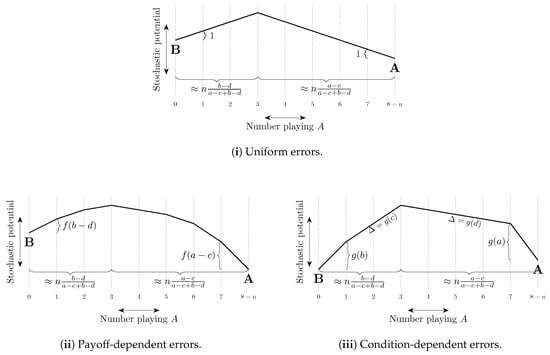
Figure 12.
Stochastic potential under perturbed best response for coordination games under rematching every period. The game in Figure 10 is played by a population of size . Updating players maximize their expected payoff over all possible opponents and the threshold between basins of attraction is approximated by as population size n becomes large. In Panel (i), as all errors have equal steepness, the convention with the longer basin of attraction, the risk dominant convention, is stochastically stable. In Panel (ii), the path exiting the risk dominant convention is not only longer, but also steeper, so it remains stochastically stable. In Panel (iii), for large enough populations, we can ignore the and terms, so that stochastic stability is determined by comparing and . In this example, the difference in steepnesses and is large enough that steepness dominates length and the maximin convention is stochastically stable.
There also exist results on stochastic stability in coordination games with an arbitrary number of strategies. Stochastically stable conventions of Nash demand games are related to subsets of the core of cooperative games and are discussed in Section 6.1. Stochastically stable conventions of coordination games with zero payoff for miscoordination are related to bargaining solutions and are discussed in Section 6.4.
4.2.3. Communication and Language
There has been considerable prior work on the evolution of language and efficient communication. Examples include Blume and Arnold [53], Blume et al. [56,57,58], Blume [61], Hurkens and Schlag [175], Kim and Sobel [196], Schlag [314,315], Sobel [332]. More recently, Heller [158] considers coordination games with a unique efficient strategy profile and a round of cheap talk before the game is played. In such settings, Demichelis and Weibull [100] showed that when there exist messages with preexisting literal meaning corresponding to elements of the strategy set and also lexicographic lying costs (so that if the expected payoff from a truthful message and a false message are equal, a player prefers to tell the truth than to lie), then the unique stable outcome is for the efficient strategy profile to be played. Heller [158] shows that the interpretation of this as relating to ‘small’ lying costs is problematic. Specifically, continuous lying costs are considered and it is shown that if these costs are small enough then inefficient equilibria perist. The method is to show that the game without lying costs has an inefficient symmetric equilibrium that assigns positive probability to every pure strategy that is a best response to itself, therefore nearby games (with small lying costs) have a nearby Nash equilibrium with the same support. As every message is used in equilibrium and the equilibrium is constructed so that lower payoffs are achieved when the same message is sent by both players, any invading mutant types attain low payoffs when playing one another, so is evolutionarily stable.
4.2.4. Best Shot and Minimum Effort Games
Boncinelli and Pin [63] consider stochastic stability in best shot network games. Players interact on a network and each can contribute or not contribute. For a given player, if none of his neighbors contribute, then his best response is to contribute. Otherwise, his best response is to not contribute. The game is effectively a model of threshold public good provision with a threshold of one. It is shown that, if the only type of errors in the model are errors which switch players from not contributing to contributing (each occurring with probability of order ), then the stochastically stable states are the Nash equilibria of the static model. This is because there always exists a transition path from any Nash equilibrium to any other Nash equilibrium that, for each transition between consecutive Nash equilibria on the path, only involves a single error. In the words of Samuelson [300], the set of Nash equilibria is a mutation-connected component. If, instead, the only type of errors in the model are errors which switch players from contributing to not contributing, then the stochastically stable states are the Nash equilibria of the static model with the maximum number of contributors. If errors in both directions are permitted at the same rate, then the results of the first case apply. Note that the directional restrictions on possible errors make them similar to uniform intentional errors as defined in Section 4.2.1, with further theoretical results described in Section 6.4 and empirics in Section 9.4.
A minimum effort game is at the opposite end of the public goods spectrum from a best shot game. Whereas in the best shot game only a single person must contribute for a good to be provided, in the minimum effort game everyone must contribute. Specifically, players each make some level of costly effort and the payoff to a player is the minimum level of effort taken by any of the players with whom he interacts, minus the cost of his own effort. There have been a few papers in recent years (Alós-Ferrer and Weidenholzer [15], Angus and Masson [21], Cui and Wang [93], Khan [193]) that consider dynamic processes and minimum effort games when the set of players with whom a player interacts is not the same as the set of players he observes when he chooses his strategy. Specifically, a player may imitate the strategy of successful players with whom he does not interact. Thus, small sets of interacting players who play high effort levels can ‘reproduce’ themselves (i.e., their strategies) by being observed to obtain high payoffs. Similar effects can be obtained in other games, such as prisoner’s dilemmas (Rivas [286]). This is effectively a story of assortativity (see Section 3) and group selection. Individual strategies that are played in successful groups are imitated. In terms of group selection, groups of players who obtain high average payoffs (e.g., a group of cooperators who interact mainly with each other) expand via selection at a group level, even though they may be outperformed in interactions with those outside the group (e.g., against defectors).
4.2.5. Cournot Oligopoly
Vega-Redondo [348] showed that in a Cournot oligopoly game, if players imitate (with uniform errors) the strategy of the player who is achieving the highest current payoff, then production of the Walrasian equilibrium quantities, and not the Nash equilibrium quantities, is uniquely stochastically stable. This is due to spite effects, as starting from Nash equilibrium quantities, if firm i makes a single error and increases its quantity, this reduces the profits of firm i but reduces the profits of the other firms even more. Hence firm i, being relatively more successful, will be imitated the following period. Alós-Ferrer [19] considers an amendment to the model whereby firms instead imitate the strategy that achieved the highest payoff in the previous m periods. That is, firms play the game with players in the present, but may imitate players in the past. In this model there can be a multiplicity of stochastically stable quantities in between the Nash equilibrium and Walrasian quantities. The reason for this multiplicity is that memory is assortative in the sense that strategies at period t generated the payoffs they generated due to other strategies at period t. If every player has played the Nash equilibrium quantity for as long as they can remember, and a player makes an error and plays a higher quantity, this will reduce the payoffs associated with the Nash equilibrium quantity in that period, but will not affect the payoffs associated with the Nash equilibrium quantity in previous periods (a similar assortativity across time is generated in a best response setting by a variant of fictitious play in Marden et al. [226], discussed in Section 8.4). This makes quantities lower than the Walrasian quantity more robust in the presence of memory. Alós-Ferrer and Shi [14] show that this effect disappears if at least one player has no memory of any strategy profile other than the current one. Such a player is immune to the lure of the payoffs of the past.
4.2.6. Prisoner’s Dilemmas
Weibull and Salomonsson [352] consider symmetric, two player games. Individuals’ fitnesses are given by a function of both their own payoff in the game and their opponent’s payoff. This sometimes leads to evolutionary stability of behavior that is not a Nash equilbrium of the game. In particular, consider an extensive form game in which players’ play a prisoner’s dilemma, following which, a player who has cooperated and his opponent defected, has the opportunity to pay a cost to punish his opponent. There is a set of rest points at which all individuals are cooperators and a sufficient number punish defection. The size and stability of this set is considered under a variety of different fitness functions, under which an individual’s fitness can increase or decrease in the payoff of his opponent. A similar extensive form model with rewards and punishments, in which fitness is considered in equilibrium and there is no explicit transformation of payoffs into fitnesses, is considered by Herold [165], discussed in Section 2.4.
Heller and Mohlin [156] consider randomly matched pairs of players who play a prisoner’s dilemma with sum of payoffs maximized at (i.e., in Figure 3) against one another. Each player in a matched pair observes a random sample of past play by their opponent against other opponents. Strategies map these observations to distributions over actions. Perturbations of the environment are considered in which some small fraction of the population comprises commitment types, where each commitment type always plays a given strategy and at least one commitment type plays a totally mixed strategy. A steady state of the unperturbed environment is said to be strictly perfect evolutionarily stable if is a limit of evolutionarily stable states of the perturbed environment as . It is shown that if , corresponding to in Figure 3, then the only strictly perfect evolutionarily stable state is for players to always defect, as by the assumed inequality, defecting can only discourage other players from defecting against you. However, if the opposite inequality holds, then full cooperation can be sustained as a strictly perfect evolutionarily stable state, as equilibrium strategies can then be such that defection increases the probability that future partners will defect against you. There is an essentially unique way in which such cooperation can be maintained, with some members of the population defecting if they observe their opponent defecting at least once, and the remainder of the population defecting if they observe their opponent defecting at least twice.
In a public goods game with prisoner’s dilemma style payoffs, Traulsen et al. [343] consider four possible player types. These are the standard cooperator and defector types, as well as loners, who do not participate in the game and receive a fixed payoff, and punishers, who cooperate and inflict costly punishment on defectors (see also Section 2.4). When error (mutation) rates are high, a positive share of each type persists in the population. In particular, a positive share of punishers persists, despite being outperformed by cooperators, who do not punish defectors and so do not suffer the associated fitness cost. Due to the positive share of punishers, defectors are punished and do not outperform cooperators. When error rates are low, the process spends most of the time at homogeneous states. Loners invade and outperform populations of defectors, cooperators or punishers invade and outperform populations of loners, and defectors invade and outperform populations of cooperators. In contrast, punishers can only be invaded by cooperators by neutral drift, so for large populations, populations of punishers are most likely to be observed in the long run.
4.3. Culture Embodied in Individuals
An example of culture embodied at an individual level is the ability to cook Yorkshire pudding. Alice and Bob can teach this skill to their son Colm. Yorkshire pudding will then persist as a cultural phenomenon as long as enough individuals know how to make it.
Montgomery [241] considers the model of intergenerational cultural transmission of Bisin and Verdier [52]. Individuals (within a continuum population) have a cultural type (from a finite set of types) that they have some probability of passing directly to their offspring via direct socialization. If that fails, then the offspring adopts a trait at random from the population. Individuals of type i choose the level of direct socialization for their offspring, trading off a quadratic cost against a desire to maximize a weighted probability over values , where represents the value that an individual of type i places on having an offspring of type j. The cultural distaste of an individual i for trait j is given by . Montgomery [241] shows that this model simplifies to a replicator dynamic on a game where is the payoff from playing strategy i against strategy j. When the number of types in a population is more than two, it is possible that the most tolerant types (low cultural distate) can go extinct. For even higher values of n, multiple equilibria and limit cycles are observed.
Cheung and Wu [85] consider the above model adapted for a continuous set of types , assuming that and hence are continuous in i and j (which implies that the assumption that T is one dimensional is meaningful). It is shown that monomorphic states are not Lyapunov stable. Furthermore, if is a strictly increasing function h of , more can be said. If h is convex, then the unique Nash equilibrium (which is Lyapunov stable) is composed of the two extreme types 0 and 1. In fact, all rest points of the dynamic are composed of two types with equal shares of the population, but unless these types are the extreme types, these rest points are not stable. If h is strictly concave, then the above-mentioned state with the two extreme types is no longer a Nash equilibrium, although it remains a rest point. Some rest points under concave h have more than two types present.
4.4. Interaction of Culture Embodied in Individuals and Society
The desire of Yorkshiremen to teach their offspring about Yorkshire pudding is a convention. We can easily imagine an alternative Yorkshire in which Lancashire hotpot is a local cuisine. This shows that sometimes individual behaviors will be socially enforced and a cultural phenomenon embodied partly at a collective and partly at an individual level.
A model that combines culture embodied at the individual level (religiosity versus secularism) and culture embodied at a societal level (equilibrium levels of wearing the Islamic veil) is that of Carvalho [79]. There are two types, religious and secular types, in a continuum population. Individuals have the option to veil themselves to some degree (between 0 and 1). Veiling is a commitment device to avoid temptation. Secular types would like to give in to temptation, but religious types would like to resist temptation. Individuals care not only about their own behavior, but also about how others view their behavior. In equilibrium, religious types veil more than secular types. Individuals can also choose to spend on religious education to increase the probability that their offspring will be religious. Religious types may wish to do this, so that their offspring will adopt a higher degree of veiling and be less likely to be tempted. Regulations that mandate (typically at 0 or 1) some degree of veiling thus lead to a reduction in religiosity, as the transmission mechanism from religiosity to behavior via veiling is removed. However, the degree of veiling that is mandated will still determine how often people give in to temptation. Moreover, it is shown that if there is an option for types to segregate themselves and avoid temptation, then banning veiling can lead to a higher degree of religiosity, as individuals seek to increase the probability that their offspring will be religious, in order that they will segregate and avoid temptation. Note that voluntary segregation is a method of endogenously determining assortativity along the lines discussed in Section 3.2.
5. Economic Applications
5.1. Macroeconomics, Market Selection and Finance
Chakrabarti and Lahkar [82] give a model in which firms choose input levels and production depends on aggregate input, with each firm’s share of production equal to their share of total input. Each firm’s payoff is given by its production minus a strictly convex input cost. The aggregate production function is concave, so input by any given firm exerts a negative externality on other firms by reducing the average return on input. This model has a potential function, hence play converges to an equilibrium under the (continuous population) logit dynamic (Hofbauer and Sandholm [167]). Due to the negative externalities in the model, equilibrium production is inefficiently high. As a consequence of this, it may occur that while the process is converging to the (unique, in this model) equilibrium, aggregate payoffs of the firms may rise before falling back down. This can occur due to states that are passed through en route to the equilibrium being closer to efficient production levels than the equilibrium is. The production function itself has a technology parameter and it is shown that when this parameter is changed, thus changing the equilibrium, boom-bust patterns of the type just discussed can be generated.
Norman [271] analyzes a variant of the model of Blume and Easley [55] (with a correction later provided by Massari [231]), in which there are many possible paths of the economy (sequences of states of nature); there is a true probability measure over these paths; and consumers have differing beliefs over these paths. The model is one of general equilibrium. Norman [271] assumes that the probability measure over the true state of nature in period is determined by the consumption shares of the consumers in period t. The beliefs of consumers are bound by the same restriction. It is shown that a perfect-foresight equilibrium, in which there exists a consumer with rational expectations who accounts for all of the consumption in the economy, need not be neutrally or Lyapunov stable, as a change in consumption shares can lead to a change in the state probabilities. However, if the process is ergodic, then there exists an invariant probability measure over states in the distant future, over which belief selection can occur. These results are used to explore the stability of inflation paths (constant versus increasing or decreasing inflation) and liquidity traps in macroeconomic examples. For further work on market selection of beliefs, see Massari [233,232], Sandroni [307,308], and for the related literature on the market selection of rules of portfolio choice see Alós-Ferrer and Ania [9], Amir et al. [20], Blume and Easley [54], De Giorgi [98], Evstigneev et al. [114,115], Hens and Schenk-Hoppé [163].
Foster and Young [123] study a process of learning to approximate Nash equilibria in repeated games by hypothesis testing. Norman [270] extends this to a model of learning rational expectations equilibria in a macro-style environment. Agents hold models of the world, given by sets of parameters, and given his model of the world, an agent will play a smoothed response that is close to a best response. Given play (data), every so often an agent will submit his model to a hypothesis test. If his hypothesis test rejects the model, he will randomly adopt another model and henceforth play accordingly. If agents’ responses are close to best responses, the hypothesis tests are sensitive enough, and enough data is used for the hypothesis tests, then, in the long run, the process spends most of the time close to a rational expectations equilibrium in that agents’ predictions are close to the actual outcomes and agents’ responses are close to optimal.
Cho and Kasa [88] analyze a similar model to Norman [270], but focus on selection amongst multiple models (corresponding to equilibria) using stochastic stability, although they do not explicitly mention stochastic stability except for a reference to Kandori et al. [191]. They find the costs of transitions that escape the basins of attraction of equilibria. These escapes correspond to model rejection events after which any alternative model may be chosen with positive probability. Hence, a model which has the uniquely highest cost of escape will be uniquely stochastically stable. Freidlin and Wentzell [125] tree arguments are not required.
5.2. Industrial Organization
Since the 1990s there has been a steady flow of evolutionary work related to pricing and competition. Examples include Alós-Ferrer and Ania [9], Alós-Ferrer et al. [16,17], Tanaka [339], Vega-Redondo [348]. Some recent work has studied the selection of market institutions (Alós-Ferrer and Kirchsteiger [12], Alós-Ferrer et al. [18]) and for a flavor of this see the discussion in Section 3.2.3. Recent work has also considered the impact that adaptive multi-agency decision making within organizations can have on corporate culture (Newton et al. [263]). This relates to the relationship between collective agency and coordination problems and has been discussed in Section 2.2.1.
Lahkar [210] analyzes the stability of equlibria in the Burdett and Judd [75] model of price dispersion and shows the emergence of price cycles. There are populations of buyers and sellers, each of which can be represented by the unit interval. Strategies of sellers are prices in the interval . The set of possible prices is discretized by Lahkar [210] to simplify analysis. A strategy for a consumer is a number of sellers to sample. Consumers sample sellers independently and each consumer chooses to buy from the seller in her sample that offers the lowest price. Some Nash equilibria of the model involve sellers charging multiple prices. Building on the analysis of Hopkins and Seymour [172], who show instability of equilibria in multiple prices under the replicator and similar dynamics, it is shown using simulation that, under logit dynamics, rest points that approximate multi-price Nash equilibria of the original model are unstable, and that play converges to limit cycles. This is shown analytically for the special case in which buyers can only sample one or two sellers.
In a similar model, Chakrabarti and Lahkar [83] let sellers choose a level of technology instead of a price, with buyers sampling multiple sellers and choosing the one which offers the highest technology. Buyers produce an output equal to the technology level that they sample. Results are very similar to those of Lahkar [210], but can instead be interpreted to show the emergence of cycles in productivity.
Dawid and Hellmann [96] consider a setup in which firms choose which other firms to form R&D partnerships with, and payoffs are then given by the Nash equilibrium of a Cournot game. Each R&D partnership in which a firm is involved costs a fixed amount f and reduces the firm’s marginal cost of production by a fixed amount. Note that firms care not only about how many partnerships they are involved in, but also in how many partnerships their partners are involved in, as their profits are affected by their partners’ marginal costs. The network of partnerships is updated according to the perturbed pairwise better response dynamic of Jackson and Watts [184], which is effectively the dynamic of Roth and Vande Vate [293] augmented with random errors in the style of Young [361] (see Section 2.2.2). The stochastically stable states of this process are shown to have one completely connected component of the network in which every firm is connected to every other firm, with the remainder of firms being isolated and not involved in any partnerships. The size of the connected component decreases monotonically in the cost of a partnership f. A comparative static analysis shows that total profits in the industry are nonmonotonic in f. As f increases, profits decrease until the connected component shrinks and profits increase (discontinuously) due to the reduced total cost of partnership formation. The discontinuity in the comparative statics in f implies a coordination failure at values of f just below the values at which total industry profits show a discontinuous increase. The dynamic is a coalitional better response dynamic in which coalitions are restricted to sizes 1 and 2, raising the question of whether the possibility of larger coalitions (e.g., of size 4) might smoothen some of these discontinuities.
6. The Evolutionary Nash Program
The Evolutionary Nash Program is the study of connections between evolutionary game theory and cooperative game theory (see Figure 13). This is similar to the standard Nash Program which studies connections between noncooperative game theory and cooperative game theory (see, e.g., Nash [248]). A cooperative game in characteristic function form is a set of players N and a characteristic function from subsets to the nonnegative real numbers. The characteristic function shows how much surplus a coalition can generate. It is typically assumed that .
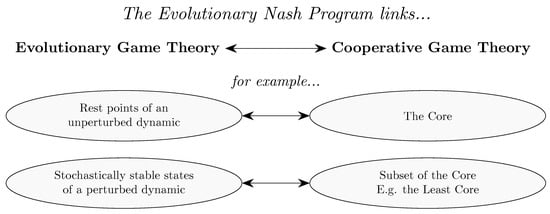
Figure 13.
The Evolutionary Nash Program. Connections are made between evolutionary game theory and cooperative game theory. For example, sometimes a state space can be derived from an underlying cooperative game. For some evolutionary dynamics, the rest points will correspond to the core of the associated cooperative game. When these dynamics are perturbed, the stochastically stable states will then correspond to a (possibly strict) subset of the core.
A characteristic function v is superadditive if, for all , , we have . A characteristic function v is supermodular if, for all , we have . Note that supermodularity implies superadditivity. The core is an allocation of surplus under the grand coalition N, such that and no coalition S can obtain a higher surplus by leaving the grand coalition: for all . A coalition for which is known as a blocking coalition.
6.1. Recontracting and Nash Demand Games
The question of how a society represented by a cooperative game might converge to the core is an old one. Feldman [117] and Green [142] give recontracting processes under which subsets of players randomly meet, and if they can do better than they do under the current allocation x, that is if , then they form a coalition with a new allocation such that . These processes eventually reach the core, assuming that the core is nonempty. Note that any such process suffers from the remainder problem: when a subcoalition leaves a coalition S, it is not clear what should happen to players in . Should they be left in a coalition on their own as in Green [142]? Should they form singleton coalitions as in Feldman [117]? Each of these makes sense in some context. For example, if eleven people constitute a discussion group, S, and two of them, , decide to go climbing instead, it makes sense for the discussion group to continue to meet as . However, if S instead formed a football team, the remainder set no longer has enough members to form a football team, so it may make more sense for them to become singletons.
Young [362] represents a two player cooperative game noncooperatively as a Nash demand game, in which the players each make a demand, and if the demands sum to no more than , then they obtain their demands. If the demands sum to more than , then they get nothing. Players have a utility function that increases in their allocation. Note that, because payoffs arise from individual strategies, the remainder problem disappears. It is shown that if players adjust their demands according to an individualistic best response dynamic with uniform errors, then the stochastically stable state corresponds to the Nash bargaining solution (Nash [246]), which is within the core.
Agastya [2,3] expands the model of Young [362] to a multiplayer environment, in which a player may (sometimes probabilistically) obtain his demand if there exists some , , such that the demands of the players in S sum to no more than . For games with a supermodular characteristic function, convergence to the core occurs under an individualistic best response dynamic. When this dynamic is perturbed with uniform errors, the stochastically stable allocations are those within the core that minimize the allocation of the wealthiest player.
Rozen [295] adjusts strategies in the Agastya [2] setup by allowing a player’s strategy to include not only a demand, but also a list of players with whom he is willing to form coalitions. Under this setup, results of Agastya [2] do not change. However, this change in the strategy space makes possible another approach, which is explored in Newton [265].
Newton [265] implements collective agency (in the style of Feldman [117], Green [142]) with individual strategies (in the style of Agastya [2], Rozen [295], Young [362]). This allows the separation of collective agency in decision making from collective generation of payoffs. For example, two players could meet and take a collective decision to not form coalitions with one another, that is to exclude one another from their sets of acceptable coalition partners. Examples along these lines are quite easy to come up with. For example, if two employees in a firm find it difficult to work with one another (perhaps their skill sets overlap too much), they may agree to request that they never be part of the same team. This would be payoff improving for both of them. The return to collective agency (compared to the individualistic rules of Agastya [2,3], Rozen [295], Young [362]) allows convergence to the core to occur for games with a superadditive characteristic function. Moreover, when the dynamic is perturbed by uniform errors, the stochastically stable state is no longer the minmax outcome as it is in Agastya [3]. Rather, when is concave and is convex, the stochastically stable state trades off maximizing the wealth of the poorest player against minimizing inequality amongst the remaining players. In the boundary case of , , only the first of these considerations matters, so stochastic stability results in ‘Rawlsian’ social choice, maximizing the wealth of the poorest player.
Arnold and Schwalbe [25] give a best response dynamic in which the state includes both a set of existing coalitions and demands which are satisfied for players in coalition S if they sum to no more than . This reintroduces the remainder problem, which is treated in the manner of Green [142]. The dynamic is individualistic, with an updating player choosing a demand and to either join an existing coalition or to form a singleton coalition. Superadditivity is not assumed. However, to obtain convergence to the core, it is assumed that outside of the core, the strategy choice of players in any potential blocking coalition is perturbed by uniform errors, and that no errors occur within the core.
Nax [255] obtains convergence to the core, where it exists, treating demands as aspirations, so that players do not best respond but instead may lower their demands when they are not fulfilled and increase their demands when there is the possibility of a higher payoff. The state includes a set of existing coalitions and the remainder problem is treated in the manner of Feldman [117]. The proof is similar to the proof of convergence in Feldman [117] in that this assumption is leveraged so that payoffs, and consequently demands, can reduce over time until a jump to a core state is possible.
All perturbations discussed so far in this section are uniform, so stochastic stability emerges from length-based selection (see Section 4.2.1 for definition). Sawa [313] uses logit errors and steepness-based selection. This recovers minmax selection by a different route. In Agastya [3], all errors are equally likely and the stochastically stable state is minmax as it is the wealthiest player who changes his response most readily to errors made by others. In Newton [265], the wealth of the wealthiest players matters (and hence, by omission, the wealth of the poorest player) as these players change their collective response most readily to errors made by the poorest player. In Sawa [313], the stochastically stable state is minmax as it is the wealthiest player who makes errors most easily. Like Newton [265], Sawa [313] has collective agency in the dynamic, specifically the coalitional logit choice rule discussed in Section 2.1.2, but returns to having a set of existing coalitions included in the state of the Markov process, hence reintroducing the remainder problem, which is treated in the manner of Feldman [117].
Following work on coordination games discussed in Section 6.4, Hwang and Rey-Bellet [178] have recently analyzed the two player model of Young [362] under logit errors, also finding the Nash bargaining solution to be stochastically stable. They obtain these results by extending the technical results of Hwang and Newton [177] (see Section 8.1.1) to coordination games that satisfy the marginal bandwagon property of Kandori and Rob [190] (see Section 8.1.1 for definition). They also give results under intentional errors (see Section 4.2.1 for definition).
The above approach deals with recontracting with transferable surplus. In contrast, Serrano and Volij [320] consider a model of recontracting over discrete goods—a ‘housing economy’. Each player is endowed with a single house (the endowment is fixed and does not evolve with the process) and may only have a single house at any allocation. Every period, some set of players may agree to reallocate their endowment in such a way that they all strictly gain relative to the current allocation. If, when this happens, the allocation of players outside S can no longer be satisfied (i.e., it depended on the endowments of players in S), then the players outside S are allocated their endowments (this is an approach to the remainder problem). Errors involve players agreeing to reallocations that are not a strict improvement for them upon the existing allocation. It is assumed that errors where a player is indifferent between the old and new allocations are much more likely than errors which involve a strict payoff loss. The only allocation for which there does not exist such that a weakly improving reallocation is possible is the competitive equilibrium allocation (Roth and Postlewaite [292]). It follows that the competitive equilibrium allocation is uniquely stochastically stable.
Open Topic 6.
Skyrms [331] finds that in (discretized) Nash demand games, the basin of attraction of the egalitarian norm increases greatly when costless signals (in the style of Lewis [217]) are added to the strategy space. It is not clear why this is the case, particularly as signaling gives players the opportunity to coordinate on different asymmetric demand splits with different types. Analysis of simulation data suggests it is related to the effect of transient information: the information transmitted by signals first grows by evolutionary selection, but later fades as the system approaches a stable state. Uncovering the mechanisms by which such information benefits some norms over others would be interesting and important.
6.2. Transferable Utility Matching—The Assignment Game
A special case of a cooperative game is the assignment game (Shapley and Shubik [327]). The player set can be divided into two disjoint sets, say (firms and workers), and all surplus is generated by pairs of players in which one player is in F and one is in W. That is, for any , implies that for some and . For , is equal to the maximum amount of surplus that can be generated by such pairs in S.
Several studies have recently shown that, under pairwise dynamics (see Section 2.2.2) of rematching and surplus sharing, convergence to the core of the assignment problem is assured (Biró et al. [51], Chen et al. [84], Klaus and Payot [200], Nax et al. [253]). A typical dynamic involves two agents meeting every period, and if they can improve upon their current allocation by matching with one another and dividing the resulting surplus, they do so.
Nax and Pradelski [250] consider a perturbed version of such a dynamic. A player’s payoff may be subject to a ‘shock’ with a probability that, like logit errors, is log-linear in the size of the shock. If a player, following a shock, has a payoff lower than that which he could achieve by a change of partner, then he can change his partner. This combination of shock and response adds a discrete element to the model, bringing it closer to non-transferable models of matching. Using arguments adapted from Newton and Sawa [261], Nax and Pradelski [250] show that, under this process, the set of stochastically stable states is a subset of the least core (Maschler et al. [230]), the set of allocations such that the minimum value of over all is as high as possible. For the assignment game, the core is nonempty, and it is clear that the least core lies within the core. Similar results for many to one matchings with transferable utility are given in Nax and Pradelski [251].
Klaus and Newton [199] analyze a different form of perturbation, allowing errors whereby the agents in a given pair remain matched yet adjust the allocation they obtain within the pair. As we shall see below, this weakens the selective power of stochastic stability relative to the model of Nax and Pradelski [250]. Errors are changes to matches and allocations that do not constitute a weak blocking by players who make them. This allows the possibility of errors in which no error-committing player loses allocation, such as when two players, previously matched to other partners, match and share surplus in such a way that they attain exactly the same allocation as before. This is not a weak blocking and is therefore an error. This is similar but not identical to the approach of Serrano and Volij [320] to errors involving indifference discussed in Section 6.1. Error probabilities are assumed to be weakly decreasing in loss of allocation. If all errors are equally likely, then no selection within the core is obtained. If errors which cause no allocation loss to the player or players who commit them are more likely than errors which cause strictly positive allocation losses, then all optimal matchings occur in some stochastically stable state, but there may be strict selection of allocations amongst players who have the same partner at every optimal matching.
Pradelski [283] considers the speed of convergence to the core of an assignment game and finds a decentralized dynamic that attains this convergence in polynomial time. Each player has a changing aspiration level of utility that he seeks to meet. The result on polynomial time convergence relies on ‘market sentiment’, by which at any point in time, players on one side of the market (i.e., either F or W players) can accept allocations slightly below their aspiration level. Interestingly, the result only holds if market sentiment does not switch too frequently from favoring one side of the market to favoring the other side of the market. Further work that uses such state variables can be found in Section 8.4. In contrast, Leshno and Pradelski [214] show that, if transitions from a given matching and allocation are such that any rematching of a firm and a worker (i) depends only on their allocations at the existing matching and (ii) is a strict blocking, then the expected time to converge to the core may increase exponentially in the number of players.
6.3. Non-Transferable Utility Matching—Marriage, College Admissions
Now consider matching with non-transferable utility (Gale and Shapley [134]). That is, the payoffs of a player depend solely on the identity of those with whom he is matched. This class of problems includes the marriage problem, in which men and women are matched in pairs; the roommate problem, in which players of any sex are matched in pairs; and the college admissions problem, in which colleges are matched to multiple students, whilst each student is only matched to one college. A college is said to have responsive preferences if its preferences over any two students are independent of the other students to whom it is matched. A college is said to have substitutable preferences if, whenever it would admit a student i from a set of students A that contains i, it would also admit student i from set , . A matching is pairwise stable if no player can gain by leaving a current partner, and no pair of players who are not currently matched to one another can gain by matching with one another. The set of pairwise stable matchings corresponds to the core in the marriage problem, roommate problem, and college admissions problem when colleges have responsive preferences.
Paths to stability results in such settings give, sometimes implicitly, pairwise dynamics (Section 2.2.2) under which convergence to stable matchings occur. Such results exist for the marriage problem (Roth and Vande Vate [293]), variants thereof (e.g., Klaus and Klijn [198]), and the roommate problem (Diamantoudi et al. [101]). Such dynamics work by randomly selecting a player or pair of players each period. If an individual is selected and can gain by leaving his or her current partner (if he or she has one) to become a singleton, then he or she does so. If a pair of players is selected and both players in the pair can gain by leaving their current partners (if they have them) and getting together, then they do so. The process is repeated until a stable matching is obtained. For college admissions problems, if a college has responsive preferences, then the problem reduces to the marriage problem by mapping each position in a college to a man, and each student to a woman. Kojima and Ünver [203] give a paths to stability result for many to many matchings when one side of the market has responsive preferences and the other has substitutable preferences.
The next step is to consider perturbed dynamics. Jackson and Watts [184] and Klaus et al. [201] do this for uniform errors and find no selection in marriage and roommate problems respectively. That is, the entire set of stable matchings is stochastically stable. The reason for this is that, under the unperturbed dynamic, from any unstable matching, it is possible to get closer (under a suitable concept of similarity) to any stable matching of one’s choice. This implies that it only ever takes one random error to exit the basin of attraction of a stable matching and eventually reach a stable matching that is closer to any given target stable matching. Freidlin and Wentzell [125] tree arguments immediately imply that every stable matching must be stochastically stable.
These arguments are taken further by Newton and Sawa [261], who, for marriage problems, roommate problems and college admissions with responsive preferences, expand the analysis to cover any perturbed dynamic (including uniform, logit, probit) for which error probabilities of an individual or a pair do not depend on the partnerships of other players. Let (for ‘one shot’) denote the set of stable matchings at which the probability of an error occuring is lowest. It is shown that, for any given , from a stable matching , following a single error, no matter what that error is, it is possible under the unperturbed dynamic to reach a stable matching y that is more similar to z than x is to z. This implies that the root of any least cost Freidlin and Wentzell [125] tree and hence any stochastically stable state will be within . In particular, under logit errors, similarly to Nax and Pradelski [250] discussed above, stochastically stable states are within a non-transferable utility version of the least core of Maschler et al. [230].
Open Topic 7.
Some interesting characterizations or examples may arise from dropping Assumption 3 of Newton and Sawa [261] and allowing error probabilities to depend on the partnerships of players other than those making the error. For example, it may be that Alice and Diane are friends and that Alice is more likely to make errors when Diane is in an unhappy partnership and has a low current payoff.
6.4. Bargaining Solutions and Coordination Games
Consider a two player coordination game, the main diagonal of which approximates the efficient frontier of a convex bargaining set, and that has zero payoffs off-diagonal. Let there be two populations, each corresponding to one of the positions in the game. Under an individualistic best response dynamic with uniform errors, Young [364] shows that stochastically stable states approximate the Kalai-Smorodinsky bargaining solution (Kalai and Smorodinsky [188]). Newton [264] extends the model to a coalitional dynamic and finds that stochastically stable states approximate the Nash bargaining solution (Nash [246]).
Naidu et al. [244] consider errors which are intentional (see Section 4.2.1) in that the only errors that a player might make are those that involve attempting to coordinate on an outcome that corresponds to a higher equilibrium payoff than the equilibrium payoff associated with his best response. Players never make errors that ask for less than their best response. Under intentional uniform errors, the stochastically stable states again approximate the Nash bargaining solution. Note that under both unintentional uniform errors and intentional uniform errors, all errors in the support of the error distribution occur with similar probability, so there is no steepness-based selection and results are driven by length-based selection (see Section 4.2.1).
Using the technical results of Hwang and Newton [177] (see Section 8.1.1), Hwang et al. [179] extend the analysis to logit dynamics. Logit errors introduce steepness-based selection as well as length-based selection. Under intentional logit errors, it turns out that length-based selection is dominated by steepness-based selection, and given that players who earn higher payoffs have more to lose from making errors and miscoordinating, stochastically stable states approximate the Egalitarian bargaining solution of Kalai [189]. This contrasts with previous justifications of Egalitarianism which have usually assumed some symmetry in the problem faced (Alexander and Skyrms [4]) or invoked ex-ante symmetry of players with respect to their position in the game (Binmore [49,50]). Under unintentional logit errors (i.e., the standard logit choice rule), length-based and steepness-based selection combine and a new (piecewise) bargaining solution, the logit bargaining solution, emerges. This solution shares features of some of the existing bargaining solutions, but exhibits some curious nonmonotonicities. Results on the relationship between bargaining solutions and the stochastically stable states of coordination games under individualistic dynamics are summarized in Figure 14.
Figure 14.
Conventions and bargaining solutions. Each bargaining solution can be justified as the stochastically stable state of a coordination game under the corresponding behavioral rule and without reference to any appealing ex-post properties that the solution might have.
7. Behavioral Dynamics
There exists a rich literature on a variety of behavioral dynamics, rules which specify the current behavior of agents in a population, given what has occurred in the past. Important earlier work includes Binmore and Samuelson [47,48], Bomze [62], Friedman [129], Hofbauer and Sigmund [169], Hofbauer and Weibull [170], Nachbar [242], Ritzberger and Weibull [285], Samuelson and Zhang [299]. This work concerns processes with both finite and infinite populations under dynamics with both discrete and continuous time steps, and sometimes the approximation of one type of process by another (Benaïm and Weibull [39]). Here we consider some recent contributions to this literature.
7.1. Reinforcement Learning
Argiento et al. [23] show that efficient signaling in a two state, two signal setting (similar to the signaling model of Lewis [217]) can be obtained asymptotically with certainty using the urn based reinforcement learning model of Roth and Erev [291] and Erev and Roth [111]. A sender observes the state of nature (state 1 or 2), and chooses a signal (A or B) by drawing a ball from an urn that corresponds to the state (urns 1 and 2). The receiver observes the signal and chooses an action (1 or 2) by drawing a ball from an urn that corresponds to the signal (urns A and B). If the receiver’s action matches the state of nature, then the players ‘win’. When they win, they each add a ball to the relevant urns. For example, if a win is attained when the state of nature is 1, the sender chooses B and the receiver chooses 1, then the sender adds a B ball to urn 1 and the receiver adds a 1 ball to urn B. This process converges to one of two possible signaling systems in which state-signal-action triplets correspond perfectly, such as when state 1 induces signal B which induces action 1 and state 2 induces signal A which induces action 2. This result contrasts, qualitatively as the models are very different, with the evolutionary stability of inefficient communication that was discussed in Section 4.2.3.
The general version of the reinforcement rule of which the above is an example involves each player, after playing a strategy, adding a number of balls (not necessarily discrete) to his urn for that strategy. Building on results that stochastic reinforcement models can be approximated by deterministic replicator dynamics (Beggs [35], Börgers and Sarin [65], Hopkins [173], Laslier et al. [213]), Ianni [180] shows that if the state (in terms of the probability of players choosing strategies) is close to a strict Nash equilibrium of the underlying game, then the amount of time that has elapsed under the process (so that the urns are full enough that learning has become slow) can be chosen so that the process converges to the Nash equilibrium with arbitrarily high probability. The proof uses the fact that trajectories of the replicator dynamic that start within the basin of attraction of a strict Nash equilibrium converge exponentially fast to show that, for small , if learning is made slow enough, the process can be made to stay within of the trajectory of the replicator dynamic with arbitrarily high probability.
An alternative model of reinforcement learning is the Cross Model (Cross [92]), under which a player updates a probability vector x according to which he plays each of a finite set of actions. After choosing action i (which occurs with probability ) and receiving a payoff from the game, the player transfers a share of the probability mass from the other actions to action i. The share that is transferred is proportional to the payoff he received. Lahkar and Seymour [209] extend this model to incorporate the possibility of negative payoffs. If i yields a negative payoff for the player, then a share of the probability mass is transferred to the other actions. The share that is transferred is proportional to the absolute value of the payoff received. It is noted that unlike the basic Cross Model, this model cannot be approximated by the replicator dynamic. In particular, any state at which every player plays strategy i with probability one and obtains a negative payoff cannot be a rest point of the dynamic (even if it corresponds to a Nash equilibrium of the game), as negative reinforcement will then transfer probability away from this strategy. Lahkar [211] shows conditions under which a continuum population playing a stag hunt under this dynamic will converge to all playing Stag or all playing Hare. If payoffs at the Hare-Hare equilibrium are negative and payoffs at the Stag-Stag equilibrium are positive and sufficiently large, then the state at which every player plays Stag is a globally asymptotically stable rest point. If Hare-Hare payoffs are positive, and the payoffs from playing Stag against Hare is negative and greater in magnitude than the difference between Stag-Stag and Hare-Hare payoffs, then the state at which every player plays Hare is an almost globally asymptotically stable rest point, and the state at which every player plays Stag is an unstable rest point. Other rest points, including polymorphic ones, exist when neither of these conditions is satisfied.
Mertikopoulos and Sandholm [236] follow Sorin [333] and Hofbauer et al. [171] in specifying reinforcement learning directly in continuous time. A choice map transforms a vector of scores (cumulative payoffs) from each action over time into mixed strategies. The choice map derives from maximizing the expected score minus a penalty function, the convexity of which encourages mixed strategies over pure strategies. Examples of such choice maps include the projection map (see, e.g., Friedman [129], Lahkar and Sandholm [208]) and the logit map (see, e.g., Littlestone and Warmuth [220], Vovk [351]), which is known to be equivalent to the replicator dynamic (see, e.g., Mertikopoulos and Moustakas [235], Rustichini [298] and citations earlier in this section). It is shown that iteratively strictly dominated strategies become extinct on solution paths and that, if penalty functions do not approach infinity at the boundaries of the simplex, then this happens in finite time. Weakly dominated strategies either become extinct or the profiles on which they are dominated become extinct. Stationary points of the dynamic correspond to Nash equilibria and strict Nash equilibria are asymptotically stable.
7.2. Imitation
Consider a setting in which two players repeatedly play a finite, symmetric game. One of the players, Alice, follows the behavioral rule imitate-if-better by which at period she imitates the action of the other player at period t if and only if the other player obtained a higher payoff than Alice did in period t. Otherwise, Alice plays the same action at as she did at t. Duersch et al. [106] consider the zero-sum game defined by the payoff differences
and find conditions under which the sum of payoffs (across time) earned by a player playing against an imitate-if-better player are bounded above as time goes to infinity. When this is the case, they say that imitation is not subject to a money pump. An imitation cycle is a cycle of action pairs
such that the non-imitative player always outperforms the imitator, , and the imitator imitates, so . It is shown that imitation is subject to a money pump if and only if there exists an imitation cycle. An imitation cycle such as (11) can be expanded into a cycle whereby a single player improves their payoff at each step,
Hence the absence of such a payoff improving cycle implies the absence of an imitation cycle. A game is a generalized ordinal potential game if and only if there does not exist such a payoff improving cycle (Monderer and Shapley [240]), therefore in such a game the imitator cannot be subject to a money pump. It is also shown that if there exists an ordering on the strategy set such that payoffs are quasiconcave in a player’s own strategy, then no money pump exists.
Sawa and Zusai [311] consider (continuum) population games with imitation rules according to which a revising player who is playing i considers an alternative strategy j drawn at random according to the strategy distribution given by the population state. With some strictly positive state dependent probability the player switches from i to j. Players can be of different types and the switching probability is assumed to be formed by adding together two nonnegative terms. The first term does not vary across types and can vary according to the identity of the strategy pair under consideration. This is standard. The second term differs across types but does not depend on . The second term, by inducing positive imitation independently of i and j, moves all types towards the average distribution of strategies in the population. Over time, the process converges towards the set of states at which there is an equal proportion of each type playing each strategy (the Wright manifold) and the process approximates standard imitative dynamics without type diversity. It is interesting to note that the variability of the non-type dependent term in the switching rate according to the strategy pair makes these generalized replicator dynamics possibly nonmonotonic in that strategies that generate higher payoffs need not have higher growth rates. Consequently, even a strategy that is strictly dominated by another (pure) strategy may survive indefinitely (Sethi [324]).
Mertikopoulos and Sandholm [237] consider a class of dynamics, Riemannian game dynamics, in which the trajectory of the dynamic is the maximizer of an expression equal to a gain function minus a cost function. For a given population state and a trajectory vector that implies a direction and speed of motion, the gain function equals the scalar product of the vector of payoffs from each action and the trajectory vector. It takes higher values for trajectories that increase the share of the population taking actions currently associated with high payoffs and grows linearly with the speed of motion. For a given population state, the cost function is a positive definite quadratic form, so that it increases quadratically in the speed of motion for any given direction. These cost functions correspond to Riemannian metrics on the state space. For example, the dynamic associated with the Euclidean metric is the projection dynamic (Nagurney and Zhang [243]) and the dynamic association with the Shahshahani metric (Shahshahani [326]) is the replicator dynamic. Results on existence and uniqueness of solution trajectories are derived and it is shown that Riemannian game dynamics satisfy positive correlation, a form of payoff monotonicity. When a Riemannian metric is the Hessian matrix of a convex function, dynamics are similar to those derived for reinforcement learning models by Mertikopoulos and Sandholm [236] (see discussion in Section 7.1). For this class, it is shown that evolutionarily stable states are asymptotically stable and, for contractive (also known as negative semi-definite) games, a Lyapunov function is derived.
Laraki and Mertikopoulos [212] consider imitative dynamics in which, rather than the growth rates of strategies in a population being determined by payoffs, the rate of change of such growth rates, or even higher order derivatives, are determined by payoffs. One difficulty with analyzing such dynamics has been that relevant second order optimization methods are defined for unconstrained problems rather than for problems constrained by a strategy space. Flåm and Morgan [120] tackle this problem by projecting velocities of orbits onto a subspace of admissible directions. Recognizing that projective methods can lead to discontinuous dynamics, Laraki and Mertikopoulos [212] instead propose a solution based on the equivalence between the replicator dynamic and logit choice according to cumulative payoff scores used in reinforcement learning (see Section 7.1 for more on this equivalence). That is, they consider dynamics on unconstrained spaces of cumulative scores, including second and higher order cumulative scores created from summing lower order cumulative scores. An equivalence exists between choice based on these higher order scores and higher order variants of the replicator dynamic. Iteratively strictly dominated strategies go extinct under these higher order dynamics and this happens n orders of magnitude as fast under the nth order replicator dynamic as it does under the first order (i.e., standard) replicator dynamic. Moreover, unlike the standard replicator dynamic, for , if the dynamic starts at rest, then weakly dominated strategies are guaranteed to go extinct. To see this, consider . If, for Alice, strategy i weakly dominates strategy j, then the acceleration towards strategy i will be greater than the acceleration towards strategy j. If the process starts from rest, this will give the dynamic a greater velocity towards strategy i relative to strategy j. This velocity advantage will be maintained even if the strategy profiles at which i has a strict advantage over j go extinct so that acceleration towards i and j becomes the same. This argument cannot be made iteratively for the following reason. It may be that following the elimination of Alice’s strategy j, Bob’s strategy k weakly dominates his strategy l. However, in the time taken for j to be eliminated, it may be the case that strategy l has gained a considerable velocity advantage relative to strategy k. Consequently, the previous argument does not work. Analogous results to those regarding stability and convergence of the standard replicator dynamic are given for the higher order dynamics.
Hofbauer et al. [171] consider the fact that logit choice according to cumulative payoffs over time is a solution of the replicator dynamic (see Section 7.1). Cumulative payoffs over time are equal to average payoffs over time multiplied by time t, so logit choice according to cumulative payoffs can be seen as logit choice according to time average payoffs multiplied by t. As t diverges to infinity, this approximates a best response to time average payoffs (we can think of t as equivalent to , with measuring perturbations from best response). However, best responses to time average payoffs are solutions to a process in which time average payoffs evolve according to a best response dynamic. Together, these results imply that the time average of the replicator dynamic is a perturbed solution to the best response dynamic, with the magnitude of perturbations vanishing over time. Accordingly, results can be derived on the long run behavior of the replicator dynamic in terms of the long run behavior of the best response dynamic on time average payoffs.
7.3. Sampling Equilibrium and Best Experienced Payoff Dynamics
Osborne and Rubinstein [275] model procedurally rational choice (Simon [330]) in the following manner. Consider a symmetric game with a finite set of actions . Let p be a probability distribution over A. Suppose that a player samples each of the actions in A once, playing the sampled action against an opponent who plays the mixed strategy given by p. Each of the actions in A is thereby associated with a realized payoff. The player who is sampling selects the action with the highest realized payoff (with uniform tie breaking). Letting be the probability that this decision rule selects action , a sampling equilibrium is a mixed strategy that satisfies for all i. Osborne and Rubinstein [275] suggest that that these equilibria can be interpreted as rest points of a process whereby players in a large population are randomly matched to play the game, any given player in the population plays the same action every time he plays, and players entering the population sample each action and select one as described above.
Sethi [325] formalizes the idea of the dynamic proposed above with a family of dynamics according to which, if the current distribution of actions in the population is p, then the share of action in the population increases if and only if . Under these dynamics, even strict Nash equilibria need not be stable, in contrast to payoff monotone dynamics (Weibull [353]). Furthermore, it can be the case that the only stable rest points are sampling equilibria in which strictly dominated strategies are played with positive probability. A symmetric action profile is inferior if, for every action , there exists such that a player’s payoff from playing when one opponent plays and the other opponents play is strictly greater than his payoff at the symmetric action profile . For games with three or more players, if a sampling equilibrium corresponds to the play of a strict Nash equilibrium that is an inferior action profile, then is unstable. We can connect this observation to the literature discussed in Section 2 by noting that if, for every alternative action , a symmetric strict Nash equilibrium in has a profitable pairwise coalitional deviation involving , then the Nash equilibrium must be inferior. Recent work by Cárdenas et al. [78] fits a model of sampling equilibrium to experimental data on games with negative externalities, replicating features of the data despite being parameter free.
Mantilla et al. [221] study public goods games under the above dynamics. It transpires that Nash equilibrium profiles, even in dominant strategies, are unstable for a broad range of payoff specifications. Instability of non contribution (resp. full contribution) can arise when a player samples the action of contribution, encounters a mutant amongst his opponents who contributes (resp. does not contribute), and misattributes the positive (resp. negative) externality from this opponent’s contribution (resp. non-contribution) to his own contribution. The precise conditions under which these effects lead to instability depend on a property of the binomial distribution.
Sandholm et al. [305] refer to the above dynamic and its variants as the best experienced payoff dynamics. In particular, they note possible alternatives for three parts of the dynamic, (i) the possibility of only sampling a subset of alternatives rather than every alternative; (ii) the size of the sample taken for each action, which as the above cited papers already discuss, can be more than one; and (iii) the tie breaking rule when several strategies give equal expected payoffs (calculated from the sample). It is emphasized that (iii) is more important in extensive form games than in normal form games, in which it generically has no effect. It is noted that these dynamics are characterized by systems of polynomial equations with rational coefficients and a discussion is given of concepts and methods relevant to solving such equations. Computer assisted proofs are used to analyze the centipede game (Rosenthal [290]) when all strategies are sampled once and the tie breaking rule is to choose the rule that defects and ends the game at the earliest decision node, thus making it more difficult to achieve cooperation. Under this rule, for centipede games with at least three decision nodes, the equilibrium corresponding to the backward induction solution is unstable. Furthermore, for centipede games with three to six decision nodes, there also exists an asymptotically stable interior rest point of the dynamic. Note that, as every Nash equilibrium of the centipede game involves the game ending after the first decision node, this stable rest point does not correspond to a Nash equilibrium. This result continues to hold even for moderately large sample sizes. However, if a best experienced payoff dynamic samples all strategies a large number of times it approaches a best response dynamic, under which, as we shall now see, results differ.
7.4. Best and Better Response
Xu [359] considers generic, finite, extensive-form games of perfect information and shows that every solution trajectory of the continuous best response dynamic (Gilboa and Matsui [138]) converges to some Nash equilibrium component (a set of Nash equilibria with the same outcome). It is further shown that, from any interior initial state, the dynamic converges to the backwards induction solution for the extensive form game. Furthermore, this last result also holds for approximate best response dynamics that are sufficiently close to the standard best response dynamic. An approximate best response dynamic is one in which updating players may play best responses to strategy profiles which are close to the current strategy profile as well as best responses to the current profile itself.
Zusai [369] defines the tempered best response dynamics, amending the continuous time best response dynamic for continuous populations. The idea is that the further the current payoff of a player is from his best response payoff, the more likely he should be to update his strategy to a best response. Hence, under these dynamics, the revision rate is strictly increasing in payoff gain from switching to a best response. Furthermore, the revision rate is zero when there is zero payoff gain, hence all Nash equilibria are rest points of the dynamic, even if they are not strict. Similar stability results to those that hold for standard best response dynamics (for potential games etc.) continue to hold. A similar dynamic is considered for finite populations in Kuzmics [206], discussed in Section 8.1.4. Zusai [371] generalizes the analysis to a broader class of dynamics in which the set of actions from which a player can choose at any given revision opportunity is allowed to vary and shows asymptotic stability of (regular) evolutionarily stable states (Taylor and Jonker [340]).
Building on the work of Ritzberger and Weibull [285], Balkenborg et al. [32] define a generalized best-reply correspondence as a correspondence that, independently for each player, maps mixed strategy profiles to sets of mixed strategies that contain at least one best response. Under some continuity assumptions, the set of such correspondences can be considered as a lattice with a minimal element, , that coincides with a standard best response correspondence on a dense set of strategy profiles. The set of independent strategy mixtures over given subsets of the pure strategies is called a minimal asymptotically stable face if it is asymptotically stable under some generalized best-reply correspondence but does not contain any other such set. Inclusion relations are given between these faces and variants of existing set-valued solution concepts, which are defined either with reference to or with reference to the standard best response correspondence.
Leslie et al. [215] consider two player, zero-sum, discounted payoff, stochastic games, in which in every period there is a state of nature (from some finite set) that determines available actions and payoffs. The actions chosen by the players affect the probability of the state of nature in the subsequent period. A stationary strategy specifies a mixture over actions for each state of nature. From such a game, an auxiliary game can be derived for each state of nature (Shapley [328]). In the auxiliary game, continuation payoffs from each state of nature in the future are assumed to be fixed. Of course, when the players optimize, these continuation payoffs are consistent with optimization in every auxiliary game. Leslie et al. [215] define a continuous time best response dynamic for such games. Under this dynamic, the state space comprises both stationary strategies and the continuation values according to which best responses are calculated. Strategies evolve according to a best response dynamic according to the payoffs in the auxiliary game, taking continuation values as given. Continuation values evolve by moving closer to the expected discounted payoffs that players believe they will obtain by best responding in the auxiliary game. The dynamic is designed so that continuation values adjust at a slower rate than strategies. It is shown that, under this dynamic, strategies converge to the set of stationary optimal strategies of the game, and that both continuation payoffs and expected discounted payoffs converge to the same value, which is consistent with the strategies.
A finite game is weakly acyclic (Young [361]) if, from any strategy profile, there exists a path to a Nash equilibrium on which, at each step of the path, the strategy of only one player is altered and this player gains payoff as a consequence. Young [361] showed that, when a game is weakly acyclic and each position in the game is occupied by one player, we can expect play to converge to Nash equilibrium under best response dynamics, provided that strategy updating by players is not so predictable that absorbing cycles exist. Arieli and Young [24] show that similar convergence can be expected when each position in the game is occupied by a finite population, the players of which update their strategies using pairwise comparison dynamics (i.e., better response). However, the time until such convergence occurs can grow exponentially with population size. The reason for this is that in order to leverage the weak acyclicity assumption, a sufficient amount of homogeneity in the play of at least some of the populations is required, and it may take a long time for this to occur. To achieve this homogeneity faster, it is assumed that for any strategy pair corresponding to a position in the game, the ability of any member of the corresponding population to switch from i to j is controlled by a state variable , which switches on and off at random. This induces sufficient homogeneity that, starting from any state, the process will be, on average, close to Nash equilibrium over a long enough time period, no matter how large the population is. See Section 8.4 for further examples of the use of state variables to achieve desirable outcomes. Also see Hurkens [176] for results on convergence under best response dynamics to sets of strategies that are closed under rational behavior (Basu and Weibull [33]).
Babichenko [29], building on Babichenko [30], considers aggregative games. The games are aggregative in that the payoff of a player only depends on his own strategy and an aggregate statistic based on the strategies of all of the players. A common example is Cournot oligopoly, in which a player’s strategy is a production quantity and aggregate production determines the price (see Section 4.2.5 for results on conventional behavior in such settings). A best react function differs from a best response in that it does not take into account the effect of a player’s strategy on the aggregate statistic. However, if this effect is small, the best react function can approximate the best response function (Alos-Ferrer and Ania [10]). Babichenko [29] considers a dynamic whereby players best react to an approximation to the aggregate statistic x given by the highest integer multiple of small that is lower than x. This makes the best react correspondence constant on small intervals of the aggregate statistic, which is then used to show that the dynamic converges to an approximate Nash equilibrium in a number of steps of order at most , where n is the number of players and is assumed to be large.
Bednarik and Hofbauer [34] consider a rock, paper, scissors game with a Nash equilibrium that corresponds to population shares e that are globally asymptotically stable under the continuous best response dynamic. They show that, when the dynamic is discretized so that a proportion of the population adjusts their strategies at every time step of length , then the formerly asymptotically stable state becomes a repeller and cyclic behavior within an attracting region becomes stable. To see why this is so, consider a state x that is close to e, but has a slightly lower proportion of players playing rock and a slightly higher proportion of players playing paper. The best response to x is then to play scissors, and when a proportion of the population best respond to x, this will lead to a state that is further from e than x is from e. This may be related to experimental evidence on non-convergence in rock-paper-scissors games, discussed in Section 9.1.
In two strategy symmetric games, a best response strategy will also be favored by the replicator dynamic, giving identical basins of attraction under the best response dynamic and the replicator dynamic. Golman and Page [139] (see also erratum) show that there exist three strategy games with arbitrarily small overlap between basins of attraction. For example, the basin of attraction of strategy i under the best response dynamic can include of the state space, while the basin of attraction of strategy j under the replicator dynamic also includes of the state space. A parameterized sequence of such games is given in which as the parameter becomes large.
Open Topic 8.There is broad scope to develop dynamics that incorporate multiple agency (Section 2) for continuum populations. Such models will answer questions such as: (i) What are sensible ways to model multiple agency (e.g., coalitional updating) in an environment in which interaction is driven by random matching? (ii) When will the presence of multiple agency give different results to individualistic models and when will it make no difference?
7.5. Continuous Strategy Sets
Several recent papers have considered dynamics on games with continuous strategy sets. In the case where the population is a continuum, the population state is then a probability measure over the strategy set. Typically, these papers show existence of a solution trajectory under some continuity assumptions on the payoffs and the dynamic, then show convergence results for some classes of games. Cheung [86] considers pairwise comparison dynamics (i.e., better response), by which any given player considers some alternative strategy (chosen from an exogenous distribution) to her current strategy, and may switch if the alternative strategy gives a greater payoff. Convergence results are proven for potential games and negative semi-definite (i.e., contractive) games. Cheung [87] considers imitative dynamics such as the replicator dynamic, in which the alternative strategies that may be imitated are determined by the state. Specifically, the distribution over alternatives that was exogenous for the pairwise comparison dynamic is set equal to the state. Convergence to restricted equilibria, Nash equilibria of the game after some subset of strategies is removed, is shown for potential games. These two papers consider weak convergence of measures, as it seems reasonable that states in which every member of the population plays a strategy that is close to strategy x (under some metric that makes sense given the model), can be thought of as close to the state at which every member of the population plays strategy x.
Lahkar and Riedel [207] consider the logit dynamic, referring to a fixed point of this dynamic as a logit equilibrium. As logit choice is stochastic, these equilibria are diffuse (non-atomic), so strong convergence of measures is not too strong a convergence concept. Results on convergence to logit equilibria are shown for potential games and negative semi-definite (i.e., contractive) games. Perkins and Leslie [280] consider a model of stochastic fictitious play in which players play according to the logit choice rule after forming their beliefs according to a fictitious play rule (see, e.g., Benaïm and Hirsch [37], Benaım and Hirsch [38], Brown [74], Fudenberg and Kreps [130], Kaniovski and Young [192]). Convergence of such a process to the logit dynamic is shown and a convergence result given for negative definite games. The paper also considers the case where measures on the strategy space represent mixed strategies rather than population states. In this case, they show convergence to logit equilibria under stochastic fictitious play for two player zero-sum games with continuous action sets.
Newton [266] considers stochastic stability (see Section 4.2.1) on general state spaces. Finite state space models of stochastic stability (Kandori et al. [191], Young [361]) dispensed with the requirement for the many regularity assumptions (compactness, continuity, bounded convergence) found in the prior literature (Freidlin and Wentzell [125], Kifer [194]). Newton [266] returns to infinite state spaces, but considers a finite set of orders of magnitude of transition probabilities. This allows a weakening of assumptions so that, for example, best response dynamics can be considered even when best response correspondences are discontinuous. Conditions are given under which the standard tools of stochastic stability can be used.
7.6. Completely Uncoupled Dynamics
A dynamic is uncoupled if the strategy choice of a player does not directly depend on the payoffs of the other players (see Hart and Mas-Colell [151]). Examples include best response dynamics, better response, and fictitious play. A dynamic is completely uncoupled if the strategy choice of a player does not depend on any information about the other players (see Foster and Young [124]). That is, when a player updates his strategy he does not take into account the payoffs or actions of other players, nor even the number of other players in the game. One agenda in this literature is to give simple dynamics that lead to convergence to Nash equilibria or approximate Nash equilibria. One example is regret testing (Foster and Young [124], Germano and Lugosi [137]) under which each player plays some current mixed strategy most of the time, but occasionally chooses a random action. Every so often, a player compares the average payoff from his strategy to his average payoffs from other actions and if the latter exceeds the former by some tolerance level , then he randomly chooses another strategy. A further example is trial and error learning (Pradelski and Young [282], Young [366]) in which a player’s proclivity to experiment with new actions is determined by a state variable, the player’s mood (see Section 8.4 for further discussion).
Another agenda is to describe possibility and impossibility results. That is, to answer the question of whether dynamics can achieve certain types of convergence. For example, there exist games for which there is no continuous adjustment dynamic—a class of dynamics based on better response, that converges to Nash equilibrium (see Section 8.6 of Hofbauer and Sigmund [168]), and even games for which no uncoupled dynamic converges to Nash equilibrium (see Hart and Mas-Colell [151]). Building on this and other work (e.g., Foster and Young [122], Hart and Mansour [149], Hart and Mas-Colell [150,152], Hart [153], Young [365]), Babichenko [28] gives bounds on what convergence is possible under completely uncoupled dynamics. Defining a completely uncoupled strategy mapping as a mapping from sets of possible actions to completely uncoupled learning rules, he shows that there is no completely uncoupled strategy mapping that leads to almost sure convergence of play to pure Nash equilibrium in every finite generic game that has a pure Nash equilibrium. However, if action sets are distinct, in that any two players’ action sets are disjoint, then such a strategy mapping exists. Moreover, if players are allowed to condition behavior on either their own identity (their index in the player set) or on the number of players in the game, then such a strategy mapping exists. If learning rules are restricted to have finite memory, then the negative results of the paper must continue to hold, whereas the positive results continue to hold if all possible payoffs can be encoded in finite memory.
Note that finding a Nash equilibrium is, in a sense, a hard problem, even without restricting search procedures to be uncoupled or completely uncoupled. In the terminology of computer science, NP problems are the class of problems whose answers can be verified in polynomial time. Daskalakis et al. [95] show that finding a (possibly mixed) Nash equilibrium belongs to a class of problems that they call PPAD-complete, a subset of NP problems. One distinguishing feature of PPAD is that a solution is known to exist for such problems. For example, it is known that a mixed strategy Nash equilibrium exists for finite games (Nash [247]). It is very likely that PPAD is not a subset of the class of problems that can be solved by an algorithm that runs in polynomial time (see discussion in Daskalakis et al. [95]).
8. General Methodology
8.1. Perturbed Dynamics and Stochastic Stability
8.1.1. Least Cost Transition Paths
Minimal cost spanning tree methods for finding stochastically stable states (see Young [363]) are conceptually simple and, given least cost transition paths between conventions, can be found in polynomial time using Edmonds’ algorithm (Chu and Liu [90], Edmonds [107]). Finding least cost transitions, however, can be tricky. Often the number of conventions remains the same as the size of a finite population increases, but the number of paths between conventions increases exponentially.
To find the cost of least cost transitions between conventions, Sandholm and Staudigl [304], building on Staudigl [337], show that, as a finite population grows large, transition costs can be approximated by solutions to continuous optimal control problems. They illustrate the method by analyzing stochastic stability under logit choice of three strategy coordination games that satisfy the marginal bandwagon property of (Kandori and Rob [190]), under which, for strategies , , we have that . That is, players of strategy i gain most from playing against strategy i compared to playing against another strategy k.
Hwang and Newton [177] consider two populations, members of which are matched to play coordination games with an arbitrary number of strategies and zero payoff off-diagonal, and who make decisions according to the logit choice rule. For large populations, the costs of escaping the basins of attraction of conventions are estimated by explicitly constructing bounding functions. See Section 6.4 for an application of these results to the relationship between bargaining solutions and stochastic stability in coordination games.
8.1.2. Cyclic Decomposition
Freidlin and Wentzell [125] (Chapter 6.6) show that there exists a cyclic decomposition of a perturbed adaptive dynamic. The underlying idea is simple and we illustrate using an example. Assume that the dynamic without perturbations converges to the set of conventions and that the costs of least cost transitions between these conventions are given by Figure 15. From each convention, consider the least cost transition to another convention, illustrated by directed edges between conventions in Figure 16, in which the edges are labeled with their associated cost. This decomposes the state space into cycles. The process will, in expectation, spend a long time within a cycle before it transits to another cycle.
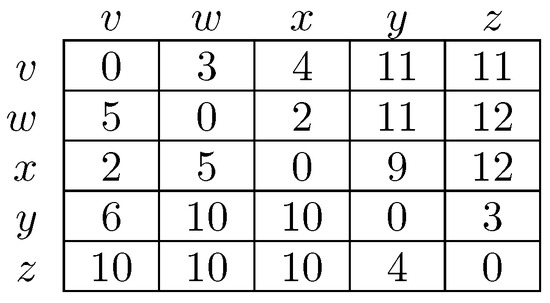
Figure 15.
Transition costs between conventions. For transitions between conventions in the set , the table gives the cost of a transition from the convention specified by the row to the convention specified by the column. For example, a transition from v to x has a cost of 4.
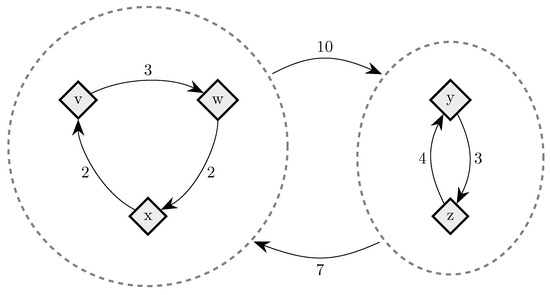
Figure 16.
Cyclic decomposition. The unperturbed dynamic converges to conventions in the set . A directed edge from a convention corresponds to a least cost transition from this convention as per Figure 15. This decomposes the set of conventions into two sets, and . Transition costs between these two sets are determined as described in the main text.
The cycles themselves can be treated as stable sets with associated transition costs. The transition cost from the set to is determined by finding the lowest cost tree on , rooted at , for some . The reader can check that this tree is which has a cost of 14. To find the cost of the transition from to we subtract from this cost the cost of the lowest cost tree on , which is rooted at v, which has a cost of 4. Hence the cost of the transition from to is 10, as illustrated in Figure 16. The cost of the transition from to can be similarly determined to be 7. Economists are likely to be familiar with such modified cost arguments via the finite state space exposition of Ellison [108], who gives corollaries of the hitting time results of Freidlin and Wentzell [125] and the finite state space stochastic stability characterization of Young [361].
The above shows that, for small perturbations, the process will spend much more time in than in , and within will spend much more time at convention v than at any other convention. The grouping of states into cycles, which in turn can be grouped together in metacycles and so on, gives an idea of the medium term behavior of the dynamic process. The cyclic decomposition has recently been described in a finite state space setup, first by Cui and Zhai [94] and then by Levine and Modica [216].
Finally, we note that Peski [281] uses Edmonds’ algorithm, which is closely related to the cyclic decomposition, to show that in symmetric, two strategy, two player coordination games played on any network under the best response dynamic with uniform errors, the convention at which every player plays the risk dominant strategy is stochastically stable, adding to existing results that the convention in the risk dominant strategy is uniquely stochastically stable on large enough complete networks (Kandori et al. [191], Young [361]), but may not be uniquely stochastically stable on some networks (Blume [60]). For completeness, consider the contrast of uniform errors with results for logit choice. Risk dominance is uniquely stochastically stable under asynchronous (only one player updates his strategy at a time) logit choice on any network. This is due to the fact that the game has a potential function and potential maximizers are stochastically stable under asynchronous logit (Blume [59]). Potential maximizing profiles need not be stochastically stable when synchronicity in strategy updating is possible (see Alós-Ferrer and Netzer [13], Marden and Shamma [224]).
8.1.3. Convergence Time
For a coordination game like Figure 4[ii] played on a network, Young [368] calls a set of players autonomous if, fixing the actions of all other players, potential is maximized when all of the players in the set play A. When this is the case, the hitting time for the process to reach a state in which all of these players play A can be bounded. If the entire network is decomposable into such sets of bounded size, then the convergence time for the whole network can be similarly bounded. Ideas of autonomy can also be used to find stochastically stable states in coordination games with heterogeneous preferences (Section 4.2.2) and to consider the relationship between the aggregation of incentives and the aggregation of agency (Section 2.4).
Norman [269] considers dynamics with a switching cost. For example, under best response, if the current strategy profile is s, player i may switch from to if and only if
where is the switching cost and corresponds to a standard best response dynamic. Consider a two player, two strategy coordination game with strategies , . A finite population has two conventions under the best response dynamic, each corresponding to one of the Nash equilibria in pure strategies. There is also a mixed Nash equilibrium of the game. For population states in which strategy shares approximate the probabilities under the mixed Nash equilibrium, individuals will be almost indifferent between and . Hence, if a switching cost is present, at such states, individuals playing either strategy will not choose to switch strategies. New conventions are created at these states due to the switching costs. These intermediate stable states will be visited by the process along transitions between the two preexisting conventions. By arguments found in Freidlin and Wentzell [125] and popularized in economics by Ellison [108], these intermediate conventions can speed the process of getting from one convention to another. For example, if, with , it takes 10 uniform errors to move between homogeneous conventions and, with , it takes 5 errors to move from a homogeneous to heterogeneous convention or vice versa, then the expected time to transit from one homogeneous convention to the other is of order when , and is of order when , as the sum of two quantities of order is also of order . This result on switching costs reducing waiting times generalizes, for which see the cited paper. Note that the potential conservative effect of coalitional behavior noted in Section 2.2.1 operates according to the same mechanism as this switching cost effect, but in the other direction, as some intermediate conventions cease to be conventions following the introduction of coalitional behavior.
Kreindler and Young [204,205] bound convergence time under the logit dynamic for coordination games (Figure 4ii) on a complete network and on any network respectively. Unlike the other papers on convergence time in this section, they deal with finite, non-vanishing amounts of noise and do not consider transitions between conventions, but give conditions under which there is a strictly positive expected per period increase in the number of players choosing A. This is a function of the error rate, the payoff and the network. For high enough error rate and high enough , they find a bound on expected waiting time that works for all networks.
8.1.4. Elimination of Weakly Dominated Strategies
Kuzmics [206] considers normal form games in which each position in the game corresponds to a finite population. A best response dynamic is considered, with an individual’s switching rate given by an increasing (from zero) function of the difference between the payoff from a best response and the payoff from his current strategy. The dynamic is perturbed by uniform errors. Error probabilities are taken to zero as population sizes approach infinity, with the product of error probability and population size approaching infinity. It is shown that, if the switching rate is insensitive to small payoff differences, then states at which a weakly dominated strategy is played may have positive probability under the limiting invariant measure. This is because the strategy profiles at which a weakly dominated strategy does worse than a strategy that dominates it may themselves become rare as . When this is the case, the payoff difference between the dominated and dominating strategies will be low, so that if the rate of switching to best responses is insensitive to small payoff differences, the flow of probability away from the weakly dominated strategy due to best responses may not always outweigh the flow of probability towards it due to errors. A similar dynamic is considered for continuum populations in Zusai [369], discussed in Section 7.4.
8.2. Further Stability Results
Ely and Sandholm [109] present a model in which players in a population have fixed types and the state of the dynamic is a Bayesian strategy that specifies a distribution over strategies for every type. The number of each type in the population, together with this strategy, then determines aggregate behavior. It is shown that, when the Bayesian strategies evolve under the best response dynamic, aggregate behavior can be described by a simplified best response dynamic that takes aggregate behavior as its state. The dynamic is aggregable. Zusai [370] studies nonaggregable dynamics. In particular, it is shown that the tempered best response dynamic (see Section 7.4) is nonaggregable: if payoff differences affect switching rates so that some types are evolving faster than others, then different Bayesian strategies that induce the same aggregate behavior may induce different aggregate trajectories. Several other common dynamics are likewise shown to be nonaggregable.
Heller [159] shows that, contrary to what was previously thought, the concept of limit evolutionarily stable strategy (limit ESS) of Selten [319] does not imply neutral stability. A limit ESS is a limit of ESSs of some sequence of perturbed games in which each strategy must be played with at least some nonnegative probability that approaches zero. This does not imply neutral stability as it may be that some strategy i is a limit ESS and that on the convergent sequences of perturbed games that make this so, strategy j does not outperform strategy i due to the small probability with which some strategy k is played. However, without the play of strategy k, it may be that i can be outperformed by an invading strategy j, contradicting neutral stability of i. Any ESS in a sequence of convergent ESS must, by definition, be robust to small invasions of other strategies. Heller [159] strengthens this requirement and defines uniform limit ESS by requiring the definition of small to remain the same along the sequence. Neutral stability is then implied in the limit by continuity.
Heller [161] analyzes the evolutionary stability of belief-free equilibria (Ely et al. [110]), a type of equilibrium of repeated games in which players do not observe the actions of their opponents but receive private signals which are correlated with those actions. A sequential equilibrium is belief-free if continuation strategies are optimal independently of beliefs about opponents’ histories of actions. Heller [161] shows that, if a belief-free equilibrium is evolutionarily stable, then it must be trivial, meaning that, independently of history, equilibrium strategies must specify that, each period, a Nash equilibrium of the stage game be played. If signals are informative, an equivalent result for neutral stability holds. In this case, a non-trivial belief-free equilibrium can be invaded by a mutant strategy that plays actions that are optimal per the specified continuation equilibrium, but uses information from the signals to induce correlation in actions so as to earn higher payoffs when playing against itself.
Van Veelen [347] considers indirect invasions, in which an incumbent strategy is invaded by a strategy that is neutral with respect to , following which another strategy invades and strictly outperform . Specifically, strategy is robust against indirect invasions (RAII) if there does not exist a sequence of mutations, , such that is neutrally unstable but not evolutionarily unstable against for , and is evolutionarily unstable against . Placing the concept within the inclusion hierarchy of existing concepts, any evolutionarily stable strategy is RAII, any RAII strategy is neutrally stable, and any neutrally stable strategy is a Nash equilibrium. Moreover, equivalence classes of strategies that are reachable from one another via sequences of neutral mutations are shown to be the same as minimal evolutionarily stable sets of strategies under the definitions of Thomas [341] and Balkenborg and Schlag [31].
Building on previous work (Bendor and Swistak [40], Boyd and Lorberbaum [72], Farrell and Ware [116], Selten and Hammerstein [318]) that has shown the non-existence of evolutionarily stable strategies in repeated games (due to mutations off the equilibrium path) and the existence of neutrally stable strategies in such games, García and van Veelen [136] consider strategies that are robust against indirect invasions as per Van Veelen [347] (discussed above). For any two player repeated game, they show that any incumbent repeated game strategy s can be neutrally invaded by a strategy that differs from s only in that its behavior after some time t no longer depends on the opponent’s action at time t. That is, making a connection to Section 3, assortativity between future action sequences played between types is unaffected by actions at time t. Consequently, (i) if profile does not lead to a Nash equilibrium of the stage game being played at t, then can be invaded by some strategy that maximizes its stage game payoff at t. Furthermore; (ii) if does not lead to efficient play at t amongst symmetric feasible action profiles, then can be invaded by some strategy that uses actions at t as a signal to induce assortativity, in that, in subsequent periods, plays efficiently when playing against and as s when playing against . The reader may recognize arguments (i) and (ii) as almost perfect parallels of the arguments supporting Nash behavior and efficient behavior in Newton [268] as discussed in Section 3.2.1. Argument (ii) is a secret handshake argument (Robson [288]), the connections to assortativity of which were remarked at the end of Section 4.1.4.
8.3. Further Convergence Results
Oyarzun and Ruf [278] consider stochastic processes in which the object of interest is a variable that takes values from zero to one, for example the rate of adoption of some technology, or the probability of choosing an optimal action in a decision problem. Sufficient conditions are given for to converge to one with high probability as . Firstly, the expected relative hazard rate, (Young [367]), is bounded below so that is a submartingale (see, e.g., Williams [354]). Secondly, the difference between successive values of is required to be sufficiently small. This convergence result is applied to the individual learning model of Börgers et al. [66]. It is further shown that if the difference between successive values of diminishes over time at an appropriate rate, convergence obtains almost surely. This result is applied to a variant of the imitative dynamic of Schlag [316] and to the reinforcement learning model of Erev and Roth [111] (see Section 7.1).
8.4. Distributed control
Rather than ask what the implications of evolutionary dynamics are for games, the literature on distributed control asks how a decentralized system can be designed to achieve some goal (Marden and Shamma [223]). It may be impossible for components (agents) within a system to communicate with some centralized decision maker, or even with each other, so it may be necessary to instead focus on the optimal design of agents’ decision rules so as to best achieve the goals of a planner. For example, swarm robotics (see, e.g., Brambilla et al. [73], Nemitz et al. [258]) aims to accomplish complex global tasks through the interactions of large groups of autonomous agents. Quijano et al. [284] discuss how distributed control can be used in urban planning to create smart cities, giving as examples the design of lighting systems, efficient power generation by microgrids and the control of drainage systems. The literature is particularly concerned with concerns of efficiency, computational complexity (difficulty of computations) and time complexity (number of iterations required for convergence).
From an efficiency perspective, it may not always be possible to design a system that achieves the optimal outcome. The price of anarchy is a measure of efficiency defined to equal the ratio of the optimal value of a goal function to the worst possible equilibrium outcome. For games of resource allocation amongst agents, recent results on the price of anarchy under Nash equilibrium and under a form of correlated equilibrium are found in Marden and Roughgarden [222] and Roughgarden [294] respectively.
One question that can be asked is whether payoffs for agents can be chosen to give a potential game structure, thus ensuring convergence under a variety of common dynamics. Again in the context of resource allocation, one possibility is for the marginal utility of a resource to an agent to be set equal to the marginal increase in the goal function, taking as given the other agents that hold the resource. Another alternative that also generates a potential game is to use a weighted Shapley value (Marden and Wierman [225]).
Regarding computational complexity, work has been done to reduce the complexity of dynamics that are known to have nice convergence properties. For example, Marden et al. [226] give a version of fictitious play in which a player, rather than considering the historical distribution of play by each of his opponents separately, instead assesses the effectiveness of actions against entire action profiles (excluding his own action) played in past periods, effectively assuming correlation in opponents’ play. In finite potential games, this dynamic is shown to converge almost surely to a pure Nash equilibrium.
Additional state variables can be added to a dynamic for the explicit purpose of obtaining desirable properties related to efficiency, complexity or convergence. Building on work of Young [366] that gives convergence to Nash equilibrium, Pradelski and Young [282] give dynamics in which an agent’s mood affects his likelihood of experimentation, and the dynamic converges to an efficient (in terms of sums of utilities) Nash equilibrium with arbitrarily high probability. Marden et al. [227] do similarly, but for efficient strategy profiles rather than just Nash equilibria. Similar use of an additional state variable is found in the use of ‘market sentiment’ in Pradelski [283], which was discussed in Section 6.2. Marden [228] extends the idea of potential to incorporate such a state variable, defining a potential function on action profiles and the state variable so that (i) fixing the value of the state variable, is a standard potential function on action profiles, and (ii) as long as the action profile remains the same, increases as the state evolves.
Open Topic 9.
Distributed control is an area in which the methods discussed in Section 2 could be especially fruitful, especially as there is no prejudice as to what may constitute an agent. Indeed, Marden and Shamma [223] note that “There is some flexibility in defining what constitutes a single player. For example in wind energy harvesting, a player could be a single turbine or a group of turbines.” Consequently, we can imagine systems in which both the wind turbine and the group of turbines exhibit agency in a complementary manner.
8.5. Software and Simulations
Izquierdo et al. [183] introduce “ABED: Agent-Based Simulation of Evolutionary Game Dynamics”, open source software that, for one and two population models, can simulate many of the dynamic processes covered in this survey (see Section 4.2 and Section 7), including imitative dynamics, dynamics based on sampling, and dynamics based on best responses. It offers options to adjust the underlying game, the size of the populations, the decision rule, the likelihood of perturbations, and the frequency and synchronicity of updating. Visual outputs track the proportions with which each strategy is played in the populations and the expected payoffs of each strategy.
Angus and Newton [22] make MatLab® code (GNU Octave Version 3.4.0 and Gnuplot 4.2.5, Massachusetts Institute of Technology, Cambridge, MA, USA) and documentation publically available for simulating games on networks under coalitional better response dynamics. The full model is a multi-generational group selection model of the evolution of the ability to participate in collective agency (discussed in Section 2.3), but the subroutines that deal with coalitional updating on networks within a single generation build on code written for Newton and Angus [259], which was published without simulations as Newton and Angus [260].
9. Empirics
It can be asked whether the type of models surveyed in the current paper are a good fit for observed behavior. “If players play game X under a best response dynamic, then they will converge to convention y” is the type of theorem that we find in these models. If a researcher attempts to replicate this implication empirically and convergence to y is not obtained, then it must be either that game X was not being played or that players did not follow a best response dynamic. Both of these things may be affected by all kinds of extraneous factors that are not in the original model. Consider Figure 17. The shaded inputs are sufficient for a player to follow a best response dynamic. The remaining inputs are then unnecessary. If a player does indeed follow a best response dynamic, his behavior will be the same whether or not he knows the payoffs of his opponents, in the same sense that if Newton’s apple were to suddenly become aware of the laws of motion, this would not affect its acceleration towards the ground. However, it may be that knowledge of his opponents’ payoffs does indeed affect a player’s choices, creating a situation in which the theoretical model does not apply. The knowledge is not part of the model, but is part of the situational context. The importance of extraneous context is something about which the theoretical models have little to say, but about which much can be learned from empirical studies.
Figure 17.
Information and context in an experiment. If only the shaded elements pertain, this is sufficient to make it possible that players follow an individualistic best response dynamic. However, all of the elements are compatible with players following such a dynamic, so there is nothing wrong with including any of them in a situational context that is being explored. Some of the elements, such as telling subjects individual best responses, might be expected to work towards inducing such a dynamic, whereas others, such as allowing subjects to talk, might be expected to work against it and in favor of some other dynamic such as coalitional best response.
Another point to consider is that distinct behavioral dynamics may differ from one another only when they are not at rest. A given state y may be a rest point under multiple dynamics which exhibit different speeds and trajectories when not at rest. It may be that players play game X and convergence to y occurs, but that we do not observe the intervening periods during which convergence occurs and, consequently, are left with multiple plausible candidates for the exact dynamic, although dynamics for which y is not a rest point can be ruled out. Furthermore, different dynamics can have very different basins of attraction corresponding to any given rest point (see, e.g., Golman and Page [139], discussed in Section 7.4), so without knowing the process, it will not be possible to infer the stability properties of the observed rest point. From an empirical perspective, this shows that it is important to observe systems that are not at rest in order to distinguish between different dynamics.
9.1. Best and Better Response
Oprea et al. [274] have subjects play a hawk-dove game in continuous time, earning flow payoffs based on the current strategy profile. Both one population and two population treatments are carried out. In the one population treatment, play converges to close to the mixed Nash equilibrium proportions. In the two population treatment, play converges to an equilibrium in which one population plays Hawk and the other plays Dove. Both of these results are in accordance with the predictions of several theoretical dynamics (best response, replicator etc.). Subjects are shown information on their own strategy and payoffs and the average strategy and payoffs of their opponents. Note that the actual payoffs in this experiment are given by the average payoff of the game played against all opponents. Payoffs in the standard theoretical models can indeed be interpreted in this way, but can also be interpreted as expected payoffs under random matching or, in continuum populations, as average realized payoffs under random matching. This emphasizes that the mapping of theory to experiment is not one to one.
Cason et al. [80] consider a similar setup to the paper above, but consider rock, paper, scissors games in both continuous and discrete time. Here we discuss the continuous case. Players choose mixed strategies from a heat map on a simplex that shows them which strategies offer the highest instantaneous payoffs. In one treatment a player moves instantly to the chosen strategy, in another treatment his strategy moves continuously towards his chosen ‘target’. Cyclic average behavior is observed. When the game payoffs are chosen so that the Nash equilibrium is stable (unstable) under the continuous best response dynamic, the amplitude of cycles is observed to decrease (increase) over time, but not as much as it would under the theoretical dynamic. In particular, in the stable case, average play (within a period) does not come to approximate the mixed strategy Nash equilibrium. This is perhaps related to the low population size of eight. In fact, the possibility of discretization in rock, paper, scissors games leading to stable cyclic behavior is suggested by the theoretical results of Bednarik and Hofbauer [34], discussed in Section 7.4.
Doraszelski et al. [105] considers the frequency response (FR) market, a market in which electricity providers are paid to adjust supply to maintain the frequency of oscillations of alternating current in the United Kingdom electric power grid within a band of 50 Hertz. A learning model is fitted to the data that has two components. (i) Suppliers of FR form beliefs about the prices offered by other suppliers through a fictitious play dynamic that, similarly to Marden et al. [226] (see Section 8.4), assumes correlation in the prices offered by the other suppliers. This dynamic is discounted so that recent periods are weighted more heavily. (ii) Suppliers learn about the model of demand for FR through adaptive learning, estimating demand as an econometrician might (Evans and Honkapohja [113]). They find that, following an initial period of disorder after the market was created, there was a period in which their model considerably outperforms equilibrium predictions. However, this outperformance does not persist into the final part of their dataset, which they interpret as indicating that suppliers had by then become more adept at rapidly adjusting to changing market conditions.
Following in the footsteps of Young and Burke [360], who use evolutionary methods to study crop sharing norms, Koch and Nax [202] study groundwater usage by farmers in the Upper Big Blue district of Nebraska in the United States of America. The model, one of common resource usage (see also Sethi and Somanathan [322]), is a stochastic game, with the state variable being the amount of groundwater at the start of a farming season. The solution concept used for the game as a whole is Markov perfect equilibrium, but holding fixed continuation values in auxiliary games for possible future groundwater states, equilibrium behavior in the current period is justified by the convergence of a better-reply (i.e., better response) dynamic (Dindoš and Mezzetti [103], Friedman and Mezzetti [127]). This is similar to the convergence of strategies, taking continuation values as given, shown by Leslie et al. [215] (discussed in Section 7.4), who also show convergence of continuation values under a best response dynamic designed specifically for stochastic games. Koch and Nax [202] find that, contrary to their model’s predictions, there is no empirical support for strategic substitutability in grou ndwater usage. To the contrary, low groundwater usage by farmers seems to induce low usage by other farmers.
9.2. Imitation
Friedman et al. [128] consider a Cournot oligopoly game (two and three player treatments). Subjects observe the actions taken and payoffs gained by themselves and their opponents in the previous period. Unlike previous experimental studies (e.g., Huck et al. [174]) that have confirmed predictions that Walrasian equilibrium will arise (see discussion in Section 4.2.5 above), they find that, after initial increases in production move play towards the Walrasian outcome, production decreases, eventually reaching levels close to collusive profit maximizing outcomes as players mimic reductions in production by their opponents. One way of interpreting this behavior is that players create a new agent, coming to adopt a new heuristic that communicates via play and improves the welfare of all (see Section 2, in particular Open Topic 2).
Clemm von Hohenberg et al. [91] study a model in which an individual has an opinion before he is subject to social influence. After he is subjected to social influence from a population with opinions distributed according to f, he has an opinion . The difference in opinion is modelled as being a linear function of the first four moments of f. The parameters in the model are linked to three theories of social influence, (i) the linear positive model in which players adjust their opinion towards average opinion, with the size of the adjustment linear in the distance they find themselves from the average; (ii) the moderated positive model in which individuals are less influenced by those with whom they have large differences of opinion; (iii) the negative influence model in which individuals are repelled by the opinions of those with whom they have large differences of opinion. The study asks participants for an opinion after reading an article and being shown a distribution of the opinions of others (or a simulacrum thereof). Data from the experiment fits model (i). Using the model to predict long run dynamics in large populations, they thus show that social influence will reduce variance in opinions. Shortly after data for the experiment were collected, the tool used to collect the data was changed so that users had to give an opinion before being shown the distribution of prior opinions. Data from after this change further supports the results of the study.
Mohlin et al. [238] consider data collected by Östling et al. [276] on the play of a lowest unique positive integer game in which, simultaneously, each player chooses a positive integer that is less than or equal to some maximum value K, and the player that chooses the lowest integer that has not been chosen by any other player wins. Mohlin et al. [238] find that a learning model they call similarity-weighted global cumulative imitation does a reasonable job of tracking the data. The model is essentially a reinforcement learning model (see Section 7.1) with two differences. Firstly, a player reinforces the weights he gives to strategies according to the outcomes of the strategies played by every player, not just the strategy he himself played. Secondly, strategies close to the winning integer, and not just the winning integer itself, are positively reinforced.
9.3. Completely Uncoupled Dynamics
Burton-Chellew et al. [76] considers three models of learning in public goods games. A particular goal of the paper is to explain declining payoffs when these games are played repeatedly over time. They consider three treatments, (i) a black box treatment in which participants are told that a black box into which they make their contribution will calculate the amount they get back according to a formula; (ii) a treatment in which participants knew they were playing a public goods game and were told the actions taken in the previous period by the other participants; and (iii) a similar treatment in which participants were also told the payoffs obtained by other participants. They test three hypotheses, (a) payoff-based (completely uncoupled—see Section 7.6) learning in which a previous increase in payoff following an increase (decrease) in contribution leads to an increase (decrease) in contribution (and vice versa for decreases in payoffs); (b) payoff-based learning under an assumption that players have altruistic concerns for the payoffs of other players; and (c) payoff-based learning plus a conditional cooperation motive that leads to an increase in contribution if other participants have increased their contributions. The evidence of the study strongly supports hypothesis (i) but not the other hypotheses, and in fact finds evidence of spite rather than altruism.
Nax et al. [254] also look at payoff-based learning in public goods games and test five specific behaviors, (i) asymmetric inertia; (ii) asymmetric volatility; (iii) asymmetric breadth, under which after a decrease (increase) in payoffs players respectively exhibit lower (higher) inertia in action choice, higher (lower) volatility in action choice, and larger (smaller) changes in their choice of action; (iv) reversion, under which a change in action that leads to a decrease (increase) in payoff is reversed (retained); and (v) directional bias, in which if there is a salient ordering on the actions, a player who has changed their action and seen a payoff increase (decrease) will change it again in the same direction (change it in the opposite direction). Evidence for all five of these features is found at a statistically significant level, regardless of whether (a) a pure black box approach is adopted or (b) players have some idea of the structure of the game.
9.4. Errors in Perturbed Dynamics
Mäs and Nax [229] study non-best response behavior (i.e., errors) in learning models. They look at two strategy coordination games on networks in which each player has a favorite strategy and the payoff of a player is the number of his neighbors who take the same strategy as he does, plus a bonus payoff if he plays his favorite strategy. Most choices (approx. 96%) are best responses to the strategies of the previous period. Errors (i) exhibit payoff-dependence, decreasing in frequency as conjectured payoff loss relative to playing a best response increases; (ii) occur with higher probability if the player changed strategy in the previous period; (iii) occur with higher probability if the players experienced a decrease in payoff in the previous period; and (iv) exhibit intentional bias (see Section 4.2.1), in that players are more likely to make an error when their best response is not their favorite strategy. Lim and Neary [219] conduct a similar experimental study, but consider the language game of Neary [257] (see Section 4.2.2) played in a population. The study also finds evidence of payoff-dependence and intentional bias in error probabilities.
Hwang et al. [179] consider two populations, players from which are matched to play a two player coordination game with zero payoffs off-diagonal (see Section 6.4). In experimental treatments in which each player in the game has five strategies, high levels of best response play (approx. 90%) are observed, as well as payoff-dependence and intentional bias in errors. As the game has five strategies instead of the two strategies in the previous studies, it is possible to understand intentional bias in the stronger sense that, for a given best response, errors that involve playing strategies associated with more preferred conventions (from the perspective of the error-making player) are more likely than errors playing strategies associated with less preferred conventions. In a two strategy model this cannot be observed, as for a given best response, there is only one strategy that can be played in error.
Open Topic 10.
There is much work to be done on evolution and empirics.
- (a)
- That the behavior of subjects in context X is approximated by dynamic Y may be non-generic in the sense that small changes to X may lead to the connection being broken. This is one reason, beyond the usual reasons, that replication is important, as any replication will never replicate X exactly (e.g., the weather outside the laboratory will be different). An important question is then the size of the set of contexts containing X that can be approximated by Y. This can be examined by including or excluding elements such as those of Figure 17. Resources permitting, for any positive results (i.e., mapping), X can be adjusted until the mapping fails.
- (b)
- Further study of separate attributes and features of decision rules, as discussed in several papers in Section 9.3 and Section 9.4, could be promising. In particular, the cues and information that influence each feature could be studied.
- (c)
- There is much real world time series data that could be considered using evolutionary models.
- (d)
- Theories of the evolution of traits, including preferences, should be tested, as suggested in Open Topic 5.
10. Conclusions
We began this survey by summarizing models of behavior as providing answers to the question who does what to whom and in what circumstances? We have seen how evolutionary game theory can be used to study and propose answers to every part of this question. Moreover, the models that arise are rich, deep and plausible, demonstrating how interaction can be complex even when decision making is not. As the survey has progressed, themes have arisen that bind together seemingly different topics. For example, assortativity has shown itself to be relevant to a broad range of subject matter. In particular, we have seen how every noncooperative way of inducing cooperation in prisoner’s dilemmas, from tit-for-tat, through secret handshakes and parochial mutant invaders, to the most arcane strategies in repeated games, all amount to inducing assortativity in the strategies that are played against one another. Another theme has been the importance of length-based and steepness-based selection in perturbed dynamics. These effects sometimes operate in isolation and sometimes interact. How they interact depends on properties of the stochastic perturbations, a fact that motivates the empirical challenge of discovering which kind of perturbations are observed in which contexts.
We conclude by mentioning some areas that the author believes warrant special attention over the coming years. Firstly, there is still much work to be done to integrate and deepen our understanding of the role of agency in evolutionary game theory (see Open Topics 1, 2, 8, 9). Work to date has only scratched the surface of understanding the role of the ‘who’ that is a fundamental part of our behavioral question. Secondly, evolutionary methods should establish themselves more firmly in applied social science. For example, there is no reason that simple evolutionary theories cannot play a significant role in the study of industrial organization. There is a need for someone to do for evolution and industrial organization what Spiegler [334] has done for bounded rationality and industrial organization. Thirdly, there should be more rigorous empirical research that gradually and carefully increases our understanding of evolution and adaptive decision making in practice (see Open Topics 5 and 10). We need to know under what conditions certain models should be used and under what conditions they should be avoided.
The author hopes that the reader has found this survey as stimulating to read as it was to write and that it strengthens the shared intention of researchers in the field that the field grow and flourish.
Funding
This research received no external funding.
Acknowledgments
For support and advice, I thank Ennio Bilancini, Leonardo Boncinelli, Samuel Bowles, Jean-Paul Carvalho, Man-Wah Cheung, Yuval Heller, Luis Izquierdo, Segis Izquierdo, Ratul Lahkar, Eduardo Gallo, Sung-Ha Hwang, Erik Mohlin, Heinrich Nax, Thomas Norman, Bary Pradelski, Alexandros Rigos, Klaus Ritzberger, Larry Samuelson, Ryoji Sawa, Rajiv Sethi, William Sandholm, Fei Shi, Matthias Staudigl, Jörgen Weibull, Zibo Xu, Peyton Young, Jiabin Wu, Dai Zusai.
Conflicts of Interest
The author declares no conflict of interest.
References
- Abbot, P.; Abe, J.; Alcock, J.; Alizon, S.; Alpedrinha, J.A.; Andersson, M.; Andre, J.B.; Van Baalen, M.; Balloux, F.; Balshine, S.; et al. Inclusive fitness theory and eusociality. Nature 2011, 471, E1. [Google Scholar] [CrossRef] [PubMed]
- Agastya, M. Adaptive Play in Multiplayer Bargaining Situations. Rev. Econ. Stud. 1997, 64, 411–426. [Google Scholar] [CrossRef]
- Agastya, M. Perturbed Adaptive Dynamics in Coalition Form Games. J. Econ. Theory 1999, 89, 207–233. [Google Scholar] [CrossRef]
- Alexander, J.; Skyrms, B. Bargaining with Neighbors: Is Justice Contagious? J. Philos. 1999, 96, 588–598. [Google Scholar] [CrossRef]
- Alger, I.; Weibull, J.W. Kinship, incentives, and evolution. Am. Econ. Rev. 2010, 100, 1725–1758. [Google Scholar] [CrossRef]
- Alger, I.; Weibull, J.W. A generalization of Hamilton’s rule—Love others how much? J. Theor. Biol. 2012, 299, 42–54. [Google Scholar] [CrossRef] [PubMed]
- Alger, I.; Weibull, J.W. Homo Moralis–Preference Evolution Under Incomplete Information and Assortative Matching. Econometrica 2013, 81, 2269–2302. [Google Scholar]
- Alger, I.; Weibull, J.W. Evolution and Kantian morality. Games Econ. Behav. 2016, 98, 56–67. [Google Scholar] [CrossRef]
- Alós-Ferrer, C.; Ania, A.B. The asset market game. J. Math. Econ. 2005, 41, 67–90. [Google Scholar] [CrossRef]
- Alos-Ferrer, C.; Ania, A.B. The evolutionary stability of perfectly competitive behavior. Econ. Theory 2005, 26, 497–516. [Google Scholar] [CrossRef]
- Alós-Ferrer, C.; Buckenmaier, J. Trader matching and the selection of market institutions. J. Math. Econ. 2017, 69, 118–127. [Google Scholar] [CrossRef]
- Alós-Ferrer, C.; Kirchsteiger, G. General equilibrium and the emergence of (non) market clearing trading institutions. Econ. Theory 2010, 44, 339–360. [Google Scholar] [CrossRef]
- Alós-Ferrer, C.; Netzer, N. The logit-response dynamics. Games Econ. Behav. 2010, 68, 413–427. [Google Scholar] [CrossRef]
- Alós-Ferrer, C.; Shi, F. Imitation with asymmetric memory. Econ. Theory 2012, 49, 193–215. [Google Scholar] [CrossRef]
- Alós-Ferrer, C.; Weidenholzer, S. Imitation and the role of information in overcoming coordination failures. Games Econ. Behav. 2014, 87, 397–411. [Google Scholar] [CrossRef]
- Alós-Ferrer, C.; Ania, A.; Vega-Redondo, F. An evolutionary model of market structure. In The Theory of Markets; van der Laan, G., Herings, P., Talman, A., Eds.; Number 177 in KNAW Series; North Holland: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Alós-Ferrer, C.; Ania, A.B.; Schenk-Hoppé, K.R. An evolutionary model of Bertrand oligopoly. Games Econ. Behav. 2000, 33, 1–19. [Google Scholar] [CrossRef]
- Alós-Ferrer, C.; Kirchsteiger, G.; Walzl, M. On the evolution of market institutions: The platform design paradox. Econ. J. 2010, 120, 215–243. [Google Scholar] [CrossRef]
- Alós-Ferrer, C. Cournot versus Walras in dynamic oligopolies with memory. Int. J. Ind. Organ. 2004, 22, 193–217. [Google Scholar] [CrossRef]
- Amir, R.; Evstigneev, I.V.; Hens, T.; Schenk-Hoppé, K.R. Market selection and survival of investment strategies. J. Math. Econ. 2005, 41, 105–122. [Google Scholar] [CrossRef]
- Angus, S.; Masson, V. The Effects of Information and Interactions on Contagion Processes; University of Adelaide: Adelaide, Australia, 2010. [Google Scholar]
- Angus, S.D.; Newton, J. Emergence of Shared Intentionality Is Coupled to the Advance of Cumulative Culture. PLOS Comput. Biol. 2015, 11, e1004587. [Google Scholar] [CrossRef] [PubMed]
- Argiento, R.; Pemantle, R.; Skyrms, B.; Volkov, S. Learning to signal: Analysis of a micro-level reinforcement model. Stoch. Process. Their Appl. 2009, 119, 373–390. [Google Scholar] [CrossRef]
- Arieli, I.; Young, H.P. Stochastic learning dynamics and speed of convergence in population games. Econometrica 2016, 84, 627–676. [Google Scholar] [CrossRef]
- Arnold, T.; Schwalbe, U. Dynamic coalition formation and the core. J. Econ. Behav. Organ. 2002, 49, 363–380. [Google Scholar] [CrossRef]
- Aumann, R. Acceptable Points in General Cooperative n-Person Games. In Contributions to the Theory of Games IV; Tucker, A.W., Luce, R.D., Eds.; Princeton University Press: Princeton, NJ, USA, 1959; pp. 287–324. [Google Scholar]
- Avrachenkov, K.; Singh, V.V. Stochastic coalitional better-response dynamics and stable equilibrium. Autom. Remote Control 2016, 77, 2227–2238. [Google Scholar] [CrossRef]
- Babichenko, Y. Completely uncoupled dynamics and Nash equilibria. Games Econ. Behav. 2012, 76, 1–14. [Google Scholar] [CrossRef]
- Babichenko, Y. Best-Reply Dynamic in Large Aggregative Games; Mimeo: New York, NY, USA, 2013. [Google Scholar]
- Babichenko, Y. Best-reply dynamics in large binary-choice anonymous games. Games Econ. Behav. 2013, 81, 130–144. [Google Scholar] [CrossRef]
- Balkenborg, D.; Schlag, K.H. Evolutionarily stable sets. Int. J. Game Theory 2001, 29, 571–595. [Google Scholar] [CrossRef]
- Balkenborg, D.; Hofbauer, J.; Kuzmics, C. Refined best reply correspondence and dynamics. Theor. Econ. 2013, 8, 165–192. [Google Scholar] [CrossRef]
- Basu, K.; Weibull, J.W. Strategy subsets closed under rational behavior. Econ. Lett. 1991, 36, 141–146. [Google Scholar] [CrossRef]
- Bednarik, P.; Hofbauer, J. Discretized best-response dynamics for the rock-paper-scissors game. J. Dyn. Games 2017, 4, 75–86. [Google Scholar] [CrossRef]
- Beggs, A.W. On the convergence of reinforcement learning. J. Econ. Theory 2005, 122, 1–36. [Google Scholar] [CrossRef]
- Belloc, M.; Bowles, S. The Persistence of Inferior Cultural-Institutional Conventions. Am. Econ. Rev. 2013, 103, 93–98. [Google Scholar] [CrossRef]
- Benaïm, M.; Hirsch, M.W. Stochastic approximation algorithms with constant step size whose average is cooperative. Ann. Appl. Probab. 1999, 216–241. [Google Scholar]
- Benaım, M.; Hirsch, M.W. Mixed equilibria and dynamical systems arising from fictitious play in perturbed games. Games Econ. Behav. 1999, 29, 36–72. [Google Scholar] [CrossRef]
- Benaïm, M.; Weibull, J.W. Deterministic approximation of stochastic evolution in games. Econometrica 2003, 71, 873–903. [Google Scholar] [CrossRef]
- Bendor, J.; Swistak, P. Types of evolutionary stability and the problem of cooperation. Proc. Natl. Acad. Sci. USA 1995, 92, 3596–3600. [Google Scholar] [CrossRef] [PubMed]
- Bergstrom, T.C. On the evolution of altruistic ethical rules for siblings. Am. Econ. Rev. 1995, 85, 58–81. [Google Scholar]
- Bergstrom, T.C. The algebra of assortative encounters and the evolution of cooperation. Int. Game Theory Rev. 2003, 5, 211–228. [Google Scholar] [CrossRef]
- Bilancini, E.; Boncinelli, L. The co-evolution of cooperation and defection under local interaction and endogenous network formation. J. Econ. Behav. Organ. 2009, 70, 186–195. [Google Scholar] [CrossRef]
- Bilancini, E.; Boncinelli, L. Social coordination with locally observable types. Econ. Theory 2015, 65, 975–1009. [Google Scholar] [CrossRef]
- Bilancini, E.; Boncinelli, L. The Evolution of Conventions under Condition-Dependent Mistakes; Working Paper; Universita’degli Studi di Firenze: Firenze, Italia, 2016. [Google Scholar]
- Bilancini, E.; Boncinelli, L.; Wu, J. The interplay of cultural intolerance and action-assortativity for the emergence of cooperation and homophily. Eur. Econ. Rev. 2018, 102, 1–18. [Google Scholar] [CrossRef]
- Binmore, K.; Samuelson, L. Drift. Eur. Econ. Rev. 1994, 38, 859–867. [Google Scholar] [CrossRef]
- Binmore, K.; Samuelson, L. Evolutionary drift and equilibrium selection. The Rev. Econ. Stud. 1999, 66, 363–393. [Google Scholar] [CrossRef]
- Binmore, K.G. Game Theory and the Social Contract: Just Playing; MIT Press: Cambridge, MA, USA, 1998; Volume 2. [Google Scholar]
- Binmore, K. Natural Justice; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Biró, P.; Bomhoff, M.; Golovach, P.A.; Kern, W.; Paulusma, D. Solutions for the Stable Roommates Problem with Payments. In Graph-Theoretic Concepts in Computer Science; Lecture Notes in Computer Science; Springer: Berlin, Germany, 2013; pp. 69–80. [Google Scholar]
- Bisin, A.; Verdier, T. The economics of cultural transmission and the dynamics of preferences. J. Econ. Theory 2001, 97, 298–319. [Google Scholar] [CrossRef]
- Blume, A.; Arnold, T. Learning to communicate in cheap-talk games. Games Econ. Behav. 2004, 46, 240–259. [Google Scholar] [CrossRef]
- Blume, L.; Easley, D. Evolution and market behavior. J. Econ. Theory 1992, 58, 9–40. [Google Scholar] [CrossRef]
- Blume, L.; Easley, D. If you’re so smart, why aren’t you rich? Belief selection in complete and incomplete markets. Econometrica 2006, 74, 929–966. [Google Scholar] [CrossRef]
- Blume, A.; Kim, Y.G.; Sobel, J. Evolutionary stability in games of communication. Games Econ. Behav. 1993, 5, 547–575. [Google Scholar] [CrossRef]
- Blume, A.; DeJong, D.V.; Kim, Y.G.; Sprinkle, G.B. Experimental evidence on the evolution of meaning of messages in sender-receiver games. Am. Econ. Rev. 1998, 88, 1323–1340. [Google Scholar]
- Blume, A.; DeJong, D.V.; Kim, Y.G.; Sprinkle, G.B. Evolution of communication with partial common interest. Games Econ. Behav. 2001, 37, 79–120. [Google Scholar] [CrossRef]
- Blume, L.E. The Statistical Mechanics of Strategic Interaction. Games Econ. Behav. 1993, 5, 387–424. [Google Scholar] [CrossRef]
- Blume, L.E. Population Games; Working Papers 96-04-022; Santa Fe Institute: Santa Fe, NM, USA, 1996. [Google Scholar]
- Blume, A. Communication, risk, and efficiency in games. Games Econ. Behav. 1998, 22, 171–202. [Google Scholar] [CrossRef]
- Bomze, I.M. Non-cooperative two-person games in biology: A classification. Int. J. Game Theory 1986, 15, 31–57. [Google Scholar] [CrossRef]
- Boncinelli, L.; Pin, P. Stochastic stability in best shot network games. Games Econ. Behav. 2012, 75, 538–554. [Google Scholar] [CrossRef]
- Boncinelli, L.; Pin, P. The stochastic stability of decentralized matching on a graph. Games Econ. Behav. 2017. [Google Scholar] [CrossRef]
- Börgers, T.; Sarin, R. Learning through reinforcement and replicator dynamics. J. Econ. Theory 1997, 77, 1–14. [Google Scholar] [CrossRef]
- Börgers, T.; Morales, A.J.; Sarin, R. Expedient and monotone learning rules. Econometrica 2004, 72, 383–405. [Google Scholar] [CrossRef]
- Bowles, S.; Gintis, H. A Cooperative Species: Human Reciprocity and Its Evolution; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Bowles, S. Microeconomics: Behavior, Institutions, and Evolution; Princeton University Press: Princeton, NJ, USA, 2004. [Google Scholar]
- Bowles, S. Is inequality a human universal. In The Social Economics of Poverty; Barrett, C.B., Ed.; Routledge: Abingdon, UK, 2005; pp. 125–145. [Google Scholar]
- Bowles, S. Group competition, reproductive leveling, and the evolution of human altruism. Science 2006, 314, 1569–1572. [Google Scholar] [CrossRef] [PubMed]
- Bowles, S. Institutional poverty traps. In Poverty Traps; Bowles, S., Durlauf, S.N., Hoff, K., Eds.; Princeton University Press: Princeton, NJ, USA, 2006; pp. 116–138. [Google Scholar]
- Boyd, R.; Lorberbaum, J.P. No pure strategy is evolutionarily stable in the repeated prisoner’s dilemma game. Nature 1987, 327, 58. [Google Scholar] [CrossRef]
- Brambilla, M.; Ferrante, E.; Birattari, M.; Dorigo, M. Swarm robotics: a review from the swarm engineering perspective. Swarm Intell. 2013, 7, 1–41. [Google Scholar] [CrossRef]
- Brown, G.W. Iterative solution of games by fictitious play. Act. Anal. Prod. Alloc. 1951, 13, 374–376. [Google Scholar]
- Burdett, K.; Judd, K.L. Equilibrium price dispersion. Econometrica 1983, 955–969. [Google Scholar] [CrossRef]
- Burton-Chellew, M.N.; Nax, H.H.; West, S.A. Payoff-based learning explains the decline in cooperation in public goods games. Proc. R. Soc. Lond. B Biol. Sci. 2015, 282, 20142678. [Google Scholar] [CrossRef] [PubMed]
- Cara, M.A.R.d.; Barton, N.H.; Kirkpatrick, M. A Model for the Evolution of Assortative Mating. Am. Nat. 2008, 171, 580–596. [Google Scholar] [CrossRef] [PubMed]
- Cárdenas, J.C.; Mantilla, C.; Sethi, R. Stable sampling equilibrium in common pool resource games. Games 2015, 6, 299–317. [Google Scholar] [CrossRef]
- Carvalho, J.P. Veiling. Q. J. Econ. 2012, 128, 337–370. [Google Scholar] [CrossRef]
- Cason, T.N.; Friedman, D.; Hopkins, E. Cycles and instability in a rock–paper–scissors population game: A continuous time experiment. Rev. Econ. Stud. 2013, 81, 112–136. [Google Scholar] [CrossRef]
- Cavalli-Sforza, L.L.; Feldman, M.W. Cultural Transmission and Evolution: A Quantitative Approach; Princeton University Press: Princeton, NJ, USA, 1981. [Google Scholar]
- Chakrabarti, A.S.; Lahkar, R. An Evolutionary Analysis of Growth and Fluctuations with Negative Externalities. Dyn. Games Appl. 2017. [Google Scholar] [CrossRef]
- Chakrabarti, A.S.; Lahkar, R. Productivity dispersion and output fluctuations: An evolutionary model. J. Econ. Behav. Organ. 2017, 137, 339–360. [Google Scholar] [CrossRef]
- Chen, B.; Fujishige, S.; Yang, Z. Random decentralized market processes for stable job matchings with competitive salaries. J. Econ. Theory 2016, 165, 25–36. [Google Scholar] [CrossRef]
- Cheung, M.W.; Wu, J. On the probabilistic transmission of continuous cultural traits. J. Econ. Theory 2018, 174, 300–323. [Google Scholar] [CrossRef]
- Cheung, M.W. Pairwise comparison dynamics for games with continuous strategy space. J. Econ. Theory 2014, 153, 344–375. [Google Scholar] [CrossRef]
- Cheung, M.W. Imitative dynamics for games with continuous strategy space. Games Econ. Behav. 2016, 99, 206–223. [Google Scholar] [CrossRef]
- Cho, I.K.; Kasa, K. Learning and model validation. Rev. Econ. Stud. 2014, 82, 45–82. [Google Scholar] [CrossRef]
- Choi, J.K.; Bowles, S. The coevolution of parochial altruism and war. Science 2007, 318, 636–640. [Google Scholar] [CrossRef] [PubMed]
- Chu, Y.J.; Liu, T.H. On the shortest arborescence of a directed graph. Sci. Sin. 1965, 14, 1396–1400. [Google Scholar]
- Clemm von Hohenberg, B.; Maes, M.; Pradelski, B.S. Micro Influence and Macro Dynamics of Opinions; SSRN Working Paper Series 2974413; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Cross, J.G. A stochastic learning model of economic behavior. Q. J. Econ. 1973, 87, 239–266. [Google Scholar] [CrossRef]
- Cui, Z.; Wang, R. Collaboration in networks with randomly chosen agents. J. Econ. Behav. Organ. 2016, 129, 129–141. [Google Scholar] [CrossRef]
- Cui, Z.; Zhai, J. Escape dynamics and equilibria selection by iterative cycle decomposition. J. Math. Econ. 2010, 46, 1015–1029. [Google Scholar] [CrossRef]
- Daskalakis, C.; Goldberg, P.W.; Papadimitriou, C.H. The complexity of computing a Nash equilibrium. SIAM J. Comput. 2009, 39, 195–259. [Google Scholar] [CrossRef]
- Dawid, H.; Hellmann, T. The evolution of R&D networks. J. Econ. Behav. Organ. 2014, 105, 158–172. [Google Scholar]
- De Borda, J.C. Mémoire sur les élections au scrutin. In Histoire de l’Academie Royale des Sciences pour 1781; Royal Society: London, UK, 1784. [Google Scholar]
- De Giorgi, E. Evolutionary portfolio selection with liquidity shocks. J. Econ. Dyn. Control 2008, 32, 1088–1119. [Google Scholar] [CrossRef]
- Dekel, E.; Ely, J.C.; Yilankaya, O. Evolution of preferences. Rev. Econ. Stud. 2007, 74, 685–704. [Google Scholar] [CrossRef]
- Demichelis, S.; Weibull, J.W. Language, meaning, and games: A model of communication, coordination, and evolution. Am. Econ. Rev. 2008, 98, 1292–1311. [Google Scholar] [CrossRef]
- Diamantoudi, E.; Xue, L.; Miyagawa, E. Random paths to stability in the roommate problem. Games Econ. Behav. 2004, 48, 18–28. [Google Scholar] [CrossRef]
- Dieckmann, U.; Doebeli, M. On the origin of species by sympatric speciation. Nature 1999, 400, 354–357. [Google Scholar] [CrossRef] [PubMed]
- Dindoš, M.; Mezzetti, C. Better-reply dynamics and global convergence to Nash equilibrium in aggregative games. Games Econ. Behav. 2006, 54, 261–292. [Google Scholar] [CrossRef]
- Dokumaci, E.; Sandholm, W.H. Large deviations and multinomial probit choice. J. Econ. Theory 2011, 146, 2151–2158. [Google Scholar] [CrossRef]
- Doraszelski, U.; Lewis, G.; Pakes, A. Just starting out: Learning and equilibrium in a new market. Am. Econ. Rev. 2018, 108, 565–615. [Google Scholar] [CrossRef]
- Duersch, P.; Oechssler, J.; Schipper, B.C. Unbeatable imitation. Games Econ. Behav. 2012, 76, 88–96. [Google Scholar] [CrossRef]
- Edmonds, J. Optimum branchings. J. Res. Natl. Bureau Stand. 1967, 71, 233–240. [Google Scholar] [CrossRef]
- Ellison, G. Basins of Attraction, Long-Run Stochastic Stability, and the Speed of Step-by-Step Evolution. Rev. Econ. Stud. 2000, 67, 17–45. [Google Scholar] [CrossRef]
- Ely, J.C.; Sandholm, W.H. Evolution in Bayesian games I: theory. Games Econ. Behav. 2005, 53, 83–109. [Google Scholar] [CrossRef]
- Ely, J.C.; Hörner, J.; Olszewski, W. Belief-free equilibria in repeated games. Econometrica 2005, 73, 377–415. [Google Scholar] [CrossRef]
- Erev, I.; Roth, A.E. Predicting how people play games: Reinforcement learning in experimental games with unique, mixed strategy equilibria. Am. Econ. Rev. 1998, 88, 848–881. [Google Scholar]
- Eshel, I.; Cavalli-Sforza, L.L. Assortment of encounters and evolution of cooperativeness. Proc. Natl. Acad. Sci. USA 1982, 79, 1331–1335. [Google Scholar] [CrossRef] [PubMed]
- Evans, G.W.; Honkapohja, S. Learning and Expectations in Macroeconomics; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Evstigneev, I.V.; Hens, T.; Schenk-Hoppé, K.R. Market Selection Of Financial Trading Strategies: Global Stability. Math. Financ. 2002, 12, 329–339. [Google Scholar] [CrossRef]
- Evstigneev, I.V.; Hens, T.; Schenk-Hoppé, K.R. Evolutionary stable stock markets. Econ. Theory 2006, 27, 449–468. [Google Scholar] [CrossRef]
- Farrell, J.; Ware, R. Evolutionary stability in the repeated Prisoner’s Dilemma. Theor. Popul. Biol. 1989, 36, 161–166. [Google Scholar] [CrossRef]
- Feldman, A.M. Recontracting Stability. Econometrica 1974, 42, 35–44. [Google Scholar] [CrossRef]
- Ferriere, R.; Michod, R.E. Inclusive fitness in evolution. Nature 2011, 471, E6. [Google Scholar] [CrossRef] [PubMed]
- Fisher, R.A. The Genetical Theory of Natural Selection, Variorum Edition (2000); Oxford University Press: Oxford, UK, 1930. [Google Scholar]
- Flåm, S.D.; Morgan, J. Newtonian mechanics and Nash play. Int. Game Theory Rev. 2004, 6, 181–194. [Google Scholar] [CrossRef]
- Foster, D.; Young, H.P. Stochastic Evolutionary Game Dynamics. Theor. Popul. Biol. 1990, 38, 219–232. [Google Scholar] [CrossRef]
- Foster, D.P.; Young, H.P. On the impossibility of predicting the behavior of rational agents. Proc. Natl. Acad. Sci. USA 2001, 98, 12848–12853. [Google Scholar] [CrossRef] [PubMed]
- Foster, D.P.; Young, H.P. Learning, hypothesis testing, and Nash equilibrium. Games Econ. Behav. 2003, 45, 73–96. [Google Scholar] [CrossRef]
- Foster, D.P.; Young, H.P. Regret testing: Learning to play Nash equilibrium without knowing you have an opponent. Theor. Econ. 2006, 1, 341–367. [Google Scholar]
- Freidlin, M.I.; Wentzell, A.D. Random Perturbations of Dynamical Systems, 2nd ed.; Springer: Berlin, Germany, 1984. [Google Scholar]
- Frenkel, S.; Heller, Y.; Teper, R. The Endowment Effect as blessing. Int. Econ. Rev. 2018. (online first). [Google Scholar] [CrossRef]
- Friedman, J.; Mezzetti, C. Learning in Games by Random Sampling. J. Econ. Theory 2001, 98, 55–84. [Google Scholar] [CrossRef]
- Friedman, D.; Huck, S.; Oprea, R.; Weidenholzer, S. From imitation to collusion: Long-run learning in a low-information environment. J. Econ. Theory 2015, 155, 185–205. [Google Scholar] [CrossRef]
- Friedman, D. Evolutionary games in economics. Econometrica 1991, 59, 637–666. [Google Scholar] [CrossRef]
- Fudenberg, D.; Kreps, D.M. Learning mixed equilibria. Games Econ. Behav. 1993, 5, 320–367. [Google Scholar] [CrossRef]
- Fudenberg, D.; Levine, D.K. Self-confirming equilibrium. Econometrica 1993, 61, 523–545. [Google Scholar] [CrossRef]
- Fujiwara-Greve, T.; Okuno-Fujiwara, M. Voluntarily separable repeated prisoner’s dilemma. Rev. Econ. Stud. 2009, 76, 993–1021. [Google Scholar] [CrossRef]
- Fujiwara-Greve, T.; Okuno-Fujiwara, M.; Suzuki, N. Voluntarily separable repeated Prisoner’s Dilemma with reference letters. Games Econ. Behav. 2012, 74, 504–516. [Google Scholar] [CrossRef]
- Gale, D.; Shapley, L.S. College Admissions and the Stability of Marriage. Am. Math. Mon. 1962, 69, 9–15. [Google Scholar] [CrossRef]
- Gamba, A. Learning and evolution of altruistic preferences in the Centipede Game. J. Econ. Behav. Organ. 2013, 85, 112–117. [Google Scholar] [CrossRef]
- García, J.; van Veelen, M. In and out of equilibrium I: Evolution of strategies in repeated games with discounting. J. Econ. Theory 2016, 161, 161–189. [Google Scholar] [CrossRef]
- Germano, F.; Lugosi, G. Global Nash convergence of Foster and Young’s regret testing. Games Econ. Behav. 2007, 60, 135–154. [Google Scholar] [CrossRef]
- Gilboa, I.; Matsui, A. Social stability and equilibrium. Econometrica 1991, 59, 859–867. [Google Scholar] [CrossRef]
- Golman, R.; Page, S.E. Basins of attraction and equilibrium selection under different learning rules. J. Evol. Econ. 2010, 20, 49–72. [Google Scholar] [CrossRef]
- Goyal, S.; Hernández, P.; Martínez-Cánovas, G.; Moisan, F.; Muñoz Herrera, M.; Sánchez, A. Integration and Segregation; CWPE Working Paper 1721; Faculty of Economics, University of Cambridge: Cambridge, UK, 2017. [Google Scholar]
- Granovetter, M. Threshold Models of Collective Behavior. Am. J. Sociol. 1978, 83, 1420–1443. [Google Scholar] [CrossRef]
- Green, J.R. The Stability of Edgeworth’s Recontracting Process. Econometrica 1974, 42, 21–34. [Google Scholar] [CrossRef]
- Güth, W.; Kliemt, H. The indirect evolutionary approach: Bridging the gap between rationality and adaptation. Ration. Soc. 1998, 10, 377–399. [Google Scholar] [CrossRef]
- Haldane, J.B.S. The Causes of Evolution; Princeton University Press: Princeton, NJ, USA, 1932. [Google Scholar]
- Hamilton, W.D. The evolution of altruistic behavior. Am. Nat. 1963, 97, 354–356. [Google Scholar] [CrossRef]
- Hamilton, W. The genetical evolution of social behaviour I. J. Theor. Biol. 1964, 7, 1–16. [Google Scholar] [CrossRef]
- Hamilton, W. The genetical evolution of social behaviour II. J. Theor. Biol. 1964, 7, 17–52. [Google Scholar] [CrossRef]
- Harsanyi, J.C. Games with Incomplete Information Played by “Bayesian” Players, I-III. Part I. The Basic Model. Manag. Sci. 1967, 14, 159–182. [Google Scholar] [CrossRef]
- Hart, S.; Mansour, Y. How long to equilibrium? The communication complexity of uncoupled equilibrium procedures. Games Econ. Behav. 2010, 69, 107–126. [Google Scholar] [CrossRef]
- Hart, S.; Mas-Colell, A. A simple adaptive procedure leading to correlated equilibrium. Econometrica 2000, 68, 1127–1150. [Google Scholar] [CrossRef]
- Hart, S.; Mas-Colell, A. Uncoupled dynamics do not lead to Nash equilibrium. Am. Econ. Rev. 2003, 93, 1830–1836. [Google Scholar] [CrossRef]
- Hart, S.; Mas-Colell, A. Stochastic uncoupled dynamics and Nash equilibrium. Games Econ. Behav. 2006, 57, 286–303. [Google Scholar] [CrossRef]
- Hart, S. Commentary: Nash equilibrium and dynamics. Games Econ. Behav. 2011, 71, 6–8. [Google Scholar] [CrossRef]
- Heifetz, A.; Shannon, C.; Spiegel, Y. What to maximize if you must. J. Econ. Theory 2007, 133, 31–57. [Google Scholar] [CrossRef]
- Heller, Y.; Mohlin, E. Coevolution of Deception and Preferences: Darwin and Nash Meet Machiavelli; Mimeo: New York, NY, USA, 2017. [Google Scholar]
- Heller, Y.; Mohlin, E. Observations on cooperation. Rev. Econ. Stud. 2017. Available online: http://www.restud.com/wp-content/uploads/2017/12/MS24086manuscript.pdf (accessed on 24 May 2018).
- Heller, Y. Overconfidence and diversification. Am. Econ. J. Microecon. 2014, 6, 134–153. [Google Scholar] [CrossRef]
- Heller, Y. Language, meaning, and games: A model of communication, coordination, and evolution: Comment. Am. Econ. Rev. 2014, 104, 1857–1863. [Google Scholar] [CrossRef]
- Heller, Y. Stability and trembles in extensive-form games. Games Econ. Behav. 2014, 84, 132–136. [Google Scholar] [CrossRef]
- Heller, Y. Three steps ahead. Theor. Econ. 2015, 10, 203–241. [Google Scholar] [CrossRef]
- Heller, Y. Instability of belief-free equilibria. J. Econ. Theory 2017, 168, 261–286. [Google Scholar] [CrossRef]
- Hellmann, T.; Staudigl, M. Evolution of Social Networks. Eur. J. Oper. Res. 2014, 234, 583–596. [Google Scholar] [CrossRef]
- Hens, T.; Schenk-Hoppé, K.R. Evolutionary stability of portfolio rules in incomplete markets. J. Math. Econ. 2005, 41, 43–66. [Google Scholar] [CrossRef]
- Herold, F.; Kuzmics, C. Evolutionary stability of discrimination under observability. Games Econ. Behav. 2009, 67, 542–551. [Google Scholar] [CrossRef]
- Herold, F. Carrot or stick? The evolution of reciprocal preferences in a haystack model. Am. Econ. Rev. 2012, 102, 914–940. [Google Scholar] [CrossRef]
- Herre, E.A.; Wcislo, W.T. In defence of inclusive fitness theory. Nature 2011, 471, E8. [Google Scholar] [CrossRef] [PubMed]
- Hofbauer, J.; Sandholm, W.H. Evolution in games with randomly disturbed payoffs. J. Econ. Theory 2007, 132, 47–69. [Google Scholar] [CrossRef]
- Hofbauer, J.; Sigmund, K. Evolutionary Games and Population Dynamics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Hofbauer, J.; Sigmund, K. Evolutionary game dynamics. Bull. Am. Math. Soc. 2003, 40, 479–519. [Google Scholar] [CrossRef]
- Hofbauer, J.; Weibull, J.W. Evolutionary selection against dominated strategies. J. Econ. Theory 1996, 71, 558–573. [Google Scholar] [CrossRef]
- Hofbauer, J.; Sorin, S.; Viossat, Y. Time average replicator and best-reply dynamics. Math. Oper. Res. 2009, 34, 263–269. [Google Scholar] [CrossRef]
- Hopkins, E.; Seymour, R.M. The stability of price dispersion under seller and consumer learning. Int. Econ. Rev. 2002, 43, 1157–1190. [Google Scholar] [CrossRef]
- Hopkins, E. Two competing models of how people learn in games. Econometrica 2002, 70, 2141–2166. [Google Scholar] [CrossRef]
- Huck, S.; Normann, H.T.; Oechssler, J. Learning in Cournot oligopoly—An experiment. Econ. J. 1999, 109, 80–95. [Google Scholar] [CrossRef]
- Hurkens, S.; Schlag, K.H. Evolutionary insights on the willingness to communicate. Int. J. Game Theory 2003, 31, 511–526. [Google Scholar] [CrossRef]
- Hurkens, S. Learning by forgetful players. Games Econ. Behav. 1995, 11, 304–329. [Google Scholar] [CrossRef]
- Hwang, S.H.; Newton, J. Payoff-dependent dynamics and coordination games. Econ. Theory 2017, 64, 589–604. [Google Scholar] [CrossRef]
- Hwang, S.; Rey-Bellet, L. Positive feedback in coordination games: stochastic evolutionary dynamics and the logit choice rule. arXiv, 2017; arXiv:1701.0487. [Google Scholar]
- Hwang, S.H.; Lim, W.; Neary, P.; Newton, J. Conventional contracts, intentional behavior and logit choice: Equality without symmetry. Games Econ. Behav. 2018. forthcoming. [Google Scholar] [CrossRef]
- Ianni, A. Learning strict Nash equilibria through reinforcement. J. Math. Econ. 2014, 50, 148–155. [Google Scholar] [CrossRef]
- Izquierdo, S.S.; Izquierdo, L.R.; Vega-Redondo, F. The option to leave: Conditional dissociation in the evolution of cooperation. J. Theor. Biol. 2010, 267, 76–84. [Google Scholar] [CrossRef] [PubMed]
- Izquierdo, L.R.; Izquierdo, S.S.; Vega-Redondo, F. Leave and let leave: A sufficient condition to explain the evolutionary emergence of cooperation. J. Econ. Dyn. Control 2014, 46, 91–113. [Google Scholar] [CrossRef]
- Izquierdo, L.R.; Izquierdo, S.S.; Sandholm, W.H. An Introduction to ABED: Agent-Based Simulation of Evolutionary Game Dynamics; Mimeo: New York, NY, USA, 2018. [Google Scholar]
- Jackson, M.O.; Watts, A. The Evolution of Social and Economic Networks. J. Econ. Theory 2002, 106, 265–295. [Google Scholar] [CrossRef]
- Jackson, M.O. Social and Economic Networks; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Jensen, M.K.; Rigos, A. Evolutionary Games and Matching Rules; Mimeo: New York, NY, USA, 2017. [Google Scholar]
- Kahneman, D.; Tversky, A. Prospect Theory: An Analysis of Decision under Risk. Econometrica 1979, 47, 263–291. [Google Scholar] [CrossRef]
- Kalai, E.; Smorodinsky, M. Other Solutions to Nash’s Bargaining Problem. Econometrica 1975, 43, 513–518. [Google Scholar] [CrossRef]
- Kalai, E. Proportional Solutions to Bargaining Situations: Interpersonal Utility Comparisons. Econometrica 1977, 45, 1623–1630. [Google Scholar] [CrossRef]
- Kandori, M.; Rob, R. Bandwagon effects and long run technology choice. Games Econ. Behav. 1998, 22, 30–60. [Google Scholar]
- Kandori, M.; Mailath, G.J.; Rob, R. Learning, Mutation, and Long Run Equilibria in Games. Econometrica 1993, 61, 29–56. [Google Scholar] [CrossRef]
- Kaniovski, Y.M.; Young, H.P. Learning dynamics in games with stochastic perturbations. Games Econ. Behav. 1995, 11, 330–363. [Google Scholar] [CrossRef]
- Khan, A. Coordination under global random interaction and local imitation. Int. J. Game Theory 2014, 43, 721–745. [Google Scholar] [CrossRef]
- Kifer, Y. Random Perturbations of Dynamical Systems; Birkhauser: Basel, Switzerland, 1988. [Google Scholar]
- Kim, N.; Hwang, S.H. Evolution of Altruistic Preferences among Boundedly Rational Agents. Korean Econ. Rev. 2015, 31, 239–266. [Google Scholar]
- Kim, Y.G.; Sobel, J. An evolutionary approach to pre-play communication. Econometrica 1995, 63, 1181–1193. [Google Scholar] [CrossRef]
- Kipling, R. Just So Stories; Macmillan and Co.: London, UK, 1902. [Google Scholar]
- Klaus, B.; Klijn, F. Paths to Stability for Matching Markets with Couples. Games Econ. Behav. 2007, 36, 154–171. [Google Scholar] [CrossRef]
- Klaus, B.; Newton, J. Stochastic stability in assignment problems. J. Math. Econ. 2016, 62, 62–74. [Google Scholar] [CrossRef]
- Klaus, B.; Payot, F. Paths to Stability in the Assignment Problem; Cahiers de recherches economiques du département d’econométrie et d’economie politique (deep); Universitéde Lausanne Facultédes HEC; DEEP: Lausanne, Suisse, 2013. [Google Scholar]
- Klaus, B.; Klijn, F.; Walzl, M. Stochastic stability for roommate markets. J. Econ. Theory 2010, 145, 2218–2240. [Google Scholar] [CrossRef]
- Koch, C.M.; Nax, H.H. Theory and Evidence of Common-Pool Resource Usage; Mimeo, Dept. of Humanities, Social and Political Sciences, ETH: Zurich, Switzerland, 2017. [Google Scholar]
- Kojima, F.; Ünver, M. Random paths to pairwise stability in many-to-many matching problems: A study on market equilibration. Int. J. Game Theory 2008, 36, 473–488. [Google Scholar] [CrossRef]
- Kreindler, G.E.; Young, H.P. Fast convergence in evolutionary equilibrium selection. Games Econ. Behav. 2013, 80, 39–67. [Google Scholar] [CrossRef]
- Kreindler, G.E.; Young, H.P. Rapid innovation diffusion in social networks. Proc. Natl. Acad. Sci. USA 2014, 111, 10881–10888. [Google Scholar] [CrossRef] [PubMed]
- Kuzmics, C. On the elimination of dominated strategies in stochastic models of evolution with large populations. Games Econ. Behav. 2011, 72, 452–466. [Google Scholar] [CrossRef]
- Lahkar, R.; Riedel, F. The logit dynamic for games with continuous strategy sets. Games Econ. Behav. 2015, 91, 268–282. [Google Scholar] [CrossRef]
- Lahkar, R.; Sandholm, W.H. The projection dynamic and the geometry of population games. Games Econ. Behav. 2008, 64, 565–590. [Google Scholar] [CrossRef]
- Lahkar, R.; Seymour, R.M. The dynamics of generalized reinforcement learning. J. Econ. Theory 2014, 151, 584–595. [Google Scholar] [CrossRef]
- Lahkar, R. The dynamic instability of dispersed price equilibria. J. Econ. Theory 2011, 146, 1796–1827. [Google Scholar] [CrossRef]
- Lahkar, R. Equilibrium selection in the stag hunt game under generalized reinforcement learning. J. Econ. Behav. Organ. 2017, 138, 63–68. [Google Scholar] [CrossRef]
- Laraki, R.; Mertikopoulos, P. Higher order game dynamics. J. Econ. Theory 2013, 148, 2666–2695. [Google Scholar] [CrossRef]
- Laslier, J.F.; Topol, R.; Walliser, B. A behavioral learning process in games. Games Econ. Behav. 2001, 37, 340–366. [Google Scholar] [CrossRef]
- Leshno, J.D.; Pradelski, B.S.R. Efficient Price Discovery and Information in the Decentralized Assignment Game; Mimeo: New York, NY, USA, 2017. [Google Scholar]
- Leslie, D.S.; Perkins, S.; Xu, Z. Best-Response Dynamics in Zero-Sum Stochastic Games; Mimeo: New York, NY, USA, 2017. [Google Scholar]
- Levine, D.K.; Modica, S. Dynamics in stochastic evolutionary models. Theor. Econ. 2016, 11, 89–131. [Google Scholar] [CrossRef]
- Lewis, D. Convention: A Philosophical Study; Harvard University Press: Cambridge, MA, USA, 1969. [Google Scholar]
- Lewontin, R.C.; Cohen, D. On population growth in a randomly varying environment. Proc. Natl. Acad. Sci. USA 1969, 62, 1056–1060. [Google Scholar] [CrossRef] [PubMed]
- Lim, W.; Neary, P.R. An experimental investigation of stochastic adjustment dynamics. Games Econ. Behav. 2016, 100, 208–219. [Google Scholar] [CrossRef]
- Littlestone, N.; Warmuth, M.K. The weighted majority algorithm. Inf. Comput. 1994, 108, 212–261. [Google Scholar] [CrossRef]
- Mantilla, C.; Sethi, R.; Cárdenas, J.C. Efficiency and Stability of Sampling Equilibrium in Public Good Games; SSRN Working Paper Series 3081506; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Marden, J.R.; Roughgarden, T. Generalized Efficiency Bounds in Distributed Resource Allocation. IEEE Trans. Autom. Control 2014, 59, 571–584. [Google Scholar] [CrossRef]
- Marden, J.R.; Shamma, J.S. Game theory and distributed control. In Handbook of Game Theory; Elsevier: Amsterdam, The Netherlands, 2012; Volume 4, pp. 861–900. [Google Scholar]
- Marden, J.R.; Shamma, J.S. Revisiting log-linear learning: Asynchrony, completeness and payoff-based implementation. Games Econ. Behav. 2012, 75, 788–808. [Google Scholar] [CrossRef]
- Marden, J.R.; Wierman, A. Distributed welfare games. Operations Research 2013, 61, 155–168. [Google Scholar] [CrossRef]
- Marden, J.R.; Arslan, G.; Shamma, J.S. Joint strategy fictitious play with inertia for potential games. IEEE Trans. Autom. Control 2009, 54, 208–220. [Google Scholar] [CrossRef]
- Marden, J.R.; Young, H.P.; Pao, L.Y. Achieving Pareto optimality through distributed learning. SIAM J. Control Optim. 2014, 52, 2753–2770. [Google Scholar] [CrossRef]
- Marden, J.R. State based potential games. Automatica 2012, 48, 3075–3088. [Google Scholar] [CrossRef]
- Mäs, M.; Nax, H.H. A behavioral study of “noise” in coordination games. J. Econ. Theory 2016, 162, 195–208. [Google Scholar] [CrossRef]
- Maschler, M.; Peleg, B.; Shapley, L.S. Geometric Properties of the Kernel, Nucleolus, and Related Solution Concepts. Math. Oper. Res. 1979, 4, 303–338. [Google Scholar] [CrossRef]
- Massari, F. Comment on If You’re so Smart, Why Aren’t You Rich? Belief Selection in Complete and Incomplete Markets. Econometrica 2013, 81, 849–851. [Google Scholar]
- Massari, F. Market Selection in Large Economies: A Matter of Luck; Mimeo: New York, NY, USA, 2015. [Google Scholar]
- Massari, F. Markets with heterogeneous beliefs: A necessary and sufficient condition for a trader to vanish. J. Econ. Dyn. Control 2017, 78, 190–205. [Google Scholar] [CrossRef]
- Matessi, C.; Gimelfarb, A.; Gavrilets, S. Long-term buildup of reproductive isolation promoted by disruptive selection: how far does it go? Selection 2002, 2, 41–64. [Google Scholar] [CrossRef]
- Mertikopoulos, P.; Moustakas, A.L. The emergence of rational behavior in the presence of stochastic perturbations. Ann. Appl. Probab. 2010, 20, 1359–1388. [Google Scholar] [CrossRef]
- Mertikopoulos, P.; Sandholm, W.H. Learning in games via reinforcement and regularization. Math. Oper. Res. 2016, 41, 1297–1324. [Google Scholar] [CrossRef]
- Mertikopoulos, P.; Sandholm, W.H. Riemannian game dynamics. arXiv, 2016; arXiv:1603.09173. [Google Scholar]
- Mohlin, E.; Östling, R.; Wang, J.T.Y. Learning by Similarity-Weighted Imitation in Games; Mimeo: New York, NY, USA, 2017. [Google Scholar]
- Mohlin, E. Evolution of theories of mind. Games Econ. Behav. 2012, 75, 299–318. [Google Scholar] [CrossRef]
- Monderer, D.; Shapley, L.S. Potential Games. Games Econ. Behav. 1996, 14, 124–143. [Google Scholar] [CrossRef]
- Montgomery, J.D. Intergenerational cultural transmission as an evolutionary game. Am. Econ. J. Microecon. 2010, 2, 115–136. [Google Scholar] [CrossRef]
- Nachbar, J.H. “Evolutionary” selection dynamics in games: Convergence and limit properties. Int. J. Game Theory 1990, 19, 59–89. [Google Scholar] [CrossRef]
- Nagurney, A.; Zhang, D. Projected dynamical systems in the formulation, stability analysis, and computation of fixed-demand traffic network equilibria. Transp. Sci. 1997, 31, 147–158. [Google Scholar] [CrossRef]
- Naidu, S.; Hwang, S.H.; Bowles, S. Evolutionary bargaining with intentional idiosyncratic play. Econ. Lett. 2010, 109, 31–33. [Google Scholar] [CrossRef]
- Naidu, S.; Hwang, S.H.; Bowles, S. The Evolution of Egalitarian Sociolinguistic Conventions. Am. Econ. Rev. Papers Proc. 2017, 107, 572–577. [Google Scholar] [CrossRef]
- Nash, John F., Jr. The Bargaining Problem. Econometrica 1950, 18, 155–162. [Google Scholar]
- Nash, J. Non-cooperative games. Ann. Math. 1951, 286–295. [Google Scholar] [CrossRef]
- Nash, J. Two-person cooperative games. Econometrica 1953, 21, 128–140. [Google Scholar] [CrossRef]
- Nax, H.H.; Perc, M. Directional learning and the provisioning of public goods. Sci. Rep. 2015, 5, 8010. [Google Scholar] [CrossRef] [PubMed]
- Nax, H.H.; Pradelski, B.S.R. Evolutionary dynamics and equitable core selection in assignment games. Int. J. Game Theory 2015, 44, 903–932. [Google Scholar] [CrossRef]
- Nax, H.H.; Pradelski, B.S.R. Core Stability and Core Selection in a Decentralized Labor Matching Market. Games 2016, 7, 10. [Google Scholar] [CrossRef]
- Nax, H.H.; Rigos, A. Assortativity evolving from social dilemmas. J. Theor. Biol. 2016, 395, 194–203. [Google Scholar] [CrossRef] [PubMed]
- Nax, H.H.; Pradelski, B.S.R.; Young, H.P. Decentralized dynamics to optimal and stable states in the assignment game. In Proceedings of the 52nd IEEE Conference on Decision and Control, Florence, Italy, 10–13 December 2013; pp. 2391–2397. [Google Scholar]
- Nax, H.H.; Burton-Chellew, M.N.; West, S.A.; Young, H.P. Learning in a black box. J. Econ. Behav. Organ. 2016, 127, 1–15. [Google Scholar] [CrossRef]
- Nax, H.H. Uncoupled Aspiration Adaptation Dynamics Into the Core. Ger. Econ. Rev. 2018. (online first). [Google Scholar] [CrossRef]
- Neary, P.R.; Newton, J. Heterogeneity in Preferences and Behavior in Threshold Models. J. Mech. Inst. Des. 2017, 2, 141–159. [Google Scholar]
- Neary, P.R. Competing conventions. Games Econ. Behav. 2012, 76, 301–328. [Google Scholar] [CrossRef]
- Nemitz, M.P.; Sayed, M.E.; Mamish, J.; Ferrer, G.; Teng, L.; McKenzie, R.M.; Hero, A.O.; Olson, E.; Stokes, A.A. HoverBots: Precise Locomotion Using Robots That Are Designed for Manufacturability. Front. Robot. AI 2017, 4, 55. [Google Scholar] [CrossRef]
- Newton, J.; Angus, S. Coalitions, Tipping Points and the Speed of Evolution; Working Papers Series 2013-02; University of Sydney Economics: Sydney, NSW, Australia, 2013. [Google Scholar]
- Newton, J.; Angus, S.D. Coalitions, tipping points and the speed of evolution. J. Econ. Theory 2015, 157, 172–187. [Google Scholar] [CrossRef]
- Newton, J.; Sawa, R. A one-shot deviation principle for stability in matching problems. J. Econ. Theory 2015, 157, 1–27. [Google Scholar] [CrossRef]
- Newton, J.; Sercombe, D. Agency, Potential and Contagion; SSRN Working Paper Series 3035245; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Newton, J.; Wait, A.; Angus, S.D. Watercooler Chat, Organizational Structure and Corporate Culture; SSRN Working Paper Series 3053174; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Newton, J. Coalitional stochastic stability. Games Econ. Behav. 2012, 75, 842–854. [Google Scholar] [CrossRef]
- Newton, J. Recontracting and stochastic stability in cooperative games. J. Econ. Theory 2012, 147, 364–381. [Google Scholar] [CrossRef]
- Newton, J. Stochastic stability on general state spaces. J. Math. Econ. 2015, 58, 46–60. [Google Scholar] [CrossRef]
- Newton, J. Shared intentions: The evolution of collaboration. Games Econ. Behav. 2017, 104, 517–534. [Google Scholar] [CrossRef]
- Newton, J. The preferences of Homo Moralis are unstable under evolving assortativity. Int. J. Game Theory 2017, 46, 583–589. [Google Scholar] [CrossRef]
- Norman, T.W. Rapid evolution under inertia. Games Econ. Behav. 2009, 66, 865–879. [Google Scholar] [CrossRef]
- Norman, T.W. Learning, hypothesis testing, and rational-expectations equilibrium. Games Econ. Behav. 2015, 90, 93–105. [Google Scholar] [CrossRef]
- Norman, T.W. Endogenous Market Selection; Mimeo: New York, NY, USA, 2017. [Google Scholar]
- Nowak, M.A.; Tarnita, C.E.; Wilson, E.O. The evolution of eusociality. Nature 2010, 466, 1057. [Google Scholar] [CrossRef] [PubMed]
- Okada, A.; Sawa, R. An Evolutionary Approach to Social Choice Problems with Q-Quota Rules; Kyoto Institute of Economic Research Discussion Paper 936; Kyoto University: Kyoto, Japan, 2016. [Google Scholar]
- Oprea, R.; Henwood, K.; Friedman, D. Separating the Hawks from the Doves: Evidence from continuous time laboratory games. J. Econ. Theory 2011, 146, 2206–2225. [Google Scholar] [CrossRef]
- Osborne, M.J.; Rubinstein, A. Games with procedurally rational players. Am. Econ. Rev. 1998, 88, 834–847. [Google Scholar]
- Östling, R.; Wang, J.T.Y.; Chou, E.Y.; Camerer, C.F. Testing game theory in the field: Swedish LUPI lottery games. Am. Econ. J. Microecon. 2011, 3, 1–33. [Google Scholar] [CrossRef]
- Otto, S.P.; Servedio, M.R.; Nuismer, S.L. Frequency-dependent selection and the evolution of assortative mating. Genetics 2008, 179, 2091–2112. [Google Scholar] [CrossRef] [PubMed]
- Oyarzun, C.; Ruf, J. Convergence in models with bounded expected relative hazard rates. J. Econ. Theory 2014, 154, 229–244. [Google Scholar] [CrossRef]
- Pennings, P.S.; Kopp, M.; Meszéna, G.; Dieckmann, U.; Hermisson, J. An analytically tractable model for competitive speciation. Am. Nat. 2008, 171, E44–E71. [Google Scholar] [CrossRef] [PubMed]
- Perkins, S.; Leslie, D.S. Stochastic fictitious play with continuous action sets. J. Econ. Theory 2014, 152, 179–213. [Google Scholar] [CrossRef]
- Peski, M. Generalized risk-dominance and asymmetric dynamics. J. Econ. Theory 2010, 145, 216–248. [Google Scholar] [CrossRef]
- Pradelski, B.S.; Young, H.P. Learning efficient Nash equilibria in distributed systems. Games Econ. Behav. 2012, 75, 882–897. [Google Scholar] [CrossRef]
- Pradelski, B.S. Decentralized Dynamics and Fast Convergence in the Assignment Game. In Proceedings of the Sixteenth ACM Conference on Economics and Computation, Portland, OR, USA, 15–19 June 2015; ACM: New York, NY, USA. [Google Scholar]
- Quijano, N.; Ocampo-Martinez, C.; Barreiro-Gomez, J.; Obando, G.; Pantoja, A.; Mojica-Nava, E. The role of population games and evolutionary dynamics in distributed control systems: The advantages of evolutionary game theory. IEEE Control Syst. 2017, 37, 70–97. [Google Scholar] [CrossRef]
- Ritzberger, K.; Weibull, J.W. Evolutionary selection in normal-form games. Econometrica 1995, 63, 1371–1399. [Google Scholar] [CrossRef]
- Rivas, J. Cooperation, imitation and partial rematching. Games Econ. Behav. 2013, 79, 148–162. [Google Scholar] [CrossRef]
- Robalino, N.; Robson, A. The evolution of strategic sophistication. Am. Econ. Rev. 2016, 106, 1046–1072. [Google Scholar] [CrossRef]
- Robson, A.J. Efficiency in evolutionary games: Darwin, Nash and the secret handshake. J. Theor. Biol. 1990, 144, 379–396. [Google Scholar] [CrossRef]
- Robson, A.J. A biological basis for expected and non-expected utility. J. Econ. Theory 1996, 68, 397–424. [Google Scholar] [CrossRef]
- Rosenthal, R.W. Games of perfect information, predatory pricing and the chain-store paradox. J. Econ. Theory 1981, 25, 92–100. [Google Scholar] [CrossRef]
- Roth, A.E.; Erev, I. Learning in extensive-form games: Experimental data and simple dynamic models in the intermediate term. Games Econ. Behav. 1995, 8, 164–212. [Google Scholar] [CrossRef]
- Roth, A.E.; Postlewaite, A. Weak versus strong domination in a market with indivisible goods. J. Math. Econ. 1977, 4, 131–137. [Google Scholar] [CrossRef]
- Roth, A.E.; Vande Vate, J.H. Random Paths to Stability in Two-Sided Matching. Econometrica 1990, 58, 1475–1480. [Google Scholar] [CrossRef]
- Roughgarden, T. Intrinsic Robustness of the Price of Anarchy. J. ACM 2015, 62, 32. [Google Scholar] [CrossRef]
- Rozen, K. Conflict leads to cooperation in demand bargaining. J. Econ. Behav. Organ. 2013, 87, 35–42. [Google Scholar] [CrossRef]
- Rusch, H. The evolutionary interplay of intergroup conflict and altruism in humans: a review of parochial altruism theory and prospects for its extension. Proc. R. Soc. B Biol. Sci. 2014, 281, 20141539. [Google Scholar] [CrossRef] [PubMed]
- Rusch, H. Shared Intentions: Collaboration Evolving; MAGKS Joint Discussion Paper Series in Economics 39; University of Marburg: Marburg, Germany, 2017. [Google Scholar]
- Rustichini, A. Optimal properties of stimulus—Response learning models. Games Econ. Behav. 1999, 29, 244–273. [Google Scholar] [CrossRef]
- Samuelson, L.; Zhang, J. Evolutionary stability in asymmetric games. J. Econ. Theory 1992, 57, 363–391. [Google Scholar] [CrossRef]
- Samuelson, L. Stochastic stability in games with alternative best replies. J. Econ. Theory 1994, 64, 35–65. [Google Scholar] [CrossRef]
- Samuelson, L. Evolutionary Games and Equilibrium Selection; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Samuelson, L. Introduction to the evolution of preferences. J. Econ. Theory 2001, 97, 225–230. [Google Scholar] [CrossRef]
- Samuelson, L. Game Theory in Economics and Beyond. J. Econ. Perspect. 2016, 30, 107–130. [Google Scholar] [CrossRef]
- Sandholm, W.H.; Staudigl, M. Large deviations and stochastic stability in the small noise double limit. Theor. Econ. 2016, 11, 279–355. [Google Scholar] [CrossRef]
- Sandholm, W.H.; Izquierdo, S.S.; Izquierdo, L.R. Best Experienced Payoff Dynamics and Cooperation in the Centipede Game; Mimeo: New York, NY, USA, 2017. [Google Scholar]
- Sandholm, W.H. Population Games and Evolutionary Dynamics; Economic Learning and Social Evolution; MIT Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Sandroni, A. Do markets favor agents able to make accurate predictions? Econometrica 2000, 68, 1303–1341. [Google Scholar] [CrossRef]
- Sandroni, A. Market selection when markets are incomplete. J. Math. Econ. 2005, 41, 91–104. [Google Scholar] [CrossRef]
- Sawa, R.; Wu, J. Prospect Dynamic and Loss Dominance; SSRN Working Paper Series 2804852; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Sawa, R.; Wu, J. Reference-Dependent Preferences, Super-Dominance and Stochastic Stability; Mimeo: New York, NY, USA, 2017. [Google Scholar]
- Sawa, R.; Zusai, D. Evolutionary imitative dynamics with population-varying aspiration levels. J. Econ. Theory 2014, 154, 562–577. [Google Scholar] [CrossRef]
- Sawa, R. Coalitional Stochastic Stability in Games, Networks and Markets. Games Econ. Behav. 2014, 88, 90–111. [Google Scholar] [CrossRef]
- Sawa, R. Stochastic Stability in Coalitional Bargaining Problems; Mimeo: New York, NY, USA, 2015. [Google Scholar]
- Schlag, K.H. Cheap Talk and Evolutionary Dynamics; University of Bonn Discussion Paper b-242; University of Bonn: Bonn, Germany, 1993. [Google Scholar]
- Schlag, K.H. When Does Evolution Lead to Efficiency in Communication Games? University of Bonn Discussion Paper b-299; University of Bonn: Bonn, Germany, 1994. [Google Scholar]
- Schlag, K.H. Why imitate, and if so, how?: A boundedly rational approach to multi-armed bandits. J. Econ. Theory 1998, 78, 130–156. [Google Scholar] [CrossRef]
- Searle, J.R. The Construction of Social Reality; Simon and Schuster: New York, NY, USA, 1995. [Google Scholar]
- Selten, R.; Hammerstein, P. Gaps in Harley’s argument on evolutionarily stable learning rules and in the logic of “tit for tat”. Behav. Brain Sci. 1984, 7, 115–116. [Google Scholar] [CrossRef]
- Selten, R. Evolutionary stability in extensive two-person games. Math. Soc. Sci. 1983, 5, 269–363. [Google Scholar] [CrossRef]
- Serrano, R.; Volij, O. Mistakes in Cooperation: the Stochastic Stability of Edgeworth’s Recontracting. Econ. J. 2008, 118, 1719–1741. [Google Scholar] [CrossRef]
- Servedio, M.R. Limits to the evolution of assortative mating by female choice under restricted gene flow. Proc. R. Soc. B Biol. Sci. 2011, 278, 179–187. [Google Scholar] [CrossRef] [PubMed]
- Sethi, R.; Somanathan, E. The evolution of social norms in common property resource use. Am. Econ. Rev. 1996, 86, 766–788. [Google Scholar]
- Sethi, R.; Somanathan, E. Preference evolution and reciprocity. J. Econ. Theory 2001, 97, 273–297. [Google Scholar] [CrossRef]
- Sethi, R. Strategy-specific barriers to learning and nonmonotonic selection dynamics. Games Econ. Behav. 1998, 23, 284–304. [Google Scholar] [CrossRef]
- Sethi, R. Stability of equilibria in games with procedurally rational players. Games Econ. Behav. 2000, 32, 85–104. [Google Scholar] [CrossRef]
- Shahshahani, S. A New Mathematical Framework for the Study of Linkage and Selection; Memoirs of the American Mathematical Society; American Mathematical Society: Providence, RI, USA, 1979; Volume 211. [Google Scholar]
- Shapley, L.; Shubik, M. The assignment game I: The core. Int. J. Game Theory 1971, 1, 111–130. [Google Scholar] [CrossRef]
- Shapley, L.S. Stochastic games. Proc. Natl. Acad. Sci. USA 1953, 39, 1095–1100. [Google Scholar] [CrossRef] [PubMed]
- Sigmund, K. The Calculus of Selfishness; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Simon, H.A. Rationality as process and as product of thought. Am. Econ. Rev. 1978, 68, 1–16. [Google Scholar]
- Skyrms, B. Signals, evolution and the explanatory power of transient information. Philos. Sci. 2002, 69, 407–428. [Google Scholar] [CrossRef]
- Sobel, J. Evolutionary stability and efficiency. Econ. Lett. 1993, 42, 301–312. [Google Scholar] [CrossRef]
- Sorin, S. Exponential weight algorithm in continuous time. Math. Programm. 2009, 116, 513–528. [Google Scholar] [CrossRef]
- Spiegler, R. Bounded Rationality and Industrial Organization; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Stahl, D.O.; Wilson, P.W. On players’ models of other players: Theory and experimental evidence. Games Econ. Behav. 1995, 10, 218–254. [Google Scholar] [CrossRef]
- Staudigl, M.; Weidenholzer, S. Constrained interactions and social coordination. J. Econ. Theory 2014, 152, 41–63. [Google Scholar] [CrossRef]
- Staudigl, M. Stochastic stability in asymmetric binary choice coordination games. Games Econ. Behav. 2012, 75, 372–401. [Google Scholar] [CrossRef]
- Strassmann, J.E.; Page Jr, R.E.; Robinson, G.E.; Seeley, T.D. Kin selection and eusociality. Nature 2011, 471, E5. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, Y. Long run equilibria in an asymmetric oligopoly. Econ. Theory 1999, 14, 705–715. [Google Scholar] [CrossRef]
- Taylor, P.D.; Jonker, L.B. Evolutionary stable strategies and game dynamics. Math. Biosci. 1978, 40, 145–156. [Google Scholar] [CrossRef]
- Thomas, B. On evolutionarily stable sets. J. Math. Biol. 1985, 22, 105–115. [Google Scholar] [CrossRef]
- Tomasello, M. A Natural History of Human Thinking; Harvard University Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Traulsen, A.; Hauert, C.; De Silva, H.; Nowak, M.A.; Sigmund, K. Exploration dynamics in evolutionary games. Proc. Natl. Acad. Sci. USA 2009, 106, 709–712. [Google Scholar] [CrossRef] [PubMed]
- Trivers, R.L. The evolution of reciprocal altruism. Q. Rev. Biol. 1971, 46, 35–57. [Google Scholar] [CrossRef]
- Van Veelen, M. Group selection, kin selection, altruism and cooperation: when inclusive fitness is right and when it can be wrong. J. Theor. Biol. 2009, 259, 589–600. [Google Scholar] [CrossRef] [PubMed]
- Van Veelen, M. The replicator dynamics with n players and population structure. J. Theor. Biol. 2011, 276, 78–85. [Google Scholar] [CrossRef] [PubMed]
- Van Veelen, M. Robustness against indirect invasions. Games Econ. Behav. 2012, 74, 382–393. [Google Scholar] [CrossRef]
- Vega-Redondo, F. The evolution of Walrasian behavior. Econometrica 1997, 65, 375–384. [Google Scholar] [CrossRef]
- Vesely, F.; Yang, C.L. On Optimal and Neutrally Stable Population Equilibrium in Voluntary Partnership Prisoner’s Dilemma Games; Mimeo: New York, NY, USA, 2010. [Google Scholar]
- Vesely, F.; Yang, C.L. Breakup, Secret Handshake and Neutral Stability in Repeated Prisoner’s Dilemma with Option to Leave: A Note; Mimeo: New York, NY, USA, 2012. [Google Scholar]
- Vovk, V. Aggregating strategies. In Proceedings of the Third Annual Workshop on Computational Learning Theory, Rochester, NY, USA, 6–8 August 1990; Fulk, M., Case, J., Eds.; Morgan Kaufmann: San Francisco, CA, USA, 1990; pp. 371–383. [Google Scholar]
- Weibull, J.W.; Salomonsson, M. Natural selection and social preferences. J. Theor. Biol. 2006, 239, 79–92. [Google Scholar] [CrossRef] [PubMed]
- Weibull, J. Evolutionary Game Theory; MIT Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Williams, D. Probability with Martingales; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Wilson, D.S.; Dugatkin, L.A. Group selection and assortative interactions. Am. Nat. 1997, 149, 336–351. [Google Scholar] [CrossRef]
- Wu, J. Evolving assortativity and social conventions. Econ. Bull. 2016, 36, 936–941. [Google Scholar]
- Wu, J. Social Hierarchy and the Evolution of Behavior. Int. Game Theory Rev. 2017, 19, 1750019. [Google Scholar] [CrossRef]
- Wu, J. Political Institutions and the Evolution of Character Traits. Games Econ. Behav. 2017, 106, 260–276. [Google Scholar] [CrossRef]
- Xu, Z. Convergence of best-response dynamics in extensive-form games. J. Econ. Theory 2016, 162, 21–54. [Google Scholar] [CrossRef]
- Young, H.P.; Burke, M.A. Competition and Custom in Economic Contracts: A Case Study of Illinois Agriculture. Am. Econ. Rev. 2001, 91, 559–573. [Google Scholar] [CrossRef]
- Young, H.P. The Evolution of Conventions. Econometrica 1993, 61, 57–84. [Google Scholar] [CrossRef]
- Young, H.P. An Evolutionary Model of Bargaining. J. Econ. Theory 1993, 59, 145–168. [Google Scholar] [CrossRef]
- Young, H.P. Individual Strategy and Social Structure; Princeton University Press: Princeton, NJ, USA, 1998. [Google Scholar]
- Young, H.P. Conventional Contracts. Rev. Econ. Stud. 1998, 65, 773–792. [Google Scholar] [CrossRef]
- Young, H.P. The possible and the impossible in multi-agent learning. Artif. Intell. 2007, 171, 429–433. [Google Scholar] [CrossRef]
- Young, H.P. Learning by trial and error. Games Econ. Behav. 2009, 65, 626–643. [Google Scholar] [CrossRef]
- Young, H.P. Innovation diffusion in heterogeneous populations: Contagion, social influence, and social learning. Am. Econ. Rev. 2009, 99, 1899–1924. [Google Scholar] [CrossRef]
- Young, H.P. The dynamics of social innovation. Proc. Natl. Acad. Sci. USA 2011, 108 (Suppl. 4), 21285–21291. [Google Scholar] [CrossRef] [PubMed]
- Zusai, D. Tempered best response dynamics. Int. J. Game Theory 2017, 47, 1–34. [Google Scholar] [CrossRef]
- Zusai, D. Nonaggregable Evolutionary Dynamics Under Payoff Heterogeneity; DETU Working Paper 17-02; Department of Economics, Temple University: Philadelphia, PA, USA, 2017. [Google Scholar]
- Zusai, D. Gains in Evolutionary Dynamics: Unifying Rational Framework for Dynamic Stability of ESS; Mimeo: New York, NY, USA, 2018. [Google Scholar]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).