Intention-Based Sharing
Abstract
:1. Introduction
2. The Social Environment
- in IG and UG, each sets an acceptance threshold (respectively ) based on the same integer restrictions for ; and
- in YN, each decides between unconditional acceptance () and rejection ().
- in UG, proposer i, with either or , earns , and responder j, with , earns when the offer is accepted, that is when ; both, proposer and responder, earn zero when the offer is rejected, that is, when ;
- in YN, proposer i, with either or , earns , and responder j, with , earns when the offer is unconditionally accepted, that is, when ; both proposer and responder earn zero when the offer is unconditionally rejected, that is, when ;
- in IG, proposer i, with either or , earns irrespective of the responder’s acceptance threshold, and responder j, with , earns when and zero otherwise.
- in IG and UG, responder i sets when and when , while in YN responder i, with , sets ;
- in each game type, proposer i, with , sets and if and if ;
- finally, anticipating leads to for and for optimal.
- the overwhelming tendency of participant is conditioning in the sense of , meaning that one anticipates to be influenced by another’s intention;
- downward adjustments, , to be on average larger than upward adjustments, , i.e., when participants adjust, they do so in a self-serving way;
- a significantly positive minority of participants does not adjust at all either due to or by avoiding information about another’s intention via , implying that is implemented, respectively via , implying that is implemented.
- a lower frequency of and, if so, an average decrease of with sanctioning power in YN than IG and when it lowest frequency when sanctioning is based on monitoring as in UG;
- persistent heterogeneity of adaptation patterns in case of , e.g., more than , and more so in IG than in YN than in UG;
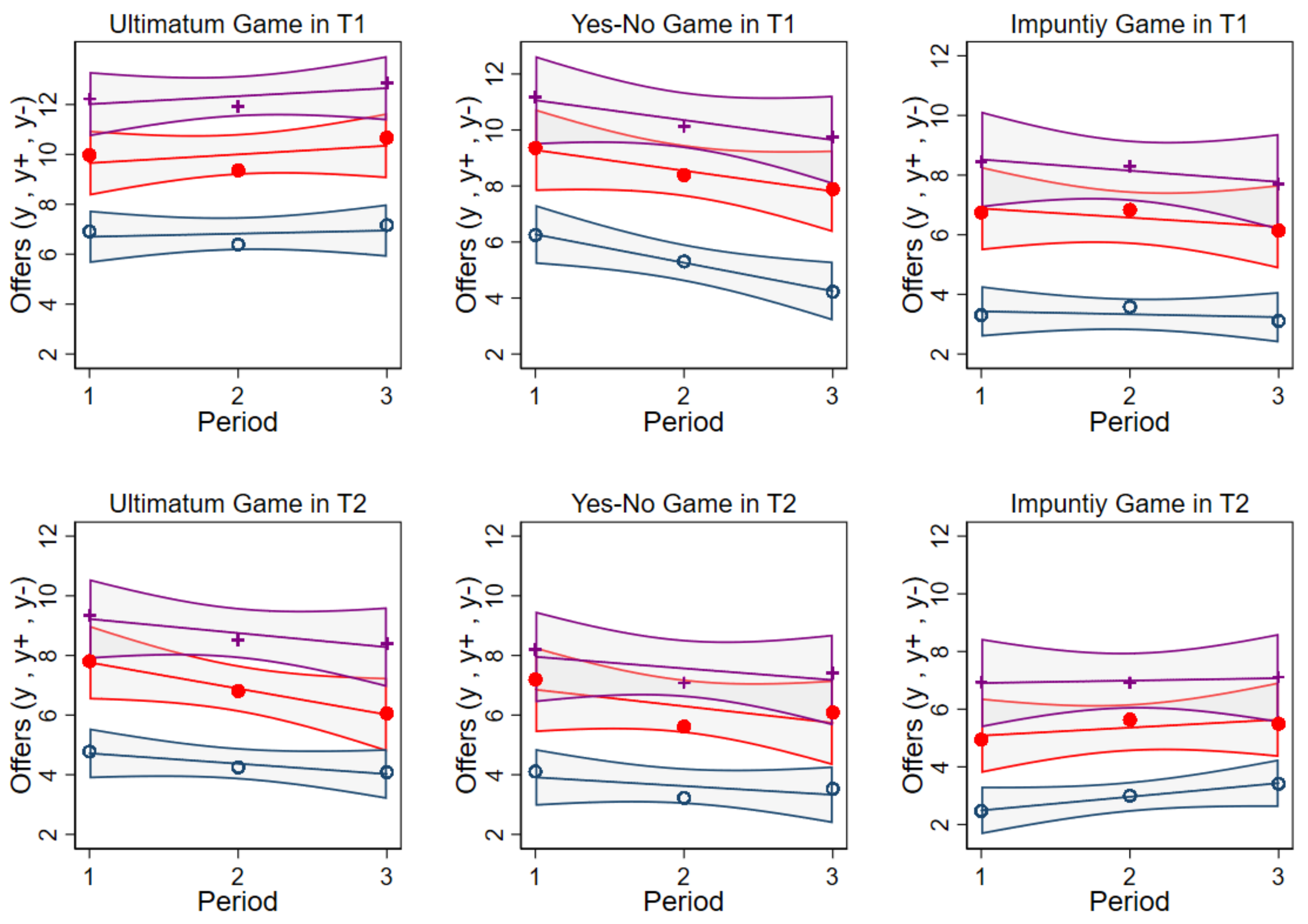
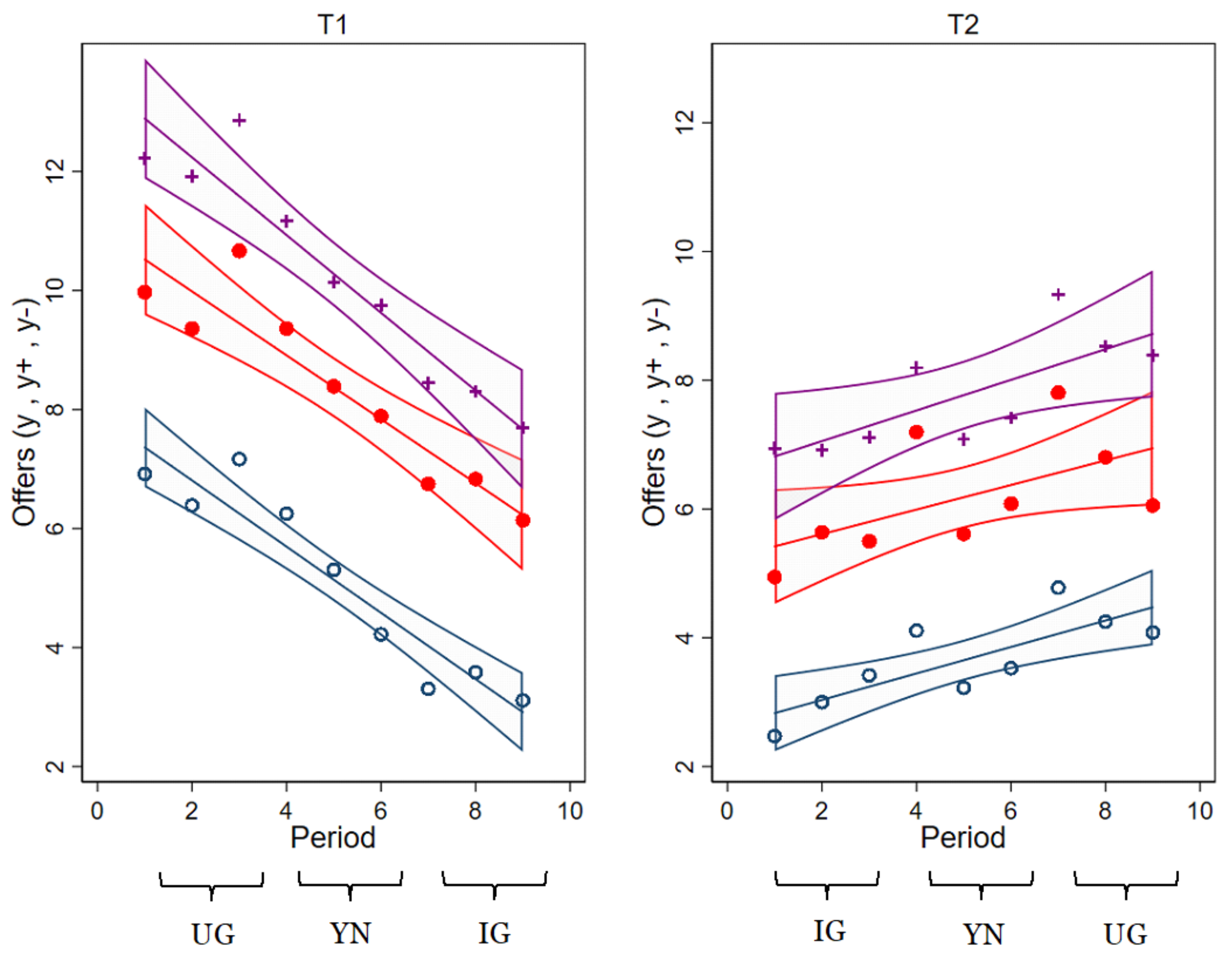
- a decline of average intended generosity and actual offers across the nine successive rounds of play which are stronger for IG than for YN than for UG.
3. Experimental Protocol
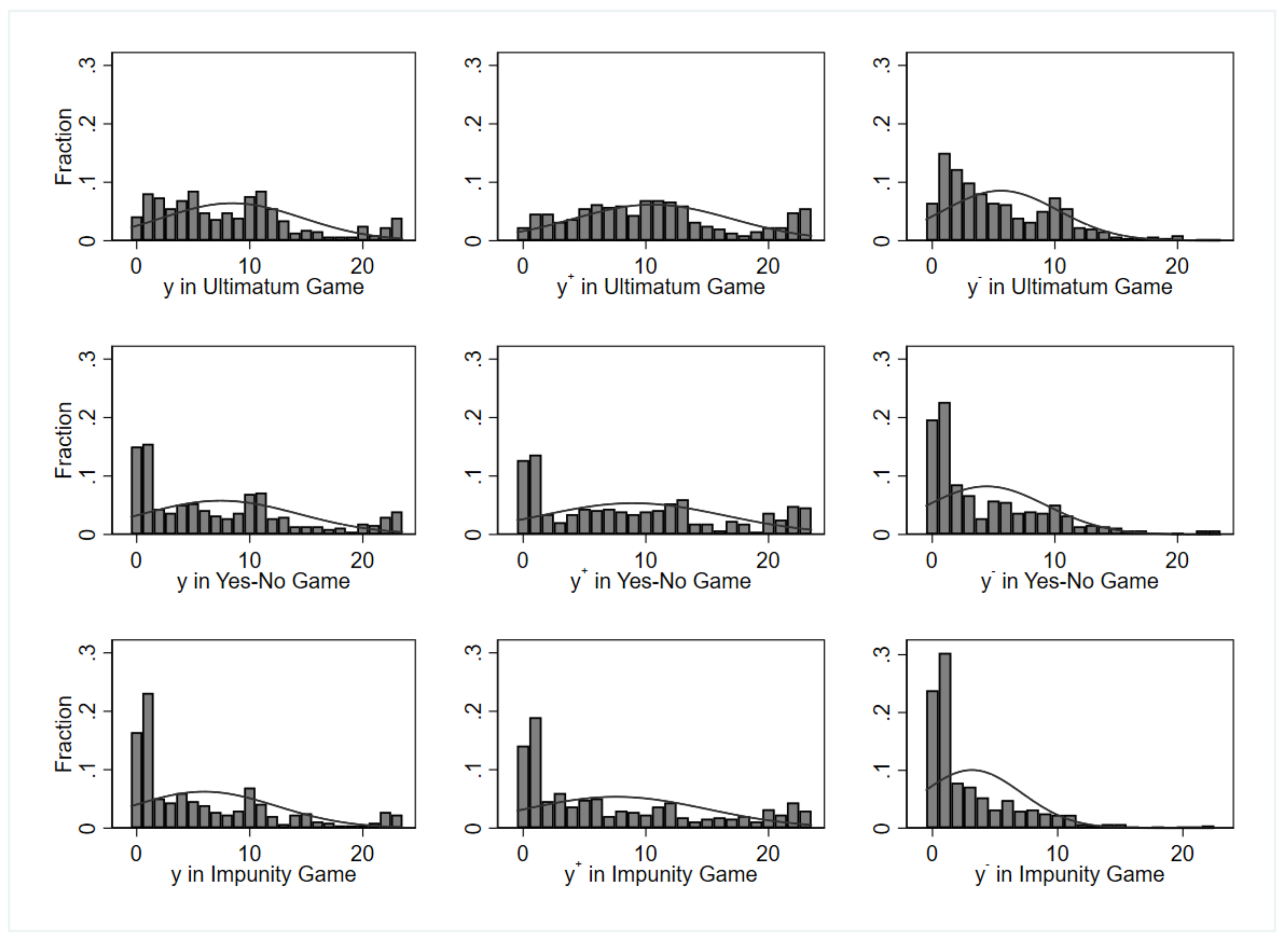
4. Data Analysis and Empirical Findings
4.1. Confirming Conditional Offering
- (i)
- for IG differences in offers and acceptance thresholds when played first or last are minor and mostly insignificant;
- (ii)
- for UG average offers and acceptance thresholds are much and significantly smaller when UG is played last; and
- (iii)
- for YN it does not matter for response behavior whether it is preceded by UG or IG but average offers are significantly smaller when YN is preceded by IG rather than by UG.
4.2. Efficiency Analysis
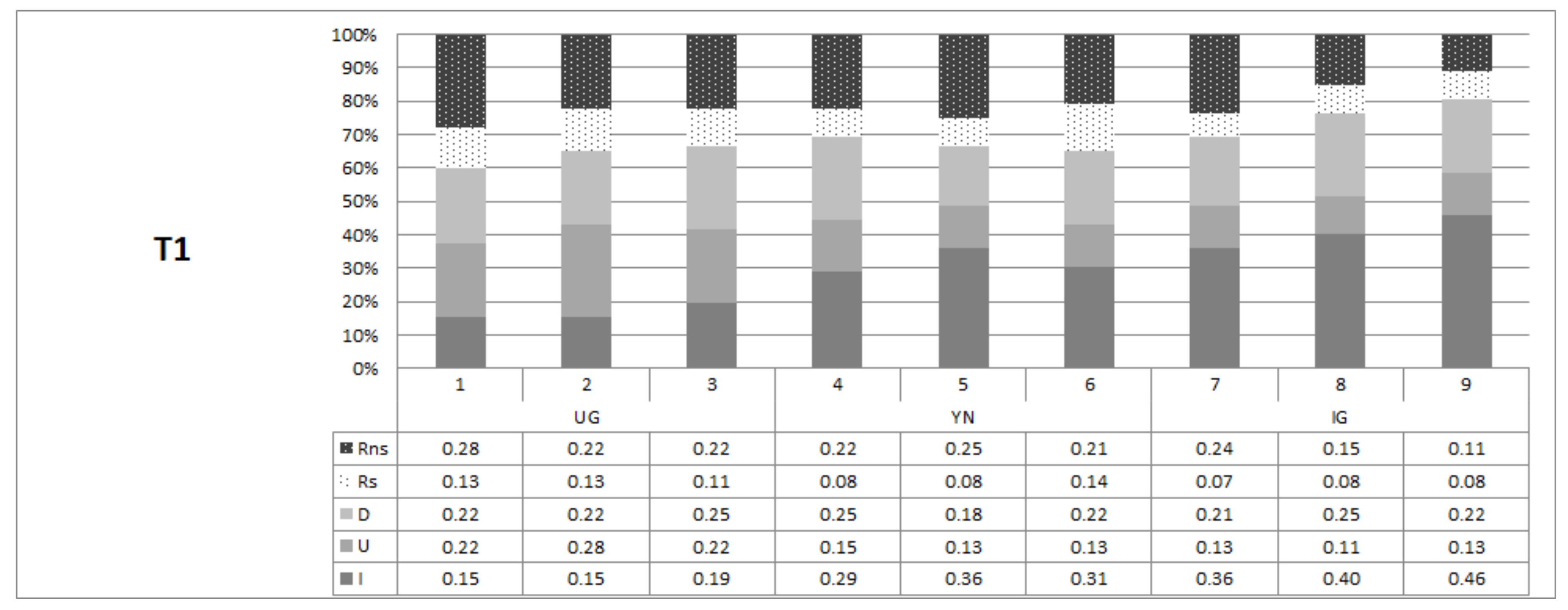
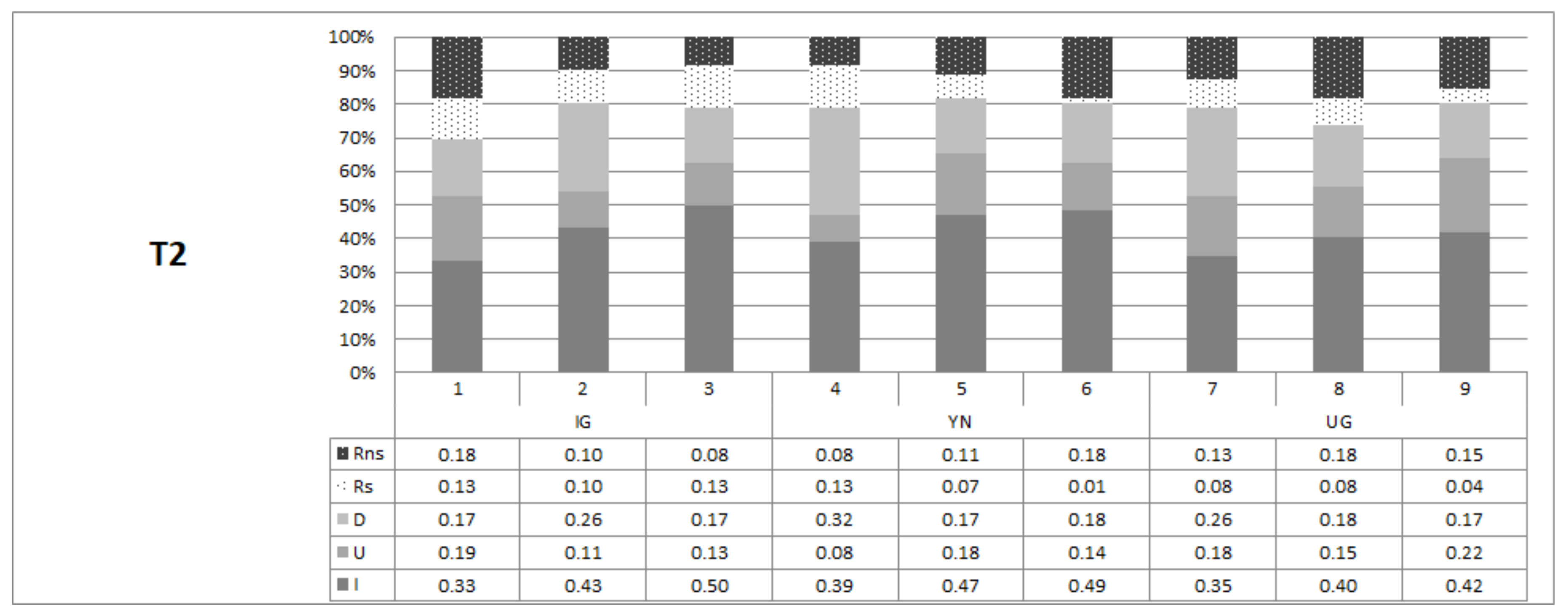
4.3. Categorization of Offer Profiles and Individual Types
- -
- Reactive (R): if and , one adjusts upward as well as downward.
- -
- Reactive selfserving (Rs): , that is, one reacts more strongly downward than upward;
- -
- Reactive non-selfserving (Rns): if , that is, one abstains from conditioning in a self-serving manner.
- -
- Adapting Downward (D): if ; and
- -
- Adapting Upward (U): if .
- -
- Immune (I): if .
5. Conclusions
Acknowledgments
Conflicts of Interest
Appendix A.
Translated instruction for treatment T2.
- first, you have to decide, individually and independently, how much of your endowment you to want to give to a responder (different from your paired participant) if you will be selected as a proposer. If you are an O(dd) participant, you can choose one between these numbers . If you are an E(ven) participant, you can choose one of the numbers .Observe that both types of participants have the same number of possible choices, i.e., twelve, and that the difference between the minimum and the maximum choice, i.e., 22€, is the same for both types of participant.
- Second, you have to decide, individually and independently, how much you want to update your initial proposal if you will be selected as a proposer in the two following situations:
- –
- the proposal of your paired participant is larger than yours; in this case you can either confirm or increase your initial proposal;
- –
- the proposal of your paired participant is smaller than your; in this case you can either confirm or decrease your initial proposal.
Remember that in each of the two cases, your updated proposal can only be an odd number or even number depending on whether you are an O or an E candidate.Note: Beware that you will be asked to update your initial proposal before knowing if the other has decided to propose more than you or less than you. - Third, you have to decide, individually and independently, what proposals you will accept if you will be selected as a responder. In particular, you have to decide an acceptance threshold such that all proposals larger than the threshold will be accepted and all proposals lower than the threshold will be rejected.Remember that the acceptance threshold can only be an odd number or even number depending on whether you are an O or an E candidate.
- adjust the proposals of each participant depending on whether the initial proposal of the paired participant is larger or smaller than the own one;
- select, for each pair of participant, who is the proposer and who is the responder;
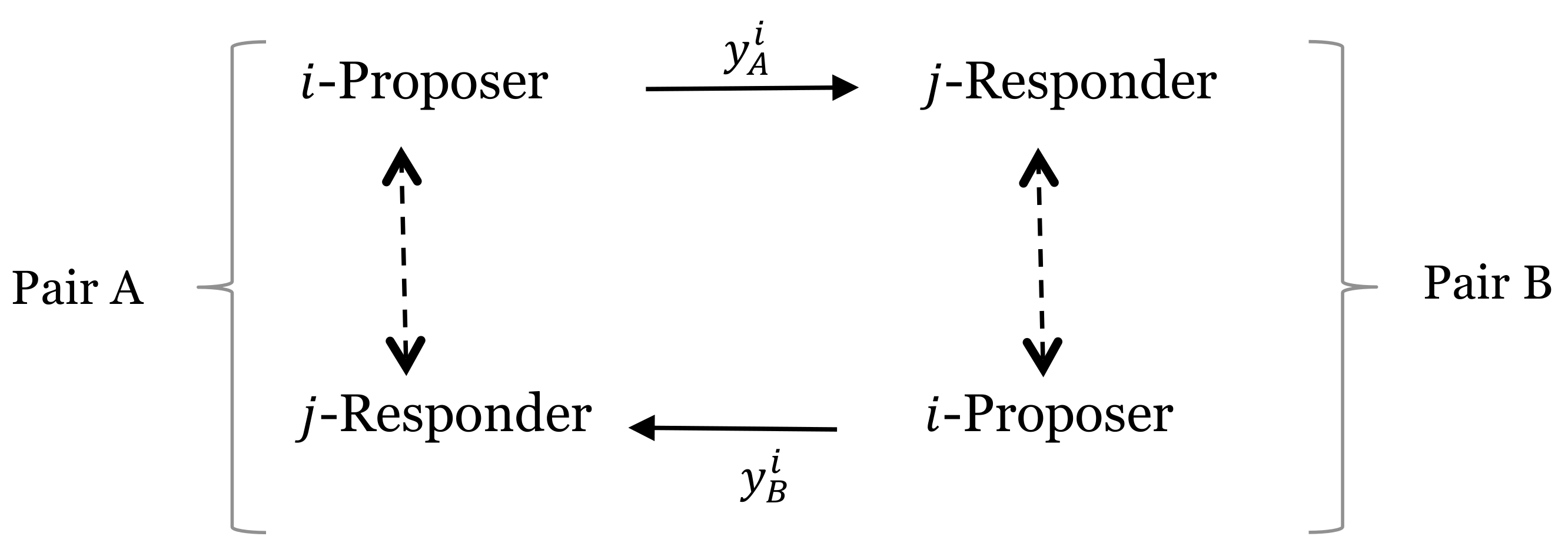
- randomly match each proposer with a responder from a different pair than the initial one and, similarly, randomly match each responder with a proposer from a different pair than the initial one.
- –
- O(dd) proposers will be matched with E(ven) receivers and that E(ven) proposers will be matched with O(dd) receivers;
- ●
- the proposal communicated to the receiver will be the adjusted one (and not the initial one).
- if you are a proposer, your payoff will be equal to your endowment minus your offer both in case the offer is above or below the responder’s acceptance threshold.
- if you are a receiver, your payoff will be equal to
- ∘
- the proposer’s proposal if this is larger than your acceptance threshold;
- ∘
- equal to zero if the proposal is smaller than your acceptance threshold.
- –
- if you are proposer or responder;
- –
- if your are a proposer, you will be communicated that you were selected as a proposer and you will be informed about your final payoff and the payoff of the responder who received your proposal;
- –
- if you are a receiver, you will be communicated that you were selected as a receiver and you will be informed about your final payoff.
- if you are a proposer, your payoff is
- ∘
- the initial endowment minus you proposal if the receiver selected the Yes option;
- ∘
- zero if the receiver selected the No option;
- if you are a receiver, your payoff
- ∘
- is the proposer’s proposal whether you accepted the offer;
- ∘
- zero whether you refused the offer.
- –
- if you are proposer or responder;
- –
- your final payoff.
- if you are a proposer, your payoff will be equal to
- ∘
- your endowment minus your offer when your offer is above the responder’s acceptance threshold;
- ∘
- Zero, when you offer is below the responder’s acceptance threshold;
- if you are a receiver, your payoff will be equal to
- ∘
- the proposer’s proposal if this is larger than your acceptance threshold;
- ∘
- equal to zero if the proposal is smaller than your acceptance threshold.
- –
- if you are proposer or responder;
- –
- your final payoff.
- –
- the payoff that you realised in the selected round;
- –
- the participation fee of €3.
Appendix B.
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | |
|---|---|---|---|---|---|---|---|---|---|
| UG | YN | IG | UG | YN | IG | UG | YN | IG | |
| L.Proposer | 0.59 | 1.39 * | 5.13 *** | 0.38 | 1.50 * | 6.37 *** | 0.52 | 1.38 ** | 4.51 *** |
| (0.39) | (0.79) | (1.48) | (0.40) | (0.84) | (1.57) | (0.33) | (0.68) | (1.32) | |
| L.Profit | −0.01 | −0.13 ** | −0.31 *** | −0.03 | −0.15 ** | −0.40 *** | −0.04 * | −0.14 *** | −0.30 *** |
| (0.03) | (0.06) | (0.08) | (0.03) | (0.06) | (0.09) | (0.02) | (0.05) | (0.07) | |
| Round | 0.16 | −0.09 | −0.36 | 0.25 | −0.16 | −0.29 | 0.25 | −0.38 | −0.15 |
| (0.26) | (0.29) | (0.28) | (0.21) | (0.27) | (0.27) | (0.25) | (0.25) | (0.32) | |
| Odd | −0.11 | 0.02 | −0.94 | 0.13 | −0.25 | −1.34 ** | −1.03 *** | −0.39 | −1.14 ** |
| (0.41) | (0.52) | (0.60) | (0.38) | (0.54) | (0.62) | (0.32) | (0.42) | (0.50) | |
| Treatment | −2.54 *** | −2.50 * | −1.24 | −1.97 ** | −3.02 ** | −1.45 | −1.60 ** | −0.91 | 0.11 |
| (0.94) | (1.40) | (1.56) | (0.93) | (1.50) | (1.80) | (0.68) | (1.09) | (1.25) | |
| Session 1 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| (.) | (.) | (.) | (.) | (.) | (.) | (.) | (.) | (.) | |
| Session 2 | 0.46 | 0.77 | 0.46 | −0.18 | 1.39 | 0.76 | −0.07 | 0.66 | 0.38 |
| (0.84) | (1.42) | (1.45) | (0.86) | (1.39) | (1.66) | (0.72) | (1.14) | (1.14) | |
| Session 3 | 0.34 | −0.63 | −0.77 | 0.66 | −0.73 | −0.93 | −0.01 | 0.45 | 0.27 |
| (0.88) | (1.32) | (1.43) | (0.87) | (1.42) | (1.55) | (0.59) | (0.98) | (1.07) | |
| Session 4 | 0.65 | 1.25 | 0.98 | 0.90 | 0.79 | 1.24 | 0.67 | 1.49 | 1.07 |
| (0.77) | (1.16) | (1.29) | (0.77) | (1.27) | (1.36) | (0.51) | (0.97) | (1.00) | |
| Session 5 | 1.89 * | 1.38 | 0.89 | 1.35 | 1.67 | 1.66 | 0.66 | −0.03 | 0.12 |
| (0.97) | (1.61) | (1.65) | (1.04) | (1.61) | (1.82) | (0.73) | (1.18) | (1.23) | |
| Session 6 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| (.) | (.) | (.) | (.) | (.) | (.) | (.) | (.) | (.) | |
| Cons | 6.32 *** | 6.37 *** | 5.13 ** | 6.72 *** | 8.58 *** | 6.51 ** | 4.28 *** | 3.44 * | 1.15 |
| (1.53) | (2.25) | (2.37) | (1.47) | (2.42) | (2.66) | (1.14) | (1.75) | (2.06) | |
| cons | 3.22 *** | 4.75 *** | 4.76 *** | 3.24 *** | 4.87 *** | 5.12 *** | 2.53 *** | 3.62 *** | 3.60 *** |
| (0.19) | (0.30) | (0.35) | (0.16) | (0.28) | (0.31) | (0.15) | (0.28) | (0.31) | |
| N | 288 | 288 | 288 | 288 | 288 | 288 | 288 | 288 | 288 |
| LL | −708.49 | −652.48 | −608.18 | −736.86 | −698.38 | −666.38 | −611.11 | −529.90 | −466.66 |
| pseudo | 0.03 | 0.02 | 0.02 | 0.03 | 0.02 | 0.03 | 0.04 | 0.02 | 0.04 |
| F | 3.49 | 2.06 | 2.80 | 3.75 | 1.87 | 3.84 | 4.45 | 2.28 | 3.28 |
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
| UG | IG | UG | IG | UG | IG | |
| L.Proposer | −1.30 * | 4.63 ** | −1.75 ** | 5.68 ** | −1.34 ** | 2.81 |
| (0.76) | (2.25) | (0.72) | (2.46) | (0.58) | (1.85) | |
| L.success | −0.70 | 0.97 | −0.41 | 1.52 | −1.00 * | 0.81 |
| (0.67) | (0.96) | (0.72) | (1.06) | (0.57) | (0.75) | |
| L.success×L.Prop | 2.97 *** | 0.56 | 3.43 *** | 0.77 | 2.83 *** | 1.67 |
| (0.93) | (1.54) | (0.87) | (1.69) | (0.70) | (1.20) | |
| L.Profit | −0.07 | −0.31 *** | −0.12 *** | −0.39 *** | −0.08 ** | −0.27 *** |
| (0.04) | (0.09) | (0.04) | (0.10) | (0.04) | (0.08) | |
| Round | 0.17 | −0.31 | 0.26 | −0.23 | 0.25 | −0.07 |
| (0.27) | (0.29) | (0.22) | (0.28) | (0.26) | (0.34) | |
| Treatment | −2.56 *** | −1.13 | −1.99 ** | −1.27 | −1.62 ** | 0.23 |
| (0.91) | (1.52) | (0.89) | (1.73) | (0.63) | (1.20) | |
| Odd | −0.19 | −0.79 | 0.04 | −1.12 * | −1.11 *** | −0.94 * |
| (0.41) | (0.60) | (0.37) | (0.62) | (0.31) | (0.49) | |
| Session 1 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| (.) | (.) | (.) | (.) | (.) | (.) | |
| Session 2 | 0.48 | 0.48 | −0.16 | 0.79 | −0.06 | 0.40 |
| (0.81) | (1.42) | (0.83) | (1.61) | (0.68) | (1.09) | |
| Session 3 | 0.36 | −0.53 | 0.74 | −0.56 | −0.02 | 0.57 |
| (0.83) | (1.42) | (0.82) | (1.54) | (0.56) | (1.06) | |
| Session 4 | 0.66 | 0.96 | 0.94 | 1.19 | 0.66 | 1.02 |
| (0.73) | (1.28) | (0.71) | (1.33) | (0.47) | (0.97) | |
| Session 5 | 1.94 ** | 1.09 | 1.40 | 1.97 | 0.68 | 0.42 |
| (0.95) | (1.60) | (1.01) | (1.74) | (0.68) | (1.15) | |
| Session 6 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| (.) | (.) | (.) | (.) | (.) | (.) | |
| Cons | 7.19 *** | 4.11 * | 7.55 *** | 4.94 * | 5.25 *** | 0.06 |
| (1.54) | (2.45) | (1.46) | (2.62) | (1.15) | (2.09) | |
| cons | 3.16 *** | 4.73 *** | 3.15 *** | 5.04 *** | 2.46 *** | 3.51 *** |
| (0.19) | (0.35) | (0.16) | (0.31) | (0.15) | (0.30) | |
| N | 288 | 288 | 288 | 288 | 288 | 288 |
| LL | −708.49 | −608.18 | −736.86 | −666.38 | −611.11 | −466.66 |
| pseudo | 0.04 | 0.02 | 0.04 | 0.03 | 0.05 | 0.05 |
| F | 3.93 | 3.27 | 5.00 | 4.85 | 5.72 | 4.26 |
References
- Andreoni, J. Giving with impure altruism: Applications to charity and Ricardian equivalence. J. Polit. Econ. 1989, 97, 1447–1458. [Google Scholar] [CrossRef]
- Andreoni, J. Impure altruism and donations to public goods: A theory of warm-glow giving. Econ. J. 1990, 100, 464–477. [Google Scholar] [CrossRef]
- Vesterlund, L. Using Experimental Methods to Understand Why and How We Give to Charity. In The Handbook of Experimental Economics; Kagel, J.H., Roth, A.E., Eds.; Princeton University Press: Princeton, NJ, USA, 2016; Volume 2, ISBN 978-0-691-13999-9. [Google Scholar]
- Selten, R. Die strategiemethode zur erforschung des eingeschränkt rationalen verhaltens im rahmen eines oligopolexperiments. In Beiträge zur Experimentellen Wirtschaftsforschung; Sauerman, H., Ed.; JCB Mohr (Paul Siebeck): Tübingen, Germany, 1967; ISSN 00442550. [Google Scholar]
- Güth, W.; Huck, S. From Ultimatum Bargaining to Dictatorship—An experimental Study of Four Games Varying in Veto-Power. Metroeconomica 1997, 48, 262–279. [Google Scholar] [CrossRef]
- Bolton, G.E.; Katok, E.; Zwick, R. Dictator Game Giving: Rules of Fairness versus Acts of Kindness. Int. J. Game Theory 1998, 27, 269–299. [Google Scholar] [CrossRef]
- Dana, J.; Weber, R.A.; Kuang, J.X. Exploiting moral wiggle room: experiments demonstrating an illusory preference for fairness. Econ. Theory 2007, 33, 67–80. [Google Scholar] [CrossRef]
- Fischer, P.; Krueger, J.I.; Greitemeyer, T.; Vogrincic, C.; Kastenmüller, A.; Frey, D.; Kainbacher, M. The bystander-effect: A meta-analytic review on bystander intervention in dangerous and non-dangerous emergencies. Psychol. Bull. 2011, 137, 517. [Google Scholar] [CrossRef] [PubMed]
- Dufwenberg, M.; Kirchsteiger, G. A Theory of Sequential Reciprocity. Games Econ. Behav. 2004, 47, 268–298. [Google Scholar] [CrossRef]
- Levine, D.K. Modeling altruism and spitefulness in experiments. Rev. Econ. Dyn. 1998, 1, 593–622. [Google Scholar] [CrossRef]
- Gächter, S.; Nosenzo, D.; Sefton, M. Peer effects in pro-social behavior: Social norms or social preferences? J. Eur. Econ. Assoc. 2013, 11, 548–573. [Google Scholar] [CrossRef] [PubMed]
- Gächter, S.; Gerhards, L.; Nosenzo, D. The importance of peers for compliance with norms of fair sharing. Eur. Econ. Rev. 2017, 97, 72–86. [Google Scholar] [CrossRef]
- Carpenter, J.P. When in Rome: Conformity and the provision of public goods. J. Socio Econ. 2004, 33, 395–408. [Google Scholar] [CrossRef]
- Bardsley, N.; Sausgruber, R. Conformity and reciprocity in public good provision. J. Econ. Psychol. 2005, 26, 664–681. [Google Scholar] [CrossRef]
- Bereby-Meyer, Y.; Niederle, M. Fairness in bargaining. J. Econ. Behav. Org. 2005, 56, 173–186. [Google Scholar] [CrossRef]
- Fischbacher, U.; Gächter, S.; Fehr, E. Are people conditionally cooperative? Evidence from a public goods experiment. Econ. Lett. 2001, 71, 397–404. [Google Scholar] [CrossRef] [Green Version]
- Fischbacher, U.; Gächter, S. Social Preferences, Beliefs, and the Dynamics of Free Riding in Public Goods Experiments. Am. Econ. Rev. 2010, 100, 541–556. [Google Scholar] [CrossRef]
- Cooper, D.J.; Kagel, J.H. Other-Regarding Preferences: A Selective Survey of Experimental Results. In The Handbook of Experimental Economics; Kagel, J.H., Roth, A.E., Eds.; Princeton University Press: Princeton, NJ, USA, 2016; Volume 2, ISBN 978-0-691-13999-9. [Google Scholar]
- Di Cagno, D.; Galliera, A.; Güth, W.; Panaccione, L. A hybrid public good experiment eliciting multi-dimensional choice data. J. Econ. Psychol. 2016, 56, 20–38. [Google Scholar] [CrossRef]
- Yamagishi, J.; Horite, Y.; Takagishi, H. The private rejection of unfair offers and emotional commitment. Proc. Nat. Acad. Sci. USA 2009, 106, 11520–11523. [Google Scholar] [CrossRef] [PubMed]
- Spiekermann, K.; Weiss, A. Objective and subjective compliance: A norm-based explanation of moral wiggle room? Games Econ. Behav. 2016, 96, 170–183. [Google Scholar] [CrossRef] [Green Version]
- Dana, J.; Cain, D.M.; Dawes, R.M. What you don’t know won’t hurt me: Costly (but quiet) exit in dictator games. Org. Behav. Hum. Decis. Proc. 2006, 100, 193–201. [Google Scholar] [CrossRef]
- Zizzo, D.J. Experimenter demand effects in economic experiments. Exp. Econ. 2010, 13, 75–98. [Google Scholar] [CrossRef]
- Greiner, B. Subject Pool Recruitment Procedures: Organizing Experiments with ORSEE. J. Econ. Sci. Assoc. 2015, 1, 114–125. [Google Scholar] [CrossRef]
- Fischbacher, U. z-Tree: Zurich toolbox for ready-made economic experiments. Exp. Econ. 2007, 10, 171–178. [Google Scholar] [CrossRef]
- Güth, W.; Kocher, M.G. More than thirty years of ultimatum bargaining experiments: Motives, variations, and a survey of the recent literature. J. Econ. Behav. Org. 2014, 108, 396–409. [Google Scholar] [CrossRef]
| 1. | Due to the strategy vector method (see Selten [4]), each participant determines independent and conditional offers in the role of proposer as well as an acceptance threshold in the role of responder. |
| 2. | |
| 3. | Dictator game experiments—except when especially interested in the “moral wiggle room” (see Dana et al. [7] —unnecessarily deprive the recipient of voice and choice in addition to excluding sanctioning power, for example, when comparing them with those of ultimatum game experiments. |
| 4. | Note that UG-equilibrium multiplicity is avoided by YN as well as by IG. |
| 5. | Gächter et al. [12] focus on uni-dimensional influence based on actual donations of two successively donating dictators in three-person dictator experiments. |
| 6. | Joint generosity is explored by running charitable donation experiments in which conditioning is investigated via providing information about other earlier donations, for example, by distinguishing larger (smaller) earlier donations (see Bereby-Meyer and Niederle [15]). |
| 7. | |
| 8. | Due to the available amount differs between o and e so as to allow both o and e to offer the whole endowment. Moreover, the fact that paired candidates have different headings (e, respectively, o) avoids the possibility of equal intentions in sharing. |
| 9. | Although equal intentions are often maintained (see Di Cagno et al. [19]), we opted against eliciting reactions to the equality of intentions since this questions qualitative comparability. |
| 10. | In the terminology of Yamagishi et al. [20] we have implemented a non-private IG. |
| 11. | For in YN both acceptance and rejection are best responses, that is, there are two (pure strategy) equilibria. |
| 12. | UG has other equilibria with other, also fair, outcomes. These, however, rely on weakly dominated response strategies which would not survive once repeated elimination. |
| 13. | We thank one of our referee for this suggestion. |
| 14. | All three sharing games were easily understood by participants and three rounds seemed sufficient to indicate learning. |
| 15. | Participants were informed about random rematching in each round but not about its specific details. |
| 16. | Participants are first asked for an intended offer and then to submit new offers conditional on the possible qualitative information about the other’s intended offer. We try to limit experimenter demand effects (see Zizzo [23]) for a comprehensive discussion on the experimenter demand effects) by neutral instructions. Furthermore, the analysis on differences between adjustments and learning analysis should partially account for it since strategic concerns are likely to weaken demand effects. |
| 17. | Details on the committee as well as the ethical code can be found on the Cesare laboratory web-page (http://economiaefinanza.luiss.it/en/research/research-centers/cesieg/cesare-centre-experimental-economics/cesare-rent). |
| 18. | Thus, guaranteed independence of the initial profiles can only be explored in case of IG and UG as YN is never the game type played first. |
| 19. | Since offer profiles with are impossible. |
| 20. | In what follows, will denote average values. |
| 21. | This is in line with previous experiments without conditioning (see Güth and Kocher [26], for references). |
| 22. | Whether or holds allows to verify participants’ consistency, in that they would not otherwise accept their own offer. Such consistency is higher in UG (71% of adjusted offers satisfy ) than in IG (43% of adjusted offers satisfy ). |
| 23. | The offers are rescaled via when and when . In this way, each offer is associated with a value between 1 and 11, consistent with the choices ranging either from 0 to 22 or from 1 to 23. |
| 24. | We estimated all models with panel data regression. The analysis is consistent when we consider the twelve possible allocations or the full offer profiles for even and odd participants; nevertheless the censored regression model was more accurate for the current analysis. We ran also a multilevel analysis to account for different groups: the likelihood ratio test (testing for the multilevel model) rejects the between-group variations. Finally, we check for sessions effects: the multilevel analysis rejects between-session variation for YN and IG, while is weakly significant for UG: when wee pool results, we reject sessions variations. |
| 25. | L.Proposer is a variable equal to 1 for those participants who are actual proposer in the previous round. |
| 26. | L.Profit is a variable which measure profits earned in the previous round. |
| 27. | Odd is a variable equal to 1 for the participants and equal to zero otherwise. |
| 28. | L.Success is a variable equal to 1 if the offer is accepted in the previous round, both for proposer and responder, and 0 otherwise. Note that L.Success is equal to 0 for proposer in IG when the offer had been refused in the previous round even though this does not have an effect on the proposer’s payoffs. |
| 29. | We rely on participants for UG and participants for IG. A participant is paired with half () of the other allocator candidates, namely those of the other type (o and e) which determines the adjusted offers of this participant. Each of them is paired with the remaining other allocator candidates () which determines the acceptance threshold of responders. In total, this yields 1,260 combinations for each individual in the first round. |
| 30. | Recall that randomly selecting a proposer candidate in one pair also selects the proposer candidate of the other pair since each interacting pair involves an and an player. |
| 31. | Since YN is never played first, there is no simulation for this game type. |
| 32. | If, for instance, an o-allocator candidate does not want to offer more than necessary, e.g. in case of impunity, but would like to trigger more generosity by the e-allocator candidate, o might strategically choose and . Thus, the robust evidence of conditioning allows to manipulate the other’s actual generosity by guaranteeing when allocator candidate e (and not o) is actually endowed. For e-allocator candidates, the corresponding behavior, namely and , would be very costly: if e is actually endowed and confronts an allocator candidate o choosing , the actual offer of e would be . |
| Endowed Proposer | Needy Responder | |
|---|---|---|
| UG game | Role and Final payoff | Role and Final payoff |
| YN game | Role and Final Payoff | Role and Final payoff |
| IG game | Role, Final payoff and Responder’s payoff | Role and Final payoff |
| All Games | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| y | WSRST | |||||||||||||
| Obs. | Mean | S.d. | Mean | S.d. | Mean | S.d. | Mean | S.d. | Mean | S.d. | ||||
| T1 and T2 | 1296 | 7.278 | 6.595 | 9.023 | 7.241 | 4.395 | 4.619 | 1.745 | 3.042 | 2.883 | 5.025 | 0.000 | ||
| T1 | 648 | 8.373 | 6.722 | 10.278 | 7.294 | 5.139 | 4.912 | 1.904 | 2.958 | 3.235 | 5.317 | 0.001 | ||
| T2 | 648 | 6.182 | 6.283 | 7.769 | 6.970 | 3.651 | 4.180 | 1.586 | 3.118 | 2.531 | 4.693 | 0.000 | ||
| WRST | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |||||||||
| ultimatum game (UG) | ||||||||||||||
| y | WSRST | |||||||||||||
| Obs. | Mean | S.d. | Mean | S.d. | Mean | S.d. | Mean | S.d. | Mean | S.d. | Mean | S.d. | ||
| T1 and T2 | 432 | 8.444 | 6.224 | 10.542 | 6.467 | 5.597 | 4.666 | 3.639 | 4.391 | 2.097 | 3.139 | 2.847 | 4.746 | 0.259 |
| T1 | 216 | 10.000 | 6.173 | 12.333 | 6.115 | 6.824 | 4.984 | 4.685 | 4.912 | 2.333 | 2.893 | 3.176 | 4.854 | 0.471 |
| T2 | 216 | 6.889 | 5.889 | 8.750 | 6.324 | 4.370 | 3.971 | 2.593 | 3.512 | 1.861 | 3.358 | 2.519 | 4.624 | 0.333 |
| WRST | 0.000 | 0.000 | 0.000 | 0.000 | 0.001 | 0.023 | ||||||||
| yes-no game (YN) | ||||||||||||||
| y | WSRST | |||||||||||||
| Obs. | Mean | S.d. | Mean | S.d. | Mean | S.d. | Mean | S.d. | Mean | S.d. | Mean | S.d. | ||
| T1 and T2 | 432 | 7.421 | 6.918 | 8.958 | 7.470 | 4.440 | 4.854 | 0.986 | 0.117 | 1.537 | 2.813 | 2.981 | 5.261 | 0.000 |
| T1 | 216 | 8.546 | 6.927 | 10.352 | 7.495 | 5.259 | 5.051 | 0.991 | 0.096 | 1.806 | 2.871 | 3.287 | 5.414 | 0.008 |
| T2 | 216 | 6.296 | 6.739 | 7.565 | 7.195 | 3.620 | 4.514 | 0.981 | 0.135 | 1.269 | 2.735 | 2.676 | 5.097 | 0.002 |
| WRST | 0.000 | 0.000 | 0.000 | 0.412 | 0.004 | 0.023 | ||||||||
| impunity game (IG) | ||||||||||||||
| y | WSRST | |||||||||||||
| Mean | S.d. | Mean | S.d. | Mean | S.d. | Mean | S.d. | Mean | S.d. | Mean | S.d. | |||
| T1 and T2 | 432 | 5.968 | 6.402 | 7.569 | 7.449 | 3.148 | 3.970 | 2.315 | 3.592 | 1.602 | 3.138 | 2.819 | 5.065 | 0.000 |
| T1 | 216 | 6.574 | 6.629 | 8.148 | 7.599 | 3.333 | 4.012 | 2.454 | 4.259 | 1.574 | 3.069 | 3.241 | 5.675 | 0.006 |
| T2 | 216 | 5.361 | 5.361 | 6.991 | 6.991 | 2.963 | 2.963 | 2.176 | 2.176 | 1.630 | 1.630 | 2.398 | 2.398 | 0.011 |
| WRST | 0.059 | 0.146 | 0.422 | 0.162 | 0.844 | 0.309 | ||||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | |
|---|---|---|---|---|---|---|---|---|---|
| UG | YN | IG | UG | YN | IG | UG | YN | IG | |
| L.Proposer | 0.61 | 1.38 * | 4.97 *** | 0.40 | 1.47 * | 6.21 *** | 0.52 | 1.36 ** | 4.48 *** |
| (0.40) | (0.79) | (1.41) | (0.41) | (0.85) | (1.49) | (0.33) | (0.67) | (1.31) | |
| L.Profit | −0.02 | −0.13 ** | −0.30 *** | −0.04 | −0.15 ** | −0.39 *** | −0.04 * | −0.14 *** | −0.30 *** |
| (0.03) | (0.06) | (0.08) | (0.03) | (0.06) | (0.08) | (0.02) | (0.05) | (0.07) | |
| Round | 0.16 | −0.09 | −0.36 | 0.25 | −0.15 | −0.30 | 0.25 | −0.38 | −0.15 |
| (0.26) | (0.28) | (0.28) | (0.21) | (0.27) | (0.27) | (0.25) | (0.25) | (0.32) | |
| Odd | −0.12 | 0.01 | −0.94 | 0.12 | −0.27 | −1.34 ** | −1.03 *** | −0.39 | −1.14 ** |
| (0.41) | (0.54) | (0.61) | (0.38) | (0.55) | (0.63) | (0.31) | (0.43) | (0.50) | |
| Treatment | −2.07 *** | −2.00 ** | −0.89 | −2.10 *** | −2.01 ** | −0.76 | −1.61 *** | −1.35 ** | −0.18 |
| (0.49) | (0.80) | (0.81) | (0.51) | (0.81) | (0.87) | (0.37) | (0.62) | (0.60) | |
| Cons | 6.23 *** | 6.08 *** | 4.88 *** | 7.40 *** | 7.58 *** | 5.95 *** | 4.53 *** | 4.52 *** | 1.91 |
| (1.05) | (1.51) | (1.44) | (1.02) | (1.55) | (1.47) | (0.84) | (1.31) | (1.29) | |
| cons | 3.27 *** | 4.79 *** | 4.77 *** | 3.29 *** | 4.90 *** | 5.14 *** | 2.56 *** | 3.67 *** | 3.60 *** |
| (0.20) | (0.31) | (0.35) | (0.17) | (0.29) | (0.32) | (0.15) | (0.29) | (0.31) | |
| N | 288 | 288 | 288 | 288 | 288 | 288 | 288 | 288 | 288 |
| LL | −708.49 | −652.48 | −608.18 | −736.86 | −698.38 | −666.38 | −611.11 | −529.90 | −466.66 |
| pseudo | 0.02 | 0.01 | 0.02 | 0.02 | 0.01 | 0.02 | 0.03 | 0.02 | 0.04 |
| F | 4.41 | 2.65 | 4.89 | 4.50 | 2.68 | 6.43 | 6.66 | 3.93 | 5.65 |
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
| UG | IG | UG | IG | UG | IG | |
| L.Proposer | −1.29 * | 4.57 ** | −1.74 ** | 5.60 ** | −1.33 ** | 2.85 |
| (0.75) | (2.20) | (0.72) | (2.39) | (0.58) | (1.84) | |
| L.success | −0.81 | 1.03 | −0.54 | 1.51 | −1.02 * | 0.80 |
| (0.70) | (0.95) | (0.75) | (1.05) | (0.57) | (0.75) | |
| L.success×L.Prop | 2.95 *** | 0.51 | 3.43 *** | 0.75 | 2.82 *** | 1.65 |
| (0.92) | (1.54) | (0.87) | (1.70) | (0.71) | (1.22) | |
| L.Profit | −0.07 | −0.30 *** | −0.12 *** | −0.38 *** | −0.08 ** | −0.27 *** |
| (0.04) | (0.09) | (0.04) | (0.10) | (0.04) | (0.08) | |
| Round | 0.17 | −0.32 | 0.26 | −0.24 | 0.25 | −0.08 |
| (0.27) | (0.29) | (0.22) | (0.28) | (0.26) | (0.34) | |
| Treatment | −2.08 *** | −0.76 | −2.12 *** | −0.56 | −1.62 *** | −0.04 |
| (0.48) | (0.82) | (0.49) | (0.87) | (0.35) | (0.59) | |
| Odd | −0.19 | −0.79 | 0.03 | −1.12 * | −1.11 *** | −0.96 * |
| (0.41) | (0.60) | (0.37) | (0.62) | (0.30) | (0.49) | |
| Cons | 7.13 *** | 3.86 ** | 8.34 *** | 4.46 *** | 5.49 *** | 0.89 |
| (1.08) | (1.65) | (1.04) | (1.61) | (0.86) | (1.45) | |
| cons | 3.21 *** | 4.74 *** | 3.20 *** | 5.06 *** | 2.48 *** | 3.52 *** |
| (0.20) | (0.36) | (0.17) | (0.32) | (0.15) | (0.30) | |
| N | 288 | 288 | 288 | 288 | 288 | 288 |
| LL | −708.49 | −608.18 | −736.86 | −666.38 | −611.11 | −466.66 |
| pseudo | 0.03 | 0.02 | 0.03 | 0.03 | 0.05 | 0.05 |
| F | 4.46 | 4.78 | 5.63 | 6.72 | 7.97 | 6.62 |
| Proposer Payoff (UG) | Responder Payoff (UG) | |||||
| Freq. | % | Mean | Std. Dev | Mean | Std. Dev | |
| Rejected deals | 126 | 29.167 | 0.000 | 0.000 | 0.000 | 0.000 |
| Accepted deals | 306 | 70.833 | 13.660 | 5.149 | 8.771 | 5.091 |
| Total | 432 | 100 | 9.676 | 7.581 | 6.213 | 5.856 |
| Proposer Payoff (YN) | Responder Payoff (YN) | |||||
| Freq. | % | Mean | Std. Dev | Mean | Std. Dev | |
| Rejected deals | 6 | 1.389 | 0.000 | 0.000 | 0.000 | 0.000 |
| Accepted deals | 426 | 98.611 | 16.958 | 5.218 | 5.521 | 5.195 |
| Total | 432 | 100 | 16.722 | 5.550 | 5.444 | 5.199 |
| Proposer Payoff (IG) | Responder Payoff (IG) | |||||
| Freq. | % | Mean | Std. Dev | Mean | Std. Dev | |
| Rejected deals | 156 | 36.111 | 21.128 | 2.054 | 0.000 | 0.000 |
| Accepted deals | 276 | 63.889 | 17.478 | 5.071 | 5.210 | 4.867 |
| Total | 432 | 100 | 18.796 | 4.581 | 3.329 | 4.624 |
| Proposer Payoff (UG) | Responder Payoff (UG) | |||||
| Freq. | % | Mean | Std. Dev | Mean | Std. Dev | |
| Rejected deals | 22528 | 24.832 | 0 | . | 0 | . |
| Accepted deals | 68192 | 75.168 | 12.024 | 4.680 | 10.531 | 4.592 |
| Total | 90720 | 100 | 9.038 | 6.592 | 7.916 | 6.046 |
| Proposer Payoff (IG) | Responder Payoff (IG) | |||||
| Freq. | % | Mean | Std. Dev | Mean | Std. Dev | |
| Rejected deals | 39725 | 43.789 | 21.292 | 1.584 | 0 | . |
| Accepted deals | 50995 | 56.211 | 16.815 | 4.601 | 5.675 | 4.609 |
| Total | 90720 | 100 | 18.775 | 4.235 | 3.190 | 4.457 |
| Ultimatum Game | |||||
| Obs. | y | ||||
| Always Immune | 72 | 4.639 | 4.639 | 4.639 | 2.000 |
| Always Reacting | 48 | 10.604 | 14.271 | 6.938 | 4.979 |
| WRST | 0.000 | 0.000 | 0.000 | 0.000 | |
| Yes-No Game | |||||
| Obs. | y | ||||
| Always Immune | 117 | 3.103 | 3.103 | 3.103 | 1.000 |
| Always Reacting | 66 | 10.212 | 13.606 | 6.455 | 0.955 |
| WRST | 0.000 | 0.000 | 0.000 | 0.020 | |
| Impunity Game | |||||
| Obs. | y | ||||
| Always Immune | 129 | 0.899 | 0.899 | 0.899 | 1.039 |
| Always Reacting | 57 | 10.263 | 15.281 | 5.526 | 3.947 |
| WRST | 0.000 | 0.000 | 0.000 | 0.000 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Cagno, D.; Galliera, A.; Güth, W.; Panaccione, L. Intention-Based Sharing. Games 2018, 9, 22. https://doi.org/10.3390/g9020022
Di Cagno D, Galliera A, Güth W, Panaccione L. Intention-Based Sharing. Games. 2018; 9(2):22. https://doi.org/10.3390/g9020022
Chicago/Turabian StyleDi Cagno, Daniela, Arianna Galliera, Werner Güth, and Luca Panaccione. 2018. "Intention-Based Sharing" Games 9, no. 2: 22. https://doi.org/10.3390/g9020022
APA StyleDi Cagno, D., Galliera, A., Güth, W., & Panaccione, L. (2018). Intention-Based Sharing. Games, 9(2), 22. https://doi.org/10.3390/g9020022




