Voluntary Disclosure of Private Information and Unraveling in the Market for Lemons: An Experiment

Abstract

We experimentally analyze a lemons market with a labor-market framing. Sellers are referred to as “workers” and have the possibility to provide “employers” with costly but credible information about their “productivity”. Economic theory suggests that in this setup, unraveling takes place and a number of different types are correctly identified in equilibrium. While we do observe a substantial degree of information disclosure, we also find that unraveling is typically not as complete as predicted by economic theory. The behavior of both workers and employers impedes unraveling in that there is too little disclosure. Workers are generally reluctant to disclose their private information, and employers enforce this behavior by bidding less competitively if workers reveal compared to the case where they conceal information.

1. Introduction

Information asymmetries are fundamentally important for many markets. In the labor market, firms seek to hire outstanding employees, but there is no way they can accurately predict which candidates will turn out best. Insurance companies or banks need to minimize their risk exposure by selecting their customers appropriately. However, they cannot easily distinguish between clients they should do business with and clients they should avoid. Hence, all these companies face the same basic problem. They need personal information on their prospective trade partners—information that enables them to make adequate decisions.

One possible way to resolve such information asymmetries is that agents voluntarily provide the other party with credible information on their type. In the economics literature this is sometimes referred to as the “certification solution to the lemons problem.” The general idea is that the agent acquires a potentially costly certificate which can be passed on to the other party. The other party then decides whether and at which price they will trade with the agent. In theory, this will trigger an unraveling process in that more and more agents will find it in their interest to disclose similar information. If the price of such certification is negligible there will be complete unraveling. That means, in equilibrium all player types are correctly identified. This approach was first suggested by Viscusi [1]. Similar concepts have, for example, been analyzed by Milgrom [2] or Milgrom and Roberts [3]. Jovanovic [4] points out that a game where revelation comes at a positive cost may result in complete, incomplete or even non-existent unraveling.

If the information to be disclosed is sensitive, unraveling may constitute a severe threat to personal privacy.1 For instance, the insurance industry has developed novel tariffs where customers may save on their premiums if they provide credible information on their behavior. In the case of car insurance, this is typically achieved using GPS devices which automatically upload data relaying the driving behavior to the insurer. Naturally, this also implies that the insurer will receive personal information such as geographical location and movement patterns. A similar innovation has been introduced in the domain of life insurance. Here, some tariffs use customers’ smartphones to measure and upload activity levels and other data. Again, customers get a discount if they disclose sensitive data about their personal lifestyle. A different example relates to the labor market. Online services such as www.mybackgroundcheck.com enable applicants to provide potential employers with verified information on their personal background. Currently, such checks are mostly limited to criminal records, but additional information may be considered if such certification becomes more popular. In theory, agents may have an incentive to provide more detailed information possibly including medical records and drug or pregnancy tests.2

In all examples, it is usually emphasized that the disclosure of personal data takes place on a voluntary basis, but because of unraveling such decisions may not be as voluntary as it initially seems. The reason is that not providing personal information may be interpreted as a bad signal such that consumers seeking insurance may find it difficult to find a tariff which does not jeopardize their privacy at a reasonable price. The intuition for this is as follows. Since the new tariffs are most attractive to those with lowest risks, such customers should sort themselves into the new tariffs. This may cause the premiums for the classical tariffs to rise because the low-risk customers are no longer participating in them. In other words, not providing similar information may be interpreted as a signal of high risk and those who do not wish to share sensitive personal information with their insurance company may face rising premiums. A similar problem may occur in the labor market. In a world where (nearly) everybody has the possibility to provide credible personal information, the refusal to do so may be interpreted as a bad signal. In this case, applicants who refuse to provide sensitive information may find it more difficult to get a job.3

In the present paper, we analyze unraveling of privacy in a laboratory experiment. We use a labor market with a lemons structure where workers have the possibility to provide employers with credible information on their productivity. We examine the unraveling problem from two different perspectives. First, we compare the degree of unraveling in the full game with a game where the computer plays the role of the employers. This enables us to infer whether the behavior of the receivers affects unraveling in a dampening or in a reinforcing manner. Note that we are not aware of another study with a direct comparison of both situations. The second dimension is the cost of revelation. We compare the situation where revelation comes at a substantial cost to a situation where the cost of revelation is negligible. The motivation for this comparison is twofold. First, in the field both situations are applicable. While installing an app on a smartphone or sharing a password for a website are practically free of charge, the other examples may involve the work of experts such as medical doctors, which may result in a significant cost of revelation. The second reason to vary the cost of revelation lies in the related literature. So far, there is only one experiment that assumes a significant cost of revelation [13]. However, the same paper also refrains from modeling employers as players such that the results cannot really be related to those of other studies which assume that revelation is free of charge and consider the full game (e.g., [14,15]).

There are three experiments which are closely related to our research.4 All these studies analyze the unraveling of private information in experimental lemons markets. The first paper is an early contribution by Forsythe et al. [14] which focuses on the bidding behavior of the buyers (employers) and which observes a substantial degree of unraveling. The experiments are framed neutrally (generic goods and valuations) and the cost of revelation is assumed to be zero. Moreover, there is only one parameterization that is repeated in each period. These aspects may have encouraged the high degree of unraveling reported by Forsythe et al. [14]. An experiment by Jin et al. [15] also tackles unraveling in a framework where revelation is free of charge and where the parameterization does not change over time. The authors report that there is less unraveling than predicted by theory. The third paper is an experiment by Benndorf et al. [13]. The authors not only use a loaded labor market frame, their setup also comprises different parameterizations and assumes positive costs of revelation. Like Jin et al. [15] the authors report that there is less unraveling than predicted by economic theory. However, the study focuses exclusively on the disclosure behavior of the workers. Employers are not played by actual lab participants, they are substituted by the computer using a suitable payoff function. This may, of course, also influence the degree of unraveling observed. In the present study, we close the gap between the papers by Forsythe et al. [14], Jin et al. [15], and Benndorf et al. [13]. We not only provide a direct comparison between the games with and without employers, but we also test whether the cost of revelation has any unpredicted effect on unraveling.

We find that introducing employers as human players promotes the early steps of unraveling but dampens later ones. In our labor market framing this means that high types of workers are more likely, and low types of workers are less likely, to disclose their productivity in the game with employers compared to the game without employers. We will argue that the latter effect is driven by the behavior of the employers who bid less competitively if the productivity of the worker is known. In other words, employers are able to extract a positive rent if the worker discloses her productivity, but they are unable to do so if the worker does not disclose her private information. These (unpredicted) profits of the employers may therefore be interpreted as an additional cost of revelation which causes the unraveling process to stop earlier than the standard model suggests. We also find that reducing the costs of revelation to a negligible degree results in a dramatic increase of unraveling, which is in line with the theoretical predictions. This is, however, not to suggest that reducing the costs generally increases the consistency of the theoretical predictions and the experimental results. In some conditions, experimental behavior is more in line with the theoretical predictions if the cost of revelation is low, but there is also one parameterization where decreasing the costs reduces consistency.

The remainder of the paper is organized as follows: Section 2 discusses the theoretic aspects of the game with employers and derives the equilibrium predictions. Section 3 describes the experimental design and procedures and comments on the parameterizations used in the experiment. In Section 4, we derive a few behavioral hypotheses. The results are presented in Section 5 and discussed in Section 6 and Section 7 concludes.

2. The Game

There are three players: one worker and two employers, and there are n different types of workers. These types are heterogeneous with respect to their productivity $\theta$ which is drawn from a set of possible productivities $\mathsf{\Theta }=\left\{{\theta }_1,{\theta }_2,\dots ,{\theta }_n\right\}$ with ${\theta }_1<{\theta }_2<\dots <{\theta }_n$. The exact realization $\theta$ is ex ante private information of the worker, but the set $\mathsf{\Theta }$ and the fact that all possible productivities are equally likely are common knowledge. The employers will competitively bid wages in order to hire the worker. They are identical and move simultaneously. All players are assumed to be risk neutral.

We first consider the timing of the revelation game. The first two stages are depicted in Figure 1. In stage zero, nature determines the worker’s type. In stage one, the worker decides whether or not to disclose her type (in other words, whether to reveal or to conceal her productivity) to the employers. In stage two, the employers simultaneously bid wages in order to hire the worker. In the final stage, the worker accepts one of the offers she received.5

Next, we describe the notation of players’ strategies. A revelation strategy of the worker is denoted by $\sigma =\{{\sigma }_1,\dots ,{\sigma }_n\}$ where ${\sigma }_i\in [0;1]$ is the probability that the worker will choose to reveal as type ${\theta }_i$.6 Employers’ bidding strategies are denoted by $b\left(H\right)$ where H refers to the different information sets the employers may reach.

Players’ payoffs can be summarized as follows: a worker accepting an employer’s bid will receive that bid as a wage payment but, if she reveals, she has to pay a fixed cost c for the certification process. The employers have an endowment $\gamma$ that is independent of their decisions. However, all further profits depend on whether or not an employer hires the worker (determined by whose bid is accepted). If b denotes the wage bid accepted by the worker, while c and $\theta$ represent the cost of revelation and the worker’s productivity, respectively, the profits of the worker (${\pi }^W$) and the employers (${\pi }^E$) are given by:

$${\pi }^W=\{\begin{array}{cc}b\hfill & \mathrm{if}\mathrm{worker}\mathrm{conceals}\hfill \\ b-c\hfill & \mathrm{if}\mathrm{worker}\mathrm{reveals}\hfill \end{array}{\pi }^E=\{\begin{array}{cc}\gamma +\theta -b\hfill & \mathrm{if}\mathrm{own}\mathrm{bid}\mathrm{was}\mathrm{accepted}\hfill \\ \gamma \hfill & \mathrm{otherwise}.\hfill \end{array}$$

The employers need to form a system of beliefs specifying a probability ${\beta }_x^H\in [0;1]$ to all decision nodes x in information set H with ${\sum }_{x\in H}{\beta }_x^H=1$ for all information sets $H\in \mathcal{H}$, where $\mathcal{H}$ is the set of employers’ information sets. From Figure 1 we learn that employers have $n+1$ information sets including n singletons that are reached upon revelation. These information sets are denoted by $H_1,\dots ,H_n$ where $H_i$ is the information set where the worker is of type ${\theta }_i$. At $H_1,\dots ,H_n$ employers’ beliefs are trivially equal to one. In our formal notation, that is, ${\beta }^{H_1}=\dots ={\beta }^{H_n}=1$. The only non-singleton information set is labeled $H_C$, and it is reached if the worker chooses to conceal. Here, employers need to form non-degenerate beliefs, i.e., they need to assign a probability to each of the n decision nodes. Let ${\beta }^{H_C}=\{{\beta }_1^{H_C},\dots ,{\beta }_n^{H_C}\}$ denote the employers’ belief at $H_C$ where ${\beta }_i^{H_C}$ is the probability the employers will assign to being matched with a worker of type ${\theta }_i$. Reaching the non-singleton $H_C$ is on the equilibrium path since at least type ${\theta }_1$ will conceal in equilibrium.7 Hence, the beliefs can be calculated using Baye’s rule. Employers’ beliefs after reaching the information set $H_C$ are therefore given by:

$$\begin{array}{c}\hfill {\beta }^{H_C}=\left\{{\beta }_1^{H_C},\dots ,{\beta }_n^{H_C}|{\beta }_i^{H_C}=\frac{1-{\sigma }_i}{{\sum }_{j=1}^{n}1-{\sigma }_j}\forall i\in \{1,\dots ,n\}\right\}\end{array}$$

The revelation game is a dynamic game with incomplete information such that the Perfect Bayesian Equilibrium (PBE) is an appropriate solution concept. In such an equilibrium, players’ strategies have to be sequentially rational, and beliefs need to be consistent with the strategies on the equilibrium path.8 Hence, any PBE of the revelation game comprises the following components:

(i)

The worker’s revelation strategy $\sigma$: a function mapping $\mathsf{\Theta }$ into reveal decisions.

(ii)

The employers’ bidding strategy $b\left(H\right)$: a function mapping all information sets $H\in \mathcal{H}$ into bids.

(iii)

The worker’s acceptance strategy: a function mapping bids into accept decisions (not formalized further for brevity).

(iv)

A system of beliefs $\beta =\{{\beta }^{H_1},\dots ,{\beta }^{H_n},{\beta }^{H_C}\}$ as described above.

In the third stage, the worker will accept the higher wage if the employers choose different bids or a random bid if they are identical. As a consequence, in the second stage, employers will bid the observed productivity if the worker chose to reveal, as the corresponding information sets are all singletons. If the worker concealed her productivity, employers need to base their decision on their beliefs ${\beta }^{H_C}$ and will bid the expected productivity given ${\beta }^{H_C}$. Hence, employers will choose the following bidding function in equilibrium:

$$b(H)=\{\begin{array}{cc}{\theta }_i\hfill & \mathit{if}H=H_i\mathrm{with}i\in \{1,\dots ,n\}\hfill \\ {\displaystyle \sum _{j=1}^n}{\beta }_j^{H_C}{\theta }_j\hfill & \mathit{if}H=H_C\hfill \end{array}$$

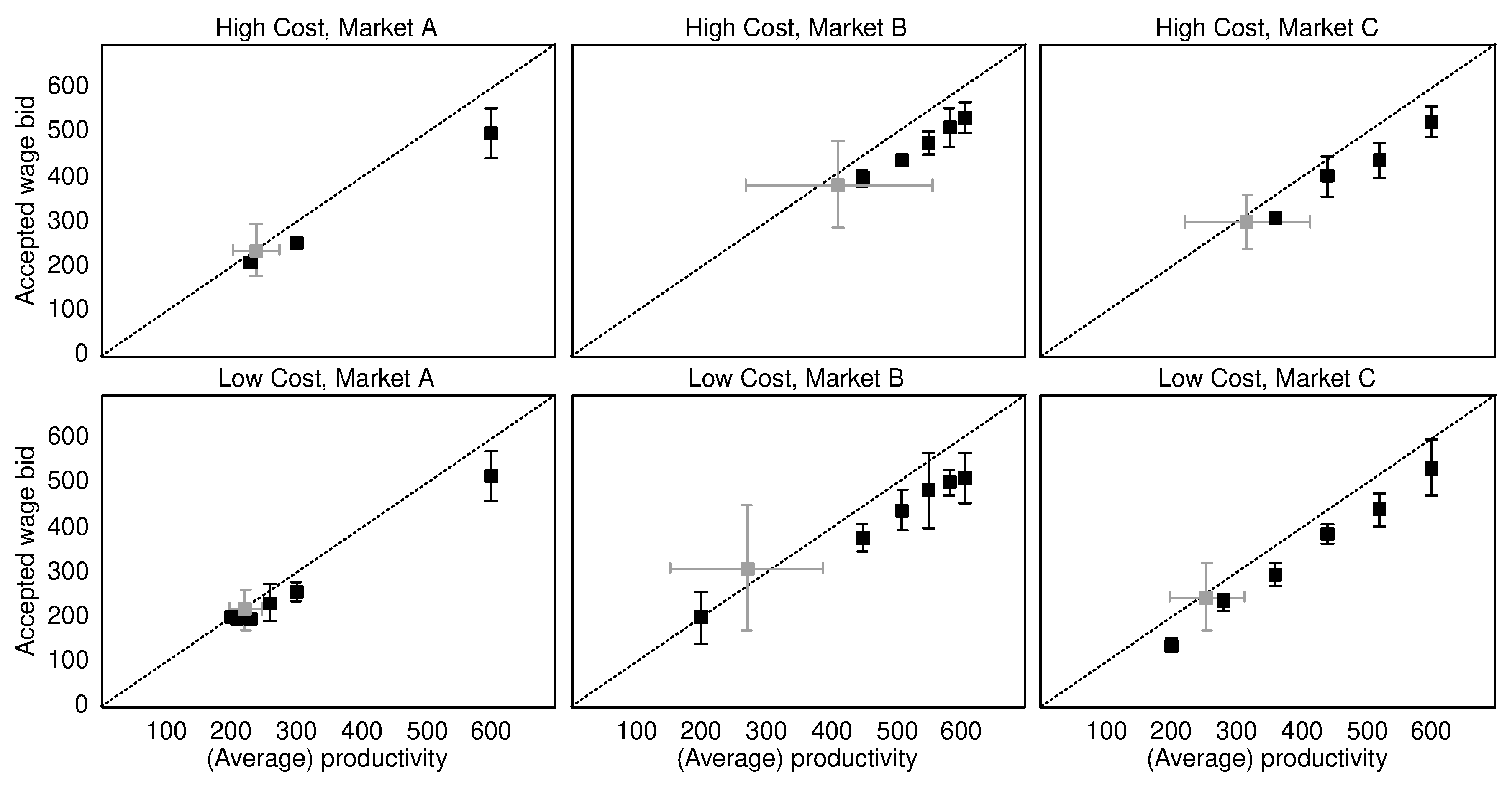
These bidding strategies imply that the worker will receive the entire (expected) rent, independent of her revelation decision. The employers gain nothing from hiring the worker. Apart from their endowment $\gamma$, they will both receive zero (expected) profits, independent of whether or not their bid is accepted.

In equilibrium, the worker’s revelation strategy $\sigma$ will have a special pattern. Since ${\theta }_1<{\theta }_2<\dots <{\theta }_n$, the first few types will choose to conceal while the last few types prefer to reveal. Assume w.l.o.g that m is the highest wage either of the employers offer after observing concealment. If type ${\theta }_j$ prefers concealing to revealing for a given amount m, all other types ${\theta }_i$ with ${\theta }_i<{\theta }_j$ prefer to conceal as well. If ${\theta }_j$ prefers to conceal, we have ${\theta }_j-c\le m$. If this inequality is satisfied for ${\theta }_j$, it is also satisfied for all types with lower productivities, i.e., for all ${\theta }_i<{\theta }_j$. An analogous argument can be made for the case where ${\theta }_j$ and all types of higher productivities prefer to reveal. Hence, for any realization of m there will always be exactly one threshold $k\in \{1,\dots ,n\}$ such that all types ${\theta }_i$ with $i\le k$ weakly prefer concealing to revealing, while all types ${\theta }_j$ with $j>k$ strictly prefer revealing to concealing. Note that depending on m, type ${\theta }_k$ herself may also be indifferent between revealing and concealing. As a consequence, in any PBE of the revelation game, the worker’s revelation strategy $\sigma$ has the form:

$$\begin{array}{cc}\hfill \sigma & =\{{\sigma }_1=\dots ={\sigma }_{k-1}=0,{\sigma }_k,{\sigma }_{k+1}=\dots ={\sigma }_n=1\}\mathrm{with}k\in \{1,\dots ,n\}\mathrm{and}{\sigma }_k\in [0;1].\hfill \end{array}$$

Applying this form of the worker’s revelation strategy to the employers’ system of beliefs as defined above, we obtain the employers’ beliefs upon observing concealment:

$$\begin{array}{c}\hfill {\beta }^{H_C}=\left\{{\beta }_1^C=\dots ={\beta }_{k-1}^C=\frac{1}{k-{\sigma }_k},{\beta }_k^C=\frac{1-{\sigma }_k}{k-{\sigma }_k},{\beta }_{k+1}^C=\dots ={\beta }_n^C=0\right\}\end{array}$$

and their bidding function:

$$b\left(H\right)=\{\begin{array}{cc}{\theta }_i\hfill & \mathit{if}H=H_i\mathrm{with}i\in \{1,\dots ,n\}\hfill \\ \frac{(1-{\sigma }_k){\theta }_k+{\sum }_{j=1}^{k-1}{\theta }_j}{k-{\sigma }_k}\hfill & \mathit{if}H=H_C\hfill \end{array}$$

The revelation strategy $\sigma$, the bidding function $b\left(H\right)$, the verbal description of the worker’s acceptance strategy, and employers’ set of beliefs $\beta$ define a PBE of the revelation game, if $\sigma$ constitutes a best response for each type of the worker given the employers’ set of beliefs $\beta$ and bidding function $b\left(H\right)$.

The equilibria depend on the parameters $\mathsf{\Theta }$ and c which define the threshold k and the corresponding ${\sigma }_k$. Note that the equilibria and the thresholds k are not necessarily unique. If there are several thresholds k, the game will also have multiple equilibria. This does not, however, occur in the parameterizations used in the experiments.9 However, multiplicity of equilibria may also arise even if there is only one threshold k. Whenever there is an equilibrium system of beliefs resulting in a bid after observing concealment leaving type ${\theta }_k$ indifferent between revealing and concealing (i.e., $b\left(H_C\right)={\theta }_k-c$), there will be up to three equilibria: one where ${\theta }_k$ conceals (${\sigma }_k=0$), one where ${\theta }_k$ reveals (${\sigma }_k=1$), and possibly one where ${\theta }_k$ chooses a completely mixed strategy with ${\sigma }_k\in [0;1]$.10 This also occurs in one of the combinations we use in the experiments. In Section 3 the corresponding parameterization is introduced as High Cost—Market C and the equilibria are described in

Table 1. Parameterizations and equilibrium predictions for the games used in the experiment.

Market A					Market B					Market C
$\mathsf{\Theta }$	LC		HC		$\mathsf{\Theta }$	LC		HC		$\mathsf{\Theta }$	LC		HC1		HC2		HC3
	$\mathit{\sigma }$	${\mathit{\beta }}^{{\mathit{H}}_{\mathit{C}}}$	$\mathit{\sigma }$	${\mathit{\beta }}^{{\mathit{H}}_{\mathit{C}}}$		$\mathit{\sigma }$	${\mathit{\beta }}^{{\mathit{H}}_{\mathit{C}}}$	$\mathit{\sigma }$	${\mathit{\beta }}^{{\mathit{H}}_{\mathit{C}}}$		$\mathit{\sigma }$	${\mathit{\beta }}^{{\mathit{H}}_{\mathit{C}}}$	$\mathit{\sigma }$	${\mathit{\beta }}^{{\mathit{H}}_{\mathit{C}}}$	$\mathit{\sigma }$	${\mathit{\beta }}^{{\mathit{H}}_{\mathit{C}}}$	$\mathit{\sigma }$	${\mathit{\beta }}^{{\mathit{H}}_{\mathit{C}}}$
200	0	1	0	$\frac{1}{5}$	200	0	1	0	1	200	0	1	0	$\frac{1}{3}$	0	$\frac{1}{2}$	0	$\frac{5}{12}$
210	1	0	0	$\frac{1}{5}$	448	1	0	1	0	280	1	0	0	$\frac{1}{3}$	0	$\frac{1}{2}$	0	$\frac{5}{12}$
230	1	0	0	$\frac{1}{5}$	510	1	0	1	0	360	1	0	0	$\frac{1}{3}$	1	0	$\frac{2}{5}$	$\frac{2}{12}$
260	1	0	0	$\frac{1}{5}$	551	1	0	1	0	440	1	0	1	0	1	0	1	0
300	1	0	0	$\frac{1}{5}$	582	1	0	1	0	520	1	0	1	0	1	0	1	0
600	1	0	1	0	607	1	0	1	0	600	1	0	1	0	1	0	1	0
k	1		5		k	1		1		k	1		3		3		3
${\sigma }_k$	0		0		${\sigma }_k$	0		0		${\sigma }_k$	0		0		1		0.4
$b\left(H_C\right)$	200		240		$b\left(H_C\right)$	200		200		$b\left(H_C\right)$	200		280		240		260

of that section.

3. Experimental Design and Procedures

In the experiments, a random matching routine was used in combination with a fixed-roles-but-random-types design. In each session, there were 18 participants who were divided into 12 employers and six workers. This role assignment remained constant during the entire experiment, the productivity of the workers and the matching were, however, subject to change at the beginning of each period. Note that the random matching only determined which employers interacted with which workers, and that there were always the same six workers in one session.

We used six different parameterizations, each comprising a set of six possible productivities. The productivity of a worker was determined by a random draw of the computer,11 where each of the six possible productivities was chosen with equal probability. The random draw was conducted without replacement, such that each of the six possible productivities was attributed to exactly one worker in each period (as was mentioned in the instructions). Finally, six groups, each consisting of two employers and one worker, were randomly formed by the computer at the beginning of each period. Because of the random matching we conservatively count one session of 18 subjects as one independent observation.

The timing of the base game was as described in Section 2. The matching took place at the beginning of each period and the productivities of the workers were also determined then. Afterwards, everybody was presented with the parameterization to be played that period, and workers were informed about their productivities. In the first stage, workers decided whether or not to disclose their productivities. In the second stage, employers were informed of the decision of the worker in their group and needed to simultaneously bid wages for that worker. The support for the wage bids was the interval $[0;800]$, it did not depend on the current parameterization or the decision of the worker. In the third stage, the workers had to accept one of the two wage bids they had received. Finally, subjects were given a summary of the results in that period. Nobody received any information about the decisions of players outside their group.

Subjects’ payoff functions were equivalent to those presented in Section 2. In the experiments, employers received an endowment of $\gamma =200$ ECU each period to avoid biased behavior due to zero profits or losses.

During all experiments, we varied the set of possible productivities (labeled $\mathsf{\Theta }$ in Section 2). The different parameterizations were referred to as markets and were addressed using a within-subjects design. That is, they were played on a rotating basis.12 Subjects played six repetitions of each market such that there were 18 periods in total. The only difference between the markets was the set of possible productivities $\mathsf{\Theta }$.

We considered three different treatments labeled High Cost (or HC), Low Cost (or LC), and No Employers (or NE) in a between-subjects design. In HC and NE, disclosing one’s productivity comes at a cost of $c=100$. In LC, these costs are reduced to $c=1$. Apart from that, HC and LC are identical. The NE treatment is equivalent to HC except that the employers are played not by actual participants, but by a computer which is programmed to best-respond against workers’ behavior. In the game without employers, workers received their own productivity minus the cost of revelation if they decided to reveal, and the average productivity of all concealing workers if they decided not to reveal. Note that the equilibrium revelation rates in HC and NE are identical.

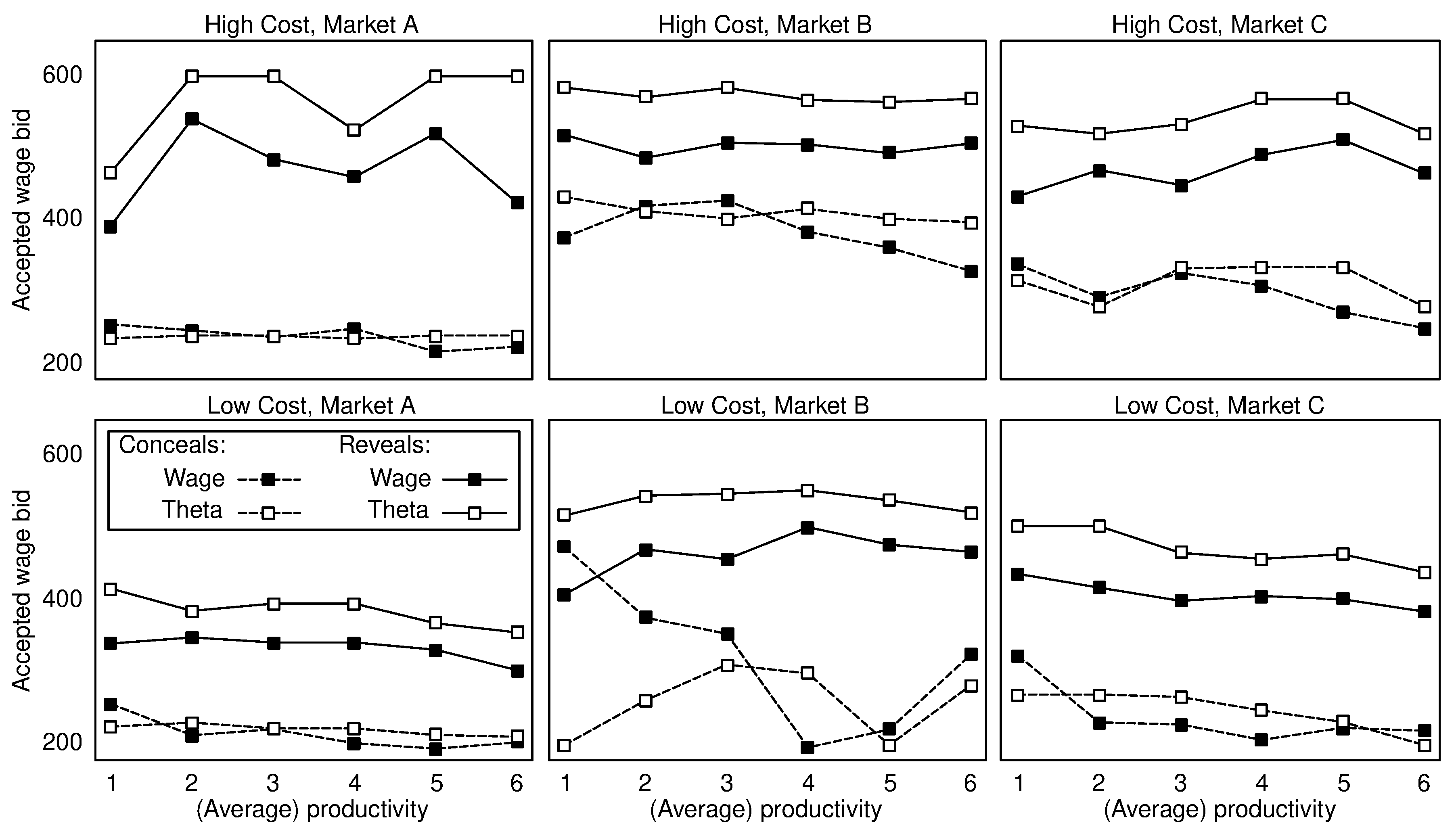
Table 1 summarizes the productivities and equilibrium predictions for the three markets in both treatments. We use the notation introduced in Section 2. Apart from the thresholds k and ${\sigma }_k$, we also report the revelation strategy of the worker $\sigma$ and employers’ beliefs and bids upon observing concealment. There is always a unique equilibrium, except for Market C in High Cost where we have three equilibria. In the table, these equilibria are denoted by HC1, HC2, and HC3. In the remainder of this paper, we only refer to HC1 and we neglect the other equilibria. HC1 is the one best in line with the experimental data, and the deviations would only be larger when comparing the data to the other equilibria.

Since the data for NE was gathered by Benndorf et al. [13] there are a few differences to the other treatments. First, the framing in NE is slightly different compared to the treatments with employers. In HC and LC, the productivity of the worker was simply referred to as “productivity” whereas it was framed as worker’s “health condition” in NE. This loaded framing might cause workers to reveal less often in the game without employers because it emphasizes the privacy aspect of the disclosure decision. We will come back to this issue in the results section. Second, there were fewer repetitions of the game (only five repetitions of each market instead of six) in NE than in other treatments. We do find that there is more learning in the game with employers compared to the game without employers, but this is not driven by the additional periods (see Section 5.3 for more details). The third difference is that we elicited subjects’ risk preferences for the game with employers, but not for the game without employers.13 Since this was separate from the main experiment, it does not appear very likely that it will affect the results in a meaningful way. Finally, the data for NE was elicited in Berlin whereas the data for HC and LC was gathered in Düsseldorf. While comparing data from two different subject pools is of course not ideal, we are, however, confident that there are no substantial subject-pool effects.14

The experiments using the game with employers (HC and LC) were conducted at the DICELab on the campus of the University of Düsseldorf. A total of 108 participants took part in these experiments, 54 of these in HC and LC, respectively. One session of the game with employers comprises 18 subjects: six workers and 12 employers. Because of the random matching, one session counts as one independent observation. Hence, we gathered a total of three independent observations for either treatment. Subjects’ earnings from the revelation game were aggregated over the 18 periods and converted into Euro at an exchange rate of ECU 400 = EUR 1. At the end of the experiment, subjects simultaneously received their payments from the revelation game and from the risk elicitation task. Average earnings were about EUR $15.66$ for an experiment that lasted about 90 min.

The data for the game without employers originates from Benndorf et al. [13]. The corresponding experiments took place in the lab at the Technical University Berlin. One session lasted about 60 min and another 72 subjects (12 independent observations) participated in these experiments.15 Average earnings in the game without employers were about EUR $10.76$.

4. Hypotheses

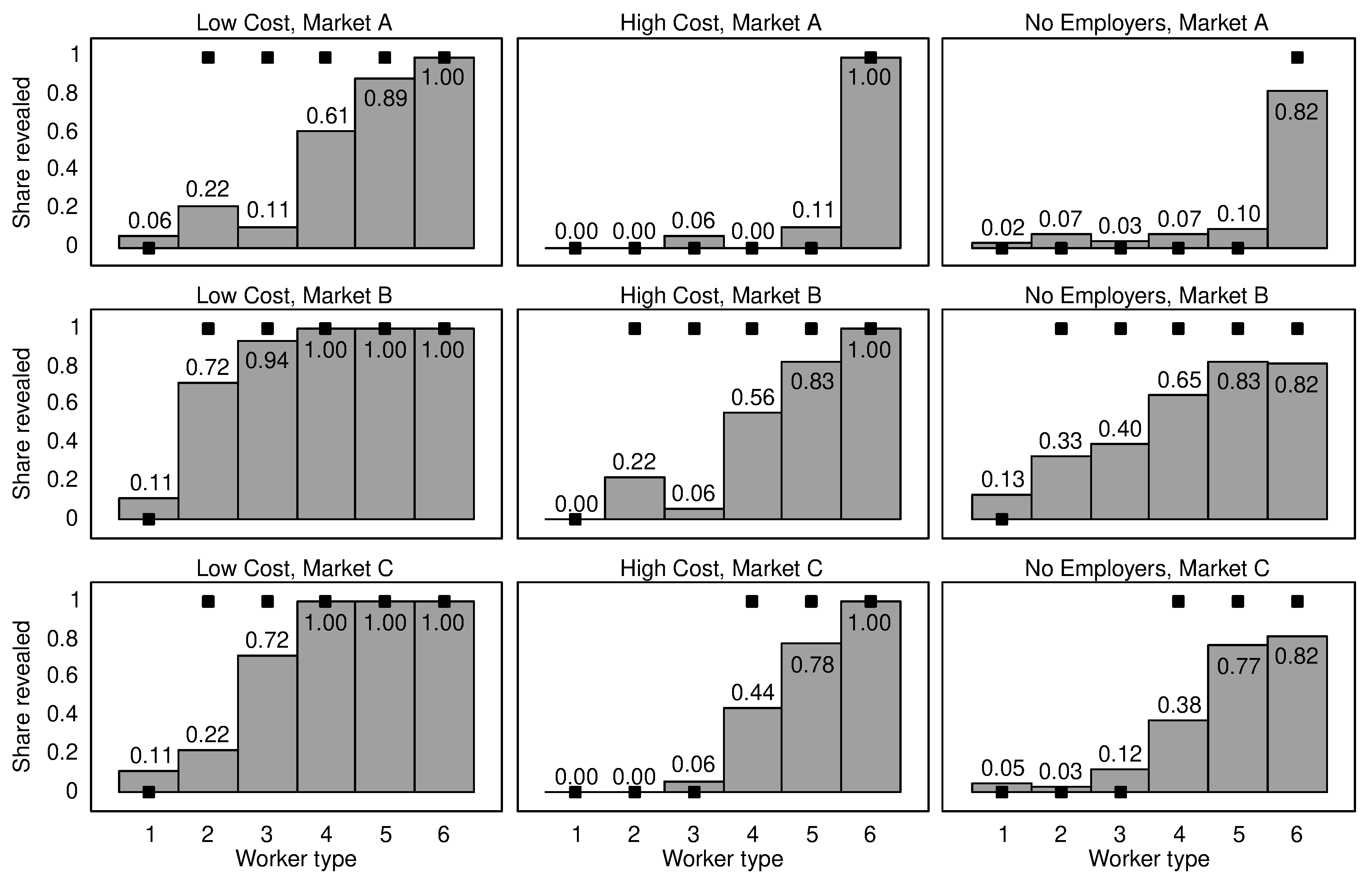
We expect revelation rates in Low Cost to be higher compared to the High Cost treatment. This expectation is in line with the theoretical predictions which suggest a global revelation rate of 83.33% in LC compared to only 50% in HC. The reason for this is as follows. The higher the cost of revelation, the less the types will have an incentive to reveal. Low-productivity types in particular would not find it in their interest to reveal their type if the cost of revelation was high.

Hypothesis 1.

Revelation rates in LC will be higher compared to HC.

The revelation rates will be lowest in Market A and highest in Market B in both our treatments. In HC, this pattern is in line with the predictions. Here, the equilibrium revelation rates are 16.67%, 83.33%, and 50% for the markets A, B, and C, respectively. This is in contrast to LC where the predicted rates are identical for all markets. However, there is still considerable variation in workers’ incentives to stick to their equilibrium actions. For instance, when deviating from revelation, a type-2 worker loses ECU 9 in Market A compared to ECU 79 and ECU 247 in markets C and B, respectively. Similar trade-offs also exist for the other types that should conceal in HC, but not in LC. Hence, we expect the ranking of revelation rates across markets to be identical in both treatments.

Hypothesis 2.

In both treatments, the degree of unraveling will be highest in Market B and lowest in Market A.

We expect to observe a positive correlation between the revelation rate and the productivity of the worker. This hypothesis is also consistent with economic theory. In our parameterizations, all worker types choose pure strategies in equilibrium. Since any pure-strategy equilibrium of the revelation game includes concealment of the first few types and revelation of types with higher productivities, the experimental data should show that low-productivity types reveal at lower frequencies compared to high-productivity types.

Hypothesis 3.

In all treatments and in all markets, we expect the revelation rates to increase in the type of the worker.

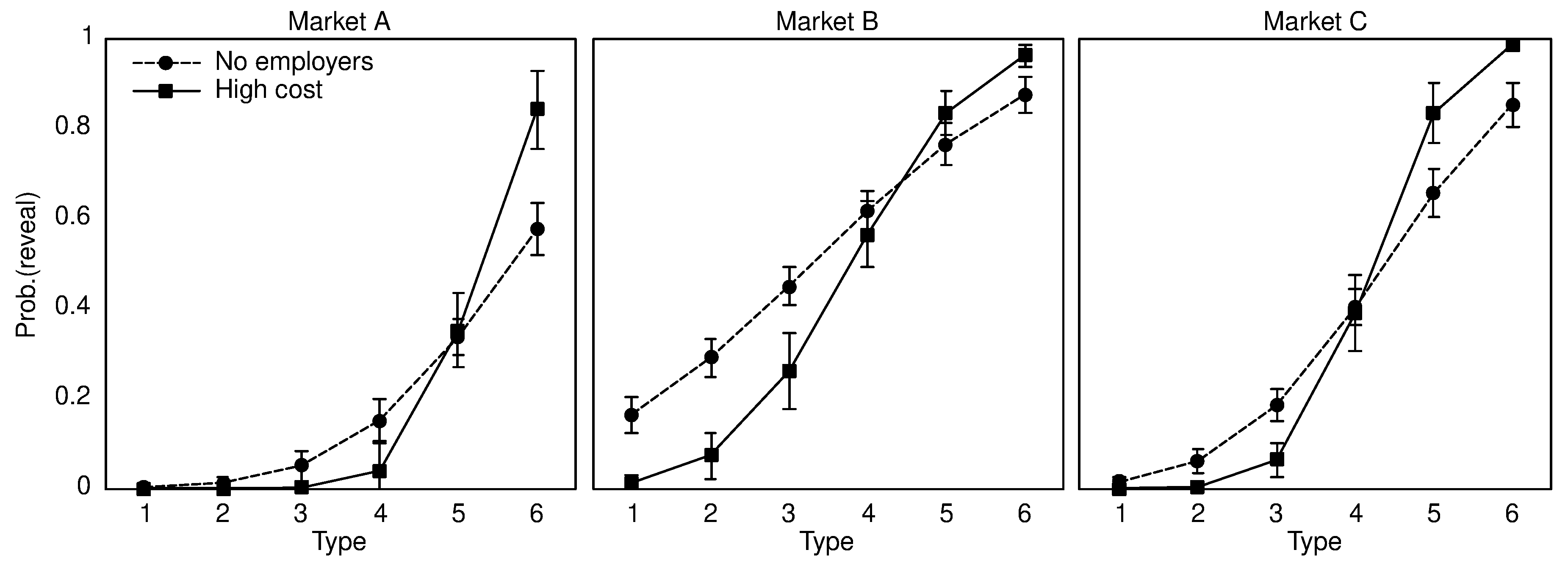
We refrain from formulating hypotheses concerning the behavior of the employers and the comparison of the games with and without employers. The reason is that it is not clear if introducing human employers affects behavior at all or whether or not there will be systematic differences when comparing the bidding behavior in the cases where the worker reveal or conceals. We will address these aspects in the results section, but these parts of the study are exploratory.

5. Results

In this section, we present our experimental results. It is structured as follows. In Section 5.1 we describe the revelation behavior of the workers. This subsection is split into two parts. In Section 5.1.1 we compare the High Cost and the Low Cost treatments, and in Section 5.1.2 the games with and without employers are compared. The behavior of the employers is described in Section 5.2. Section 5.3 comments on the development of decisions over time.

In total, we have 12 independent observations for the game without employers (NE) and three independent observations for either treatment of the game with employers (HC and LC). The reason for this discrepancy is that one independent observation for the game with employers comprises three times as many participants as one observation for the game without employers (12 employers and six workers instead of just six workers).16

5.1. Workers’ Decisions

The workers’ revelation decisions from all experiments are summarized in Figure 2. Each chart depicts the share of workers that choose to reveal as a certain type in a certain market in one of the three treatments. The charts are arranged such that the rows contain the observations from our markets A, B, and C, and the columns summarize the different treatments. Note that the charts also contain the equilibrium predictions which are indicated by black markers.

5.1.1. HC vs. LC

The data depicted in Figure 2 supports our first hypothesis: There is more revelation in High Cost compared to Low Cost. We find that about 65% of the workers’ decisions imply revelation in LC compared to only about 34% in HC. This difference is significant at the 5% level (one-sided Mann-Whitney U-test, $p=0.050$) which is evidence for Hypothesis 1.

As for the different markets, we find support for Hypothesis 2. Our HC data shows that about 19.4%, 44.4%, and 38.0% of the workers’ decisions imply revelation in markets A, B, and C, respectively. In our three HC sessions the average revelation rates were always lowest in Market A and always highest in Market B. This ranking is significant at the 5% level (one-sided Friedman test, $p=0.028$). In LC, we observe the same pattern, despite the fact that the revelation rates should be identical in equilibrium. However, because of the structure of workers’ incentives, this is not entirely unexpected. The ranking for LC is just as significant as the one for HC (one-sided Friedman test, $p=0.028$).

In the figure, there is also evidence for Hypothesis 3. Types with higher productivity generally reveal at higher frequencies compared to lower types. We find that there is a positive correlation between the workers’ types and their revelation decisions. To test this, we calculated Spearman’s $\rho$ between the workers’ revelation decisions and their type ranks (i.e., rank i, not type ${\theta }_i$) for our six independent observations and found that $\rho$ is significantly larger than zero (one-sided sign test, $p=0.016$).

Figure 2 also shows that types who should reveal in equilibrium more often deviate from their equilibrium action than types who should conceal in equilibrium. This is especially obvious in High Cost Market B and Low Cost Market A. Here, 100% and 94% of the types who conceal in equilibrium stick to their equilibrium action compared to only 53% and 57% of the types who reveal in equilibrium. This result may be qualified by the fact that in both parameterizations five out of six types should reveal in equilibrium. However, the only parameterization with a balanced prediction—Market C in High Cost—features numbers of comparable magnitude. Here, we have 98% equilibrium-consistent choices when subjects should conceal compared to about 74% if they should reveal. When averaging across both treatments and all markets, we find that 96% of the types who should conceal actually do so, while only 72% of the types who should reveal choose their equilibrium action. This difference is significant at the 5% level (one-sided Wilcoxon signed-rank test, $p=0.016$).

5.1.2. HC vs. NE

In this section, we compare the data with and without employers. Our treatment High Cost is comparable to the game without employers in that the parameterization and the equilibrium predictions are identical across these two treatments. This is obviously not the case for the Low Cost treatment, and the corresponding data is therefore excluded from the analyses in the following paragraphs.

We find that the revelation rates of type-six workers are higher in HC compared to NE. The data in Figure 2 documents that in HC 100% of the revelation decisions by type-six workers imply revelation compared to only about 82% in NE. Both shares are remarkably stable. In No Employers the share of type-six workers who choose to reveal is constant across all three markets, and there is literally no variation concerning these decisions in High Cost. When testing the markets separately, all differences are significant at the 5% level (one-sided Mann-Whitney U-test). Testing all markets at the same time returns $p\le 0.001$ (one-sided Mann-Whitney U-test).

We also conduct a regression analysis.

Table 2. Probit regressions and linear probability models as robustness check. Note: the standard errors presented in the table are clustered at the subjects-level. Clustering at the group or session-level does not change the results qualitatively. In such regressions, all the effects identified are significant at the 1% level.

Revealed	Probit			Linear Probability Model
	Market A	Market B	Market C	Market A	Market B	Market C
High Cost	−3.827	−1.661 **	−2.435 ***	−0.103	−0.300 ***	−0.124 **
	(2.866)	(0.653)	(0.860)	(0.0732)	(0.0893)	(0.0581)
Type	0.611 ***	0.425 ***	0.650 ***	0.118 ***	0.148 ***	0.180 ***
	(0.132)	(0.0578)	(0.0912)	(0.0124)	(0.0148)	(0.0142)
HC × Type	0.773	0.382 **	0.601 ***	0.0327	0.0619 ***	0.0406 **
	(0.534)	(0.148)	(0.201)	(0.0237)	(0.0194)	(0.0192)
Constant	−3.474 ***	−1.404 ***	−2.850 ***	−0.230 ***	0.0111	−0.269 ***
	(0.699)	(0.209)	(0.379)	(0.0383)	(0.0588)	(0.0425)
Observations	468	468	468	468	468	468
R-squared	0.397	0.265	0.430	0.308	0.319	0.455

Standard errors are clustered at the subjects level *** p < 0.01, ** p < 0.05, * p < 0.1.

reports the results from probit and OLS regressions where the revelation decision is the dependent variable. The regressions were conducted separately for the three markets, and both estimation methods yield similar results. In Market A, we do not find significant differences between HC and NE. Neither the treatment dummy for High Cost nor its interaction with the worker type is significant. In the markets B and C all regressors are significant. Here, we find that low-productivity types reveal less often in the game with employers, while high-productivity types reveal less often in the game without employers. The treatment dummy is significantly negative in both cases. This captures that low-productivity types reveal less frequently in High Cost. The interaction term is significantly positive for both markets, indicating more revelation by high-productivity types in High Cost. In addition, note that the worker type and the interaction term between HC and type are positive in all markets. Thus, the regression results deliver additional support for our Hypothesis 3 where we argue that revelation rates should increase with the type of worker.

Consider Figure 3 next. The figure visualizes the predictions of the probit regressions for all types of workers in both treatments. The black and gray lines represent the probability that a worker of a specific type will choose to reveal in a given market in No Employers and in High Cost, respectively. In all three markets, we observe that as long as the worker’s type does not exceed four, the black lines remain above the gray lines. In Market A, the error bars for low-productivity workers overlap. However, low-productivity types are less likely to reveal in High Cost in markets B and C. Then, the lines for HC and NE intersect between types four and five, and the predicted revelation rates for workers of type five and six are higher for HC compared to NE. Note that the error bars for type-six workers do not overlap in any market. In other words, high-productivity types are more likely to reveal in High Cost.

A possible explanation for the differences we observe for the high types are fairness considerations. In No Employers, subjects can only compare their payoffs to the payoffs of other workers, and revelation causes the profits of the concealing workers to decrease. In other words, those workers who reveal exert a negative externality on those workers who conceal. Consequently, fairness considerations may cause the workers with high productivities to refrain from revealing. This is not necessarily the case in the game with employers. In HC, the workers primarily interact with the employers in the same group and are therefore more likely to compare their payoffs with the employers’ payoffs. Since revelation does not harm the employers, high-productivity types will not refrain from revealing because of fairness considerations. Another possible explanation is that the framing in the game without employers emphasizes the privacy aspect of the revelation decision, which is not the case in the game with employers. Consequently, high-productivity workers in the game without employers may have been more reluctant to disclose their private information than those workers in the game with employers.

The explanation for the behavior of low-productivity workers is less ambiguous. Low-productivity workers reveal less frequently in the game with employers compared to the game without employers. This pattern cannot be explained by differences in the procedures and it is not a reaction to the changed behavior of the high types. If high types reveal more frequently, types with lower productivity should also reveal more frequently. The intuition is that employers should bid less upon observing concealment because the probability of being matched with a high type is relatively low. This is in contrast to our experimental data. In Section 5.2 we will show that the behavior of the employers is biased in a certain way, and in Section 6 we will argue that the behavior of the low types is a reaction to this bias.

5.2. Employers’ Bids

Figure 4 visualizes the market wages and relates them to the productivity of the corresponding worker. The scatter plots depict the average wage bid that was accepted by the worker. The plots also contain information on the standard deviation of these bids. The black entries refer to the cases where the worker reveals her type, the gray entries represent workers who conceal. In the case of concealment, we use the average productivity of a concealing worker in the corresponding combination of market and treatment. The dashed lines indicate equality of wages and productivity. In theory, all entries should be located along these dashed lines.

From Figure 4 we learn that employers’ bids fall behind the worker’s productivity if the worker chose to reveal. In most cases, the black entries are considerably below the dashed line. More often than not, the difference between the average accepted wage bid upon revelation and the productivity of the worker is larger than one standard deviation of the wage bid. On average, we find that employers aim for a rent of about ECU 94.70 or 19.13% of the observed productivity of the worker. The employers whose bids were accepted make profits of about ECU 67.76 or 13.42% of the worker’s productivity. In the case of revelation, the accepted wage bids are significantly lower than the productivity of the worker (one-sided Wilcoxon signed-rank test, $p=0.016$). Hence, employers earn positive profits from hiring a worker of known productivity.

Hiring a worker who chose to conceal is hardly profitable for the employers.17 Figure 4 suggests that average wages and productivities coincide rather well in the case of concealment. All the gray entries are close to the dashed line. The differences between the average productivity and the average wage bid appear negligible, especially when compared to the standard deviation of the wage bid. The fact that the average accepted wage bid plus one standard deviation always exceeds the average productivity of a concealing worker, documents that employers often realize losses when they hire a worker who chose to conceal. On average, employers earn about ECU 7.48 if they hire a worker of unknown productivity. In relative terms, employers even make losses when the worker conceals. On average, they realize a margin of about −5.24% of the worker’s productivity.18 If the worker chose to conceal, accepted bids are not significantly different from the productivity of the worker (one-sided sign test, $p=0.656$).

5.3. Learning

There is moderate learning in our experiments. Figure 5 visualizes the development of the share of workers opting for their equilibrium action over time. As shown in the figure, this share is superior in later periods. In the final period, between 65% and 100% of all revelation decisions are in line with the theoretic predictions. Averaging across the markets, we find that in both treatments with employers (LC and HC), 88.89% of the workers’ revelation decisions in the final period are in line with the predictions. In NE this share is 82.41%.

There appears to be better learning in the experiments with employers. In both treatments, equilibrium consistency increases by about 15%. This is in line with Forsythe et al. [14] who also emphasize that there is more unraveling in later periods.

In general, Figure 5 documents that the theoretic predictions capture workers’ revelation behavior rather well. A majority of workers’ decisions are in line with the predictions. In some cases, all or nearly all workers behave according to the predictions. Having said that, it should be noted that there are also some exceptions. For instance, in Market B in HC, approximately 35% of the decisions depart from the predictions in the final period. Given the pattern of the revelation rates depicted in Figure 2, this implies that three out of six worker types manage to pool even though they should not be able to do so.

There is one further interesting aspect concerning the degree of equilibrium consistency. It does not directly depend on the cost of revelation. In Market A, the share of equilibrium-consistent revelation decisions is significantly higher in High Costs compared to Low Cost while the opposite is true in Market B. Here, the share of equilibrium-consistent revelation decisions is higher in Low Cost compared to High Cost (one-sided Mann-Whitney U tests, $p=0.050$ in both cases).

Figure 6 visualizes the development of the market wages (i.e., the bids accepted by the workers) and relates them to the average productivity of the workers. The solid lines capture the case where the worker chose to reveal, the dashed lines represent cases where the worker concealed.

The figure documents that the differences in the profits employers realize when hiring workers that revealed or concealed, are stable over time. In Section 5.2 we reported that employers realize positive profits in the case of revelation, but not in the case of concealment. From Figure 6 we learn that this effect does not alleviate over time. Throughout our experiments, the average market wages fall behind the average productivity in the case of revelation, whereas average wages and average productivities coincide rather well in the case of concealment.

6. Discussion

The differences in the profits employers can realize depending on the worker’s revelation decision have an important implication for unraveling. If the worker chooses to reveal, employers manage to extract positive rents from hiring the worker. As they are unable to do so if the worker conceals, the profits employers can realize upon revelation can be considered as an additional, endogenous cost of revelation which workers have to pay whenever they choose to reveal. Therefore, fewer workers will find it in their interest to reveal their productivity. As the cost of revelation increases, the threshold k we used to define the highest type of the worker that chooses to conceal in equilibrium, will also increase. Hence, workers of low productivity in particular will reveal less frequently in the game with employers compared to the game without employers. Note that this is perfectly in line with the workers’ revelation behavior as reported in Section 5.1.

Such endogenous costs of revelation may explain why unraveling is not necessarily complete even if the exogenous cost of revelation is negligible as in Low Cost. From Figure 6 we learn that the profits employers realize upon revelation are rather constant across treatments and markets. As noted above, they are roughly ECU 68 on average. Taking this amount into account when deriving the equilibria results in different equilibrium predictions. For instance, assume that workers actually have to pay ECU 69 instead of ECU 1 in Low Cost. In this case, the equilibrium predictions change as follows. In Market A there is an equilibrium where only types five and six reveal, in Market C type two may deviate to concealment and the predictions for Market B remain unaffected. Even though these new predictions do not match the observed revelation rates perfectly, they still capture the experimental data far better than those predictions that do not account for the positive profits employers receive in the case of revelation.

7. Conclusions

In this paper, we analyze workers’ willingness to disclose private information in a lab experiment. We follow Benndorf et al. [13] by using a similar game with a similar parameterization. We extend their work in two dimensions and close the gap to the existing literature.

Comparing the games with and without human employers, we find a somewhat inconclusive effect on unraveling. In the game with employers, high-productivity types reveal more frequently whereas low-productivity types reveal less frequently. The first aspect might be explained by differences in the framing and/or by horizontal fairness considerations, which are less likely to play a role in the game with employers. The explanation for the second aspect is the bidding behavior of the employers whose bids after observing revelation are less competitive than their bids upon concealment. This behavior causes fewer types of workers to reveal. Hence, while the overall effect of introducing employers is inconclusive, the consequences induced by their behavior are unambiguous. Employers’ wage bids impede unraveling.

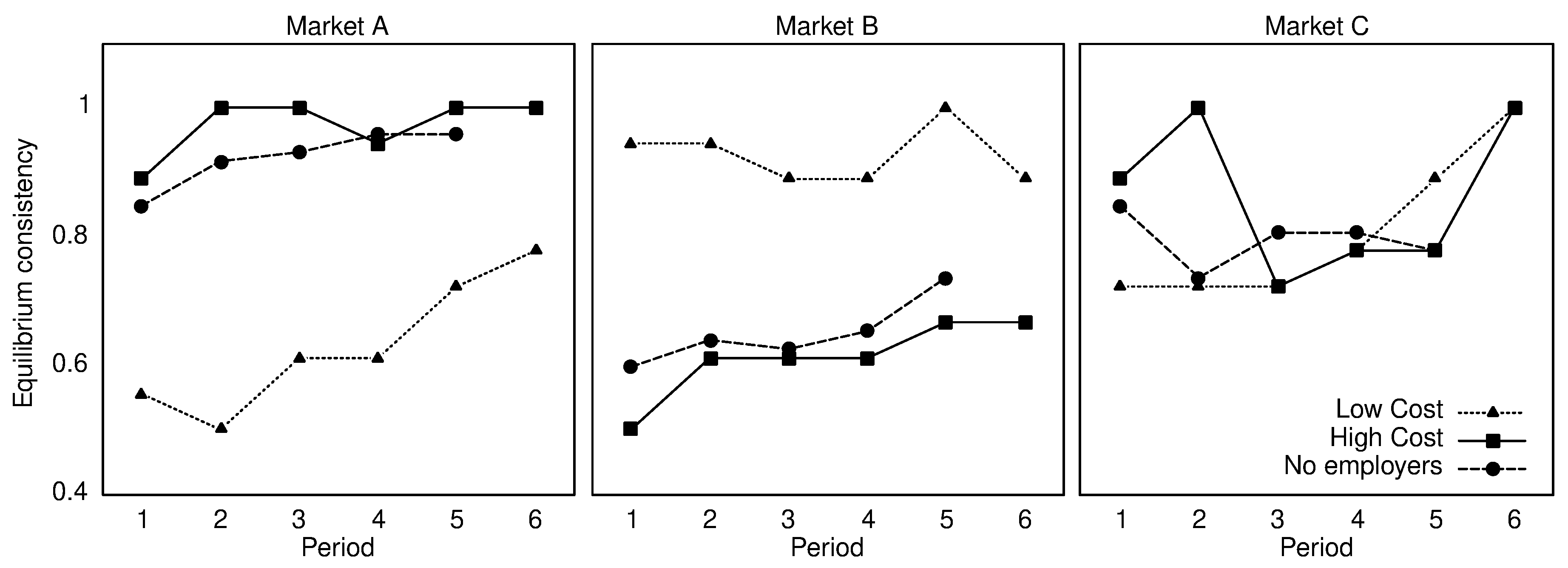
The second dimension we consider is the cost of revelation. We find that reducing the cost of revelation to a negligible degree increases the revelation rates dramatically. However, this is already captured by the game-theoretic predictions. Averaging across all markets, the degree of equilibrium consistency appears to be rather independent of this cost. There is, however, one further interesting aspect. While the degree of consistency is highest in Market A and lowest in Market B in High Cost, the opposite is true for Low Cost. Here, the equilibrium consistency of workers’ revelation decision is lowest in Market A and highest in Market B. This suggests that reducing the cost of revelation results in more revelation, but may result in a lower, higher, or equal share of equilibrium-consistent revelation decisions.

The policy implications we can derive from our results are as follows. The unraveling problem is not quite as severe as suggested by economic theory. In all our experiments, we find a bias against revelation in that those who should reveal in equilibrium deviate from their equilibrium action more frequently than those who should conceal. The result is consistent with other experimental studies on unraveling [13,15]. It is, however, not to suggest that unraveling is unproblematic from a privacy point of view. Our experiments document that there is a substantial degree of unraveling even though the behavior of workers and employers impedes the process. Hence, the voluntary disclosure of personal information does constitute a threat to privacy. The ex-ante uninformed parties are able to use the information to their benefit, and only relatively few types of the worker manage to conceal their private information. Overall, we agree with Peppet [12] in that further regulation may be required.