Game Theoretic Interaction and Decision: A Quantum Analysis
Abstract
1. Introduction
- Interaction systems provide a general model for interaction and decision-making. Their analysis with vector space methods yields isomorphic representations in real and complex space, which also suggests quantum theoretic interpretations.
- Hermitian eigenvalue theory of interaction exhibits measurements on interaction and decision systems as stochastic variables that measure these eigenvalues.
- The dual interpretation of decision systems refines the model of multichoice games and reveals fuzzy games as cooperative systems without entangled states. Moreover, the probabilistic interpretation of decision analysis refines Penrose’s model for human decision-making.
- A comprehensive theory of Fourier transformation exists for interaction systems.
- The dual interpretation suggests novel concepts of “Markov evolution” of cooperation.
2. Interaction Systems
- and
3. Symmetry Decomposition and Hermitian Representation
3.1. Binary Interaction
- (i)
- I: no proper interaction, the two agents have the same unit activity level.
- (ii)
- : no proper interaction, opposite unit activity levels.
- (iii)
- : no proper activity, symmetric interaction: there is a unit “interaction flow” from x to y and a unit flow from y to x.
- (iv)
- : no proper activity, skew-symmetric interaction: there is just a unit flow from x to y or, equivalently, a -flow from y to x.
3.2. Spectral Theory
4. Measurements
- Cooperative games. A linear value for a player in a cooperative game (sensu Example 1) is a linear functional on the collection of diagonal interaction matrices V. Clearly, any such functional extends linearly to all interaction matrices A. Thus, the Shapley value [21] (or any linear value (probabilistic, Banzhaf, egalitarian, etc.) can be seen as a measurement. Indeed, taking the example of the Shapley value, for a given player , the quantitywith , acts linearly on the diagonal matrices V representing the characteristic function v. Similar conclusions appl+y to bicooperative games.
- Communication Networks. The literature on graphs and networks13 proposes various measures for the centrality (Bonacich centrality, betweenness, etc.) or prestige (Katz prestige index) of a given node in the graph, taking into account its position, the number of paths going through it, etc. These measures are typically linear relative to the incidence matrix of the graph and thus represent measurements.
4.1. Probabilistic Interpretation
5. Decision Analysis
5.1. The Case
5.1.1. Decisions and Interactions
5.1.2. Decision Probabilities
- (i)
- Influence networks: While it may be unusual to speak of “influence” if there is only a single agent, the possible decisions of this agent are its opinions (‘yes’ or ’no’), and the state of the agent hesitating between ‘yes’ and ‘no’ is described by (with probability to say ‘no’ and to say ‘yes’).
- (ii)
- Cooperative games: As before, “cooperation” may sound odd in the case of a single player. However, the possible decisions of the player are relevant and amount to being either active or inactive in the given game. Here, represents a state of deliberation of the player that results in the probability for being active (resp. inactive).
5.1.3. Quantum Bits
5.1.4. Non-Binary Alternatives
5.2. The Case
5.2.1. Entanglement and Fuzzy Systems
5.3. Linear Transformations
5.3.1. Möbius Transform
5.3.2. Hadamard Transform
5.3.3. Fourier Transformation
5.4. Decision and Quantum Games
6. Markov Evolutions
- (i)
- There is some such that holds for all .
- (ii)
- The limit exists.
- (ii)
- The evolution sequence is mean ergodic.
- (ii)
- For every linear functional , the statistical averagesconverge.
6.1. Markov Chains
Schrödinger’s Wave Equation
6.2. Markov Decision Processes
7. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
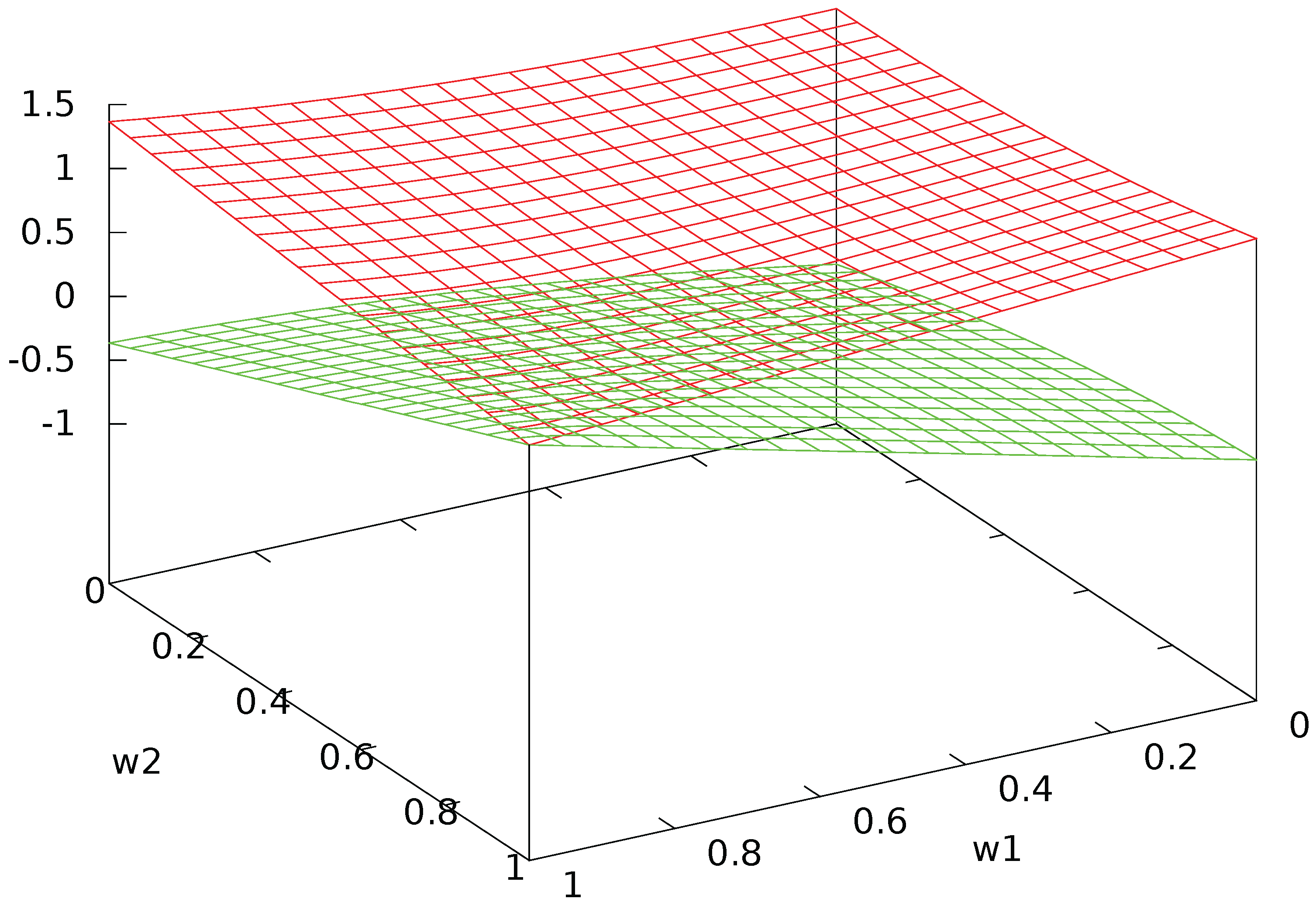
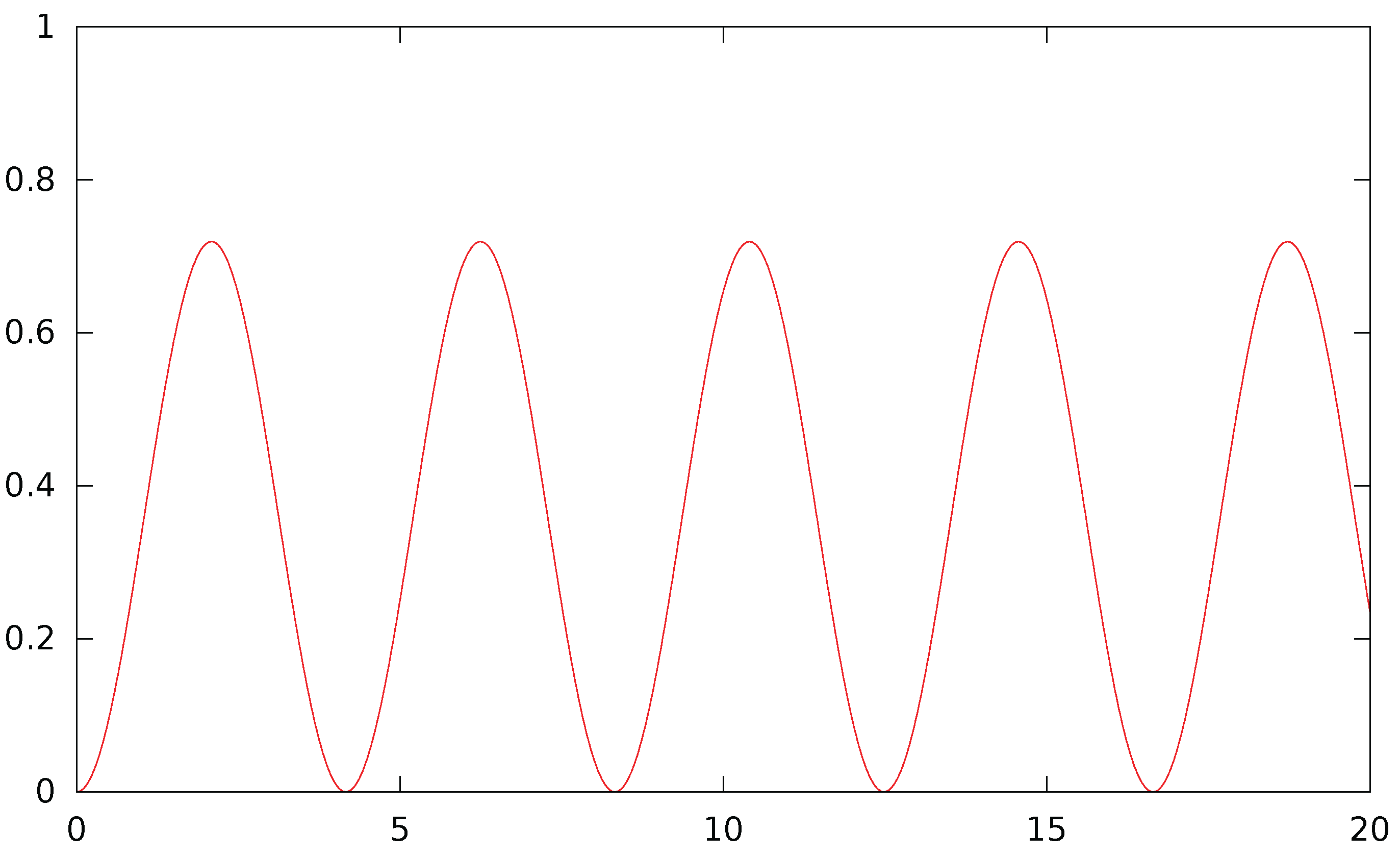
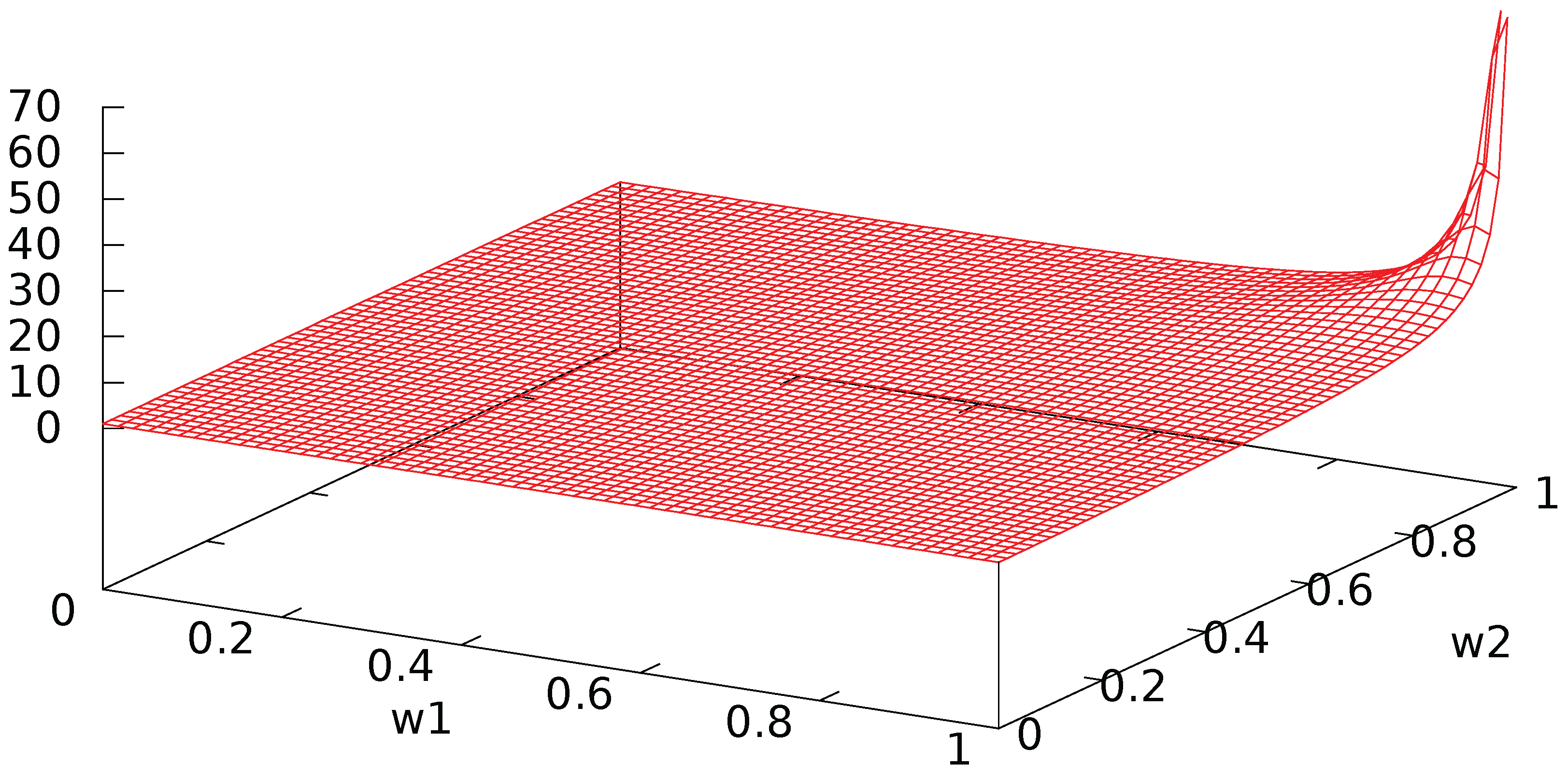
Appendix A. An Example with Two Agents

References
- Owen, G. Multilinear extensions of games. Manag. Sci. 1972, 18, 64–79. [Google Scholar] [CrossRef]
- Grabisch, M.; Roubens, M. An axiomatic approach to the concept of interaction among players in cooperative games. Int. J. Game Theory 1999, 28, 547–565. [Google Scholar] [CrossRef]
- Faigle, U.; Grabisch, M. Bases and linear transforms of TU-games and cooperation systems. Int. J. Game Theory 2016, 45, 875–892. [Google Scholar] [CrossRef]
- Penrose, R. Shadows of the Mind; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Grabbe, J.O. An Introduction to Quantum Game Theory. arXiv 2005, arXiv:quant-ph/050621969. [Google Scholar]
- Guo, H.; Zhang, J.; Koehler, G.J. A survey of quantum games. Decis. Support Syst. 2008, 46, 318–332. [Google Scholar] [CrossRef]
- Eisert, J.; Wilkens, M.; Lewenstein, M. Quantum games and quantum strategies. Phys. Rev. Lett. 1999, 83, 3077–3080. [Google Scholar] [CrossRef]
- Vourdas, A. Comonotonicity and Choquet integrals of Hermitian operators and their applications. J. Phys. A Math. Theor. 2016, 49, 145002. [Google Scholar] [CrossRef]
- Zhang, Q.; Saad, W.; Bennis, M.; Debbah, M. Quantum Game Theory for Beam Alignment in Millimeter Wave Device-to-Device Communications. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Next Generation Networking Symposium, Washington, DC, USA, 4–8 December 2016. [Google Scholar]
- Iqbal, A.; Toor, A.H. Quantum cooperative games. Phys. Lett. A 2002, 293, 103–108. [Google Scholar] [CrossRef]
- Levy, G. Quantum game beats classical odds–Thermodynamics implications. Entropy 2017, 17, 7645–7657. [Google Scholar] [CrossRef]
- Wolpert, D.H. Information theory–The bridge connecting bounded rational game theory and statistical physics. In Complex Engineered Systems; Springer: Berlin, Germany, 2006; pp. 262–290. [Google Scholar]
- Aubin, J.-P. Cooperative fuzzy games. Math. Oper. Res. 1981, 6, 1–13. [Google Scholar] [CrossRef]
- Nielsen, M.; Chuang, I. Quantum Computation; Cambrigde University Press: Cambrigde, UK, 2000. [Google Scholar]
- Aumann, R.J.; Peleg, B. Von Neumann-Morgenstern solutions to cooperative games without side payments. Bull. Amer. Math. Soc. 1960, 66, 173–179. [Google Scholar] [CrossRef]
- Bilbao, J.M.; Fernandez, J.R.; Jiménez Losada, A.; Lebrón, E. Bicooperative games. In Cooperative Games on Combinatorial Structures; Bilbao, J.M., Ed.; Kluwer Academic Publishers: New York, NY, USA, 2000. [Google Scholar]
- Labreuche, C.; Grabisch, M. A value for bi-cooperative games. Int. J. Game Theory 2008, 37, 409–438. [Google Scholar] [CrossRef]
- Faigle, U.; Kern, W.; Still, G. Algorithmic Principles of Mathematical Programming; Springer: Dordrecht, the Netherlands, 2002. [Google Scholar]
- Grabisch, M.; Rusinowska, A. Influence functions, followers and command games. Games Econ. Behav. 2011, 72, 123–138. [Google Scholar] [CrossRef]
- Grabisch, M.; Rusinowska, A. A model of influence based on aggregation functions. Math. Soc. Sci. 2013, 66, 316–330. [Google Scholar] [CrossRef]
- Shapley, L.S. A value for n-person games. In Contributions to the Theory of Games; Kuhn, H.W., Tucker, A.W., Eds.; Princeton University Press: Princeton, NJ, USA, 1953; Volume II, pp. 307–317. [Google Scholar]
- Jackson, M.O. Social and Economic Networks; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Hsiao, C.R.; Raghavan, T.E.S. Monotonicity and dummy free property for multi-choice games. Int. J. Game Theory 1992, 21, 301–332. [Google Scholar] [CrossRef]
- Marichal, J.-L. Weighted lattice polynomials. Discret. Math. 2009, 309, 814–820. [Google Scholar] [CrossRef]
- Rota, G.C. On the foundations of combinatorial theory I. Theory of Möbius functions. Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete 1964, 2, 340–368. [Google Scholar] [CrossRef]
- Walsh, J. A closed set of normal orthogonal functions. Am. J. Math. 1923, 45, 5–24. [Google Scholar] [CrossRef]
- Hammer, P.L.; Rudeanu, S. Boolean Methods in Operations Research and Related Areas; Springer: New York, NY, USA, 1968. [Google Scholar]
- Kalai, G. A Fourier-theoretic perspective on the Condorcet paradox and Arrow’s theorem. Adv. Appl. Math. 2002, 29, 412–426. [Google Scholar] [CrossRef]
- O’Donnell, R. Analysis of Boolean Functions; Cambridge University Press: Cambrigde, UK, 2014. [Google Scholar]
- Meyer, D.A. Quantum strategies. Phys. Rev. Lett. 1999, 82, 1052–1055. [Google Scholar] [CrossRef]
- Faigle, U.; Schönhuth, A. Asymptotic Mean Stationarity of Sources with Finite Evolution Dimension. IEEE Trans. Inf. Theory 2007, 53, 2342–2348. [Google Scholar] [CrossRef]
- Faigle, U.; Grabisch, M. Values for Markovian coalition processes. Econ. Theory 2012, 51, 505–538. [Google Scholar] [CrossRef]
- Bacci, G.; Lasaulce, S.; Saad, W.; Sanguinetti, L. Game Theory for Networks: A tutorial on game-theoretic tools for emerging signal processing applications. IEEE Signal Process. Mag. 2016, 33, 94–119. [Google Scholar] [CrossRef]
- Faigle, U.; Gierz, G. Markovian statistics on evolving systems. Evol. Syst. 2017. [Google Scholar] [CrossRef]
- Puterman, M. Markov Decision Processes: Discrete Stochastic Dynamic Programming; John Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Lozovanu, D.; Pickl, S. Optimization of Stochastic Discrete Systems and Control on Complex Networks; Springer: Cham, Switzerland, 2015. [Google Scholar]
| 1 | see also Grabisch and Roubens [2] for a general approach |
| 2 | |
| 3 | |
| 4 | Iqbal and Toor [10] discuss a 3 player situation |
| 5 | see, e.g., Levy [11] |
| 6 | cf. Wolpert [12] |
| 7 | see, e.g., Nielsen and Chang [14] |
| 8 | Non Transferable Utility game; cf. Aumann and Peleg [15] |
| 9 | |
| 10 | see also the discussion in Section 7 |
| 11 | see, e.g., [18] |
| 12 | |
| 13 | see, e.g., Jackson [22] |
| 14 | see, e.g., Penrose [4] |
| 15 | see, e.g., Nielsen and Chuang [14] |
| 16 | Hammer and Rudeanu [27] |
| 17 | |
| 18 | |
| 19 | |
| 20 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faigle, U.; Grabisch, M. Game Theoretic Interaction and Decision: A Quantum Analysis. Games 2017, 8, 48. https://doi.org/10.3390/g8040048
Faigle U, Grabisch M. Game Theoretic Interaction and Decision: A Quantum Analysis. Games. 2017; 8(4):48. https://doi.org/10.3390/g8040048
Chicago/Turabian StyleFaigle, Ulrich, and Michel Grabisch. 2017. "Game Theoretic Interaction and Decision: A Quantum Analysis" Games 8, no. 4: 48. https://doi.org/10.3390/g8040048
APA StyleFaigle, U., & Grabisch, M. (2017). Game Theoretic Interaction and Decision: A Quantum Analysis. Games, 8(4), 48. https://doi.org/10.3390/g8040048



