1. Introduction
Thailand’s agricultural industries not only generate billions of baht a year in economic value, they have also been an important part of Thai life, which revolves around agriculture. Every 10 years, the National Statistical Office of Thailand [
1] conducts an Agriculture Census, and the latest data, collected in 2013, show that the country has 5.9 million agricultural holdings representing 25.9% of total number of households. That same year, agriculture contributed 10.4% of value to Gross Domestic Product (GDP) [
2], and Thailand ranked 15th among the world’s exporters of agricultural products [
3].
Thailand’s No. 1 crop is rice, whose waste—rice straws—produce massive amounts of GHGs when burned. In the last 20–30 years, corn has been added to the agricultural mix, and corn cultivation area in the northern region now comprises 71.33 percent of the nation’s total corn farmland area. According to 2013 data from the Land Development Department, 54.11 percent of the north’s corn cultivation area is supposed to be forest area. To make matters worse, with the popularity of contract farming, corn growing has increased to 2, 3 or even 4 crops a year, a practice that generates substantial amounts of biomass, which is typically eliminated by burning. The open incineration out in the fields is a major cause of the smoke pollutions that plagued Chiang Mai and other northern provinces yearly during February–April. In 2015, recorded amounts of PM10-bound polycyclic aromatic hydrocarbons in Chiang Mai were as high as 299 µg/m
3 compared to the EPA’s annual mean standard of 50 µg/m
3 and daily concentration standard of 150 µg/m3 [
4]. The same year, Chiang Mai International airport canceled record numbers of flights, daily, as a result of smoke pollution. During January–May 2014, more than 200,000 of Chiang Mai’s population showed symptoms associated with this smoke. Government agencies, including the Energy Research and Development Institute, have been trying to educate and support local farmers to transform agricultural waste to Refuse-derived fuel (RDF), biochar, fertilizer or even landfill.
GHGs, especially man-made GHGs, contribute appreciably towards climate change. Global warming potential (GWP) is defined as the warming influence over a 100-year horizon relative to that of CO
2. The GWPs of the six main greenhouse gases range from over 1000 for F-gases to 21 for methane. CO
2, with GWP being 1, is the most important GHG and accounts for more than 76% of the total amount of greenhouse gases [
5]. There have been global, national and some local initiatives aimed at limiting corporate greenhouse gas emissions. In Thailand, even though a Nationally Appropriate Mitigation Action (NAMA) plan to lower greenhouse gases below the business as usual (BaU) level by 2020 was submitted to the UN in the year 2015, problems related to the pollution have been on the rise. Farmers still prefer to burn agricultural wastes in the fields, which shows that such initiatives have not taken root at the local level [
6].
Farms in Northern Thailand are usually small and scattered around mountainous terrains. Most corn growers’ holdings are smaller than 25
rai (4 ha) and located away from industrial mills [
1]. In a typical Thai agricultural supply chain, growers simply pack and sell their products without any post-harvest control. Growers use small trucks or traditional transport vehicles to transport their crop to the mills or middlemen. Some growers hire contractors to handle crop deliveries. Agricultural waste, typically eliminated by open incineration right on the fields, has never been included in the product distribution network, an important component in supply chain management. Together, the combination of extra fuel consumption from this activity and open incineration of farm waste product drives up CO
2 equivalent emissions in Thailand’s crop supply chain to very high levels. For the waste elimination problem with the aim of reducing CO
2 equivalent emission, the solution could lie in transforming biomass at these integration points into energy or some other useful products. The resulting products could then be transported to customers in the waste supply chain system, where transportation cost is practically the only cost. Therefore, the clustering problem is studied in order to group product/waste integrating points (in this case, co-ops) and their clients (in this case, fields). Since the CO
2 emission from transportation is directly related to the transportation cost, the cluster created should reduce not only the system’s transportation cost but its CO
2 emission as well.
Related works on clustering problems include Kusiak [
7], who studied five different integer programming formulations of the clustering problem and developed heuristic algorithms to find the solution for these clustering problems. Bramel and Simchi-Levi [
8] presented a general framework for modeling routing problems and applied it to the capacitated vehicle routing problem and the inventory routing problem. Later in [
9], they proposed a heuristic for finding the routing in the CVRP where their clusters are found by a model similar to the second model presented in this paper. Negreiros and Palhano [
10] proposed the capacitated centered clustering problem (CCCP), which has to do with finding a set of clusters with limited capacity and minimum dissimilarity within each cluster by using non-Euclidean distance measures. Two variations of this problem were proposed and solved with their heuristic after clustering. The work by Expósito-Izquierdo et al. [
11], in the year 2016, proposed a two-Level solution approach to finding the clusters with minimum total travel cost of the routes that fulfill the demands.
Most research works on agricultural supply chain management in Thailand are about sugarcane management systems, which by nature contain a large number of distribution centers (DCs). Algorithms have been proposed by Saranwong and Likasiri [
12] to solve bi-level problems where the upper and lower parts are to find the minimum transportation cost of shipping products from plants to DCs and from DCs to customers, respectively. They also compare the solutions with that of the single-level problem. In a study of sugarcane management system in Northeastern Thailand, Khamjan et al. [
13] proposed a single-level mixed integer programming model to find the increased capacity of existing sugarcane loading stations, the locations of new loading stations and small farmer allocations in order to minimize the total cost. They proposed a heuristic algorithm based on the relaxation of the model and a greedy algorithm to tackle industrial-size problems such as a case study problem consisting of 3000 grower fields. Neungmatcha et al. [
14] proposed, via single-level programming, an adaptive genetic algorithm to solve the sugarcane loading station problem with multi-transloaders. According to their work, DCs, which the authors called sugarcane loading stations, contain transloaders that transfer sugarcanes from the grower’s small trucks (under 5 ton capacity) to larger trucks (18–20 ton capacity) or trailer trucks (35–38 ton capacity). They applied a fuzzy logic control in the crossover and mutation processes to improve the genetic algorithm’s search ability.
This paper is organized as follows: In
Section 2, various models are proposed to find the best clusters with minimum transportation cost for several constraints sets. Since the best transportation system in each cluster is not known, the resulting clusters are further solved via TSP to compare with their original objective function values. Then, in
Section 3, complexity of the models and simulation results are conducted to show the efficiency of the proposed models. The featured case study, shown in
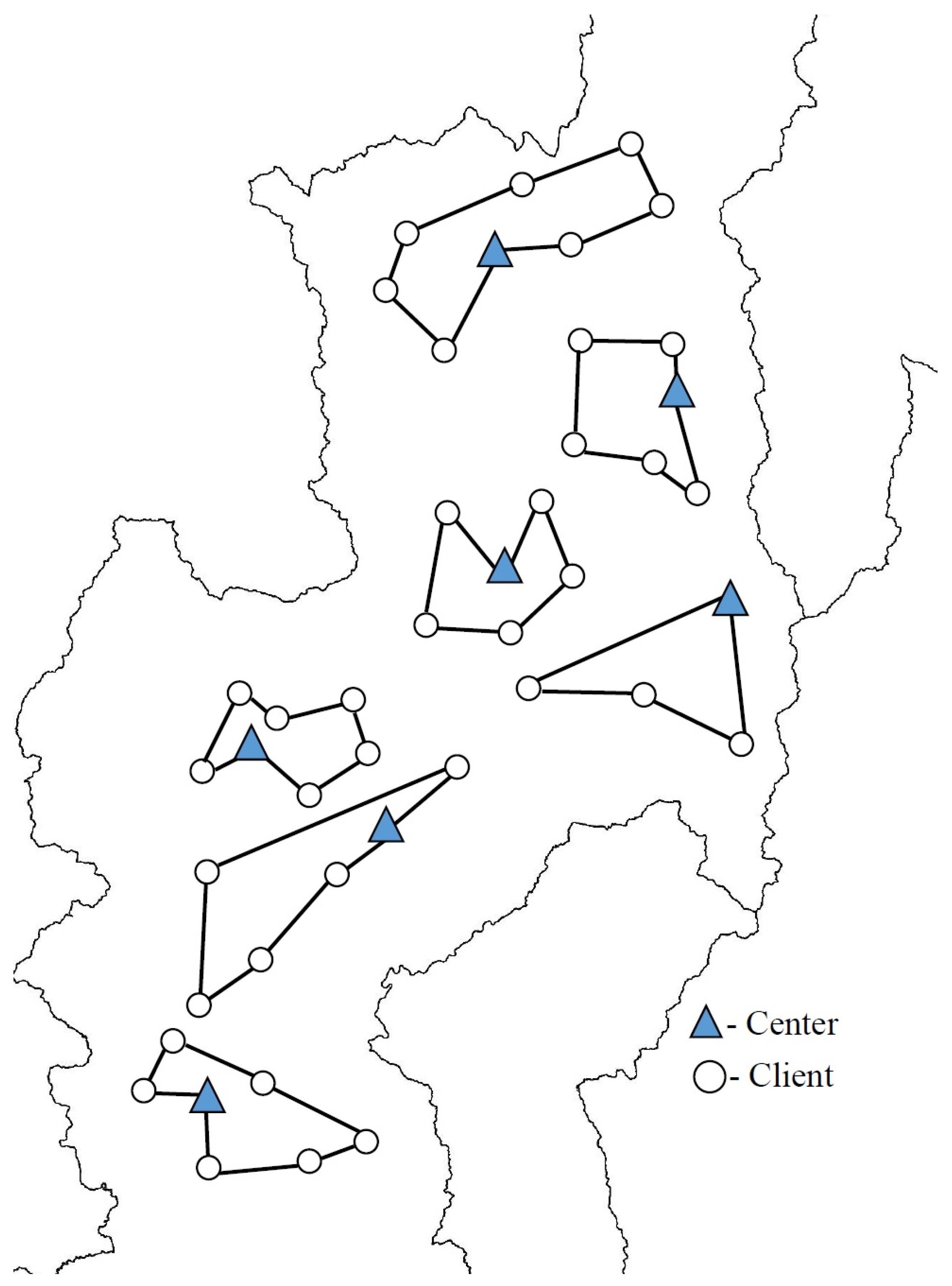
Section 4, involves finding optimal clusters for centers in Chiang Mai’s as well as Northern Thailand’s corn product/waste management systems similar to
Figure 1. We address the total CO
2 emissions from the waste elimination processes, open burning and transforming to biomass pellets in this section.
2. Model Development
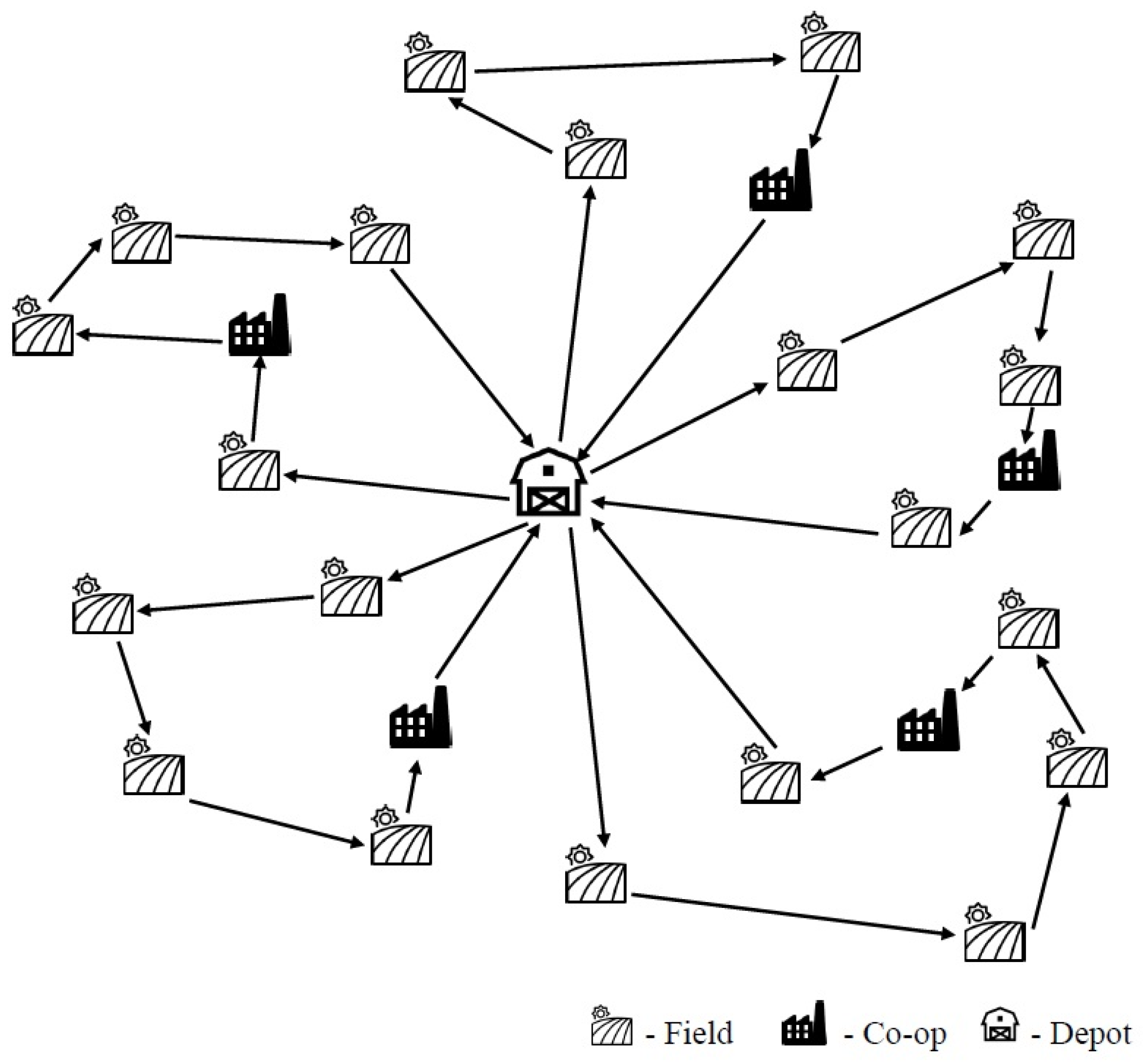
We start with a model to cluster customers into groups with associated centers where, in each group, the clients’ total supplies match up with their center’s capacity. With the assumption that the center does all the pickups, CVRP with the objective of finding the optimal routing is considered. New variables are added to the CVRP model to represent the centers, and the resulting model is called the capacitated vehicle routing problem with centers (CVRPC), with a corresponding network similar to that in
Figure 2. In order to cluster groups of customers with their centers in the case study, a dummy node with zero distance to all other nodes is added and set as a depot in the CVRPC model.
The CVRPC is defined by a graph
where
denotes the set of nodes, and
denotes the set of edges between node
and
. The routing denoted as
starts and ends at node
, which is the depot. The customers are indexed as
with a demand for each customer denoted as
The centers are indexed as
with a capacity for each center denoted as
and a fixed cost for each center denoted as
The transportation cost from node
to node
is denoted as
, which can be described in terms of the distance or time traveled. Decision variables are:
where
where
The CVRPC can be written as follows:
subject to
Objective function (1) is to minimize the total cost including transportation cost and fixed cost. Constraints (2) ensure that each routing starts from the depot. Constraint (3) implies that the number of routings cannot exceed a predetermined number. Constraints (4) and (5) ensure that each customer can only be on one route. Constraint (6) guarantees that the entering arc to each customer (node) and the leaving arc from this node are on the same route. Constraint (7) ensures that the total supplies from the customers on any one route do not exceed the capacity of the center serving that route. Constraint (8) ensures that each route has only one center. Constraint (9) ensures that only one center appears in each route. Constraint (10) ensures that there is an edge from node to center whenever the center is on route . Constraint (11) ensures that each route contains no more than one center. Constraint (12) means that there will be no cycle with nodes (i.e., no subtour of these sizes). Constraints (13) and (14) are binary constraints.
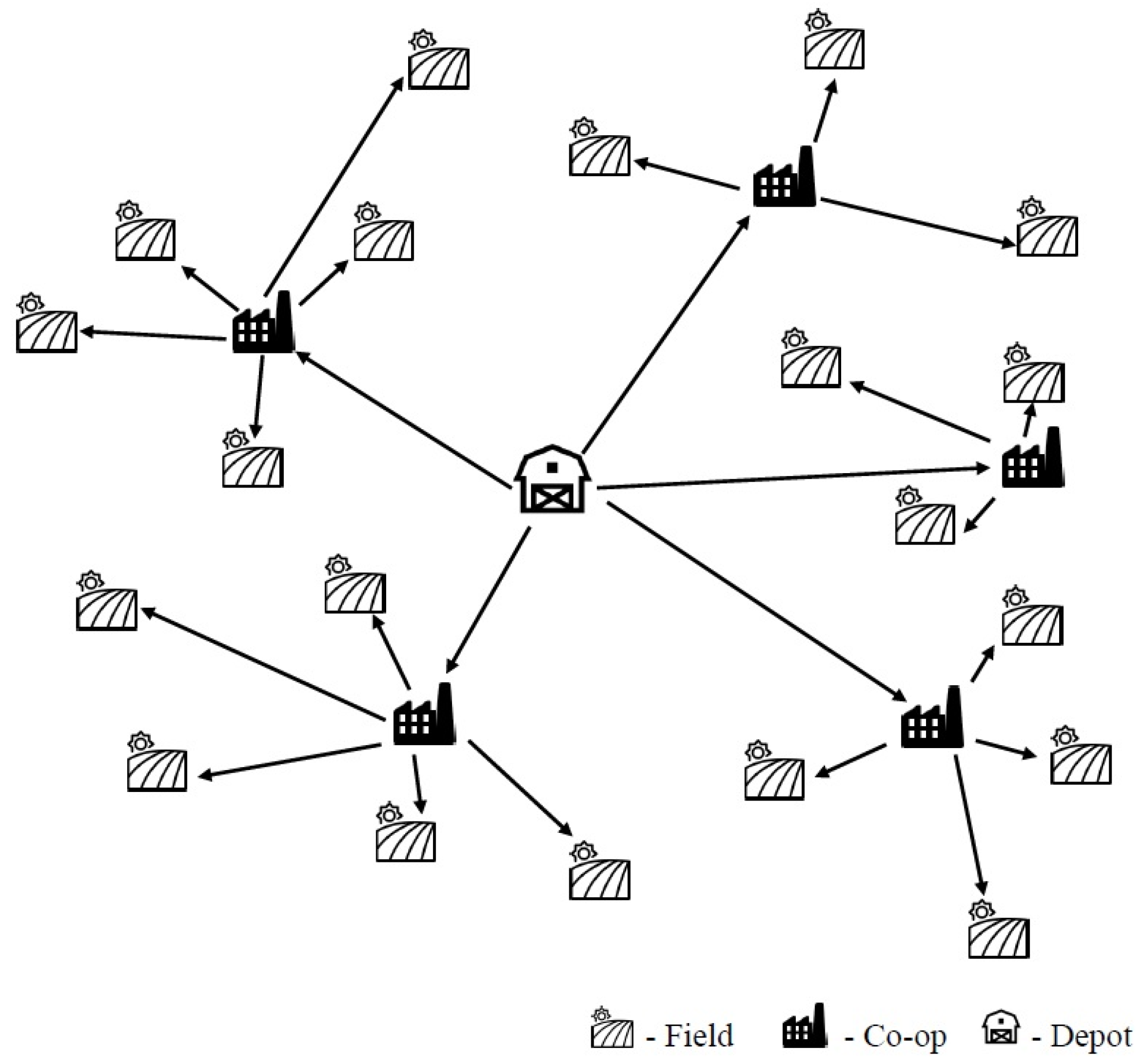
The second model carries the assumption that all customers deliver the products to the center. Hence, the centers are required to literally be the centers of the clusters. Since the resulting clusters are stars, the proposed model is called the star-capacitated vehicle routing problem (SCVRP). Its network is similar to that in
Figure 3.
The SCVRP is defined by a graph
where
denotes the set of nodes and
denotes the set of edges between node
and
. The clusters join at node
, which is the depot. The number of clusters is
. The customers are indexed as
, with the demand for each customer denoted as
; and the centers are indexed as
, with the capacity for each center denoted as
. The transportation cost from node
to node
is denoted as
, and is described in terms of the distance or time traveled. Decision variables are as follows:
SCVRP model can be written as:
subject to
Objective function (15) is to minimize the total cost, including transportation cost. Constraint (16) ensures that the number of clusters is equal to a predetermined number. Constraints (17) and (18) imply that customers can be served by only one center. Constraint (19) ensures that each cluster will have only one center. Constraint (20) ensures that no customer is served by another customer. Constraint (21) ensures that the demand of customers in a cluster does not exceed the capacity of that cluster’s center. Constraint (22) is a binary constraint.
4. Some Real-World Experiences
We then tested the models on real-world problems, focusing on a transportation system for corn production waste elimination, using data on biomass fuel demands and supplies, and the locations for its production from Thailand’s Energy Technology for Research Center. The locations of corn fields and centers (in this case, co-ops to collect the agricultural products and residues from the fields and produce the biomass fuels) are located on the maps. As of 2016, there are 75 fields, 16 co-ops and 74 potential customers in Chiang Mai involved in the waste control program. Those numbers for the 9 provinces in Northern Thailand are 571, 74 and 222, respectively. Almost half (48.85%) of the nation’s maize production is from the North. The corn production systems in Chiang Mai and in the 9 provinces in the North including Chiang Mai produce 48,391 and 699,768 tons of corncobs and husks, respectively. Only 15% of the products in Chiang Mai are sold to the co-ops. Therefore, only 7258.61 tons out of 48,391 tons of the waste in Chiang Mai are sold to potential customers. The unprocessed waste sells for 500 baht (around 14.5 USD) per ton whereas the transformed waste (in the form of pellets) sells for 2000 baht per ton.
Open burning of corn is classified into 2 types, i.e., corn stalks and leaves burning, and corn cobs and husks burning. Emissions of CO, NO
x, SO
2, CO
2 and particulates from corn stalks and leaves burning are 63.74, 2.31, 0.54, 1147.43 and 3.39 g per kg of dry biomass, respectively, whereas emissions from corn cobs and husks burning are 68.68, 3.57, 0.46, 1917.69 and 23.38 g per kg of dry biomass, respectively [
6]. In this work, only the CO
2 emissions from the burning of corn cobs and husks are considered, since they are normally transported to the co-ops as part of the unprocessed products and, when burned, they emit a higher CO
2 per weight. According to the collected data, CO
2 emissions from this burning process in Chiang Mai and in the 9 provinces of Northern Thailand are 92,798.46 and 1,341,938.25 ton/year, respectively. Since the CO
2 emission of biomass pellet production is 107 kg/ton [
16], CO
2 emissions from the transformation process are 5,177.81 and 74,875.18 ton/year in Chiang Mai and the 9 provinces of Northern Thailand, respectively. Together with pellet burning, which produces 1547.80 grams of the CO
2 per kilogram [
17], which can be transformed into 74,899.20 and 1,083,101.03 tons per year, transforming the waste to pellets will release 80,077.01 and 1,157,979.48 tons per year, respectively, from Chiang Mai and the 9 provinces of Northern Thailand. This still reduces the general CO
2 emissions. However, this does not include the CO
2 emissions from agricultural waste transportation to the pellet production sites, and from the sites to their potential customers.
To find the minimum transportation cost (i.e., CO
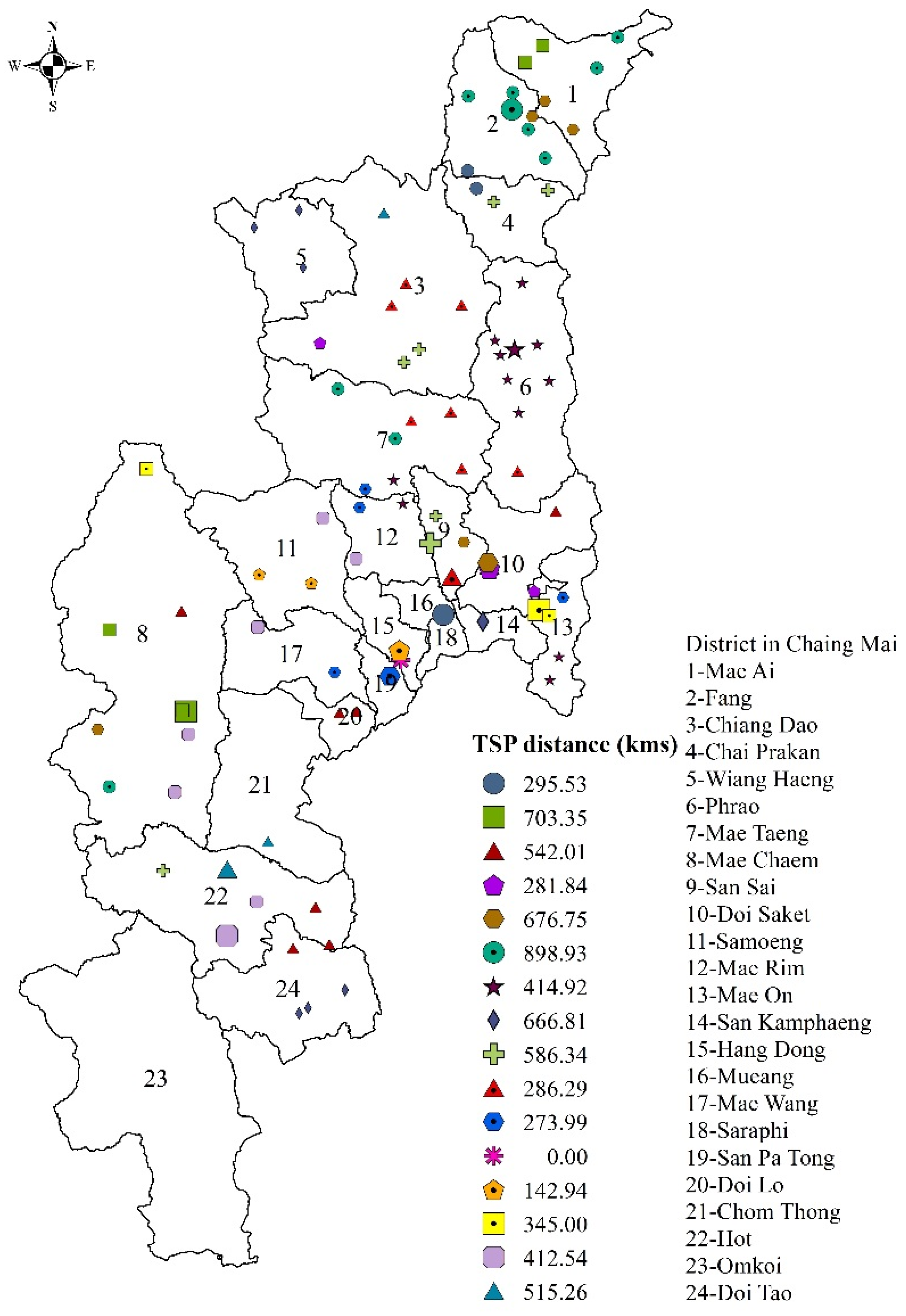
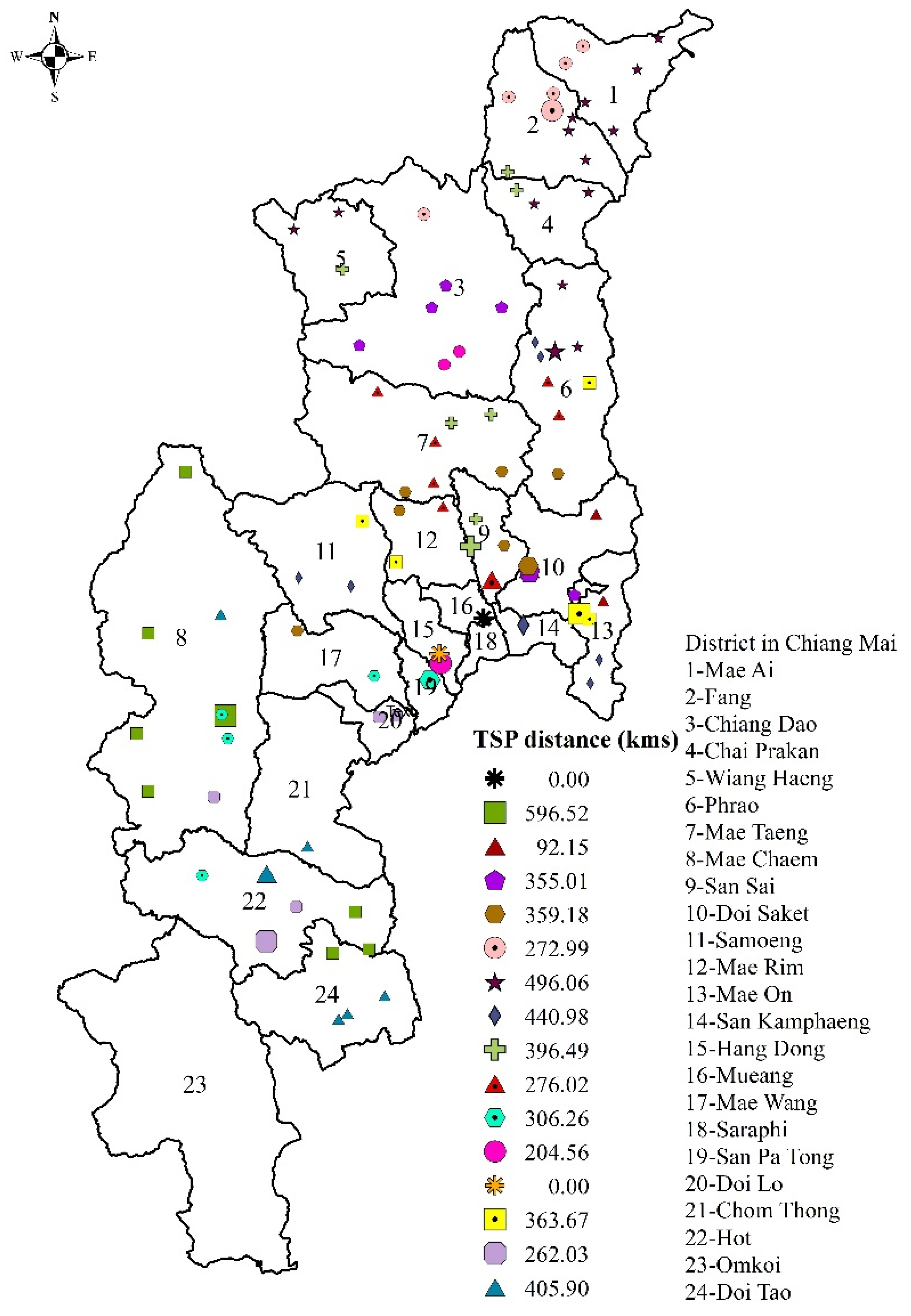
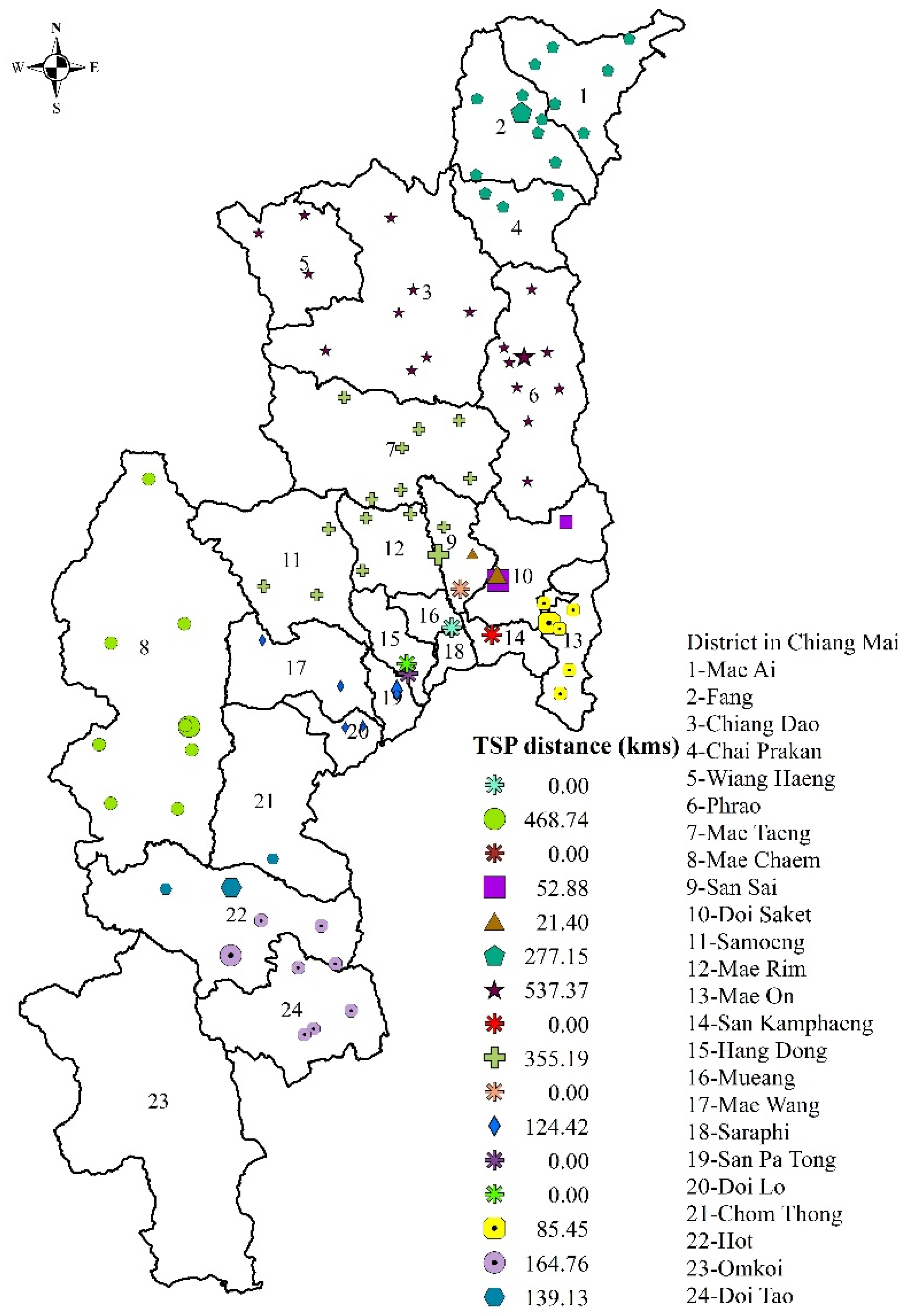
2 emissions) of this system, we wrote a program on Google Apps to find the shortest distance and time traveled between each pair of nodes (fields, co-ops and customers), which were obtained as GPS coordinates via Google maps. Since the number of nodes in the system exceeds the limitations of CVRPC, the solutions for this problem are found via Relaxed CVRPC, Relaxed CVPRC with fixed radius and SCVRP. The clusters found through these 3 models are shown in
Figure 4,
Figure 5 and
Figure 6. The optimal travel distance obtained from Relaxed CVRPC is 1162.65 km; after solving TSP in each cluster, it is 7042.50 km with an execution time of 130.19 s. The optimal solution of Relaxed CVRPC with a fixed radius of 128 km is 1294.27 km; after TSP, it is 4827.82 km with an execution time of 112.92 s; and those of the SCVRP model are 5296.84 and 2226.49 km, with an execution time of 157.90 s.
Since the Relaxed CVRPC model for the larger case study cannot be optimally solved via AIMMS, this system of the 9 provinces is solved via the SCVRP model. The optimal total distance obtained is 33,335.17 km and, after solving for TSP in each cluster, the total distance is 11,752.66 km.
Since the CO
2 emission of agricultural waste transportation is 0.0728 kgCO
2/tkm [
18], CO
2 emission transportation in Chiang Mai using the Relaxed CVRPC, the Relaxed CVRPC with fixed radius, and SCVRP are 2255.42, 1546.15, and 713.05 ton/year, respectively. In the 9 provinces of Northern Thailand, CO
2 emission of transportation is 3763.89 ton/year. Adding these figures to the CO
2 emissions from transforming the waste to pellets, the biomass pellet production process will reduce CO
2 emissions from open burning of corn residues. CO
2 emissions from biomass pellet production with agricultural waste transportation using the Relaxed CVRPC, the Relaxed CVRPC with fixed radius, and SCVRP in Chiang Mai will reduce be reduced by 10,466.03, 11,175.30 and 12,008.40 tons per year, respectively. CO
2 emissions from biomass pellet production in the 9 provinces of Northern Thailand with transportation using SCVRP will decrease by 180,198.14 tons per year. This system includes only 15% of corn cob and husk residues produced in the studied areas.
5. Discussions and Conclusions
In this work, mathematical formulations of the capacitated vehicle routing problem are proposed to identify clusters for centers and their clients. Each cluster can be served by only one center while satisfying the supplies/demands in that cluster and the capacity of the center. Since the best transportation criterion in the system has not yet been determined, we investigated several objective functions for the problem. Two distinct transportation criteria are considered in this work, i.e., either the centers pick up products/waste from their clients, or all clients deliver their products/waste to their centers. The first two initiative models were constructed to capture these two criteria. The first model, CVRPC, was developed to find clusters whose individual centers each have minimum total transportation costs similar to the capacitated vehicle routings with capacity (CVRP). The depot of the CVRP, if not utilized, will be a dummy node having zero distance to all the nodes in the system. The second model developed is the SCVRP where the second transportation criterion is involved. In this model, each cluster has a center and all clients connect to its center, while the depot (which can also be a dummy) joins all the centers together.
Since CVRPC has a very long processing time, the Relaxed CVRPC model is obtained by dropping the subtour elimination constraints (the cause of long processing time) off the CVRPC model. The resulting model’s complexity, hence, the computation time needed to solve the model, is much lower than that of the CVRPC, but the optimal solution obtained is much worse than that from the CVRPC. Consequently, the Relaxed CVRPC with a fixed radius is developed by limiting the distances between the nodes and its center.
Each of the clusters obtained from all of these models is solved by TSP to find alternative transportation scheme for the cluster. All 4 models constructed are solved using AIMMS on an Intel® Core ™ i7-2600 CPU@3.40 GHz with 16 GB of RAM, or an Intel® Xeon® CPU 2.30 GHz 2.29 GHz (2 processors) with 64 GB of RAM when the former is unable or takes too long to solve the problems. Statistical tests are also conducted to compare the models’ efficiency. The total distances of the CVRPC in the simulation results indicates the model’s superiority over the others in small scale problems. However, for practical problems with larger scale, CVRPC cannot be executed within a reasonable processing time.
CVRPC cannot be solved for both of the real-world problems studied. Supplies, demands, locations of all fields and centers, and the distances between every pair of nodes are collected. In the simulation results, Relaxed CVRPC after TSP solutions is generally worse than Relaxed CVRPC with a fixed radius in all cases, and is worse than the SCVRP in larger cases. The simulations also show that Relaxed CVRPC with a fixed radius gives the best results among the three models in all cases.
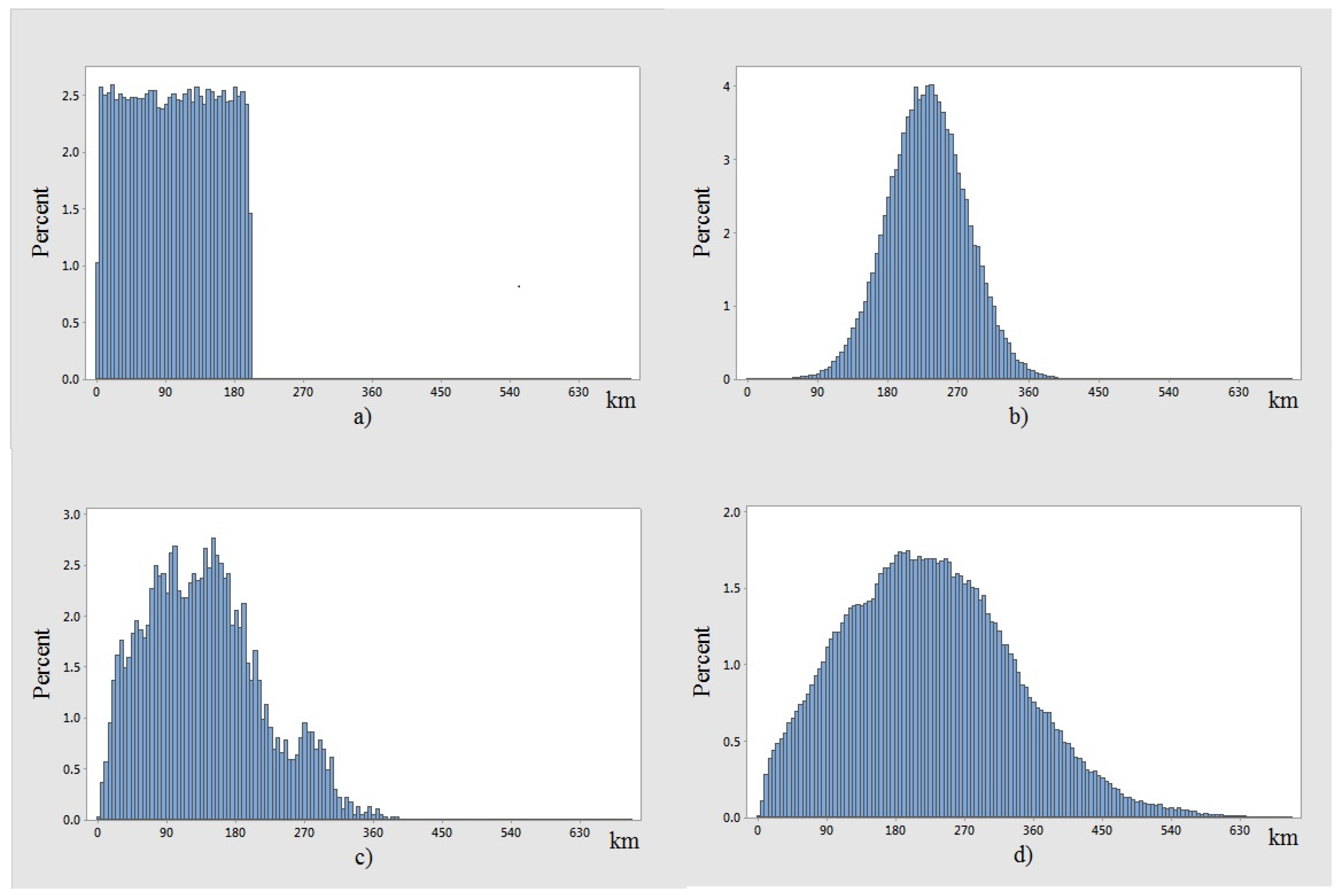
However, the results from the SCVRP are better than those from the other two models for both real-world problems. This is counterintuitive, since one might assume that SCVRP should be worse than the other two models. From our investigation of the distributions of each set of data solved as shown in
Figure 7, we found that, in the case study, the distances between the two nodes are a right skewed normal distribution, while those in the simulated problems are uniformly or normally distributed. These differences may be caused by a discrepancy between the distributions of random distances in the simulations and real-world problems. So when solving a real world problem, SCVRP might be a good candidate since it can provide a good solution and is more flexible in the sense that the solution to both transportation criteria can be obtained.
In the case study, the transportation of corn residues is solved via the three solvable models. Then the total CO2 emissions in the corn residue elimination process is calculated. It is found that total CO2 emissions is reduced even with more transportation involved in the system. In this particular system, only CO2 emissions from corn cob and husk eliminations are considered. This could save up to 12,008.40 tons per year of CO2 emissions in Chiang Mai and 180,198.14 tons per year in the 9 provinces of Northern Thailand. Since only 15% of corn production (and by extension, only the same amount of residues) are transported to the co-ops, the figures can be improved if we expand the co-ops to include more farms. This can be done if incentives are offered to the farmers. More investigation should be made in order to reduce transportation cost, and policies on incentives to the farmers can be made based on further investigation.