Abstract
We report an experiment designed to study bargaining behavior between one buyer and multiple sellers with complementarity and how it is influenced by fairness concern and information transparency. We base our setup on a structured alternating-offer bargaining model in which a buyer procures complementary items from two heterogeneous sellers with endogenous choice of the order of bargaining. In addition, we implemented an information transparency manipulation regarding whether the sellers were informed about each other’s offers/counteroffers with the buyer. Experimental behavior exhibited deviations from equilibrium predictions that did not differ significantly by information condition, suggesting that sellers were not significantly influenced by direct social comparison between each other. Further analysis suggests that each seller demanded splitting the value of the deal approximately half-half with the buyer as a normative fairness benchmark. The buyers, on the other hand, did not have a demand for fairness that was based on a fairness benchmark.
Keywords:
one-to-many bargaining with complementarity; fairness; transparency; social comparison; normative fairness benchmarks; experiments JEL Classification:
C72; C78; C92; D63
1. Introduction
Bargaining that involves multiple parties abound in all domains of life; a common subset is one-to-many bargaining with complementarity, where the “one” must reach an agreement with all or a subset of the “many” to derive any benefit from the overall deal. Examples include land assembly [1], where a property developer needs to purchase contiguous parcels of land from multiple landowners in order to complete a project. Likewise, when the U.S. Federal Communications Commission (FCC) seeks to repurpose spectrum, it faces a one-to-many bargaining challenge where a profitable reallocation requires acquiring large contiguous spectrum blocks, but spectrum ownership rights are fragmented among many independent sellers. One-to-many bargaining with complementarity also occurs widely in modern manufacturing of products from consumer electronics to automobiles and aircraft, where original equipment manufacturers (OEMs) in a supply chain need to purchase inputs from multiple independent suppliers [2,3]. Other examples include the formation of a coalition government where the designated prime minister needs to negotiate separately with multiple parties in order to form a majority coalition, a labor negotiation process in which an employer needs to reach wage deals with different unions separately, or a pharmaceutical development project in which a firm needs to bargain with multiple patent holders to commercialize a treatment. Also, in financial crises, firms in dire circumstances need to deal with multiple creditors and often bargain with multiple unions with different timelines.
Fairness concern could have a key influence in these and many other instances of one-to-many bargaining with complementarity, as the voluminous behavioral research on fairness concern in two-party bargaining behavior suggests [4]. However, fairness concern in one-to-many bargaining with complementarity could be more complex than in two-party bargaining. Consider, for example, a setting in which a buyer needs to close price deals with most or all of multiple sellers each holding a complementary item [5]. There could be two different types of fairness concerns. First, direct social comparison between the sellers regarding the deals and offers they receive could induce inequity aversion [6] that reflects a “horizontal” fairness concern [7]. Secondly, bargainers might also be influenced by a highly localized and normative “vertical” fairness concern [7], with which a deal between the buyer and a seller is fair as long as the deal offers a division of the “pie” (value of the deal) between the two that is considered fair.
An example of “horizontal” fairness concern was studied by [8], who analyzed two identical ultimatum games played sequentially by a leader and two followers. Using laboratory experimental data and a social comparison model adapted from [6] model of inequity aversion, those authors estimated that horizontal fairness between the followers is two-times stronger than distributional fairness between leader and follower. However, in that study the two followers were symmetric and engaged in two ultimatum games that were independent in terms of the size of the “pie” (value to be divided), so that equal treatment might appear to be a natural fairness norm that would also induce direct social comparison between the followers. Moreover, in [8] setting, the first agreement (or disagreement) does not constrain the value of the pie to be divided in the second stage. This is very different from our setting—which is more pertinent to realistic one-to-many bargaining—where a single “pie” is to be divided sequentially and the first division puts a limit on how much the leader can offer the second follower. Further, to derive any value, the leader must reach an agreement with both followers. It is not clear if [8] findings will hold when the leader is negotiating a multiparty split of the same “pie” with highly asymmetric followers like in many cases of one-to-many bargaining, including the experimental setting to be reported. In fact, in a previous two-party bargaining experiment that involved a three-way split among the bargaining parties plus an inactive “dummy” [9,10], a very different picture emerged: the study showed that responding bargainers might be largely influenced by their own “vertical” fairness benchmarks (in terms of the proportion of the “pie” that is considered a fair share for themselves) regardless of how much the dummy was receiving, so that direct social comparison did not play a significant role.
A major objective of the present research is to examine, through a laboratory experiment, how the two different types of fairness concern might influence behavior in one-to-many bargaining with complementarity. In our experiment, human subjects assumed the roles of bargaining players with corresponding economic incentives in a game that was based on an alternating-offer one-buyer–two-sellers bargaining model [11] were the buyer could choose the order of bargaining. Through our setup, we could analyze various aspects of bargaining behavior at a granular level during the process of bargaining, such as the buyer’s choice of bargaining order, the players’ offers/counteroffers, and responses to them, as well as the final bargaining outcomes. We could then obtain evidence regarding whether/how these observations of bargaining behavior might deviate from strategic benchmarks obtained from standard game-theoretic analysis, and, if so, in what ways might the different types of fairness concern be able to explain the deviations.
Our experimental design also included a between-subjects information transparency manipulation. Under the full information condition, the two sellers were fully informed about the bargaining histories of each other with the buyer. Under the partial information condition, each seller was not informed about the offers/counteroffers the other seller received from/gave to the buyer or the price of the deal the buyer and the other seller have reached and was only informed if a deal had been reached or not. Our information manipulation allowed us to detect “horizontal” fairness concern between the sellers, as it provided each seller access to information about the deals of the other seller, which might then facilitate direct social comparison. Equilibrium predictions under standard assumptions of self-interest maximization would be the same for both information conditions. However, if direct social comparison between sellers was an important influence on their behavior, we might be able to observe significant differences in bargaining behavior across the information conditions. Previous behavioral research on bargaining and other market behavior has also found that fairness perceptions might vary with the level of provision of information in different settings [12,13,14,15]; it is thus also of interest to investigate how information transparency might or might not make any difference in a setting of one-to-many bargaining with complementarity, as we realize here.
Our information manipulation was additionally motivated by transparency issues in real-life one-to-many bargaining. Traditionally, deals between a buyer and each seller might often be kept confidential from other sellers. However, increasing social concern for governance has pushed bargaining deals toward greater information transparency in domains such as land [16], Chapter 2 and supply chain [17], where one-to-many bargaining is common. Our experimental design is therefore aligned with a public policy interest to examine whether transparency can make a difference in such scenarios.
The data from our experiment present a number of major findings. First, behavior differed from equilibrium predictions significantly. While equilibrium prescribes that the buyer should bargain with the weaker seller (in terms of the income stream that the seller receives before making a deal) first, buyers in the experiment chose to bargain with either seller first with approximately equal likelihood, irrespective of the information condition. Moreover, deal prices with the weaker (stronger) seller were higher (lower) than in equilibrium, also irrespective of the information condition. We also observed that information transparency had little influence on behavior in our experiment. Further analysis of the possible influence of fairness concern in the form of direct social comparison between sellers reinforces the implication of the non-significant effect of information transparency, namely that sellers were not significantly influenced by direct social comparison or a “horizontal” fairness concern.
We next analyze our response data using a fairness model that is adapted from [18], through which we estimate the bargainers’ normative fairness benchmarks for deals as a “vertical” fairness concern. Our estimations suggest that sellers consider splitting the value of the deal approximately half–half with the buyer to be fair, and their fairness benchmark did not vary with factors such as the asymmetry between the sellers. The observed seller responses reflect a tradeoff between normative fairness demand, the pecuniary value of the deal price, and the seller’s income stream. The buyers, on the other hand, did not have a demand for fairness that was based on a fairness benchmark. In sum, robust normative fairness benchmarks, as a “vertical” fairness concern—an entrenched demand of a fair share of the current bargained value with the buyer—played a significant role in bargaining behavior in our experiment, including its deviations from equilibrium predictions.
Our work contributes to research on behavior in one-to-many bargaining and more generally multiparty bargaining. Existing behavioral experiments on one-to-many bargaining tend to focus on specific major applications such as land assembly [1,19,20,21] and supply chain [22,23]. Other types of multiparty bargaining experiments have examined contexts such as market design [24] and legislative voting [25] In terms of bargaining protocols, both freeform [23,26] and structured bargaining approaches [27,28,29,30,31,32,33,34,35,36] have been adopted. The research objectives of these studies cover a host of bargaining variables including contingent vs. non-contingent contracts, buyer proposes vs. sellers propose, sequential vs. simultaneous offers, number of sellers, strict complementarity vs. partial complementarity, and whether the buyer can invoke eminent domain. However, our experiment is the first to focus on fairness concern as well as information transparency in a structured one-to-many bargaining setup, which facilitates the study of behavior during the bargaining process. In particular, our investigation into fairness concern distinguishes between direct social comparison between sellers as a “horizontal” fairness concern, and normative benchmarks of fair split between each seller and the buyer as a “vertical” fairness concern—issues that have been scarcely explored in previous related research 1.
In the rest of this paper, we first introduce the bargaining game on which the experiment was based. We discuss the equilibrium predictions for the model and then the information manipulation. We then report our data analysis findings including our analysis and estimations on the influence of fairness. Finally, we offer a concluding discussion on our findings and their implications.
2. Experimental Design
2.1. The Theoretical Model: Motivations and Outline
In proceeding with our investigation, we sought to base our experimental bargaining game on a theoretical model that captures several common characteristics in one-to-many bargaining scenarios, including the examples at the beginning of this article. These characteristics include: (1) a buyer needs to purchase complementary items from multiple sellers, (2) the sellers are heterogeneous, (3) the buyer endogenously chooses the order of bargaining, and (4) there could be multiple periods of interactions between the buyer and the same seller before a deal is closed with that seller. In addition, we looked for theoretical models with unique equilibrium outcomes that could be used as unambiguous point predictions.
Earlier theoretical treatment of one-to-many bargaining typically assumed an exogenous ordering protocol [44,45,46,47]. Subsequently, [37,38,39,40,48] study endogenous sequencing in one-buyer–multiple-seller bargaining where the buyer interacts with each seller only once. A number of recent studies look at endogenous order of bargaining between one buyer and multiple heterogeneous sellers in a sequential context involving potentially repeating offers and counteroffers [49], in a contingent contract setting (under which payoffs are realized only after the buyer has completed making deals with all the sellers), and [50], in a setting where the sellers’ items are non-complementary to the buyer, both obtain multiplicity results. The few works of this kind that yield unique equilibrium predictions include [11], who analyze models with perfect complementarity and binding cash-offer contracts, so that a seller receives the agreed price in cash once a deal is reached and leaves the game immediately. The sellers are, moreover, heterogeneous in having different inside options. Ref. [11] shows that there is a unique equilibrium if the sellers’ inside options are not too large and are sufficiently different from each other; in equilibrium, the buyer prefers to negotiate with the seller with the lower inside option first 2.
As such, we based our experimental game on an infinite horizon version of [11]’s model, which exhibits the common characteristics mentioned above and offers a unique equilibrium outcome that could be used as unambiguous point predictions. In the model, a buyer seeks to purchase two perfectly complementary items from two sellers. Each seller owns one item. Each item by itself has zero value to the buyer, but the value of the combined items to the buyer is VB > 0. Bilateral bargaining takes place sequentially with a series of offers and counteroffers that are time-discounted by a common per-period discount factor δ and follows an endogenous order determined by the buyer as the game proceeds. Seller i (i {L, H}) earns a per-period income of vi (1 − δ) from their item as long as they own it, which is the seller’s inside option. The value vi is thus the total time-discounted income stream obtained if a deal is never reached. The sellers are heterogeneous in having unequal per-period incomes. Assume, without loss of generality, that vL < vH, so that Seller L is the seller with the lower inside option value and will henceforth be called the low-value seller. Seller H will henceforth be called the high-value seller.
2.2. Experimental Implementation of the Model
To implement the model in the experiment, one player was assigned the role of Buyer and the other two players the roles of Sellers. To operationalize time discounting in the laboratory, we adopted an experimental procedure that makes use of the equivalency between such a game and a multi-period game with random termination [52,53]. In our design, each experimental game consists of an indefinite number of periods and, conditioned on the game being played currently, there is always a fixed probability r that the game would continue to the next period. This continuation probability is equivalent to the common time discount factor δ = r in an expected utility framework, so that the experimental bargaining process mimics an infinite horizon with time discount factor δ. The game ends if the Buyer makes deals with both Sellers or if the game is terminated randomly before that.
As in the theoretical model, the experimental game involves a sequence of price offers and counteroffers. It takes one period to make and accept/reject an offer. In the first period of the game, the Buyer makes an offer to the Seller of their choice. This Seller can accept or reject the offer. If the Seller accepts the offer, a deal is made, their item is sold, and this Seller leaves the game. If the Seller rejects the offer, they stay in the game. If the game continues to the next period (with a probability of r), this Seller makes a counteroffer to the Buyer for the sale of their item. If the Buyer rejects the counteroffer and the game continues to yet another period, the Buyer makes an offer to one of the Sellers that are still in the game; if both Sellers are still in the game, the Buyer can choose which of them to make an offer to.
The parameters in our experimental game are VB = 100, vL = 10, vH = 50, and r = δ = 0.9. That is, the incomes per period for the low-value and high-value Sellers are vL (1 −δ) = 1 and vH (1 − δ) = 5, respectively, and the Buyer earns 100 if and only if deals have been agreed with both Sellers. All of the parameter values are common knowledge in the experimental game. The time discount factor δ = 0.9 is implemented as a random continuation probability r = 0.9 for the game to proceed to another period.
2.3. Equilibrium Predictions
[11]’s theoretical findings, based on standard game-theoretic equilibrium analysis assuming self-interest maximization, common rationality, and subgame perfection, are used to generate the theoretical predictions for our experiment. Our experimental parameters satisfy the conditions of [11]’s Proposition 4, so that the experimental game has a unique equilibrium outcome. The specific equilibrium offers and subgame equilibrium offers/acceptance thresholds along off-the-equilibrium paths for our experimental parameters can be calculated using the results in [11] and are listed in Table 1; see Appendix A for more details about the calculation of equilibrium predictions. The equilibrium prescribes that the Buyer makes a relatively low offer of 16.48 to the low-value Seller first and the low-value Seller accepts the offer. If the game continues to the next period in the experiment, the Buyer makes a relatively high offer of 73.68 to the high-value Seller, which is also accepted, thus concluding the game. Notably, the Buyer and the high-value Seller would not make a deal in any off-the-equilibrium play before a deal was made with the low-value Seller—the Buyer and the high-value Seller should prefer to wait for a deal with the low-value Seller being reached first.

Table 1.
Overall equilibrium offers and subgame equilibrium offers/acceptance thresholds along off-the-equilibrium paths.
Although both Sellers have equal “vetoing” power from the point of view of the Buyer—the Buyer can make any gains only after reaching deals with both Sellers—in equilibrium, the low-value Seller reaches a deal with a lower price than the high-value Seller. This is because each Seller has to trade off between continuing to earn their inside option and reaching a deal (when they will stop earning the inside option); this tradeoff, including the opportunity costs involved, leads to asymmetric considerations from the Sellers’ point of view despite the apparent symmetry in their “vetoing” power from the point of view of the Buyer. The Buyer, factoring these in, would then find it strategically optimal and feasible in equilibrium to make different offers to different Sellers as prescribed.
2.4. The Information Manipulation
As discussed earlier, we also manipulated, across two between-subjects experimental conditions, the information that was available to each Seller, so that the level of information transparency between Sellers was different across conditions. In the full information condition, each Seller was fully informed about the bargaining history between the Buyer and the other Seller. This included the value of each offer/counteroffer, and, if agreement had been reached, the price that was agreed upon. In the partial information condition, each Seller was only partially informed about the bargaining history between the Buyer and the other Seller. The Seller was only informed about the fact that bargaining was taking place between the Buyer and the other Seller and, after bargaining, whether a deal had been reached—but not about the deal price.
In terms of game-theoretic analysis, the only strategically relevant information to a Seller would be whether the other Seller was still in the game (i.e., whether a deal had been reached with that Seller or not) but not the offers/counteroffers between the Buyer and the other Seller, nor their agreed deal price (if any). That is, all equilibrium predictions are the same across the information conditions. However, as discussed, the full information condition could behaviorally facilitate direct social comparison and induce inequity aversion [6] that influences behavior as a “horizontal” fairness concern.
3. Method
3.1. Subjects
Two hundred and nineteen subjects, students from a large Western US university, volunteered to participate in an interactive decision-making experiment with payoff contingent on performance. The subjects were divided into 24 experimental sessions. Two sessions had 6 subjects each (one session in each information condition), 19 sessions had 9 subjects each (nine sessions in the full information condition and 10 sessions in the partial information condition), and three sessions had 12 subjects each (two sessions in the full information condition and one session in the partial information condition). That is, 111 subjects were assigned across 12 sessions in the full information condition and 108 subjects were assigned across 12 sessions in the partial information condition. Each subject participated in a single computer-controlled session that lasted about 100 min and included 15 games. The first 3 games were for practice and the next 12 games were for payment. At the end of the session, subjects were paid their average earnings from the 12 for-payment games in addition to a fixed $8 show-up fee. On average, subjects were paid $31.56 each.
3.2. Procedure
Upon arrival at the laboratory, subjects were randomly assigned to separate cubicles and handed printed instructions. A sample of the instructions is available in Appendix B. After reading the instructions, subjects were asked to complete an online quiz that tested their understanding of the instructions. While answering the questions, subjects could consult the instructions. If an answer was incorrect, feedback with an explanation for the correct answer was provided. The first practice game started after all subjects in the session answered all the questions correctly.
The two Sellers were labeled Seller Blue and Seller Green. In the experimental decision interface, which was similarly designed for all players, Seller Blue was always presented on the left side of the screen and Seller Green was always presented on the right side (Figure 1). To mitigate potential confounds with psychological biases associated with these presentation features, in 13 of the sessions, Seller Blue was the low-value Seller (vBlue = vL = 10) and Seller Green was the high-value Seller (vGreen = vH = 50). In the rest of the sessions, the inside options were reversed between Seller Blue and Seller Green.
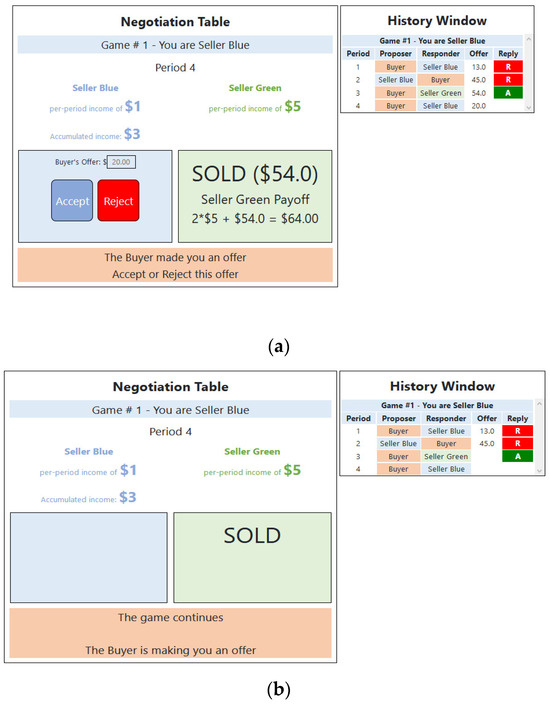
Figure 1.
Sample decision screens in the experiment. (a) Full information condition: low-value Seller at the point of responding to an offer from the Buyer. (b) Partial information condition: low-value Seller at the point of waiting for an offer from the Buyer.
During the three practice games, each subject played each role once. During the 12 for-payment games, each subject played each role four times. In addition, the three-player groups within every session were randomly re-matched from game to game. The bargaining protocol and computer–subject interface were implemented in oTree [54]. The players’ screen was divided into a Negotiation Table and a History Window (Figure 1). In the Negotiation Table, the active player could make an offer or respond to an offer from another player. In order to offer ample information for subjects to learn to play the game strategically, the History Window presents the history of all previous games (by period) and the history of the current game up to the current period. The difference between the information conditions was that a Seller could (could not) see the offers/counteroffers between the other Seller and the Buyer in the full (partial) information condition—as is evident from a comparison of the two panels in Figure 1.
4. Preliminary Analysis of the Experimental Data
In assessing bargaining behavior in our experiment, we focus on the for-payment games in the experimental sessions. Figure 2 presents a breakdown of these games in terms of the type of deals made (if at all). We also divide the 12 for-payment games in each session into two blocks of six games and aggregate data separately in each block, in order to test for learning effects upon repeated play. Table 2 lists the means of major dependent variables by block and information condition, with notations that indicate deviations from equilibrium predictions and learning across blocks. Note that the unit of observation in this set of statistical analysis is an experimental session, within each of which subjects were re-matched into three-player groups from game to game. Further analysis is reported in Appendix C.
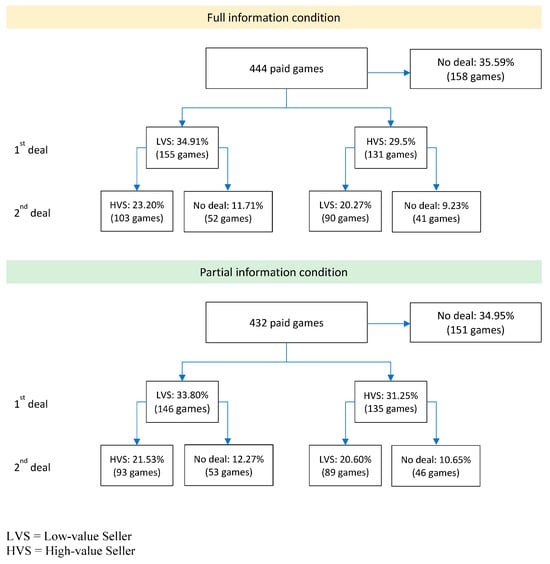
Figure 2.
Breakdown of games by deals.

Table 2.
Means of major dependent variables.
Overall, bargaining behavior in our experiment deviated significantly from equilibrium predictions:
- (1)
- An equilibrium prediction is that the Buyer would make an offer in Period 1 to the low-value Seller. However, offers that were made to the low-value Seller in the experiment accounted for only around 50% of the Period 1 offers over much of the session. Statistical analysis of the evolution of this choice variable across blocks does not yield significant learning effects. Further analysis with aggregation over all paid games (see Table 3 for relevant summary statistics) shows the following, according to paired t-tests at a 95% significance level: (a) the period at which the first deal was made did not differ significantly according to whether the first deal was made with the low-value or high-value Seller; and (b) the price at which a deal was made with a particular type of Seller (low-value/high-value) did not differ significantly according to whether the deal was the first or the second to be made within a game. Both findings deviate from equilibrium predictions, including the prediction that a deal with the high-value Seller could never occur before a deal with the low-value Seller (Table 1);
 Table 3. Breakdown of mean number of periods to deals and deal prices by order of deals agreed.
Table 3. Breakdown of mean number of periods to deals and deal prices by order of deals agreed. - (2)
- Equilibrium analysis predicts that the bargaining game should not be more than two periods long. A deal with the low-value Seller should be reached in Period 1, followed by the second and final deal with the high-value Seller in Period 2—which would happen with 90% probability in the experiment due to random termination. However, Figure 2 shows that the proportion of games with two deals, which is between 40% and 45% across information conditions, is clearly lower than 90%. Moreover, the bargaining process was, in general, much longer than the equilibrium prediction: it took, on average, more than five periods to reach a deal with any Seller in the experiment. Table 2 also suggests that the number of periods to make a deal with the low-value Seller was, in general, about the same as that for the high-value Seller. This is supported by paired t-tests for Block 1 in the full information condition and for both blocks in the partial information condition with p > 0.1 in all three tests;
- (3)
- Table 2 indicates that, on average, the low-value (high-value) Seller made deals with a higher (lower) price than the corresponding equilibrium prediction;
- (4)
- Table 2 also shows that, in each block and information condition, compared with equilibrium predictions, the Buyer earned about as much or lower payoff on average, the low-value Seller earned significantly higher payoff on average, and the high-value Seller earned significantly lower payoff on average. Moreover, the welfare was significantly lower than the equilibrium prediction on average.
In Sectiona 1 to 4 of Appendix C, we report a set of additional analyses of the bargaining dynamics in the experiment with respect to offers/counteroffers and responses to them. In particular, the analysis reported in Appendix B suggests the following:
- (5)
- Subjects were insufficiently strategic and did not base their decisions in the bargaining game on the number of Sellers still in the game (which makes crucial differences in the equilibrium), nor the previous deal price (if any) in the full information condition (see also Section 5.1);
- (6)
- Buyers had a tendency of bargaining with the same Seller repeatedly until the Seller accepted a deal;
- (7)
- There is some evidence of offers and counteroffers exhibiting reciprocal gradualism [55], by which the two parties made mutual, reciprocal concessions in their interactions.
Information Manipulation
As reflected in Table 2, there was significant learning across blocks (at p < 0.05 level for within-subjects block effects) in terms of Period 1 offers and deal price with the low-value Seller under the partial information condition. Under the full information condition, there was only significant learning across blocks in terms of the number of periods to make a deal with high-value Seller. It thus seems that, at least for some of the dependent variables, full information did quicken learning so that the variables stabilized early on in the session, while under partial information there was more gradual learning throughout the session.
The above effects, however, did not translate to significant impacts on deal prices. We analyze the mean deal prices in a 2 (Seller role) × 2 (Block) × 2 (Information condition) mixed-design ANOVA, where Seller role and block are within-subjects factors and information condition is a between-subjects factor. We find a significant main effect in Seller role (F(1,22) = 56.70, p < 0.01) but no other main or interaction effects at p < 0.05. The significant main effect in Seller role highlights the high disparity in deal prices by Seller roles that is apparent from Table 2. However, additional information in the full information condition did not bring about a difference in the disparity of deal prices among Sellers relative to the partial information condition—as we might have observed had the full information condition facilitated direct social comparison that influenced behavior.
5. Further Analysis Regarding Fairness Concern
5.1. Testing for the Potential Influence of Direct Social Comparison between the Sellers in the Full Information Condition
We conduct further logistic regression analysis focusing on the full information condition and in situations when there was only one Seller in the game, so that one deal had previously been reached in the game, and the other Seller was responding to an offer from the Buyer. Our regression model specifically tests the influence of direct social comparison in those situations, and the regressors are informed by [6] model of inequity aversion. Denote the Buyer’s offer as x and the previous deal reached as p−1. Then, the regressors are x, max (p−1–x, 0) (a measure of disadvantageous inequity of the offer relative to the previous deal), and max (x–p−1, 0) (a measure of advantageous inequity of the offer relative to the previous deal). We conduct the regressions for the low-value and high-value Sellers separately but aggregating over blocks in each case to achieve a larger number of data points. The results are presented in Table 4. We find that the response of the remaining Seller to offers did not depend on the deal with the other Seller in terms of disadvantageous and advantageous inequity—the corresponding coefficients are not significantly different from zero at significance level p < 0.05 for both Sellers.

Table 4.
Tests for possible direct social comparison between the Sellers in the full information condition: logistic regression analysis of Seller’s response to offers when a deal had already been reached with the other Seller.
In sum, our analysis suggests that subjects in the experiments were not significantly influenced by the previous deal price (if any) in the full information condition and the direct social comparison thus implied.
5.2. Estimating Bargainers’ Normative Fairness Benchmarks
Our data analysis so far suggests that, while our experimental results deviated significantly from equilibrium predictions, bargaining outcomes were largely consistent and stable across periods, games, and information conditions. Bargainers also did not seem to be significantly impacted by direct social comparison as a “horizontal” fairness concern. We now explore whether fairness might impact behavior in our experiment in another way, namely that players might base their decisions on simple, normative fairness benchmarks [56], so that negative deviation from the benchmark incurs disutility [10,18]. That is, robust normative fairness benchmarks as a “vertical” fairness concern—an entrenched demand of a fair share of the current bargained value with the buyer—might have played a significant role in bargaining behavior. As such, we conduct a further analysis that is aimed to estimate these fairness benchmarks.
Note that, despite our earlier finding that direct social comparison of an offer with a previous deal did not seem to impact bargaining outcomes significantly, a previous deal could still have an indirect influence on a Seller’s fairness concern in the current analysis. This is because the previous deal determined the current value of the deal and thus the absolute amount (= current “pie” × fair share percentage) that the supplier demanded as fair. The fairness implication of this indirect influence underlies part of the analysis to be reported. Note also that the actual bargaining outcomes (i.e., deal prices) are not necessarily the benchmarks themselves. This is because a bargaining outcome could be the result of a tradeoff between demand for fairness and strategic self-interest factors such as income stream. A responder might have accepted an offer that was worse than their fairness benchmark for the sake of the immediate value gain. Alternatively, a responder might reject an offer that was better than their fairness benchmark if they thought that, by rejecting, they might gain even higher expected benefits in further periods of bargaining. Our objective is to tease out the relative influence of immediate self-interest (the pecuniary value gained from the current offer if it is accepted), fairness concern (the disutility from unfair offers), and the strategic considerations (the expected utility from rejecting the current offer and waiting) on subjects’ behavior.
To proceed, we adapt the equity–reciprocity–competition (ERC) model of fairness [57] to our setting. The ERC model has been shown to be useful in understanding the influence of fairness in sequential bargaining behavior [18]. An essential component of the model is the assumption of a normative fairness benchmark (in bargaining contexts, the proportion of the value of the deal that is considered a fair share) such that an unfair outcome relative to the norm could incur disutility to the individual. However, previous applications of this model were largely in two-party bargaining and the fairness benchmark was typically assumed at the outset to be half of the total bargained value. Here, the fairness benchmark is not obvious at the outset since there are three players with roles of a very different nature and very different inside options. A central aim here is thus to estimate the fairness benchmarks of the roles.
As in any empirical estimations, we allow for random errors in players’ decisions, so that decisions would be probabilistic in general. We also limit our analysis to the part of the data that record the responses to offers or counteroffers. This is because estimations from the offer/counteroffer decisions themselves would require modelling the beliefs of the player making the offer/counteroffer regarding the responder’s probabilistic response to every potential offer/counteroffer. The modelling of such wide-ranging beliefs could lead to confounds depending on the background assumptions. For instance, a systematic, internally consistent approach to modelling these beliefs would be the quantal response equilibrium (QRE) framework [58], which has been used to analyze two-party finite sequential bargaining [18]. However, to our knowledge, there is no QRE theoretical treatment for games with infinite horizon, and hence we find the current QRE framework inapplicable to the present setting. Meanwhile, we can more readily adapt an existing two-party bargaining model of fairness—based on [18]—to the responses in our three-party bargaining setup.
5.2.1. Model Specifications
In our model, the fairness of an offer/counteroffer is appreciated in proportion to the value of the deal. To be precise, we define the value of the deal as the maximum feasible price that the Seller can obtain from making a deal at the point of observation without incurring a certain net loss to the Buyer in the whole game (i.e., a net loss even if both deals are completed). This definition indicates the amount that the Seller can ever gain from the bargaining game at that point. Consider player i in the role of a Seller in a hypothetical game. Suppose that i is at the point in a game when the Buyer has made an offer to i, and i is deciding whether to accept or reject, or i has made a counteroffer to the Buyer and the Buyer is deciding whether to accept or reject. In both cases, the offer/counteroffer is the price that i will earn if a deal is made. Denote the value of the deal at that point as c. Then, according to our definition, c = VB = 100 if no Seller has accepted a deal yet (i.e., there are still two Sellers in the game), and c = VB − x = 100 − x if the other Seller has already received x from an agreed deal in an earlier period.
A complication regarding the value of the deal arises in observations in the partial information condition where there is only one Seller left in the game who is a responder (488 or 8.69% of all the response observations in the analyzed data). This is because the Seller, in this condition, is uninformed about the value of the deal, as the Seller has no knowledge about the previous deal with the other Seller. We adopt a simple, linear formulation of the Seller’s belief of c in that case. Suppose that, in such a case, the Seller is i, and the offer from the Buyer to the Seller is pi. Then, we assume that i uses pi as a signal to form a proxy for c such that:
where m = m0 + δi,high mhigh with δi,high = 1 if Seller i is a high-value Seller and is 0 otherwise; m0 and mhigh are parameters to be estimated under constraints that guarantee that VB ≥ cbelief ≥ 0 as long as the offer pi is within the reasonable range of VB ≥ pi ≥ 0 (see Section 5 of Appendix C). Hence, cbelief is close to m when pi is very low and is close to VB = 100 when pi is very high. This is intuitive as Seller i would be expected to form a higher belief of the value of the deal the higher the value of the offer is. Our formulation is also supported by the finding of [59] that, in an ultimatum game where the responder only knows the proposer’s offer but not the residual amount that the proposer is keeping, the responder estimates the actual size of the pie in a manner similar to what we assume here.
c = cbelief = m + (VB -m)(pi/VB) = m + (100 − m)(pi/100),
Referring to the hypothetical game introduced earlier, suppose the offer/counteroffer is for the Seller i to receive cσi, so that 1 ≥ σi ≥ 0 is the share of the value of the deal for the Seller. Also, as discussed above, while c is the actual value of the deal in all cases in the full information condition and in cases when there are two Sellers in the game in the partial information condition, it is cbelief as defined previously in cases where there is one Seller left in the game in the partial information condition, and the Seller is the responder. We next specify the full model via the following steps:
(a) Consider first cases when the Buyer is making an offer (σi) to a Seller, i, so that Seller i is the responder. Adapting [18], we model Seller i’s utility from the offer (if accepted) as follows:
where a ≥ 0 and bi ≥ 0 are the weightings on the immediate self-interest and the fairness concern components of the utility function (as can be seen below, we model the actual response according to a binary logistic choice model. We opt to have a coefficient parameter to be estimated for every term in the utilities to accommodate the noise factor, rather than normalize one of the parameters). The parameter a will be estimated in our analysis. Meanwhile, we also allow for the possibility that the Sellers’ fairness concern could vary according to the information condition and role (high-value Seller or low-value Seller), as the salience of fairness concern may be different in different conditions. Therefore, we assume the following:
bi = b0 + δi,pinfo bpinfo,
The quantity fi is the modelled fairness benchmark, that is, the share of c that the Seller i considers as a fair offer. As mentioned earlier, in studies such as [18] on two-party bargaining, fi is typically assumed to be 1/2. Here, fi is an estimated quantity. More specifically, we shall test whether fi can be dependent on the Seller’s role as well as how many Sellers are still in the game. This can be expressed as follows:
fi = f0 + δi,high fhigh + δi,state fstate + δi,high δi,state fhigh,state,
As such, the fairness term in the utility function measures the disutility of an offer σ to Seller i that is less than fi (i.e., when σ < fi), which captures i’s fairness benchmark in terms of what Seller i considers as a fair offer. Note that, following [18], we assume that Seller i does not assign additional utility to an offer that is more than fair (i.e., when σi > fi).
If Seller i rejects the offer, they will still be in the game. Seller i, therefore, can form a belief of the utility that they may receive by rejecting and staying on. This belief can be abstracted as an expected utility term which we label as Ui,reject:
Ui,reject = cui + rvi,
Therefore, Ui, reject captures the strategic considerations of Seller i in deciding whether to accept or reject the offer. Note that Ui, reject includes both a bargaining gain component as well as the income stream component, as waiting could potentially lead to a deal in the future while also accruing additional income;
(b) Consider now the case when Seller i is making a counteroffer to the Buyer, so that the Buyer is the responder. The Buyer’s split of the value of the deal is c(1 − σi). Note that, when there is one Seller left in the game, the Buyer does receive a payoff equal to this split upon agreeing to the deal. However, when there are two Sellers in the game, this split is only a book value that is not yet realized as an actual payoff. As such, we allow for the parameter for immediate self-interest in the latter case to be a possibly different parameter from a, which we label as aB. Otherwise, the formulation for the Buyer when the Buyer is the responder is similar to that for the Seller when the Seller is the responder. When there are two Sellers in the game, the Buyer’s utility from the deal upon being made a counteroffer of σi from Seller i is as follows:
while, when there is one Seller left in the game, the Buyer’s utility upon being made a counteroffer of σi from Seller i is the following:
where fB = fB0 + δi,high fBhigh + δi,state fBstate + δi,high δi,state fBhigh,state with similar definitions of δi,high and δi,state as before, while fB0, fBhigh, fBstate, and fBhigh,state are parameters to be estimated (under constraints that guarantee that 1 ≥ fB ≥ 0; see Section 5 of Appendix C) along with a, aB, and b. While a ≥ 0 and b ≥ 0 are parameters common to both Sellers and Buyers, aB ≥ 0 and the parameters that make up fB are specific to the Buyer.
Finally, we define the Buyer’s expected utility from rejecting a counteroffer as follows:
UB,reject = c uB,
(c) We then assume that the responders could make random errors in their decisions, so that the actual responses (accept or reject) follow a logistic binomial choice model. When the responder is Seller i, these probabilities are as follows:
When the responder is the Buyer, these probabilities are the following:
5.2.2. Estimation Results and Discussion
We use maximum likelihood estimation to estimate the parameters on the dataset under the parameter constraints discussed above (see Section 5 of Appendix C). Our estimation results, utilizing all the 5614 response observations in the for-payment games, are summarized in Table 5. We also compare, in Table 5, estimations of the full model with estimations of a similar model without fairness concern (i.e., the terms with b, f, and fB all become zero) and find that the full model does improve performance. Our results suggest the following:

Table 5.
Results of the fairness model estimations.
- (1)
- Sellers’ fairness concern, in relation to their self-interest and strategic considerations, did not vary with the information condition (bpinfo is non-significantly different from zero), which is consistent with our earlier analysis;
- (2)
- Sellers’ fairness benchmarks, as quantified as what they considered to be a fair share of the value of the deal, did not differ by their inside option or the state of the game (i.e., how many Sellers were still in the game). In fact, the estimated fairness benchmark was close to half of the value of the deal (f0 = 0.46 and is significantly different from zero). This means that, when in a state of the game in which both Sellers were still in the game (so that the deal value was VB = 100), the low-value (high-value) Sellers typically considered that they were entitled to a higher (lower) share of the value of the deal than suggested by the equilibrium deal prices (Table 1). Also, in equilibrium, only the high-value Seller may become the only Seller in the game. In that case, the high-value Seller demands 88.2% (= 100% × 73.86/(100 − 16.48) from the equilibrium prices in Table 1) of the value of the deal, which is also higher than the estimated fairness benchmark. All in all, Sellers seemed to bargain as if they were in a two-party bargaining situation where an approximately 50-50 split would typically be the norm;
- (3)
- The Buyer did not exhibit significant fairness concern. The fairness benchmark parameters for the Buyer are all non-significantly different from zero except for fBhigh,state, but the actual fairness benchmark that would involve that parameter, namely, when the Buyer is responding to a high-value Seller when that is the only Seller left, is fB0 + fBhigh + fBstate + fBhigh,state, which reaches the constraint zero in the estimation. That is, the Buyer considered a zero share as fair when responding to a counteroffer, implying no fairness concern. It seems that the Buyer, under the pressure of having to make deals with both Sellers, did not have their own demand for fairness that was based on a normative fairness benchmark. This does not imply that the Buyer tended to accept any counteroffer. The Buyer was still driven by strategic self-interest factors in their decisions in the experiment, and our result only means that the Buyer traded off immediate gain and expected utility from rejection without consideration of fairness, when responding to a counteroffer.
Overall, subjects in our experiment seemed to adhere to a norm of “piecewise 50-50 split” when they were Sellers, i.e., the Seller demanded as fair a 50-50 split of the current value of the deal with the Buyer in the current period. This was the case regardless of the type of the Seller role (low-value or high-value). However, when the subjects were the Buyer in the game, there was little concern for fairness, so that the impact of fairness concern on the experimental results was predominantly driven by the Sellers.
6. Concluding Discussion
Our findings, including the fairness benchmark estimations, highlight how entrenched normative concern could be in one-to-many bargaining settings, as in other kinds of settings investigated in previous research such as [60]. Specifically, our fairness model estimations show that Sellers considered splitting the value of the deal approximately half–half with the buyer as fair, which highlights the significant influence of a localized, “vertical” fairness concern [7]. This contributed to a mitigated difference in deal prices and payoffs of the two Sellers than under equilibrium predictions, as if the Sellers were not as responsive to their inside options as theoretically predicted (see also the findings of [61]). Our fairness model estimations suggest that the observed responses and outcomes reflect a tradeoff between demand for fairness and strategic self-interest factors such as the asymmetric income streams. However, the Buyers did not have a demand for fairness that was based on a fairness benchmark.
Moreover, information to each Seller about offers/counteroffers and deal prices with the other Seller did not influence bargaining behavior significantly—even though such information might have facilitated direct social comparison between Sellers as a “horizontal” fairness concern [7]. This finding seems to be in contrast with previous research (as discussed in the Section 1) which shows, largely in bilateral bargaining settings, that information could impact fairness perceptions. However, it does not necessarily imply that the Sellers in our experiment did not harbor direct social comparison. Rather, from our fairness model estimations, their focal concern for fairness in the current context seemed to lie in a normatively fair split with the buyer, a concern that dominated direct social comparison in its influence on behavior.
In terms of major aspects of the observed bargaining behavior, it first appears that the localized fairness concern eliminated potential gains for the Buyers in strategically choosing the order of bargaining, so that Buyers in the experiment were approximately equally likely to bargain with either Seller first. Regarding deal prices, given the 50-50 local split fairness benchmark, the first Seller approached by the Buyer would have reached a deal at VB/2 = 50 and the second would have reached a deal at VB/4 = 25, had the Sellers demanded only what they considered fair and had strategic self-interest factors not been impactful as tradeoff factors. Comparing these illustrative numbers with the equilibrium predictions in Table 1 highlights how our fairness account is consistent with the observation that deals with the low-value Seller were higher than equilibrium price while deals with the high-value Seller were lower than their equilibrium. In essence, fairness concern seemed to have mitigated the disparity in deal prices based on strategic considerations alone.
A number of further observations follow with regard to the current context. First, while the 50-50 split in two-party bargaining is a natural fairness benchmark, it is not straightforward to intuit a priori that the same benchmark would be adopted by the Sellers in our experiment. In order to understand this finding, we might start with the equal split outcome in a three-party context (1/3-1/3-1/3). For such a benchmark to be established, all three players must conceptualize themselves as participating in a three-way group task of dividing a “pie” with perceived interdependence. Such perception has been shown to induce cooperation [62]. However, in the current setup, while such perception would seem to be valid for the Buyer, the Sellers are bargaining independently of each other (in the sense that they do not directly interact). As a result, the Sellers might perceive each interaction with the Buyer as a simple two-party bargaining interaction that justifies the adoption of a local 50-50 split. This would have been reinforced by the sequential nature of the bargaining game, as previous research has shown that sequential movers are likely to develop a sense of separateness in their interactions [63].
Second, the local 50-50 benchmark resembles the social norm of the “advantage of the early mover” identified in the sequential resource dilemmas literature [64]. That is, the first Seller to strike a deal might not have been concerned with “leaving enough value” to the second Seller, nor did the second Seller consider the first deal (if known) to be a relevant direct social comparison benchmark, as we have found.
Third, in our experiment, the Buyer’s demand for fairness seemed to be suppressed by the high cost of doing so [65]. It seems that, after striking a deal with the first Seller, any deal with the second Seller that did not incur a loss was considered a fair deal by the Buyer.
Our work could be the starting point for further research on one-to-many bargaining. One possible direction is how the bargaining is contextualized; previous research has shown that the way a relationship is described can affect fairness perceptions in bargaining behavior in the relationship [66]. Also, the way a bargaining position was obtained (e.g., by the bargainers’ own previous performance, as opposed to exogenous assignment as in our experiment) might lead to the bargainer developing entitlements [67] that could affect behavior. Another direction is to examine different bargaining protocols. These include, for example, the possibility of contingent contracting [46]—agreeing on a contract with a seller that will be executed only when deals with other sellers have all been made—so that all contracts will be executed simultaneously even if the bargaining is sequential. Such research might uncover institutional factors that could mitigate or exacerbate the influence of the weaker sellers and improve the incentives for players to participate in the bargaining process.
Author Contributions
Conceptualization, V.M. and R.Z.; Methodology, V.M. and R.Z.; Formal analysis, V.M. and R.Z.; Writing—original draft, V.M.; Writing—review & editing, R.Z. and V.M. All authors have read and agreed to the published version of the manuscript.
Funding
This project has been funded by a grant from the UCR School of Business.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data will be made available on request.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Note on the Calculation of Equilibrium Predictions
The rules of the game in [11]’s model with infinite horizon and two Sellers is as described in Section 2.1 and implemented in the experiment (with the time discount factor δ operationalized as a period-to-period continuation probability). While VB in [11]’s analysis is normalized to 1, all theoretical predictions for the experiment can be derived from the original analysis upon applying a scaling factor of 100. Also, the Sellers are indexed as 1, 2, … in [11]’s notations with v1 > v2 > … Hence the high-value Seller is seller 1 and the low-value Seller is seller 2 when we calculate equilibrium predictions using Xiao’s results.
The relevant unique equilibrium solution in [11] for VB = 1 and two Sellers in infinite horizon (Proposition 4) requires the following inequalities to be satisfied (inequalities (11) and (12) in [11]:
These inequalities express the requirements that the Sellers’ inside options are not too large and are sufficiently different in order to guarantee a unique equilibrium outcome (Proposition 4). Next, define Equation (8) in Xiao (2018):
which ([11], Lemma 1) are the equilibrium results in subgames where only one Seller remains (i.e., the other has already made a deal with the Buyer).
Next, for each seller i, define the function:
Hi,t ≡ vi(1 − δ)[1 + δ + … + δt−1].
We then further define Equations (13)–(16) in [11] under Proposition 4:
Ref. [11]’s equilibrium solution (Proposition 4) is such that, for any or such that > and < , the strategies below constitute a unique equilibrium:
- (i)
- Seller 1 suggests a price of and accepts a price no less than ;
- (ii)
- Seller 2 suggests a price of and accepts a price no less than ;
- (iii)
- The Buyer bargains with Seller 2 until an agreement is reached; suggests a price to Seller 2 and to Seller 1; and accepts a price no more than from Seller 2 and no more than from Seller 1.
The above imply that, in equilibrium, the Buyer reaches a deal with Seller 2 at price in period 1, and then a deal with Seller 1 at price in period 2. The time-discounted payoffs are Equations (17)–(19) in [11]:
The experimental parameters are vL = 10, vH = 50, and r = δ = 0.9. That is, the incomes per period for the low-value and high-value Sellers are vL (1 − δ) = 1 and vH (1 − δ) = 5, respectively. The Buyer earns VB = 100 if and only if deals have been agreed with both Sellers.
We first substitute the experimental parameters into [11]’s inequalities (11) and (12) with v1 = vH/100 = 0.5, v2 = vL/100 = 0.1, and δ = 0.9. Indeed, the parameters satisfy both inequalities. We next substitute the experimental parameters into the set of Equation (8) in [11] and we then substitute these results together with the experimental parameters into Equations (13)–(16) and apply Proposition 4 to obtain the rest of the equilibrium results. Finally, we scale these results by 100 to obtain the actual equilibrium predictions for the experiment as listed in Table 1. The equilibrium time-discounted payoff predictions (Table 2; corresponding to expected payoff predictions for the experiment) can be derived from the deal prices with appropriate time discounting for any payment/payoff realized after period 1; alternatively, they can be obtained from Equations (17)–(19) in [11].
Appendix B. Sample of Experimental Instructions
- Buyer/Sellers Negotiation
- Instructions
This is a 3-player game with one Buyer and two Sellers (Seller Blue and Seller Green). The other two players in each game will be played by other participants who are now at the lab.
Seller Blue owns the Blue item. She would be happy to sell it for the right price. The Blue item provides Seller Blue a per-period income of $1 as long as she owns it.
Seller Green owns the Green item. He would be happy to sell it for the right price. The Green item provides Seller Green a per-period income of $5 as long as he owns it.
The Buyer would like to buy both items. The value of the combined items to the Buyer is $100. Each item by itself has no value to the Buyer.
The Buyer negotiates with the Sellers to buy the items.
- The Negotiation Process
The bargaining process is a sequence of price offers. It takes one period to make and accept/reject an offer. At the end of every period, the computer randomly selects whether the game terminates or whether it continues to the next period: there is a 10% chance that the game terminates, and a 90% chance that the game continues to the next period.
The game ends if the Buyer buys both items, or if the game terminates randomly before the Buyer bought both items.
In the first period, the Buyer makes an offer to the Seller of his choice. This Seller can either accept or reject the offer. If the Seller accepts the offer, his/her item is sold, and this Seller leaves the game. If the Seller rejects the offer, he/she stays in the game. If the game continues to the next period (with 90% chance), this Seller makes a counteroffer to the Buyer for the sale of his/her item.
Starting in the second period and in each period until the end of the game, either one of two things may happen:
- (a)
- The Buyer makes an offer to the Seller of his choice (if both Sellers are still in the game) or to the single Seller remaining in the game, or
- (b)
- One of the Sellers makes a counteroffer to the Buyer. A Seller can make an offer to the Buyer only as a counteroffer—that is, only if in the previous period this Seller rejected an offer made by the Buyer and the game continued to the current period. If the Buyer rejects the counteroffer and the game continues to yet another period, the Buyer makes an offer as in (a)
| Profit/Loss in a Game | ||
| Buyer | ||
| Possible Outcomes | Profit/Loss | |
| The game terminates before the Buyer buys any of the items | $0 | |
| The Buyer buys item Blue for $X and item Green for $Y | $100-$X-$Y | |
| The Buyer buys item Blue for $X but the game terminates before she buys item Green | -$X (lose $X) | |
| The Buyer buys item Green for $Y but the game terminates before she buys item Blue | -$Y (lose $Y) | |
| Sellers | ||
| Possible Outcomes | Seller Blue | Seller Green |
| The game terminates after period n before a Seller sells his item | n × $1 | n × $5 |
| A Seller sells his item in period n for $Z | $Z + (n − 1) × $1 | $Z + (n − 1) × $5 |
| Information | |
| This header is not part of the instructions | |
| <Full information condition> | If you are a seller, you will be fully informed of the negotiation between the buyer and the other seller. |
| <partial information condition> | If you are a seller, you will not be fully informed of the negotiation between the buyer and the other seller. Only that negotiation takes place and if agreement has been reached. |
- Games and roles
You will play the game 15 times. The first 3 games are for practice and the next 12 games are “for cash”. During the 15 games, you will play each role 5 times.
The other two players in each game, will change from game to game.
- Payment
At the end of the session we will pay you your average earnings from the 12 “for cash” games. In addition, you will receive a fixed $8 show-up fee.
Next, we would like to ask you few questions. You can consult these instructions when answering the questions. If you answer a question incorrectly, you will receive feedback with explanation to the correct answer. When you are ready, please click the NEXT button on the screen.
Appendix C. Additional Data Analysis
In the analysis reported in the main text, we focus on a number of major dependent variables across the paid games. In this Appendix and its accompanying tables, we report further analysis in more detail. First, Table A1 reports the means of dependent variables among only games with two deals (see also Section 4 in the main text). Next, in the following sections, we examine in more detail the offers and counteroffers.
- 1.
- Offers/Counteroffers
Table A2 lists the means of offers and counteroffers distinguishing between the type of interaction (e.g., whether the low-value Seller or the high-value Seller was involved), whether one or both Sellers were still in the bargaining game at the time of offer/counteroffer, as well as block and information condition.
The overall picture is that:
(1) Offers and counteroffers involving the low-value Seller were generally around the same as or significantly higher than equilibrium prediction when the high-value Seller was still in the game. However, when the low-value Seller was the only Seller left, the offers/counteroffers were, in general, significantly lower than equilibrium predictions;
(2) Offers and counteroffers involving the high-value Seller were generally consistent with equilibrium predictions when the low-value Seller was still in the game; note that equilibrium predictions in those cases were either strict upper bound of offers or strict lower bound of counteroffers, and the observed means satisfy those bounds statistically speaking. When the high-value Seller was the only Seller left, the offers/counteroffers were, in general, significantly lower than equilibrium predictions.
Further data analysis, represented in Table A3 and Table A4, brings out some additional observations. First, when both Sellers were still in game, many offers/counteroffers should be rejected according to the thresholds in Table 1, and, regardless of whether they should be so, acceptance rates were generally lower than 50%. Second, when there was only one Seller remaining, offers and counteroffers were predominantly lower than the acceptance thresholds prescribed in Table 1. In the case of counteroffers, this should lead to high acceptance rates, which was, however, not the case. Clearly, the players maintained very different response strategies from what is prescribed by game-theoretic analysis.
- 2.
- Contingent Strategy Analysis
An interpretation of the pattern in Table A2 is that, controlling for the type of interaction, the player making the offer/counteroffer did not adjust their decision according to the number of Sellers still in the game—what we shall henceforth call the “state” of the game.
This is borne out by our contingent strategy analysis that involves linear regression of offers/counteroffers on two variables that are their potential antecedents, namely the state and the period in the game. We choose period as a potential antecedent as we surmise that Buyers would make higher offers the higher the number of periods, while Sellers would correspondingly make lower counteroffers the higher the number of periods—both as attempts to increase the likelihood of a deal based on a gambler’s-fallacy type of fear that the game might end soon. In addition, Sellers might be affected by the perception that they had been accumulating income from their inside options as the number of periods increased, which could then make them more compromising.
The results are displayed in Table A5. The table confirms that period affected offers positively and counteroffers negatively across blocks and information conditions. However, the dependence on state was non-significant, which is consistent with Table A2.
We also conduct a set of contingent strategy analyses that involves logistic regression of responses to offers/counteroffers. The regressors are the value of the offer/counteroffer as well as state and period. The detailed results are presented in Table A6. As expected, Sellers were generally more likely to accept a higher offer (i.e., a positive dependence) and Buyers were generally more likely to reject a higher counteroffer (i.e., a negative dependence). There is also a general positive dependence on period among Sellers, i.e., controlling for the value of an offer, a Seller was more likely to accept the offer the higher the period number, possibly based on a gambler’s-fallacy type of fear that the game might end soon. For responses of Buyers to counteroffers, however, evidence for this dependence is much weaker. More importantly, the contingent strategy analysis of responses does not reveal a general dependence on the state, especially in Block 2. That is, players did not become more or less inclined to accept offers/counteroffers with different number of Sellers still in the game.
- 3.
- The Buyer’s Tendency to Continue Bargaining with the Same Seller until a Deal was Reached
Equilibrium analysis suggests that, after a Seller has made a counteroffer that is rejected by the Buyer, if there remain two Sellers in the game, the Buyer should next make an offer to the low-value Seller and “restart” the equilibrium path as if it was back to period 1. This means that the Buyer should switch (not switch) to the other Seller if the previous counteroffer was with the high-value (low-value) Seller.
In the experiment, the Buyer switched to another Seller in 38.86% of all the relevant observations. This proportion is similar whether the previous Seller was low-value (38.21%) or high-value (39.51%); further analysis shows that it is similar across information conditions. We next conduct a logistic regression on these observations where the binary decision variable is whether to stay with the same Seller (switch = 0, stay = 1). The previous Seller (low-value/high-value) as well as information condition (complete/partial) are the control variables and variances are clustered at the nested levels of subject and session. The regression analysis confirms this tendency: intercept estimate = 0.464, S.E. = 0.152, p < 0.01, N = 1297, generalized χ2 = 1123.73, while the control variables do not yield coefficients that are significantly different from zero.
Our analysis thus suggests that, overall, Buyers had a tendency to bargain with the same Seller even after a set of offer/counteroffer did not result in any deal—a behavioral regularity that is consistent with escalation of commitment [68].
- 4.
- Evidence of Reciprocal Gradualism
We carry out an analysis regarding reciprocal gradualism in the sense of [55]. We explore whether the offers/counteroffers between a Buyer and a specific Seller within the same game gradually converged in reciprocal fashion. That is, the more concession a Buyer made toward a Seller when making an offer (relatively to the Buyer’s previous offer), the more concession the Seller would reciprocate with when next making a counteroffer (assuming the Seller rejected the Buyer’s offer). To proceed, for the low-value Seller, index the interactions with the Buyer within the same game by tL(= 1, 2 …), where tL= 1 denotes the first period in which the Buyer made an offer to the low-value Seller, tL= 2 is the following period in which the low-value Seller made a counteroffer to the Buyer, etc. Note that if a Buyer did not get to make any offers to the low-value Seller in a game, the set of tLs in that game is an empty set. Likewise, define the index tH (=1,2 …) for the high-value Seller. Also, define pL(tL) as the offer/counteroffer made in the tL-th interaction between the Buyer and the low-value Seller in the game; define pH(tH) similarly for interactions between the Buyer and the high-value Seller.
To investigate reciprocal gradualism, we calculate γL(tL) in every interaction between the Buyer and the low-value Seller where tL > 2 and γL(tL) is obtained from the following defining relationship:
pL(tL) = γL(tL) pL(tL − 1) + (1 − γL(tL)) pL(tL − 2);
Similarly, we calculate γH(tH) in every interaction between the Buyer and the high-value Seller with tH > 2, and γH(tH) is obtained from the following defining relationship:
pH(tH) = γH(tH) pH(tH − 1) + (1 − γH(tH)) pH(tH − 2).
Note that γL(tL) is undefined if pL(tL − 1) = pL(tL − 2), which happened in only one instance. Likewise, γH(tL) is undefined if pL(tH − 1) = pL(tH − 2), which also happened in only one instance. We drop both of these observations in subsequent analysis. We also define pL(0) = pH(0) = VB = 100, which are the maximum amount that these Sellers could ever receive from a Buyer who did not want to go into the red in a game. The magnitudes of γL(tL) and γH(tH) are measures of players’ concessions toward their opponents. For example, a higher γL(tL) means that the player making an offer or counteroffer in interaction tL anchors their offer/counteroffer closer to the opponent’s previous counteroffer/offer, which indicates more concession toward the opponent.
Reciprocal gradualism, as analyzed by [5], implies a positive relationship between γL(tL) and γL(tL − 1), and likewise between γH(tH) and γH(tH − 1). For example, if the Buyer and the low-value Seller in an experimental game followed reciprocal gradualism, then the more concession a Buyer made toward the low-value Seller in interaction t L − 1, the more the concession the low-value Seller would reciprocate toward the Buyer in interaction tL. To test if this is the case for the data as a whole, we regress γL(tL) on γL(tL − 1) for all tL > 3 and separately γH(tH) on γH(tH − 1) for all tH > 3, with the information condition as a control variable. Reciprocal gradualism would be manifested as a positive coefficient for the lag variables γL(tL − 1) and γH(tH − 1) in the regressions.
The results are presented in Table A7. As can be seen from the table, there is only statistically significant evidence of reciprocal gradualism in the interactions between the Buyer and the low-value Seller. Moreover, in the regression results for these interactions, the information condition control variable has a statistically significant coefficient, suggesting that these dependencies could differ between information conditions. We next conduct a further set of regressions separately for each information condition. For interactions between the Buyer and the low-value Seller, we find that the coefficient for γL(tL − 1) is statistically significant at a 95% significance level only under the partial information condition (estimate = 0.074, s.e. = 0.034, p = 0.029; N = 665, AIC = 592.94) but not under the full information condition. For interactions between the Buyer and the high-value Seller, the coefficient for γH(tH − 1) remains non-significant in either information condition.
To conclude, our analysis provides evidence of reciprocal gradualism between the Buyer and the low-value Seller in the partial information condition. However, the analysis does not provide evidence for reciprocal gradualism between the Buyer and the high-value Seller in the partial information condition nor between the Buyer and any Seller in the full information condition.
- 5.
- Parameter Constraints in the Fairness Model Estimation (Section 5.2)
We subject the parameters to the following constraints in the maximum likelihood estimation for the model of fairness in Section 5.2:
- General constraints:
- a ≥ 0, b0 ≥ 0, and b0 + bpinfo ≥ 0.
- Constraints specific to the Sellers:
- To guarantee 1 ≥ fi ≥ 0: 1 ≥ f0 ≥ 0, 1 ≥ f0 + fhigh ≥ 0, 1 ≥ f0 + fstate ≥ 0, 1 ≥ f0 + fhigh + fstate + fhigh,state ≥ 0;
- To guarantee 1 ≥ ui ≥ 0:
1 ≥ u0 ≥ 0, 1 ≥ u0 + u0,pinfo ≥ 0, 1 ≥ u0 + uhigh ≥ 0, 1 ≥ u0 + u0,pinfo + uhigh + uhigh,pinfo ≥ 0;
1 ≥ u0 + ustate ≥ 0, 1 ≥ u0 + u0,pinfo + ustate + ustate,pinfo ≥ 0;
1 ≥ u0 + uhigh + ustate + uhigh,state ≥ 0, 1 ≥ u0 + u0,pinfo + uhigh + uhigh,pinfo + ustate + uhigh,state + uhigh,state,pinfo ≥ 0;
- To guarantee non-zero expected payoff from the inside option upon rejection of the current offer: r ≥ 0;
- To guarantee VB ≥ cbelief ≥ 0: VB ≥ m0 ≥ 0, VB ≥ m0 + mhigh ≥ 0 (with VB = 100).
- Constraints specific to the Buyer:
- aB ≥ 0;
- To guarantee 1 ≥ fB ≥ 0:
1 ≥ fB0 ≥ 0, 1 ≥ fB0 + fBhigh ≥ 0, 1 ≥ fB0 + fBstate ≥ 0, 1 ≥ fB0 + fBhigh + fBstate + fBhigh,state ≥ 0;
- To guarantee 1 ≥ uB ≥ 0:
1 ≥ uB0 ≥ 0, 1 ≥ uB0 + uB0,pinfo ≥ 0, 1 ≥ uB0 + uBhigh ≥ 0, 1 ≥ uB0 + uB0,pinfo + uBhigh + uBhigh,pinfo ≥ 0;
1 ≥ uB0 + uBstate ≥ 0, 1 ≥ uB0 + uB0,pinfo + uBstate + uBstate,pinfo ≥ 0;
1 ≥ uB0 + uBhigh + uBstate + uBhigh,state ≥ 0;
1 ≥ uB0 + uB0,pinfo + uBhigh + uBhigh,pinfo + uBstate + uBhigh,state + uBhigh,state,pinfo ≥ 0.

Table A1.
Means of major dependent variables for games with two deals.
Table A1.
Means of major dependent variables for games with two deals.
| Full Information Condition (N = 12) | Partial Information Condition (N = 12) | Equilibrium | |||
|---|---|---|---|---|---|
| Block 1 (Games 1–6) | Block 2 (Games 7–12) | Block 1 (Games 1–6) | Block 2 (Games 7–12) | ||
| % games with two deals | 42.56% ** (23.44%) | 43.99% ** (14.04%) | 43.80% ** (15.32%) | 40.26% ** (9.86%) | 90% |
| Among games with two deals: | |||||
| # periods to make both deals | 7.27 ** (2.44) | 8.76 ** + (2.81) | 7.64 ** (2.23) | 7.16 ** (2.38) | 2 |
| # periods to make a deal with low-value Seller | 5.84 (1.98) | 6.07 (2.41) | 6.20 (2.50) | 5.60 (2.43) | 1 |
| # periods to make a deal with high-value Seller | 5.63 ** (2.48) | 7.66 **++ (2.64) | 5.85 ** (1.94) | 5.65 ** (1.73) | 2 |
| % games in which deal was made with low-value Seller first | 41.80% (22.76%) | 61.45% + (21.51%) | 51.12% (19.84%) | 53.05% (16.89%) | 100% |
| Deal price with low-value Seller | 28.10 ** (6.30) | 30.23 ** (4.74) | 24.21 ** (4.66) | 28.05 **++ (4.86) | 16.48 |
| Deal price with high-value Seller | 42.60 ** (6.57) | 42.86 ** (5.25) | 40.93 ** (8.33) | 42.34 ** (7.10) | 73.68 |
| Buyer’s payoff | 29.30 ** (10.38) | 26.91 ** (6.22) | 34.86 ** (10.53) | 29.61 **+ (8.90) | 9.84 |
| Low-value Seller’s payoff | 32.94 ** (5.82) | 35.30 ** (5.57) | 29.41 ** (5.97) | 32.65 **++ (6.52) | 16.48 |
| High-value Seller’s payoff | 65.75 ** (13.82) | 76.18 ++ (14.95) | 65.17 ** (14.97) | 65.57 ** (13.42) | 78.68 |
| Welfare | 127.99 ** (13.95) | 138.39 **+ (15.03) | 129.44 ** (11.75) | 127.82 ** (10.70) | 105 |
Note. The unit of observation is session. S.d. in parentheses. Where a mean is significantly different from the equilibrium value according to a t-test, the entry is marked by one or more asterisks (* p < 0.05, ** p < 0.01). Exceptions include: (i) % games in which deal made with low-value Seller first and (ii) number of periods to make a deal with the low-value Seller, since the equilibrium predictions for those two variables are boundary values. Where there is significant learning across the blocks according to a paired t-test, the Block 2 entry is marked by one or more plus signs (+ p < 0.05, ++ p < 0.01).

Table A2.
Means of offers and counteroffers.
Table A2.
Means of offers and counteroffers.
| Full Information Condition (N = 12) | Partial Information Condition (N = 12) | Equilibrium/ Off-the-Equilibrium Prediction | |||
|---|---|---|---|---|---|
| Block 1 (Games 1–6) | Block 2 (Games 7–12) | Block 1 (Games 1–6) | Block 2 (Games 7–12) | ||
| Offer: Buyer → Low-value Seller | |||||
| Two Sellers still in the game | 19.27 (6.86) | 20.30 * (5.34) | 18.24 (3.99) | 20.86 * a (5.12) | 16.48 |
| One Seller still in the game | 22.26 ** (6.12) | 24.07 ** (5.34) | 19.51 ** (4.06) | 21.25 ** (5.22) | 52.63 |
| Buyer → High-value Seller | |||||
| Two Sellers still in the game | 31.76 ** (8.39) | 32.20 ** (5.31) | 29.50 ** (5.25) | 32.85 ** (6.03) | 67.27 ^ |
| One Seller still in the game | 33.34 ** (4.63) | 34.40 ** (10.19) | 32.14 ** (6.07) | 34.45 ** (9.43) | 73.68 |
| Counteroffer: Low-value Seller → Buyer | |||||
| Two Sellers still in the game | 36.90 ** (9.82) | 36.19 ** (3.38) | 38.87 ** (9.97) | 37.92 ** (7.94) | 17.20 |
| One Seller still in the game | 34.92 ** (13.71) | 35.15 ** (7.77) | 31.73 ** (7.75) | 35.68 ** (7.83) | 57.37 |
| High-value Seller → Buyer | |||||
| Two Sellers still in the game | 55.72 ** b (7.13) | 54.32 ** (8.02) | 56.65 ** (14.48) | 55.96 ** (14.13) | 36.15 ^^ |
| One Seller still in the game | 61.38 (29.99) | 50.67 ** (6.21) | 53.20 ** (7.98) | 50.14 ** (9.47) | 76.32 |
Note. The unit of observation is session. S.d. in parentheses. Where a mean is significantly different from the equilibrium value according to a t-test, the entry is marked by one or more asterisks (* p < 0.05, ** p < 0.01). Where there is significant learning across the blocks according to a paired t-test, the Block 2 entry is marked by one or more plus signs (+ p < 0.05, ++ p < 0.01). ^ Strict upper bound; asterisks for this variable indicate significant difference from the upper bound. ^^ Strict lower bound; asterisks for this variable indicate significant difference from the lower bound. Bold and underlined: offers along the overall equilibrium path. a Test for learning effect yields p = 0.053. b An outlier offer of 42,069.00, which appeared in Game 6, Period 6 in one of the sessions, has been excluded. The mean (s.d.) for this cell without excluding the outlier would be 185.38 (450.34).

Table A3.
Sellers’ responses to Buyers’ offers.
Table A3.
Sellers’ responses to Buyers’ offers.
| Full Information Condition (N = 12) | Partial Information Condition (N = 12) | |||||
|---|---|---|---|---|---|---|
| No. of Obs. (Games 1–12) | Mean Acceptance Rate (%) | No. of Obs. (Games 1–12) | Mean Acceptance Rate (%) | |||
| Block 1 (Games 1–6) | Block 2 (Games 7–12) | Block 1 (Games 1–6) | Block 2 (Games 7–12) | |||
| Buyer → Low-value Seller Two Sellers still in the game | ||||||
| Offer < Threshold (16.48) | 1329 | 4.17 (9.99) | 11.16 (28.43) | 1341 | 8.80 (15.02) | 1.58 (4.99) |
| Offer ≥ Threshold (16.48) | 1101 | 23.26 (26.56) | 20.05 (12.22) | 951 | 27.04 (25.89) | 21.04 (0.09) |
| One Seller still in the game | ||||||
| Offer < Threshold (52.63) | 2427 | 28.69 (27.06) | 25.25 (21.73) | 2292 | 24.59 (15.39) | 18.92 (17.98) |
| Offer ≥ Threshold (52.63) | 3 | No obs. | 100 (0.00) | 0 | No obs. | No obs. |
| Buyer → High-value Seller Two Sellers still in the game | ||||||
| Offer < Threshold (67.27) | 2448 | 11.60 (7.76) | 16.29 (8.98) | 2355 | 13.31 (6.75) | 15.25 (7.59) |
| Offer ≥ Threshold (67.27) | 9 | 100 (0.00) | 50.00 (70.71) | 6 | 100 (0.00) | 0.00 (0.00) |
| One Seller still in the game | ||||||
| Offer < Threshold (73.68) | 2454 | 17.98 (18.01) | 24.47 (27.57) | 2361 | 24.13 (11.78) | 16.55 (9.5) |
| Offer ≥ Threshold (73.68) | 3 | No obs. | 100 (0.00) | 0 | No obs. | No obs. |
Note. If response strategies follow overall equilibrium or subgame equilibria, we should see 100% (0%) acceptance rate whenever offer ≥ threshold (offer < threshold) in Table A3. For the mean acceptance rate, the unit of observation is session, with s.d. in parentheses; we have not detected any learning across blocks at p < 0.05 using paired t-tests with the same approach as in previous tables. Bold and underlined: the overall equilibrium path.

Table A4.
Buyer’s responses to Sellers’ counteroffers.
Table A4.
Buyer’s responses to Sellers’ counteroffers.
| Full Information Condition (N = 12) | Partial Information Condition (N = 12) | |||||
|---|---|---|---|---|---|---|
| No. of Obs. (Games 1–12) | Mean Acceptance Rate (%) | No. of Obs. (Games 1–12) | Mean Acceptance Rate (%) | |||
| Block 1 (Games 1–6) | Block 2 (Games 7–12) | Block 1 (Games 1–6) | Block 2 (Games 7–12) | |||
| Low-value Seller → Buyer Two Sellers still in the game | ||||||
| Offer ≤ Threshold (17.20) | 516 | 37.50 (47.87) | 50.00 (0.00) | 540 | 83.33 (40.82) | 100 (0.00) |
| Offer > Threshold (17.20) | 1326 | 19.78 (10.01) | 13.24 (8.50) | 1173 | 18.67 (18.38) | 21.09 (13.55) |
| One Seller still in the game | ||||||
| Offer ≤ Threshold (57.37) | 1797 | 35.47 (28.72) | 30.74 (34.27) | 1683 | 27.82 (27.19) | 39.67 (32.49) |
| Offer > Threshold (57.37) | 45 | 0.00 (0.00) | 0.00 (0.00) | 30 | 0.00 (0.00) | 0.00 (0.00) |
| High-value Seller → Buyer Two Sellers still in the game | ||||||
| Offer ≤ Threshold (36.15) | 759 | 50.00 (46.29) | 35.00 (41.83) | 666 | 53.33 (42.89) | 75.00 (25.00) |
| Offer > Threshold (36.15) | 1173 | 15.93 (8.84) | 19.44 (26.53) | 1149 | 12.88 (12.84) | 20.27 (19.27) |
| One Seller still in the game | ||||||
| Offer ≤ Threshold (76.32) | 1890 | 29.59 (20.92) | 22.46 (13.24) | 1794 | 20.11 (17.93) | 33.97 (26.64) |
| Offer > Threshold (76.32) | 42 | 0.00 (0.00) | 0.00 (0.00) | 21 | 8.33 (16.67) | No obs. |
Note. If response strategies follow overall equilibrium or subgame equilibria, we should see 0% (100%) acceptance rate whenever offer > threshold (offer ≤ threshold). For the mean acceptance rate, the unit of observation is session, with s.d. in parentheses; we have not detected any learning across blocks at p < 0.05 using paired t-tests with the same approach as in previous tables.

Table A5.
Contingent strategy analysis: linear regression analysis of offers/counteroffers.
Table A5.
Contingent strategy analysis: linear regression analysis of offers/counteroffers.
| Type of Interaction and Regressor /Estimated Coefficient | Full Information Condition | Partial Information Condition | ||
|---|---|---|---|---|
| Block 1 (Games 1–6) | Block 2 (Games 7–12) | Block 1 (Games 1–6) | Block 2 (Games 7–12) | |
| Offer: | ||||
| Buyer → Low-value Seller | N = 365 | N = 445 | N = 386 | N = 378 |
| State | −1.19 (0.99) | −0.24 (0.93) | 1.34 (1.02) | −0.12 (1.01) |
| Period | 0.42 ** (0.10) | 0.51 ** (0.09) | 0.96 ** (0.11) | 0.45 ** (0.12) |
| Buyer → High-value Seller | N = 401 | N = 418 | N = 410 | N = 377 |
| State | −0.72 (1.42) | 0.04 (1.54) | 3.60 (2.38) | 2.02 (1.46) |
| Period | 0.41 ** (0.15) | 0.29 (0.17) | 1.72 ** (0.29) | 0.29 (0.15) |
| Counteroffer: | ||||
| Low-value Seller → Buyer | N = 280 | N = 334 | N = 291 | N = 280 |
| State | 2.74 (4.11) | −0.86 (1.36) | 6.34 (3.35) | −2.59 (1.88) |
| Period | 0.42 (0.49) | −0.85 ** (0.13) | −0.05 (0.37) | −1.36 ** (0.21) |
| High-value Seller → Buyer | N = 315 | N = 328 | N = 312 | N = 293 |
| State | −0.92 a (2.05) | 0.95 (1.34) | 4.29 (2.80) | 3.58 (4.90) |
| Period | −0.91 ** (0.25) | −1.58 ** (0.15) | −1.92 ** (0.30) | −1.65 ** (0.60) |
Note. The unit of observation is an individual offer decision. The “State” variable is 1 if there were two Sellers still in the game and is 0 otherwise. Variances are clustered at the nested levels of subject and session. Standard errors in parentheses. Intercept estimates and goodness-of-fit statistics have been omitted for expositional convenience. Where an estimate is significantly different from zero, the entry is marked by one or more asterisks (* p < 0.05, ** p < 0.01).

Table A6.
Contingent strategy analysis: logistic regression analysis of responses to offers/counteroffers.
Table A6.
Contingent strategy analysis: logistic regression analysis of responses to offers/counteroffers.
| Type of Interaction and Regressor /Estimated Coefficient | Full Information Condition | Partial Information Condition | ||
|---|---|---|---|---|
| Block 1 (Games 1–6) | Block 2 (Games 7–12) | Block 1 (Games 1–6) | Block 2 (Games 7–12) | |
| Buyer → Low-value Seller | N = 365 | N = 445 | N = 386 | N =378 |
| Offer | 0.14 ** (0.02) | 0.14 ** (0.02) | 0.07 ** (0.02) | 0.12 ** (0.02) |
| State | 0.14 (0.42) | −0.19 (0.38) | −0.31 (0.39) | 0.08 (0.42) |
| Period | 0.12 * (0.05) | 0.05 (0.04) | 0.13 ** (0.05) | 0.10 (0.05) |
| Buyer → High-value Seller | N = 401 | N = 418 | N = 410 | N = 377 |
| Offer | 0.08 ** (0.02) | 0.09 ** (0.02) | 0.07 ** (0.01) | 0.07 ** (0.02) |
| State | 0.05 (0.44) | 0.02 (0.38) | −0.16 (0.40) | −0.12 (0.40) |
| Period | 0.19 ** (0.05) | 0.19 ** (0.05) | 0.20 ** (0.05) | 0.13 * (0.05) |
| Low-value Seller → Buyer | N = 280 | N = 334 | N = 291 | N = 280 |
| Counteroffer | Analysis routine | −0.09 ** (0.02) | Analysis routine | −0.15 ** (0.03) |
| State | does not | −0.33 (0.48) | does not | −0.41 (0.45) |
| Period | converge | 0.02 (0.05) | converge | 0.005 (0.06) |
| High-value Seller → Buyer | N = 316 | N = 328 | N = 312 | N = 293 |
| Counteroffer | Analysis routine | −0.09 ** (0.02) | −0.07 ** (0.01) | Analysis routine |
| State | does not | 0.07 (0.41) | −0.90 * (0.42) | does not |
| Period | converge | 0.08 (0.05) | −0.12 * (0.06) | converge |
Note. The unit of observation is an individual response to an offer. The dependent variable is equal to 1 for acceptance of an offer and is 0 otherwise. The “State” variable is 1 if there were two Sellers still in the game and is 0 otherwise. Variances are clustered at the nested levels of subject and session (the routine for our analysis, which uses PROC GLIMMIX in SAS, does not converge in a few cases as indicated). Standard errors in parentheses. Intercept estimates and goodness-of-fit statistics have been omitted for expositional convenience. Where an estimate is significantly different from zero, the entry is marked by one or more asterisks (* p < 0.05, ** p < 0.01).

Table A7.
Results of the regression analysis regarding reciprocal gradualism.
Table A7.
Results of the regression analysis regarding reciprocal gradualism.
| Buyer/Low-Value Seller Interactions (DV: γL(tL)) | Buyer/High-Value Seller Interactions (DV: γH(tL)) | ||
|---|---|---|---|
| N | 1415 | N | 1494 |
| γL(tL−1) | 0.063 * (0.026) | γH(tL−1) | −0.001 (0.026) |
| Information condition | −0.058 * (0.025) | Information condition | −1.673 (1.658) |
| Intercept | 0.163 ** (0.020) | Intercept | 0.176 (1.199) |
| AIC | 1875.21 | AIC | 14,596.08 |
Note. The unit of observation is an individual offer/counteroffer decision. The “Information condition” variable is 1 if the data point is from the full information condition and is 0 otherwise. Variances are clustered at the nested levels of subject and session. Standard errors in parentheses. Intercept estimates and goodness-of-fit statistics have been omitted for expositional convenience. Where an estimate is significantly different from zero, the entry is marked by one or more asterisks (* p < 0.05, ** p < 0.01).
Notes
| 1 | Note also that our research objective regarding information transparency is different in nature from previous theoretical analysis of confidentiality/transparency in one-to-many bargaining, such as [37,38,39,40,41]. These works typically examine transparency in a payoff-relevant asymmetric information framework rather than with a focus on direct social comparison. Regarding the use of information manipulation to examine fairness concern in bargaining behavior, previous examples include [42,43] in the context of the ultimatum game. |
| 2 | In relation, ref. [51] finds that, among the two exogenously given bargaining order protocols in his model, the buyer prefers the one that starts with negotiating with the lower-valuation seller. |
References
- Portillo, J.E. Land-assembly experiments: A survey. In Experimental Law and Economics; Isaac, R.M., Kitchens, C., Eds.; Research in Experimental Economics; Emerald Publishing Limited: Bingley, UK, 2022; Volume 21, pp. 11–34. [Google Scholar]
- Laussel, D. Buying back subcontractors: The strategic limits of backward integration. J. Econ. Manag. Strategy 2008, 17, 895–911. [Google Scholar] [CrossRef]
- Davis, A.M.; Hu, B.; Hyndman, K.; Qi, A. Procurement for assembly under asymmetric information: Theory and evidence. Manag. Sci. 2021, 68, 2694–2713. [Google Scholar] [CrossRef]
- Galeotti, F.; Montero, M.; Poulsen, A. Efficiency versus equality in bargaining. J. Eur. Econ. Assoc. 2019, 17, 1941–1970. [Google Scholar] [CrossRef]
- Gupta, D.; Sarkar, S. Assembly Problems. In Game Theory and Networks; Borkotokey, S., Kumar, R., Mukherjee, D., Rao, K.S.M., Sarangi, S., Eds.; Indian Statistical Institute Series; Springer: Singapore, 2021; pp. 89–104. [Google Scholar]
- Fehr, E.; Schmidt, K.M. A theory of fairness, competition, and cooperation. Q. J. Econ. 1999, 114, 817–868. [Google Scholar] [CrossRef]
- Güth, W.; Königstein, M.; Kovács, J.; Zala-Mezo, E. Fairness within firms: The case of one principal and multiple agents. Schmalenbach Bus. Rev. 2001, 53, 82–101. [Google Scholar] [CrossRef]
- Ho, T.H.; Su, X. Peer-induced fairness in games. Am. Econ. Rev. 2009, 99, 2022–2049. [Google Scholar] [CrossRef]
- Güth, W.; van Damme, E. Information, strategic behavior and fairness in ultimatum bargaining: An experimental study. J. Math. Psychol. 1998, 42, 227–247. [Google Scholar] [CrossRef]
- Bolton, G.E.; Ockenfels, A. Strategy and equity: An ERC-analysis of the Güth–van Damme game. J. Math. Psychol. 1998, 42, 215–226. [Google Scholar] [CrossRef] [PubMed]
- Xiao, J. Bargaining orders in a multi-person bargaining game. Games Econ. Behav. 2018, 107, 364–379. [Google Scholar] [CrossRef]
- Anbarci, N.; Feltovich, N. Pricing in competitive search markets: The roles of price information and fairness perceptions. Manag. Sci. 2018, 64, 1101–1120. [Google Scholar] [CrossRef]
- Comola, M.; Fafchamps, M. Experimental Evidence on Covert Bargaining Markets. 2023. Available online: https://ssrn.com/abstract=4323550 (accessed on 13 January 2023).
- Huang, J.; Kessler, J.B.; Niederle, M. Fairness has less impact when agents are less informed. Exp. Econ. 2024, 27, 155–174. [Google Scholar] [CrossRef]
- Mitzkewitz, M.; Nagel, R. Experimental results on ultimatum games with incomplete information. Int. J. Game Theory 1993, 22, 171–198. [Google Scholar] [CrossRef]
- Monbiot, G.; Grey, R.; Kenny, T.; Macfarlane, L.; Powell-Smith, A.; Shrubsole, G.; Stratford, B. Land for the Many. 2019. Available online: https://landforthemany.uk/ (accessed on 28 December 2022).
- Sodhi, M.S.; Tang, C.S. Research opportunities in supply chain transparency. Prod. Oper. Manag. 2019, 28, 2946–2959. [Google Scholar] [CrossRef]
- De Bruyn, A.; Bolton, G.E. Estimating the influence of fairness on bargaining behavior. Manag. Sci. 2008, 54, 1774–1791. [Google Scholar] [CrossRef]
- Eckart, W. On the land assembly problem. J. Urban Econ. 1985, 18, 364–378. [Google Scholar] [CrossRef]
- Winn, A.M.; McCarter, M.W. Who’s holding out? An experimental study of the benefits and burdens of eminent domain. J. Urban Econ. 2018, 105, 176–185. [Google Scholar] [CrossRef]
- Chaturvedi, R. Fairness and partial coercion in land assembly. Games Econ. Behav. 2020, 120, 325–335. [Google Scholar] [CrossRef]
- Lovejoy, W.S. Bargaining chains. Manag. Sci. 2010, 56, 2282–2301. [Google Scholar] [CrossRef]
- Leider, S.; Lovejoy, W.S. Bargaining in supply chains. Manag. Sci. 2016, 62, 3039–3058. [Google Scholar] [CrossRef]
- Goeree, J.K.; Lindsay, L. The exposure problem and market design. Rev. Econ. Stud. 2020, 87, 2230–2255. [Google Scholar] [CrossRef]
- Baranski, A.; Morton, R. The determinants of multilateral bargaining: A comprehensive analysis of Baron and Ferejohn majoritarian bargaining experiments. Exp. Econ. 2022, 25, 1079–1108. [Google Scholar] [CrossRef]
- Bolton, G.E.; Chatterjee, K.; McGinn, K.L. How communication links influence coalition bargaining: A laboratory investigation. Manag. Sci. 2003, 49, 583–598. [Google Scholar] [CrossRef]
- Cadigan, J.; Schmitt, P.; Shupp, R.; Swope, K. An experimental study of the holdout problem in a multilateral bargaining game. South. Econ. J. 2009, 76, 444–457. [Google Scholar] [CrossRef]
- Cadigan, J.; Schmitt, P.; Shupp, R.; Swope, K. The holdout problem and urban sprawl: Experimental evidence. J. Urban Econ. 2011, 69, 72–81. [Google Scholar] [CrossRef][Green Version]
- Swope, K.J.; Cadigan, J.; Schmitt, P. That’s my final offer! Bargaining behavior with costly delay and credible commitment. J. Behav. Exp. Econ. 2014, 49, 44–53. [Google Scholar] [CrossRef]
- Collins, S.M.; Isaac, R.M. Holdout: Existence, information, and contingent contracting. J. Law Econ. 2012, 55, 793–814. [Google Scholar] [CrossRef]
- Parente, M.D.; Winn, A.M. Bargaining behavior and the tragedy of the anticommons. J. Econ. Behav. Organ. 2012, 84, 475–490. [Google Scholar] [CrossRef]
- Zillante, A.; Schwarz, P.M.; Read, D.C. Land aggregation using contingent and guaranteed payments. South. Econ. J. 2014, 80, 702–727. [Google Scholar] [CrossRef]
- Kitchens, C.; Roomets, A. Dealing with eminent domain. J. Behav. Exp. Econ. 2015, 54, 22–31. [Google Scholar] [CrossRef]
- Isaac, R.M.; Kitchens, C.; Portillo, J.E. Can buyer “mobility” reduce aggregation failures in land-assembly? J. Urban Econ. 2016, 95, 16–30. [Google Scholar] [CrossRef]
- Portillo, J.E. Land-assembly and externalities: How do positive post-development externalities affect land aggregation outcomes? Reg. Sci. Urban Econ. 2019, 77, 104–124. [Google Scholar] [CrossRef]
- DeSantis, M.; McCarter, M.W.; Winn, A.M. Land assembly with taxes, not takings. Appl. Econ. Lett. 2019, 26, 604–607. [Google Scholar] [CrossRef]
- Noe, T.H.; Wang, J. Fooling all of the people some of the time: A theory of endogenous sequencing in confidential negotiations. Rev. Econ. Stud. 2004, 71, 855–881. [Google Scholar] [CrossRef]
- Krasteva, S.; Yildirim, H. On the role of confidentiality and deadlines in bilateral negotiations. Games Econ. Behav. 2012, 75, 714–730. [Google Scholar] [CrossRef]
- Krasteva, S.; Yildirim, H. Payoff uncertainty, bargaining power, and the strategic sequencing of bilateral negotiations. RAND J. Econ. 2012, 43, 514–536. [Google Scholar] [CrossRef]
- Krasteva, S.; Yildirim, H. Strategic ignorance in sequential procurement. Am. Econ. J. Microecon. 2019, 11, 131–172. [Google Scholar] [CrossRef]
- Chowdhury, P.R.; Sengupta, K. Transparency, complementarity and holdout. Games Econ. Behav. 2012, 75, 598–612. [Google Scholar] [CrossRef]
- Straub, P.G.; Murnighan, J.K. An experimental investigation of ultimatum games: Information, fairness, expectations, and lowest acceptable offers. J. Econ. Behav. Organ. 1995, 27, 345–364. [Google Scholar] [CrossRef]
- Croson, R.T. Information in ultimatum games: An experimental study. J. Econ. Behav. Organ. 1996, 30, 197–212. [Google Scholar] [CrossRef]
- Horn, H.; Wolinsky, A. Worker substitutability and patterns of unionisation. Econ. J. 1988, 98, 484–497. [Google Scholar] [CrossRef]
- Stole, L.A.; Zwiebel, J. Intra-firm bargaining under non-binding contracts. Rev. Econ. Stud. 1996, 63, 375–410. [Google Scholar] [CrossRef]
- Cai, H. Delay in multilateral bargaining under complete information. J. Econ. Theory 2000, 93, 260–276. [Google Scholar] [CrossRef]
- Cai, H. Inefficient Markov perfect equilibria in multilateral bargaining. Econ. Theory 2003, 22, 583–606. [Google Scholar] [CrossRef]
- Marx, L.M.; Shaffer, G. Rent shifting and the order of negotiations. Int. J. Ind. Organ. 2007, 25, 1109–1125. [Google Scholar] [CrossRef]
- Ko, C.Y.; Li, D. Decentralized one-to-many bargaining. Int. Econ. Rev. 2020, 61, 1139–1172. [Google Scholar] [CrossRef]
- Gao, H.; Xu, H. Multilateral bargaining with an endogenously determined procedure. Econ. Lett. 2021, 209, 110148. [Google Scholar] [CrossRef]
- Sarkar, S. Bargaining order and delays in multilateral bargaining with heterogeneous sellers. Math. Soc. Sci. 2016, 80, 1–20. [Google Scholar] [CrossRef]
- Zwick, R.; Rapoport, A.; Howard, J.C. Two-person sequential bargaining behavior with exogenous breakdown. Theory Decis. 1992, 32, 241–268. [Google Scholar] [CrossRef]
- Fréchette, G.R.; Yuksel, S. Infinitely repeated games in the laboratory: Four perspectives on discounting and random termination. Exp. Econ. 2017, 20, 279–308. [Google Scholar] [CrossRef]
- Chen, D.L.; Schonger, M.; Wickens, C. oTree—An open-source platform for laboratory, online, and field experiments. J. Behav. Exp. Financ. 2016, 9, 88–97. [Google Scholar] [CrossRef]
- Backus, M.; Blake, T.; Larsen, B.; Tadelis, S. Sequential bargaining in the field: Evidence from millions of online bargaining interactions. Q. J. Econ. 2020, 135, 1319–1361. [Google Scholar] [CrossRef]
- Cappelen, A.W.; Hole, A.D.; Sørensen, E.Ø.; Tungodden, B. The pluralism of fairness ideals: An experimental approach. Am. Econ. Rev. 2007, 97, 818–827. [Google Scholar] [CrossRef]
- Bolton, G.E.; Ockenfels, A. ERC: A theory of equity, reciprocity, and competition. Am. Econ. Rev. 2000, 90, 166–193. [Google Scholar] [CrossRef]
- McKelvey, R.D.; Palfrey, T.R. Quantal response equilibria for normal-form games. Games Econ. Behav. 1995, 10, 6–38. [Google Scholar] [CrossRef]
- Rapoport, A.; Sundali, J.A. Ultimatums in two-person bargaining with one-sided uncertainty: Offer games. Int. J. Game Theory 1996, 25, 475–494. [Google Scholar] [CrossRef]
- Kimbrough, E.O.; Vostroknutov, A. Norms make preferences social. J. Eur. Econ. Assoc. 2016, 14, 608–638. [Google Scholar] [CrossRef]
- Anbarci, N.; Feltovich, N. How sensitive are bargaining outcomes to changes in disagreement payoffs? Exp. Econ. 2013, 16, 560–596. [Google Scholar] [CrossRef]
- Yamagishi, T.; Terai, S.; Kiyonari, T.; Mifune, N.; Kanazawa, S. The social exchange heuristic: Managing errors in social exchange. Ration. Soc. 2007, 19, 259–291. [Google Scholar] [CrossRef]
- Abele, S.; Ehrhart, K.M. The timing effect in public good games. J. Exp. Soc. Psychol. 2005, 41, 470–481. [Google Scholar] [CrossRef]
- Budescu, D.V.; Au, W.T. A model of sequential effects in common pool resource dilemmas. J. Behav. Decis. Mak. 2002, 15, 37–63. [Google Scholar] [CrossRef]
- Zwick, R.; Chen, X.P. What price fairness? A bargaining study. Manag. Sci. 1999, 45, 804–823. [Google Scholar] [CrossRef]
- Hossain, T.; Lyons, E.; Siow, A. Fairness considerations in joint venture formation. Exp. Econ. 2020, 23, 632–667. [Google Scholar] [CrossRef]
- Gächter, S.; Riedl, A. Moral property rights in bargaining with infeasible claims. Manag. Sci. 2005, 51, 249–263. [Google Scholar] [CrossRef]
- Arkes, H.R.; Blumer, C. The psychology of sunk cost. Organ. Behav. Hum. Decis. Process. 1985, 35, 124–140. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).