Social Learning for Sequential Driving Dilemmas
Abstract
1. Introduction
2. Related Work
Contributions of This Paper
- We propose a social learning framework to investigate sequential driving dilemmas (SDD) in autonomous driving systems.
- We develop a reinforcement learning algorithm for AVs’ policy learning to estimate SDDs in traffic scenarios.
- We apply the proposed algorithm to two traffic scenarios: an unsignalized intersection and a highway, in order to identify SDDs.
3. Preliminaries
3.1. Social Dilemma in a Matrix Game
- : Agents prefer mutual cooperation to mutual defection;
- : Agents prefer mutual cooperation to unilateral cooperation;
- : Agents prefer mutual cooperation over an equal probability of unilateral cooperation and defection;
- : Agents prefer unilateral defection to mutual cooperation,: Agents prefer mutual defection to unilateral cooperation.
- : Prisoner’s dilemma;
- : Chicken game;
- : Stag hunt game.
3.2. Sequential Driving Dilemma in a Markov Game
- m. There are m adaptive AVs in the agent pool, denoted by .
- . The environment state s in the driving environment, denoted by , refers to global information such as the spatial distribution of all road users and road conditions. It is important to note that there may also be other road users, such as background vehicles, who are non-strategic players in the Markov game. The environment state space is denoted by . However, it should be noted that the environment state s is not fully observable to agents, making the Markov game a partially observable Markov decision process (POMDP).
- . Each agent draws a private observation from their neighborhood environment, which is a subset of the global environment state s. Specifically, agent draws a private observation denoted by , where is the observation space of agent i. The joint observation space for all agents is denoted by , which captures the overall observation of the driving environment by all agents. It is important to note that each agent is limited to only observing their surroundings and not the entire environment state.
- . For simplicity, we adopt discrete action space. Joint action is , where and is the action set. Actions in different traffic scenarios will be detailed in Section 5.
- . After taking action a in state s, an agent arrives at a new state with transition probability . The agent interacts with the environment to gain state transition experiences, i.e., .
- . Agent receives a reward at each time step, which can be the travel cost in the driving environment.
- . The discount factor is used to discount the future reward. In this study, we take , because drivers usually complete trips in a finite horizon and they value future and immediate rewards equally.
- : Agents prefer mutual cooperation to mutual defection when starting from state;
- : Agents prefer mutual cooperation to unilateral cooperation when starting from state;
- : When starting from state , agents prefer mutual cooperation over an equal probability of unilateral cooperation and defection;
- : When starting from state , agents prefer unilateral defection to mutual cooperation,: Agents prefer mutual defection to unilateral cooperation.
4. Social Learning Framework
4.1. Social Learning Scheme
4.2. Social Learning Algorithm
| Algorithm 1 DQN-SDD |
|
5. Numerical Experiments
5.1. Scenario 1: Unsignalized Intersection
5.1.1. Environment Set-Up
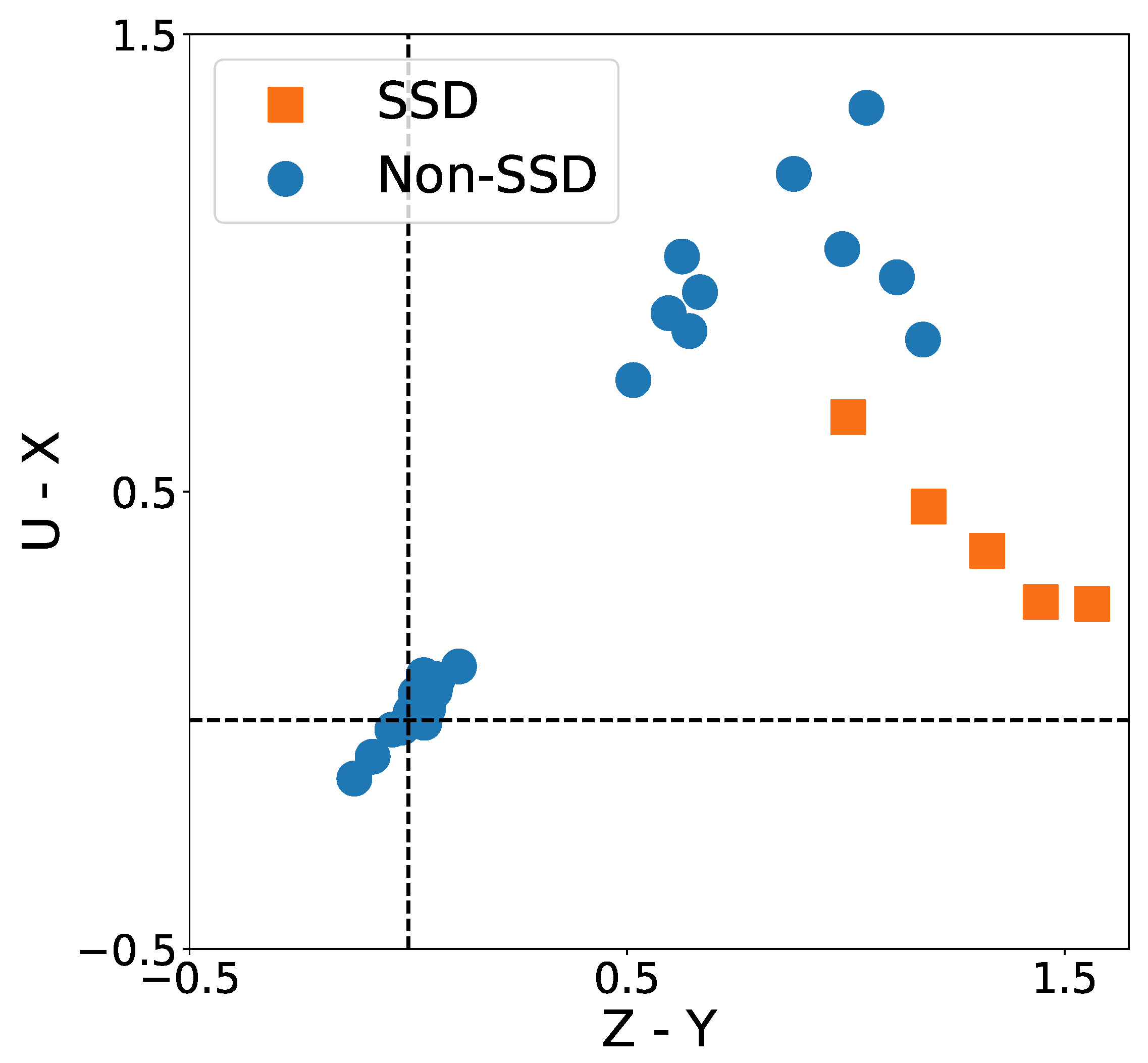
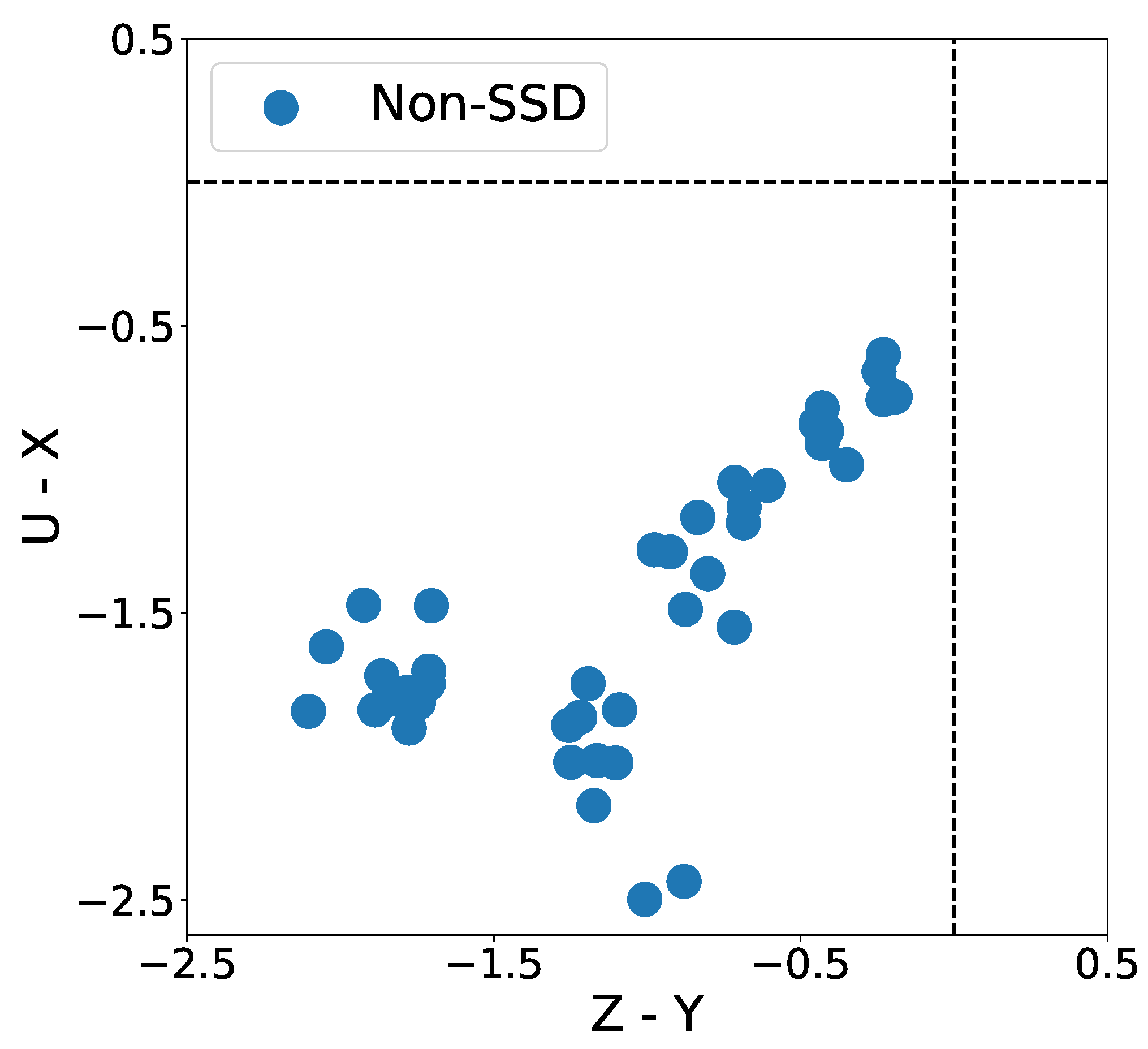
5.1.2. SDD Results
5.2. Scenario 2: Highway
5.2.1. Environment Set-Up
5.2.2. SDD Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sadigh, D.; Sastry, S.; Seshia, S.A.; Dragan, A.D. Planning for Autonomous Cars that Leverage Effects on Human Actions. In Proceedings of the Robotics: Science and Systems, Ann Arbor, MI, USA, 12–16 July 2016. [Google Scholar]
- Fisac, J.F.; Bronstein, E.; Stefansson, E.; Sadigh, D.; Sastry, S.S.; Dragan, A.D. Hierarchical Game-Theoretic Planning for Autonomous Vehicles. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 9590–9596. [Google Scholar] [CrossRef]
- Di, X.; Shi, R. A survey on autonomous vehicle control in the era of mixed-autonomy: From physics-based to AI-guided driving policy learning. Transp. Res. Part Emerg. Technol. 2021, 125, 103008. [Google Scholar] [CrossRef]
- Huang, K.; Chen, X.; Di, X.; Du, Q. Dynamic driving and routing games for autonomous vehicles on networks: A mean field game approach. Transp. Res. Part Emerg. Technol. 2021, 128, 103189. [Google Scholar] [CrossRef]
- Shou, Z.; Chen, X.; Fu, Y.; Di, X. Multi-agent reinforcement learning for Markov routing games: A new modeling paradigm for dynamic traffic assignment. Transp. Res. Part Emerg. Technol. 2022, 137, 103560. [Google Scholar] [CrossRef]
- Pedersen, P.A. A Game Theoretical Approach to Road Safety; Technical Report, Department of Economics Discussion Paper; University of Kent: Canterbury, UK, 2001. [Google Scholar]
- Pedersen, P.A. Moral hazard in traffic games. J. Transp. Econ. Policy (JTEP) 2003, 37, 47–68. [Google Scholar]
- Chatterjee, I.; Davis, G. Evolutionary game theoretic approach to rear-end events on congested freeway. Transp. Res. Rec. J. Transp. Res. Board 2013, 2386, 121–127. [Google Scholar] [CrossRef]
- Chatterjee, I. Understanding Driver Contributions to Rear-End Crashes on Congested Freeways and Their Implications for Future Safety Measures. PhD Thesis, University of Minnesota, Minneapolis, MN, USA, 2016. [Google Scholar]
- Yoo, J.H.; Langari, R. Stackelberg game based model of highway driving. In Proceedings of the ASME 2012 5th Annual Dynamic Systems and Control Conference joint with the JSME 2012 11th Motion and Vibration Conference, Fort Lauderdale, FL, USA, 17–19 October 2012; American Society of Mechanical Engineers: New York, NY, USA, 2012; pp. 499–508. [Google Scholar]
- Yoo, J.H. A Game Theory Based Model of Human Driving with Application to Autonomous and Mixed Driving. Doctoral Dissertation, Texas A & M University, College Station, TX, USA, 2014. [Google Scholar]
- Talebpour, A.; Mahmassani, H.; Hamdar, S. Modeling Lane-Changing Behavior in a Connected Environment: A Game Theory Approach. Transp. Res. Part Emerg. Technol. 2015, 59, 216–232. [Google Scholar] [CrossRef]
- Yu, H.; Tseng, H.E.; Langari, R. A human-like game theory-based controller for automatic lane changing. Transp. Res. Part Emerg. Technol. 2018, 88, 140–158. [Google Scholar] [CrossRef]
- Leibo, J.Z.; Zambaldi, V.; Lanctot, M.; Marecki, J.; Graepel, T. Multi-agent Reinforcement Learning in Sequential Social Dilemmas. In Proceedings of the AAMAS ’17, 16th International Conference on Autonomous Agents and MultiAgent Systems, Sao Paulo, Brazil, 8–12 May 2017. [Google Scholar]
- Allen, B.; Lippner, G.; Chen, Y.T.; Fotouhi, B.; Momeni, N.; Yau, S.T.; Nowak, M.A. Evolutionary dynamics on any population structure. Nature 2017, 544, 227–230. [Google Scholar] [CrossRef]
- McAvoy, A.; Allen, B.; Nowak, M.A. Social goods dilemmas in heterogeneous societies. Nat. Hum. Behav. 2020, 4, 819–831. [Google Scholar] [CrossRef]
- Su, Q.; McAvoy, A.; Wang, L.; Nowak, M.A. Evolutionary dynamics with game transitions. Proc. Natl. Acad. Sci. USA 2019, 116, 25398–25404. [Google Scholar] [CrossRef]
- Hilbe, C.; Štěpán Šimsa, Š.; Chatterjee, K.; Nowak, M.A. Evolution of cooperation in stochastic games. Nature 2018, 559, 246–249. [Google Scholar] [CrossRef] [PubMed]
- Bonnefon, J.F.; Shariff, A.; Rahwan, I. The social dilemma of autonomous vehicles. Science 2016, 352, 1573–1576. [Google Scholar] [CrossRef] [PubMed]
- Schwarting, W.; Pierson, A.; Alonso-Mora, J.; Karaman, S.; Rus, D. Social behavior for autonomous vehicles. Proc. Natl. Acad. Sci. USA 2019, 116, 24972–24978. [Google Scholar] [CrossRef] [PubMed]
- Eccles, T.; Hughes, E.; Kramár, J.; Wheelwright, S.; Leibo, J.Z. Learning Reciprocity in Complex Sequential Social Dilemmas. arXiv 2019, arXiv:1903.08082. [Google Scholar]
- Badjatiya, P.; Sarkar, M.; Sinha, A.; Singh, S.; Puri, N.; Subramanian, J.; Krishnamurthy, B. Inducing Cooperative behaviour in Sequential-Social dilemmas through Multi-Agent Reinforcement Learning using Status-Quo Loss. arXiv 2020, arXiv:2001.05458. [Google Scholar]
- Gupta, G. Obedience-Based Multi-Agent Cooperation for Sequential Social Dilemmas. Master Thesis, University of Waterloo, Waterloo, ON, Canada, 2020. [Google Scholar]
- Sen, S.; Airiau, S. Emergence of Norms through Social Learning. In Proceedings of the IJCAI’07, 20th International Joint Conference on Artifical Intelligence, Hyderabad, India, 6–12 January 2007; Morgan Kaufmann Publishers Inc: San Francisco, CA, USA, 2007; pp. 1507–1512. [Google Scholar]
- Lewis, D. Convention: A Philosophical Study; Wiley: Hoboken, NJ, USA, 1970. [Google Scholar]
- Boella, G.; Lesmo, L. A Game Theoretic Approach to Norms and Agents; Universita di Torino: Torino, Italy, 2001. [Google Scholar]
- Boella, G.; van der Torre, L. Norm governed multiagent systems: The delegation of control to autonomous agents. In Proceedings of the IAT 2003, IEEE/WIC International Conference on Intelligent Agent Technology, Halifax, NSA, Canada, 13–17 October 2003; pp. 329–335. [Google Scholar] [CrossRef]
- Epstein, J. Learning to Be Thoughtless: Social Norms and Individual Computation. Comput. Econ. 2001, 18, 9–24. [Google Scholar] [CrossRef]
- O’Callaghan, D.; Mannion, P. Tunable Behaviours in Sequential Social Dilemmas Using Multi-Objective Reinforcement Learning; International Foundation for Autonomous Agents and Multiagent Systems: Richland, SC, USA, 2021; pp. 1610–1612. [Google Scholar]
- Delgado, J. Emergence of social conventions in complex networks. Artif. Intell. 2002, 141, 171–185. [Google Scholar] [CrossRef]
- Villatoro, D.; Sabater-Mir, J.; Sen, S. Social Instruments for Robust Convention Emergence. In Proceedings of the Twenty-Second International Joint Conference on Artificial Intelligence, Barcelona, Spain, 16–22 July 2011; pp. 420–425. [Google Scholar] [CrossRef]
- Yu, C.; Zhang, M.; Ren, F.; Luo, X. Emergence of Social Norms through Collective Learning in Networked Agent Societies. In Proceedings of the AAMAS ’13, 2013 International Conference on Autonomous Agents and Multi-Agent Systems, St. Paul, MN, USA, 6–10 May 2013; International Foundation for Autonomous Agents and Multiagent Systems: Richland, SC, USA, 2013; pp. 475–482. [Google Scholar]
- Franks, H.; Griffiths, N.; Jhumka, A. Manipulating convention emergence using influencer agents. Auton. Agents-Multi-Agent Syst. 2013, 26, 315–353. [Google Scholar] [CrossRef]
- Chen, X.; Li, Z.; Di, X. Social Learning In Markov Games: Empowering Autonomous Driving. In Proceedings of the 2022 IEEE Intelligent Vehicles Symposium (IV), Aachen, Germany, 4–9 June 2022; pp. 478–483. [Google Scholar] [CrossRef]
- Macy, D.; Flache, A. Learning Dynamics in Social Dilemmas. Proc. Natl. Acad. Sci. USA 2002, 99 (Suppl. 3), 7229–7236. [Google Scholar] [CrossRef]
- Bouderba, S.; Moussa, N. Evolutionary dilemma game for conflict resolution at unsignalized traffic intersection. Int. J. Mod. Phys. 2019, 30, 189. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.A.; Fidjeland, A.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Di, X. Legal Framework for Rear-End Crashes in Mixed-Traffic Platooning: A Matrix Game Approach. Future Transp. 2023, 3, 417–428. [Google Scholar] [CrossRef]


| Matrix Game -Fixed Player | Matrix Game -Social Learning | Markov Game -Fixed Player | Markov Game -Social Learning | |
|---|---|---|---|---|
| Social dilemma | [15,16,17,18] | — | [14,21,22,23,29] | This work |
| Social norm | [24,30,31,32,33] | [24] | — | [34] |
| πC | πD | |
| πC | X, X | Y, U |
| πD | U, Y | Z, Z |
| Hyperparameter | Value |
|---|---|
| Optimizer | Adam |
| Number of hidden layers | 3 |
| Dropout rate | 0.2 |
| Activation function | ReLU |
| Learning rate | 0.0001 |
| Initial epsilon | 1.0 |
| Epsilon decay | 0.01 |
| Final epsilon | 0.01 |
| Replay buffer size | 200 |
| Update period | 50 |
| Update parameter | 0.2 |
| Number of training episodes T | 20,000 |
| Unsignalized Intersection | Highway | |
|---|---|---|
| Cooperation | one vehicle yields to another | vehicles merge and form a car platoon |
| Defection | vehicles do not yield to each other | vehicles stay in their own lanes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Di, X.; Li, Z. Social Learning for Sequential Driving Dilemmas. Games 2023, 14, 41. https://doi.org/10.3390/g14030041
Chen X, Di X, Li Z. Social Learning for Sequential Driving Dilemmas. Games. 2023; 14(3):41. https://doi.org/10.3390/g14030041
Chicago/Turabian StyleChen, Xu, Xuan Di, and Zechu Li. 2023. "Social Learning for Sequential Driving Dilemmas" Games 14, no. 3: 41. https://doi.org/10.3390/g14030041
APA StyleChen, X., Di, X., & Li, Z. (2023). Social Learning for Sequential Driving Dilemmas. Games, 14(3), 41. https://doi.org/10.3390/g14030041







