Abstract
When we play competitive games, the opponents that we face act as predictors of the outcome of the game. For instance, if you are an average chess player and you face a Grandmaster, you anticipate a loss. Framed in a reinforcement learning perspective, our opponents can be thought of as predictors of rewards and punishments. The present study investigates whether facing an opponent would be processed as a reward or punishment depending on the level of difficulty the opponent poses. Participants played Rock, Paper, Scissors against three computer opponents while electroencephalographic (EEG) data was recorded. In a key manipulation, one opponent (HARD) was programmed to win most often, another (EASY) was made to lose most often, and the third (AVERAGE) had equiprobable outcomes of wins, losses, and ties. Through practice, participants learned to anticipate the relative challenge of a game based on the opponent they were facing that round. An analysis of our EEG data revealed that winning outcomes elicited a reward positivity relative to losing outcomes. Interestingly, our analysis of the predictive cues (i.e., the opponents’ faces) demonstrated that attentional engagement (P3a) was contextually sensitive to anticipated game difficulty. As such, our results for the predictive cue are contrary to what one might expect for a reinforcement model associated with predicted reward, but rather demonstrate that the neural response to the predictive cue was encoding the level of engagement with the opponent as opposed to value relative to the anticipated outcome.
1. Introduction
In head-to-head competition, knowing one’s opponent can offer strategic advantage. For instance, in the Netflix series “The Queen’s Gambit” after learning from previous losses Beth Harmon uses her knowledge of her opponent on her way to victory against Chess Master Vasily Borgov. Knowing one’s opponent can also indicate the likelihood of a favorable (or unfavorable) outcome. Consider the expectations of a tennis player about to face 23-time Grand Slam Champion Serena Williams, versus a match against a random opponent from a neighboring tennis club. Here, we sought to use electroencephalography (EEG) to examine the cognitive processes underlying competitive games. While not as skill based as the aforementioned examples, given some of the limiting methodological factors of EEG, we decided to explore real-world competitive contexts by using simple games.
Indeed, simple games are fruitful tools for our efforts to understand the mind in a competitive setting. Games such as Rock, Paper, Scissors (RPS) or Tic-Tac-Toe are widely known, and thus are easy to explain to experimental participants. They are often enjoyable to play, leading to increased engagement in the experimental task relative to prototypical model tasks used to explore cognition [1]. They are also well-understood from a game theory perspective [2,3]. As such, optimal and sub-optimal strategies can be easily recognized, and the experimental factors that induce these outcomes can be identified. At the same time, simple games like RPS are more complex than many commonly used decision-making tasks. These games therefore provide an opportunity to expand what we know about the neural basis of learning and decision making to more ecologically valid or naturalistic scenarios [4].
Linking back to above, it is implausible to imagine a victory over a local tennis opponent would be as meaningful, or career-defining, as a victory over the greatest tennis champion of all time. This intuition about the difference between an expected win and an unexpected win is captured by the principles of reinforcement learning. Within a reinforcement learning context, learning occurs when outcomes are unexpected-that is, when outcomes are better or worse than expected. The degree to which an outcome deviates from our expectation is called a prediction error. In humans and other animals prediction errors are represented in the midbrain by the neurotransmitter dopamine [5] and transmitted to medial frontal cortex [6]. Prediction errors can be measured non-invasively in humans using electroencephalography (EEG). Specifically, an ERP component called the reward positivity (The reward positivity goes by several names, including the feedback-related negativity (FRN). See [7] for a full discussion.) can be computed by comparing the neural response to wins to the neural response to losses [8]. Unexpected wins and losses are known to elicit a larger prediction error, and correspondingly a larger reward positivity, compared to expected wins and losses [9,10]. Interestingly, cues that predict future reward can themselves elicit a reward positivity [11,12]. This result extends to faces; a reward positivity is elicited when fair and unfair opponent faces are contrasted during the ultimatum game [13,14,15]. With that said, it is not clear how perceptions of an opponent’s ability impacts prediction errors and thus the reward positivity.
Here, we examine the extent to which an opponent’s ability affects neural processing in advance, and after learning the outcome, of a simple game of RPS. RPS is a simple game that has been used to explore aspects of decision-making, such as factors affecting sub-optimal choices [16], and outcome-based reactive behavior [17]. In our study, participants played RPS against three separate opponents: a hard opponent who disproportionately wins, an easy opponent who disproportionately loses, and an average opponent who wins, loses, and ties at equal frequency. Participants were not informed regarding the opponent difficulty manipulation, rather their subjective assessments of opponent difficulty were surveyed at various time points in the experiment.
Our hypotheses about how participants would process opponents and outcomes initially came from a reinforcement learning perspective. We first considered how feedback-locked prediction errors should vary across conditions. For example, wins should be unexpected when playing the hard opponent but expected against the easy opponent. We therefore predicted that the amplitude of the reward positivity, which tracks prediction errors, should depend on outcome expectancy (larger amplitude for more unexpected outcomes). We further predicted that processing opponents themselves should follow the principles of reinforcement learning. For example, finding out you are playing the hard opponent should elicit a negative prediction error since this event is worse than expected, i.e., worse compared to playing an opponent of average ability. Put another way, playing a hard opponent is predictive of a future loss, and should elicit a negative prediction error relative to playing an easy opponent and thus reduce the amplitude of the reward positivity.
However, a posthoc examination of our data revealed no reward positivity for opponent faces. Instead, we observed a prominent signal that was both earlier and more centrally located on the scalp compared to the reward positivity. The evoked response we observed resembled the P3a, an ERP subcomponent of the well-known P3 complex [18]. An exploratory analysis was therefore conducted to determine if the face-locked P3a would differentiate between opponents. There are theoretical reasons to believe this might be the case. Although originally associated with infrequent novel stimuli, the P3a has more recently been linked with attentional processes in general [18]. Thus, while novel or rare items can grab our attention, eliciting an enhanced P3a, other types of stimuli can as well-speech sounds [19], emotional stimuli [20], and television advertisements [21]. Faces are also known to elicit a P3a component. Specifically, it has been demonstrated that activity in this time range is greater for emotional faces compared to neutral faces [22,23] and for normal compared to distorted or inverted faces [24,25] (Here we include studies on both the P3a and the P250, as these are thought to be the same component [26,27]). Our exploratory analysis asked whether the P3a component is also sensitive to opponent ability.
2. Method
2.1. Participants
Participants were recruited from the subject pool at Dalhousie University. 21 people took part in the study over the course of a single, 2.5 h session. They were compensated with course credit (0.5/30 min) for their time. All participants provided informed consent approved by the Health Sciences Research Ethics Board at Dalhousie University.
2.2. Stimuli & Procedure
Participants were seated 75 cm in front of a 22-inch LCD monitor (75 Hz, 2 ms response rate, 1680 by 1050 pixels, LG W2242TQ-GF, Seoul, Korea). Visual stimuli were presented using the Psychophysics Toolbox Extension [28,29] for MATLAB (Version 8.2, Mathworks, Natick, MA, USA). Participants were given both verbal and written instructions in which they were asked to minimize head and eye movements.
Participants played 150 blocks of RPS against three virtual opponents. The opponents were well known celebrities of the same gender as the participant. Each block consisted of three rounds (one for each opponent), and the order of opponents within each block was randomized. Rounds began with the presentation of a central fixation cross for 600–1000 ms. The opponent’s face then appeared above the fixation cross for 1500–2000 ms, followed by the appearance of three hand shapes indicating the possible choices (rock, paper, or scissors). This was the participant’s cue to choose, which they did by clicking on the appropriate hand shape using a computer mouse. The participant’s choice then appeared in the lower center of the screen for 600–1000 ms. Finally, feedback-the opponent’s choice-was displayed for 1200–1500 ms. See Figure 1 for a sample round. All jittered intervals were drawn from random uniform distributions. See Supplementary Material for the script that was read to participants.
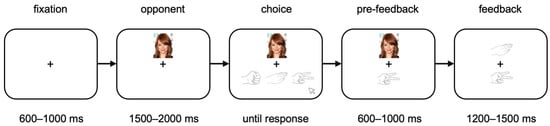
Figure 1.
RPS task, with timing details. Participants were first shown their opponent’s face, then used the mouse to make their choice. Feedback came when participants saw the opponent’s choice.
Unbeknownst to participants, we varied opponent difficulty by controlling the number of wins, losses, and ties. The “hard” opponent won approximately 60% of the time, lost 20% of the time, and tied 20% of the time. The “easy” opponent was the reverse-they lost 60% of the time, won 20% of the time, and tied 20% of the time. The “average” opponent won, lost, and tied with equal probability. These outcome frequencies were achieved by sampling from a random uniform distribution prior to the start of the experiment in order to generate the predetermined outcome sequence. Opponent choice was then determined at the time of participant choice according to the predetermined outcome, e.g., if the predetermined outcome was “win” and the participant chose “scissors” then the opponent choice was “paper”. To gauge their perception of opponent difficulty, participants completed an “opponent ability” survey prior to the study, at two points during the study, and at the end of the study. See Supplementary Figures S1 and S2 for the opponent ability surveys.
2.3. Data Collection
Our experimental software recorded the identity of each opponent (hard, easy, average), the participant choice (rock, paper, scissors), response time, and trial outcome (tie, loss, win). The “opponent ability” scores for each opponent (hard, easy, mid) and time point (pre-study, break 1, break 2, post-study) were recorded on paper and later transcribed.
EEG was recorded from 64 electrode locations using Brain Vision PyCorder software (Version 1.0.4, Brain Products GmbH, Munich, Germany). The electrodes were mounted in a fitted cap with a standard 10–20 layout and were recorded with respect to a virtual ground built into the amplifier. Electrode impedances were below 20 kΩ when the recording began and the EEG was sampled at 500 Hz and amplified (ActiCHamp, Brainproducts GmbH, Munich, Germany).
2.4. Data Analysis
2.4.1. Behavioral
The data file for one participant was lost. For the remaining 20 participants, we computed the mean number of each outcome type and mean response time for each opponent. Questionnaires for four participants also went missing.
2.4.2. EEG
The EEG was analyzed using the EEGLAB library for MATLAB [30]. The EEG was first downsampled to 250 Hz, then filtered through a 0.1–30 Hz bandpass filter. Next, we applied a 60 Hz notch filter to reduce line noise power. The data were then re-referenced to the average of the two mastoid channels, which were removed from subsequent analysis. Next, noisy channels were removed from the dataset. On average, we removed 0.67 channels, 95% CI [0.25, 1.08]. No more than three channels were removed for any participant.
We then used independent component analysis (ICA) to identify and correct ocular artifacts. First, the ICA was trained on three-second epochs starting at the presentation of the opponent’s face. Epochs with large artifacts (voltage change exceeding 500 µV) were excluded from the ICA training. We then used the iclabel function to identify components that were more likely to be eye-related than brain-related, which we removed from the data. Finally, any electrodes that were previously removed due to noise were interpolated.
Feedback-locked and face-locked ERPs were constructed by first creating epochs from 200 ms pre-feedback to 600 ms post-feedback. Epochs were excluded from further analysis according to the following artifact rejection criteria: a voltage exceeding +/− 100 uV, a voltage difference exceeding 100 uV, a sample-to-sample difference of more than 40 uV, or all voltages below 0.1 uV. On average, we removed 1.50% of feedback-locked epochs, 95% CI [0.87, 2.12], and 2.27% of face-locked epochs, 95% CI [1.35, 3.20].
Wins, Losses, and Ties. Feedback-locked epochs were then averaged for each participant and outcome condition (win, loss, tie). To define a reward positivity score, we used the method of difference waves, subtracting the loss waveform from the win waveform for each participant. To capture the peak of this difference wave, we focused on electrode FCz, a known scalp location of the reward positivity [8].
We then identified the time points at which 75% of the maximum voltage was reached in the grand average difference waveform: 284–365 ms, which is compatible with previous studies [31]. Finally, we computed the mean voltage in this time window for each participant and condition (win, loss, tie).
Outcome Expectancy. To examine the effect of expectancy on feedback processing, we also created average “win” and “loss” waveforms for each opponent type (hard, easy, mid). Win and loss waveforms were then subtracted in such a way that feedback expectancy was matched. For example, we compared easy opponent losses to hard opponent wins–in both cases, the outcomes were rare. Matching outcomes in this way is important because expectancy is a known confound of the reward positivity [8]. Difference waves were created for each expectancy condition (low, medium, high) and a reward positivity score was computed by averaging at the same scalp location and over the same time window as before–that is, the time window identified from collapsing across all conditions, a method that is unbiased towards any of the expectancy conditions [32].
Opponent Faces. Finally, we examined the face-locked response by averaging over each opponent type (hard, easy, average) for each participant. Epochs were excluded from the average using the same artifact detection procedure as before. Upon examining the face-locked waveforms, we noted that the pattern of deflections did not match that of a typical reward positivity–there was no prominent negative deflection in any of the conditions [7,8]. Rather, we observed a prominent positive deflection in each condition, which appeared to scale to opponent difficulty. The effect appeared to be in the P3a time range, and an exploratory analysis was conducted. To isolate the effect, we constructed a difference wave by subtracting the “easy” face from the “hard” face. We then calculated the mean voltage within a time window (220–256 ms) and electrode (Cz) where the difference was greatest.
2.4.3. Inferential Statistics
Response times were analyzed using a one-way repeated-measures ANOVA. Of the three response time conditions, two failed the Shapiro-Wilk test of normality (easy and mid). However, no corrections were made as the one-way ANOVA is robust to violations of normality. Opponent ratings were analyzed using a 3 (opponent: hard, easy, mid) X 4 (time: pre-study, break 1, break 2, post-study) repeated-measures ANOVA. Participant response choice 3 (rock, paper, scissors) relative to opponent ability 3 (easy, mid, hard) was analyzed with a repeated-measures ANOVA. The assumption of sphericity was tested using Mauchly’s test for all repeated-measures ANOVAs and was not violated thus no corrections were applied. For each EEG analysis (outcome type, outcome expectancy, opponent) we analyzed the resulting scores using a one-way repeated-measures ANOVA after verifying the assumption of normality using the Shapiro-Wilk test. For the one-way ANOVAs, we computed two effect sizes: partial eta squared (ηp2) and generalized eta squared (ηg2).
3. Results
3.1. Behavioral Results
The mean response time did not differ by opponent type (Figure 2), hard: 1.42 s, 95% CI [1.17, 1.73], easy: 1.38 s, 95% CI [1.12, 1.63], average: 1.48 s, 95% CI [1.19, 1.77], F(2,38) = 2.69, p = 0.081, ηp = 0.12, ηg = 0.01. Opponent ratings did however vary by opponent type, F(1,16) = 1404, p < 0.001, ηp = 0.99, ηg = 0.96, and over time, F(1,16) = 1416, p < 0.001, ηp = 0.99, ηg = 0.95. There was also a significant opponent X time interaction, F(1,16) = 1351, p < 0.001, ηp = 0.99, ηg = 0.95. When we examined the distribution of response preferences (Figure 3), we noted a main effect of response, F(2,40) = 39.31, p < 0.001, ηp = 0.66, ηg = 0.66, suggesting that participants did indeed have a preferred response. However, there was no effect of opponent, F(2,40) = 0.59, p = 0.56, ηp = 0.03, ηg = 0.00, and no opponent X response interaction, F(4,80) = 1.15, p = 0.34, ηp = 0.05, ηg = 0.05. In other words, the distribution of responses was not influenced by opponent. We collapsed across opponent type and conducted three post-hoc tests against a Bonferroni-adjusted alpha value of 0.017 (0.05/3). The tests showed that participants chose their first-ranked response more often than their second-ranked response, t(20) = 4.70, p < 0.001, Cohen’s d = 1.03, and their third-ranked response, t(20) = 7.02, p < 0.001, Cohen’s d = 1.53. The total number of second-ranked responses exceeded the total number of third-ranked responses, t(20) = 11.99, p < 0.001, Cohen’s d = 2.62.
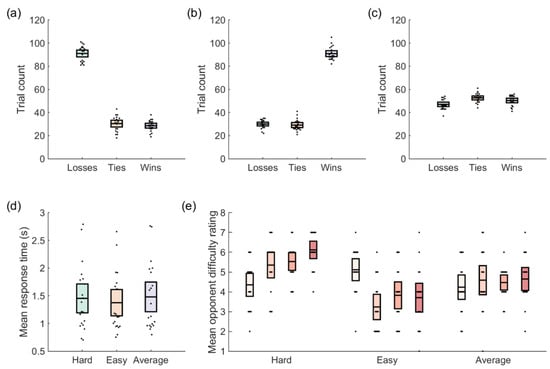
Figure 2.
Behavioral data. Mean number of outcomes of each type for the (a) hard, (b) easy, and (c) average opponents. (d) Response times did not differ between opponent types. (e) Participant ratings of each opponent type at four different times during the experiment (pre-experiment, first rest break, second rest break, and post-experiment).
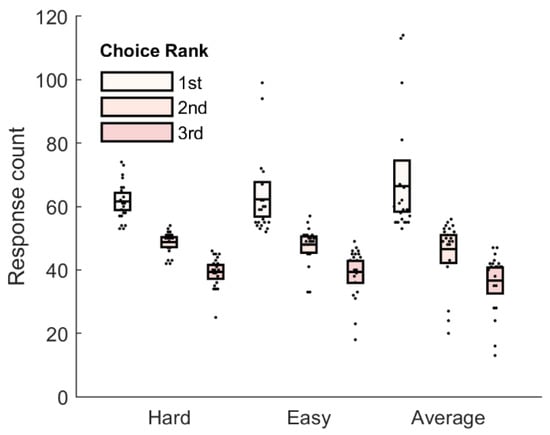
Figure 3.
Behavioural data. Mean response count as a function of ranked preference against each of the hard, easy, and average opponents.
3.2. Electroencephalographic Results
3.2.1. Feedback Processing: Tie, Lose, Win
An analysis of the average waveforms locked to the onset of each feedback type (win, tie, loss) revealed an effect of feedback type on the average voltage in a time range (284–365 ms) and location (FCz) consistent with the reward positivity, F(2,40) = 4.46, p = 0.018, ηp2 = 0.18, ηg2 = 0.02 (see Table 1 and Figure 4). Three post-hoc tests against a Bonferroni-adjusted alpha value of 0.017 (0.05/3) were done to compare final opponent ratings. The tests showed a difference between the final “hard” rating and the final “easy” rating, t(16) = 5.51, p < 0.001, Cohen’s d = 1.34, between the final “hard” rating and final “average” rating, t(16) = 4.41, p < 0.001, Cohen’s d = 1.07, and between the final “average” rating and the final “easy” rating, t(16) = 2.99, p = 0.009, Cohen’s d = 0.73.

Table 1.
Mean Reward Positivity and P3a for each ERP analysis, with 95% confidence intervals.
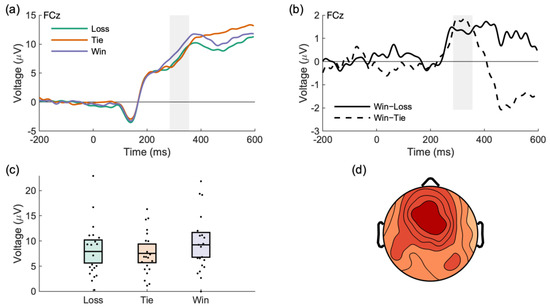
Figure 4.
Neural response to feedback differentiated wins from losses and ties. (a) A positive deflection for wins was observed relative to ties/losses. The shaded area shows the region of analysis. (b) The difference waves show the effect to be in a time range and scalp location consistent with the reward positivity component. (c) Reward positivity scores for each outcome type. Error bars indicate 95% confidence intervals. (d) The reward positivity was located at a frontal-central scalp location.
3.2.2. Feedback Processing: Expectancy
When compared on expectancy (high, medium, low) we observed no difference in the reward positivity as defined above, F(2,40) = 0.86, p = 0.430, ηp2 = 0.04, ηg2 = 0.02 (see Table 1 and Supplementary Figure S3).
3.2.3. Face Processing
An analysis of the average waveforms locked to the onset of the face of each opponent type (hard, easy, average) revealed an effect of opponent type on the average voltage from 220–256 ms at electrode Cz, F(2,40) = 12.18, p < 0.001, ηp2 = 0.39, ηg2 = 0.04 (Figure 5). Three post-hoc comparisons were made against a Bonferroni-adjusted alpha value of 0.017 (0.05/3). The tests revealed that the “hard” response exceeded both the “easy” response, t(20) = 5.50, p < 0.001, Cohen’s d = 1.20 and the “average” response, t(20) = 2.78, p = 0.012, Cohen’s d = 0.61. The difference between the “average” response and the “easy” response did not survive the adjustment for multiple comparisons, t(20) = 2.32, p = 0.031, Cohen’s d = 0.51.
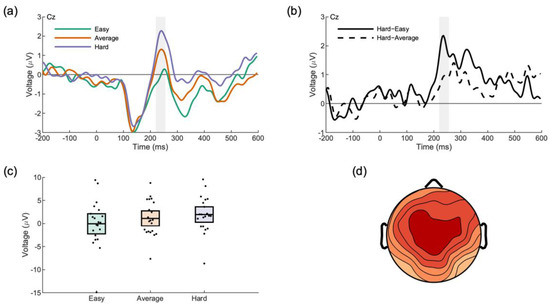
Figure 5.
Neural response to opponent faces distinguishes opponent difficulty. (a) A prominent positivity is noted in response to each face. The shaded area shows the region of our exploratory analysis. (b) Difference waves showing the time range of the effect. (c) Mean component scores for each opponent. (d) Scalp distribution of the P3a difference between the hard opponent and the easy opponent.
4. Discussion
In the present experiment we had participants play RPS against three virtual opponents-one that was “hard” and won most of the time, one that was “average” and won, lost, and tied with equal frequency, and one that was “easy” and lost to participants most of the time. In terms of our behavioral results, we found what was expected-participants lost more against the hard opponent, won more against the easy opponent, and had equivalent outcomes against the average opponent. Interestingly, we did not find a difference in response time for participants moves against any of the three opponents-thus a speed-accuracy tradeoff was not observed [33,34]. Further, we did not find any difference in response selection in relation to opponent ability (see Figure 3). This is important, as it suggests that participants were engaged and trying to “outwit” their opponents. Moreover, it suggests that when competitive contexts are constantly changing, participants are likely to defer to a stable gameplay strategy regardless of the learned difficulty of their immediate opponent. It would be interesting to explore whether this stability in response selection strategy persists under conditions wherein competitive contexts are less dynamic (i.e., if one faces the same opponent for multiple sequential trials).
In terms of our ERP data, we observed a clear reward positivity when comparing wins and losses. A similar difference was seen when we compared wins to ties (Figure 4). This finding is in line with a wide range of work showing that feedback indicating the outcome of a choice elicits a reward positivity [6,7,8,11,35]. Further, this finding also suggests that, to some extent, a reinforcement learning system in the brain was engaged during gameplay. However, contrary to our hypothesis and contrary to previous work [9,10], we did not find the reward positivity to be modulated by expectancy. What about the neural responses to the opponents themselves? Again, contrary to our hypothesis, and contrary to previous literature on the evoked response to predictive cues [13,14,15], the faces of the opponents did not elicit a reward positivity. One potential reason for this is that we used faces instead of the simple stimuli that were used in previous experiments like colored shapes. With that said, this is not a likely explanation because faces have been shown to elicit a reward positivity when playing the ultimatum game [13,14,15]. At this time, we are uncertain why the faces in our experiment did not elicit a reward positivity and further work is needed.
However, and interestingly, we did observe a clear P3a ERP response that differentiated opponents faces (Figure 5). As discussed previously, there are theoretical reasons why the P3a-indicative of attentional orienting [18] may differentiate between opponent types. Our results suggest a scaling of attentional orienting to opponent ability—the harder they are to beat, the more attention is engaged at the onset of the opponent’s face. We can imagine two reasons for this. The first is that the P3a indicates a marshalling of resources in preparation for the upcoming response. Supporting this hypothesis, the P3a has been linked to enhanced cognitive control [36,37]. For instance, previous work has associated the P3a with task-set uncertainty [38]. It has also been postulated to reflect stimulus entropy, or the amount of information associated with a stimulus over and above stimulus-response-outcome probabilities, and may represent an aspect of the central bottleneck of attentional control [39].
A second explanation for our ERP results for faces relates to the meaning of the faces-not as low-level stimuli, but as opponents in a game. Under this view, the P3a could reflect the allocation of attention to facilitate learning of opponents’ strategies, a task known to activate a “mentalizing” network in the brain [40]. This view harkens back to the context updating theory of the P300, which states that this component is related to revising an internal model of the world [41]. Unlike simulated players in the ultimatum game, who tend to be consistently fair or unfair, we presented participants with three opponents, each generating a distribution of three possible responses. Of relevance in RPS of course is the likelihood of each response for each opponent. Under this view, participants learned about opponents by updating an internal model of opponent strategies, not through a low-level association with rewards/punishments. While it is beyond the scope of this paper, this is an issue that is pertinent to model-based versus model-free reinforcement learning [42,43].
We note a potential issue with our choice of fixed outcome rates as opposed to variable outcome rates. Although participants “played” RPS, outcome likelihoods were fixed throughout the experiment. Thus, participants’ actions did not influence outcomes, unlike in real-life RPS. The use of fixed outcome rates has a long precedence in reward positivity research [6,9,10,12,44,45,46,47,48,49,50,51,52,53,54]. In some studies, fixed outcome rates are a convenient way to investigate the effect of expectancy on the reward positivity (e.g., [9,10]). In others, they provide an important means of controlling “frequency confounds” across experimental conditions [8]. However, fixing outcome rates–and untethering actions from outcomes–may come at the cost of ecological validity [4]. For example, it is yet unknown whether our results would replicate while playing actual RPS against real opponents. While acknowledging this issue, we argue that the use of simple games in neuroscience (and the benefits they afford) sometimes involves methodological compromise [8].
We also note limitations related to our choice of game. Here we relied on RPS to explore interactions with an opponent–a game that requires little skill. Potentially, future work could address this as EEG studies have been done with games such as Blackjack [50] and Chess [55]. Another potential limitation of the present work is that our experimental design did not allow us to discern whether participants thought opponents were actually “better” or whether they were just lucky. Further, a fundamental assumption of the present study was that all participants were familiar with RPS, something that we did not check but should have. Additionally, our game was structured (for methodological reasons) so that the participant always went first. It would be interesting to probe the neural response to opponent goes first trials however this of course is beyond the scope of the present experiment.
5. Conclusions
Here we used EEG and specifically ERPs to examine how the face on an opponent was processed while playing RPS. Our principal finding was that viewing an opponent’s face—as a predictor of their ability—did not engage reward processing systems within the brain. Instead, we found that viewing an opponent’s face activates the brain’s attentional system with the harder opponent drawing more attention than the average or easy opponents. We interpret this result as an indicator of strategy learning, but not via a reinforcement learning process but rather via the updating of memory for the opponent.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/g12030062/s1, Figure S1: Opponent ability survey for female participants/opponents, Figure S2: Opponent ability survey for male participants/opponents, Figure S3: Feedback-locked waveforms for (a) expected feedback, (b) somewhat unexpected feedback, (c) unexpected feedback, and associated scalp topographies (d–f).
Author Contributions
Conceptualization, C.D.H. and O.E.K.; Data curation, G.A.G. and C.D.H.; Formal analysis, G.A.G., C.C.W. and C.D.H.; Funding acquisition, O.E.K.; Investigation, R.S.R. and C.C.W.; Methodology, R.S.R. and C.C.W.; Project administration, R.S.R. and O.E.K.; Resources, O.E.K.; Software, C.D.H.; Supervision, O.E.K.; Visualization, G.A.G. and C.D.H.; Writing—original draft, R.S.R., C.D.H. and O.E.K.; Writing—review & editing, R.S.R., C.D.H. and O.E.K. All authors have read and agreed to the published version of the manuscript.
Funding
The following work was made possible by numerous sources of support: RSR (NSERC CGS-D; Killam Doctoral Award), CCW (NSERC CGS-D), CDH (NSERC PDF), OEK (NSERC Discovery Grant).
Institutional Review Board Statement
The study was conducted according to the guidelines of the Declaration of Helsinki, and approved by the Institutional Review Board (or Ethics Committee) of DALHOUSIE UNIVERSITY (protocol code 2010-2287).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Data for this study can be found by contacting the corresponding author.
Acknowledgments
The following work was made possible by numerous sources of support: RSR (NSERC CGS-D; Killam Doctoral Award), CCW (NSERC CGS-D), CDH (NSERC PDF), OEK (NSERC Discovery Grant).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Klein, R.M.; Vallis, E.H.; Chisholm, J.D. A Comparison of Engagement between the Attention Network Test and a Videogame-Like Version, Called the AttentionTrip. Int. J. Hum. Comput. Interact. 2019, 35, 1813–1819. [Google Scholar] [CrossRef]
- Von Neumann, J.; Morgenstern, O. Theory of Games and Economic Behavior (Commemorative Edition); Princeton University Press: Princeton, NJ, USA, 2007; ISBN 978-0-691-13061-3. [Google Scholar]
- Smith, J.M. Evolution and the Theory of Games; Cambridge University Press: Cambridge, UK, 1982; ISBN 978-0-521-28884-2. [Google Scholar]
- Mobbs, D.; Trimmer, P.C.; Blumstein, D.T.; Dayan, P. Foraging for foundations in decision neuroscience: Insights from ethology. Nat. Rev. Neurosci. 2018, 19, 419–427. [Google Scholar] [CrossRef]
- Schultz, W.; Dayan, P.; Montague, P.R. A Neural Substrate of Prediction and Reward. Science 1997, 275, 1593–1599. [Google Scholar] [CrossRef]
- Holroyd, C.B.; Coles, M.G. The neural basis of human error processing: Reinforcement learning, dopamine, and the error-related negativity. Psychol. Rev. 2002, 109, 679–709. [Google Scholar] [CrossRef]
- Proudfit, G.H. The reward positivity: From basic research on reward to a biomarker for depression. Psychophysiology 2015, 52, 449–459. [Google Scholar] [CrossRef]
- Krigolson, O.E. Event-related brain potentials and the study of reward processing: Methodological considerations. Int. J. Psychophysiol. 2017, 132, 175–183. [Google Scholar] [CrossRef]
- Holroyd, C.B.; Krigolson, O.E. Reward prediction error signals associated with a modified time estimation task. Psychophysiology 2007, 44, 913–917. [Google Scholar] [CrossRef]
- Williams, C.C.; Hassall, C.D.; Trska, R.; Holroyd, C.B.; Krigolson, O.E. When theory and biology differ: The relationship between reward prediction errors and expectancy. Biol. Psychol. 2017, 129, 265–272. [Google Scholar] [CrossRef]
- Krigolson, O.E.; Hassall, C.D.; Handy, T.C. How We Learn to Make Decisions: Rapid Propagation of Reinforcement Learning Prediction Errors in Humans. J. Cogn. Neurosci. 2014, 26, 635–644. [Google Scholar] [CrossRef]
- Holroyd, C.B.; Krigolson, O.E.; Lee, S. Reward positivity elicited by predictive cues. NeuroReport 2011, 22, 249–252. [Google Scholar] [CrossRef]
- Kaltwasser, L.; Hildebrandt, A.; Wilhelm, O.; Sommer, W. Behavioral and neuronal determinants of negative reciprocity in the ultimatum game. Soc. Cogn. Affect. Neurosci. 2016, 11, 1608–1617. [Google Scholar] [CrossRef]
- Li, D.; Meng, L.; Ma, Q. Who Deserves My Trust? Cue-Elicited Feedback Negativity Tracks Reputation Learning in Repeated Social Interactions. Front. Hum. Neurosci. 2017, 11, 307. [Google Scholar] [CrossRef]
- Osinsky, R.; Mussel, P.; Öhrlein, L.; Hewig, J. A neural signature of the creation of social evaluation. Soc. Cogn. Affect. Neurosci. 2014, 9, 731–736. [Google Scholar] [CrossRef][Green Version]
- Dyson, B.J.; Wilbiks, J.M.P.; Sandhu, R.; Papanicolaou, G.; Lintag, J. Negative outcomes evoke cyclic irrational decisions in Rock, Paper, Scissors. Sci. Rep. 2016, 6, 20479. [Google Scholar] [CrossRef]
- Forder, L.; Dyson, B.J. Behavioural and neural modulation of win-stay but not lose-shift strategies as a function of outcome value in Rock, Paper, Scissors. Sci. Rep. 2016, 6, 33809. [Google Scholar] [CrossRef] [PubMed]
- Polich, J. Updating P300: An integrative theory of P3a and P3b. Clin. Neurophysiol. 2007, 118, 2128–2148. [Google Scholar] [CrossRef]
- Fisher, D.J.; Labelle, A.; Knott, V.J. Auditory hallucinations and the P3a: Attention-switching to speech in schizophrenia. Biol. Psychol. 2010, 85, 417–423. [Google Scholar] [CrossRef]
- Hartikainen, K.M.; Ogawa, K.H.; Knight, R.T. Orbitofrontal cortex biases attention to emotional events. J. Clin. Exp. Neuropsychol. 2012, 34, 588–597. [Google Scholar] [CrossRef]
- Treleaven-Hassard, S.; Gold, J.; Bellman, S.; Schweda, A.; Ciorciari, J.; Critchley, C.; Varan, D. Using the P3a to gauge automatic attention to interactive television advertising. J. Econ. Psychol. 2010, 31, 777–784. [Google Scholar] [CrossRef]
- Wang, J.; Liu, L.; Yan, J.H. Implicit power motive effects on the ERP processing of emotional intensity in anger faces. J. Res. Pers. 2014, 50, 90–97. [Google Scholar] [CrossRef]
- Campanella, S.; Gaspard, C.; Debatisse, D.; Bruyer, R.; Crommelinck, M.; Guerit, J.-M. Discrimination of emotional facial expressions in a visual oddball task: An ERP study. Biol. Psychol. 2002, 59, 171–186. [Google Scholar] [CrossRef]
- Milivojevic, B.; Clapp, W.C.; Johnson, B.W.; Corballis, M.C. Turn that frown upside down: ERP effects of thatcherization of misorientated faces. Psychophysiology 2003, 40, 967–978. [Google Scholar] [CrossRef]
- Halit, H.; De Haan, M.; Johnson, M.H. Modulation of event-related potentials by prototypical and atypical faces. NeuroReport 2000, 11, 1871–1875. [Google Scholar] [CrossRef]
- Brown, C.R.; Clarke, A.R.; Barry, R.J. Inter-modal attention: ERPs to auditory targets in an inter-modal oddball task. Int. J. Psychophysiol. 2006, 62, 77–86. [Google Scholar] [CrossRef]
- García-Larrea, L.; Lukaszewicz, A.-C.; Mauguiére, F. Revisiting the oddball paradigm. Non-target vs neutral stimuli and the evaluation of ERP attentional effects. Neuropsychologia 1992, 30, 723–741. [Google Scholar] [CrossRef]
- Brainard, D.H. The Psychophysics Toolbox. Spat. Vis. 1997, 10, 433–436. [Google Scholar] [CrossRef]
- Pelli, D.G. The VideoToolbox software for visual psychophysics: Transforming numbers into movies. Spat. Vis. 1997, 10, 437–442. [Google Scholar] [CrossRef]
- Delorme, A.; Makeig, S. EEGLAB: An Open Source Toolbox for Analysis of Single-Trial EEG Dynamics Including Independ-ent Component Analysis. J. Neurosci. Methods 2004, 134, 9–21. [Google Scholar] [CrossRef]
- Sambrook, T.D.; Goslin, J. A Neural Reward Prediction Error Revealed by a Meta-Analysis of ERPs Using Great Grand Aver-ages. Psychol. Bull. 2015, 141, 213–235. [Google Scholar] [CrossRef]
- Luck, S.J.; Gaspelin, N. How to get statistically significant effects in any ERP experiment (and why you shouldn’t). Psychophysiology 2017, 54, 146–157. [Google Scholar] [CrossRef]
- Lee, M.J.C.; Tidman, S.J.; Lay, B.S.; Bourke, P.D.; Lloyd, D.G.; Alderson, J.A. Visual Search Differs But Not Reaction Time When Intercepting a 3D Versus 2D Videoed Opponent. J. Mot. Behav. 2013, 45, 107–115. [Google Scholar] [CrossRef]
- Slezak, D.F.; Sigman, M. Do not fear your opponent: Suboptimal changes of a prevention strategy when facing stronger opponents. J. Exp. Psychol. Gen. 2012, 141, 527–538. [Google Scholar] [CrossRef]
- Holroyd, C.B.; Hajcak, G.; Larsen, J.T. The good, the bad and the neutral: Electrophysiological responses to feedback stimuli. Brain Res. 2006, 1105, 93–101. [Google Scholar] [CrossRef]
- Chaillou, A.-C.; Giersch, A.; Hoonakker, M.; Capa, R.L.; Bonnefond, A. Differentiating Motivational from Affective Influence of Performance-contingent Reward on Cognitive Control: The Wanting Component Enhances Both Proactive and Reactive Control. Biol. Psychol. 2017, 125, 146–153. [Google Scholar] [CrossRef]
- Morales, J.; Yudes, C.; Gómez-Ariza, C.J.; Bajo, M.T. Bilingualism modulates dual mechanisms of cognitive control: Evidence from ERPs. Neuropsychologia 2015, 66, 157–169. [Google Scholar] [CrossRef]
- Barceló, F.; Periáñez, J.A.; Knight, R.T. Think differently: A brain orienting response to task novelty. NeuroReport 2002, 13, 1887–1892. [Google Scholar] [CrossRef]
- Barcelo, F.; Escera, C.; Corral, M.J.; Periáñez, J.A. Task Switching and Novelty Processing Activate a Common Neural Network for Cognitive Control. J. Cogn. Neurosci. 2006, 18, 1734–1748. [Google Scholar] [CrossRef]
- Hampton, A.N.; Bossaerts, P.; O’Doherty, J.P. Neural correlates of mentalizing-related computations during strategic interactions in humans. Proc. Natl. Acad. Sci. USA 2008, 105, 6741–6746. [Google Scholar] [CrossRef]
- Donchin, E. Surprise!? Surprise? Psychophysiology 1981, 18, 493–513. [Google Scholar] [CrossRef]
- Daw, N.D.; Gershman, S.J.; Seymour, B.; Dayan, P.; Dolan, R.J. Model-Based Influences on Humans’ Choices and Striatal Prediction Errors. Neuron 2011, 69, 1204–1215. [Google Scholar] [CrossRef]
- Collins, A.G.E.; Cockburn, J. Beyond dichotomies in reinforcement learning. Nat. Rev. Neurosci. 2020, 21, 576–586. [Google Scholar] [CrossRef]
- Cohen, M.X.; Elger, C.E.; Ranganath, C. Reward expectation modulates feedback-related negativity and EEG spectra. NeuroImage 2007, 35, 968–978. [Google Scholar] [CrossRef] [PubMed]
- Dyson, B.J.; Musgrave, C.; Rowe, C.; Sandhur, R. Behavioural and neural interactions between objective and subjective performance in a Matching Pennies game. Int. J. Psychophysiol. 2020, 147, 128–136. [Google Scholar] [CrossRef]
- Hajcak, G.; Holroyd, C.B.; Moser, J.S.; Simons, R.F. Brain potentials associated with expected and unexpected good and bad outcomes. Psychophysiology 2005, 42, 161–170. [Google Scholar] [CrossRef]
- Holroyd, C.B.; Nieuwenhuis, S.; Yeung, N.; Cohen, J.D. Errors in reward prediction are reflected in the event-related brain potential. NeuroReport 2003, 14, 2481–2484. [Google Scholar] [CrossRef]
- Eppinger, B.; Kray, J.; Mock, B.; Mecklinger, A. Better or worse than expected? Aging, learning, and the ERN. Neuropsychologia 2008, 46, 521–539. [Google Scholar] [CrossRef]
- Hajcak, G.; Moser, J.S.; Holroyd, C.B.; Simons, R.F. It’s worse than you thought: The feedback negativity and violations of reward prediction in gambling tasks. Psychophysiology 2007, 44, 905–912. [Google Scholar] [CrossRef]
- Hewig, J.; Trippe, R.; Hecht, H.; Coles, M.G.H.; Holroyd, C.B.; Miltner, W.H.R. Decision-Making in Blackjack: An Electro-physiological Analysis. Cereb. Cortex 2006, 17, 865–877. [Google Scholar] [CrossRef]
- Holroyd, C.B.; Krigolson, O.E.; Baker, R.; Lee, S.; Gibson, J. When is an error not a prediction error? An electrophysiological investigation. Cogn. Affect. Behav. Neurosci. 2009, 9, 59–70. [Google Scholar] [CrossRef] [PubMed]
- KreuSSel, L.; Hewig, J.; Kretschmer, N.; Hecht, H.; Coles, M.G.H.; Miltner, W.H.R. The influence of the magnitude, probability, and valence of potential wins and losses on the amplitude of the feedback negativity. Psychophysiology 2012, 49, 207–219. [Google Scholar] [CrossRef]
- Masaki, H.; Takeuchi, S.; Gehring, W.J.; Takasawa, N.; Yamazaki, K. Affective-motivational influences on feedback-related ERPs in a gambling task. Brain Res. 2006, 1105, 110–121. [Google Scholar] [CrossRef]
- Santesso, D.L.; Dzyundzyak, A.; Segalowitz, S.J. Age, sex and individual differences in punishment sensitivity: Factors influencing the feedback-related negativity. Psychophysiology 2011, 48, 1481–1489. [Google Scholar] [CrossRef]
- Fuentes-García, J.P.; Villafaina, S.; Collado-Mateo, D.; Cano-Plasencia, R.; Gusi, N. Chess Players Increase the Theta Power Spectrum When the Difficulty of the Opponent Increases: An EEG Study. Int. J. Environ. Res. Public Health 2019, 17, 46. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).