Abstract
In simple dyadic games such as rock, paper, scissors (RPS), people exhibit peculiar sequential dependencies across repeated interactions with a stable opponent. These regularities seem to arise from a mutually adversarial process of trying to outwit their opponent. What underlies this process, and what are its limits? Here, we offer a novel framework for formally describing and quantifying human adversarial reasoning in the rock, paper, scissors game. We first show that this framework enables a precise characterization of the complexity of patterned behaviors that people exhibit themselves, and appear to exploit in others. This combination allows for a quantitative understanding of human opponent modeling abilities. We apply these tools to an experiment in which people played 300 rounds of RPS in stable dyads. We find that although people exhibit very complex move dependencies, they cannot exploit these dependencies in their opponents, indicating a fundamental limitation in people’s capacity for adversarial reasoning. Taken together, the results presented here show how the rock, paper, scissors game allows for precise formalization of human adaptive reasoning abilities.
1. Introduction
At a basic level, human conflict and coordination are rooted in the ability to predict the behavior of others and make plans accordingly. While this may sometimes involve ad hoc coordination from first principles, such as well-known Schelling point behavior [1], more often we find ourselves in repeated interactions, wherein we have the opportunity to adapt to past outcomes. Everyday life is replete with such dynamics, whether playing basketball or chess, or simply commuting in traffic among other drivers that are all trying to get home as fast as possible. Broadly, competitive interactions highlight our ability to anticipate and respond to others in diverse settings. What cognitive processes underlie our remarkable ability to anticipate and adapt to the behavior of others around us across repeated interactions? We argue that this question can be addressed by examining people’s behavior in repeated adversarial games, such as the rock, paper, scissors game, where success is a matter of outsmarting one’s opponent, often by identifying predictable patterns in their choices.
To better understand how people manage the cognitive challenges of adapting to others in adversarial interactions, researchers have traditionally turned to iterated zero-sum games. Zero-sum games have the unique character that any player’s gain comes at a loss to their opponent: they are the “limiting case of pure conflict” [2]. Here, we focus on the rock, paper, scissors (RPS) game, or roshambo. In this game, two players simultaneously produce a hand signal indicating their choice of “rock”, “paper”, or “scissors”. The rules are simple: “rock” beats “scissors”, “paper” beats “rock”, and “scissors” beats “paper”. The game is perhaps most popular with children, but it has been used in official contexts to settle court disputes [3] and art auctions [4]. Large-scale RPS tournaments have been held with human entrants [5], while the potential to test a diverse set of algorithmic strategies has also inspired tournaments modeled after [6] in which various bots compete against each other [7,8] (and more recently on the data science site Kaggle, see https://www.kaggle.com/c/rock-paper-scissors (accessed on 13 July 2021)). Finally, the dynamics of the game have made it popular for modeling diverse biological ecosystems [9,10,11,12,13,14], offering predictions in evolutionary game theory [15,16,17,18,19], and even studying large-scale market behavior [20,21,22,23,24,25,26].
Beyond its role in popular culture and in various academic disciplines, the rock, paper, scissors game offers a unique means of studying human adversarial behavior during repeated interactions. Here, our focus is on decision making across many iterated rounds against a stable opponent—often hundreds, rather than the “best of 3” used to resolve household disputes. In such laboratory studies of the rock, paper, scissors game, the large number of interactions allow people to detect and adapt to potentially complex patterns in their opponent’s behavior. In fact, due to the game’s simple rules and constrained space of choices, better performance by one individual over many rounds will not likely be a result of general game “expertise”, but rather a result of superior reasoning about dependencies in their specific opponent’s move choices. This reliance on adaptation to a particular opponent, rather than general game expertise, distinguishes RPS from other adversarial games like chess, and makes it a purer form of adversarial reasoning. Finally, RPS, like other mixed strategy equilibrium games, is characterized by its Nash Equilibrium solution [27], which dictates random move selection, a strategy which presents unique cognitive challenges for human players. For these reasons, a large body of literature has examined human behavior over repeated interactions in the rock, paper, scissors game, motivated by diverse questions about the nature of human learning, sequential behavior, and perceptions of randomness [28,29,30].
In the present work, we argue that the rock, paper, scissors game represents an ideal means of studying human adaptive, adversarial reasoning capacities, i.e., the ability to outwit another person by discovering patterns in their behavior, and offer a novel set of results illustrating the limits of this ability. First, we briefly examine the findings from previous literature on the rock, paper, scissors game with an eye to what existing results tell us about human adversarial reasoning. We argue that by focusing on failures of Nash Equilibrium and on coarse heuristics, prior work has largely overlooked the question of how people adapt to a fallible human opponent over repeated interactions. In this vein, we next discuss how the structure of the game offers a tractable way of describing the flexibility and limitations of people’s adaptive reasoning capacities. To illustrate this, we present an analysis of existing results which suggests that the ability to recognize and exploit sequential patterns in RPS is highly constrained, revealing the limits of human adaptive reasoning.
2. Human RPS Behavior Reflects Adversarial Reasoning
First, we consider what is known about human behavior in iterated rock, paper, scissors games. This literature often starts with the behavioral economics perspective of comparing human behavior to optimal play and, upon finding a difference, seeks to explain it in terms of human heuristics or biases. In RPS, optimal behavior is taken to be uniform random choices, and failures to achieve such randomness are explained as human failures to generate random sequences. Here, we instead argue that the deviations from optimality documented in this literature are more consistent with people attempting to adapt to, and outwit, their opponent, rather than trying and failing to generate truly random move choices. In short, we argue that the existing literature supports the claim that human RPS behavior reflects adaptive adversarial reasoning.
2.1. Normative Strategies
The starting point for exploring human behavior in the rock, paper, scissors game has traditionally focused on whether people adhere to the normative standards of Nash Equilibrium [27], in which a strategy is chosen to optimize performance under the assumption of an equivalently rational, optimizing opponent. RPS belongs to the class of zero-sum cyclic dominance games [31]. Their cyclic nature is best illustrated with the well-known rules of RPS, where “rock” beats “scissors” and “paper” beats “rock”, but “paper” is beaten by “scissors” (see Figure 1a for an illustration of this). Thus, every choice is dominated by one other and no choice is better than another, unless you have some information about what the opponent will choose. Such games are not limited to three-choice paradigms like RPS; cyclic games with many more choices provide a unique means of studying large-scale group behaviors [32].
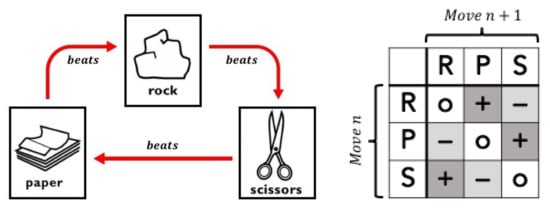
Figure 1.
The rock, paper, scissors game. (a) Shows the cyclic dominance relations of the three move choices: “rock” beats “scissors”, “scissors” beats “paper”, “paper” beats “rock”. (b) The cyclic dominance structure means that the relationship between one move and the next can be characterized into one of three “transitions”: a “positive” transition or shift “up” to the move that would beat the previous move (+), a “negative” transition or shift “down” to the move that would lose to the previous move (−), and a “stay” transition which repeats the same move (0).
Given that no move is better than any other in a cyclic dominance game, how should one make strategic decisions in the rock, paper, scissors game? The zero-sum nature of the game ensures that for a single player, their opponent’s win is always their loss, so any degree to which a player’s decisions are predictable will allow their opponent to exploit them for a greater gain. Therefore, the best strategy for a rational player paired with an equally rational opponent is to choose moves so as to not create any exploitable patterns in their choices: to choose the three options randomly, with equal probability. Cyclic dominance games belong to the broader class of mixed strategy equilibrium (MSE) games (see [33] ch. 3 for review), with a single Nash Equilibrium (NE) [27] that requires a mixed strategy of playing each move (e.g., “rock”, “paper”, and “scissors”) in equal proportion, with no conditional dependence from one game to the next. Indeed, the appeal of studying decision making in RPS and other similar games has been in large part due to the fact that they impose such strong, testable constraints on optimal play; constraints that human behavior often fails to exhibit.
2.2. Human Behavior Exhibits Sequential Patterns
Some of the earliest research in mixed strategy equilibrium games like RPS puzzled over whether people could in fact meet the high standards of random play under the Nash Equilibrium strategy [34,35,36]; for an overview of significant early results, see [33] ch. 3. A large body of work has shown that in the rock, paper, scissors game and other MSE games, people exhibit a range of sequential regularities or dependencies in their move choices that run counter to equilibrium play. A full review of these results is beyond the scope of the current paper, but here we offer a sample, surveying evidence for sequential dependencies in order of increasing behavioral complexity [28].
A first pass analysis of people’s behavior in the rock, paper, scissors game often looks at whether their overall distribution of move choices is consistent with the mixed strategy equilibrium proportions of 1/3 for each move. In repeated rounds of RPS, a number of studies have found people to have a slight overall bias towards “rock”, though this is not always significant [37,38,39,40,41]. Further, other results have observed a modest preference for “paper” or “scissors” [42] and in many cases people show no distinguishable preference at all [43,44,45,46]. In the broader space of MSE games, it is noted in [33] that marginal choice probabilities tend to align with equilibrium proportions.
Though marginal move distributions are often approximately consistent with equilibrium random selection, a key feature of the Nash Equilibrium strategy is that players not display any conditional dependence on their own or their opponents’ previous moves. Thus, a player that continually cycles from “rock” to “paper” to “scissors” will produce an overall distribution of moves that appears identical to the mixed strategy equilibrium but the statistical dependence on their own previous move will be highly exploitable by a perceptive opponent. Following prior work [28], we will refer to a transition from one move to the move that beats it (e.g., “rock” to “paper”) as shifting up (denoted with a + in tables and figures); a transition from one move to the same move (e.g., “rock” to “rock”) as staying (denoted with a 0 in tables and figures), and a transition from one move to the move that loses to it (e.g., “rock” to “scissors”) as shifting down (denoted with a − in tables and figures). See Figure 1b for a complete illustration of the transitions between moves.
Evidence of transition dependencies in people’s moves is not widespread, but [40] find a slight overall preference for staying compared to shifting up or down which diminishes with the relative value of wins over ties, suggesting that stronger reward incentives may improve people’s tendency to approximate equilibrium play. Indeed, related work has argued for a relationship between transition dependencies in competitive settings and limitations in executive control; it was found in [47] that people with schizophrenia had a strong dependence on their opponent’s previous move, tending to select moves that would beat what their opponent had just played (this is often referred to as a Cournot Best Response strategy [48]). Finally, evidence is presented in [39] for a stickiness of transition dependencies, namely that participants who shifted up in a previous transition were more likely to continue shifting up and participants who shifted down in a previous transition were more likely to shift down again (no such persistence was found for staying).
The best documented higher-order move dependencies in the rock, paper, scissors game are transitions conditioned on prior outcome. This is exemplified by win-stay, lose-shift (WSLS) behavior. In the context of the rock, paper, scissors game, such a strategy amounts to changing the rates of particular transitions (+, −, 0) depending on whether the preceding game outcome was a win, loss, or tie. The appeal of WSLS as a possible explanatory mechanism for people’s decisions in games like RPS comes from its prominence in other settings where it can be seen as a computationally simple heuristic that enables broadly adaptive behavior [49,50]. A number of studies have found evidence of outcome-dependent transition behavior in the rock, paper, scissors game [40,41,51,52,53]. Subsequent work has further explored the separability of win-stay and lose-shift behaviors [38], as well as the factors mediating their respective magnitudes [37,39,54].
Finally, it was found in [55] that in many rounds of paired human dyad play, people exhibit a range of additional dependencies, with more complex dependencies being more pronounced. Taken together, these results have broad agreement that people’s move choices exhibit unique sequential dependencies which violate NE. This raises an important question: given the failure to implement equilibrium strategies in mixed strategy games like RPS, what accounts for people’s behavior, particularly the various sequential dependencies in their move choices?
2.3. Existing Accounts of Empirical Behavior Are Insufficient
The most prominent account of why human behavior in the rock, paper, scissors game and other MSE games displays such sequential dependencies focuses on people’s misapprehensions about what it means to be random in the first place. A large body of work on subjective randomness has revealed that people often have poor intuitions about what constitutes a random sequence [56,57]. Concretely, when prompted to evaluate or produce a sequence of simulated coin flips (or simulate any other random variable) people tend to favor sequences that (i) have an equal number of heads and tails, (ii) under-represent “runs” (e.g., HHH) and (iii) over-represent alternations (HTH) [58,59]. In a series of studies exploring these biases in adversarial settings, Rapoport and Budescu propose a model in which randomness is a matter of “local representativeness” across a limited memory of prior events [30,60,61]. Essentially, their model suggests that behavior in mixed strategy equilibrium games like the rock, paper, scissors game represents people doing their best to produce random outcomes. With only a limited memory for prior events, participants will make choices that exemplify the features of subjective randomness exhibited in prior literature.
While there is ample evidence that our judgments of random events depart systematically from true randomness, this is unlikely to explain human behavior in repeated rounds of the rock, paper, scissors game. Empirical support for behaviors that show a conditional dependence on opponent choices and prior outcomes suggests that people are doing something more complicated than merely attending to the (subjective) randomness of their own move choices (see [62] for discussion of complex opponent-responsive properties). What then can explain people’s behavior, particularly the sequential patterns they exhibit, in repeated MSE games?
Another common explanation is that people may be using stable heuristics that produce winning, or at least adequate, outcomes in the long run. For instance, win-stay, lose-shift (WSLS) is a “fast and frugal” decision rule [49] that can be applied in a variety of adversarial settings; indeed, WSLS outperforms the well-known “tit-for-tat” strategy in evolutionary Prisoner’s Dilemma simulations [63]. This finding fits within a broad literature on the evolution of cooperation examining the strength of various heuristic-based strategies across many interactions, though such findings typically describe population dynamics rather than individual behavior [6,64,65,66]. Nonetheless, fixed heuristics like WSLS might drive people’s choices in repeated adversarial interactions and may explain behavioral regularities in the rock, paper, scissors game [29,39,40]. The authors of [54] propose a variation of a stable heuristic like win-stay, lose-shift, suggesting that it is not one heuristic, but a result of two independent heuristic processes that separately react to reward and loss. Consistent with this, participants respond more quickly to losses than wins [54] and exhibit fairly distinct EEG signatures when responding to different game outcomes [37,54]. Further, it appears that win-stay behavior may not arise as consistently as lose-shift [37,39] and may be more vulnerable to fluctuations in game rewards [38]. Whether win-stay and lose-shift reflect a single mechanism or not, this class of accounts suggests that human behavior in the rock, paper, scissors game is best explained by a conjunction of stable heuristics.
While win-stay, lose-shift and other heuristic strategies may offer people a simple decision process, they are also insufficient to explain human behavior in repeated rounds of the rock, paper, scissors game. For one, dependencies in people’s move choices extend beyond such heuristics to a variety of other complex sequential regularities which cannot be as easily accounted for [55]. Second, an emphasis on heuristics as a basis of people’s decision making in repeated RPS interactions fails to address the ways in which people exhibit more dynamic, adaptive behavior, such as exploiting biases in their opponent’s choices [44,46,62].
Recent Results Suggest People Are Trying to Outwit Their Opponents
A complete account of human behavior in repeated MSE games like the rock, paper, scissors game should accommodate the adaptive character of people’s decision making over many interactions. Consider, for example, playing repeated rounds with an opponent that simply plays “rock” over and over. Here, subjective randomness or win-stay, lose-shift responding would be surprising. Though trivial, this illustrates a critical underlying dynamic in repeated MSE games: Optimal play depends on the predictability of the opponent. Heuristics or subjectively random behavior may be adaptive against an unexploitable opponent, and may serve as a useful fallback when one is losing, but they are not the best policy when facing a fallible opponent. In large-scale algorithmic RPS tournaments, random strategies often under-perform precisely because they fail to detect stable dependencies in their opponent’s moves that could be exploited [7,8].1
Despite its intuitive appeal, the role of adaptive, adversarial reasoning in repeated RPS interactions has been largely overlooked in the prior literature. Most empirical studies of rock, paper, scissors behavior pair participants either against automated opponents employing a random strategy [37,38,39,43,44,46,54,67], or against a shuffled group of human opponents [32,40,41,51,52]. In both cases, participants cannot adapt to the dependencies of their opponent. Random computer choices are simply unexploitable, while random assignment of opponents ensures that sequential choices are independent and identically distributed, and thus equally unexploitable through more sophisticated adversarial reasoning. Thus, these results cannot address whether decision making over repeated interactions, including the sequential regularities observed in prior empirical work, may result from an effort to outwit one’s opponent.
What happens when people play against opponents that are exploitable, such as stable human adversaries? A handful of recent studies asking this question yield behavior consistent with flexible, adaptive reasoning, rather than simple heuristics or subjective randomness. First, in repeated interactions with opponents that exhibit a strong bias towards certain moves, people often show an above-chance capacity to exploit the opponent [44,46] consistent with basic reinforcement learning mechanisms [68]. Notably, this adaptability appears to be limited to very strong opponent biases, even over many trials [69,70,71]. However, efforts to outwit a stable opponent extend beyond reinforcement learning and draw on more structured pattern recognition abilities when opponent behavior is more nuanced. The authors of [43] find that people adapt to bots that exhibit a Cournot Best Response transition strategy, but their ability to do so is limited by prior exposure to an opponent with a simple move bias, suggesting a strong role of context in adversarial reasoning. The authors of [62] provide a relatively thorough investigation of people’s ability to adapt to neural network opponents with a memory for various numbers of previous moves, showing that people are reliably able to beat a lag1 opponent whose moves are primarily based on the previous move, but behave more similarly to a lag2 opponent that draws on the two previous rounds. However, recent work has found that people can detect even more complex transition and outcome-dependent transition strategies over many rounds [37,54,72]. Finally, results in [73] indicate that when paired with opponents that exploit regularities in participants’ own move choices, people are able to counteract such exploitation for simpler behavioral dependencies. Taken together, these results suggest that over many RPS interactions with a stable opponent, people are highly attuned to the structured dependencies which make players themselves and their opponents exploitable.
In sum, recent results suggest that people’s behavior over many rounds against a potentially exploitable opponent can be explained by the desire to outwit that opponent, rather than merely attempting to respond randomly or relying on stable heuristics. But how flexible is this ability, and what are its limitations? What sorts of hypotheses about behavioral structure can people entertain and track on the basis of an opponent’s sequential decisions? Addressing these questions requires characterizing the space of uniquely identifiable strategies that may be exploited, and estimating whether people attend to these regularities when playing repeated rounds of RPS. The rest of this paper focuses on these technical challenges.
3. RPS Behavior Reveals Structure of Adversarial Reasoning
Human behavior during repeated interactions in mixed strategy games like the rock, paper, scissors game may be explained by ongoing attempts to outwit one’s opponent. However, it remains an open question how people are able to adapt to regularities in an opponent’s behavior. What kind of dependency structures can people detect and respond to? Prior work has examined the ways that different sequential patterns in RPS can be categorized [28]. Building on these results, we begin by providing an overview of how the complex dependencies observed in people’s move decisions are structured and show how people’s exploitability along these dimensions can be quantified. We then demonstrate how such measures can be used to explore which behavioral regularities people successfully exploit against a stable opponent. We apply these methods to experimental data from prior work by [55] to explore how well different sequential regularities predict people’s move decisions and the degree to which they successfully exploit regularities in an opponent’s behavior. In this way, we show that behavior in the rock, paper, scissors game offers novel insights into how people perform adaptive, adversarial reasoning.
3.1. Sequential Dependencies in RPS Can Be Systematically Described
3.1.1. Individual Dependencies
The level at which people are able to outwit their opponents (i.e., the scope of their adversarial reasoning abilities) is reflected in the structure and complexity of the sequential dependencies they can detect and exploit, and how much they do so over many rounds. How can we define this structure, and how do we then assess whether these dependencies are exploited by a savvy player? In the rock, paper, scissors game, the space of exploitable dependencies can be described in increasing order of complexity based on the number of prior events that impact a player’s move choices [28,55]. In other words, sequential dependencies in a player’s RPS moves are expressible in terms of how the probability of a particular decision—either a move selection or a transition between moves—is statistically impacted by some form of previous event: the player’s own previous move, their opponent’s previous move, etc. If a player or bot is behaving randomly, the probability of any decision will be equal no matter what previous event is considered; every move or transition is just as likely given every previous move or outcome. However, to the degree that a player’s behavior is exploitable, they will exhibit non-uniform move or transition probabilities conditioned on a particular event, such as their previous move. The greater the departure from a uniform distribution conditioned on the prior event, the more exploitable a player is, i.e., the more they exhibit this dependency. Broadly, the more prior events required to evaluate the dependency, the more complex it is. Questions about a person’s adversarial reasoning abilities in RPS therefore come down to measuring whether and how much they can recognize these dependencies in their opponent.
To illustrate, the tables in Figure 2 show how outcome-based transition dependencies like win-stay, lose-shift can be represented. Here, each state of a dependency event like previous outcome is given a unique row on the left side of the table. The dependencies in Figure 2 have a row for each possible outcome from the previous round—win (W), tie (T), and loss (L)—but a simpler dependency based on, e.g., one’s own previous move might instead have a row for “rock”, “paper”, and “scissors”. Each column indicates a possible decision based on that row-wise dependency event. In Figure 2, these decisions are move transitions: shift up (+), stay (0), or shift down (−). Once again, a simple dependency in which move choices are based on one’s own previous move could be expressed with possible move decisions (“rock”, “paper”, “scissors”) in each column instead of transitions. Each cell in the tables in Figure 2 then represents the probability that the player chooses the action in the cell’s column following the dependency event in the corresponding row. If players did not exhibit any dependency on a row-wise outcome, the probabilities in each cell in that row would be 1/3, signaling that each transition (column value) is equally likely given that row value. However, the more a player exhibits a particular dependency, the greater the disparity between their transition probabilities given each possible outcome. This encoding of patterned behavior therefore allows us to express each unique class of dependencies that a player could exploit in their opponent through the choice of different row-wise events and column-wise actions. The ability to express RPS dependencies in this way is not limited to outcomes affecting transition choices, as in Figure 2, but applies at every level of behavioral complexity. This structure for expressing classes of sequential patterns therefore provides a formal mechanism for outlining the hypothesis space of behavioral regularities people exhibit and can adapt to. In the next section, we discuss this space, in particular, the relationship between different dependencies.
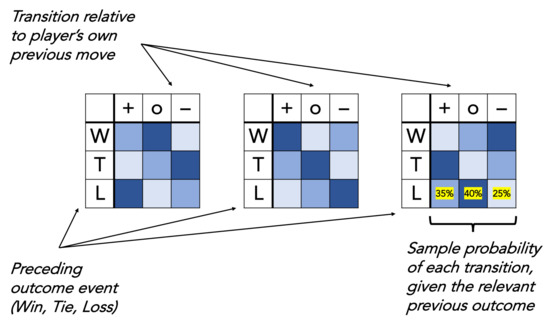
Figure 2.
Sample schematic for illustrating dependencies exhibited during rock, paper, scissors play. Above are three distinct versions of an outcome-dependent transition dependency like win-stay, lose-shift. Shaded squares indicate gradations in the probability of a given transition (column) given each prior event (row).
3.1.2. Combining Dependencies
Critically, the various classes of sequential dependencies that a player can exhibit in her move choices are not independent, but rather are arranged in an expressive hierarchy. Dependencies exhibited at one level will affect other levels that rely on the same information. For example, a player’s distribution over moves given her previous move subsumes her marginal distributions over transitions and moves—any pattern in her overall move or transition distributions will be reflected in the distribution of moves given her previous move. Why is this important when describing people’s adaptive behavior? If a player exhibits a tendency toward a particular move following each previous move, this will in part reflect any lower-level biases in their moves and transitions. Describing their behavior as following a strategy of gravitating toward particular moves after each previous move must factor in the degree to which they are simply favoring some moves or transitions. Similarly, if a player is able to exploit an opponent seemingly on the basis of regularities in the opponent’s moves following each previous move, we want to know that they are not primarily sensitive to simpler dependencies in the opponent’s transition or move base rates. Broadly, the dependency signal for a given dependency structure will include the dependency signal from its lower-level subsidiaries.
The schematic in Figure 3 shows the inheritance relationship among increasingly complex sequential move and transition dependencies. As the dependencies become more complex, they inherit from a greater number of simpler regularities. While this does not show the full space of possible regularities (such a space is technically infinite), we include any behavioral dependencies that have been observed in prior work (i.e., all of those discussed in our review of existing literature) or in previous attempts to frame these structures [28,73]. For researchers attempting to quantify how much people are exploitable or are successfully exploiting opponents on the basis of these dependencies, this structure poses a credit assignment problem: how to identify when a dependency is being exploited above and beyond the lower-level dependencies it is based on? The key to attributing behavior at the right level of complexity is to use this hierarchical dependency structure when evaluating the regularities in people’s move choices. In other words, to untangle the unique contribution of a higher-order dependency structure from the exploitability arising from its subsidiaries, we partial out the subsidiary dependencies based on the relationships in Figure 3. This allows us to ask how much each dependency contributes to explaining individual behavior. As we show below, this logic can be applied not only to estimating a given player’s level of exploitability within a given structure, but also to estimating how much this dependence is exploited by their opponent.
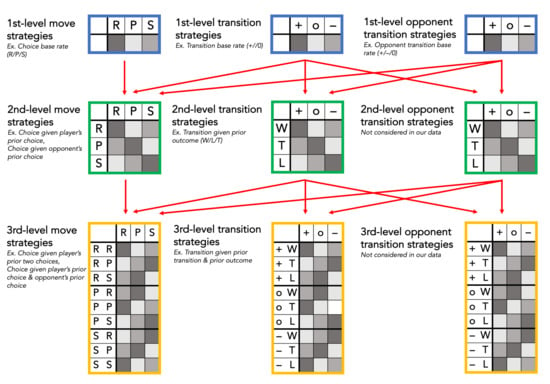
Figure 3.
Schematic for quantifying complexity of dependencies exhibited during rock, paper, scissors play. On the left are three levels of increasing complexity for regularities in players’ move choices. In the middle and right columns are equivalent complexity levels for dependencies players exhibit in their transitions between moves, either relative to their own previous move, or relative to the opponent’s. The arrows illustrate the hierarchical relationship across these regularities, indicating for example how second-level move dependencies carry some of the dependency signal captured by first-level move and transition dependencies.
3.2. Quantifying How Much People Exhibit and Exploit Sequential Dependencies
In the previous section, we showed that the exploitable dependencies people exhibit over repeated rounds of the rock, paper, scissors game can be described in terms of how events like previous moves or outcomes impact the probability of subsequent move decisions. We further showed that the relationship among different dependencies of this sort prevents us from treating them independently without correcting for the shared structure across dependencies. How then can we quantify how much a player exhibits a given dependency and, relatedly, how much their opponent is able to exploit it?
3.2.1. Measuring Exploitability with Information Gain
We measure how predictable a player’s behavior is subject to a particular dependency via conditional entropy and information gain. In the rock, paper, scissors game, the player has three choices, . This action space A can either represent the move choices (“rock”, “paper”, and “scissors”), or the transitions (+, −, 0) relative to the player’s previous move or relative to the opponent’s previous move (the set of transitions encodes additional information about either the player or their opponent’s previous move but is otherwise the same). A player’s propensity to make some choices more than others in a given context c (i.e., how exploitable they are in this context), can be summarized as the probability distribution . The Shannon entropy [74] of the distribution over those choices describes how unpredictable they are:
and will take on a value, in bits, between 0—for completely deterministic behavior, where one of the three actions is always chosen in a given context—and for uniform behavior where all three actions are equally likely.
In the base case, where the context, c is an empty set, this definition is sufficient, and reduces to entropy over actions . However, for all non-trivial contexts, we calculate the Shannon entropy for each possible state in the context and average over them. For instance, a strategy such as “win-stay, lose-shift” describes a distribution over self-transitions that varies with context defined as the outcome of the preceding round. Our entropy calculation must factor in the full partition over contexts that a dependency structure imposes. In the case of win-stay, lose-shift, the relevant dependency structure defined by the context partition is: . The unpredictability of choices given a context partition is therefore given by the conditional entropy marginalized over the contexts in that dependency structure:
To characterize how much behavioral regularity may be captured via a particular dependency structure defined by the partition over contexts (), we ask how much information is gained about actions by taking that dependency structure into account. Specifically, we can subtract the conditional entropy under that dependency structure from a uniform distribution over choices, to calculate the information gained by using that dependency structure to predict a player’s moves or transitions:
Intuitively, this measure quantifies the improvement gained by predicting a player’s moves or transitions using a particular dependency relative to a random baseline. Large information gain for a given dependency structure suggests that a player is highly exploitable via that dependency. Low values suggest that their behavior is not easily distinguished from random choices given the prior events in .
While information gain provides an intuitive measure for how much a player exhibits a particular dependency, it fails to reflect the hierarchical structure of dependencies described previously. In other words, the information gain associated with a given dependency structure will not capture just the information unique to that structure. For instance, if a player shows a bias toward choosing “rock”, that predictable dependency will also show up in the information gain over each move conditioned on the previous move. To uniquely identify the information gained for a particular dependency structure, we must consider the hierarchical structure of different dependencies shown in Figure 3.
Given the hierarchical relationship among dependency structures in Figure 3, we can define an operation which yields all the upstream nodes (parents, grandparents, etc.) of a given dependency structure. For instance, the dependency structure capturing the tendency to choose “rock”, “paper”, or “scissors” given one’s previous choice has two parents: an overall move bias to choose “rock”/“paper”/“scissors”, and a preference for particular self-transitions (+/−/0). Using this, we can calculate a corrected information gain for a particular dependency structure by subtracting the information gained from the parent dependency structures:
This calculation yields a measure of the information about actions that can be uniquely captured in a given dependency structure. The ability to attribute sequential patterns in behavior to a particular dependency structure is critical for understanding the cognitive processes underlying adversarial reasoning in the rock, paper, scissors game. Prior work has shown that certain patterns of outcome-based transition behavior (i.e., win-stay, lose-shift) are isomorphic to much simpler patterns of Cournot best responding when a player’s self-transitions are re-cast as transitions relative to their opponent’s previous move [28]. Because of this isomorphism, conclusions about whether a savvy player is exploiting complex outcome-based patterns in their opponent, or is simply sensitive to the pattern of Cournot transition responses may be ambiguous. Here, by correcting the information gain for a given dependency structure to reflect all upstream parents, we can identify the extent to which people exhibit dependencies of a certain complexity, without being misled by the possibility of a complex dependency being mimicked by a simpler one. More broadly, this provides a means of quantifying how much players exhibit rich and complex patterns in their move choices over many rounds. Answering this allows us to then address questions at the heart of adversarial reasoning in the rock, paper, scissors game: which behavioral patterns do people exploit in their opponents? Generally, what is the relationship between how much people exhibit a particular behavioral regularity and how much their opponents are able to exploit it?
3.2.2. Measuring How Much Players Are Exploited with Expected Win Count Differentials
To understand the relationship between a player’s exploitable behavior patterns and whether their opponent in fact uses these patterns to their advantage, we extend the information gain measure described previously to reflect the outcomes that might be expected by fully exploiting a given dependency in a player’s moves. Intuitively, the level at which a player’s decisions over repeated rounds are exploitable can be thought of as the number of games their opponent could expect to win by taking advantage of the patterns their choices exhibit. We refer to this as the expected win count differential for a given dependency structure. The win count differential is simply the number of games that one player wins over the course of many rounds minus the number of games won by their opponent. A positive win count differential for one player indicates that they were able to win more often than their opponent and higher win count differentials indicate more successful exploitation of the opponent. The expected win count differential, then, captures how much advantage a player could theoretically obtain by choosing moves which maximally exploit a particular dependency in their opponent’s moves. Given a non-uniform (exploitable) distribution over an opponent’s actions , a player’s expected win count differential for a given action is equal to , where is the outcome of playing a particular move against the opponent’s move : increasing the player’s win count by 1, decreasing by 1, or tying for a change of 0. Given this, the player has an optimal action that maximizes their expected win count differential over all possible opponent moves:
This optimal choice in turn yields an expected win-count differential of: . And averaging over all contexts (for example, the set of all previous moves by the player), this yields:
The expected win count differential for a given dependency context captures how exploitable a player is along that dimension, much like the information gain measure described previously. In fact, the difference between the expected win count differential and the information gain for a particular dependency structure is often small, since lots of information in a given dependency will translate directly into expected win count differentials. However, not all low-entropy distributions are equally exploitable. For instance, a player that chooses their moves with the distribution 60% “rock”, 30% “paper”, and 10% “scissors” can be exploited to achieve an average win count differential (per round) of 0.5 by playing “paper”. Meanwhile, a move distribution of 60% “rock”, 10% “paper”, and 30% “scissors” only yields an expected win count differential of 0.3 (by playing “scissors”; playing “paper” yields an expected win count differential of only 0.2). These two distributions have the same entropy and information gain, but one is nearly twice as exploitable as the other, in terms of the achievable win count differential. Thus, expected win count differential tells us not just how much information is available at a given dependency structure, but how exploitable such information is.
As a measure of how exploitable a player’s behavior is, expected win count differential also enables us to investigate the relationship between how much a player’s opponent could theoretically exploit patterns in their behavior, and how much their opponent actually did so. This is because expected win count differentials can be directly compared to observed win count differentials in dyads, indicating whether regularity at a particular dependency structure might explain the observed pattern of advantage seen in a pair of players. Given a set of many repeated RPS games between pairs of stable opponents, we can use each player’s level of exploitability for a given dependency—their expected win count differential—as predictors in a regression over the true win count differentials in each dyad. This provides a first approximation of how much of the variance in empirical win count differentials can be explained by the different ways that players exhibit exploitable behavior across many dyads.
However, this approach faces the same fundamental challenge as the uncorrected information gain measure described earlier; expected win count differentials for different behavioral regularities will be influenced by the rich interdepencence of these regularities shown in Figure 3. Thus, predicting empirical win count differentials using raw expected win count differentials fails to accommodate the role of lower-level dependencies in higher-level expected win count differentials. In this context, to correct expected win count differentials for upstream dependencies, we cannot simply subtract them, as we can for information gain. Instead, we correct for the hierarchy in Figure 3 within the observed win count differential regression itself. To illustrate, when predicting observed win count differentials across experimental dyads, we only use the simplest dependencies in Figure 3 as direct predictors. To partial out the role of these lower-level dependencies in more complex dependencies, we include the residuals from separate regressions of expected win count differentials for each higher-level dependency predicted by expected win count differentials for the dependencies they inherit from. For example, a player’s level of exploitability using second-level move strategies in Figure 3, such as their choice given their prior choice, can be predicted based on their exploitability using first-level move strategies (base rate of “rock”, “paper”, and “scissors”) and first-level transition strategies (base rate of +, −, and 0 transitions). The residuals from this prediction using expected win count differentials indicate how much of the variance in a given second-level move strategy cannot be accounted for by the first-level strategies. These residuals can then serve as predictors for the second-level variables in the original regression of observed dyad win count differentials. In this manner, we can isolate the unique dependency arising at a certain level of behavior, rather than attributing lower-level dependencies to the more abstract, higher-order structure.
To summarize, we have argued that behavior in repeated rounds of the rock, paper, scissors game provides a window into how people perform the sort of adaptive, adversarial reasoning that allows them to outwit a stable opponent. We first showed that a player’s exploitable behavior—patterns that their opponent might use to their advantage—contains structure illustrated in their conditional move or transition probabilities subject to various contingencies like their previous move. We further showed how these regularities are hierarchically arranged. Given this, we next showed how a player’s exploitability, i.e., the degree to which they exhibit a given dependency structure, can be quantified using measures of information gain and expected win count differential. The former indicates exactly how much signal is contained in a player’s patterned behavior, and the latter incorporates the way this signal can be exploited. Finally, we showed how the level of exploitability that a player exhibits can be used to investigate which sources of exploitability contribute to the observed pattern of players exploiting their opponents, thus providing clues about the underlying nature of people’s adversarial reasoning in this setting. In the next section, we show how these measures can be applied to empirical data to explore the flexibility and limitations of people’s ability to outwit an opponent.
4. Adversarial Reasoning in RPS Relies on Detecting Simple Regularities
In the previous section, we showed how sequential regularities in people’s move decisions in the rock, paper, scissors game can be formally described and quantified. This might serve as the basis for a more precise characterization of the dependencies people exhibit in their own behavior in adversarial settings, as well as the patterns they can detect and exploit in opponents. In other words, this framework offers a unified view of the decision-making biases shown in the rock, paper, scissors game move choices [39,40,47,55], and the complexities of modeling opponent behavior in the same setting [43,54,62,72,73].
Here, we show how the measures from the previous section can be applied to empirical data from a set of rock, paper, scissors dyads. In [55] 116 participants were paired into stable dyads and data were collected for 300 rounds of the rock, paper, scissors game in each dyad. Because participants in this experiment were playing with the same opponent for 300 consecutive rounds, players had ample time to try and learn sequential patterns in their opponent’s moves. Indeed, the authors find that the distribution of empirical win count differentials across the 58 dyads is overall significantly larger than would be expected under random play, suggesting that players found ways to outwit their opponents. How did some participants perform the adaptive, adversarial reasoning necessary to gain a steady advantage over their opponents? Here, we attempt to answer this question using the measures outlined in the previous section. We first examine the average information gain for a range of sequential dependencies proposed in [55] to quantify how much participants exhibited exploitable patterns. Next, we explore the relationship between observed win count differentials and expected win count differentials to assess which patterns best explain participants’ ability to outwit their opponents.
4.1. People Exhibit Complex Behavioral Dependencies
The data from [55] suggest that across 300 rounds, people exhibit stable predictable behaviors that might form the basis of exploitation by their opponents. Here, we ask how predictable their behavior was for a range of sequential regularities. In particular, we ask how the Shannon entropy over RPS choices for a given player is reduced when conditioning on some prior dependency. As outlined above, the reduction in entropy compared to chance behavior represents the information gain from taking each dependency structure into account. Figure 4 shows average information gain across participants for eight different dependency structures that increase in complexity from left to right. We plot the “uncorrected” information gain values for each dependency alongside the “corrected” information gain to account for the hierarchical structure of these dependencies as described previously. Larger information gain (in bits) indicates a greater level of predictability for that particular dependency. The uncorrected values show a steady increase in information gain as the complexity of the dependency increases on x, suggesting greater and greater predictability for more complex sequential patterns. However, the corrected values suggest that some of this increase can be attributed to higher-level patterns carrying signal from lower-level ones. Nonetheless, the complex dependencies at the right retain some signal even after correction, providing evidence that people’s move choices are exploitable using a range of sequential patterns that vary in their complexity.
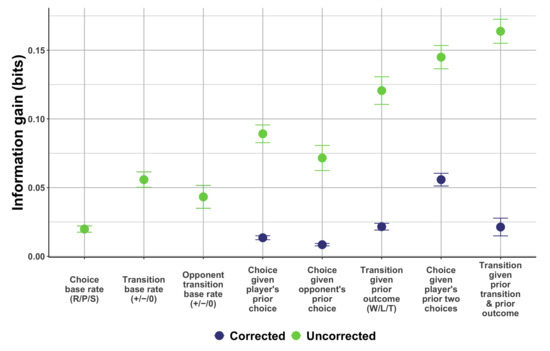
Figure 4.
Change in average information gain (bits) as a result of incorporating the hierarchical structure in Figure 3. The information gain reflects how exploitable individuals were for each of the dependencies shown. For more complex dependencies, individual exploitability decreases when corrected for simpler low-level dependencies. Error bars show one SEM.
4.2. Players Exploit Simple Behavioral Dependencies in Their Opponents
Across repeated rounds of the rock, paper, scissors game with a stable opponent, Ref. [55] show that some players are able to reliably outwit their opponents. But among dyads that exhibit higher win count differentials, what kinds of regularities in one player’s move choices form the basis of this exploitation by their opponent? In other words, which dependencies do people successfully exploit?
As described in the previous section, we can begin to address this question by exploring the relationship between the observed win count differentials in each dyad and the average expected win count differentials in each dyad for each of the sequential dependencies that players may have relied on to exploit their opponent. Critically, we correct for the hierarchical relationship among dependencies using the residuals from separate regressions for complex dependencies where some of the predictability may derive from simpler underlying dependencies. Using the dyad results from [55] as the basis for this regression, we find that expected win count differential based on transition dependencies (the transition base rate (+/−/0)) and opponent previous move dependencies (player’s choice given opponent’s prior choice) are both significant predictors of empirical win count differentials in each dyad (transition: = 0.19, p = 0.027; opponent previous choice: = 0.45, p = 0.015). In other words, the degree to which players exploit their opponents over 300 rounds is best explained by simple biases that players in the dyad exhibit toward particular transitions, as well as regularities in player moves given their opponent’s previous move.
But what might the regression look like if we did not correct for the hierarchical structure of the dependencies? Figure 5 plots the correlation between expected win count differentials—how much players in each dyad exhibited each dependency—and true win count differentials, i.e., how much players in each dyad exploited their opponents overall. Critically, we first plot these correlations using the expected win count differentials for each dependency (“uncorrected” correlations), and then substitute them for the the residuals as described in the previous section (the “corrected” correlations). Figure 5 illustrates the importance of this correction; revised correlations are broadly lower across the board, but especially for the most complex dependencies on the right. Therefore, incorporating the hierarchical structure of the dependencies into the correlation shows that people’s use of complex regularities when exploiting their opponent may in fact draw heavily on simpler, low-level behavioral patterns.
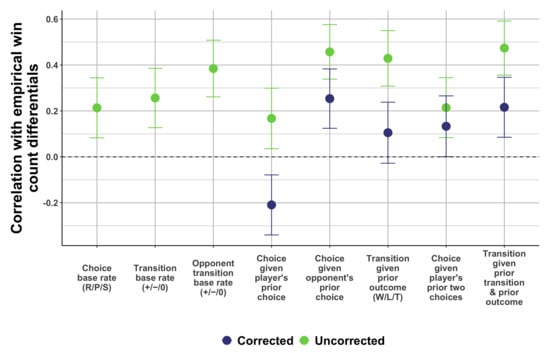
Figure 5.
Change in the relationship between expected win count differential for each behavioral dependency and empirical win count differentials as a result of incorporating the hierarchical structure in Figure 3. For more complex dependencies, the role they play in exploitation among dyads decreases when we factor in the role of lower-level dependencies. Error bars show one SEM.
5. Discussion
Here, we argued that games like rock, paper, scissors offer a precise and tractable way to study adaptive adversarial reasoning. We started with the observation that human play in simple cyclic-dominance games, such as matching pennies or rock, paper, scissors, systematically deviates from the mixed strategy Nash Equilibrium of purely random play. In particular, people exhibit a range of sequential regularities in their move choices that are most consistent with an intuitive but understudied account: people are constantly trying to outwit their opponents, and behavioral dependencies arise from such adaptive reasoning.
How can we make sense of the behavioral regularities that emerge as a result of adaptive reasoning in the rock, paper, scissors game? Building on prior work exploring the cognitive and computational resources required to identify such dependencies [28], we outline a schema for formally describing the ways that rock, paper, scissors behavior can reflect stable patterned regularities. We show that the predictability and subsequent exploitability of a given dependency can be precisely quantified using measures of conditional entropy and expected win count differentials. Prior work in this space raised important concerns about the identifiability of complex dependency structures in a player’s behavior due to isomorphisms between different patterns in behavior which make distinctly different cognitive demands of an adaptive opponent [28]. To overcome this challenge, we introduce analytical techniques that can correct for the hierarchical inheritance structure among different dependencies, and can thus identify both the extent to which people exhibit, and exploit, complex behavioral patterns.
Finally, we validate our approach by applying the proposed measures of exploitability and adversarial reasoning to a large empirical dataset comprised of repeated rock, paper, scissors games between a set of stable dyads from [55]. Our results show that incorporating the hierarchical structure of sequential dependencies into analysis of human behavior allows for a clear description of how each dependency is reflected in individual decisions. Concretely, our results offer two key findings which highlight the value of repeated rock, paper, scissors interactions in understanding human adaptive reasoning capacities. First, we show that over many rounds against a stable opponent, people exhibit a range of exploitable dependencies, including some that reflect a high level of complexity. These however, are attenuated by the expression of simpler dependencies. Next, we show that despite the range of predictable behavior patterns in people’s decisions, their opponents largely fail to exploit these same dependencies. Instead, people rely on simple transition and previous move dependencies in order to outwit their opponents, an intuitive finding that our results provide concrete, quantitative support for.
The current results show that the rock, paper, scissors game can be fruitfully used to study the flexibility of human adversarial reasoning. In particular, we show how people’s behavior across repeated interactions reveals the limits of our capacity to detect and adapt to sequential behavior patterns. Critically, rock, paper, scissors presents just one avenue by which these and other similar questions can be addressed. Applying a similar approach to other mixed strategy equilibrium games, or even a broader set of strategic interactions altogether, may reveal further insights about adversarial reasoning. In particular, one interpretation of the current results is that the failure to exploit more complex dependencies arises from limits in memory. Prior work has considered the impact of memory length on strategic behavior in a range of domains including RPS [50,62]; the current results may open the door to a more precise account of such resource limits in adversarial reasoning.
Together, our results show how the simple rock, paper, scissors game can support a quantitative perspective on the rich adaptive reasoning and opponent modeling that underlies human competition. What kinds of complex, patterned behavior can people detect and adapt to in strategic settings, and how does dyadic behavior reflect exploitation of these patterns across repeated interactions? We hope that our framework for constructing and analyzing dependencies in the rock, paper, scissors game allows researchers to better characterize human adaptive adversarial capacities.
Author Contributions
Conceptualization, E.B. and E.V.; methodology, E.B. and E.V.; software, E.B.; validation, E.B.; formal analysis, E.B. and E.V.; investigation, E.B.; resources, E.V.; data curation, E.B.; writing—original draft preparation, E.B.; writing—review and editing, E.V.; visualization, E.B.; supervision, E.V.; project administration, E.B. and E.V.; funding acquisition, E.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partly supported by UCSD Research Award #A139946 awarded to Edward Vul.
Institutional Review Board Statement
The study was conducted according to the guidelines of the Declaration of Helsinki, and approved by the Institutional Review Board of University of California, San Diego (protocol number 101191, April 2019).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data presented in this study are openly available in github at https://github.com/erik-brockbank/rps-games-analysis.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Note
| 1 | Successful algorithmic strategies in a recent Kaggle RPS tournament highlight this dynamic: https://www.kaggle.com/c/rock-paper-scissors (accessed on 13 July 2021). |
References
- Schelling, T.C. The Strategy of Conflict; Harvard University Press: Cambridge, MA, USA; London, UK, 1980. [Google Scholar]
- Schelling, T.C. The strategy of conflict. Prospectus for a reorientation of game theory. J. Confl. Resolut. 1958, 2, 203–264. [Google Scholar] [CrossRef]
- Liptak, A. Lawyers Won’t End Squabble, So Judge Turns to Child’s Play. New York Times, 9 June 2006. [Google Scholar]
- Vogel, C. Rock, Paper, Payoff: Child’s Play Wins Auction House an Art Sale. The New York Times, 29 April 2005. [Google Scholar]
- Hegan, K. Hand to Hand Combat. Rolling Stone, 7 January 2004; p. 38. [Google Scholar]
- Axelrod, R. The Evolution of Cooperation; Basic Books: New York, NY, USA, 1984. [Google Scholar]
- Billings, D. Thoughts on roshambo. ICGA J. 2000, 23, 3–8. [Google Scholar] [CrossRef]
- Billings, D. The first international RoShamBo programming competition. ICGA J. 2000, 23, 42–50. [Google Scholar] [CrossRef]
- Sinervo, B.; Lively, C.M. The rock–paper–scissors game and the evolution of alternative male strategies. Nature 1996, 380, 240–243. [Google Scholar] [CrossRef]
- Zhang, R.; Clark, A.G.; Fiumera, A.C. Natural genetic variation in male reproductive genes contributes to nontransitivity of sperm competitive ability in Drosophila melanogaster. Mol. Ecol. 2013, 22, 1400–1415. [Google Scholar] [CrossRef] [PubMed]
- Kerr, B.; Riley, M.A.; Feldman, M.W.; Bohannan, B.J. Local dispersal promotes biodiversity in a real-life game of rock–paper–scissors. Nature 2002, 418, 171–174. [Google Scholar] [CrossRef] [PubMed]
- Kirkup, B.C.; Riley, M.A. Antibiotic-mediated antagonism leads to a bacterial game of rock–paper–scissors in vivo. Nature 2004, 428, 412–414. [Google Scholar] [CrossRef] [PubMed]
- Claussen, J.C.; Traulsen, A. Cyclic dominance and biodiversity in well-mixed populations. Phys. Rev. Lett. 2008, 100, 058104. [Google Scholar] [CrossRef]
- Allesina, S.; Levine, J.M. A competitive network theory of species diversity. Proc. Natl. Acad. Sci. USA 2011, 108, 5638–5642. [Google Scholar] [CrossRef]
- Toupo, D.F.; Strogatz, S.H. Nonlinear dynamics of the rock-paper-scissors game with mutations. Phys. Rev. E 2015, 91, 052907. [Google Scholar] [CrossRef]
- Yang, Q.; Rogers, T.; Dawes, J.H. Demographic noise slows down cycles of dominance. J. Theor. Biol. 2017, 432, 157–168. [Google Scholar] [CrossRef]
- da Silva, L.G.; Castro, S.B. Cyclic dominance in a two-person rock–scissors–paper game. Int. J. Game Theory 2020, 49, 885–912. [Google Scholar] [CrossRef]
- Hu, W.; Zhang, G.; Tian, H.; Wang, Z. Chaotic Dynamics in Asymmetric Rock-Paper-Scissors Games. IEEE Access 2019, 7, 175614–175621. [Google Scholar] [CrossRef]
- Szolnoki, A.; Mobilia, M.; Jiang, L.L.; Szczesny, B.; Rucklidge, A.M.; Perc, M. Cyclic dominance in evolutionary games: A review. J. R. Soc. Interface 2014, 11, 20140735. [Google Scholar] [CrossRef]
- Lakhar, R. The dynamic instability of dispersed price equilibria. J. Econ. Theory 2011, 146, 1796–1827. [Google Scholar]
- Cason, T.N.; Friedman, D.; Wagener, F. The dynamics of price dispersion, or Edgeworth variations. J. Econ. Dyn. Control. 2005, 29, 801–822. [Google Scholar] [CrossRef]
- Hopkins, E.; Seymour, R.M. The stability of price dispersion under seller and consumer learning. Int. Econ. Rev. 2002, 43, 1157–1190. [Google Scholar] [CrossRef]
- Lach, S. Existence and persistence of price dispersion: An empirical analysis. Rev. Econ. Stat. 2002, 84, 433–444. [Google Scholar] [CrossRef]
- Noel, M.D. Edgeworth price cycles: Evidence from the Toronto retail gasoline market. J. Ind. Econ. 2007, 5, 69–92. [Google Scholar] [CrossRef]
- Hauert, C.; Monte, S.D.; Hofbauer, J.; Sigmund, K. Volunteering as red queen mechanism for cooperation in public goods games. Science 2002, 296, 1129–1132. [Google Scholar] [CrossRef] [PubMed]
- Semmann, D.; Krambeck, H.J.; Milinski, M. Volunteering leads to rock–paper–scissors dynamics in a public goods game. Nature 2003, 425, 390–393. [Google Scholar] [CrossRef]
- Nash, J.F. Equilibrium points in n-person games. Proc. Natl. Acad. Sci. USA 1950, 36, 48–49. [Google Scholar] [CrossRef]
- Dyson, B.J. Behavioural isomorphism, cognitive economy and recursive thought in non-transitive game strategy. Games 2019, 10, 32. [Google Scholar] [CrossRef]
- Zhou, H.J. The rock–paper–scissors game. Contemp. Phys. 2016, 57, 151–163. [Google Scholar] [CrossRef]
- Budescu, D.V.; Rapoport, A. Subjective randomization in one- and two-person games. J. Behav. Decis. Mak. 1994, 7, 261–278. [Google Scholar] [CrossRef]
- Morgenstern, O.; Neumann, J.V. Theory of Games and Economic Behavior; Princeton University Press: Princeton, NJ, USA, 1953. [Google Scholar]
- Frey, S.; Goldstone, R.L. Cyclic game dynamics driven by iterated reasoning. PLoS ONE 2013, 8, e56416. [Google Scholar] [CrossRef]
- Camerer, C.F. Behavioral Game Theory: Experiments in Strategic Interaction; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Kalisch, G.; Milnor, J.; Nash, J.; Nering, E. Some Experimental n-Person Games. In Decision Processes; Thrall, R.M., Coombs, C.H., Davis, R.L., Eds.; John Wiley & Sons, Inc.: New York, NY, USA, 1954; pp. 301–327. [Google Scholar]
- Brown, J.N.; Rosenthal, R.W. Testing the minimax hypothesis: A re-examination of O’Neill’s game experiment. Econom. J. Econom. Soc. 1990, 58, 1065–1081. [Google Scholar] [CrossRef]
- O’Neill, B. Nonmetric test of the minimax theory of two-person zerosum games. Proc. Natl. Acad. Sci. USA 1987, 84, 2106–2109. [Google Scholar] [CrossRef]
- Dyson, B.J.; Steward, B.A.; Meneghetti, T.; Forder, L. Behavioural and neural limits in competitive decision making: The roles of outcome, opponency and observation. Biol. Psychol. 2020, 149, 107778. [Google Scholar] [CrossRef]
- Forder, L.; Dyson, B.J. Behavioural and neural modulation of win-stay but not lose-shift strategies as a function of outcome value in Rock, Paper, Scissors. Sci. Rep. (Nat. Publ. Group) 2016, 6, 33809. [Google Scholar] [CrossRef]
- Dyson, B.J.; Wilbiks, J.M.P.; Sandhu, R.; Papanicolaou, G.; Lintag, J. Negative outcomes evoke cyclic irrational decisions in Rock, Paper, Scissors. Sci. Rep. (Nat. Publ. Group) 2016, 6, 20479. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Xu, B.; Zhou, H.J. Social cycling and conditional responses in the Rock-Paper-Scissors game. Sci. Rep. 2014, 4, 5830. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.; Zhou, H.J.; Wang, Z. Cycle frequency in standard rock–paper–scissors games: Evidence from experimental economics. Phys. A Stat. Mech. Its Appl. 2013, 392, 4997–5005. [Google Scholar] [CrossRef][Green Version]
- Aczel, B.; Bago, B.; Foldes, A. Is there evidence for automatic imitation in a strategic context? Proc. R. Soc. Biol. Sci. USA 2012, 279, 3231–3233. [Google Scholar] [CrossRef]
- Stöttinger, E.; Filipowicz, A.; Danckert, J.; Anderson, B. The effects of prior learned strategies on updating an opponent’s strategy in the rock, paper, scissors game. Cogn. Sci. 2014, 38, 1482–1492. [Google Scholar] [CrossRef] [PubMed]
- Lie, C.; Baxter, J.; Alsop, B. The effect of opponent type on human performance in a three-alternative choice task. Behav. Process. 2013, 99, 87–94. [Google Scholar] [CrossRef]
- Cook, R.; Bird, G.; Lünser, G.; Huck, S.; Heyes, C. Automatic imitation in a strategic context: Players of rock–paper–scissors imitate opponents’ gestures. Proc. R. Soc. B Biol. Sci. 2012, 279, 780–786. [Google Scholar] [CrossRef]
- Kangas, B.D.; Berry, M.S.; Cassidy, R.N.; Dallery, J.; Vaidya, M.; Hackenberg, T.D. Concurrent performance in a three-alternative choice situation: Response allocation in a Rock/Paper/Scissors game. Behav. Process. 2009, 82, 164–172. [Google Scholar] [CrossRef]
- Baek, K.; Kim, Y.T.; Kim, M.; Choi, Y.; Lee, M.; Lee, K.; Hahn, S.; Jeong, J. Response randomization of one-and two-person Rock–Paper–Scissors games in individuals with schizophrenia. Psychiatry Res. 2013, 207, 158–163. [Google Scholar] [CrossRef] [PubMed]
- Cournot, A. Recherches sur les Principes Mathematiques de la Theorie des Richesses (Research into the Mathematical Principles of the Theory of Wealth); English Translation; Bacon, N., Translator; Hachette: Paris, France, 1838. [Google Scholar]
- Gigerenzer, G.; Goldstein, D.G. Reasoning the fast and frugal way: Models of bounded rationality. Psychol. Rev. 1996, 103, 650. [Google Scholar] [CrossRef] [PubMed]
- Posch, M. Win–stay, lose–shift strategies for repeated games—Memory length, aspiration levels and noise. J. Theor. Biol. 1999, 198, 183–195. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Xu, B. Incentive and stability in the Rock-Paper-Scissors game: An experimental investigation. arXiv 2014, arXiv:1407.1170. [Google Scholar]
- Hoffman, M.; Suetens, S.; Nowak, M.A.; Gneezy, U. An experimental test of Nash equilibrium versus evolutionary stability. In Proceedings of the Fourth World Congress of the Game Theory Society, Istanbul, Turkey, 22–26 July 2012; Volume 145. [Google Scholar]
- Cason, T.N.; Friedman, D.; Hopkins, E. Cycles and instability in a rock–paper–scissors population game: A continuous time experiment. Rev. Econ. Stud. 2014, 81, 112–136. [Google Scholar] [CrossRef]
- Dyson, B.J.; Sundvall, J.; Forder, L.; Douglas, S. Failure generates impulsivity only when outcomes cannot be controlled. J. Exp. Psychol. Hum. Percept. Perform. 2018, 44, 1483. [Google Scholar] [CrossRef]
- Brockbank, E.; Vul, E. Recursive Adversarial Reasoning in the Rock, Paper, Scissors Game. In Proceedings of the 42nd Annual Conference of the Cognitive Science Society, Toronto, ON, Canada, 29 July–1 August 2020; pp. 1015–1021. [Google Scholar]
- Lopes, L.L. Doing the impossible: A note on induction and the experience of randomness. J. Exp. Psychol. Learn. Mem. Cogn. 1982, 8, 626. [Google Scholar] [CrossRef]
- Bar-Hillel, M.; Wagenaar, W.A. The perception of randomness. Adv. Appl. Math. 1991, 12, 428–454. [Google Scholar] [CrossRef]
- Tversky, A.; Kahneman, D. Belief in the law of small numbers. Psychol. Bull. 1971, 76, 105. [Google Scholar] [CrossRef]
- Lopes, L.L.; Oden, G.C. Distinguishing between random and nonrandom events. J. Exp. Psychol. Learn. Mem. Cogn. 1987, 13, 392. [Google Scholar] [CrossRef]
- Rapoport, A.; Budescu, D.V. Generation of random series in two-person strictly competitive games. J. Exp. Psychol. Gen. 1992, 121, 352. [Google Scholar] [CrossRef]
- Rapoport, A.; Budescu, D.V. Randomization in individual choice behavior. Psychol. Rev. 1997, 104, 603–617. [Google Scholar] [CrossRef]
- West, R.L.; Lebiere, C. Simple games as dynamic, coupled systems: Randomness and other emergent properties. Cogn. Syst. Res. 2001, 1, 221–239. [Google Scholar] [CrossRef]
- Nowak, M.; Sigmund, K. A strategy of win-stay, lose-shift that outperforms tit-for-tat in the Prisoner’s Dilemma game. Nature 1993, 364, 56–58. [Google Scholar] [CrossRef]
- Nowak, M.; Sigmund, K. The evolution of stochastic strategies in the prisoner’s dilemma. Acta Appl. Math. 1990, 20, 247–265. [Google Scholar] [CrossRef]
- Nowak, M.A.; Sigmund, K. Tit for tat in heterogeneous populations. Nature 1992, 355, 250–253. [Google Scholar] [CrossRef]
- Nowak, M.A.; Sigmund, K. Evolutionary dynamics of biological games. Science 2004, 303, 793–799. [Google Scholar] [CrossRef] [PubMed]
- Gallagher, H.L.; Jack, A.I.; Roepstorff, A.; Frith, C.D. Imaging the intentional stance in a competitive game. Neuroimage 2002, 16, 814–821. [Google Scholar] [CrossRef] [PubMed]
- Sepahvand, N.M.; Stöttinger, E.; Danckert, J.; Anderson, B. Sequential decisions: A computational comparison of observational and reinforcement accounts. PLoS ONE 2014, 9, e94308. [Google Scholar]
- Danckert, J.; Stöttinger, E.; Quehl, N.; Anderson, B. Right hemisphere brain damage impairs strategy updating. Cereb. Cortex 2012, 22, 2745–2760. [Google Scholar] [CrossRef] [PubMed]
- Stöttinger, E.; Filipowicz, A.; Marandi, E.; Quehl, N.; Danckert, J.; Anderson, B. Statistical and perceptual updating: Correlated impairments in right brain injury. Exp. Brain Res. 2014, 232, 1971–1987. [Google Scholar] [CrossRef] [PubMed]
- Filipowicz, A.; Anderson, B.; Danckert, J. Adapting to change: The role of the right hemisphere in mental model building and updating. Can. J. Exp. Psychol./Revue Canadienne de Psychologie Expérimentale 2016, 70, 201. [Google Scholar] [CrossRef]
- Brockbank, E.; Vul, E. Rock, Paper, Scissors Reveals Limits of a “Behaviorist” Theory of Mind. In prep.
- Brockbank, E.; Vul, E. Humans fail to outwit adaptive rock, paper, scissors opponents. In Proceedings of the 43nd Annual Conference of the Cognitive Science Society, Vienna, Austria, 26–29 July 2021. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).