Abstract
We consider a demand management problem in an energy community, in which several users obtain energy from an external organization such as an energy company and pay for the energy according to pre-specified prices that consist of a time-dependent price per unit of energy as well as a separate price for peak demand. Since users’ utilities are their private information, which they may not be willing to share, a mediator, known as the planner, is introduced to help optimize the overall satisfaction of the community (total utility minus total payments) by mechanism design. A mechanism consists of a message space, a tax/subsidy, and an allocation function for each user. Each user reports a message chosen from her own message space, then receives some amount of energy determined by the allocation function, and pays the tax specified by the tax function. A desirable mechanism induces a game, the Nash equilibria (NE), of which results in an allocation that coincides with the optimal allocation for the community. As a starting point, we design a mechanism for the energy community with desirable properties such as full implementation, strong budget balance and individual rationality for both users and the planner. We then modify this baseline mechanism for communities where message exchanges are allowed only within neighborhoods, and consequently, the tax/subsidy and allocation functions of each user are only determined by the messages from their neighbors. All of the desirable properties of the baseline mechanism are preserved in the distributed mechanism. Finally, we present a learning algorithm for the baseline mechanism, based on projected gradient descent, that is guaranteed to converge to the NE of the induced game.
1. Introduction
Resource allocation is an essential task in networked systems such as communication networks, energy/power networks, etc. [1,2,3]. In such systems, there is usually one or multiple kinds of limited and divisible resources allocated among several agents. When full information regarding agents’ interests is available, solving the optimal resource allocation problem reduces to a standard optimization problem. However, in many interesting scenarios, strategic agents may choose to conceal or misreport their interests in order to obtain more resources. In such cases, it is possible that appropriate incentives are designed so that selfish agents are incentivized to truly report their private information, thus enabling optimal resource allocation [4].
In existing works related to resource allocation problems, mechanism design [5,6] is frequently used to address the agents’ strategic behavior mentioned above. In the framework of mechanism design, the participants reach an agreement regarding how they exchange messages, how they share the resources, and how much they pay (or get paid). Such agreements are designed to incentivize the agents to provide the information needed to solve the optimization problem.
Contemporary energy systems have witnessed an explosion of emerging techniques, such as smart meters and advanced metering infrastructure (AMI) in the last decade. These smart devices and systems facilitate the transmission of users’ data via communication networks and enable dynamic pricing and demand response programs [7], making it possible to implement mechanism design techniques on energy communities for improved efficiency. In this paper, we develop mechanisms to solve a demand management problem in energy communities. In an energy community, users obtain energy from an energy company and pay for it. The pre-specified prices dictated by the energy company consist of a time-dependent price per unit of energy as well as a separate price for peak demand. Users’ demand is subject to constraints related to equipment capacity and minimum comfort level. Each user possesses a utility as a function of their own demand. Utilities are private information for users. The welfare of the community is the sum of utilities minus energy cost. If users were willing to truthfully report their utilities, one could easily optimize energy allocations to maximize social welfare. However, since users are strategic and might not be willing to report utilities directly, to maximize the welfare, we need to find an appropriate mechanism that incentivizes them to reveal some information about their utilities, so that optimal allocation is reached even in the presence of strategic behaviors. These mechanisms are usually required to possess several interesting properties, among which are full implementation in Nash equilibria (NE), individual rationality, and budget balance [6,8,9]. Moreover, in environments with communication constraints, it is desirable to have “distributed” mechanisms, whereby energy allocation and tax/subsidies for each user can be evaluated using only local messages in the user’s neighborhood. Finally, for actual deployment of practical mechanisms, we hope that the designed mechanism has convergence properties that guarantee that NE is reached by the agents by means of a provably convergent learning algorithm.
1.1. Contributions
This paper proposes a method of designing a mechanism for implementing the optimal allocation of the demand management problem in an energy community, where there are strategic users communicating over a pre-specified message exchange network. The main contributions of our work are as follows:
- (a)
- We design a baseline, “centralized” mechanism for an environment with concave utilities and convex constraints. A “centralized” mechanism allows for messages from all users to be communicated to the planner [6,8,9]. To avoid excessive communication cost brought about by direct mechanisms (due to messages being entire utility functions), the mechanisms proposed in this paper are indirect, non-VCG type [10,11,12], with messages being real vectors with finite (and small) dimensionality. Unlike related previous works [13,14,15,16], a simple form of allocation function is adopted, namely, allocation equals demand. The mechanism possesses the properties of full implementation, budget balance, and individual rationality [6,8,9]. Although we develop the mechanism for demand management in energy communities, the underlying ideas can be easily adapted to other problems and more general environments. Specifically, environments with non-monotonic utilities, external fixed unit prices, and the requirement of peak shaving are tractable with the proposed mechanism.
- (b)
- Inspired by the vast literature on distributed non-strategic optimization [17,18,19,20,21], as well as our recent work on distributed mechanism design (DMD) [22,23], we modify the baseline mechanism and design a “distributed” version of it. A distributed mechanism can be deployed in environments with communication constraints, where users’ messages cannot be communicated to the central planner; consequently the allocation and tax/subsidy functions for each user should only depend on messages from direct neighbors. The focus of our methodology is to show how a centralized mechanism can be modified into a decentralized one in a systematic way by means of introducing extra message components that act as proxies of the messages not available to a user due to communication constraints. An added benefit of this systematic design is that the new mechanism preserves all of the desirable properties of the centralized mechanism.
- (c)
- Since mechanism design (centralized or distributed) deals with equilibrium properties, one relevant question is how equilibrium is reached when agents enter the mechanism. Our final contribution in this paper is to provide “learning” algorithms [24,25,26,27,28] that address this question for both cases of the proposed centralized and decentralized mechanisms. The algorithm is based on the projected gradient descent method in optimization theory ([29] Chapter 7). Learning proceeds through price adjustments and demand announcements according to the prices. During this process, users do not need to reveal their entire utility functions. Convergence of the message profile toward one NE is conclusively proven, and since the mechanism is designed to fully implement the optimal allocation in NE, this implies that the allocation corresponding to the limiting message profile is the social welfare maximizing solution.
1.2. Related Literature
The model for demand management in energy communities investigated in this paper originates from network utility maximization (NUM) problems, which is one typical category of resource allocation problems in networks (see [30], Chapter 2, for a detailed approach to models and algorithms for solving NUM problems). There are two distinct research directions that have emanated from the standard centralized formulations of optimization problems.
The first direction addresses the problem of communication constraints when solving an optimization problem in a centralized fashion. Taking into account these communication constraints, several researchers have proposed distributed optimization methods [17,18,19,20,21] whereby an optimization problem is solved by means of message-passing algorithms between neighbors in a communication network. The works have been further refined to account for possible users’ privacy concerns during the optimization processes [31,32,33,34]. Nevertheless, the users are assumed to be non-strategic in this line of works.
The second research direction, namely mechanism design, addresses the presence of strategic agents in optimization problems in a direct way. The past several decades have witnessed applications of this approach in various areas of interest, such as market allocations [14,35,36], spectrum sharing [37,38,39], data security [40,41,42], smart grid [43,44,45], etc. The well-known VCG mechanism [10,11,12] has been utilized extensively in this line of research. In VCG, users have to communicate utilities (i.e., entire functions), which leads to a high cost of information transmission. To ease the burden of communication, Kelly’s mechanism [13] (and extensions to multiple divisible resources [46]) has been proposed as a solution, which uses logarithmic functions as surrogates of utilities. The users need to only report a real number and thus the communication cost reduces dramatically, at the expense of efficiency loss [47] and/or the assumption of price-taking agents. A number of works extend Kelly’s idea to reduce message dimensionality in strategic settings [48,49,50]. Other indirect mechanisms guaranteeing full implementation in environments with allocative constraints have been proposed in [51,52] using penalty functions to incentivize feasibility and in [13,14,15] using proportional allocation or its generalization, radial allocation [16,53]. All aforementioned works on mechanism design can be categorized as “centralized” mechanisms, which means that agents’ messages are broadcasted to a central planner who evaluates allocation and taxation for all users.
The first contribution of this paper (contribution (a)) relates to the existing research detailed above in the following way. Instead of adopting the classic VCG framework as in [10,11,12], the proposed centralized mechanism is indirect with finite message dimensionality. In line with previous works [14,15,16,53], our centralized mechanism guarantees full implementation in contrast to some other indirect mechanisms (e.g., Kelly’s mechanism [13,46,47]). Additionally, compared to the works in [13,14,15,16,53], the form of allocation functions in our centralized mechanism is simpler, while at the same time, it enables the use of the mechanism in more general environments (e.g., environments allowing negative demands, non-monotonic utilities, extra prices, etc.).
The first attempts in designing decentralized mechanisms were reported in [22,23], where mechanisms are designed with the additional property that the allocation and tax functions for each agent depend only on the messages emitted by neighboring agents. As such, allocation and taxation can be evaluated locally.
Similar to the works in [22,23], the centralized mechanism in our work can be modified into a decentralized version (contribution (b)). Unlike the previous two works, however, the distributed mechanism in this paper has a straightforward form for the allocation function, making the proofs much less involved. In addition and partially due to this simplification, these decentralized mechanisms can be applied to a broader range of environments.
Recently, there has also been a line of research designing mechanisms over networks. The works of [54,55] present mechanisms for applications such as prize allocation and peer ranking, where agents are aware of their neighbors’ private characteristic (e.g., suitability, ability, or need). We caution the reader not to confuse the networks in the context of [54,55] with the message exchange networks introduced in our work in the context of contribution (b). Indeed, the networks in the two works listed above reveal how much of the private information of other agents is available to each agent, but it does not put restrictions on allocation/tax functions. On the other hand, the message exchange networks in our work treat utilities as each agent’s strictly private information and puts restrictions on the form of allocation/tax functions.
Finally, learning in games is motivated by the fact that NE is, theoretically, a complete information solution concept. However, since users do not know each-others’ utilities, they cannot evaluate the designed NE offline. Instead, there is a need for a process (learning), during which the NE is learnt by the community. The classic works [24,25,26] adopted fictitious play, while in [27], a connection between supermodularity and convergence of learning dynamics within an adaptive dynamics class was made and was further specialized in [56] to the Lindahl allocation problem. A general class of learning dynamics named adaptive best response was discussed in [57] in connection with contractive games. Learning in monotone games [28,58] was investigated in [59,60,61,62,63,64], with further applications in network optimization [65,66]. Recently, learning NE by utilizing reinforcement learning has been reported in [67,68,69,70,71].
In the last contribution of this paper (contribution (c)), we develop a learning algorithm for the proposed mechanisms. Most of the learning algorithms mentioned above require a strong property for induced games. For example, the learning algorithm of [27] requires supermodularity and the adaptive best response class of dynamics in [57] only applies to contractive games. Unfortunately, guaranteeing such strong properties limits the applicability of the mechanism. We overcome this difficulty with the proposed learning algorithm based on a PGD of the dual problem, thus guaranteeing convergence to NE with more general settings than the ones described in [27,57].
2. Model and Preliminaries
2.1. Demand Management in Energy Communities
Consider an energy community consisting of N users and a given time horizon T, where T can be viewed as the number of days during one billing period. Each user i in the user set has their own prediction of their usage across one billing period denoted by , where is the predicted usage of user i on the tth time slot of the billing period. Regarding notation, throughout the paper we use superscripts to denote users and constraints, and subscripts to denote time slots. Note that can be a negative number due to the potential possibility that users in the electrical grid can generate power through renewable technologies (e.g., photovoltaic) and can return the surplus back to the grid. The users are characterized by their utility functions as
The energy community, as a whole, pays for the energy. The unit prices are given separately for every time slot t, denoted by . These prices are considered given and fixed (e.g., by the local utility company). In addition, the local utility company imposes a unit peak price in order to incentivize load balancing and to lessen the burden of peaks in demand. To conclude, the cost of energy to the community is as follows:
where is a concatenation of demand vectors .
The centralized demand management problem for the energy community can be formulated as
The meaning of the feasible set is to incorporate possible lower bounds on each user’s demand (e.g., minimal indoor heating or AC) and/or upper bounds due to the capacities of the facilities as well as transmission line capacities.
In order to solve the optimization problem (2) using convex optimization methods, the following assumptions are made.
Assumption 1.
All of the utility functions s are twice differentiable and strictly concave.
Assumption 2.
The feasible set is a polytope formed by several linear inequality constraints, and is coordinate convex, i.e., if , then setting any of the components of to 0 does not let it fall outside of set .
By Assumption 2, can be written as for some and , where L is the number of linear constraints in , and
The coordinate convexity in Assumption 2 is mainly used for the outside option required by the individual rationality. Under this assumption, for a feasible allocation , if any user i changes their mind and chooses not to participate in the mechanism, the mechanism yields a feasible allocation with fixed.
With Assumptions 1 and 2, the energy community faces an optimization problem with a strictly concave and continuous objective function over a nonempty compact convex feasible set. Therefore, from convex optimization theory, the optimal solution for this problem always exists and should be unique [29].
Substituting the max function in (1) with a new variable w, the optimization problem in (2) can be equivalently restated as
The proof of this equivalency can be found in Appendix A. The new optimization problem has a differentiable concave objective function with a convex feasible set, which means that it is still a convex optimization, and therefore, KKT conditions are sufficient and necessary conditions for a solution to be the optimal solution, where are the Lagrange multipliers for each linear constraint in constraint and are the Lagrange multipliers for (3c). The KKT conditions are listed as follows:
- Primal Feasibility:
- Dual Feasibility:
- Complementary Slackness:
- Stationarity:where is the first order derivative of .
We conclude this section by pointing out once more that our objective is not to solve (3a)–(3c) or (4a)–(4g) in a centralized or decentralized fashion. Such a methodology is well established and falls under the research area of centralized or decentralized (non-strategic) optimization. Furthermore, such a task can be accomplished only under the assumption that users report their utilities (or related quantities, such as derivatives of utilities at specific points) truthfully, i.e., they do not act strategically. Instead, our objective is to design a mechanism (i.e., messages and incentives) so that strategic users are presented with a game, the NE of which is designed so that it corresponds to the optimal solution of (3a)–(3c) or (4a)–(4g).
2.2. Mechanism Design Preliminaries
In an energy community, utilities are users’ private information. Due to privacy and strategic concerns, users might not be willing to report their utilities. As a result, (3a)–(3c) or (4a)–(4g) cannot be solved directly. In order to solve (3a)–(3c) and (4a)–(4g) under the settings stated above, we introduce a planner as an intermediary between the community and the energy company. To incentivize users to provide necessary information for optimization, the planner signs a contract with users, which prespecifies the messages needed from users and rules for determining the allocation and taxes/subsidies from/to the users. The planner commits to the contract. Informally speaking, the design of such contract is referred to as mechanism design.
More formally, a mechanism is a collection of message sets and an outcome function [8]. Specifically, in resource allocation problems, a mechanism can be defined as a tuple , where is the space of message profile; is an allocation function determining the allocation according to the received message profile ; and is a tax function that defines the payments (or subsidies) of users based on m (specifically, with defining the tax/subsidy function for user i). Once defined, the mechanism induces a game . In this game, each user i chooses her message from the message space , with the objective to maximize her payoff . The planner charges taxes and pays for the energy cost to the company, so the planner’s payoff turns out to be (the net income of the planner).
For the mechanism-induced game , NE is an appropriate solution concept. At the equilibrium point , if coincides with the optimal allocation (i.e., the solution of (3a)–(3c)), we say that the mechanism implements the optimal allocation at . A mechanism has the property of full implementation if all of the NE s implement the optimal allocation.
There are other desirable properties in a mechanism. Individual rationality is the property that everyone volunteers to participate in the mechanism-induced game instead of quitting. For the planner, this means that the sum of taxes collected at NE is larger than the cost paid to the energy company . In the context of this paper, strong budget balance is the property that the sum of taxes is exactly the same as the cost paid to the energy company, so no additional funds are required by the planner or the community to run the mechanism other than the true energy cost paid to the energy company. In addition, if we use the solution concept of NE, one significant problem is how the users know the NE without full information. Therefore, some learning algorithm is needed to help users learn the NE. If under a specific class of learning algorithm, the message profile m converges to NE , then we say that the mechanism has learning guarantees with this certain class.
3. The Baseline “Centralized” Mechanism
In this section, we temporarily assume that there are no communication constraints, i.e., all of the message components are accessible for the calculations of the allocation and taxation. The mechanism designed under this assumption is called a “centralized” mechanism. In the next section, we extend this mechanism to an environment with communication constraints.
In the proposed centralized mechanism, we define user i’s message as
Each message component above has an intuitive meaning. Message can be regarded as the demand for time slot t announced by user i. Message is the additional price that user i expects to pay for constraint l, which corresponds to the Lagrange multiplier . Message is proportional to the peak price that user i expects to pay at time t. Intuitively, setting one greater than means that user i thinks day t is more likely to be the day with the peak demand rather than . This component corresponds to the Lagrange multiplier . Message is the prediction of user ’s usage at time t by user i. This message is included for technical reasons that will become clear in the following (for a user index , let and denote modulo N operations).
Denote the message space of user i by , and the space of the message profile is represented as . The allocation functions and the tax functions are functions defined on . The allocation functions follow the simple definition:
i.e., users obtains exactly what they request.
Prior to the definition of the tax functions, we want to find some variable that acts similar to at NE. Although is designed to be proportional to , it does not guarantee , which is the KKT condition (4f). To solve this problem, we utilize a technique similar to the proportional/radial allocation in [13,14,15,16,53] to shape the suggested peak price vector into a form that satisfies (4f). For a generic T-dimensional peak price vector and a generic T-dimensional total demand vector , define a radial pricing operator as
where
and represents the number of elements in that are equal to the maximum value.
The output of the radial pricing is taken as the peak price in the subsequent tax functions. When the given suggested price vector is a nonzero vector, the unit peak price is allocated to each day proportional to . If the suggested price vector , then divide to the days with peak demand with equal proportion.
The tax functions are defined as
where
and
and is defined as .
The tax function for user i consists of three parts. The first part is the cost for the demand. According to this part, user i pays a fixed price and the peak price for their demand. Note that the peak price at time t, , is generated by the vector of peak prices from all other agents, , and the total demand from all other agents (agent i’s demand at time t is approximated by ). As a result, the peak price is not controlled by user i at all. The second part ( stands for “proxy-”) is a penalty term for the imprecision of prediction that incentivizes to align with at NE. The third part consists of two penalty terms and for each constraint and each peak demand inequality , respectively. Both of them have a quadratic term that incentivizes consensus of the messages and among agents, respectively. In addition, they possess a form that looks similar to the complementary slackness conditions (4d) and (4e). This special design facilitates the suggested price to come to an agreement and ensures that the primal feasibility and complementary slackness hold at NE, which are shown in Lemma 2.
The main property we want from this mechanism is full implementation. We expect the allocation scheme under the NE of the mechanism-induced game to coincide with that of the original optimization problem. Full implementation can be shown in two steps. First, we show that, if there is a (pure strategy) NE, it must induce the optimal allocation. Then, we prove the existence of such (pure strategy) NE.
From the form of the tax functions, we can immediately obtain the following lemma.
Lemma 1.
At any NE, for each user i, the demand proxy is equal to the demand of their neighbor, i.e., for all t.
Proof.
Suppose that m is an NE, where there exists at least one user i whose message does not agree with the next user’s demand, i.e., . Say, for some t. Then, we can find a profitable deviation that keeps everything other than the same as m but modifies with . Compare the payoff value before and after the deviation:
Thus, if there is some , user i can always construct another announcement , such that user i gets a better payoff. □
It can be seen from Lemma 1 that the messages play an important role in the mechanism. They appear in two places in the tax functions: first, in the expression of which is the total demand at time t used in user i’s tax function, and second, in the expression for excess demand for the lth constraint. Note that we do not want user i to control these terms with their messages (specifically ) because they already control their allocation directly and this creates technical difficulties. Indeed, quoting the self-announced demand in the tax function raises the possibility of unexpected strategic moves for user i to obtain extra profit. Instead, using the proxy instead of eliminates user i’s control on their own slackness factor, while Lemma 1 guarantees that, at NE, these quantities become equal.
With the introduction of these proxies, we show in the following lemmas that, at NE, all KKT conditions required for the optimal solution are satisfied. First, we prove that primal feasibility (KKT 1) and complementary slackness (KKT 3) are ensured by the design of the penalty terms “pr”s and constraint-related terms “con”s, if we treat and as the Lagrange multipliers.
Lemma 2.
At any NE, users’ suggested prices are equal:
Furthermore, users’ announced demand profile satisfies , and equal prices, together with the demand profile, satisfy complementary slackness:
which implies
where z is the peak demand during the billing period.
Proof.
The proof can be found in Appendix B. □
Dual feasibility (KKT 2) holds trivially by definition. We now show that stationarity condition (KKT 4) holds at NE by imposing a first-order condition on the partial derivatives of user i’s utility w.r.t. their message component .
Lemma 3.
At NE, stationarity holds, i.e.,
Proof.
The proof is in Appendix C. □
With Lemmas 1–3, it is straightforward to derive the first part of our result, i.e., efficiency of the allocation at any NE.
Theorem 1.
Proof.
If is an NE, from Lemmas 1 and 2, we know that, at NE, and that all of the prices , , and all of the are the same among all users . We denote these equal quantities by and .
Consider the solution . From Lemma 2, the solution satisfies (4a)–(4e) (primal feasibility and complementary slackness). From Lemma 3, has (4g) and (4f) (stationarity). The dual feasibility (4c) holds because of the nonnegativity of and .
Therefore, satisfies all four KKT conditions, which means that the allocation is the optimal allocation. □
The following theorem shows the existence of NE.
Theorem 2.
For the mechanism-induced game , there exists at least one NE.
Proof.
From the theory of convex optimization, we know that the optimal solution of (3a)–(3c) exists. Based on this solution, one can construct a message profile that satisfies all of the properties we present in Lemmas 1–3 and prove that there is no unilateral deviation for all users. The details are presented in Appendix D. □
Full implementation indicates that, if all users are willing to participate in the mechanism, the equilibrium outcome is the optimal allocation. For each user i, the payoff at NE is
In other words, the users pay for their own demands via the aggregated unit prices given by the consensus at NE. By counting the planner as a participant of the mechanism with utility , a strong budget balance is automatically achieved. However, there are still two questions remaining. Are the users willing to follow this mechanism or would they rather not participate? Will the planner have to pay extra money for implementing such mechanism? The two theorems below answer these questions.
Theorem 3
(Individual Rationality for Users). Assume that agent i obtains and pays nothing if they choose not to participate in the mechanism. Then, at NE, participating in the mechanism is weakly better than not participating, i.e.,
Proof.
The main idea for the proof of Theorem 3 is to find a message profile with , in which user i’s payoff is , and then, we can argue that following NE is not worse since is a best response to . The details of the proof can be found in Appendix E. □
Theorem 4
(Individual Rationality for the Planner). At NE, the planner does not need to pay extra money for the mechanism:
Moreover, by slight modification of the tax functions defined in (7), the total payment of users and the energy cost achieve a balance at NE:
Proof.
The individual rationality of the planner can be verified by substituting in (14) directly. By redistributing the income of the planner back to the users in a certain way, the total payment of users is exactly , and consequently, no money is left after paying the energy company. The details are left to Appendix F. □
4. Distributed Mechanism
In the previous mechanism, allocation functions and tax functions of users depend on the global message profile m. If one wants to compute the tax for a certain user i, all messages for all are needed. Such mechanisms are not desirable for environments with communication constraints, where such a global message exchange is restricted. To tackle this problem, we provide a distributed mechanism, in which the calculation of the allocation and tax of a certain user depends only on the messages from the “available” users and therefore satisfies the communication constraints. In this section, we first introduce communication constraints using a message exchange network model. We then develop a distributed mechanism, which accommodates the communication constrains and preserves the desirable properties of the baseline centralized mechanism.
4.1. Message Exchange Network
In an environment with communication constraints, all of the users are organized in a undirected graph , where the set of nodes is the set of users and the set of edges indicates the accessibility to the message for each user. If , user i can access the message of user j, i.e., the message of j is available for user i when computing the allocation and tax of user i, and vice versa. Here, we state a mild requirement for the message exchange network:
Assumption 3.
The graph is a connected and undirected graph.
In fact, the mechanism we show works for the cases where is an undirected tree. Although an undirected connected graph is not necessarily a tree, since we can always find a spanning tree from such graph, it is safe to consider the mechanism under the assumption that the given network has a tree structure. If that is not the case, the mechanism designer can claim a spanning tree from the original message exchange network and design the mechanism only based on the tree instead of the whole graph (essentially some of the connections of the original graph are never used for message exchanges).
The basic idea behind the decentralized modification of the baseline mechanism is intuitively straightforward. Looking at the tax function for user i in the centralized mechanism, we observe that several messages required do not come from i’s immediate neighbors. For this reason, we define new “summary” messages that are quoted by i’s neighbors and represent the missing messages. At the same time, for this to work, we add additional penalty terms that guarantee that the summary messages indeed represent the needed terms at NE.
Notice that, in the previous mechanism, user i is expected to announce a equal to the demand of the next user . However, here, we might have , and owing to the communication constraint, we are not able to compare with . Instead, should be a proxy of the demand of user i’s direct neighbor. This motivates us to define the function , where ; is the set of user i’s neighbors (excluding i); and denotes that, in user i’s tax function, the proxy variable used for user i’s terms in their tax function is provided by user j. In other words, is a “helper” for user i who quotes a proxy of their demand whenever needed.
In the next part, we use the summaries of the demands to deal with the distributed issue. For the sake of convenience, we define as the nearest user to user k among the neighbors of user i and user i itself. is well-defined because of the tree structure. The proof is omitted here. The details can be found in ([72] Chapter 4, Section 7.1).
4.2. The Message Space
In the distributed mechanism, the message in user i’s message space is defined as
Here, is a summary for demands of users related to constraint l and connected to user i via j, as depicted in Figure 1. Message serves a similar role for the peak demand.
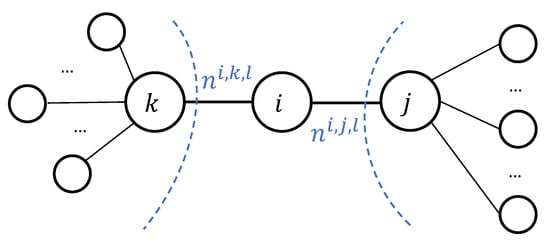
Figure 1.
Proxies in the Message Exchange Network: for constraint l, user i announces as a summary of demands for the tree on the left of i (starting from k) and as a summary of demands for the tree on the right of i (starting from j).
4.3. The Allocation and Tax Functions
The allocation functions are still straightforward. There are some modifications on tax functions, including adjustments on prices, consensus of new variables, and terms for complementary slackness.
where
and
In order to intuitively see how the decentralized mechanism works, take as an example the term in (18b), which is a modified version of (8c), repeated here for convenience related to the l-th constraint. Other than the quadratic term, which is identical in both expressions, the difference between the centralized and decentralized versions is in the expressions and , respectively. The second term in each of these expressions relates to the proxy , which in the decentralized version is substituted by the proxy due to the fact that the proxy for is not provided by user anymore but is provided by user i’s helper . The first term, , which cannot be directly evaluated in the decentralized version (since it depends on messages outside the neighborhood of i) is now evaluated as . It should now be clear that the role of the new messages quoted by the neighbors of i is to summarize the total demands of other users. Furthermore, the additional quadratic penalty terms has to effectuate this equality. This idea is made precise in the next section.
4.4. Properties
It is clear that this mechanism is distributed, since all of the messages needed for the allocation and tax functions of user i come from neighborhood and the user themselves. Due to way the messages and taxes are designed, the proposed mechanism satisfies properties similar to those in Lemmas 2 and 3, and, consequently, Theorems 1 and 2. The reason is that the components n and behave in the same manner as the absent in user i’s functions at NE, which makes the proofs of the properties in previous mechanism still work here. We elaborate on these properties in the following.
Lemma 4.
At any NE, we have the following results regarding the proxy messages:
Proof.
Now, based on the structure of the message exchange network, we have
Lemma 5.
At any NE, and satisfy
Proof.
The proof is presented in Appendix G. □
With Lemma 5, we immediately obtain the following results.
Lemma 6.
At any NE, for all user i, we have
Proof.
At NE, by directly substitution,
The third equality holds by the fact that the users in set are the ones that are not in the subtree starting from a single branch with root j, which is exactly .
Equation (26) holds for a similar reason. □
Lemma 6 plays a similar role to Lemma 1. With Lemma 6, the properties in Lemmas 2 and 3 can be reproduced in the distributed mechanism. We then obtain the following theorem.
Theorem 5.
For the mechanism-induced game , NE exists. Furthermore, any NE of game induces the optimal allocation.
Proof.
By substituting (25) and (26) in (17), we obtain exactly the same form of tax function in a centralized mechanism on equilibrium, which yields desirable results, as shown in Lemmas 2 and 3. We conclude that any NE induces the optimal allocation. The existence of NE can be proved by a construction similar to that of Theorem 2. □
As was true in the baseline centralized mechanism, in the distributed case, the planner may also have concerns about whether the users have an incentive to participate and whether the mechanism requires external sources of funds to maintain the balance. As it turns out, Theorems 3 and 4 still hold here. As a result, the users are better off joining the mechanism, and the market has a balanced budget. The proofs and the construction of the subsidies can be performed in a manner similar to the centralized case and therefore are omitted.
5. Learning Algorithm
5.1. A Learning Algorithm for the Centralized Mechanism
The property of full implementation ensures that social welfare maximization can be reached if all participants reach NE in the mechanism-induced game and no one obtains a unilateral profitable deviation at NE. Nevertheless, it is troublesome for participants to anticipate NE as being the outcome if none of them knows (or can calculate) NE without knowledge of other users’ utilities. To settle this issue, one can design a learning algorithm to help participants learn the NE in an online fashion. In this section, we present such a learning algorithm for the centralized mechanism discussed in Section 3. Instead of using Assumption 1, here, we make a stronger assumption in order to obtain a convergent algorithm.
Assumption 4.
All of the utility functions s are proper, twice differentiable concave functions with δ-strong concavity.
Here, -strong concavity of a function is defined by the -strong convexity of . A function is strongly convex with parameter if
The design of the learning algorithm involves three steps. First, we find the relation between NE and the optimal solution of the original optimization problem. This step was performed in the proof of Theorem 1: we see in NE that coincides with in the optimal allocation, that equals , and that the components of are proportional to the components of . Then, by Slater’s condition, strong duality holds here, so we connect the Lagrange multipliers with the optimal solution of the dual problem. Due to the strong concavity of the utilities and stationarity, given and , the optimal allocation can be uniquely determined. Finally, if we can find an algorithm to solve the dual problem, the design is completed.
The first two steps are straightforward. For the third one, we can see that the dual problem is also a convex optimization problem, so projected gradient descent (PGD) is one of the choices for the learning algorithm. The proof of convergence of PGD is not trivial. In the proof developed in [29], the convergence of PGD holds when (a) the objective function is -smooth and (b) the feasible set is closed and convex. In Appendix H, we show that (a) is satisfied by Assumption 4. To check (b), we need to find a feasible set for the dual variables. Since in PGD of the dual problem, the gradient of the dual function turns out to be a combination of functions of the form , the feasible set should satisfy two requirements: first, all of the elements are in the domain of the dual function’s gradient in order to make every iteration valid; second, is in the feasible set so that we do not miss it. With these requirements in mind, we make Assumption 5 and construct a feasible set for the dual problem based on that.
Assumption 5.
For each utility , there exist satisfying
- 1.
- , ,
- 2.
- , .
Before we explain this assumption, we define
- , ,
- , andwhere ⊗ represents the Kronecker product of matrices. Then, we define a set of proper prices as the feasible set for the dual problem:
Observe that, by stationarity, the th entry of equals in the optimal solution. Consequently, Assumption 5 implies two things: first, ; second, all can be a vector of s on some if . Hence, with Assumption 5, it is safe to narrow down the feasible set of the dual problem to without changing the optimal solution. Furthermore, for all of the price vectors in , in PGD can be evaluated. Back to condition (b) stated above, since is closed and convex, PGD is convergent in this case.
Based on all of the assumptions and the PGD method, we propose Algorithm 1 as a learning algorithm for the NE of the centralized mechanism.
The convergence of PGD yields the convergence of proposed learning algorithm:
Theorem 6.
Choose a step size , where is A’s spectral norm and is the parameter of strong concavity of the centralized objective function. As the number of iterations K grows, the distance between the computed price vector and the optimal price vector is non-increasing. Furthermore, , where is the NE.
Proof.
See Appendix H. □
| Algorithm 1: Learning algorithm for the centralized mechanism. |
 |
5.2. A Learning Algorithm for the Distributed Mechanism
Algorithm 1 cannot be applied in a distributed environment because lines 4 and 5 for the price adjustments require global user messages. Luckily, the price adjustment is the only part requiring messages from other users during an iteration. Based on this fact, the main modification of the algorithm is to figure out a way for users to obtain the aggregated demand of each constraint, which was indeed the same problem we needed to address when we modified the centralized mechanism to a distributed one. Naturally, we can utilize the proxies to help exchange the necessary messages, as we did in the design of the distributed mechanism. If the proxies and n behave the same way as described in Lemma 5, then we can modify line 4 and 5 in Algorithm 1 as follows and we can expect the same output as that of the original algorithm:
To make sure the proxies behave the same way as described in Lemma 5, some additional message exchanges are required in the beginning of each iteration before price adjustments. We design the maintenance algorithm for in Algorithms 2 and 3.
It is worth noting that a deadlock does not occur during the proxy maintenance and that the proxies after maintenance behave the way we expect in Lemma 5. The reason is that the distributed mechanism uses an acyclic subgraph of the network, so there are no loops. Notice that the proof of Lemma 5 (see Appendix G) uses an iterative process to justify the statement. Indeed, what happens during the maintenance process described here is exactly the same as the process depicted in the proof of Lemma 5. The termination signal is used to notify users when to proceed to the price adjustment step.
With the assistance of proxy maintenance Algorithms 2 and 3, we arrive at an extended version of the original learning algorithm for the distributed mechanism stated as Algorithm 4.
| Algorithm 2: Maintenance algorithm for proxy . |
 |
| Algorithm 3: Maintenance algorithm for proxy . |
 |
With the support of Lemma 5 and Theorem 6, this modified learning algorithm is also guaranteed to converge to NE in the distributed mechanism. Nevertheless, this algorithm is not as fast as the original one. We can observe that one user can do nothing but wait if any of the dependencies for their calculations is absent. As a result, this scheme has a mixed sequential and concurrent operation. To be more precise, the extra time for the modified algorithm is proportional to the length of the longest path of the chosen spanning tree in the network (one can derive this result following the procedures detailed in Lemma 5 by focusing on the steps for the transmission of the message from one side of the network to another side). Thus, the algorithm time complexity is impacted by the network structure.
| Algorithm 4: Learning algorithm for user i in the distributed mechanism. |
 |
6. A Concrete Example
To give a sense of how the two mechanisms and the learning algorithm work, we provide a simple non-trivial example here. We first present the original centralized problem for the example, and then identify the NE of the centralized mechanism based on the properties we found. For the distributed mechanism, we illustrate how the proxy variables at NE are determined with a simple example of a message exchange network. Lastly, we implement the learning algorithm for the centralized mechanism.
6.1. The Demand Management Optimization Problem
In the energy community, assume that there are three users in the user set and days in a billing period. Suppose user i on day t has the following utility function:
Set , , and the peak price . We adopt the following centralized problem as a concrete example:
where .
The exact solution to this problem is , , , and for , . for , . The interested readers can verify it by using KKT conditions. For the sake of convenience, we adopt the following approximate results:
The lower bound constraint for and the upper bound constraint for the sum are active. Thus, according to KKT conditions, for , , and by stationarity. The total demands of Day 1 and Day 2 are and , respectively, so Day 2 has the peak demand , Day 1 charges no peak price (), and Day 2 has an extra unit peak price .
6.2. The Centralized Mechanism
For this example, in the centralized mechanism, user i needs to choose their message with the following components:
For the sake of brevity, let us take user 1 for example. In this problem setting, user 1 needs to report their demands for two days (); suggest a set of prices for constraints 1–7 (), suggest unit peak prices for two days (quantities and do not necessarily sum up to ); and lastly, provide proxies and for user 2’s demands.
User 1’s tax function is
where
and according to the definition (6a) and (6b) of the radial pricing operator, we have
From Theorem 1, we know that, at NE, user 1’s message is such that corresponds to the optimal solution , equals the optimal Lagrange multiplier , equals , and finally is proportional to the Lagrange multiplier .
6.3. The Distributed Mechanism
In this subsection, we first demonstrate the modifications on message spaces compared with the centralized mechanism and then show how the newly introduced components n and work. The specific NE can be determined in a similar way to that of the centralized mechanism and is therefore omitted.
Assume that the energy community has communication constraints with the message exchange network depicted in Figure 2. Apart from the network topology, the -relation that indicates the responsibility of proxy is also an important part of distributed mechanism. Here, we set . Then, for proxy variables , in user 1’s tax is provided by user 2, in user 2’s tax is provided by user 1, and in user 3’s tax is provided by user 2.
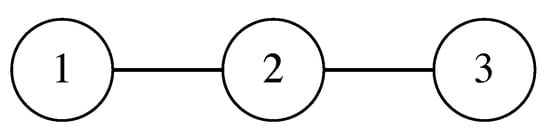
Figure 2.
Message exchange network: Users 1 and 2, and users 2 and 3 are neighbors. User 1’s message is invisible to user 3, and vice versa.
For this message exchange network, the message components for each user are
Therefore, in the distributed mechanism, users are still required to provide their demands , suggested unit prices , and suggested unit peak prices . Different from the centralized mechanism, there are no among user 3’s message components, while user 2 needs to provide two s, namely . In addition, for each constraint l, every user needs to announce variable n to each of their neighbors; for each day t, every user also needs to provide variable to each of their neighbors.
For the rest of this subsection, we focus on user 3 and consider how the n variables play their roles in the tax evaluation. With this message exchange network, we can write down user 3’s tax function explicitly:
where
and
In user 3’s tax function, there are no terms because user 3 is not assigned to any other users for providing proxies.
To figure out how the proxies n work, here, we focus on the seventh constraint, and see how the corresponding constraint term is evaluated in user 3’s tax function. The reason why other ns and s work is similar. For user 3, the constraint term is
In the centralized mechanism, the slackness part turns out to be at NE. What we want to show is that, with the distributed mechanism, the same outcome can be realized at NE. Similar to the centralized mechanism, at NE, so . By Lemma 4, , so it remains to show that .
Let us trace how the is generated at NE. From (21),
Notice that , so is empty. As a result, at NE, .
6.4. The Learning Algorithm
Before the algorithm is implemented, one might want to check whether the problem setting satisfies Assumptions 4 and 5.
First, we can check Assumption 5. Suppose for the specific environment that we have and . Then, for the first condition in Assumption 5, since each has a lower bound , we have
Additioanlly, every is upper bounded by 7 because, from the seventh constraint, we have
and thus
For the second condition in Assumption 5, for all , we have
so Assumption 5 is verified.
With the s and s chosen above, a dual feasible set is constructed. Within this price set , Algorithm 1 evaluates the function only in the interval . Consequently, in running Algorithm 1, we only need to define on the interval .
Regarding Assumption 4, we need to show that is strongly concave on . Since one can verify that the function is convex on for , every is strong concave, and thus, Assumption 4 holds (this is based on the fact that f is strongly convex with parameter iff is convex.).
To choose an appropriate step size for the algorithm, we need to investigate further the parameter . In our environment, the sum of utility functions is strongly concave on with parameter because each component of f is a strongly concave function with parameter and the parameter is additive: . By calculation, , so one possible step size can be . According to Algorithm 1, the updates required are (define for convenience):
To verify the convergence of the learning algorithm, we run it with the initial price set to . After iterations, we observe the convergence for both the suggested prices and the corresponding announced demands . Figure 3 shows the process of convergence and verifies that the convergence rate is exponential, as expected.
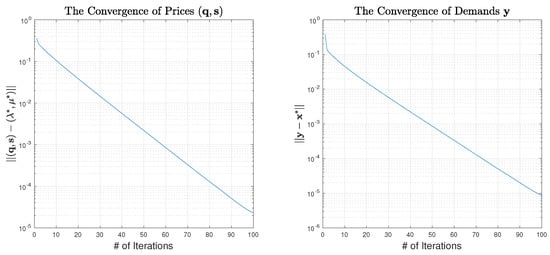
Figure 3.
The convergence of the learning algorithm.
7. Conclusions
Motivated by the work of mechanism design for NUM problems, we proposed a new class of (indirect) mechanisms, with application in demand management in energy communities. The proposed mechanisms possess desirable properties including full implementation, individual rationality, and budget balance and can be easily generalized to different environments with peak shaving and convex constraints. We showed how the original “centralized” mechanism can be modified in a systematic way to account for environments with communication constraints. This modification leads to a new type of mechanisms that we call “decentralized” mechanisms and can be thought of as the analog to decentralized optimization (developed for optimization problems with non-strategic agents) for environments with strategic users. Finally, motivated by the need for practical deployment of these mechanisms, we introduced a PGD-based learning algorithm for users to learn the NE of the mechanism-induced game.
Possible future research directions include seeking more efficient learning algorithms for the distributed mechanism as well as co-design of a (distributed) mechanism and characterization of the class of convergent algorithms for this design.
Author Contributions
X.W.—conceptualization, formal analysis, investigation, methodology, software, visualization, original draft, review and editing; A.A.—conceptualization, formal analysis, funding acquisition, investigation, methodology, project administration, resources, supervision, review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received funding from National Science Foundation.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Equivalence of Centralized Optimization Problem (2) and Original Problem (3a)–(3c)
We first prove this sufficiency by showing that we can always derive the optimal solution of (2) from the optimal solution of newly constructed (3a)–(3c). Suppose that the optimal solution of (3a)–(3c) is . We claim that is the optimal solution of the original problem (2). First, the feasibility of in (2) is ensured by (3b) in the newly constructed problem.
Now, we check the optimality. Suppose that is not the optimal for (2), and instead, is the optimal. In the new problem, construct
then it is easy to verify that is feasible for the new optimization. Notice that
The first inequality follows the optimality of in the original optimization (2); the second inequality comes from the constraint (3c) in the new optimization. By this inequality chain, we find a with a better objective function value in (3a)–(3c) than , which contradicts the assumption that is an optimal solution of (3a)–(3c).
Therefore, by contradiction, we shows that, if is optimal solution of (3a)–(3c), must be the optimal solution for the original optimization (2).
For the other direction, we need to show if is optimal solution of (2), then we are able to construct an optimal solution of (3a)–(3c) based on . We construct and and argue that this is the optimal for (3a)–(3c). Assume that is the optimal for (3a)–(3c); then, we still obtain the same inequality chain as (A1) (except that, for the second line, there should be a “greater than or equal” sign instead), and the equality and inequalities hold for the same reasons, as stated above. This shows that has the same objective value as the optimal solution of (3a)–(3c), and thereforem constructed from of the original problem is also the optimal for the new problem.
Appendix B. Proof of Lemma 2
Proof.
At NE , for the constraint l in , consider the message components for each user i. In user i’s tax function, denote the part relative to by . We have
by Lemma 1.
For any user i, there is no unilateral profitable deviation on . Hence, if we fix and all of the message components of except , it is a necessary condition that user i cannot find a better response than .
Consider the best response of in different cases of .
Case 1., i.e., the constraint l is inactive at NE. Note that is a quadratic function of of the following form
Without considering the nonnegative restriction, the best choice should be . Since , the best choice for would be (here, ), which is unique with fixed .
Therefore,
Observe that . Equality holds only if and . Thus, for all i, , equality holds only if and . In other words, if for one user i we have , then all of the .
Notice that implies that is smaller than one of the among user , which means that is not the largest. Assume that for all i; then, no can be the largest among , but we also know that is a finite set, and therefore, it must have a maximum. Here comes the contradiction. As a result, there must exist at least one i such that , which implies that all of the .
Case 2., i.e., the constraint l is active at NE. In this case, . It is clear that every user’s best response is to make their own price align with the average of others.
Notice that, if , then is equal to the average of all . Consequently, for all .
Case 3., i.e., the constraint l is violated at NE. In this case,
which leads to a condition for all user i as
In a finite set, if one number is strictly larger than the average of the others, it means that it is not the smallest number in the set. If this condition is true for all user i, it means there is no smallest number among the set, which is impossible. Therefore, Case 3 does not occur at NE.
In summary, at NE, we always have , and s are equal. Moreover, . These prove the primal feasibility, equal prices, and complementary slackness on prices q in the Lemma 2.
Now, for time t, consider the message component for each user i. In user i’s tax function, denote the part relative to by . We have
where .
Different from the proof of previous part, here, we only need to consider two cases of because, by definition of z, is always nonnegative. Another thing we can observe is that there exists at least one t such that , i.e., at least one time t is the time for the peak demand. Define the set as the time set containing all time t with peak demand.
Check the best response of separately. For all , , then following the similar steps shown above, we know for all i. For those , we have already had . For those t, the best response is , which is true for every user i. As a result, we also have the equal prices and complementary slackness for .
For , , so
Adiitionally, we know that such a has . Therefore, for , for either branch in the definition of radial pricing , . Hence, (10) holds for . □
Appendix C. Proof of Lemma 3
Proof.
At NE, for user i, the can be treated as a function of , with fixed. By the assumption of the existence of NE, must have a global maximizer with respect to . Given , all of the auxiliary variables and functions only determined by are constants here, and one can check that the other terms in (5) and (7) are differentiable. Necessary conditions for the global maximizer are
Therefore,
which is exactly the equation (11).
Equation (12) follows directly from the definition of operator. □
Appendix D. Proof of Theorem 2
Proof.
By assumption, the centralized problem is a convex optimization problem with a non-empty feasible set, so there must exist an optimal solution and corresponding Lagrange multipliers which satisfy KKT conditions (4a)–(4g).
Consider the message profile consisting of
If for arbitrary user i, no profitable unilateral deviations exist, i.e., there does not exist an such that , then is a NE of the game .
We can focus on of user i to see whether they have a profitable deviation given . For user i, we have
Therefore, in the interest of user i, they want to maximize the following
The last term of (A2) is the only term related to , which is a quadratic terms. As a strategic agent, it is clear that user i does not deviate from ; otherwise, they pay for the penalty.
The second and third terms of (A2) are quite similar: they both consist of a quadratic term and a term for complementary slackness. For the second term, let us consider constraint l. If l is active in the optimal solution, the complementary slackness term goes to 0. To avoid extra payment, user i does not deviate from the price suggested by optimal solution . If l is inactive, the price suggested by optimal solution is 0. Then, the penalty of constraint l for user i is
where user i can only select a nonnegative price . There are no better choices better than choosing . A similar analysis works for the third term of (A2). As a result, there are no unilateral profitable deviations on for all l and for all t.
Now, we denote the terms in the parentheses in the first part of (A2) by . Since these four terms are disjoint in the aspect of inputted variables, achieves its maximum if and only if every achieves its maximum, and the other three terms equal their minimum. For the first part, due to the strict concavity of , the second-order derivative of for each t is negative, which indicates that is strictly concave as well. We can find the maxima of by the first-order condition:
By (4g) in the KKT conditions, we know that the only that makes (A3) hold is for all t. The reason is that, by the strict concavity assumption of utility function , the first-order derivative of strictly decreases, and therefore, for one aggregated price, there is at most one demand value x that makes equal that price.
Therefore, for any agent i, if others send messages , the only best response of agent i is to announce . Under this circumstance, sending messages other than does not increase agent i’s payoff . Consequently, is an NE of the induced game . □
Appendix E. Proof of Theorem 3
Proof.
For any user i, if they choose to participate with other users, when everyone anticipates the NE, user i’s payoff is of the form (13) if they only consider modifying and keeps other components unchanged. Thus, user i faces the following optimization problem:
By the definition of NE, is one of the best solutions, which yields a payoff . User i can also choose . Denote the corresponding message by . Then, the payoff value becomes , which coincides with the payoff for not participating. Since is the best response to , we have . In other words, if every one anticipates the NE as the outcome, to participate is at least not worse than not participating. □
Appendix F. Proof of Theorem 4
Proof.
Suppose that the optimal solution for the original problem given by NE is ; then, the tax for user i is
The total amount of tax is
For each constraint l, by the complementary slackness, we have
Therefore,
which shows that, at NE, the planner’s payoff is nonnegative.
Furthermore, in order to save unnecessary expenses on the planner, the energy community can adopt the mechanism with the following tax function instead
Note that user i has no control on the additional term because no components of are in that term, and thus, the additional term does not change NE. Since the prices are equal at NE, the planner actually gives back to the users. Hence,
As a side comment, the choice of is not unique. Any adjustment works here as long as it does not depend on for each and sums up to at NE. □
Appendix G. Proof of Lemma 5
Proof.
Here, we provide a non-rigorous proof of (24). The proof of (23) is quite similar. For a detailed version of the proof, we refer the interested readers to 7.1, Chapter 4, of [72].
Before we show the proof of this part, for the sake of convenience, we define as the nearest user among the neighbors of user i and user i itself to user k. is well-defined because one can show that provides a partition for all the users.
Equation (24) can be shown by applying (22) iteratively. Recall that the message exchange network is assumed to be a undirected acyclic graph (i.e., a tree). First, consider the user j on the leaves (the nodes with only one degree). Suppose the neighbor of user j is i, then . By (22), we have . Since no k satisfies other than j themselves, (24) holds for , where j is a leaf node.
For more general cases, to compute , it is safe to only consider the subgraph that contains only node i and node k such that . When applying (22), it is impossible to have node involved because, if it occurs when expanding “” term for some , l is a neighbor of . We know that there is a route from i to , say route . Since , , there exists a route that does not involve any node in the branch starting from node j, such that , which results in a loop .
Then, by using (22) iteratively, we can see that (1) every node in is visited at least once and gives a corresponding demand “y”; (2). each is given only once (except root i, which does not give in this procedure); and (3) when it proceeds to the leaf nodes, the iteration terminates because there are no more “” terms to expand. Hence, , and we can easily verify that is nothing but . □
Appendix H. Convergence of the Learning Algorithm for Centralized Mechanism
The convergence of the proposed learning algorithm can be shown in the three steps mentioned in Section 5. THe first step shows the connection between and of the optimal solution for the original optimization, which has already been clarified in Section 5. As a result, learning NE is equivalent to learning the optimal solution of the original optimization problem. For the second step, as a convex optimization problem with a non-empty feasible set defined by linear inequalities, Slater’s condition is easy to check. Therefore, we have a strong duality in this problem, which means we can obtain the optimal solution of the original problem as long as we solve the dual problem. The last step is to identify the dual problem and to find a convergent algorithm for it. This part of appendix explains how to pin down the dual function and the dual feasible set, and shows the convergence of PGD algorithm on this dual problem.
Before we identify the dual function of the original problem, for the sake of convenience, in constraint (3c) of the original problem, move w to the left-hand side and rewrite (3b) and (3c) into one matrix form
where is defined in (27), and
Suppose that ; then, the objective function can be written as . Observe that, by Assumption 4, s are also strongly concave without cross terms. Sequently, by the definition of strong concavity one can show directly that, as the sum of these strongly concave functions, is strongly concave as well. Let ; then, is strongly convex with parameter . Denote by the conjugate function of .
With these notations in mind, the dual function of the original problem is
Here, we should be cautious about the domain of . In the second line, is only defined when the coefficient , i.e., . Therefore, we get the following dual problem:
Now, we derive the dual problem for the original optimization. To find the optimal solution, one direct thought is to use a projected gradient descent. Luckily, we have the following theorem, which ensures the convergence of PGD algorithm.
Theorem A1.
For a minimization problem on a closed and convex feasible set with objective function , suppose that is the set of optimal solutions. If f is convex and β-smooth on , by using PGD with step size , there exists , such that
Proof.
The proof can be found in ([29] Theorem 1, Section 7.2). □
Theorem A1 indicates that, if the dual problem satisfies certain conditions, the solution converges to the set of optimal solutions. Although it is not clear whether the dual problem has a unique solution, by strong duality and the uniqueness of the solution to the primal problem, no matter which dual optimal solution is achieved, the corresponding primal solution can only be the unique optimal one and results in the same outcome.
Now, for the dual problem, we need to check the conditions required by Theorem A1. First, check the objective function. It is clear that any conjugate functions are convex, so is convex and, consequently, is convex in as a composition of convex function and affine function. Thus, the objective function is convex. Since is strongly convex with parameter , by the result mentioned in [73], the -strong convexity of implies that its conjugate is -smooth. Then, we have
which indicates that the objective function is -smooth with . However, we are not sure whether the objective function is well-defined on the whole feasible set. Fortunately, by Assumption 5, we know that the optimal price vector lies in and we can verify that is a subset of the feasible set generated by (A5) and (A6). Therefore, by solving the following optimization problem, we can obtain the same optimal solution, and Theorem A1 is applicable here.
By applying PGD to (A7) with step size , the update rules are as follows:
where represents the jth entry of the inputted vector. To modify these rules into a learning algorithm for a centralized mechanism, by the relation between and the optimal solution of the original problem and the dual, one might want to substitute with for each user i. However, is not tractable for users as they do not know the utilities of the others. Thankfully, users can obtain the values of -related terms by cooperation without revealing their entire utility functions. This method is realized by inquiries for the demands under given prices from each user. A key point for this implementation is to build a connection between and the marginal value function for each demand .
A useful result of subgradient of function f and its conjugate can be used here, which is quoted as Theorem A2.
Theorem A2.
Suppose is the conjugate of , then
Proof.
The proof can be found in [73]. □
Since h is closed (because h is proper convex and continuous) and strictly convex by assumption, is differentiable (see [73]), and therefore, the subgradient of on a fixed is a singleton. As a result,
The last equivalent sign comes from the fact that
Thus, in every iteration of PGD, before using (A8) and (A9), one can first evaluate
and then, (A8) and (A9) become
Arranging (A10)–(A13) in an appropriate order, we obtain an algorithm with the same convergent property of the original PGD, and significantly, no is in the algorithm. By substituting and with and (by making duplications of (A12) and (A13) for each user i) and by substituting with , we obtain Algorithm 1. Consequently, Theorem 6 follows directly from the convergence of PGD indicated in Theorem A1.
References
- Schmidt, D.A.; Shi, C.; Berry, R.A.; Honig, M.L.; Utschick, W. Distributed resource allocation schemes. IEEE Signal Process. Mag. 2009, 26, 53–63. [Google Scholar] [CrossRef]
- Nair, A.S.; Hossen, T.; Campion, M.; Selvaraj, D.F.; Goveas, N.; Kaabouch, N.; Ranganathan, P. Multi-agent systems for resource allocation and scheduling in a smart grid. Technol. Econ. Smart Grids Sustain. Energy 2018, 3, 1–15. [Google Scholar] [CrossRef]
- HamaAli, K.W.; Zeebaree, S.R. Resources allocation for distributed systems: A review. Int. J. Sci. Bus. 2021, 5, 76–88. [Google Scholar]
- Menache, I.; Ozdaglar, A. Network games: Theory, models, and dynamics. Synth. Lect. Commun. Netw. 2011, 4, 1–159. [Google Scholar] [CrossRef]
- Hurwicz, L.; Reiter, S. Designing Economic Mechanisms; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Börgers, T.; Krahmer, D. An Introduction to the Theory of Mechanism Design; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- United States Department of Energy. 2018 Smart Grid System Report; United States Department of Energy: Washington, DC, USA, 2018.
- Garg, D.; Narahari, Y.; Gujar, S. Foundations of mechanism design: A tutorial part 1-key concepts and classical results. Sadhana 2008, 33, 83. [Google Scholar] [CrossRef]
- Garg, D.; Narahari, Y.; Gujar, S. Foundations of mechanism design: A tutorial Part 2-Advanced concepts and results. Sadhana 2008, 33, 131. [Google Scholar] [CrossRef][Green Version]
- Vickrey, W. Counterspeculation, auctions, and competitive sealed tenders. J. Financ. 1961, 16, 8–37. [Google Scholar] [CrossRef]
- Clarke, E.H. Multipart pricing of public goods. Public Choice 1971, 11, 17–33. [Google Scholar] [CrossRef]
- Groves, T. Incentives in teams. Econom. J. Econom. Soc. 1973, 41, 617–631. [Google Scholar] [CrossRef]
- Kelly, F.P.; Maulloo, A.K.; Tan, D.K. Rate control for communication networks: Shadow prices, proportional fairness and stability. J. Oper. Res. Soc. 1998, 49, 237–252. [Google Scholar] [CrossRef]
- Yang, S.; Hajek, B. Revenue and stability of a mechanism for efficient allocation of a divisible good. Preprint 2005. Available online: https://www.researchgate.net/publication/238308421_Revenue_and_Stability_of_a_Mechanism_for_Ecient_Allocation_of_a_Divisible_Good (accessed on 14 May 2021).
- Maheswaran, R.; Başar, T. Efficient signal proportional allocation (ESPA) mechanisms: Decentralized social welfare maximization for divisible resources. IEEE J. Sel. Areas Commun. 2006, 24, 1000–1009. [Google Scholar] [CrossRef]
- Sinha, A.; Anastasopoulos, A. Mechanism design for resource allocation in networks with intergroup competition and intragroup sharing. IEEE Trans. Control Netw. Syst. 2018, 5, 1098–1109. [Google Scholar] [CrossRef]
- Rabbat, M.; Nowak, R. Distributed optimization in sensor networks. In Proceedings of the 3rd International Symposium on Information Processing in Sensor Networks, Berkeley, CA, USA, 26–27 April 2004; pp. 20–27. [Google Scholar]
- Boyd, S.; Parikh, N.; Chu, E. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers; Now Publishers Inc.: Hanover, MA, USA, 2011. [Google Scholar]
- Wei, E.; Ozdaglar, A.; Jadbabaie, A. A distributed Newton method for network utility maximization–I: Algorithm. IEEE Trans. Autom. Control 2013, 58, 2162–2175. [Google Scholar] [CrossRef]
- Alvarado, A.; Scutari, G.; Pang, J.S. A new decomposition method for multiuser DC-programming and its applications. IEEE Trans. Signal Process. 2014, 62, 2984–2998. [Google Scholar] [CrossRef]
- Di Lorenzo, P.; Scutari, G. Distributed nonconvex optimization over time-varying networks. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 4124–4128. [Google Scholar]
- Sinha, A.; Anastasopoulos, A. Distributed mechanism design with learning guarantees for private and public goods problems. IEEE Trans. Autom. Control 2020, 65, 4106–4121. [Google Scholar] [CrossRef]
- Heydaribeni, N.; Anastasopoulos, A. Distributed Mechanism Design for Network Resource Allocation Problems. IEEE Trans. Netw. Sci. Eng. 2020, 7, 621–636. [Google Scholar] [CrossRef]
- Brown, G.W. Iterative solution of games by fictitious play. Act. Anal. Prod. Alloc. 1951, 13, 374–376. [Google Scholar]
- Monderer, D.; Shapley, L.S. Fictitious play property for games with identical interests. J. Econ. Theory 1996, 68, 258–265. [Google Scholar] [CrossRef]
- Hofbauer, J.; Sandholm, W.H. On the global convergence of stochastic fictitious play. Econometrica 2002, 70, 2265–2294. [Google Scholar] [CrossRef]
- Milgrom, P.; Roberts, J. Rationalizability, learning, and equilibrium in games with strategic complementarities. Econom. J. Econom. Soc. 1990, 58, 1255–1277. [Google Scholar] [CrossRef]
- Scutari, G.; Palomar, D.P.; Facchinei, F.; Pang, J.S. Monotone games for cognitive radio systems. In Distributed Decision Making and Control; Springer: Berlin/Heidelberg, Germany, 2012; pp. 83–112. [Google Scholar]
- Polyak, B. Introduction to Optimization; Optimization Software Inc.: New York, NY, USA, 1987. [Google Scholar]
- Srikant, R.; Ying, L. Communication Networks: An Optimization, Control, and Stochastic Networks Perspective; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Huang, Z.; Mitra, S.; Vaidya, N. Differentially private distributed optimization. In Proceedings of the 2015 International Conference on Distributed Computing and Networking, Goa, India, 4–7 January 2015; pp. 1–10. [Google Scholar]
- Cortés, J.; Dullerud, G.E.; Han, S.; Le Ny, J.; Mitra, S.; Pappas, G.J. Differential privacy in control and network systems. In Proceedings of the 2016 IEEE 55th Conference on Decision and Control (CDC), Las Vegas, NV, USA, 12–14 December 2016; pp. 4252–4272. [Google Scholar]
- Nozari, E.; Tallapragada, P.; Cortés, J. Differentially private distributed convex optimization via objective perturbation. In Proceedings of the American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 2061–2066. [Google Scholar]
- Han, S.; Topcu, U.; Pappas, G.J. Differentially private distributed constrained optimization. IEEE Trans. Autom. Control 2017, 62, 50–64. [Google Scholar] [CrossRef]
- Groves, T.; Ledyard, J. Optimal allocation of public goods: A solution to the “free rider” problem. Econom. J. Econom. Soc. 1977, 45, 783–809. [Google Scholar] [CrossRef]
- Hurwicz, L. Outcome functions yielding Walrasian and Lindahl allocations at Nash equilibrium points. Rev. Econ. Stud. 1979, 46, 217–225. [Google Scholar] [CrossRef]
- Huang, J.; Berry, R.A.; Honig, M.L. Auction-based spectrum sharing. Mob. Netw. Appl. 2006, 11, 405–418. [Google Scholar] [CrossRef]
- Wang, B.; Wu, Y.; Ji, Z.; Liu, K.R.; Clancy, T.C. Game theoretical mechanism design methods. IEEE Signal Process. Mag. 2008, 25, 74–84. [Google Scholar] [CrossRef]
- Wang, S.; Xu, P.; Xu, X.; Tang, S.; Li, X.; Liu, X. TODA: Truthful online double auction for spectrum allocation in wireless networks. In Proceedings of the 2010 IEEE Symposium on New Frontiers in Dynamic Spectrum (DySPAN), Singapore, 6–9 April 2010; pp. 1–10. [Google Scholar]
- Ghosh, A.; Roth, A. Selling privacy at auction. In Proceedings of the 12th ACM Conference on Electronic Commerce, San Jose, CA, USA, 5–9 June 2011; pp. 199–208. [Google Scholar]
- Khalili, M.M.; Naghizadeh, P.; Liu, M. Designing cyber insurance policies: Mitigating moral hazard through security pre-screening. In Proceedings of the International Conference on Game Theory for Networks, Knoxville, TN, USA, 9 May 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 63–73. [Google Scholar]
- Pal, R.; Wang, Y.; Li, J.; Liu, M.; Crowcroft, J.; Li, Y.; Tarkoma, S. Data Trading with Competitive Social Platforms: Outcomes are Mostly Privacy Welfare Damaging. IEEE Trans. Netw. Serv. Manag. 2020. [Google Scholar] [CrossRef]
- Caron, S.; Kesidis, G. Incentive-based energy consumption scheduling algorithms for the smart grid. In Proceedings of the 2010 First IEEE International Conference on Smart Grid Communications, Gaithersburg, MD, USA, 4–6 October 2010; pp. 391–396. [Google Scholar]
- Samadi, P.; Mohsenian-Rad, H.; Schober, R.; Wong, V.W. Advanced demand side management for the future smart grid using mechanism design. IEEE Trans. Smart Grid 2012, 3, 1170–1180. [Google Scholar] [CrossRef]
- Muthirayan, D.; Kalathil, D.; Poolla, K.; Varaiya, P. Mechanism design for demand response programs. IEEE Trans. Smart Grid 2019, 11, 61–73. [Google Scholar] [CrossRef]
- Iosifidis, G.; Gao, L.; Huang, J.; Tassiulas, L. An iterative double auction for mobile data offloading. In Proceedings of the 2013 11th International Symposium and Workshops on Modeling and Optimization in Mobile, Ad Hoc and Wireless Networks (WiOpt), Tsukuba, Japan, 13–17 May 2013; pp. 154–161. [Google Scholar]
- Johari, R.; Tsitsiklis, J.N. Efficiency loss in a network resource allocation game. Math. Oper. Res. 2004, 29, 407–435. [Google Scholar] [CrossRef]
- Yang, S.; Hajek, B. VCG-Kelly mechanisms for allocation of divisible goods: Adapting VCG mechanisms to one-dimensional signals. IEEE J. Sel. Areas Commun. 2007, 25, 1237–1243. [Google Scholar] [CrossRef][Green Version]
- Johari, R.; Tsitsiklis, J.N. Efficiency of scalar-parameterized mechanisms. Oper. Res. 2009, 57, 823–839. [Google Scholar] [CrossRef]
- Farhadi, F.; Golestani, S.J.; Teneketzis, D. A surrogate optimization-based mechanism for resource allocation and routing in networks with strategic agents. IEEE Trans. Autom. Control 2018, 64, 464–479. [Google Scholar] [CrossRef]
- Kakhbod, A.; Teneketzis, D. An Efficient Game Form for Unicast Service Provisioning. IEEE Trans. Autom. Control 2012, 57, 392–404. [Google Scholar] [CrossRef]
- Kakhbod, A.; Teneketzis, D. Correction to “An Efficient Game Form for Unicast Service Provisioning” [Feb 12 392-404]. IEEE Trans. Autom. Control 2015, 60, 584–585. [Google Scholar] [CrossRef]
- Sinha, A.; Anastasopoulos, A. A General Mechanism Design Methodology for Social Utility Maximization with Linear Constraints. ACM Sigmetrics Perform. Eval. Rev. 2014, 42, 12–15. [Google Scholar] [CrossRef]
- Baumann, L. Self-Ratings and Peer Review. 2018. Available online: https://www.amse-aixmarseille.fr/sites/default/files/events/JMPLeonieBaumann_0.pdf (accessed on 30 July 2021).
- Bloch, F.; Olckers, M. Friend-Based Ranking in Practice. Available online: https://arxiv.org/abs/2101.02857 (accessed on 14 May 2021).
- Chen, Y. A family of supermodular NAvailable online: Ash mechanisms implementing Lindahl allocations. Econ. Theory 2002, 19, 773–790. [Google Scholar] [CrossRef]
- Healy, P.J.; Mathevet, L. Designing stable mechanisms for economic environments. Theor. Econ. 2012, 7, 609–661. [Google Scholar] [CrossRef]
- Scutari, G.; Facchinei, F.; Pang, J.S.; Palomar, D.P. Real and complex monotone communication games. IEEE Trans. Inf. Theory 2014, 60, 4197–4231. [Google Scholar] [CrossRef]
- Gharesifard, B.; Cortés, J. Distributed convergence to Nash equilibria in two-network zero-sum games. Automatica 2013, 49, 1683–1692. [Google Scholar] [CrossRef]
- Ye, M.; Hu, G. Game design and analysis for price-based demand response: An aggregate game approach. IEEE Trans. Cybern. 2016, 47, 720–730. [Google Scholar] [CrossRef]
- Grammatico, S. Dynamic control of agents playing aggregative games with coupling constraints. IEEE Trans. Autom. Control 2017, 62, 4537–4548. [Google Scholar] [CrossRef]
- Yi, P.; Pavel, L. Distributed generalized Nash equilibria computation of monotone games via double-layer preconditioned proximal-point algorithms. IEEE Trans. Control Netw. Syst. 2018, 6, 299–311. [Google Scholar] [CrossRef]
- Paccagnan, D.; Gentile, B.; Parise, F.; Kamgarpour, M.; Lygeros, J. Nash and Wardrop equilibria in aggregative games with coupling constraints. IEEE Trans. Autom. Control 2018, 64, 1373–1388. [Google Scholar] [CrossRef]
- Parise, F.; Ozdaglar, A. A variational inequality framework for network games: Existence, uniqueness, convergence and sensitivity analysis. Games Econ. Behav. 2019, 114, 47–82. [Google Scholar] [CrossRef]
- Xiao, Y.; Hou, X.; Hu, J. Distributed solutions of convex-concave games on networks. In Proceedings of the 2019 American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019; pp. 1189–1194. [Google Scholar]
- Bimpikis, K.; Ehsani, S.; Ilkılıç, R. Cournot competition in networked markets. Manag. Sci. 2019, 65, 2467–2481. [Google Scholar] [CrossRef]
- Zhang, K.; Yang, Z.; Başar, T. Policy optimization provably converges to Nash equilibria in zero-sum linear quadratic games. arXiv 2019, arXiv:1906.00729. [Google Scholar]
- uz Zaman, M.A.; Zhang, K.; Miehling, E.; Bașar, T. Reinforcement learning in non-stationary discrete-time linear-quadratic mean-field games. In Proceedings of the 2020 59th IEEE Conference on Decision and Control (CDC), Jeju, Korea, 14–18 December 2020; pp. 2278–2284. [Google Scholar]
- Roudneshin, M.; Arabneydi, J.; Aghdam, A.G. Reinforcement learning in nonzero-sum Linear Quadratic deep structured games: Global convergence of policy optimization. In Proceedings of the 2020 59th IEEE Conference on Decision and Control (CDC), Jeju, Korea, 14–18 December 2020; pp. 512–517. [Google Scholar]
- Shi, Y.; Zhang, B. Multi-agent reinforcement learning in Cournot games. In Proceedings of the 2020 59th IEEE Conference on Decision and Control (CDC), Jeju, Korea, 14–18 December 2020; pp. 3561–3566. [Google Scholar]
- Sohet, B.; Hayel, Y.; Beaude, O.; Jeandin, A. Learning Pure Nash Equilibrium in Smart Charging Games. In Proceedings of the 2020 59th IEEE Conference on Decision and Control (CDC), Jeju, Korea, 14–18 December 2020; pp. 3549–3554. [Google Scholar]
- Sinha, A. Mechanism Design with Allocative, Informational and Learning Constraints. Ph.D. Thesis, 2017. Available online: http://web.eecs.umich.edu/~anastas/anastas/docs/northwestern_2017.pdf (accessed on 14 May 2021).
- Zhou, X. On the Fenchel duality between strong convexity and Lipschitz continuous gradient. arXiv 2018, arXiv:1803.06573. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).