Rock-Paper-Scissors Play: Beyond the Win-Stay/Lose-Change Strategy
Abstract
:1. Introduction
1.1. Literature Review
1.2. Current Study
2. Experiment 1
2.1. Methods
2.1.1. Participants
2.1.2. Design
2.1.3. Procedure
2.2. Results
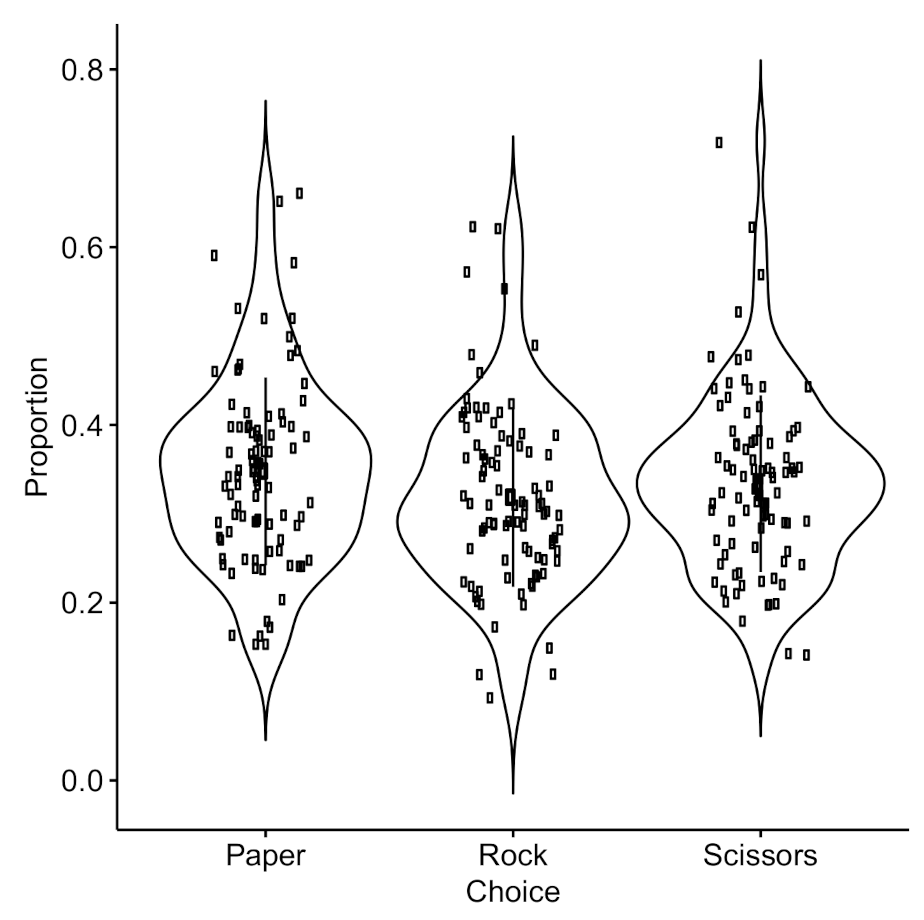
2.2.1. Random or Nash Strategies
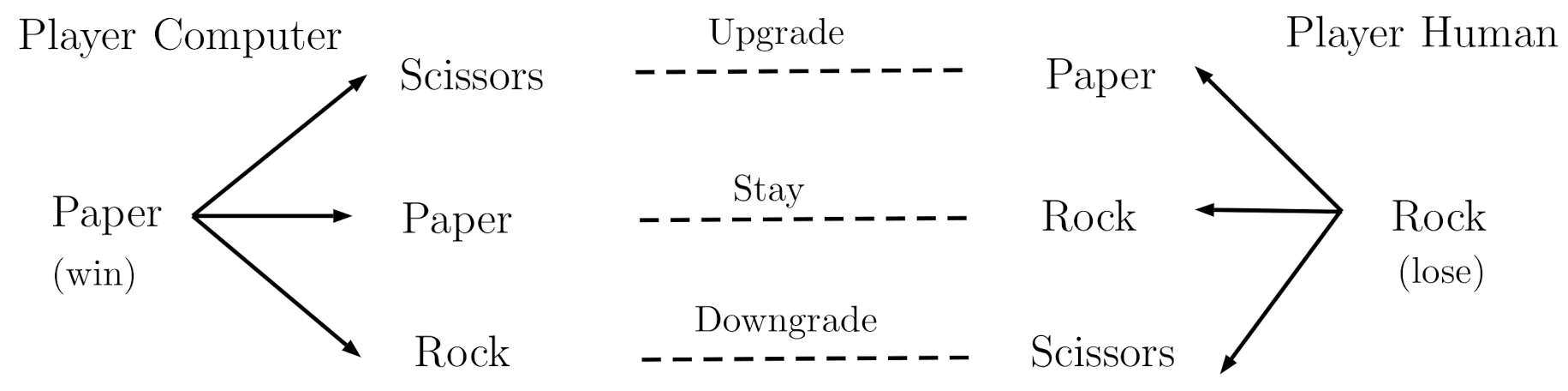
2.2.2. Win-Stay/Lose-Change
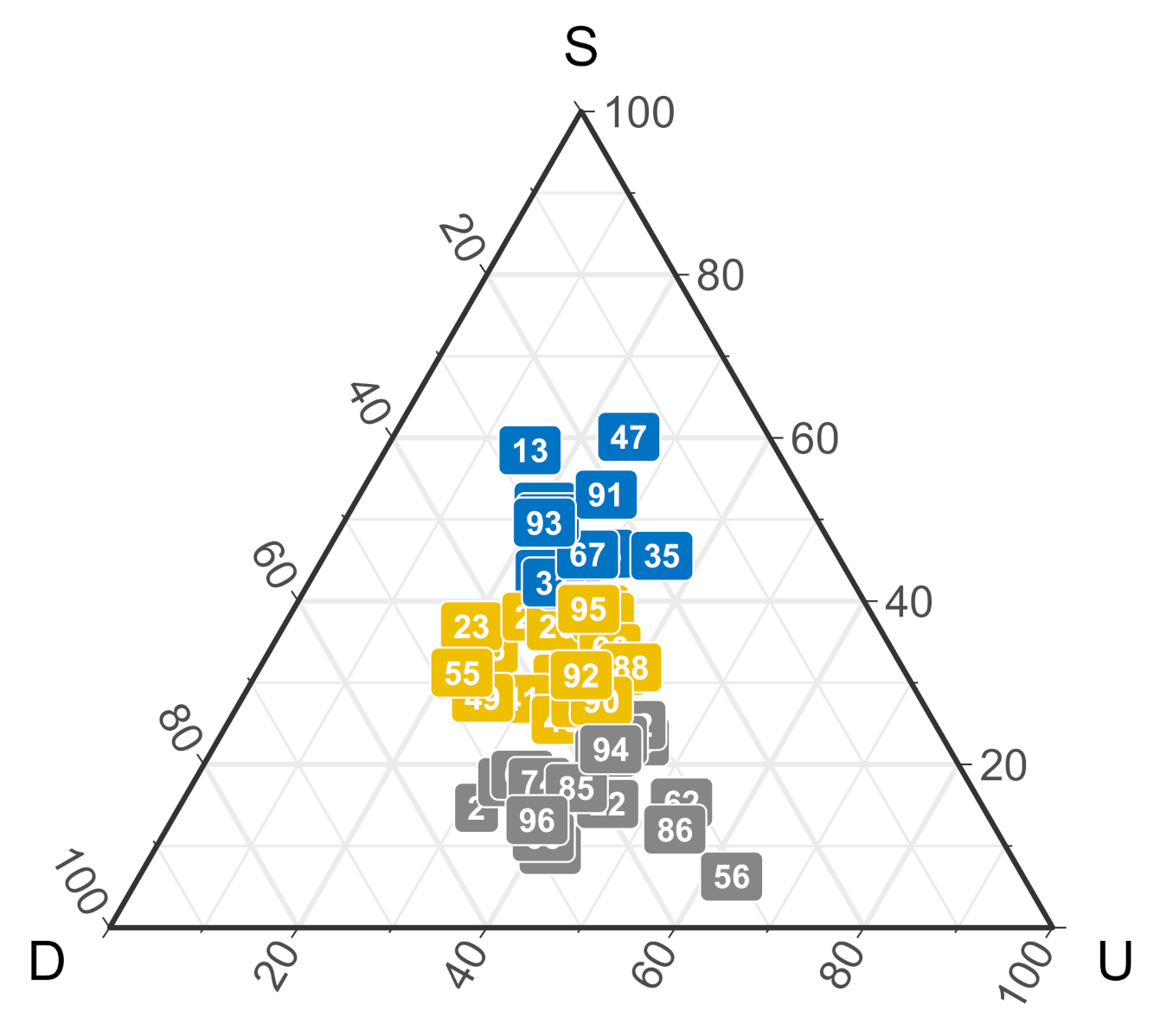
2.2.3. Cluster Analysis
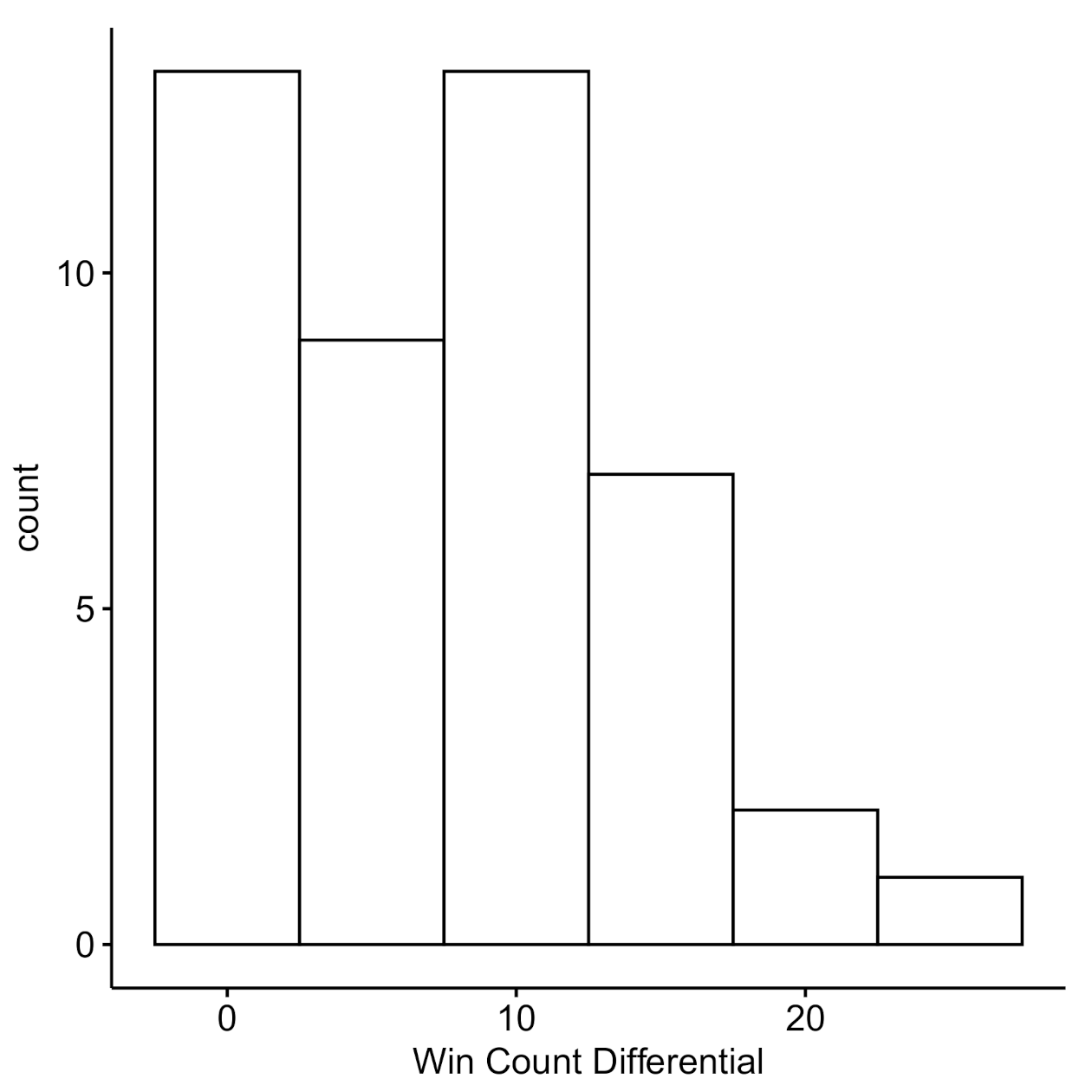
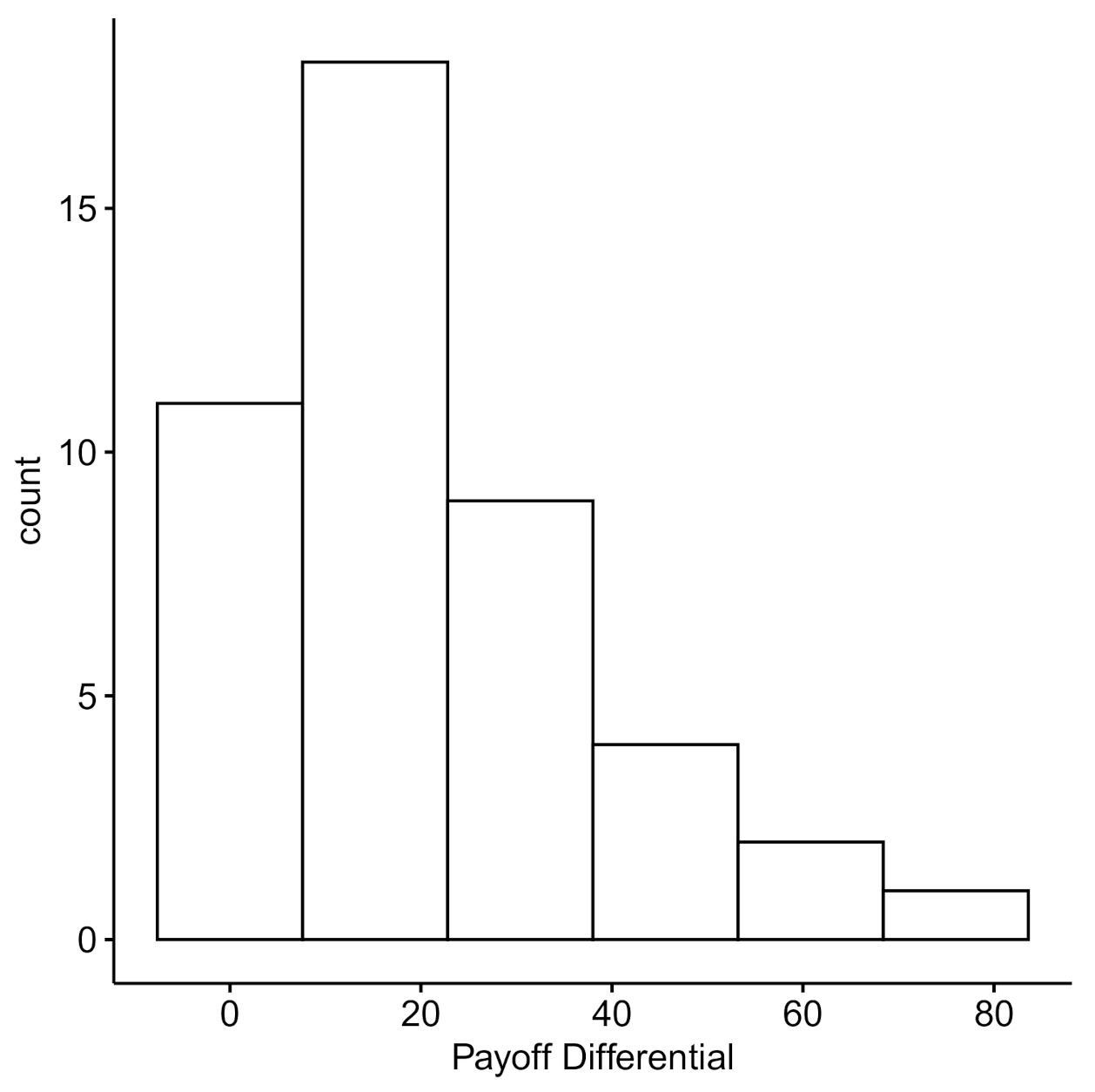
2.2.4. Dyad-Level Payoffs
2.3. Discussion
3. Experiment 2
3.1. Methods
3.1.1. Participants
3.1.2. Design
3.2. Procedure
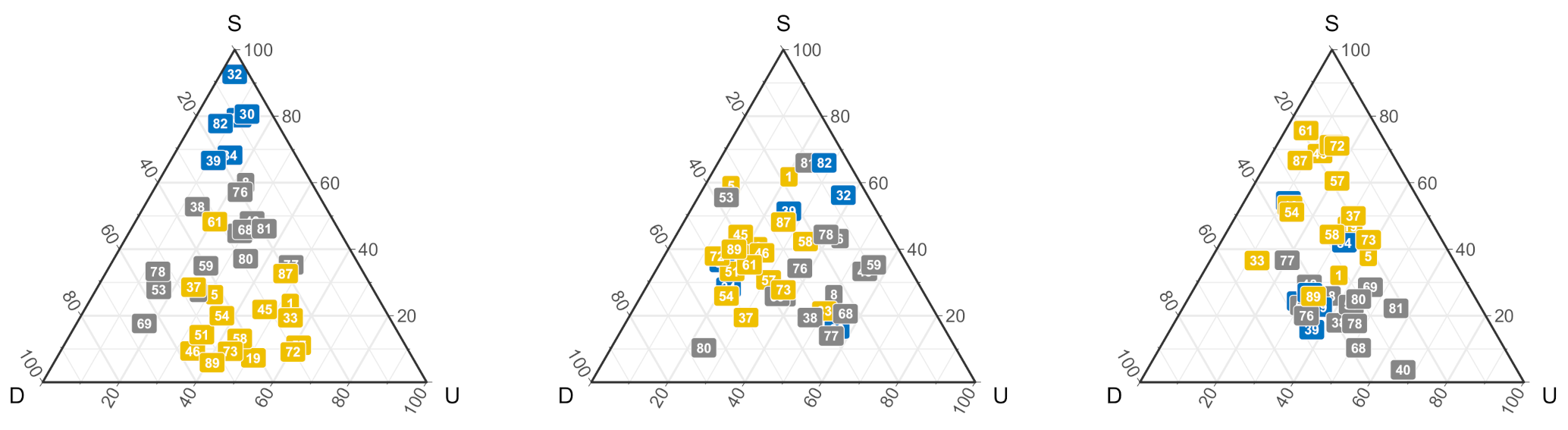
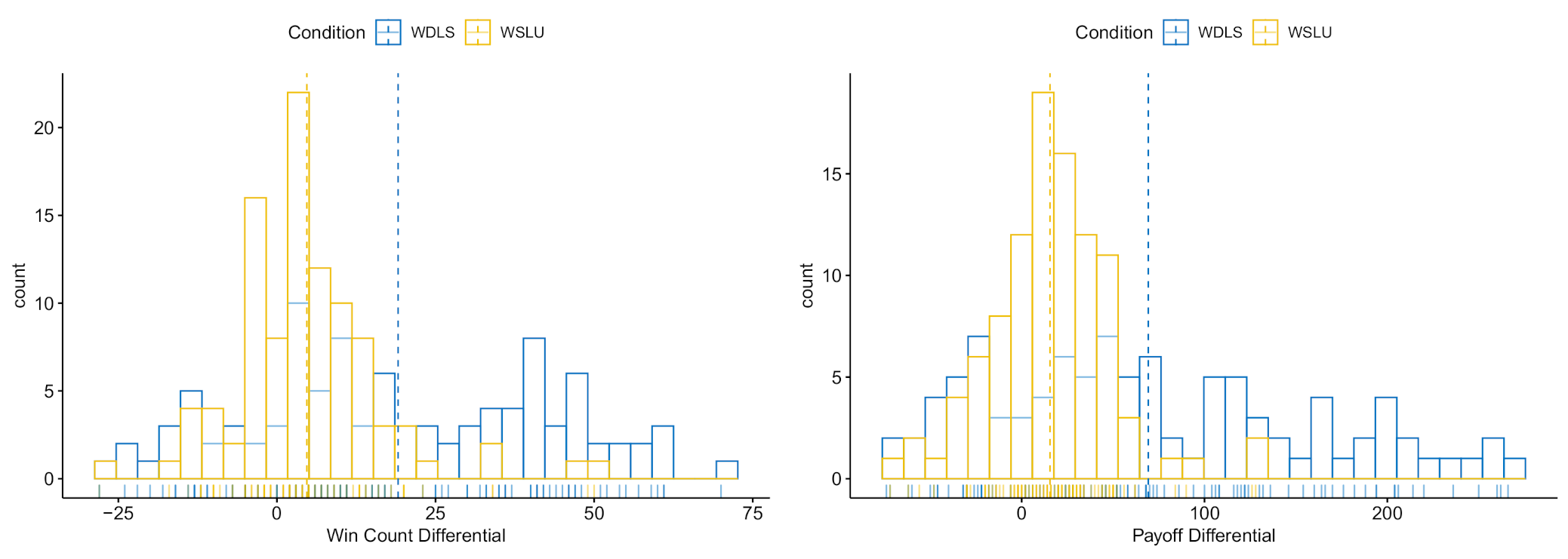
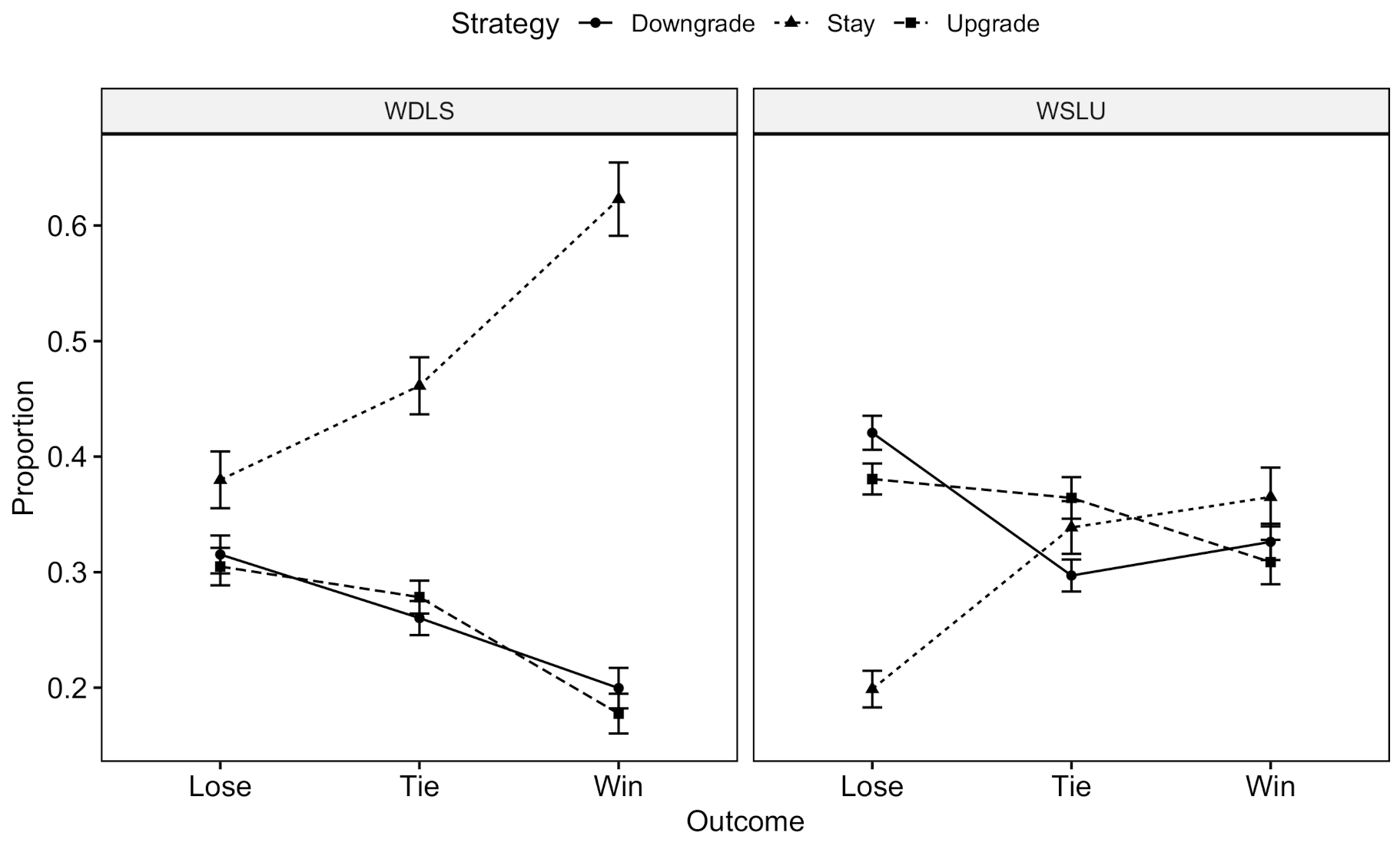
3.3. Results
3.4. Discussion
4. General Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fisher, L. Rock, Paper, Scissors: Game Theory in Everyday Life; Basic Books: New York, NY, USA, 2008. [Google Scholar]
- Gilovich, T.; Vallone, R.; Tversky, A. The hot hand in basketball: On the misperception of random sequences. Cogn. Psychol. 1985, 17, 295–314. [Google Scholar] [CrossRef]
- Dyson, B.J. Behavioural isomorphism, cognitive economy and recursive thought in non-transitive game strategy. Games 2019, 10, 32. [Google Scholar] [CrossRef] [Green Version]
- Eyler, D.; Shalla, Z.; Doumaux, A.; McDevitt, T. Winning at Rock-Paper-Scissors. Coll. Math. J. 2009, 40, 125–128. [Google Scholar]
- Wang, Z.; Xu, B.; Zhou, H.J. Social cycling and conditional responses in the Rock-Paper-Scissors game. Sci. Rep. 2014, 4, 5830. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dyson, B.J.; Wilbiks, J.M.P.; Sandhu, R.; Papanicolaou, G.; Lintag, J. Negative outcomes evoke cyclic irrational decisions in Rock, Paper, Scissors. Sci. Rep. 2016, 6, 20479. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Forder, L.; Dyson, B.J. Behavioural and neural modulation of win-stay but not lose-shift strategies as a function of outcome value in Rock, Paper, Scissors. Sci. Rep. 2016, 6, 33809. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- West, R.L.; Lebiere, C. Simple games as dynamic, coupled systems: Randomness and other emergent properties. Cogn. Syst. Res. 2001, 1, 221–239. [Google Scholar] [CrossRef]
- Batzilis, D.; Jaffe, S.; Levitt, S.; List, J.A.; Picel, J. Behavior in Strategic Settings: Evidence from a Million Rock-Paper-Scissors Games. Games 2019, 10, 18. [Google Scholar] [CrossRef] [Green Version]
- De Weerd, H.; Verbrugge, R.; Verheij, B. How much does it help to know what she knows you know? An agent-based simulation study. Artif. Intell. 2013, 199, 67–92. [Google Scholar] [CrossRef]
- Kahneman, D. Thinking, Fast and Slow; Macmillan: New York, NY, USA, 2011. [Google Scholar]
- Rutledge-Taylor, M.; West, R. Using DSHM to model paper, rock, scissors. In Proceedings of the Annual Meeting of the Cognitive Science Society, Boston, MA, USA, 20–23 July 2011; Volume 33. [Google Scholar]
- Rutledge-Taylor, M.; West, R. Cognitive Modeling Versus Game Theory: Why cognition matters. In Sixth International Conference on Cognitive Modeling; Psychology Press: New York, NY, USA, 2004; pp. 255–260. [Google Scholar]
- Cook, R.; Bird, G.; Lünser, G.; Huck, S.; Heyes, C. Automatic imitation in a strategic context: Players of rock–paper–scissors imitate opponents’ gestures. Proc. R. Soc. B Biol. Sci. 2012, 279, 780–786. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hedden, T.; Zhang, J. What do you think I think you think? Strategic reasoning in matrix games. Cognition 2002, 85, 1–36. [Google Scholar] [CrossRef]
- Premack, D.; Woodruff, G. Does the chimpanzee have a theory of mind? Behav. Brain Sci. 1978, 1, 515–526. [Google Scholar] [CrossRef] [Green Version]
- MacLean, E.L. Unraveling the evolution of uniquely human cognition. Proc. Natl. Acad. Sci. USA 2016, 113, 6348–6354. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- JASP Team. JASP (Version 0.14.1) [Computer Software]. 2020. Available online: https://jasp-stats.org/ (accessed on 22 June 2021).
- Cichosz, P. Data Mining Algorithms: Explained Using R; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Xu, R.; Wunsch, D. Clustering; John Wiley & Sons: Hoboken, NJ, USA, 2008; Volume 10. [Google Scholar]
- De Weerd, H.; Diepgrond, D.; Verbrugge, R. Estimating the use of higher-order theory of mind using computational agents. BE J. Theor. Econ. 2018, 18. [Google Scholar] [CrossRef]
- Brockbank, E.; Vul, E. Recursive Adversarial Reasoning in the Rock, Paper, Scissors Game. In Proceedings of the Annual Meeting of the Cognitive Science Society, Online, 29 July–1 August 2020. [Google Scholar]
- Camerer, C.F.; Ho, T.H.; Chong, J.K. A cognitive hierarchy model of games. Q. J. Econ. 2004, 119, 861–898. [Google Scholar] [CrossRef] [Green Version]
- Frey, S.; Goldstone, R.L. Cyclic game dynamics driven by iterated reasoning. PLoS ONE 2013, 8, e56416. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Frey, S.; Goldstone, R.L. Going with the group in a competitive game of iterated reasoning. In Proceedings of the Annual Meeting of the Cognitive Science Society, Boston, MA, USA, 20–23 July 2011; Volume 33. [Google Scholar]

| Player 1 | ||||
|---|---|---|---|---|
| Rock | Paper | Scissor | ||
| Player 2 | Rock | (2,2) | (1,3) | (4,0) |
| Paper | (3,1) | (2,2) | (1,3) | |
| Scissor | (0,4) | (3,1) | (2,2) | |
| Player | Strategy | Computer | Human | Computer | Human |
|---|---|---|---|---|---|
| Outcome | Win | Lose | Lose | Win | |
| WSLC | Stay | Downgrade | Upgrade | Upgrade | |
| Downgrade | Downgrade | ||||
| WCLS | Upgrade | Stay | Stay | Stay | |
| Downgrade | Upgrade |
| Algorithm | Outcome | Strategy | ||
|---|---|---|---|---|
| Stay | Upgrade | Downgrade | ||
| (1) Win-Stay/Lose-Upgrade (WSLU) | Lose | 0.1 | 0.8 | 0.1 |
| Tie | 0.33 | 0.33 | 0.33 | |
| Win | 0.8 | 0.1 | 0.1 | |
| (2) Win-Downgrade/Lose-Stay (WDLS) | Lose | 0.8 | 0.1 | 0.1 |
| Tie | 0.33 | 0.33 | 0.33 | |
| Win | 0.1 | 0.1 | 0.8 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Moisan, F.; Gonzalez, C. Rock-Paper-Scissors Play: Beyond the Win-Stay/Lose-Change Strategy. Games 2021, 12, 52. https://doi.org/10.3390/g12030052
Zhang H, Moisan F, Gonzalez C. Rock-Paper-Scissors Play: Beyond the Win-Stay/Lose-Change Strategy. Games. 2021; 12(3):52. https://doi.org/10.3390/g12030052
Chicago/Turabian StyleZhang, Hanshu, Frederic Moisan, and Cleotilde Gonzalez. 2021. "Rock-Paper-Scissors Play: Beyond the Win-Stay/Lose-Change Strategy" Games 12, no. 3: 52. https://doi.org/10.3390/g12030052
APA StyleZhang, H., Moisan, F., & Gonzalez, C. (2021). Rock-Paper-Scissors Play: Beyond the Win-Stay/Lose-Change Strategy. Games, 12(3), 52. https://doi.org/10.3390/g12030052






